Received 20 November 2015; accepted 22 January 2016; published 25 January 2016

ABSTRACT

In this study, we first give the definitions of (s,t)-Jacobsthal and (s,t)-Jacobsthal Lucas sequence. By using these formulas we define (s,t)-Jacobsthal and (s,t)-Jacobsthal Lucas matrix sequences. After that we establish some sum formulas for these matrix sequences.

Keywords:

Jacobsthal Numbers, Jacobsthal Lucas Numbers, Matrix Sequences

1. Introduction

There are so many studies in the literature that are concern about special number sequences such as Fibonacci, Lucas, Pell, Jacobsthal, and Padovan in [1] [2] . They are widely used in many research areas as Engineering, Architecture, Nature and Art in [3] -[6] . For example, microcontrollers (and other computers) use conditional instructions to change the flow of execution of a program. In addition to branch instructions, some micro- controllers use skip instructions which conditionally bypass the next instruction. This winds up being useful for one case out of the four possibilities on 2 bits, 3 cases on 3 bits, 5 cases on 4 bits, 21 on 6 bits, 43 on 7 fits, 85 on 8 fits, ..., which are exactly the Jacosthal numbers [7] . 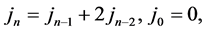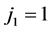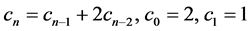Jacobsthal and Jacobsthal Lucas numbers are given by the recurrence relations and for 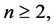res- pectively in [7] - [9] . Generalization of number sequences is studied in many articles. For example the gener- alization of Jacobsthal sequences is defined in [10] . We can see any properties of these numbers in [7] - [9] [11] [12] . Some properties of these sequences were deduced directly from elementary matrix algebra in [13] [14] . By using matrix algebra H. Civciv and R. Turkmen defined Fibonacci and Lucas matrix sequences in [15] [16] . Similarly K. Uslu and Ş. Uygun defined Jacosthal and Jacosthal Lucas matrix se- quences and by using them found some properties of Jacobsthal numbers in [17] .

Definition 1. The (s,t)-Jacobsthal sequence 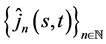and (s,t)-Jacobsthal Lucas sequence 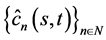are defined by the recurrence relations

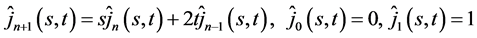(1)

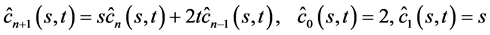(2)

respectively, where 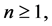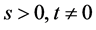and 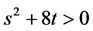[10] .

Some basic properties of these sequences are given in the following:

In the following definition, (s,t)-Jacosthal and (s,t)-Jacosthal Lucas matrix se- quences are defined by carrying to matrix theory (s,t)-Jacosthal and (s,t)-Jacosthal Lucas sequences.

Definition 2. The (s,t)-Jacobsthal matrix sequence and (s,t)-Jacobsthal Lucas matrix sequence are defined by the recurrence relations

(3)

(4)

respectively, where and

Throughout this paper, for convenience we will use the symbol instead of and the symbol instead of. Similarly we will use the symbol instead of and instead of

Proposition 3. Let us consider and The following properties are hold:

1) and

2) For

3) For

4) For

For their proofs you can look at the Ref. [17] .

2. The Generating Functions of Jacobsthal and Jacobsthal-Lucas Matrix Sequences

Theorem 4. For we have the generating function of Jacobsthal matrix sequence in the following:

(5)

Proof. By using the expansion of geometric series and proposition 3, we can write

■

Corollary 5. Let Then for (s,t)-Jacobsthal sequence we have

and

Corollary 6. Let Then we have

Corollary 7. Let Then we have we have the generating function of Jacobsthal-Lucas matrix sequence in the following:

(6)

Proof. It can be seen easily by using theorem 4 and the property of ■

Corollary 8. Let Then for (s,t)-Jacobsthal Lucas matrix sequence we have

Corollary 9. Let Then for (s,t)-Jacobsthal Lucas sequence we have

and

Theorem 10. For let be r is odd positive integer and

Then we have

and for r is even positive integer

Proof. By using proposition 3 (iv), the nth element of (s,t)-Jacobsthal matrix sequence can be written in the following:

From this equality we have

If r is an odd positive integer, then we have

If r is an even positive integer, then we have

■

3. Partial Sums of Jacobsthal and Jacobsthal-Lucas Matrix Sequences

Theorem 11. The partial sum of (s,t)-Jacobsthal matrix sequence for is given in the following

Proof. Let. By multiplying two sides of the equality, we get

By adding two sides of the equality, we get

The inverse of is available for. Then we get

By using following equalities and

we get

■

Corollary 12. The partial sums of (s,t)-Jacobsthal sequence for are given in the following:

and

Proof. It is proved by the equality of matrix sequences and from Theorem 11. ■

Theorem 13. The partial sum of (s,t)-Jacobsthal Lucas matrix sequence for is given in the follow-

ing

Proof. By using and Theorem 11 we get

If the product of matrices is made the desired result is found. ■

Corollary 14. The partial sums of (s,t)-Jacobsthal Lucas sequence for are given in the following:

and

Proof. It is proved by the equality of matrix sequences and from Theorem 11. ■

Theorem 15. Let and Then for we get

Proof. By multiplying two sides of the equality, we get

By adding two sides of the equality, we get

■

Corollary 16. The odd and even elements sums of (s,t)-Jacobsthal sequence for and are given in the following:

In the following theorem we will show the partial sum of Jacobsthal Lucas matrix sequence of the elements of power of n.

Theorem 17. For (s,t)-Jacobsthal matrix sequence the equality is hold.

Proof. By using the equality of we can write By using it

■

Acknowledgements

Thank you very much to the editor and the referee for their valuable comments.

Cite this paper

ŞükranUygun, (2016) Some Sum Formulas of ( s , t )-Jacobsthal and ( s , t )-Jacobsthal Lucas Matrix Sequences. Applied Mathematics,07,61-69. doi: 10.4236/am.2016.71005

References