Applied Mathematics
Vol.06 No.12(2015), Article ID:61201,8 pages
10.4236/am.2015.612177
A Two-Point Boundary Value Problem by Using a Mixed Finite Element Method
Pedro Pablo Cárdenas Alzate, José Rodrigo González Granada
Department of Mathematics, Universidad Tecnológica de Pereira, Pereira, Colombia

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 October 2015; accepted 15 November 2015; published 18 November 2015
ABSTRACT
This paper describes a numerical solution for a two-point boundary value problem. It includes an algorithm for discretization by mixed finite element method. The discrete scheme allows the utilization a finite element method based on piecewise linear approximating functions and we also use the barycentric quadrature rule to compute the stiffness matrix and the L2-norm.
Keywords:
Two-Point BVP, Galerkin’s Method, Non-Symmetric Problem

1. Introduction
Finite element methods in which two spaces are used received the domination of mixed finite element method. Sometimes a second variable is introduced in the formulation of the problem by its physical study, for example in the case of elasticity equations and also the Stokes equations where the mixed formulation is the natural one. The mathematical analyses of mixed finite element have been widely developed in the seventies. A general analysis was first developed by [1] . We also have to mention to [2] and [3] which introduced of the fundamental ideas for the analysis of mixed finite elements. We also refer to [4] and [5] where general results are obtained.
An outline of the paper is as follows. We derive the mixed variational formulation for bilinear form non- symmentric problem and we define the related discrete elements and the error analysis of the associated finite element method is made [6] . We generalize the results to mixed methods using rectangular elements and we use the barycentric quadrature rule to compute the stiffness matrix, the load vector and the L2-norm. Finally, numerical experiments are given to illustrate the present theory [7] .
2. Error in the Finite Element Solution
Recall that 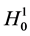 in one dimension by Sobolev’s inequality, so that
in one dimension by Sobolev’s inequality, so that 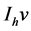 is defined for
is defined for . We can prove that with
. We can prove that with  and
and 

and

In fact, by definition we have
 (1)
(1)
where 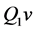 is the polynomial of degree 1 approximating v in
is the polynomial of degree 1 approximating v in , then we have
, then we have
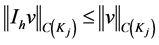
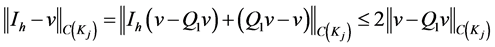

therefore, the error is of order  because the fitting is until the second derivative, then
because the fitting is until the second derivative, then

Now, we know that
So, we can write 
then we obtain
So
To write the norm in
Next, integrate with respect to 
Taking the square root finally we obtain
3. Galerkin’s Method
Galerkin’s method: Let 

and 






and with 


In fact, let 



Now, from the assumptions of the Lax-Milgram lemma we have


Divide by 
Now, using (5), we get that
Finally, we can prove (4)
Now, for the symmetric 
Similar to previous proof, we have
Therefore
As for the norm in V, we have

From the assumptions we obtain
With 

Using this inequality, (6) becomes
We know that
from Equation (4) which was proven in the previous section, therefore
4. FEM for Bilinear Form Non-Symmetric Problem
We consider the problem
in 





Next, integrate over the domain
Now, the left hand side can be written using integrating by parts:
Therefore we have the bilinear form
and the linear functional
The space 




The bilinear form is also bounded:
Now, we would like to minimize the residual
Also we have (see [2] )
where
which for our case become
5. BVP by Finite Element Method
We consider the boundary value problem
Figure 1. Mesh used to solve the problem (7) by using (8).
Figure 2. (a) Solution of the system (7) using

Figure 3. Logarithmic plot of the L2-norm of the error vs. the choice of h.

We want to solve it by the finite element method

based on piecewise linear approximating functions on the partition





Therefore we obtain
・ 


・ The Barycentric Quadrature Rule were used to evaluate the integral on the right hand side,
where
where K is each triangle in the mesh, 
・ Figure 2 shows the solution of (7) for 

the errors are shown in (panel B) and (panel C) respectively.
・ 
Acknowledgments
We thank the editor and the referee for their comments and group GEDNOL of the Universidad Tecnológica de Pereira-Colombia.
Cite this paper
Pedro Pablo Cárdenas Alzate,José Rodrigo González Granada, (2015) A Two-Point Boundary Value Problem by Using a Mixed Finite Element Method. Applied Mathematics,06,1996-2003. doi: 10.4236/am.2015.612177
References
- 1. Brezzi, F. (1974) On the Existence, Uniqueness and Approximation of Saddle Points Problems Arising from Lagrangian Multipliers. ESAIM: Mathematical Modelling and Numerical Analysis—Modélisation Mathématique et Analyse Numérique, 8, 129-151.
- 2. Larsson, S. and Thome, V. (2009) Partial Differential Equations with Numerical Methods. Springer-Verlag, New York.
- 3. Canuto, C. and Hussaini, M. (1988) Spectral Methods in Fluids Dynamics. Springer Series in Computational Physics, Springer-Verlag, Berlin.
http://dx.doi.org/10.1007/978-3-642-84108-8 - 4. Fortin, M. (1977) An Analysis of the Convergence of Mixed Finite Element Methods. R.A.I.R.O, 11, 341-354.
- 5. Guzman, J. (2010) A Unified Analysis of Several Mixed Methods for Elasticity with Weak Stress Symmetric. Journal of Scientific Computing, 4, 156-169.
http://dx.doi.org/10.1007/s10915-010-9373-2 - 6. Yao, C. and Jia, S. (2014) Asymptotic Expansion Analysis of Nonconforming Mixed Finite Element Methods for Time-Dependent Maxwell’s Equations in Debye Medium. Applied Mathematics and Computation, 229, 34-40.
http://dx.doi.org/10.1016/j.amc.2013.12.016 - 7. Pal, M. and Lamine, S. (2015) Validation of the Multiscale Mixed Finite-Element Method. International Journal for Numerical Methods in Fluids, 77, 206-223.
http://dx.doi.org/10.1002/fld.3978














































