Received 30 August 2015; accepted 27 November 2015; published 30 November 2015

ABSTRACT

Let 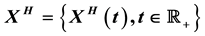be a subfractional Brownian motion in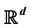. We prove that 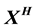is strongly locally nondeterministic.

Keywords:

Sub-Fractional Brownian Motion, Fractional Brownian Motion, Self-Similar Gaussian Processes, Strong Local Non-Determinism

1. Introduction

The fractional Brownian motion (fBm for short) is the best known and most used process with long-dependence property for models in telecommunications, turbulence, image processing and finance. This process is first introduced by [1] and later studied by [2] . The self-similarity and stationarity of the increments are two main properties for which fBm enjoy success as a modeling tool. The fBm is the only continuous Gaussian process which is self-similar and has stationary increments; see [3] . Many authors have also proposed for using more general self-similar Gaussian processes and random fields as stochastic models; see e.g. [4] -[9] . Such applications have raised many interesting theoretical questions about self-similar Gaussian processes and fields in general. However, in contrast to the extensive studies on fractional Brownian motion, there has been little systematic investigation on other self-similar Gaussian processes until [10] fills the gap by developing systematic ways to study sample path properties of a class of self-similar Gaussian process, namely, the bifractional Brownian motion. Their main tools are the Lamperti transformation, which provides a powerful connection between self-similar processes and stationary processes; see [11] , and the strong local non-determinism of Gaussian processes; see [12] . In particular, for any self-similar Gaussian processes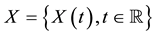, the Lamperti transformation leads to a stochastic integal representation for X.

An extension of Bm which preserves many properties of the fBm, but not the stationarity of the increments, is so called sub-fractional Brownian motion (sub-fBm, in short) introduced by [13] . The sub-fBm is another class of self-similar Gaussian process which has properties analogous to those of fBm; see [13] -[15] . Given a constant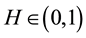, the sub-fractional Brownian motion in 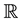is a centered Gaussian process 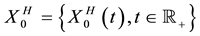with covariance function

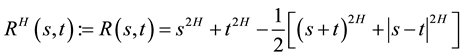(1)

and.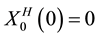

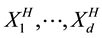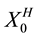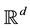Let be independent copies of. We define the Gaussian process with values in by

(2)

By (1), one can verify easily that 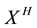is a self-similar process with index H, that is, for every constant,

(3)

where means that the two processes have the same finite dimensional distributions. Note that does not have stationary increments.

The strong local non-determinism is an important tool to study the sample path properties of self-similar Gaussian process, such as the small ball probability and Chung’s law of the iterated logarithm. In this paper, we apply the Lamperti transformation to prove the strong local non-determinism of. Throughout this paper, a specified positive and finite constant is denoted by which may depend on H.

2. Strong Local Non-Determinism

Theorem 1. For all constants, is strongly locally -nondeterministic on with. That is, there exist positive constants and such that for all and all,

(4)

Proof. By Lamperti’s transformation (see [11] ), we consider the centered stationary Gaussian process defined by

(5)

The covariance function is given by

(6)

where is an even function. By (6) and Taylor expansion, we verify that, as, where. It follows that. Also, by using (6) and the Taylor expansion again, we also have

(7)

Using Bochner’s theorem, has the following stochastic integral representation

(8)

where W is a complex Gaussian measure with control measure whose Fourier transform is. The measure is called the spectral measure of.

Since, the spectral measure of has a continuous density function which can be represented as the inverse Fourier transform of:

(9)

We would like to prove that f has the following asymptotic property

(10)

where is an explicit constant depending only on H.

In the following we give a direct proof of (10) by using (9) and an Abelian argument similar to that in the proof of Theorem 1 of [16] . Without loss of generality, we assume that. Applying integration-by-parts to (9), we get

(11)

with

(12)

We need to distinguish three cases:, and. In the first case, it can be verified from (12) that, hence, and

(13)

We will also make use of the properties of higher order derivatives of. It is elementary to compute and verify that, when, we have

(14)

and as which implies.

The behavior of the derivatives of is simpler when. (12) becomes

(15)

and

(16)

Hence, we have, , and both and are in.

When, it can be shown that (14) still holds, and as.

Now, we proceed to prove (10). First, we consider the case when. By a change of variable, we can write

(17)

Hence,

(18)

Let be a fixed constant. It follows from (13) and the dominated convergence theorem that

(19)

On the other hand, integration-by-parts yields

(20)

By Riemann-Lebesgue lemma,

(21)

Moreover, since by (13) and as, we have as. It follows that

(22)

Then for all large enough, we derive

(23)

Hence, we have

(24)

Combining (18), (19), and (24), we have

(25)

Then we see that, when, (10) holds with.

Secondly, we consider the case. Since is continuous and, (19) becomes

(26)

Using (20) and integration-by-parts again we derive

(27)

It follows from the (27), (16) and Riemann-Lebesgue lemma that

(28)

We see from the above and (17) that

(29)

This verifies that (10) holds when.

Finally we consider the case. Note that (19) and (24) are not useful anymore and we need to modify the above argument. By using integration-by-parts to (11) we obtain

(30)

Note that we have. Hence is integrable in the neighborhood of. Consequently, the proof for this case is very similar to the case of. From (30) and (14), we can verify that (10) holds as well and the constant is explicitly determined by H. Hence we have proved (10) in general.

It follows from (10) and Lemma 1 of [17] (see also [12] for more general results) that is strongly locally -nondeterministic on any interval with in the following sense: There exist positive constants and such that for all and all,

(31)

Now we prove the strong local nondeterminism of on I. To this end, note that for all. We choose. Then for all with we have

(32)

Hence, it follows from (31) and (32) that for all and,

(33)

where. This proves Theorem 1.

Funding

Supported by NSFC (No. 11201068) and “The Fundamental Research Funds for the Central Universities” in UIBE (No. 14YQ07).

Cite this paper

NanaLuan, (2015) Strong Local Non-Determinism of Sub-Fractional Brownian Motion. Applied Mathematics,06,2211-2216. doi: 10.4236/am.2015.613194

References