Received 26 July 2015; accepted 15 September 2015; published 18 September 2015

ABSTRACT

This paper discusses a special class of mathematical programs with equilibrium constraints. At first, by using a generalized complementarity function, the discussed problem is transformed into a family of general nonlinear optimization problems containing additional variable m. Furthermore, combining the idea of penalty function, an auxiliary problem with inequality constraints is presented. And then, by providing explicit searching direction, we establish a new conjugate projection gradient method for optimization with nonlinear complementarity constraints. Under some suitable conditions, the proposed method is proved to possess global and superlinear convergence rate.

Keywords:

Mathematical Programs with Equilibrium Constraints, Conjugate Projection Gradient, Global Convergence, Superlinear Convergence

1. Introduction

Mathematical programs with equilibrium constraints (MPEC) include the bilevel programming problem as its special case and have extensive applications in practical areas such as traffic control, engineering design, and economic modeling. So many scholars are interested in this kind of problems and make great achievements, (see [1] -[10] ).

In this paper, we consider an important subclass of MPEC problem, which is called mathematical program with nonlinear complementarity constraints (MPCC):

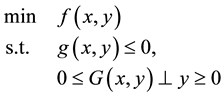(1.1)

where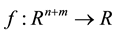, , 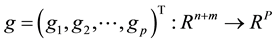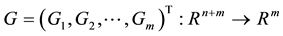are all continuously differential functions,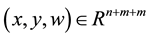. 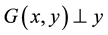denotes orthogonality of the vectors y and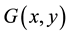, i.e.,.

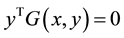In order to eliminate the complementary constraints, which can not satisfy the standard constraint qualification [11] , we introduce the generalized nonlinear complementary function

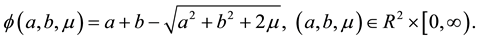
Obviously, the following practical results about function 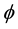hold:

• if 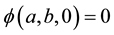and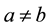, then

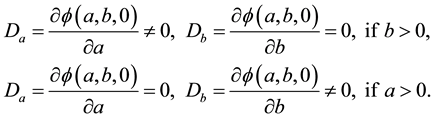(1.2)

•

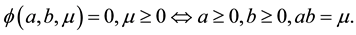(1.3)

By means of the function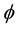, problem (1.1) is transformed equivalently into the following standard nonlinear optimization problem

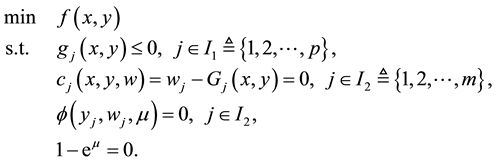(1.4)

Similar to [12] , we define the following penalty function

where is a penalty parameter. Therefore, our approach consists of solving an auxiliary inequality constrained problem which is defined by

(1.5)

2. Preliminaries and Algorithm

For the sake of simplicity, we denote

(2.1)

Throughout this paper, the following basic assumptions are assumed.

H 2.1. The feasible set of (1.1) is nonempty, i.e.,.

H 2.2. The functions are twice continuously differentiable.

H 2.3., the vectors are linearly independent.

The following definition and proposition can be refereed to in [13] .

Definition 2.1. Suppose that satisfies the so-called nondegeneracy condition:

(2.2)

If there exists multipliers such that

(2.3)

(2.4)

hold, then is said to be a point of (1.1).

Proposition 2.1. Suppose that satisfies the so-called nondegeneracy condition (2.2), then is a point of (1.1) if and only if satisfies

(2.5)

(2.6)

where

(2.7)

and.

Proposition 2.2. (1) s is a feasible point of (1.1) if and only if with is a feasible point of (1.4).

(2) is a point of (1) if and only if with is a point of (1.4).

Proof. (1) According to the property of function, the conclusion follows immediately from (1.3).

(2) Suppose that is a point of (1.1). If set and, then, from (1), we see is a feasible point of (1.4). While, it follows from proposition 2.1 that there exists vector such that (2.5) and (2.6) hold. Define

(2.8)

So, it is not difficult to prove that satisfies the system of (1.4), according to (1.3), (2.5) and (2.6).

Conversely, if is a point of (1.4), then it follows that

and,

which shows that is a feasible point of (1.1). Suppose is a multiplier corresponding to of (1.4). Define as follows:

(2.9)

Then, it is easy to see, from (1.2) and the system of (4) at, that with the multiplier satisfies (2.5) and (2.6). Therefore, we assert is a point of (1.1) according to proposition 2.1.

Now, we present the definition of multiplier function associated with -active set [14] .

Definition 2.2. A continuous function is said to a multiplier function, if satisfies the system of (1.5) with corresponding multipliers.

Firstly, for a given point, by using the pivoting operation, we obtain an approximate active.

Algorithm A:

Step 1. For the current point and parameter. Set,;

Step 2. If, let, stop; otherwise, goto Step 3, where

(2.10)

Step 3., , go back to Step 2.

Lemma 2.1. For any iteration index k, algorithm A terminates in finite iteration.

For the current point and -active set, compute

(2.11)

Now we give some notations and the explicit search direction in this paper.

(2.12)

(2.13)

(2.14)

(2.15)

(2.16)

where.

According to the above analysis, the algorithm for the solution of the problem (1.1) can be stated as follows.

Algorithm B:

Step 0. Given a starting point, and an initial symmetric positive definite matrix.

Choose parameters.

Step 1. By means of Algorithm A, compute and.

Step 2. Compute according to (2.13). If, stop; otherwise, compute according to (2.14). If

(2.17)

goto Step 3; otherwise, goto Step 4.

Step 3. Let.

(1) If

(2.18)

(2.19)

Set, goto Step 5.

(2) Let. if, goto Step 4; otherwise, repeat (1).

Step 4. Obtain feasible descent direction from (2.16), and compute β_k, the first number β in the sequence

satisfying

(2.20)

(2.21)

Let.

Step 5. Define, and set

(2.22)

and. Obtain by updating the positive definite matrix using some quasi- Newton formulas, and set k = k + 1. Go back to Step 1.

In the remainder of this section, we give some results to show that Algorithm B is correctly stated.

Lemma 2.2. (1) If, then we have

(2.23)

(2.24)

(2) If the sequence is bounded, then there exists a constant such that

(2.25)

Proof. (1) If, then

In view of, we get. Since

so we have

(2.26)

(2) Note that the boundedness of sequence and positive definite, we know that are bounded. By (2.16), there exists constant such that. Thus, there exists constant such that

So, the claim holds.

According to Lemma 2.2 and the continuity of functions and, the following result is true.

Lemma 2.3. Algorithm B is well defined.

3. Global Convergence

In this section, we consider the global convergence of the algorithm B. Firstly, we show that is an exact stationary point of (1.1) if the Algorithm B terminates at the current iteration point.

Lemma 3.1. (1) is a K − T point of (1.5) if and only if.

(2) If is a point of (1.5), then with is a K − T point of (1.4).

Proof. (1) If is a K − T point of (1.5), then from the definition of index set J_k, we know the K − T multiplier corresponding to constraints about index is 0. Thus, there exists vector such that

(3.1)

Note that matrix is full of column rank, and positive definite. Thus we have exists. Furthermore, it follows from (3.1) that

By (2.14) and (3.1), we have

so

On the other hand, it is easy to verify that

It follows from that

From the positive definiteness of and (2.12), (2.13) and (2.14), we have

(3.2)

which implies that is a point of (1.5).

(2) In view of the definition of, we obtain from (3.2) that

(3.3)

Since the vectors are linearly independent, we have

i.e.

Thus, we deduce

(3.4)

In view of the definition of penalty parameter, from (3.4), we have

(3.5)

Combining with (3.2) and (3.5), it holds that

(3.6)

Let where. From (3.3) and (3.6), we can easily see that is a K − T point pair of (1.4).

Theorem 3.1. Suppose the nondegeneracy condition holds at. If is a K − T point of (1.4), then is a K − T point of (1.1).

Proof. According to the K − T system of (1.4) and the relationship of index i and j in (2.1), we see that

(3.7)

Then, combining with Proposition 2.1 and Proposition 2.2, we can conclude that is a K − T point of (1.1).

In the sequel, it is assumed that the Algorithm B generates an infinite sequence. The following further assumption about is required in subsequent discussions.

H 3.1. (1) The sequence is bounded.

(2) The accumulation point of infinite sequence satisfies (2.2).

From H 3.1 and the fact that there are only finitely many choices for sets, we may assume that there exists a subsequence K, such that

(3.8)

where J is a constant set. Correspondingly, the following results hold:

Lemma 3.2. Suppose, then for large enough, we have

(1) there exists a constant such that.

(2) there exists a constant such that.

Proof. (1) suppose, by contradiction, that there exists an index set such that. Let. For large enough, from Algorithm A, we have

(3.9)

Since there are only finite possible subsets of, there must be an infinite subset such that for any. Thus, it follows from (3.9) that

(3.10)

which contradicts the condition H 2.3.

(2) Suppose by contradiction, there exists a subsequence such that, then from the definition of, we have

(3.11)

From the finite selectivity of, we can suppose without loss of generality that. By (1), we can see that is bounded, i.e., for some. Let M be such an integer that, then we have

a contradiction, and the result is proved.

Lemma 3.3. Suppose that, and which is generated by Step 4 and Step 5. If is not a point of (1.5), then we have

(1),

(2).

Proof. (1) Suppose. Since is not a of (1.5), so we have and

Therefore, for large enough, we obtain

(3.12)

(2) For (2.20), denote

From (3.12), for large enough and small enough, it holds that.

For (2.21), when, the fact and the continuity of imply that (4.5) holds. When, it holds that. From (3.12), for large enough and small enough, we have

According to the analysis above, the result is true.

Lemma 3.4. Algorithm B generates infinite sequence, whose any accumulation points are points of (1.1).

Proof. Suppose that. From (2.17), (2.18), (2.20) and Lemma 2.2, we know that is a descent sequence. While, for, it is obvious that. So

(3.13)

Now we consider the following two cases:

(1) Suppose there exists an infinite subset such that

which is obtained by Step 3 and Step 5. In view of in Step 3, it follows from (2.17) and (2.18) that

Obvious,. Again, , so we have. Imitating the proof of Lemma 3.1, it is easy to see that is a point of (1.5).

(2) Assume the iteration is generated by Step 4 and Step 5. Suppose by contradiction that is not a point of (1.5). Then, from (3.12) and Lemma 3.3, we have

which is a contradiction. Thus, the claim holds.

Theorem 3.2. The point of (1.5) must be the one of (1.4), where.

Proof. If is a point of (1.5), then there exists multiplier such that

(3.14)

Set

Obvious,. While, from (3.14) we get

i.e.

Thereby,

(3.15)

According to the definition of, it is clear that

(3.16)

In addition, combining with (3.2) (3.16), we obtain

(3.17)

Let, where. It follows from (3.14) and (3.17) that is a point pair of (1.4).

Theorem 3.3. Suppose (2.2) holds at. If is a point of (1.4), then is a point of (1.1).

Proof. According to Theorem 3.2 and (2.1), Proposition 2.1 and Proposition 2.2 imply is a point of (1.1).

4. Superlinear Convergence

Now we discuss the convergence rate of the Algorithm B, and prove that the sequence generated by the Algorithm B is one-step superlinearly convergent. For this purpose, we add some stronger regularity assumptions.

H 4.1. The bounded sequence possesses an accumulation point, at which second-order sufficiency condition and strict complementary slackness hold, where is the corresponding multiplier of.

Lemma 4.1. Under H 2.1-H 4.2, we have that

Proof. For generated by Step 3 and Step 5, from (2.17) and (2.18), it holds that

While, for generated by Step 4 and Step 5, from (2.17), (2.20) and Lemma 2.2, we have

So

Passing to the limit and from (3.13), we obtain

Thereby

Theorem 4.1. The entire sequence converges to, i.e.,.

In order to obtain the superlinear convergence rate, we make the following assumption.

H 4.2. positive definite.

Lemma 4.2. If H 2.1-H 4.2 hold, then we get that

(1) for k large enough,.

(2).

Proof. (1) On one hand, by Lemma 3.2, for k large enough, there exists a constant such that in Algorithm A. It follows from H 4.1 and the fact that, for k large enough,.

On the other hand, we assert that. Otherwise, there exists some index t and infinite subset K such that

Let, then

It is a contradiction with the complementary slackness condition, which shows that, i.e.,.

(2) According to and, the fact implies. Again, since is a point of (1.5), imitating the proof of Lemma 3.1, we get that

So the uniqueness of multiplier shows.

Lemma 4.3. Under H 2.1-H 4.2, for k large enough, with the corresponding multiplier

is a point of the following quadratic program

(4.1)

Proof. Suppose that is a point pair of (4.1). From (2.12), (2.14) and (4.1), it holds that

In addition, for k large enough, holds from fact and strict complementarity condition. While, from the definition of, it holds that. So the claim holds.

Lemma 4.4. (1) For k large enough, there exist constants such that

(4.2)

(2) obtained by (2.15) satisfies

(4.3)

Proof. (1) Since, and for k large enough, , it is easy to see

(4.4)

Obviously, for k large enough,. Thereby, there exists a constant such that

In addition, from Lemma 4.3, we see

(4.5)

So

(4.6)

(2) Since

we know

From and the boundedness of, it follows that

So, the result is true.

In order to obtain the superlinear convergence rate, we make another assumption.

H 4.3. The sequence of symmetric matrices satisfies

where

Lemma 4.5. For k large enough, Algorithm B is not implemented on Step 4, and

holds in Step 3.

Proof. According to and Lemma 4.4, we have

which shows (2.17) hold. Now we prove that, the arc search (2.19) and (2.18) eventually accept unit step, i.e., , for k large enough.

Firstly, for (2.19), when, the fact that and the continuity of imply

when, using Taylor expansion, we get

(4.7)

Again, from

we see

Thus, (4.7) yields

(4.8)

In view of, (2.19) obviously holds when.

Secondly, we prove that, for k large enough, (2.18) holds for. Denote

(4.9)

From (4.5), we have

Also, by (4.8), it holds that

So

Thus, (4.6) yields

Denote, then. Set

(4.10)

Clearly,

while, from (2) and (10), it holds that

So

which implies the theorem hold.

According to Lemma 4.3, Lemma 4.4 and Lemma 4.5, combining with Theorem 12.3.3 in [15] , the following state holds.

Theorem 4.2. The Algorithm B is superlinearly convergent, i.e.,

5. Conclusion

By means of perturbed technique and generalized complementarity function, we, using implicit smoothing strategy, equivalently transform the original problem into a family of general optimization problems. Based on the idea of penalty function, the discussed problem is transformed an associated problem with only inequality constraints containing parameter. And then, by providing explicit searching direction, a new variable metric gradient projection method for MPCC is established. The smoothing factor regarded as a variable ensures that we can obtain an exact stationary point of original problem once the algorithm terminates in finite iteration. What’s more, the proposed algorithm adjusts penalty parameter automatically. Under some mild conditions, the global convergence is obtained as well as the superlinear convergence rate.

Acknowledgements

The authors are indebted to the anonymous referees for valuable comments and remarks that helped them improve the original version of the paper.

Funding

This work was supported in part by the National Natural Science Foundation (No. 11361018), the Natural Sci- ence Foundation of Guangxi Province (No. 2014GXNSFFA118001), the Key Program for Science and Techno- logy in Henan Education Institution (No. 15B110008) and Huarui College Science Foundation (No. 2014qn35) of China.

Cite this paper

CongZhang,LiminSun,ZhibinZhu,MingleiFang, (2015) An Implicit Smooth Conjugate Projection Gradient Algorithm for Optimization with Nonlinear Complementarity Constraints. Applied Mathematics,06,1712-1726. doi: 10.4236/am.2015.610152

References

NOTES

^*Corresponding author.