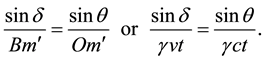Applied Mathematics
Vol.06 No.09(2015), Article ID:58762,9 pages
10.4236/am.2015.69138
Rays’ Change of Directions between Inertial Frames and Stellar Aberration
Caesar P. Viazminsky1, Piere K. Vizminiska2
1Department of Physics, Illinois Institute of Technology, Chicago, IL, USA
2Department of Computer Engineering, University of Detroit Mercy, MI, USA
Email: kaysarv2@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 July 2015; accepted 9 August 2015; published 12 August 2015
ABSTRACT
The path of a light’s signal is one and the same in the universal space regardless of the inertial frame by which it is identified. However, only one frame can be taken stationary and identified with the universal space while all other frames are moving. The direction of the path of a light’s pulse in a moving frame is determined in terms of its direction in the stationary one; the result is utilized to explain stellar aberration and show that the tilted direction in the moving frame depends only on its velocity. The aberration increment vector is introduced and employed to determine the apparent position of a star at each point of the earth orbit. Aberration in an earth satellite relative to the geocentric frame is presented. The direction’s change of a light beam between graded inertial frames promotes explaining aberration in an earth’s satellite in parallel to stellar aberration on earth.
Keywords:
Direction’s Change of Light Rays, Stellar Aberration, Aberration in a Satellite, Aberration Increment, Graded Inertial Frames

1. Introduction
In earlier works [1] [2] the fundamentals of the theory of universal space and time (UST) were presented. According to the UST, time intervals in an inertial frame S are essentially measured by corresponding spatial intervals travelled by light signals. Equivalently, the geometric distance
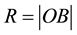 between two points B and O in S is measurable by the time duration
between two points B and O in S is measurable by the time duration
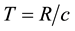 (or geometric time) of a light trip
(or geometric time) of a light trip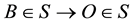 , which is the same as the duration of the light trip
, which is the same as the duration of the light trip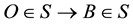 . The latter simple relation which is valid only when B and O are stationary in S, puts geometric time and length on equal footing as equivalent measures of the same distance. The physical, or universal space, can be identified by one arbitrary inertial frame S (or s), which is considered stationary while any other inertial frame s (S) is moving relative to S (s); and a light’s trip thus follows the same path in the universal space whether identified by S or s [1] .
. The latter simple relation which is valid only when B and O are stationary in S, puts geometric time and length on equal footing as equivalent measures of the same distance. The physical, or universal space, can be identified by one arbitrary inertial frame S (or s), which is considered stationary while any other inertial frame s (S) is moving relative to S (s); and a light’s trip thus follows the same path in the universal space whether identified by S or s [1] .
The light path is seen in the moving frame tilted from its direction in the stationary frame by the aberration angle. In the heliocentric frame the direction of the earth’s velocity, due to its orbital motion, keeps changing, resulting in every received starlight continuously changing its direction in the geocentric frame. The latter fact is manifested in a periodic change in the apparent position of distant stars throughout the year. The phenomenon of the annual apparent motion of celestial objects about their locations, named stellar aberration, was discovered by Bradley in 1727 [3] [4] , who also explained it employing the corpuscular model of light [3] [5] . One can also account for aberration in terms of light’s waves traveling through the ether, provided the ether remains completely undisturbed by the earth’s motion [6] . Bradley’s explanation of stellar aberration however, proved inadequate since it couldn’t account for the negative results of Airy Experiment [4] .
The following items summarize the goals that we seek in this work and the plan of its presentation.
We start by an outline of the structure and relevant results of UST theory.
Find the relation between the path of a light’s pulse in the stationary and moving frames.
Utilize the relation that we found to explain the aberration phenomenon and obtain a new expression for stellar aberration angle. Although different from Bradley’s and the relativistic expressions, our formula is in accord with experiment results and it determines the aberration angle at each instant of the year.
The concepts of the aberration increment and aberrated vector are introduced and used to determine the apparent motion of a given star and the direction at which the telescope should be pointed at various times of the year.
The direction’s change of light beams between graded inertial frame is introduced and employed to quantify aberration in an earth’s satellite.
Basics and discussions of stellar aberration can be found in many textbooks and articles [3] -[8] .
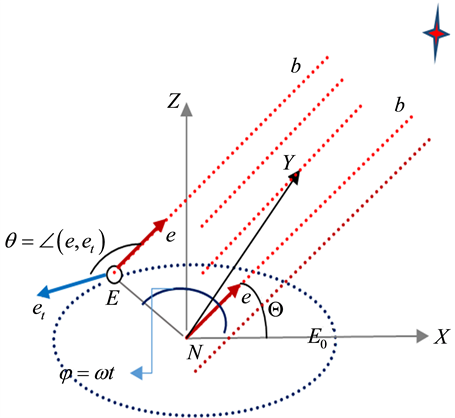
2. Universal Direction of a Light’s Ray
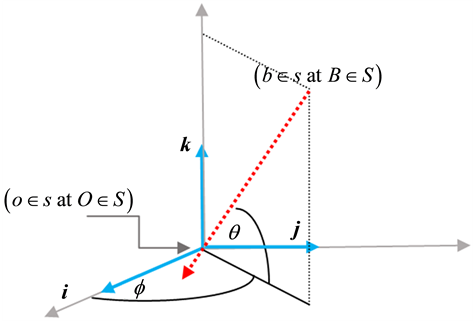
Let S be an inertial frame in which a source of light b is moving at a constant velocity u, and s be another inertial frame in standard configuration with S and co-moving with b. We found in [1] that a pulse of light emanating from
 and received by the conjugate observers
and received by the conjugate observers
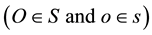 follows the same path in the universal space whether identified by S or s. The pulse’s path is realized within each frame, S or s when considered stationary, as propagating along the same vector
follows the same path in the universal space whether identified by S or s. The pulse’s path is realized within each frame, S or s when considered stationary, as propagating along the same vector
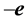 which is identified by
which is identified by
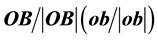 when S (s) is the stationary frame [1] , i.e.
when S (s) is the stationary frame [1] , i.e.
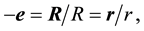 (2.1)
(2.1)
where R is the geometric radius vector of the point (b at B) in S (in s) when stationary. The relation (2.1) implies that the direction of the radius vector of (b at B) as measured within the stationary frame, S or s, is the same one thing. If e is specified in a basis of unit vectors of S or s (when stationary) then the directional angles are the same in both frames [1] :
is the geometric radius vector of the point (b at B) in S (in s) when stationary. The relation (2.1) implies that the direction of the radius vector of (b at B) as measured within the stationary frame, S or s, is the same one thing. If e is specified in a basis of unit vectors of S or s (when stationary) then the directional angles are the same in both frames [1] :
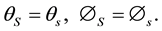 (2.2)
(2.2)
This shows that no matter was the magnitude of the source’s velocity in S, or equivalently, regardless of the frame S in which the source b was viewed, the direction of the light’s path as observed within S is identical to its direction as observed within the frame s in which the source b is stationary (the word “within” here implies that the frame concerned is considered stationary). This means that all observers conjugate to o, each within his frame, are in accord with the direction’s measurements obtained by o, and consequently with each other. Therefore, the direction of the path of a light’s pulse, as measured within each inertial frame, is independent of the relative velocity between the source and the receiver; the same values of the directional angles are obtained by all inertial conjugate observers, each within his inertial frame (Figure 1). The latter statements manifest the absolute character of the path direction of light.
In the rest of this section we brief some basic concepts and results of UST that is relevant to our current work.
Suppose that at an instant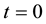 , corresponding to
, corresponding to
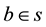 occupying the point
occupying the point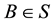 , light emanates from
, light emanates from
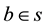 . The light arrives at
. The light arrives at
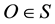 (and hence at the contiguous observer
(and hence at the contiguous observer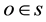

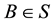
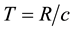
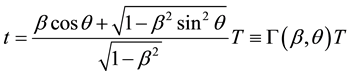
where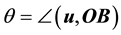
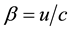
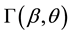
It was shown [1] [2] that when the pulse arrives at O, i.e. at the instant t, the moving object b occupies a position
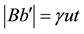
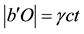
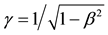
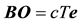
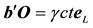
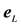
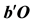
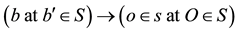
Note that if the pulse emanates from B, then as before, the pulse follow
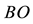

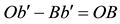
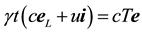
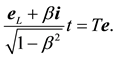
Taking the cross product of both sides with
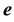
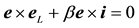

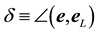
Figure 1. The pulse follows one and the same path (in red) in the universal space whether identified by S or s.
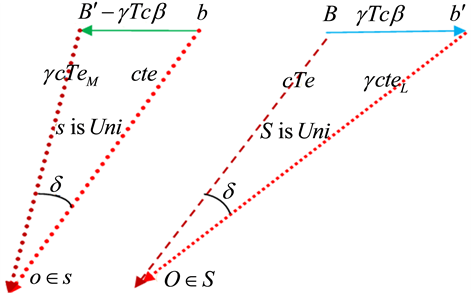
Figure 2. (a) The pulse path is
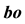
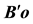
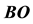

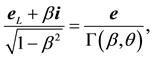
or
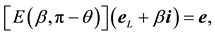
where
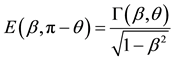
is the Euclidean factor [2] .
In the UST theory, time is an absolute entity and hence the duration of a light trip is the same in all inertial frames, but its direction and spatial length may differ. Therefore, if S is the universal frame, the duration of the trip
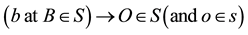
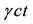
If the frame s is chosen the universal frame (stationary), then in the first case the time duration of the trip
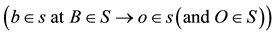
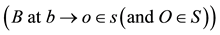
In parallel to the relations (2, 4 - 6) we have when s is stationary
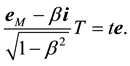
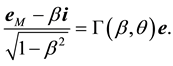

or
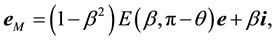
which all are obtained through replacing
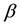
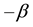
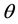
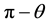

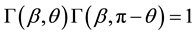
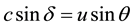
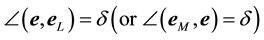
3. The Ray’s Direction in a Moving Frame―Aberration Angle
Consider a parallel beam of light propagating in the universal frame S parallel to the direction
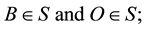
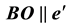

The path of the ray in M is also determined by two points in M. Let m be a point in M and assume that when at
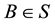
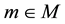
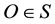
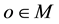
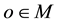


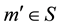
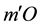

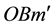
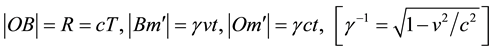
Thus the direction of the ray is observed in M tilted from a fixed direction
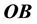

which yields

where
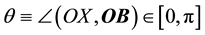

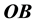
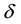
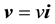
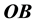
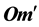
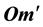
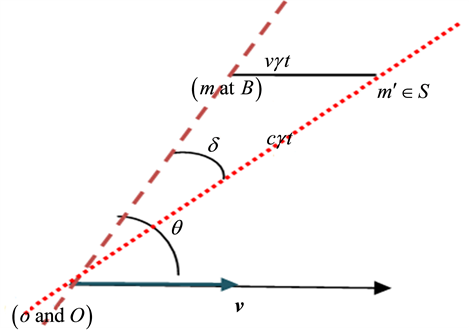
The source of light b (a star for instance) can be seen by a telescope, with ocular and objective lenses r and o respectively, only if the telescope ro is set along the direction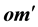
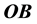
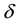
4. Stellar Aberration
Consider a “distant” star b, in the sense that the radius of the earth’s orbit is negligible in comparison with the distance between the star and the sun. In this context, the phrase “the vicinity of the sun at some instant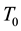
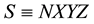
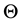
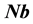
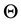
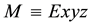
All S-observers (in vicinity of the sun) see the rays from the star b throughout the year coming along the
Figure 3. The same beam is seen along OB in S and
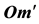
Figure 4. In order to see the star b, a telescope in M with ocular o must points along om'.
negative direction of the vector

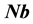
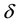
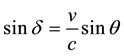
and
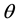
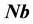

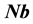
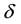
The vector velocity
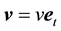
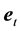
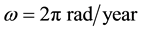
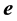
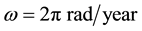
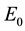
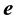
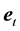
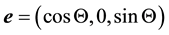
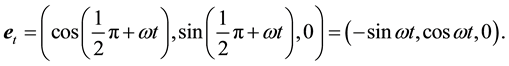
where we assume in writing (4.2b) that the earth orbit is approximately circular. The cosine of the angle
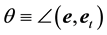

Identifying
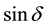
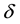
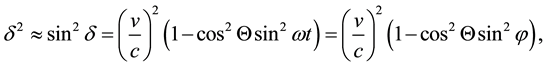
where
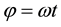
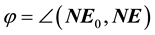
Figure 5. Because the star b is too far, Nb and Eb are essentially parallel. The true position of b is along the same direction in the heliocentric and geocentric frames S and M.
aberration angle
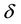

By (4.5) the aberration angle attains its maximal values
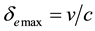
for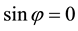
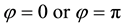
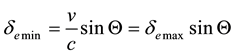
for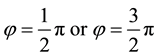
Substituting for v and c in (4.6) by
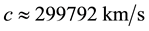
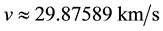

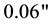
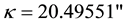
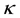
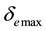
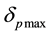
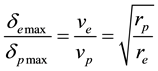
where
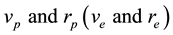
Recalling that the telescope in s is tilted by
tude of the star is highest for
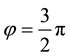
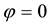
remains unchanged because the telescope is tilted horizontally (by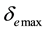
Two Special Cases: (i) For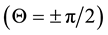
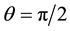
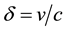
(ii) The distant star b is in the ecliptic: Setting
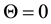

The aberration occurs in the ecliptic attaining its maximal absolute value (4.6) at
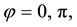
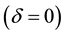
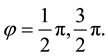
the earth’s velocity and minimum when the earth directly approach the star or recedes from it.
5. The Aberration Increment and Aberration Direction
The aberrated direction is the momentary direction along which the star is seen from Earth. Being in the aberration plane, its unit vector
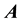
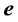
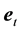
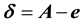
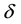

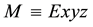
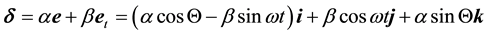
Since
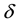

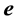
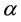
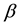

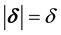
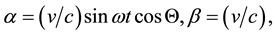

The aberration vector
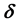
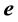
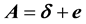
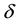

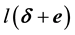
Two particular independent directions of
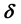
(i) At
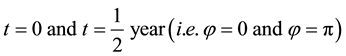
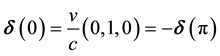
which shows that, when the Earth’s velocity is perpendicular to the line of sight to b, the telescope is tilted horizontally in the direction of motion by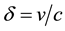
(ii) For
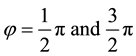

As the z-component is positive for
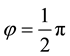

It is convenient to decompose the aberration increment into a horizontal (east-west) and “vertical” (north- south) components,
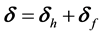
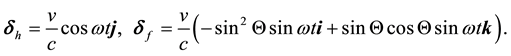
It is clear that the triad
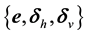
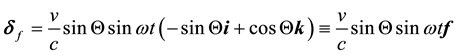
where f is a unit vector defined by the quantity in the parentheses. It is clear that f is perpendicular to
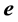

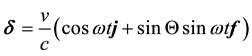
From the parametric representation
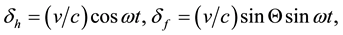

Likewise, the aberrated vector
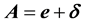
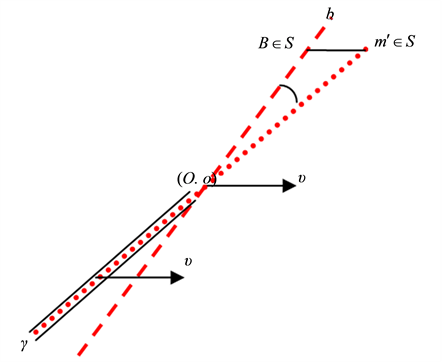
Aberration in Graded Inertial Frames:
When S and M are equally inertial the star is seen in each frame when taken universal along the same direction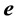
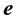
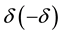
The aberrated direction in the geocentric frame M is determined with reference to a fixed direction in the heliocentric frame S. But it is known [10] [11] that our sun is revolving about the center of the galaxy at about 8 times the earth’s orbital velocity and making a full round in about 230 million years (a galactic year) [10] [11] . As observed from the sun, the aberration increment vector concerning a extragalactic object is given by an equation like (5.2) in which v is replaced by 8v and
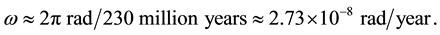
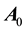
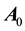
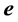
In reality no frame is exactly inertial, but there are graded inertial frames in which one frame is more inertial than another. For instance, the set of non-rotating frames with origins at the center of mass of, the galaxy (G), the solar system (S), the earth-moon system (M), an earth satellite, is graded. Indeed, the motion of S can be counted uniform for thousands of years, whereas the duration of uniformity of earth’s motion in S ranges from minutes to hours depending on the required degree of accuracy. The apparent position
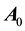

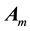

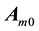
6. Observing Aberration from an Earth’s Satellite
Suppose that a satellite is orbiting the earth in a low circular orbit that lies in the ecliptic. During the orbital period
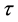
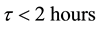

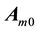
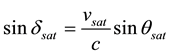
where


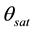
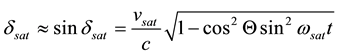
where
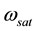
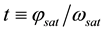
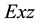
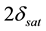
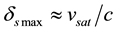
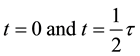
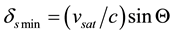

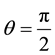

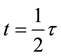
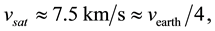

The apparent motion of the star b repeats itself once a year when observed from the earth, and

7. Conclusion
The UST theory provides a neat explanation of the stellar aberration phenomenon that highlights its independence from the velocity of the light source. By introducing the concept of the aberration increment vector we were able to find an approximate formula for the apparent position of the celestial object at each moment of the year. The concept of graded inertial frames makes it clear why annual stellar aberration depends only on the velocity of the earth relative to the heliocentric frame. Employing the same concept enables us to treat aberration when observed from a satellite in parallel to its treatment when observed from the earth.
Cite this paper
Caesar P.Viazminsky,Piere K.Vizminiska, (2015) Rays’ Change of Directions between Inertial Frames and Stellar Aberration. Applied Mathematics,06,1553-1562. doi: 10.4236/am.2015.69138
References
- 1. Viazminsky, C.P. and Vizminiska, P.K. (2014) On Universal Space and Time. Applied Mathematics, 5, 2530-2546.
http://dx.doi.org/10.4236/am.2014.516243 - 2. Viazminsky, C.P. and Vizminiska, P.K. (2014) On Universal Mechanics and Superluminal Velocities. Applied Mathematics, 5, 2728-2738.
http://dx.doi.org/10.4236/am.2014.517260 - 3. Bradley, J. (1728) Account on a New Discovered Motion of the Fix’d (Fixed) Stars. Philosophical Transactions of the Royal Society of London, 35, 637-660.
http://dx.doi.org/10.1098/rstl.1727.0064 - 4. French, A.P. (1968) Special Relativity. Butler & Tanner Ltd., Frome and London, Ch. 2 & 3.
- 5. Russo, D. (2007) Stellar Aberration: The Contradiction between Einstein and Bradley. Apeiron, 14, 95-112.
- 6. Stokes, G.G. (1845) On the Aberration of Light. Philosophical Magazine, 27, 9-15.
- 7. Phipps Jr., T.E. (2005) Testing Relativity for One-Way Light Propagation. Apeiron, 12, 136-143.
- 8. Rindler, W. (1977) Essential Relativity. Springer-Verlag, New York.
http://dx.doi.org/10.1007/978-3-642-86650-0 - 9. http://www.britannica.com/topic/constant-of-aberration
- 10. http://www.thefullwiki.org/Aberration_of_light
- 11. https://en.wikipedia.org/wiki/Aberration_of_light