Applied Mathematics
Vol.06 No.04(2015), Article ID:55757,8 pages
10.4236/am.2015.64062
Variational Homotopy Perturbation Method for Solving Benjamin-Bona-Mahony Equation
Fadhil H. Easif1, Saad A. Manaa1, Bewar A. Mahmood2, Majeed A. Yousif1
1Department of Mathematics, Faculty of Science, University of Zakho, Zakho, Iraq
2Department of Mathematics, Faculty of Science, Univresity of Duhok, Duhok, Iraq
Email: b.m.numerical@uod.ac
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 March 2015; accepted 14 April 2015; published 17 April 2015
ABSTRACT
In this article, the application of variational homotopy perturbation method is applied to solve Benjamin-Bona-Mahony equation. Then, we obtain the numerical solution of BBM equation using the initial condition. Comparison with Adomian’s decomposition method, homotopy perturbation method, and with the exact solution shows that VHPM is more effective and accurate than ADM and HPM, and is reliable and manageable for this type of equation.
Keywords:
Variational Homotopy Perturbation Method, Benjamin-Bona-Mahony Equation

1. Introduction
Most scientific problems arise in real-world physical problems such as plasma physics, fluid mechanic, solid state physics and in many branches of chemistry [1] . The Benjamin-Bona-Mahony (BBM) equation is inherently of nonlinearity. We know that except a limited number of these problems, most of them do not have analytical solution. Therefore, these nonlinear equations should be solved using numerical methods: variational iteration method (VIM) [2] and homotopy-perturbation method (HPM) [3] . These methods are the most effective and convenient ones for both weakly and strongly nonlinear equations. In this article, VHPM is used to solve nonlinear Benjamin-Bona-Mahony [4] and [5] . The Benjamin-Bona-Mahony equation (BBM equation) is the partial differential equation
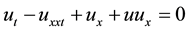 (1.1)
(1.1)
This equation was introduced in (Benjamin T. B., Bona J. L. & Mahony J. J. 1972) [5] as an improvement of the Korteweg-de Vries equation (KdV equation) for modeling long waves of small amplitude in 1 + 1 dimensions.
The main goal of this paper is to find the approximate solution of the BBM by the variational homotopy perturbation method that has already been successfully applied to several nonlinear problems.
2. Mathematical Model
The generalized BBM (Benjamin-Bona-Mahony) equation has a higher order nonlinearity of the form
 (2.1)
(2.1)
where a is constant.
The case 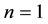 corresponds to the BBM equation
corresponds to the BBM equation
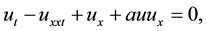 (2.2)
(2.2)
which was first proposed in 1972 by Benjamin et al. [5] . This equation is an alternative to the Korteweg-de Vries (KdV) equation, and describes the unidirectional propagation of small-amplitude long waves on the surface of water in channel. The BBM equation is not only convenient for shallow water waves but also for hydro magnetic waves, acoustic waves, and therefore it has more advantages compared with the KdV equation. When , Equation (2.1) is called the modified BBM equation:
, Equation (2.1) is called the modified BBM equation:
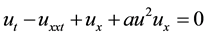 (2.3)
(2.3)
3. Materials and Methods
3.1. Variational Iteration Method
To clarify the basic ideas of VIM, we consider the following differential equation
 (3.1)
(3.1)
where L is a linear operator is defined by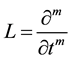 ,
, 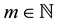 , N is a nonlinear operator and
, N is a nonlinear operator and 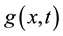 is a known
is a known
analytic function. According to VIM, we can write down a correction functional as follows:
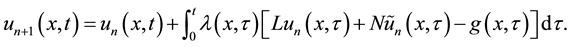 (3.2)
(3.2)
where 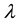 is a general lagrangian multiplier [6] defined as:
is a general lagrangian multiplier [6] defined as:
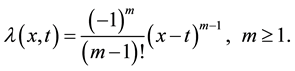 (3.3)
(3.3)
The subscript n indicates the nth approximation and 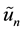 is considered as a restricted variation [7] .
is considered as a restricted variation [7] .
3.2. Homotopy Perturbation Method
To illustrate the basic ideas of this method, we consider the following nonlinear differential equation
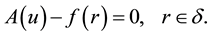 (3.2.1)
(3.2.1)
With the following boundary conditions
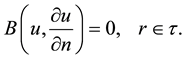 (3.2.2)
(3.2.2)
where A is a general differential operator, B a boundary operator, 


Equation (3.2.1) can be written as follows:

By using the homotopy technique, we construct a homotopy:

Which are satisfies:

or

where 



The changing process of p forms zero to unity is just that of 


And assume that the solution of Equations (3.2.5) and (3.2.6) can be written as a power series in p:

Setting

The combination of the perturbation method and the homotopy method is called the homotopy perturbation method (HPM), which has eliminated the limitations of the traditional perturbation methods. On the other hand, this technique can have full advantage of the traditional perturbation techniques.
The series (3.2.10) is convergent for most cases. Some criteria are suggested for convergence of the series (3.2.10) [8] .
3.3. Variational Homotopy Perturbation Method
To illustrate the concept of the variational homotopy perturbation method, we consider the general differential Equation (3.1). We construct the correction functional (3.2) and apply the homotopy perturbation method (3.2.9) to obtain:

As we see, the procedure is formulated by the coupling of variational iteration method and homotopy perturbation method. A comparison of like powers of p gives solutions of various orders [9] .
4. Numerical Example
Example:
Consider the nonlinear Benjamin-Bona-Mahony equation where 

And initial condition

And exact solution

The correct functional is given as

where 


Applying the variational homotopy perturbation method, we have:

Comparing the coefficient of like powers of p, we have




Then


The other components of the VHPM can be determined in a similar way. Finally, the approximate solution of Equation (4.1) in a series form is

5. Figures and Tables
In this section, the results obtained by VHPM are tabulated in the following tables, followed by their figures (Figures 1-12) and comparisons.
6. Conclusions
In this paper, we have successfully used variational homotopy perturbation method for solving the Benjamin- Bona-Mahony equation, it is apparently seen that VHPM is very powerful and efficient technique in finding
Figure 1. Exact solution at −50 ≤ x ≤ 50, 0 ≤ t ≤ 0.5.
Figure 2. VHPM at −50 ≤ x ≤ 50, 0 ≤ t ≤ 0.5.
Figure 3. Exact solution at −5 ≤ x ≤ 5, 0 ≤ t ≤ 1.
Figure 4. VHPM at −5 ≤ x ≤ 5, 0 ≤ t ≤ 1.
Figure 5. Exact solution at 0 ≤ x ≤ 50, 0 ≤ t ≤ 5.
Figure 6. VHPM at 0 ≤ x ≤ 50, 0 ≤ t ≤ 5.
Figure 7. Exact solution and VHPM at −5 ≤ x ≤ 5, t = 0.1.
Figure 8. Exact solution and VHPM at −5 ≤ x ≤ 5, t = 0.5.
Figure 9. Exact solution and VHPM at −50 ≤ x ≤ 50, t = 0.5.
Figure 10. Exact solution and VHPM at −50 ≤ x ≤ 50, t = 1.
Figure 11. Exact solution and VHPM at −50 ≤ x ≤ 50, t = 5.
Figure 12. Exact solution and VHPM at 0 ≤ x ≤ 50, t = 0.5.
Table 1. Comparing absolute error of ADM, HPM obtained [10] and present method with exact solution.
Table 2. Absolute error of VHPM with exact solution.
Table 3. Absolute error between VHPM and exactsolution.
Table 4. Absolute error between VHPM and exact solution.
analytical solutions for wide classes of nonlinear problems. They also do not require large computer memory. This method is reliable and manageable. The results show that:
・ As shown in (Table 1) VHPM is more accurate than ADM and HPM obtained [10] .
・ As shown in (Table 2) and (Figure 1, Figure 2, Figure 9, Figure 10 and Figure 12), when the time small in a wide space the solution by VHPM approaches to exact solution.
・ As shown in (Table 3) and (Figure 3, Figure 4, Figure 7 and Figure 8), when the time small in a small space the error decreases.
・ As shown in (Table 4) and (Figure 5, Figure 6 and Figure 11), when time increases in a wide space the error increases.
・ In general, whenever a space gets extended the error decreases and closer gets to zero.
Acknowledgements
The authors thank the University of Zakho for their support.
Cite this paper
Fadhil H.Easif,Saad A.Manaa,Bewar A.Mahmood,Majeed A.Yousif, (2015) Variational Homotopy Perturbation Method for Solving Benjamin-Bona-Mahony Equation. Applied Mathematics,06,675-683. doi: 10.4236/am.2015.64062
References
- 1. Wazwaz, A.M. (2005) Nonlinear Variants of KDV and Application to Thin Film Flow. Central European Journal of Physics, KP Equations with Compactons, Solitons and Periodic, 3, 648-653.
- 2. He, J.H. (1999) Variational Iteration Method—A Kind of Non-Linear Analytical Technique: Some Examples. International Journal of Non-Linear Mechanics, 34, 699-708.
http://dx.doi.org/10.1016/S0020-7462(98)00048-1 - 3. He, J.H. (1999) Homotopy Perturbation Technique. Computer Methods in Applied Mechanics and Engineering, 178, 257-262.
http://dx.doi.org/10.1016/S0045-7825(99)00018-3 - 4. Benjamin, T.B. (1974) Lectures on Nonlinear Wave Motion. Lecture Notes in Applied Mathematics, 15, 3-47.
- 5. Benjamin, T.B., Bona, J.L. and Mahony, J.J. (1972) Model Equations for Long Waves in Nonlinear Dispersive System. Philos. Trans. Soc., London S. R., A., 272, 47-78.
- 6. Wu, G.C. (2013) Challenge in the Variational Iteration Method—A New Approach to Identification of the Lagrange Multipliers. Journal of King Saud University, 25, 175-178.
http://dx.doi.org/10.1016/j.jksus.2012.12.002 - 7. He, J.H. (1997) A New Approach to Nonlinear Partial Differential Equations. Communications in Nonlinear Science and Numerical Simulation, 2, 230-235.
http://dx.doi.org/10.1016/S1007-5704(97)90007-1 - 8. He, J.H. (1999) Homotopy Perturbation Technique. Computer Methods in Applied Mechanics and Engineering, 178, 257-262.
http://dx.doi.org/10.1016/S0045-7825(99)00018-3 - 9. Muhammad, A.N. and Syed, T.M. (2008) Variational Homotopy Perturbation Method for Solving Higher Dimensional Initial Boundary Value Problems. Mathematical Problems in Engineering, Article ID: 696734, 11 p.
- 10. Hasan, B., Mehmet, H.B., Seyma, T. and Tojga, A. (2011) A Comparison between HPM and ADM for the Nonlinear Benjamin-Bona-Mahony Equation. International Journal of Basic and Applied Science, 11, 117-127.

















