Applied Mathematics
Vol.06 No.02(2015), Article ID:53792,8 pages
10.4236/am.2015.62025
Energy Identities of ADI-FDTD Method with Periodic Structure
Rengang Shi1,2, Haitian Yang3
1Department of Applied Mathematics, Dalian University of Technology, Dalian, China
2College of Science, China University of Petroleum, Qingdao, China
3Department of Engineering Mechanics, Dalian University of Technology, Dalian, China
Email: srg831@163.com, haitian@dlut.edu.cn
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 January 2015; accepted 28 January 2015; published 4 February 2015
ABSTRACT
In this paper, a new kind of energy identities for the Maxwell equations with periodic boundary conditions is proposed and then proved rigorously by the energy methods. By these identities, several modified energy identities of the ADI-FDTD scheme for the two dimensional (2D) Maxwell equations with the periodic boundary conditions are derived. Also by these identities it is proved that 2D-ADI-FDTD is approximately energy conserved and unconditionally stable in the discrete L2 and H1 norms. Experiments are provided and the numerical results confirm the theoretical analysis on stability and energy conservation.
Keywords:
Stability, Energy Conservation, ADI-FDTD, Maxwell Equations

1. Introduction
The alternative direction implicit finite difference time domain (ADI-FDTD) methods, proposed in [1] [2] , are interesting and efficient methods for numerical solutions of Maxwell equations in time domain, and cause many researchers’ work since ADI-FDTD overcomes the stability constraint of the FDTD scheme [3] . For example, it was proved by Fourier methods in [4] -[8] that the ADI-FDTD methods are unconditionally stable and have reasonable numerical dispersion error; Reference [9] studied the divergence property; Reference [10] studied ADI-FDTD in a perfectly matched medium; Reference [11] gave an efficient PML implementation for the ADI-FDTD method. By Poynting’s theorem, Energy conservation is an important property for Maxwell equations and good numerical method should conform it. In 2012, Gao [12] proposed several new energy identities of the two dimensional (2D) Maxwell equations with the perfectly electric conducting (PEC) boundary conditions and proved that ADI-FDTD is approximately energy conserved and unconditionally in the discrete L2 and H1 norms. Is there any other structure which can keep energy conservation for Maxwell equations? Is there any other energy identity for ADI-FDTD method? This two interesting questions promote us to find other energy- conservation structure.
In this paper, we focus our attention on structure with periodic boundary conditions and propose energy identities in L2 and H1 norms of the 2D Maxwell equations with periodic boundary conditions. We derive the energy identities of ADI-FDTD for the 2D Maxwell equations (2D-ADI-FDTD) with periodic boundary conditions by a new energy method. Several modified energy identities of 2D-ADI-FDTD in terms of the discrete L2 and H1 norms are presented. By these identities it is proved that 2D-ADI-FDTD with the periodic boundary conditions is unconditionally stable and approximately energy conserved under the discrete L2 and H1 norms. To test the analysis, experiments to solve a simple problem with exact solution are provided. Computational results of the energy and error in terms of the discrete L2 and H1 norms confirm the analysis on the energy conservation and the unconditional stability.
The remaining parts of the paper are organized as follows. In Section 2, energy identities of the 2D Maxwell equations with periodic conditions in L2 and H1 norms are first derived. In Section 3, several modified energy identities of the 2D-ADI-FDTD method are derived, the unconditional stability and the approximate energy conservation in the discrete L2 and H1 norms are then proved. In Section 4, the numerical experiments are presented.
2. Energy Conservation of Maxwell Equations and 2D-ADI-FDTD
Consider the two-dimensional (2D) Maxwell equations:
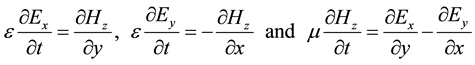 (2.1)
(2.1)
in a rectangular domain with electric permittivity ε and magnetic permeability μ, where ε and μ are positive constants; 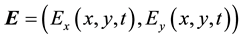 and
and 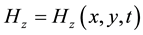 denote the electric and magnetic fields,
denote the electric and magnetic fields, 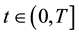 ,
, .
.
We assume that the rectangular region Ω is surrounded by periodic boundaries, so the boundary conditions can be written as
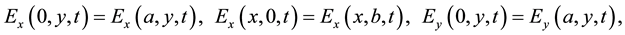 (2.2)
(2.2)
 (2.3)
(2.3)
We also assume the initial conditions
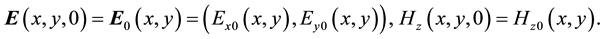 (2.4)
(2.4)
It can be derived by integration by parts and the periodic boundary conditions (2.2)-(2.3) that the above Maxwell equations have the energy identities:
Lemma 2.1 Let  and
and 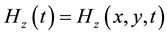 be the solution of the Maxwellsystems (2.1)-(2.4). Then
be the solution of the Maxwellsystems (2.1)-(2.4). Then
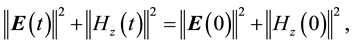 (2.5)
(2.5)
where and in what follows,  denotes the L2 norm with the weights ε (corresponding electric field) or µ (magnetic field). For example,
denotes the L2 norm with the weights ε (corresponding electric field) or µ (magnetic field). For example,
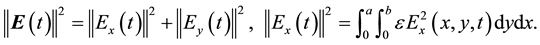 (2.6)
(2.6)
Identity (2.5) is called the Poynting Theorem and can be seen in many classical physics books. Besides the above energy identities, we found new ones below.
Theorem 2.2 Let 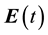 and
and  be the solution of the Maxwell systems (2.1)-(2.4), the same as those in Lemma 2.1. Then, the following energy identities hold
be the solution of the Maxwell systems (2.1)-(2.4), the same as those in Lemma 2.1. Then, the following energy identities hold
 (2.7)
(2.7)

where u = x or y, and 





Proof. First, we prove Equation (2.7) with u = x. Differentiating each of the Equations in (2.1) with respect to x leads to

By the integration by parts and the periodic boundary conditions (2.2)-(2.3), we have

where

Multiplying the Equations (2.9) by




From (2.1) and the boundary conditions (2.2)-(2.3) we note that

So,

The 2D-ADI-FDTD Scheme
The alternating direction implicit FDTD method for the 2D Maxwell equations (denoted by 2D-ADI-FDTD) was proposed by (Namiki, 1999). For convenience in analysis of this scheme, next we give some notations. Let
where Δx and Δy are the mesh sizes along x and y directions, ∆t is the time step, I, J and N are positive integers. For a grid function
where u = x, y or t. For


Other norms:



the approximations of 

Stage 1:



Stage 2:



For simplicity in notations, we sometimes omit the subscripts of these field values without causing any ambiguity. By the definition of cross product of vectors, the boundary conditions for (2.2)-(2.3) become

where 



3. Modified Energy Identities and Stability of 2D-ADI-FDTD in H1 Norm
In this Section we derive modified energy identities of 2D-ADI-FDTD and prove its energy conservation and unconditional stability in the discrete H1 norm.
Theorem 3.1 Let




where for

Proof. First we prove (3.1). Applying 






Multiplying both sides of the equations, (3.3)-(3.4) by 




Applying summation by parts, we see that

where we have used that 


So, if summing each of the Equalities (3.9)-(3.11) over their subscripts, adding the updated equations, multiplying both sides by ΔxΔy, and using the two identities, (3.12) and (3.13), together with the norms defined in Subsection 2.2, we arrive at

Similar argument is applied to the second Stage (3.6)-(3.8), we have

Combination of (3.14) and (3.15) leads to the identity (3.1). Identity (3.2) is similarly derived by repeating the above argument from the operated Equations (2.14)-(2.19) by
In the above proof, if taking 
Theorem 3.2 Let



Combining the results in Theorems 3.1 and 3.2 we have
Theorem 3.3 If the discrete H1 semi-norm and H1 norm of the solution of 2D-ADI-FDTD are denoted respectively by
then, the following energy identities for 2D-ADI-FDTD hold


Remark 3.4 It is easy to see that the identities in Theorems 3.1, 3.2 and 3.3converge to those in Lemma 2.1 and Theorem 2.2 as the discrete step sizes approach zero. This means that2D-ADI-FDTD is approximately energy-conserved and unconditionally stable in the modified discrete form of the L2 and H1 norms.
4. Numerical Experiments
In this section we solve a model problem by 2D-ADI-FDTD, and then test the analysis of the stability and energy conservation in Section 3 by comparing the numerical solution with the exact solution of the model. The model considered is the Maxwell equations (2.1) with


lution is:
It is easy to compute the norms of this solution are
4.1. Simulation of the Error and Stability
To show the accuracy of 2D-ADI-FDTD, we define the errors:
where


where log is the logarithmic function.
Table 1 gives the error and relative error of the numerical solution of the model problem computed by 2D- ADI-FDTD in the norms, and the convergence rates with different time step sizes Δt = 4h, 2h and h, when Δx = Δy = h = 0.01 is fixed and T = 1. From these results we see that the convergence rate of 2D-ADI-FDTD with respect to time is approximately 2 and that 2D-ADI-FDTD is unconditionally stable (when Δt = Δx = Δy = h,
the CFL number
Table 2 lists the similar results to Table 1 when Δt = 0.1h is fixed, Δx = Δy varies from 2h, h and 0.5h, and the time length T = 1. From the columns “Rate” we see that 2D-ADI-FDTD is of second order in space under the discrete L2 and H1 norm.
4.2. Simulation of the Energy Conservation of 2D-ADI-FDTD
In this subsection we check the energy conservation of 2D-ADI-FDTD by computing the modified energy norms derived in Section 3 for the solution to the scheme. Denote these modified energy norms by
In Table 3 are presented the energy norms 

Table 1. Error of 
Table 2. Error of 
Table 3. Energy of 
5. Conclusion
In this paper, the modified energy identities of the 2D-ADI-FDTD scheme with the periodic boundary conditions in the discrete L2 and H1 norms are established which show that this scheme is approximately energy conserved in terms of the two energy norms. By the deriving methods for the energy identities, new kind of energy identities of the Maxwell equations are proposed and proved by the new energy method. Numerical experiments are provided and confirm the analysis of 2D-ADI-FDTD.
References
- Namiki, T. (1999) A New FDTD Algorithm Based on Alternating-Direction Implicit Method. IEEE Transactions on Microwave Theory and Techniques, 47, 2003-2007. http://dx.doi.org/10.1109/22.795075
- Zheng, F., Chen, Z. and Zhang, J. (2000) Toward the Development of a Three-Dimensional Unconditionally Stable Finite- Difference Time-Domain Method. IEEE Transactions on Microwave Theory and Techniques, 48, 1550-1558. http://dx.doi.org/10.1109/22.869007
- Yee, K. (1966) Numerical Solution of Initial Boundary Value Problems Involving Maxwell’s Equations in Isotropic Media. IEEE Transactions on Antennas and Propagation, 14, 302-307. http://dx.doi.org/10.1109/TAP.1966.1138693
- Namiki, T. and Ito, K. (2000) Investigation of Numerical Errors of the Two-Dimensional ADI-FDTD Method [for Maxwell’s Equations Solution]. IEEE Transactions on Microwave Theory and Techniques, 48, 1950-1956. http://dx.doi.org/10.1109/22.883876
- Zheng, F. and Chen, Z. (2001) Numerical Dispersion Analysis of the Unconditionally Stable 3D ADI-FDTD Method. IEEE Transactions on Microwave Theory and Techniques, 49, 1006-1009. http://dx.doi.org/10.1109/22.920165
- Zhao, A.P. (2004) Consistency of Numerical Dispersion Relation Expressed in Different Forms for the ADI-FDTD Method. Microwave and Optical Technology Letters, 40, 12-13. http://dx.doi.org/10.1002/mop.11272
- Garcia, S.G., Rubio, R.G., Bretones, A.B. and Martin, R.G. (2006) On the Dispersion Relation of ADI-FDTD. IEEE Microwave and Wireless Components Letters, 16, 354-356. http://dx.doi.org/10.1109/LMWC.2006.875619
- Fu, W. and Tan, E.L. (2007) Stability and Dispersion Analysis for ADI-FDTD Method in Lossy Media. IEEE Transactions on Antennas and Propagation, 55, 1095-1102. http://dx.doi.org/10.1109/TAP.2007.893378
- Smithe, D.N., Cary, J.R. and Carlsson, J.A. (2009) Divergence Preservation in the ADI Algorithms for Electromagnetics. Journal of Computational Physics, 228, 7289-7299. http://dx.doi.org/10.1016/j.jcp.2009.06.025
- Gedney, S.D., Liu, G., Roden, J.A. and Zhu, A. (2001) Perfectly Matched Layer Media with CFS for an Unconditional Stable ADI-FDTD Method. IEEE Transactions on Antennas and Propagation, 49, 1554-1559. http://dx.doi.org/10.1109/8.964091
- Wang, S. and Teixeira, F.L. (2003) An Efficient PML Implementation for the ADI-FDTD Method. IEEE Microwave and Wireless Components Letters, 13, 72-74. http://dx.doi.org/10.1109/LMWC.2003.808705
- Gao, L. (2012) Stability and Super Convergence Analysis of ADI-FDTD for the 2D Maxwell Equations in a Lossy Medium. Acta Mathematica Scientia, 32, 2341-2368. http://dx.doi.org/10.1016/S0252-9602(12)60184-2




















