Received 25 August 2014; revised 20 September 2014; accepted 12 October 2014

ABSTRACT

We show that the non-linear semi-quantum Hamiltonians which may be expressed as 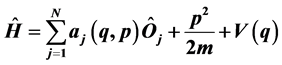(where 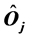is the set of generators of some Lie algebra and 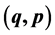are the classical conjugated canonical variables) always close a partial semi Lie algebra under commutation and, because of this, it is always possible to integrate the mean values of the quantum degrees of freedom of the semi-quantum non-linear system in the fashion: 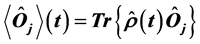(where 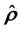is the Maximum Entropy Principle density operator) and, so, these kind of Hamiltonians always have associated dynamic invariants which are expressed in terms of the quantum degrees of freedom’s mean values. Those invariants are useful to characterize the kind of dynamics (regular or irregular) the system displays given that they can be fixed by means of the initial conditions imposed on the semi-quantum non-linear system.

Keywords:

Non-linear semiquantum dynamics, Lie algebras, Maximum entropy principle

1. Introduction

There exists certain kind of semiquantum non-linear systems which can be represented by the following Hamiltonian [1] -[3]

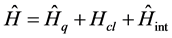, (1)

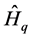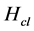where and stand for the pure quantum and pure classical parts of the system, respectively, and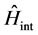

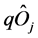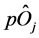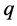is an interaction term where a classical interacts with a quantum one in the fashion or; and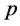

being the classical canonically conjugated variables of position and momentum, respectively, and 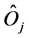is an ar-

bitrary quantum operator. Many of the systems given by Equation (1) may be expressed as a linear superposition

of quantum operators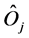, as follows:

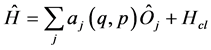, (2)

where the coefficients belonging to the linear superposition, , may (or may not) contain the classical degrees of freedom. We refer to them as non-linear systems, the non-linearity being given only by the interaction between a classical and a quantum variable. The Hamiltonians (2) exhibit some advantages that make them easy to tackle by means of the Maximum Entropy Principle approach (MEP). Indeed, 1) as the classical degrees of freedom act as they were parameters in the quantum commutation operation [3] , then Equation (2), for adequate operators, closes a partial Lie algebra under commutation with the generators of some Lie algebra, 2) as a consequence of the algebra’s closure, it is always possible to obtain the Maximum Entropy statistical operator as prescribed by Alhassid & Levine in [4] , which enables us to integrate the system’s quantum degrees

of freedom in the fashion. This also allows for the integration of the mean value of the semi-

quantum Hamiltonian given by Equation (2), , provided that it is a linear superposition of the

generators of some Lie algebra, 3) the mean value of the semiquantum Hamiltonian, is taken to coincide

with a Hamiltonian function [2] [3] [5] [6] that, in turn, generates the temporal evolution of the classical degrees of freedom and, 4) accordingly, since some Lie algebra has been associated to the semiquantum system, it will be possible to derive some dynamic invariants which, in turn, can be expressed in terms of the mean val-

ues, , of the quantum degrees of freedom, 5) these dynamic invariants are of help so as to

study the dynamics of these systems, that generally display two kind of regimes: regular and irregular. Such regimes can be differentiated by means of the values that the invariants adopt (and these values are fixed by the initial conditions imposed on the system). The interested reader may consult [3] and [5] to see how the invariants are used to study the classical limit of a semiquantum system [5] , and how the value of a special invariant, the uncertainty principle, may serve as an indicator of regular or irregular regime [3] . The purpose of the present review is to derive the invariants of the motion exhibited by a semiquantum system as a consequence of the algebra’s closure, illustrating things with reference to several interesting systems.

The paper is organized as follows: Section 2 introduces the basic tools of MEP approach. In Section 3, we focus attention on the specific Hamiltonian representation of semiquantum non-linear systems. In Section 4, we apply MEP tools to our semiquantum non-linear systems and integrate the quantum degrees of freedom. In Section 5, we show how the general dynamics invariants emerge out of the algebra’s closure and derive the specific dynamic invariants associated to SU(2), Heisenberg, SO(2,1), and SU(1,1) Lie algebras. Finally, some conclusions are drawn in Section 6.

2. Maximum Entropy Principle Formalism Tools

The description of the quantum state of a system is made by means of the density or statistical operator [4] [7] [8] while, the entropy associated to the state is defined as [4] [7]

. (3)

According to Jayne’s Information Theory [9] [10] , the statistical operator is constructed starting from the knowledge of the expectation values of operators termed as the “relevant” constraints

(4)

where the subindex 0 refers to the normalization condition

(5)

given that the identity operator must be included in order to fulfill condition, Equation (5). As it was

established by Alhassid & Levine [4] , the constraints must be linearly independent but not necessarily commuting ones. The statistical operator that maximizes the entropy is given by [4]

(6)

which is expressed in terms of Lagrange multipliers. is the one associated to the identity operator which must be included into the relevant set in order to fulfill the normalization condition given in Equation (5). Thus, is obtained as

(7)

The normalized statistical operator of maximal entropy given by Equation (6) enables one to obtain the en-

tropy at the maximum as (replacing Equation (6) into Equation (3)) [4]

. (8)

The statistical operator, its surprisal, , as well as any analytical function f of follow the same equation of motion [4]

(9)

where is the Hamiltonian of the system which may or may not explicitly depend on time. Alhassid &

Levine in [4] prescribed a procedure to specify the statistical operator of maximum entropy for any time. Departing from an initial state of maximum entropy at, given by Equation (6), they determined that, in order for Equation (6) to be valid for all time (i.e. in order for Equation (6) be an exact solution of Equation (9)), there must exist a set of relevant operators (termed as the constraints) that fulfill the well-known closure condition [4]

(10)

“so that the equation of motion of the density operator has thus been converted to a set of coupled equations of motion for the Lagrange parameters. The number of coupled equations equals the number of constraints” [4] .

(11)

“the boundary conditions of the equation of motion are determined by the requirement that the initial state

be the state of maximum entropy, Equation (6), subject to the constraints” [4] ( see Equations (4)).

As a consequence of the fact that the statistical operator obeys Equation (9), the entropy (8) is a constant of the motion, i.e.

(12)

for any two times,. In [11] , Equation (12) has been used to derive the time evolution of the expectation values of the constraints generated by Equation (19), so as to obtain

. (13)

Equation (13) is known as the generalized Eherenfest theorem. Finally, one can obtain the mean values of the relevant operators for all times as [4]

. (14)

3. Hamiltonian Representation of Physical Semiquantum Systems

Semiquantum Hamiltonians are often found in the literature [1] [3] [5] [6] [12] - [22] . In [12] , L. E. Ballentine defines a semi-quantum system as:

“one composed by a quantum part coupled to a classical part. The essential structure of all these models is a classical part acting directly on the quantum part, with the quantum part reacting back on the classical part through the expectation value of some observable [...] we refer to a system as semiquantum if one part is treated classically and the other part quantum mechanically” [12] .

Thus, the Hamiltonian representing a semi-quantum system may be expressed in the form given by Equation

(1) [1] - [3] where and stand for the quantum and classical parts of the system respectively and

is an interaction term coupling quantum and classical degree of freedom. This term makes the system (1)

to be a non-linear one. The semiquantum Hamiltonians we are interested in are those in which the part is

given by a linear superposition of, say, quantum operators, , that are the generators of some Lie alge-

bra. These quantum operators are the quantum degrees of freedom of the semiquantum system. The classical degrees of freedom are the canonical conjugate variables and. The interaction term, , is generally

cast as so that the and terms must be expressed as a linear superposition of the generators of

some Lie algebra. Thus, Equation (1) (or its equivalent Equation (2)) may be re-written in the fashion [3]

(15)

where the first term includes the and terms, the classical variables are contained in the

coefficients, and the second term is a purely classical one. Semiquantum Hamilto-

nians are used to model some nanotechnology devices (like molecular transistors, nanotubes, quantum dots and SQUIDS, for instance [20] ) because they can be thought of as quantum billiards in which a quantum particle of mass, confined in a potential well (generated by a classical mass) undergoes elastic interactions

[20] [23] . Accordingly, the classical part of Hamiltonian given by Equation (15) has the form,

where represents the quantum particle’s mass, its classical momentum and its classical position.

The Maximum Entropy Principle Approach (MEP) is able to generate a semiquantum formalism to deal with semi-quantum non-linear Hamiltonians like Equation (15) for which a set of relevant operators is invoked so as to fulfill the closure condition expressed in Equation (10) (the generators of some Lie algebra). This formalism was developed in [1] - [3] [5] and, in the following, we are going to outline it.

4. Maximum Entropy Approach to Semiquantum Systems

Let us consider a mixed physical system represented by the semiquantum Hamiltonian represented by Equation (15) with a coupling term [1] [12] [20] [24] - [26] . As the classical degrees of freedom act like as if they were parameters, the Hamiltonian given by Equation (15) may be cast as [3] [23]

, (16)

with the identity. As the Hamiltonian (16) may be expressed as a linear superposition of some Lie algebra’s generators, we speak of a partial Lie algebra under commutation with if the commutator of with any of the generators can be expressed as a linear superposition of these generators [3] [4] [23]

(17)

With the coefficients of such linear superposition. The semiquantum closure condition defines a

matrix. The terms in Equation (16) may involve the system’s classic degrees of

freedom. Since the identity operator commutes with the Hamiltonian, the classical term does not appear in the final result of the quantum commutation operation given by Equation (17). Accordingly, it is possible to generalize the prescription given by Alhassid & Levine in [4] for the semi-quantum case, i.e., to find the sufficient number of required constraints of the kind given by Equation (4) so as to obtain a statistical operator of maximum entropy like in Equation (6) valid for any time t and still retain the maximum entropy statistical operators’ form given by Equation (6) even for the semi-quantum case. Introduce now the surprisal

(18)

into the Equation (9) of motion. The time dependence of is contained only in the Lagrange parameters. The quantum operators do not depend explicitly on time in Schrödinger representation [4] , so

, and we regain Alhassid & Levine’s expression

(19)

where is the non-linear semi-quantum Hamiltonian given by Equation (16) which may or may not explicitly depend upon time. Equation (18) is an exact solution of Equation (9) if the set of constraints fulfill the semi-quantum closure condition (17) [3] . As in [4] , we replace Equation (17) into Equation (19) and, as the relevant operators generated by Equation (17) are linearly independent, we obtain [3]

. (20)

Thus, the equation of motion for the density operator (9) has been converted into a set of coupled Equation (20). Nevertheless, there exist a difference with respect to the full quantum case of [4] : while the set of Equation (11) is a set of coupled linear equations, Equation (20) correspond to a set of non-linear coupled equations since the coefficients may contain the classical degrees of freedom and. On the other side, for the mean values of the system's quantum degrees of freedom we obtain [3] [11]

. (21)

The normalization Equation (5) enables us to obtain the Lagrange parameter in a completely similar way as in the full quantum case (see Equation (7)). defines the differentiable manifold

(22)

where the’s appearing in it obeys the non-linear Equations of motion (21).

The integration of non-linear semiquantum differential Equation (21) can be accomplished in the fashion

(23)

exclusively on account of the fact it was possible to close the algebra by means of Equation (17) as we will show in the following [23] [27] . If we take the time derivative of Equation (23), we obtain

. (24)

Since in the Schrödinger representation the quantum operators do not depend on time explicitly, all the time

dependence is contained in the MEP density operator through the time dependence of the Lagrange pa-

rameters. Accordingly, from Equation (24) we obtain (see also Equation (9))

. (25)

Take now into account the invariance of the trace under commutation operation [4] [28]

(26)

Finally, taking into account the semi-quantum closure condition, Equation (17), we can replace the operator

and then Equation (26) adopts the form

(27)

which is the generalized Ehrenfest theorem given by Equation (21). In short, if we are able to close a semi Lie algebra under commutation with the semiquantum non-linear Hamiltonian (16), then we can integrate the equations of motion of the quantum degrees of freedom even though the Hamiltonian exhibits a nonlinearity via the

[23] .

Equation (23) can also be written in the fashion [4]

. (28)

The density operator of maximum entropy may be used to calculate the mean value of the Hamiltonian given by Equation (16)

(29)

and the entropy at the maximum acquires the form

(30)

and is a constant of the motion [3] [4] .

Summing up: as it is possible to close a semi Lie algebra under commutation with the non-linear semiquantum Hamiltonian, Equation (16), it is also possible to obtain the maximum entropy density operator, Equation (6). This density operator enables us to integrate the quantum degrees of freedom in the way given by Equation (23). A consequence of the algebra’s closure is that the semiquantum Hamiltonian exhibits certain kinds of motion invariants closely related to the Lie algebra associated to the system through Equation (17). These motion invariants always may be expressed in terms of the quantum degrees of freedom's mean values given by Equation (23).

Concerning the system's classical degrees of freedom, the energy is taken to coincide with the quantum expectation value of the semiquantum Hamiltonian [1] [2] [6] [17] [21] given by Equation (29) and the temporal evolution of the classical variables is given by [2] [3]

, (31)

. (32)

Thus, the semiquantum non-linear dynamics displayed by Hamiltonians of the type given by Equation (16) may be represented in a semiquantum phase space

(33)

whose dimension is with quantum variables that are linearly independent plus 2 classical ones. In this semiquantum phase space, the quantum mean values span the quantum manifold of the system

whose dimension is and, the classical variables span the classical ma-

nifold of the system whose dimension is 2. One has [3] .

5. Lie Algebras and Motion Invariants

Non-linear dynamics of semiquantum Hamiltonians of the type given by Equation (16), exhibits two kinds of invariants: 1) general dynamic invariants [29] which are independent on the specific Lie algebra invoked to close the algebra. These invariants appear only as a consequence of just having closed the algebra, 2) the second kind of dynamic invariants does depend upon the Lie algebra associated to the Hamiltonian given by Equation (16) once we have closed the algebra by means of Equation (17).

5.1. General Dynamic Invariants: The Second Order Centered Invariant

The density operatorand its surprisal obey the Liouville Equation (9) of motion [4] . Moreover,

they obey a special case of Equation (9) which is

(34)

and holds for any positive integer. In [29] , it has been demonstrated that, from Equation (34) it is possible to obtain the following dynamic invariant

. (35)

Taking into account that

(36)

the invariant given by Equation (35) may be expressed as

(37)

where the’s are the generators of some Lie algebra obtained through the Equation (17) (whose mean values obey the evolution non-linear Equation (21)) and the’s are their associated Lagrange multipliers (which evolve according to the non-linear Equations (20)).

We are interested in the particular form which the former invariant acquires for the case

(38)

in terms of the so-called quantum correlation coefficients [30] belonging to a set of non-commuting

quantum operators

. (39)

Equation (21) enables us to obtain the non-linear evolution equation for the quantum correlation coefficients

. (40)

The motion invariant given by Equation (38) is the so-called second order centered invariant of [29] [31] and its value can be fixed through the initial conditions imposed on the system by means of Equations (20) and (21). Our interest in the particular case given by Equation (38) lies in the fact that it is possible to demonstrate that Equation (38) represents a positive definite quadratic form [32] . Accordingly, the quantum correlation matrix

(whose elements are defined through Equation (39)) is a positive definite matrix and it can be

associated to an inner product (see [31] for more details).

Any non-linear semiquantum Hamiltonian of the type given by Equation (16) which fulfills the closure condi-

tion (17) with the generators of some Lie algebra exhibits the second order centered invariant (38) as a

dynamic invariant. This is of importance because, from it, it is possible to recover the generalized uncertainty principle [3] [33] that must be obeyed by the system's quantum degrees of freedom. This uncertainty relation is obtained as the summation over the principal minors of order 2 belonging to the correlation matrix. In fact, for any pair of non-commuting operators belonging to the relevant set and generated by Equation (17), the uncertainty relation always holds [30]

(41)

The left hand side of Equation (41) is a principal minor of order 2 belonging to the correlation matrix,

where. Keeping in mind that through Equation (17) we are able to find a finite set of

non-commuting operators, we can define the following expression, which is obtained as the summation over the

principal minors of order 2 belonging to the metric matrix [33] - [35]

(42)

We call Equation (42) the generalized uncertainty principle [33] , valid for a set of non-commuting operators. Equation (42) is a direct consequence of the algebra's closure given by Equation (10). Through it one generates a set of non-commuting operators termed “the relevant set of operators” [4] which, in turn, are the generators of some Lie algebra.

The uncertainty principle given by Equation (42) imposes strong constraints on the system and avoids the making of wrong choices for the initial conditions in their semiquantum non-linear equations of motion.

5.2. Invariants Associated to the Anti-Symmetry of Matrix G

The semiquantum closure condition (17) defines a matrix whose elements are the coefficients

. When this matrix is an anti-symmetric one, the semiquantum system given by Equation (16) exhibits

a particular kind of dynamic invariants that we will enumerate in the following.

Let be the set of relevant quantum operators which arises from the semiquantum closure

Equation (17) (i.e. the generators of some Lie algebra). We define the operator where

and are two operators belonging to the relevant set. It is easy to see that and.

On the other side, the closure Equation (17) enables us to obtain the following commutation relations [34]

(43)

(44)

where the are the coefficients of matrix. Making use of Equations (21) and taking into account Equations (43) and (44), we obtain the temporal evolution equations [3] [33]

, (45)

(46)

(47)

Equations (45) and (46) and (43) and (47) have terms that couple quantum and classical degrees of freedom. With the help of these equations it is possible to demonstrate that the anti-symmetry of matrix is a sufficient condition for the existence of the following dynamic invariants [3] [34]

· The invariant [5] [34]

(48)

· The Bloch “hypersphere” invariant [34]

(49)

· The invariant [34]

, (50)

· The invariant [34]

(51)

· The summation over the principal minors of order belonging to the correlation matrix [34] :

The summation over the principal minors of order belonging to the correlation matrix gives

the coefficients of the secular equation of the correlation matrix [3] [35]

(52)

where. For the sake of clarity we will illustrate things for the case (i.e. if we have a relevant

set composed only by non-commuting operators)

1) case [34]

(53)

2) case [34]

(54)

3) case [34]

(55)

With.

The methodology to demonstrate that the expressions given by Equations (53) to (55) are invariants is the same for all of them. We restrict ourselves to the case of invariant related to the generalized uncertainty principle (GUP) of [3] [33] (see Equation (42) (the interested readers can find those demonstrations on [34] ). If we take time derivative on Equation (54), we obtain [23] [33]

(56)

From Equation (56) it can be seen that if matrix is an anti-symmetric one, then the quantity is an invariant of the motion and this invariant turns out to be the generalized uncertainty principle (see Equation (42)).

5.3. The SU(2) Lie Algebra Invariants

It is well-known that is a basis of the SU(2) algebra. The operators fulfill the following commuta-

tion rules [36] .

, (57)

where are the generators of SU(2). When the SU(2) Lie algebra is associated to the Hamiltonian given by Equation (16), it adopts the form

, (58)

Proposition 1: If a set of operators, which fulfills the commutation relation, Equation (57), closes a commutation algebra with a Hamiltonian of the type given by Equation (58), then the semiquantum matrix of the system, defined by means of the closure condition, Equation (17), is an anti-symmetric one [34] .

Every Hamiltonian that closes an algebra with the SU(2) generators is accompanied by the invariants given by Equations (48) to (55). Some examples of these Hamiltonians (58) are:

· Spin 1/2 particle interacting with the classical harmonic oscillator [3] [14]

(59)

and are the classical canonically conjugated variables, are spin operators, is the external magnetic field’s frequency, is the classical harmonic oscillator’s frequency and its mass. The non-linear term is where is the coupling constant between classical and quantum degrees of freedom. Equation (17) yields to the following anti-symmetric matrix

(60)

· Spin 1/2 particle interacting with a biquadratic oscillator [12] [37]

(61)

and are the classical canonically conjugated variables, are spin operators, is the external mag-

netic field's frequency, the classical mass. The non-linear term is where is the coupling con-

stant between classical and quantum degrees of freedom. Equation (17) yields to the following anti-symmetric

matrix

(62)

· Spin 1/2 particle interacting with the double well [26]

. (63)

Equation (17) yields to the following anti-symmetric matrix

.(64)

Note that Equations (59), (61) and (63) give rise to anti-symmetric matrices given by Equations (60), (62) and (64), they all exhibit the dynamic invariants given by Equations (48) to (55). Particularly, the dynamic invariants given by Equations (53), (54) and (55) adopts the forms respectively [3] [34]

, (65)

, (66)

(67)

with. The invariant given by Equation (66) is the left hand side the uncertainty

principle (42), so and, i.e., the uncertainty principle for the SU(2)

Lie algebra, that can be expressed in the guise

(68)

defining the celebrated Bloch sphere of the system. The quantum degrees of freedom’s mean values can be obtained from the density operator [38]

(69)

with, , and

(see [3] for more details). The quantum degrees of freedom are integrated

by means of, and we obtain [33]

, (70)

, (71)

. (72)

In virtue of Equations (70)-(72), we can obtain the relationship [33]

(73)

corresponding to the invariant (see Equation (51)) and the invariant given by Equation (49).

5.4. The Heisenberg Group Invariants

The Heisenberg group closes a partial Lie algebra with Hamiltonians of the form [34]

(74)

i.e. Hamiltonians that are quadratic in and, where. The matrix which arises

from Equation (17) has the following form [34]

. (75)

The correlation matrix's characteristic polynomial has two coefficients:

, (76)

, (77)

but only is an invariant of the motion as we will see below. There exists non-linear semiquantum Ha-

miltonians of the type given by Equation (74) which close a partial Lie algebra with:

· The Hamiltonian representing the production of charged meson pairs [5] [18]

(78)

With, are canonically conjugated classical while and are quantum operators of position and

momentum respectively and, while is a constant. The Hamiltonian of Equation (78) is refe-

renced in literature as representative of the zeroth mode contribution of an strong external field to the production of charged meson pairs [18] [39] [40] . The Hamiltonian given by Equation (78) may be cast in the following fashion

(79)

where is a pure classical term and is a nonlinear interaction term given that a clas-

sical variable and a quantum one are coupled. The corresponding matrix is

(80)

· The generalized harmonic oscillator [41]

Let us consider the following generalized harmonic oscillator Hamiltonian [42]

(81)

where. If is a function of canonically conjugated classical variables or (i.e.

or, the system given in Equation (81) turns out to be a semi-quantum one and its cor-

responding matrix is

. (82)

Proposition 2: Let us have generators which close a partial Lie algebra under commuta-

tion with a semiquantum Hamiltonian. If the closure condition, Equation (17), gives rise to a

matrix such that, then the correlation matrix’s determinant is an invariant of the motion.

Proof: The correlation matrix’s determinant is

. (83)

If we take time derivative in Equation (83) and use Equation (40), we obtain

(84)

As since the correlation matrix is a definite positive one, it is easy to see that if

then is a dynamic invariant of the system.

As matrices and have null traces, then the non-linear semiquantum Hamiltonians (see Equation (79)) and (see Equation (81)) share the following dynamic invariant: the uncertainty relation

. (85)

The quantum degrees of freedom's mean values were integrated as, were the

density operator is [23] [42]

(86)

where: and, are the creation and annihilation operators respec-

tively (see [23] [42] and references therein for more details) and

. (87)

5.5. The SO(2,1) Lie Algebra Invariants

We revisit now the Hamiltonian given by Equation (79) and the generators of the SO(2,1) Lie algebra,

, given by the commutation relations [43] [44]

, (88)

, (89)

. (90)

Let us define

(91)

(92)

(93)

such that and

(94)

. (95)

Accordingly, the Hamiltonian from Equation (79) may be recast as

(96)

so that the commutation relations

, (97)

, (98)

(99)

lead to the following antisymmetric semi-quantum matrix

(100)

which enables us to obtain the semi-quantum non-linear equations of motion

(101)

(102)

. (103)

Taking into account Equations (99) and/or Equation (103), we can easily see that

(104)

is an invariant of the motion when the Hamiltonian (79) is associated to the SO(2,1) Lie algebra. Further, as the matrix given by Equation (100) is an antisymmetric one, we can ensure the invariance of the principal minors of order, 2 and 3, belonging to the covariant metric tensor which, respectively, read

, (105)

, (106)

, (107)

With and. Notice that the invariant (106) is the left

hand side of the generalized uncertainty principle, Equation (42) which, for this particular case, remains as a constant of the motion.

5.6. The SU(1,1) Lie Algebra Invariants

Let’s consider again the Hamiltonian [5] [18]

(108)

With, are canonically conjugated classical while and are quantum operators of position and

momentum respectively and, while is a constant. The Hamiltonian given by Equation (108)

is referenced in literature as representative of the zeroth mode contribution of an strong external field to the production of charged meson pairs [18] [39] [40] . The Hamiltonian given by Equation (108) may be recast as

(109)

where is a pure classical term and, , is a nonlinear interaction term given that the

classical position variable and a quantum one are coupled. It is known [42] the harmonic oscillator

closes a partial Lie algebra either with the Heisenberg group or with the SU(1,1)

one. Thus, as it was done in [42] , we select the operators belonging to these algebras

as relevant operators.From the semi-quantum closure condition, Equation (17),

we obtain the following semi-quantum matrix [23]

(110)

which is a block diagonal one, i.e. we see how the subspaces corresponding to the Heisenberg and SU(1.1) algebras are independent one from each other.

Making use of Equations (20), (21), (31) and (32) we obtain the equations of motion for the quantum (mean values and s) and classical degrees of freedom [5]

, (111)

, (112)

, (113)

, (114)

, (115)

, (116)

, (117)

Information Theory tells us that the statistical operator is [42]

. (118)

The inclusion of the Hamiltonian into the relevant set does not modify the dynamics of the system but transforms it in a thermodynamic one (see [42] and [45] for more details). In order to achieve the required diagonalization of the statistical operator, we express the relevant set in terms of the creation and annihilation operators

and }, with [28] . One writes

, (119)

, (120)

, (121)

, (122)

, (123)

, (124)

with

. (125)

If we replace Equations (119)-(124) into Equation (118) (the reader may find in [23] [42] the details of the diagonalization of the density operator), one finds

(126)

with

(127)

and

(128)

with. In virtue of Equation (126), it is possible to integrate the quantum degrees of freedom of the

system and write [23] [42]

, (129)

, (130)

, (131)

, (132)

(133)

With. As the matrix given by Equation (110) is a block diagonal one, we can consider the

sub-matrix associated to the Heisenberg group

(134)

which is the same as that given by Equation (75) (a null trace one), so, the the dynamic invariant

reappears here (see Equation (85)). Notice that

this invariant was used in [5] to analyze the classical limit of the system given by Equation (108). Concerning the second block matrix

(135)

we are going to see that it corresponds to the SU(1,1) Lie algebra. In fact, lets consider first the quantum opera-

tors [46] , , which fulfill the following SU(1,1) commutation relation

, (136)

, (137)

, (138)

As in [46] , if we introduce the vector operator components

, (139)

one has

. (140)

On the other side, remembering that

, (141)

, (142)

, (143)

we can make the identification, , so that the set

is that of the generators of the SU(1,1) Lie algebra. Thus, the Casimir operator cor-

responding to the SU(1,1) Lie algebra [46]

(144)

may be expressed in terms of, , and operators as

. (145)

It is easy to see that the Casimir operator given by Equation (145) commutes with the semiquantum Hamiltonian given by Equation (108). Accordingly, this Hamiltonian exhibits an SU(1,1) structure and the following dynamic invariant

. (146)

It is also possible to demonstrate the invariance of Equation (146), making use of Equations (21) and (17) (within the MEP context).

6. Conclusion

We have discussed properties of non-linear semi-quantum Hamiltonians of the form

are, are the generators of some Lie algebra. and are classical

conjugated canonical variables. We saw that this Hamiltonian always closes a partial Lie algebra under commutation with the. As a consequence, we were able to integrate the mean values of the quantum degrees of freedom of our systems in the fashion; using as the Maximum Entropy Principle’s density operator. It was

seen that these Hamiltonians are always associated to dynamic invariants, which are expressed in terms of

the quantum degrees of freedom’s mean values. These invariants were shown to be useful to

characterize the kind of dynamics that the system displays, as several examples have amply illustrated.

References