Applied Mathematics
Vol.5 No.11(2014), Article
ID:47062,13
pages
DOI:10.4236/am.2014.511161
Some Improvement on Convergence Rates of Kernel Density Estimator
Xiaoran Xie, Jingjing Wu
Department of Mathematics and Statistics, University of Calgary, Calgary, Canada
Email: xiaxie@ucalgary.ca, jinwu@ucalgary.ca
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 March 2014; revised 10 April 2014; accepted 18 April 2014
ABSTRACT
In this paper two kernel density estimators are introduced and investigated. In order to reduce bias, we intuitively subtract an estimated bias term from ordinary kernel density estimator. The second proposed density estimator is a geometric extrapolation of the first bias reduced estimator. Theoretical properties such as bias, variance and mean squared error are investigated for both estimators. To observe their finite sample performance, a Monte Carlo simulation study based on small to moderately large samples is presented.
Keywords:Kernel Density Estimation, Geometric Extrapolation, Bias Reduction, Mean Squared Error, Convergence Rate

1. Introduction
Many efforts have been devoted to investigating the optimal performance of kernel density estimator since it has been the most widely used nonparametric method in the last decades. Suppose we use  to denote the kernel estimator of the true density function
to denote the kernel estimator of the true density function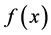 . Normally we use mean squared error (MSE) and its two components, namely bias and variance, to quantify the accuracy of an estimator. Note that the MSE of
. Normally we use mean squared error (MSE) and its two components, namely bias and variance, to quantify the accuracy of an estimator. Note that the MSE of  is decomposed into two parts:
is decomposed into two parts:

There have been numerous literatures that discuss approaches to improving the performance of kernel estimators, while reducing the bias has been the most commonly considered one. Article [1] obtained the best asymptotic convergence rate 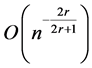 of MSE for orthogonal kernel estimators. Article [2] introduced geometric extrapolation of nonnegative kernels, while [3] discussed the number of vanishing moments of kernel order using Fourier transformation. Variable kernel estimation in [4] successfully reduced the bias by employing larger smoothing parameters in low density regions, while [5] introduced the idea of inadmissible kernels which also results in reduced bias. On the other hand, [6] proposed an estimator using some probabilistic arguments which achieves the goal of bias reduction. Article [7] suggested a locally parametric density estimator, a semiparametric technique, which effectively reduces the order of bias. Article [8] proposed algorithms relevant to quadratic polynomial and
of MSE for orthogonal kernel estimators. Article [2] introduced geometric extrapolation of nonnegative kernels, while [3] discussed the number of vanishing moments of kernel order using Fourier transformation. Variable kernel estimation in [4] successfully reduced the bias by employing larger smoothing parameters in low density regions, while [5] introduced the idea of inadmissible kernels which also results in reduced bias. On the other hand, [6] proposed an estimator using some probabilistic arguments which achieves the goal of bias reduction. Article [7] suggested a locally parametric density estimator, a semiparametric technique, which effectively reduces the order of bias. Article [8] proposed algorithms relevant to quadratic polynomial and  cumulative distribution function (c.d.f.) which accommodates possible poles at boundaries and in consequence reduces the bias at boundaries. Article [9] introduced a bias reduction method using estimated c.d.f. via smoothed kernel transformations. Article [10] introduced a two-stage multiplicative bias corrected estimator. Article [11] developed a skewing method to reduce the bias while the variance is only increased by a moderate constant factor. In addition, some recent works discussed approaches of obtaining smaller bias of the estimator via several other methods. Article [12] worked out a bias reduced kernel relative to the classical kernel estimator via Lipschitz condition. Article [13] introduced an adjusted kernel density estimator in which the kernel is adapted to the data but not fixed. This method naturally leads to an adaptive-choice of the smoothing parameters which can reduce the bias.
cumulative distribution function (c.d.f.) which accommodates possible poles at boundaries and in consequence reduces the bias at boundaries. Article [9] introduced a bias reduction method using estimated c.d.f. via smoothed kernel transformations. Article [10] introduced a two-stage multiplicative bias corrected estimator. Article [11] developed a skewing method to reduce the bias while the variance is only increased by a moderate constant factor. In addition, some recent works discussed approaches of obtaining smaller bias of the estimator via several other methods. Article [12] worked out a bias reduced kernel relative to the classical kernel estimator via Lipschitz condition. Article [13] introduced an adjusted kernel density estimator in which the kernel is adapted to the data but not fixed. This method naturally leads to an adaptive-choice of the smoothing parameters which can reduce the bias.
Although the variance reduction method is not as approachable as the bias reduction method, there still have been a lot of scholars working on it. Article [14] suggested an approach to reduce the variance in local linear regression employing the idea of the skewing method. Article [15] also used the skewing method on bias reduction and variance reduction at the same time which in turn reduces the MSE.
Many of above mentioned bias reduction methods result in complex kernel density estimators. In this paper, we introduce a novel but intuitive and feasible bias reduced kernel density estimator. In Section 2, we present the bias reduced estimator and investigate its asymptotic bias, variance and MSE. A second estimator is proposed and studied in Section 3 as a geometric extrapolation of the bias reduced kernel. To examine the finite sample performance of both estimators, a simulation study is carried out in Section 4. Finally some remarks are given in Section 5.
2. A Bias Reduced Kernel Estimator
Kernel density estimator was first introduced in [16] and [17] . Suppose 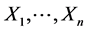 is a simple random sample from the unknown density function f. Let K be a function on real line, i.e. the “kernel”, and let h be a positive value, i.e. the “bandwidth”. Then the kernel density estimator of f is defined as
is a simple random sample from the unknown density function f. Let K be a function on real line, i.e. the “kernel”, and let h be a positive value, i.e. the “bandwidth”. Then the kernel density estimator of f is defined as
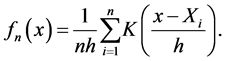 (2.1)
(2.1)
To make the estimator meaningful, the kernel function is usually required to satisfy conditions ,
,  and
and . Both [18] and [19] pointed out that if
. Both [18] and [19] pointed out that if  and f is twice continuously differentiable in a neighborhood of x, then
and f is twice continuously differentiable in a neighborhood of x, then
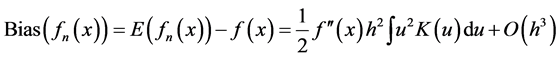 (2.2)
(2.2)
and
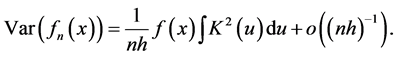 (2.3)
(2.3)
Then from (2.2) and (2.3) we have
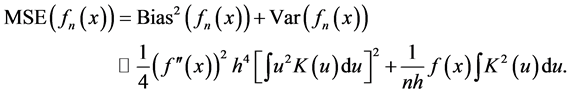
We can easily see that the optimized bandwidth is 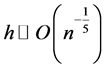 and then the optimal MSE is of the order
and then the optimal MSE is of the order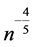 .
.
In order to reduce the bias of ordinary kernel density estimator, we can intuitively subtract the leading bias term 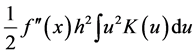 in (2.2) from it. Since the leading term of the bias is unavailable due to the unknown f, we can simply use its estimation, i.e.
in (2.2) from it. Since the leading term of the bias is unavailable due to the unknown f, we can simply use its estimation, i.e.
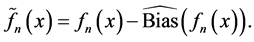
One could use any type of estimation of the bias term. We could simply replace f with the kernel estimator fn since it is readily available. As a result, our proposed estimator is
 (2.4)
(2.4)
From the way of construction, this new estimator should be able to reduce the bias and thus the MSE. To see whether this is the case or not, we next calculate the bias and the variance of . We make the following regularity condition on f, K and h:
. We make the following regularity condition on f, K and h:
1)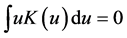 .
.
2)  is fourth differentiable in a neighbourhood of x.
is fourth differentiable in a neighbourhood of x.
3) 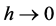 and
and 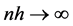 as
as .
.
Theorem 2.1. Under 1), 2) and 3),
 (2.5)
(2.5)
and
 (2.6)
(2.6)
Consequently,
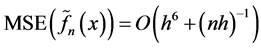
and the optimal MSE is of the order  with
with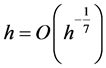 .
.
Proof. By Taylor expansion we have
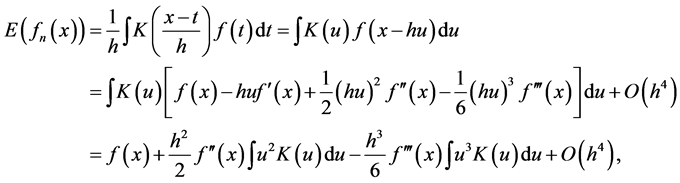
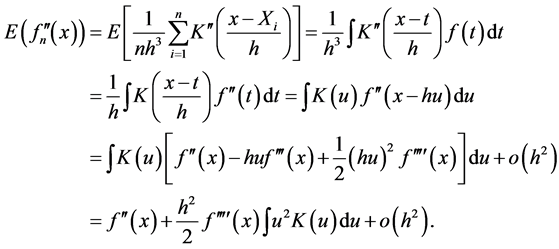 (2.7)
(2.7)
Thus we have
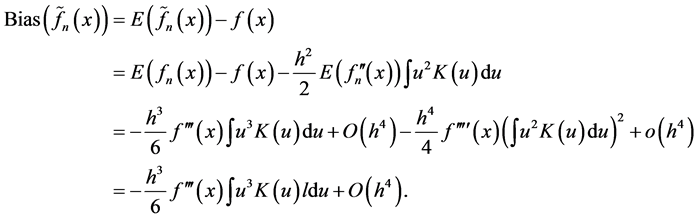 (2.8)
(2.8)
On the other hand,
 (2.9)
(2.9)
Note that (2.7) gives
 (2.10)
(2.10)
Finally (2.9) and (2.10) together with (2.3) gives (2.6). Remark 2.1. From Theorem 2.1 we can see that if K is symmetric, i.e. , then all the odd moments of K are zero and, as a result, the bias of
, then all the odd moments of K are zero and, as a result, the bias of 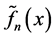 will be improved to a higher order of
will be improved to a higher order of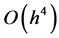 . In this case, the optimal MSE is further reduced to
. In this case, the optimal MSE is further reduced to 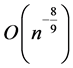 with
with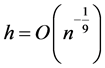 .
.
Remark 2.2. From the definition of  in (2.4), this estimator could be possibly negative on some points x. In order to make it meaningful in practice, i.e. make it a positive density estimator, one can use the following variation of the proposed bias deducted estimator
in (2.4), this estimator could be possibly negative on some points x. In order to make it meaningful in practice, i.e. make it a positive density estimator, one can use the following variation of the proposed bias deducted estimator

where 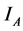 is an indicator function that takes value one on set A and zero otherwise. Note that the first term on the right hand side of Equation (2.4) converges to
is an indicator function that takes value one on set A and zero otherwise. Note that the first term on the right hand side of Equation (2.4) converges to  in probability, while the second term is of the order
in probability, while the second term is of the order
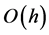 , which goes to zero as
, which goes to zero as  under 3). Thus
under 3). Thus  converges to
converges to 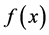 in probability, and as a result
in probability, and as a result  is positive in probabililty at any point
is positive in probabililty at any point  with
with  the support of f. Therefore,
the support of f. Therefore,  has similar performance and properties as
has similar performance and properties as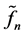 , especially when sample size is large.
, especially when sample size is large.
3. A Geometric Extrapolated Kernel Estimator with Bias Reduction
Geometric extrapolation was introduced in kernel density estimation by [2] . Consider the ordinary kernel density estimator with two different bandwidths h and 2h:
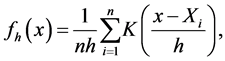

Suppose the kernel function K above is symmetric so that all the odd moments of K are zero. Article [2] proposed the following estimator
 (3.1)
(3.1)
Note that  doesn’t have integral one. In order to improve the MSE of order
doesn’t have integral one. In order to improve the MSE of order  of the ordinary kernel estimator, one has to relax the constraint of integrating to one. The powers
of the ordinary kernel estimator, one has to relax the constraint of integrating to one. The powers  and
and  are selected to reduce the bias of the ordinary kernel estimator to
are selected to reduce the bias of the ordinary kernel estimator to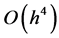 . Consequently, the MSE of
. Consequently, the MSE of 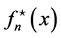 is improved to the order of
is improved to the order of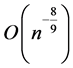 , which is a faster convergence rate than the rate
, which is a faster convergence rate than the rate  of the ordinary kernel estimator.
of the ordinary kernel estimator.
Instead of using the ordinary kernel estimator, we propose to use the bias reduced kernel estimator, presented in Section 2, in the construction of geometric extrapolated kernel (3.1). Denote the bias reduced kernel estimator with two bandwidths h and 2h as
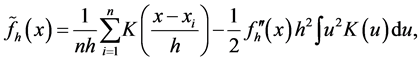

Now the geometric extrapolated kernel estimator with bias reduction is proposed as
 (3.2)
(3.2)
Since the bias reduced kernel estimator has improved bias and MSE over the ordinary kernel estimator, especially when K is symmetric, we expect that with geometric extrapolation it will achieve further improvement.
Theorem 3.1. Under 1), 2) and 3),

and

Consequently,
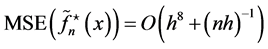
and the optimal MSE is of the order  with
with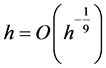 .
.
Proof. We calculate 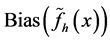 first. Similar argument to (2.8) gives
first. Similar argument to (2.8) gives

Let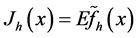 , then
, then
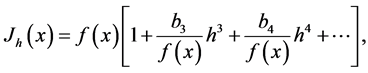 (3.3)
(3.3)
where

Taking logarithm of (3.3) gives
 (3.4)
(3.4)
Here we want to construct a geometric extrapolated kernel estimator of the form 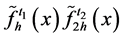 that possibly reduces the bias. In another word, we need
that possibly reduces the bias. In another word, we need  has term
has term 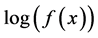 but has
but has  term disappear. Thus
term disappear. Thus  and
and  have to satisfy
have to satisfy
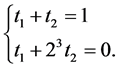
The solution to above equation system is 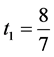 and
and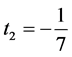 , and this gives our proposed estimator (3.2). Now
, and this gives our proposed estimator (3.2). Now
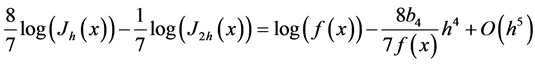
and a series expansion for exponential function gives
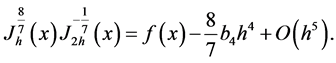 (3.5)
(3.5)
We rewrite

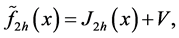
where U and V are both of order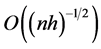 , and have expectations zero and variances and covariances of order
, and have expectations zero and variances and covariances of order . As a result,
. As a result,

and then
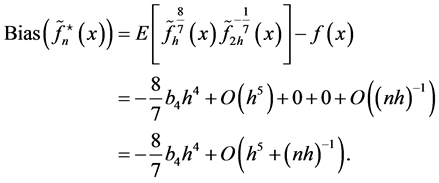
Since 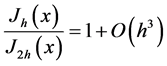 by (3.4), the variance of
by (3.4), the variance of 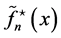 is
is

Remark 3.1. Article [2] proposed the geometric extrapolation of ordinary kernel estimator which results in optimal MSE of the order . Though here we achieve the same order of optimal MSE, we don’t impose the assumption that K is symmetric while [2] does.
. Though here we achieve the same order of optimal MSE, we don’t impose the assumption that K is symmetric while [2] does.
Remark 3.2. When K is symmetric, we propose another estimator
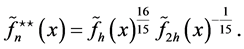
This estimator reduces the bias to 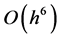 and has improved optimal MSE of the order
and has improved optimal MSE of the order 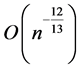 with
with .
.
4. Simulation Study
In this section, we carry out a simulation study designed to demonstrate the finite sample performance of the proposed bias reduced kernel estimator (BRK)  given in (2.4) and the proposed geometric extrapolation of bias reduced kernel estimator (GEBRK)
given in (2.4) and the proposed geometric extrapolation of bias reduced kernel estimator (GEBRK)  given in (3.2). Particularly, we compare their bias and MSE with the ordinary kernel density estimator (OK)
given in (3.2). Particularly, we compare their bias and MSE with the ordinary kernel density estimator (OK) 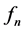 in (2.1) and the geometric extrapolation of ordinary kernel estimator (GEOK)
in (2.1) and the geometric extrapolation of ordinary kernel estimator (GEOK)  in (3.1).
in (3.1).
Without loss of generality, we suppose f is the standard normal density. We randomly select 1000 independent samples of size n = 20, 50, 100 or 200. We choose arbitrarily the points x = 0, 0.5, 1, 1.5, 2, 2.5 and 3 at which the kernel estimators are calculated and compared. Since the properties of kernel estimators do not depend much on which particular kernel is used, we choose the standard normal as the kernel function K without loss of generality. For the bandwidth h, we use the optimal one for each individual kernel estimator. In another word, since here K is symmetric, by Remarks 2.1 and 3.2, we choose 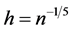 for OK,
for OK,  for both BRK and GEOK and
for both BRK and GEOK and  for GEBRK. The bias, variance and MSE are estimated respectively by
for GEBRK. The bias, variance and MSE are estimated respectively by


and
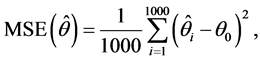
where 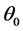 is the true parameter and
is the true parameter and 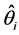 is the estimate value
is the estimate value 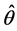 based on the i-th sample. In our case,
based on the i-th sample. In our case, 
 and
and  is either
is either ,
, 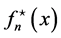 ,
,  or
or  for fixed x = 0, 0.5, 1, 1.5, 2, 2.5 or 3. The simulation results are presented in Tables 1-7.
for fixed x = 0, 0.5, 1, 1.5, 2, 2.5 or 3. The simulation results are presented in Tables 1-7.
From Tables 1-7 we can see that BRK consistently has smaller bias and MSE than OK except for x = 1. This is simply due to the fact that  which in turn reduces the bias of OK to
which in turn reduces the bias of OK to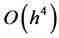 . Apparently this is of the same order as the bias of BRK, however this is a special case that is only true at point x = 1 here and the
. Apparently this is of the same order as the bias of BRK, however this is a special case that is only true at point x = 1 here and the
conclusion cannot be generalized. When the two estimators with geometric extrapolation are compared, GEBRK generally has smaller bias and MSE than GEOK, especially when sample size is large. When BRK and GEBRK are compared, GEBRK tends to have smaller variance and MSE but larger bias than BRK. In terms of bias, BRK and GEBRK perform much better than OK and GEOK while BRK and GEBRK are very competitive. Geometric extrapolation reduces the variance and MSE in general, i.e. GEOK and GEBRK perform better than OK and BRK in terms of variance and MSE. When MSE is concerned, GEBRK performs best and then GEOK. These observations are somehow different at point x = 1 due to the fact that 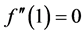 as mentioned above.
as mentioned above.
5. Concluding Remarks
In this paper, we first propose a very intuitive and feasible kernel density estimator which reduces the bias and MSE significantly compared with the ordinary kernel density estimator. Secondly, we construct a geometric extrapolation of the bias reduced kernel estimator which further improves the convergence rates of both bias and MSE. Our simulation study shows that for finite sample size both estimators perform competitively well and better than the ordinary kernel estimator and its geometric extrapolation.
For the bias reduced kernel density estimator presented in Section 2, we may find that part of the curve is under zero, especially at the tails. Taking standard normal density as an example, at point x = 4 the estimator may give a negative value. Apparently, this is unreasonable. Though in Remark 2.2 we suggest a modified version of the estimator, further work is necessary to deal with this problem.
Acknowledgements
The authors acknowledge with gratitude the support of this research by Discovery Grants from National Sciences and Engineering Research Council (NSERC) of Canada, and would like to thank the anonymous referees for their constructive comments.
References
- Farrell, R.H. (1972) On the Best Obtainable Asymptotic Rates of Convergence in Estimation of a Density Function at a Point. The Annals of Mathematics and Statistics, 43, 170-180. http://dx.doi.org/10.1214/aoms/1177692711
- Terrell, G.R. and Scott, D.W. (1980) On Improving Convergence Rates for Nonnegative Kernel Density Estimators. The Annals of Statistics, 8, 1160-1163. http://dx.doi.org/10.1214/aos/1176345153
- Hall, P. and Marron, J.S. (1988) Choice of Kernel Order in Density Estimation. The Annals of Statistics, 16, 161-173. http://dx.doi.org/10.1214/aos/1176350697
- Abramson, I.S. (1982) On Bandwidth Variation in Kernel Estimates—A Square Root Law. The Annals of Statistics, 10, 1217-1223. http://dx.doi.org/10.1214/aos/1176345986
- Samiuddin, M. and El-Sayyad, G.M. (1990) On Nonparametric Kernel Density Estimates. Biometrica, 77, 865-874. http://dx.doi.org/10.1093/biomet/77.4.865
- El-Sayyad, G.M., Samiuddin, M. and Abdel-Ghaly, A.A. (1992) A New Kernel Density Estimate. Journal of Nonparametric Statistics, 3, 1-11. http://dx.doi.org/10.1080/10485259308832568
- Cheng, M.Y., Choi, E., Fan, J. and Hall, P. (2000) Skewing Methods for Two-Parameter Locally Parametric Density Estimation. Bernoulli, 6, 169-182. http://dx.doi.org/10.2307/3318637
- Marron, J.S. and Ruppert, D. (1992) Transformations to Reduce Boundary Bias in Kernel Density Estimation. Journal of the Royal Statistical Society: Series B, 4, 653-671.
- Ruppert, D. and Cline, D.B.H. (1994) Bias Reduction in Kernel Density Estimation by Smoothed Empirical Transformations. The Annals of Statistics, 22, 185-210. http://dx.doi.org/10.1214/aos/1176325365
- Jones, M.C., Linton, O. and Nielsen, J.P. (1995) A Simple Bias Reduction Method for Density Estimation. Biometrica, 82, 327-338. http://dx.doi.org/10.1093/biomet/82.2.327
- Kim, C., Kim, W. and Park, B.U. (2003) Skewing and Generalized Jackknifing in Kernel Density Estimation. Communications in Statistics: Theory and Methods, 32, 2153-2162. http://dx.doi.org/10.1081/sta-120024473
- Mynbaev, K. and Martins-Filho, C. (2010) Bias Reduction in Kernel Density Estimation via Lipschitz Condition. Journal of Nonparametric Statistics, 22, 219-235. http://dx.doi.org/10.1080/10485250903266058
- Srihera, R. and Stute, W. (2011) Kernel Adjusted Density Estimation. Statistics and Probability Letters, 81, 571-579. http://dx.doi.org/10.1016/j.spl.2011.01.013
- Cheng, M.Y., Peng, L. and Wu, S.H. (2007) Reducing Variance in Univariate Smoothing. The Annals of Statistics, 35, 522-542. http://dx.doi.org/10.1214/009053606000001398
- Kim, J. and Kim, C. (2013) Reducing the Mean Squared Error in Kernel Density Estimation. Journal of the Korean Statistical Society, 42, 387-397. http://dx.doi.org/10.1016/j.jkss.2012.12.003
- Rosenblatt, M. (1956) Remarks on Some Nonparametric Estimates of a Density Function. The Annals of Mathematical Statistics, 27, 832-837. http://dx.doi.org/10.1214/aoms/1177728190
- Parzen, E. (1962) On Estimation of a Probability Density Function and the Mode. The Annals of Mathematical Statistics, 33, 1065-1076. http://dx.doi.org/10.1214/aoms/1177704472
- Silverman, B.W. (1986) Density Estimation for Statistics and Data Analysis. Chapman & Hall, London. http://dx.doi.org/10.1007/978-1-4899-3324-9
- Wand, M.P. and Jones, M.C. (1995) Kernel Smoothing. Chapman & Hall, London. http://dx.doi.org/10.1007/978-1-4899-4493-1


