Applied Mathematics
Vol.5 No.7(2014), Article ID:44812,8 pages DOI:10.4236/am.2014.57102
Special Numbers on Analytic Functions
Yilmaz Simsek
Department of Mathematics, Faculty of Science, University of Akdeniz, Antalya, Turkey
Email: ysimsek@akdeniz.edu.tr
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 30 January 2014; revised 28 February 2014; accepted 9 March 2014
ABSTRACT
The aim of this paper is to give some analytic functions which are related to the generating functions for the central factorial numbers. By using these functions and p-adic Volkenborn integral, we derive many new identities associated with the Bernoulli and Euler numbers, the central factorial numbers and the Stirling numbers. We also give some remarks and comments on these analytic functions, which are related to the generating functions for the special numbers.
Keywords:Bernoulli Numbers, Euler Numbers, The Central Factorial Numbers , Array Polynomials, Stirling Numbers of the First Kind and the Second Kind, Generating Function, Functional Equation, Analytic Functions

1. Introduction, Definitions and Preliminaries
Throughout this paper, we use the following standard notations:
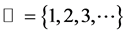 ,
,  and
and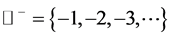 . Here,
. Here,  denotes the set of integers,
denotes the set of integers, 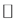 denotes the set of real numbers and
denotes the set of real numbers and  denotes the set of complex numbers. We assume that
denotes the set of complex numbers. We assume that 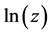 denotes the principal branch of the multi-valued function
denotes the principal branch of the multi-valued function 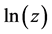 with the imaginary part
with the imaginary part  constrained by
constrained by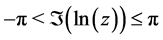 . Furthermore,
. Furthermore, 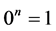 if
if , and,
, and, 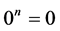 if
if .
.
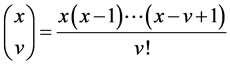
(cf. [1] -[19] ).
The generating functions have been used in many branches of Mathematics and Mathematical Physics. By using p-adic Volkenborn integral, analytic functions and these generating functions, we derive many functional equations and differential equations. By using these equations, we derive many new identities and combinatorics relations related to these numbers and polynomials.
The Stirling numbers of the first and the second are used in pure and applied Mathematics. The Stirling number of the second kind, denoted by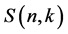 , is the number of ways to partition a set of
, is the number of ways to partition a set of  objects into
objects into  groups. These numbers occur in combinatorics and in the theory of partitions. The Stirling numbers of the second kind
groups. These numbers occur in combinatorics and in the theory of partitions. The Stirling numbers of the second kind  are defined by means of the following generating function:
are defined by means of the following generating function:
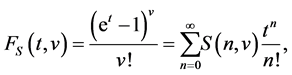
(cf. [1] -[19] ). These numbers are computed by the following formula:

or

From the above equation, one has

with

and  (
(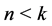 or
or ) (cf. [1] -[19] ).
) (cf. [1] -[19] ).
The Stirling numbers of the first kind  are defined by means of the following generating function:
are defined by means of the following generating function:
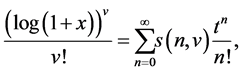
(cf. [19] ). These numbers are computed by the following formula:

From the above equation, one has

with
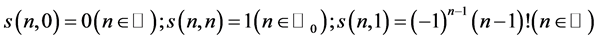
and 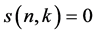 (
(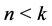 or
or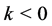 ) (cf. [19] ).
) (cf. [19] ).
The array polynomials  are defined by means of the following generating function:
are defined by means of the following generating function:
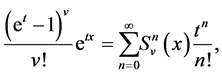
(cf. [1] [13] ).
From the above generating function, one has
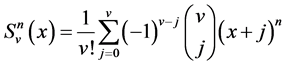
with
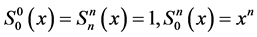
and for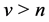 ,
, 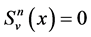 (cf. [1] [13] ).
(cf. [1] [13] ).
2. Identities and Relations on the Central Factorial Numbers 
In this section, we study on generating functions for the central factorial numbers 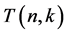 on analytic functions. By using these functions, we derive are some functional equations. Applying these functions and equations, we give some identities and relations related to the central factorial numbers
on analytic functions. By using these functions, we derive are some functional equations. Applying these functions and equations, we give some identities and relations related to the central factorial numbers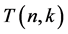 , which are defined by means of the following generating function (cf. [3] [19] ):
, which are defined by means of the following generating function (cf. [3] [19] ):
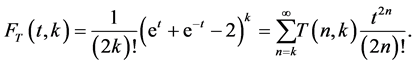 (2.1)
(2.1)
Srivastava and Liu [19] gave many properties and applications of the central factorial numbers.
In the work of Srivastava and Liu [19] , one has the following relations:
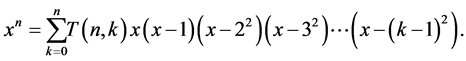
Combining the above equation with (1), we also have
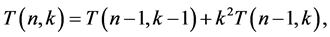
where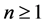 ,
, 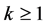 ,
, . For
. For ,
,  ,
, 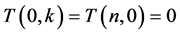 and
and  (cf. [19] ).
(cf. [19] ).
In [2] , Cigler gave the following formula for the numbers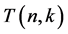 :
:

Some properties of the function 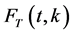 are given as follows:
are given as follows:
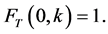
From this property, one has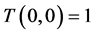 . The function
. The function 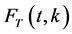 is related to the hyperbolic functions and generating functions for the special numbers. Thus we get the following functional equation:
is related to the hyperbolic functions and generating functions for the special numbers. Thus we get the following functional equation:
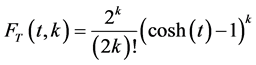
The function  is related to the generating function for the Stirling numbers of the second kind,
is related to the generating function for the Stirling numbers of the second kind, . That is
. That is
 (2.2)
(2.2)
where

and
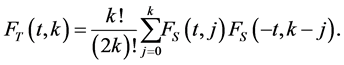 (2.3)
(2.3)
We are going to differentiate (1) with respect to 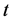 to derive a recurrence relation or identities for the central factorial numbers.
to derive a recurrence relation or identities for the central factorial numbers.
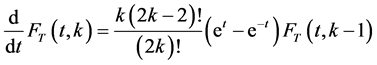 (2.4)
(2.4)
or
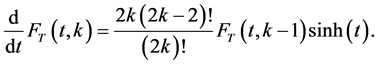 (2.5)
(2.5)
Lemma 1 ([9] , Lemma 11, Equation (7)]
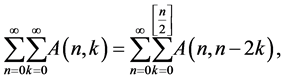
where 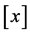 denotes the greatest integer function.
denotes the greatest integer function.
Remark 1 Lemma 1 was generalized by Srivastava et al. [16] . By using these generalization, one may generalize Theorem 1.
Theorem 1
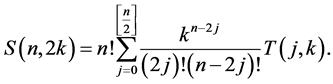
Proof. By combining (2) with (1), we get

By using Lemma 1, we obtain
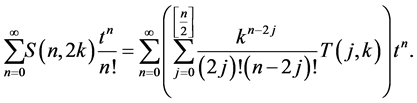
Comparing the coefficients of 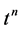 on both sides of the above equation, we arrive at the desired result. □
on both sides of the above equation, we arrive at the desired result. □
Theorem 2
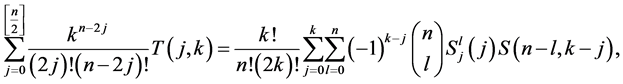
where 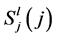 denotes the array polynomials.
denotes the array polynomials.
Proof. By using (3), we derive the following functional equation:
 (2.6)
(2.6)
where 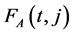 denotes generating function for the array polynomials
denotes generating function for the array polynomials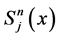 . By combining (2.6) with (2.1), we obtain
. By combining (2.6) with (2.1), we obtain
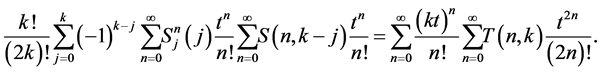
By using Lemma 1, we obtain

Comparing the coefficients of 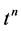 on both sides of the above equation, we arrive at the desired result. □
on both sides of the above equation, we arrive at the desired result. □
Remark 2 By using functional equation in (2.3), (2.4) and (2.5), one may also obtain an interesting identities and relationships between the Stirling numbers of the second kind and the central factorial numbers.
3. Identities Related to the p-Adic Volkenborn Integral and the Central Factorial Numbers
In this section, we give applications of the p-adic integral on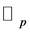 , set of p-adic integers. By using the Witt’s formula for the Bernoulli and Euler numbers related to the p-adic Volkenborn integral and the Mahler coefficients, we derive many interesting and novel identities associated with the central factorial numbers, the family of numbers
, set of p-adic integers. By using the Witt’s formula for the Bernoulli and Euler numbers related to the p-adic Volkenborn integral and the Mahler coefficients, we derive many interesting and novel identities associated with the central factorial numbers, the family of numbers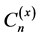 , the Stirling numbers of the first and the second kind and also combinatorics identities.
, the Stirling numbers of the first and the second kind and also combinatorics identities.
We use notations of the work of Kim [4] for the 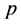 -adic
-adic  -Volkenborn integral. Let
-Volkenborn integral. Let 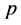 be a fixed prime. It is known that
be a fixed prime. It is known that

is a distribution on  for
for 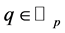 with
with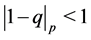 , cf. [4] . Let
, cf. [4] . Let 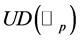 be the set of uniformly differentiable functions on
be the set of uniformly differentiable functions on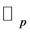 . The
. The 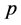 -adic
-adic 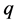 -integral of the function
-integral of the function  is defined by Kim [4] as follows:
is defined by Kim [4] as follows:
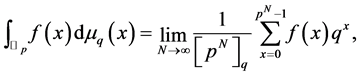
where

The bosonic 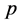 -adic integral (
-adic integral (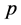 -adic Volkenborn integral) was considered from a physical point of view to the bosonic limit
-adic Volkenborn integral) was considered from a physical point of view to the bosonic limit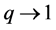 , as follows ([4] ):
, as follows ([4] ):
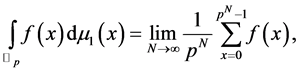 (3.1)
(3.1)
where

The  -adic
-adic 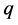 -integral is used in many branch of mathematics, mathematical physics and other areas (cf. [4] [11] [14] [18] ).
-integral is used in many branch of mathematics, mathematical physics and other areas (cf. [4] [11] [14] [18] ).
By using (7), we have the Witt’s formula for the Bernoulli numbers 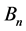 as follows:
as follows:
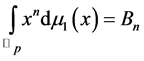 (3.2)
(3.2)
(cf. [4] [5] [11] [14] [18] ).
We consider the fermionic integral in contrast to the bosonic integral, which is called the fermionic 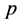 -adic Volkenborn integral on
-adic Volkenborn integral on 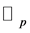 cf. [5] . That is
cf. [5] . That is
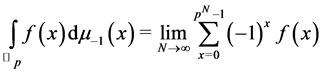 (3.3)
(3.3)
where
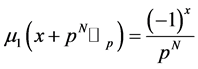
(cf. [5] ). By using (9), we have the Witt’s formula for the Euler numbers 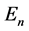 as follows:
as follows:
 (3.4)
(3.4)
(cf. [5] [6] [11] [18] ).
Theorem 3
 (3.5)
(3.5)
Proof of Theorem 3 was given by Schikhof [14] .
Theorem 4
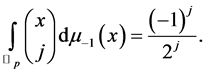
Proof of Theorem 4 was given by Kim et al. ([7] [8] ).
The family of numbers 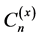 was defined by Srivastava and Liu [19] . These numbers are related to the Stirling numbers of the first and the second kind, which are given by the following theorem.
was defined by Srivastava and Liu [19] . These numbers are related to the Stirling numbers of the first and the second kind, which are given by the following theorem.
Theorem 5 ([19] , Theorem 1]) Let 
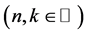 and
and
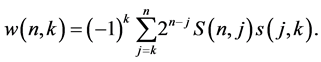
Then
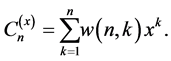 (3.6)
(3.6)
In [19] , Equation-(2.3)], Srivastava and Liu also gave the following relation:
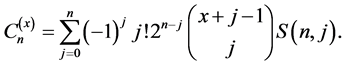 (3.7)
(3.7)
By using the above formulae, we derive the following identities related to the numbers , the Stirling numbers, the Bernoulli numbers and the Euler numbers.
, the Stirling numbers, the Bernoulli numbers and the Euler numbers.
According to the work of Kim at al. ([7] [8] ), we get
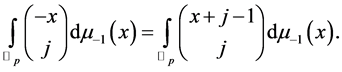
Combining Theorem 4 with the above equation, we get
 (3.8)
(3.8)
Integrating both sides of (3.7) with respect to the fermionic integral on , and than using (3.8), we obtain the following Lemma:
, and than using (3.8), we obtain the following Lemma:
Lemma 2

Integrating both sides of (3.6) with respect to the fermionic integral on , and than using (3.4), we obtain the following Lemma:
, and than using (3.4), we obtain the following Lemma:
Lemma 3
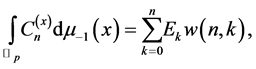
where  denotes the Euler numbers.
denotes the Euler numbers.
By using Lemma 2 and Lemma 3, we arrive at the following theorem:
Theorem 6

Similarly, according to the work of Kim et al. ([7] [8] ), we get

Combining Theorem 3 with the above equation, we get
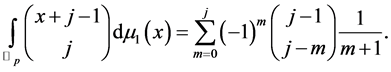 (3.9)
(3.9)
Integrating both sides of (3.7) with respect to the bosonic 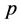 -adic integral on
-adic integral on , and than using (3.9), we obtain the following lemma:
, and than using (3.9), we obtain the following lemma:
Lemma 4
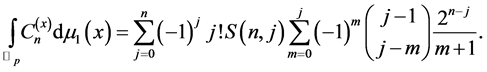
Integrating both sides of (3.6) with respect to the fermionic integral on , and than using (3.2), we obtain the following lemma:
, and than using (3.2), we obtain the following lemma:
Lemma 5

where 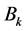 denotes the Bernoulli numbers.
denotes the Bernoulli numbers.
By using Lemma 4 and Lemma 5, we arrive at the following theorem:
Theorem 7
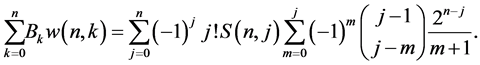
Acknowledgements
The paper was supported by the Scientific Research Project Administration of Akdeniz University.
References
- Chang, C.-H. and Ha, C.-W. (2006) A Multiplication Theorem for the Lerch Zeta Function and Explicit Representations of the Bernoulli and Euler polynomials. Journal of Mathematical Analysis and Applications, 315, 758-767. http://dx.doi.org/10.1016/j.jmaa.2005.08.013
- Cigler, J. Fibonacci Polynomials and Central Factorial Numbers. Preprint. http://homepage.univie.ac.at/johann.cigler/preprints/central-factorial.pdf
- Comtet, L. (1974) Advanced Combinatorics: The Art of Finite and Infinite Expansions. Reidel, Dordrecht and Boston, (Translated from the French by J. W. Nienhuys).
- Kim, T. (2002) q-Volkenborn integration. Russian Journal of Mathematical Physics, 19, 288-299.
- Kim, T. (2006) q-Euler Numbers and Polynomials Associated with p-Adic q-Integral and Basic q-zeta Function. Trends in International Mathematics and Science Study, 9, 7-12.
- Jang, L.C. and Kim, T. (2008) A New Approach to q-Euler Numbers and Polynomials. Journal of Concrete and Applicable Mathematics, 6, 159-168.
- Kim, D.S. and Kim, T. (2013) Daehee Numbers and Polynomials. Applied Mathematical Sciences, 7, 5969-5976.
- Kim, D.S., Kim, T. and Seo, J. (2013) A Note on Changhee Numbers and Polynomials. Advanced Studies in Theoretical Physics, 7, 993-1003.
- Rainville, E.D. (1960) Special Functions. The Macmillan Company, New York.
- Simsek, Y. (2010) On q-Deformed Stirling numbers. International Journal of Computer Mathematics, 15, 70-80.
- Simsek, Y. (2010) Complete sum of products of (h,q)-Extension of Euler Polynomials and Numbers. Journal of Difference Equations and Applications, 16, 1331-1348. http://dx.doi.org/10.1080/10236190902813967
- Simsek, Y. (2013) Identities Associated with Generalized Stirling Type Numbers and Eulerian Type Polynomials. Mathematical and Computational Applications, 18, 251-263.
- Simsek, Y. (2013) Generating Functions for Generalized Stirling type Numbers, Array Type Polynomials, Eulerian Type Polynomials and Their Applications. Fixed Point Theory and Applications, 87, 343-1355.
- Schikhof, W.H. (1984) Ultrametric Calculus: An Introduction to p-Adic Analysis. Cambridge Studies in Advanced Mathematics 4, Cambridge University Press, Cambridge.
- Srivastava, H.M. (2011) Some Generalizations and Basic (or q-) Extensions of the Bernoulli, Euler and Genocchi Polynomials. Applied Mathematics & Information Sciences, 5, 390-444.
- Srivastava, H.M., Ozarslan, M.A. and Kaanoğlu, C. (2010) Some Families of Generating Functions for a Certain Class of Three-Variable Polynomials. Integral Transforms and Special Functions, 21, 885-896. http://dx.doi.org/10.1080/10652469.2010.481439
- Srivastava, H.M. and Choi, J. (2012) Zeta and q-Zeta Functions and Associated Series and Integrals. Elsevier Science Publishers, Amsterdam, London and New York.
- Srivastava, H.M., Kim, T. and Simsek, Y. (2005) q-Bernoulli Numbers and Polynomials Associated with Multiple q-Zeta Functions and Basic L-Series. Russian Journal of Mathematical Physics, 12, 241-268.
- Srivastava, H.M. and Liu, G.-D. (2009) Some Identities and Congruences Involving a Certain Family of Numbers. Russian Journal of Mathematical Physics, 16, 536-542. http://dx.doi.org/10.1134/S1061920809040086

