Applied Mathematics
Vol.5 No.2(2014), Article ID:42165,7 pages DOI:10.4236/am.2014.52027
Fixed-Point Iteration Method for Solving the Convex Quadratic Programming with Mixed Constraints
Department of Mathematics & Physics, Beijing Institute of Petrochemical Technology, Beijing, China
Email: wangruopeng@bipt.edu.cn
Received October 24, 2013; revised November 24, 2013; accepted December 3, 2013
ABSTRACT
The present paper is devoted to a novel smoothing function method for convex quadratic programming problem with mixed constrains, which has important application in mechanics and engineering science. The problem is reformulated as a system of non-smooth equations, and then a smoothing function for the system of non-smooth equations is proposed. The condition of convergences of this iteration algorithm is given. Theory analysis and primary numerical results illustrate that this method is feasible and effective.
Keywords:Fixed-Point Iteration; Convex Quadratic Programming Problem; Convergence; Smoothing Function
1. Introduction
Consider the following convex quadratic programming problem
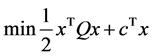
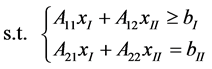 (1)
(1)
where 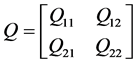 is an
is an  symmetrical positive semi-definite partitioned matrix,
symmetrical positive semi-definite partitioned matrix, 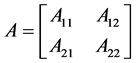 is an
is an 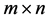 partitioned matrix,
partitioned matrix, 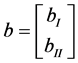 and
and 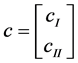 are vectors in
are vectors in  and
and 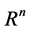 , respectively. And
, respectively. And 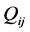 ,
,
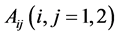 are the partitioned matrix of
are the partitioned matrix of 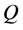 and
and 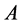 respectively.
respectively.
As is well known, this problem models a large spectrum of applications in computer science. Operation research and engineering as the nonlinear programming is solved eventually based on the convex quadratic programming problem. Therefore, the study on its effective solvers becomes a prolonged research subject.
Common effective algorithm is proposed related to certain schemes of convex quadratic programming problem, see [1-5]. Moreover, these methods are not polynomial algorithm in [6]. And the theory and algorithm of quadratic programming are presented completely. According to the optimization condition (KKT) and the duality theory of quadratic programming, the fixed-point iteration method is obtained for equality constrained (see [7]) and inequality constrained (see [8]) convex quadratic programming problem respectively. In fact, equality and inequality can be converted with inputting artificial variables and slack variables. The main default is to increase the scale and numerical difficulty while introduces these variables. Motivated by smoothing methods of
[9-11] and fixed-point method of [7,8], the paper mainly concerns about the mixed constraint quadratic programming and the fixed-point iteration method is given. And also the rank of the coefficient matrix is not full. The method considering is fulfilled efficiently. Thus the proposing question in [8] is solved.
2. Scheme of Algorithm
According to the dual theory, the dual problem of primal problem (1) is
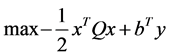
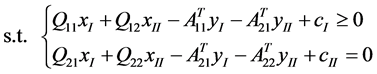 (2)
(2)
where .
.
Let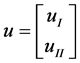 ,
,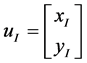 ,
,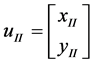 , we know if
, we know if 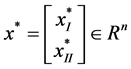 is the optimal solution of (1),there exists a vector
is the optimal solution of (1),there exists a vector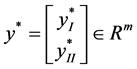 , an
, an 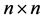 symmetrical positive semi-definite partitioned matrix, and
symmetrical positive semi-definite partitioned matrix, and 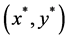 is the optimal solution of (2).
is the optimal solution of (2).
Let us define the following notation
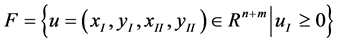
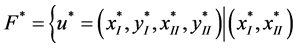 is the optimal solution of (1) and
is the optimal solution of (1) and 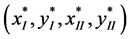 is the optimal solution of (2) }.
is the optimal solution of (2) }.
It is easy to verify that  is a close set.
is a close set.
Suppose that the feasible region  is not empty. A necessary and sufficient condition for a optimal solution is that:
is not empty. A necessary and sufficient condition for a optimal solution is that:
1) Primal feasibility
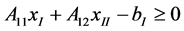

2) Dual feasibility
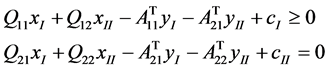
3) Complementary condition
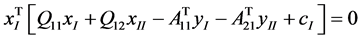
![]()
The scheme are rewritten below
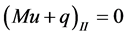
![]() (3)
(3)
Where
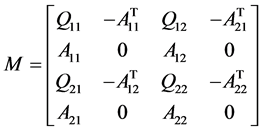
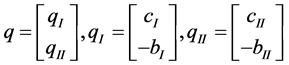
More formally, the following link fixed-point iteration problem is performed
 (4)
(4)
The component form is
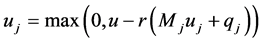 (5)
(5)
Where![]() .
.
The question (5) is non-smooth optimization problem, and the Newton-type methods cannot be applied directly. In the paper, we converted the problem into a smooth optimization.
At the beginning, we introduce a function mapping 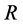 into
into 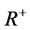 , and have the following properties.
, and have the following properties.
Property 1 Let 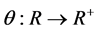 be a real function, and such that:
be a real function, and such that:
1) 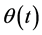 is strictly convex and differentiable;
is strictly convex and differentiable;
2)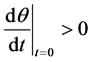 ;
;
3)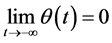 ;
;
4) 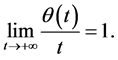
We assumed that 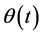 is a convex and differentiable function, which indicate one can apply the classical Newton-type algorithm directly. And the assumption
is a convex and differentiable function, which indicate one can apply the classical Newton-type algorithm directly. And the assumption 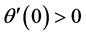 means that 0 is not a sub-gradient of
means that 0 is not a sub-gradient of ![]() at 0. The hypothesis (3) and (4) indicate the approximate function
at 0. The hypothesis (3) and (4) indicate the approximate function 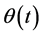 has the same numerical properties as the max-function.
has the same numerical properties as the max-function.
We consider the following function, and 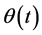 describe as above
describe as above
 (6)
(6)
For any  ,
, 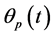 satisfies the following properties:
satisfies the following properties:
Theorem 1 Let be a function given as (6), then for any arbitrary 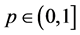 ,
,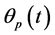 is strictly convex and differentiable, and we have
is strictly convex and differentiable, and we have 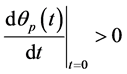 .
.
Proof According to property 1 and (6), the convexity and differentiability are straightforward.
Nothing that
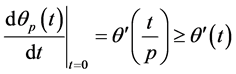
The property (2) implies 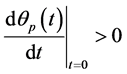 .
.
Theorem 2 Let ![]() be a function given as (6), then
be a function given as (6), then  . That is, the function
. That is, the function 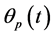 uniformly converges to the max-function, when the adjustable parameter
uniformly converges to the max-function, when the adjustable parameter ![]() approaches
approaches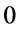 .
.
Proof For  fixed, we can compute
fixed, we can compute

If ![]() , then
, then 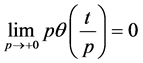 ; otherwise, change variable
; otherwise, change variable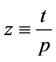 ,
,

Hence, 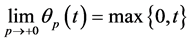 for all
for all .
.
From the discussion above, we introduce the following function in the paper
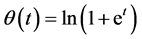
and
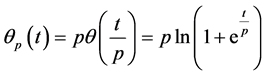
It is easily known that satisfies the properties (1) to (4), together with theorem 1 and 2. Thus, the max-function in (3) replaced by  , and the fixed-point iteration which basing on smoothing function is obtained.
, and the fixed-point iteration which basing on smoothing function is obtained.
Algorithm
Step 1 Set a initial point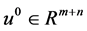 , choose
, choose ![]() ,
, 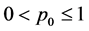 ,
,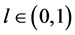 , let
, let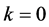 ;
;
Step 2 Apply fixed-point algorithms to solve

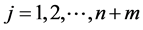 (7)
(7)
Step 3 Terminal condition: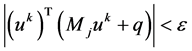 , stop; otherwise, go to Step 4;
, stop; otherwise, go to Step 4;
Step 4 Let 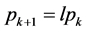 ,
, , go to step 2.
, go to step 2.
The Jacobian matrix in (7) is shown
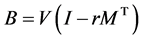 (8)
(8)
Where
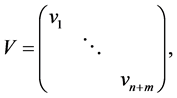
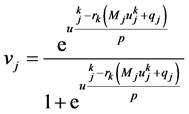
3. Convergence Analyses
Now we discuss the convergence of the algorithm. To begin with, two simple lemmas are introduced that is the basis of our theoretical analysis. Since their proof can be found in reference [12], we here omit the proof due to space.
Lemma 1 [12] A necessary and sufficient condition for the fixed-point iteration method to be convergent is that the spectral radius of Jacobian matrix B satisfies 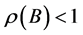 , where the spectral radius
, where the spectral radius 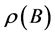 be defined as
be defined as
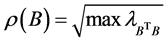 , and denotes the eigenvalue of matrix
, and denotes the eigenvalue of matrix 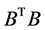 .
.
Lemma 2 [12] Suppose 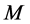 is a matrix, whose eigenvalues can be ordered from the smallest to largest, i.e.
is a matrix, whose eigenvalues can be ordered from the smallest to largest, i.e. 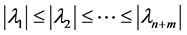 , and V is diagonal matrix with nonnegative diagonal elements, then the maximum norm of the matrix
, and V is diagonal matrix with nonnegative diagonal elements, then the maximum norm of the matrix ![]() ’s eigenvalue such that
’s eigenvalue such that .
.
Theorem 3 suppose 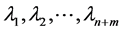 be the eigenvalues of the Jacobian matrix
be the eigenvalues of the Jacobian matrix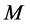 , if one of the following conditions is true, then we can select the proper parameter
, if one of the following conditions is true, then we can select the proper parameter 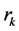 makes the algorithm convergent:
makes the algorithm convergent:
(1) The real part of ![]() is positive, that is
is positive, that is 
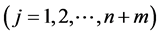 ;
;
(2) All of the eigenvalues 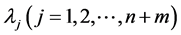 of matrix
of matrix  are real.
are real.
Proof Suppose 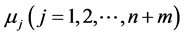 are eigenvalues of the Jacobian matrix in (8), and matrix
are eigenvalues of the Jacobian matrix in (8), and matrix ![]() eigenvalues denote as
eigenvalues denote as 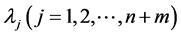 .
.
Let  (where
(where 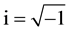 ).
).
Note that
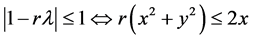
If ![]() , for all positive number of
, for all positive number of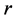 ; while
; while ![]() , we know
, we know 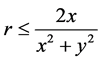 .
.
1) If 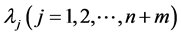 is positive, we let
is positive, we let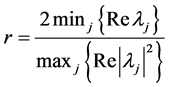 , and have
, and have 
 ;
;
2) If all of the eigenvalues  of matrix
of matrix  are real, we let
are real, we let 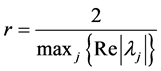 , and have
, and have 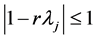
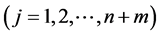 .
.
For all discussed above, associate with Lemma 1, we know that the matrix 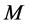 has the eigenvalues of
has the eigenvalues of 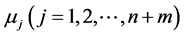 , such that
, such that
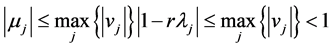
According to the theorem above, the algorithm is always convergent if the parameter 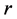 is chosen properly. Thus the recent relevant results in reference [8] are extended.
is chosen properly. Thus the recent relevant results in reference [8] are extended.
4. Numerical Experiment and Conclusion
In this section, we implement algorithm for solving system of inequalities in MATLAB7.0 in order to demonstrate the behavior of the algorithm. Due to page limit, we omit to test the effectiveness of our method in generating highly quadratic programming problems.
Example 1 Consider
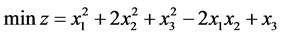
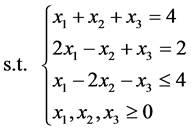
The exact optimal solution is  , and the optimal value of objective function is
, and the optimal value of objective function is 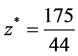 .
.
Example 2 Consider
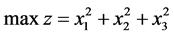

The exact optimal solution is 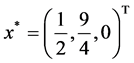 , and the optimal value of objective function is
, and the optimal value of objective function is 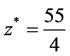 .
.
The results are shown in Table1
From the table, we can see that the algorithm is very simple and only applies the traditional fixed-point method. The implementation of this algorithm is rather easy.
Example 3 Consider
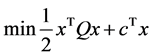
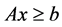
And
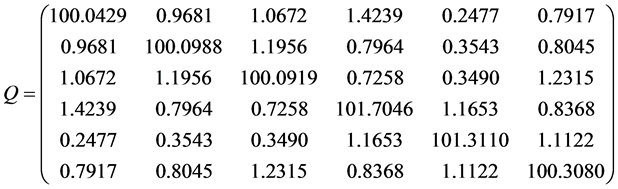
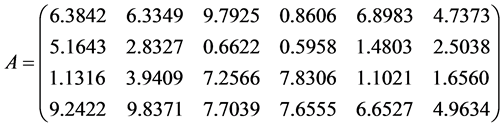
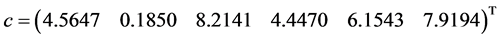

The exact optimal solution is
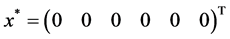 and the optimal value of objective function is
and the optimal value of objective function is 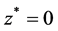 .
.
Appling the method proposed, the iterations consuming time are shown in Table2
Acknowledgements
This work is supported by the Beijing Municipal Commission of Education Science and Technology Program (KM201310017006) and the Beijing URT Program (2012J00018).
REFERENCES
- D. Goldfarb and A. Idinabi, “A Numerical Stable Dual Method for Solving Strictly Convex Quadratic Programs,” Mathematical Programming, Vol. 27, No. 2, 1983, pp. 1-33. http://dx.doi.org/10.1007/BF02591962
- Y. Ye and E. Tse, “An Extension of Kamarker’s Algorithm to Convex Quadratic Programming,” Mathematical Programming, Vol. 47, No. 4, 1989, pp. 157-179. http://dx.doi.org/10.1007/BF01587086
- J. L. Zhang and X. S. Zhang, “A Predictor-Corrector Method for Convex Quadratic Programming,” Journal of System Science and Mathematical Science, Vol. 23, No. 3, 2003, pp. 353-366.
- R. D. Monteiro, I. Adler and M. G. Resende, “A Polynomial-Time Primal-Dual Affine Scaling Algorithm for Linear and Convex Quadratic Programming and Its Powerseries Extension,” Mathematics of Operations Research, Vol. 15, No. 2, 1990, pp. 191-214. http://dx.doi.org/10.1287/moor.15.2.191
- M. W. Zhang and C. C. Huang, “A Primal-Dual Infeasible Interior Point Algorithm for Convex Quadratic Programming Problem with Box Constraints,” Journal of Engineering Mathematics, Vol. 18, No. 2, 2001, pp. 85-90.
- Y. X. Yuan and W. Y. Sun, “Optimization Theory and Method,” Science Press, 2002, pp. 111-117.
- R. P. Wang, “Fixed Iterative Method for Solving the Equality Constrained Convex Quadratic Programming Problem,” Journal of Beijing Institute of Petro-Chemical Technology, Vol. 16, No. 3, 2008, pp. 64-66.
- R. P. Wang, “Fixed Iterative Method for Solving the Inequality Constrained Quadratic Programming Problem,” Journal of Beijing Institute of Petro-Chemical Technology, Vol. 15, No. 1, 2007, pp. 1-4.
- X. S. Li, “An Effective Algorithm for Non-differentiable Problem,” Science in China (Series A), Vol. 23, No. 3, 1994, pp. 353- 366.
- G. Q. Chen and Y. Q. Chen, “An Entropy Function Method for Nonlinear Complementary Problems,” Acta Scientiarum Naturalium Universitatis NeiMongol, Vol. 31, No. 5, 2000, pp. 447-451.
- H. W. Tang and L. W. Zhang, “An Entropy Function Method for Nonlinear Programming Problems,” Chinese Science Bulletin, Vol. 39, No. 8, 1994, pp. 682-684.
- Q. Y. Li, Z. Z. Mo and L. Q. Qi, “Numerical Method for System of Nonlinear Equations,” Beijing Science Press, Beijing, 1999.


