Applied Mathematics
Vol.4 No.12A(2013), Article ID:41074,10 pages DOI:10.4236/am.2013.412A005
On the Intersection Equation of a Hyperboloid and a Plane
Clausthal University of Technology, Clausthal-Zellerfeld, Germany
Email: klein@rz.tu-clausthal.de
Copyright © 2013 Peter Paul Klein. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2013 are reserved for SCIRP and the owner of the intellectual property Peter Paul Klein. All Copyright © 2013 are guarded by law and by SCIRP as a guardian.
Received October 25, 2013; revised November 25, 2013; accepted December 2, 2013
Keywords: Hyperboloid; Intersection Equation of Hyperboloid and Plane
ABSTRACT
In this note, the ideas employed in [1] to treat the problem of an ellipsoid intersected by a plane are applied to the analogous problem of a hyperboloid being intersected by a plane. The curves of intersection resulting in this case are not only ellipses but rather all types of conics: ellipses, hyperbolas and parabolas. In text books of mathematics usually only cases are treated, where the planes of intersection are parallel to the coordinate planes. Here the general case is illustrated with intersecting planes which are not necessarily parallel to the coordinate planes.
1. Introduction
The problem of a hyperboloid being intersected by a plane is described in Section 1. The means to treat the problem are provided in Sections 2, 3 and 4. In the end of Section 4 first results can be formulated in Corollaries 3 and 4. Further results concerning the center of the conic of intersection are given in Section 5. Finally in Section 6 the case of a parabola as intersecting curve is treated.
Let a hyperboloid be given with the three positive semi axes a, b, c
 (1)
(1)
where 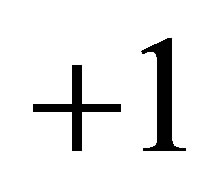 on the right hand side of (1) corresponds to a hyperboloid of one sheet,
on the right hand side of (1) corresponds to a hyperboloid of one sheet,  on the right hand side of (1) to a hyperboloid of two sheets. Let furthermore a plane be given with the unit normal vector
on the right hand side of (1) to a hyperboloid of two sheets. Let furthermore a plane be given with the unit normal vector
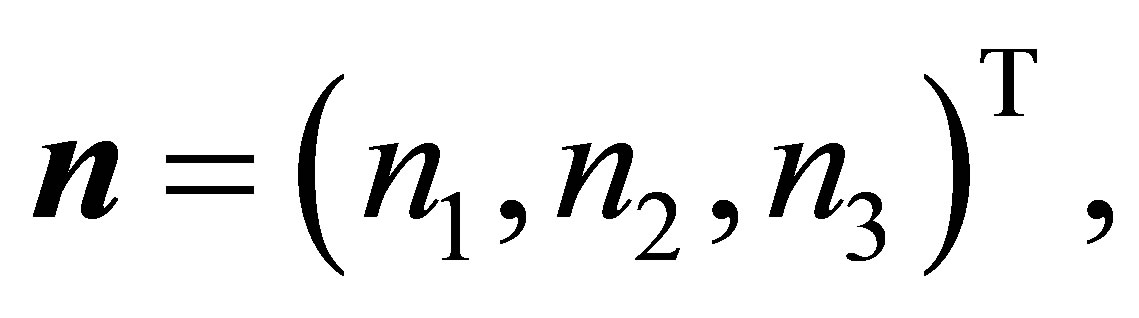
which contains an interior point or a boundary point 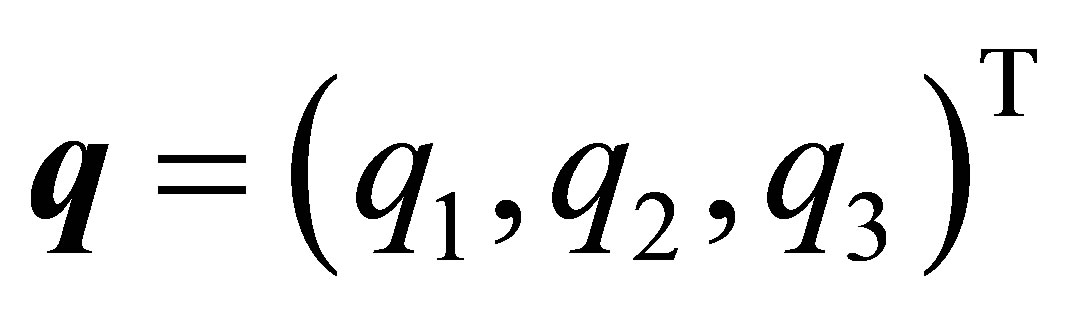 of hyperboloid (1). A plane spanned by vectors
of hyperboloid (1). A plane spanned by vectors ,
, 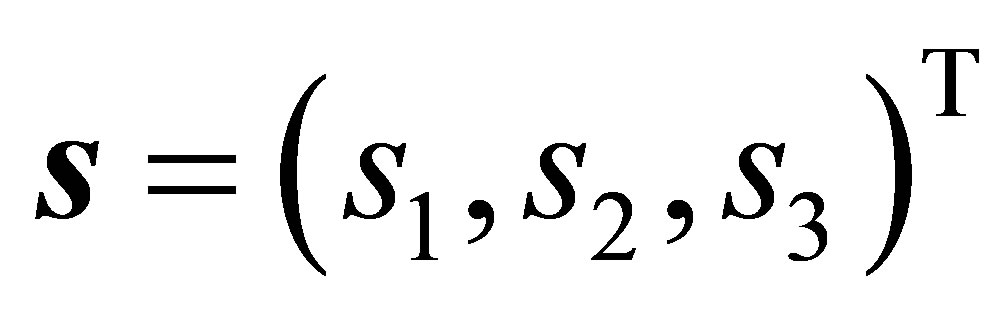 and containing the point
and containing the point  is described in parametric form by
is described in parametric form by
 (2)
(2)
Inserting the components of ![]() into the Equation of hyperboloid (1) leads to the line of intersection as a quadratic form in the variables
into the Equation of hyperboloid (1) leads to the line of intersection as a quadratic form in the variables  and
and![]() . Let the scalar product in
. Let the scalar product in  for two vectors
for two vectors 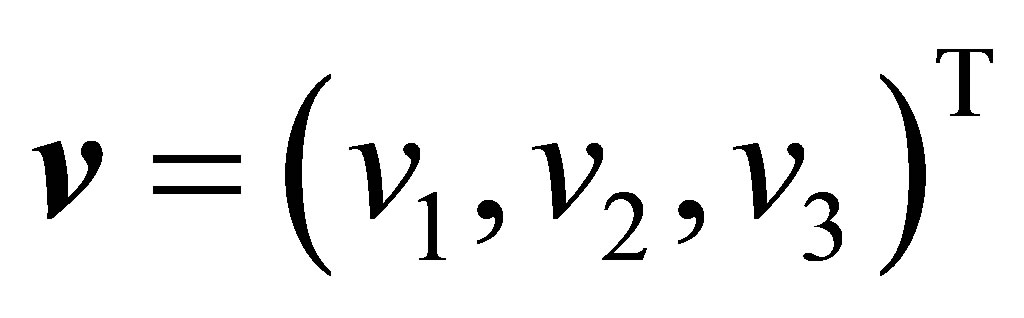 and
and  be denoted by
be denoted by
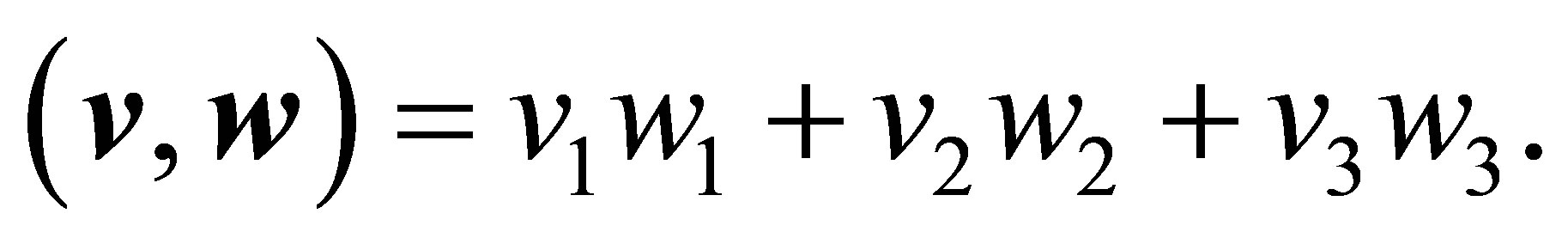
With the diagonal matrices

the line of intersection has the form:
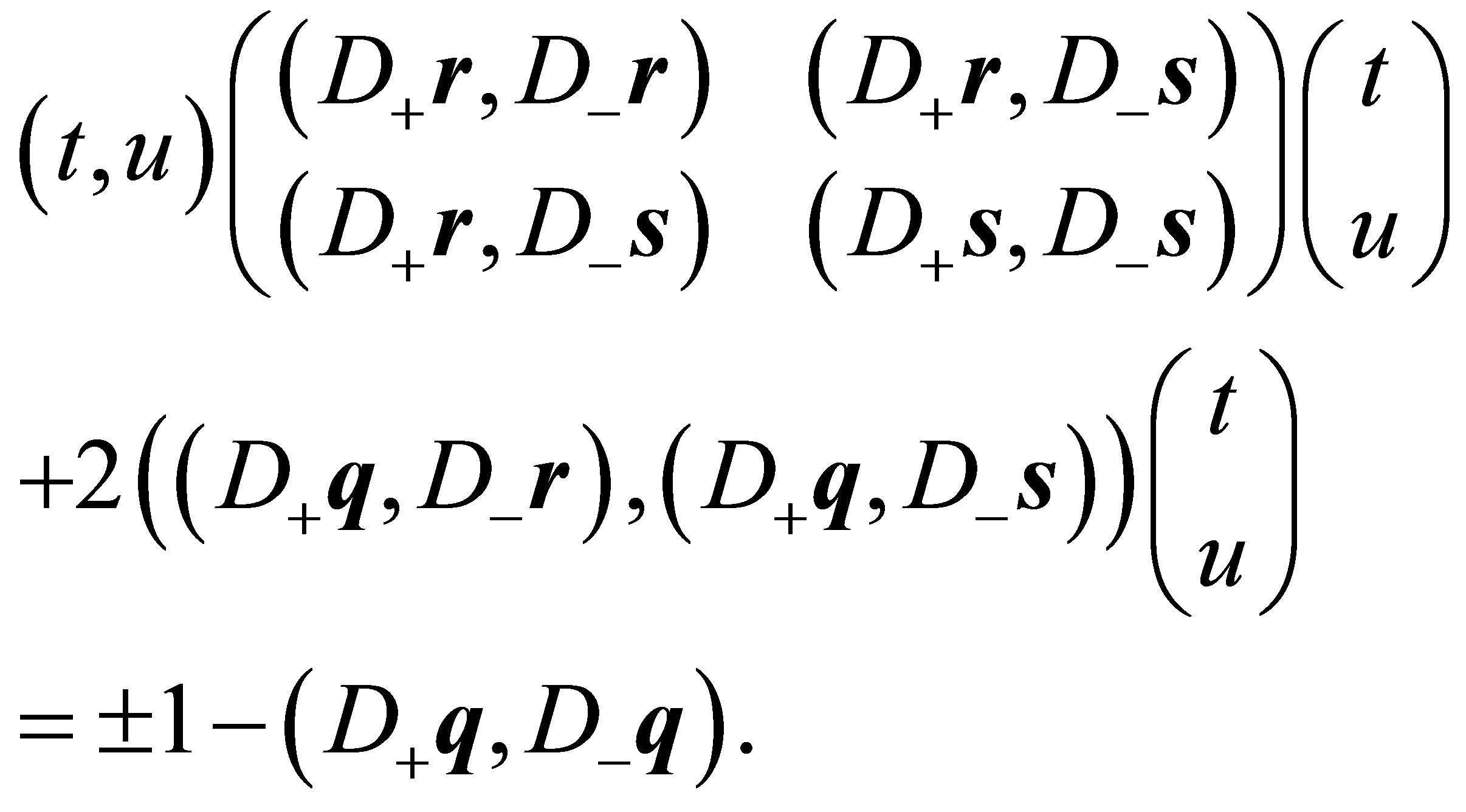 (3)
(3)
As  is an interior point or a boundary point of hyperboloid (1) the right-hand side of Equation (3) is nonnegative. Since
is an interior point or a boundary point of hyperboloid (1) the right-hand side of Equation (3) is nonnegative. Since  need not be a scalar product in
need not be a scalar product in , the
, the  matrix in Equation (3) is in general no Gram matrix. If the
matrix in Equation (3) is in general no Gram matrix. If the  matrix in (3) is positive definite, then the line of intersection is an ellipse.
matrix in (3) is positive definite, then the line of intersection is an ellipse.
Let  and
and ![]() be unit vectors orthogonal to the unit normal vector
be unit vectors orthogonal to the unit normal vector ![]() of plane (2)
of plane (2)
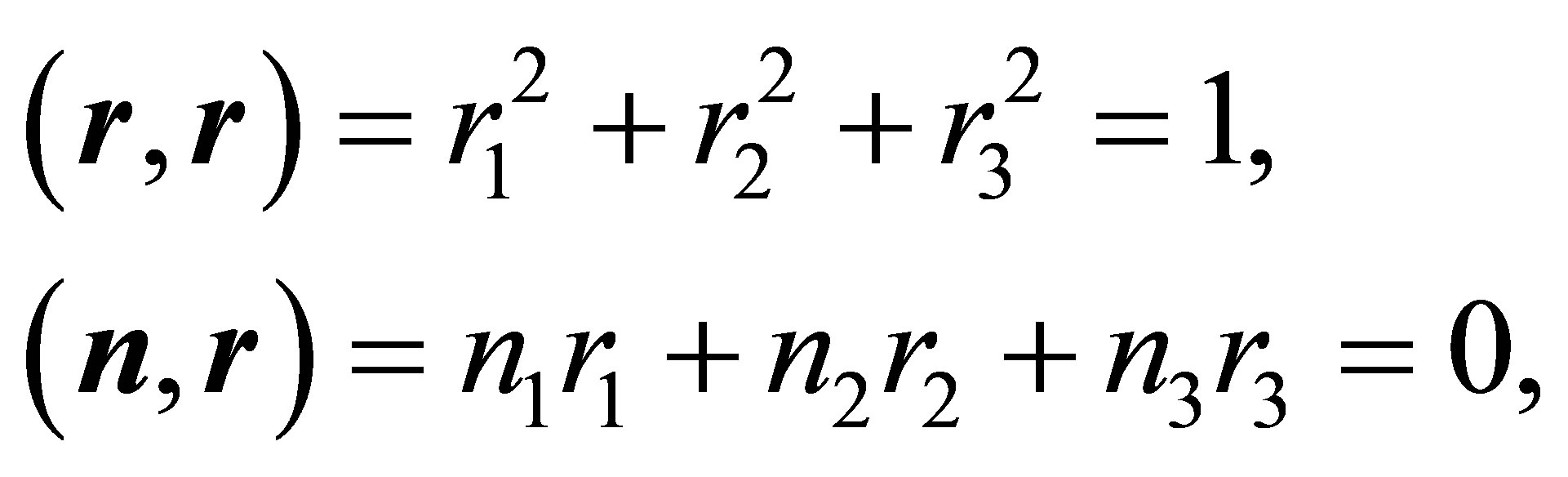 (4)
(4)
 (5)
(5)
and orthogonal to eachother
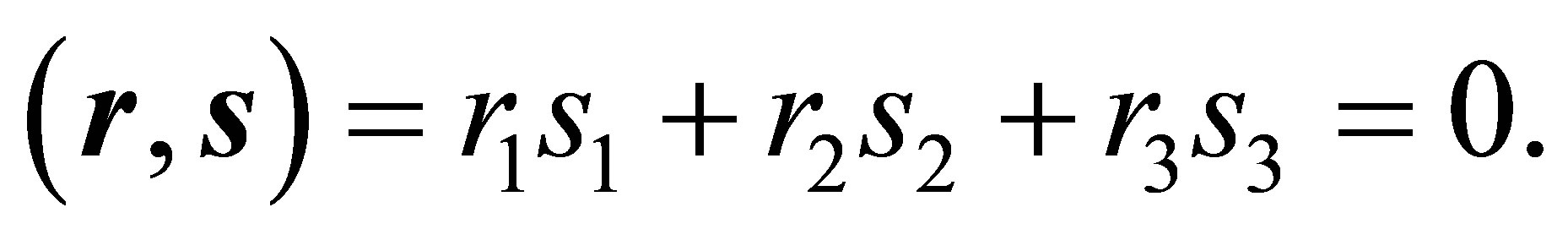 (6)
(6)
Furthermore vectors  and
and ![]() may be chosen such that
may be chosen such that
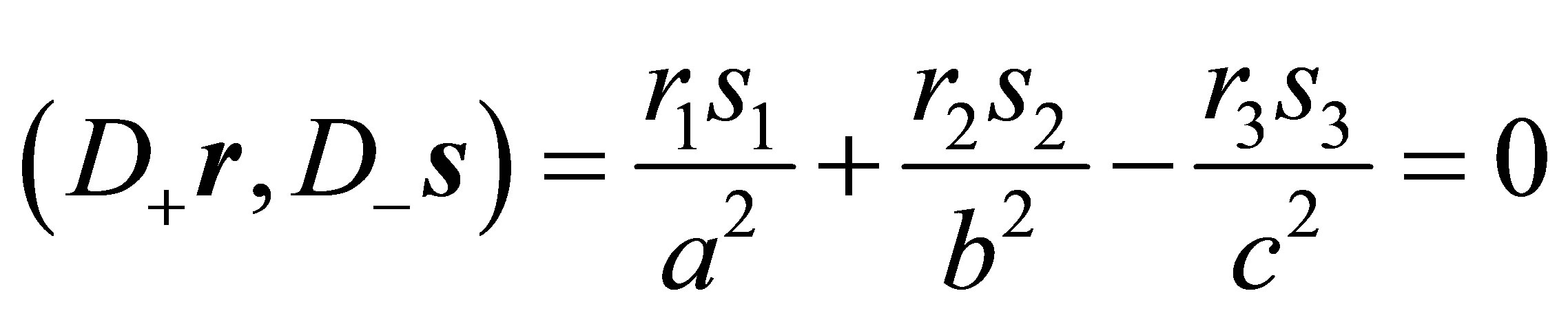 (7)
(7)
holds. This will be shown in the next Section. Condition (7) ensures that the  matrix in (3) has diagonal form.
matrix in (3) has diagonal form.
In case 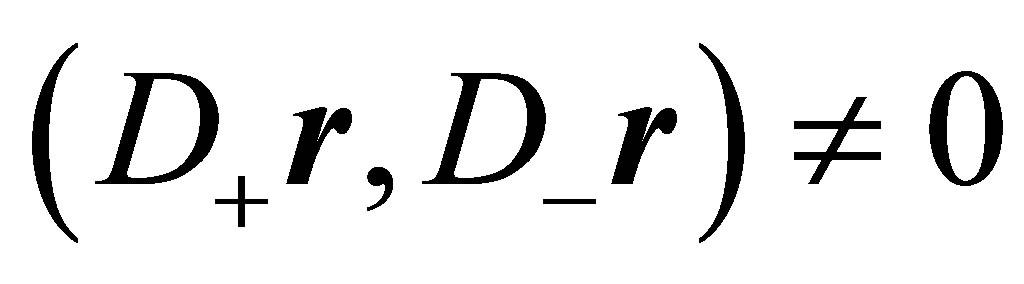 and
and 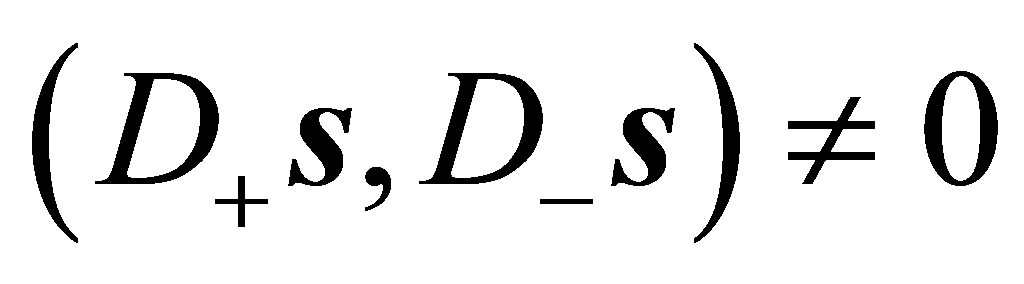 the line of intersection reduces to
the line of intersection reduces to
 (8)
(8)
with
 (9)
(9)
and
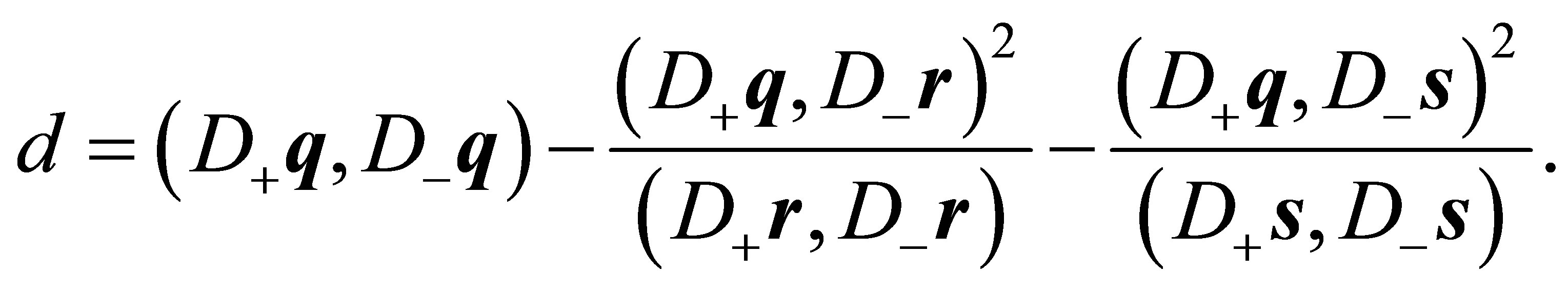 (10)
(10)
In case 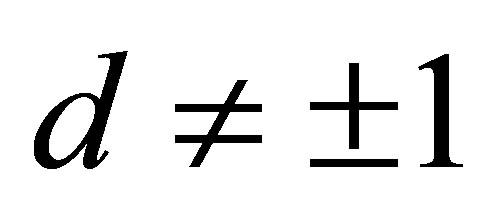 Equation (8) can be written as a conic in translational form
Equation (8) can be written as a conic in translational form
 (11)
(11)
in the variables 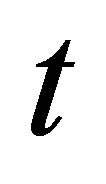 and
and ![]() with
with
 (12)
(12)
For 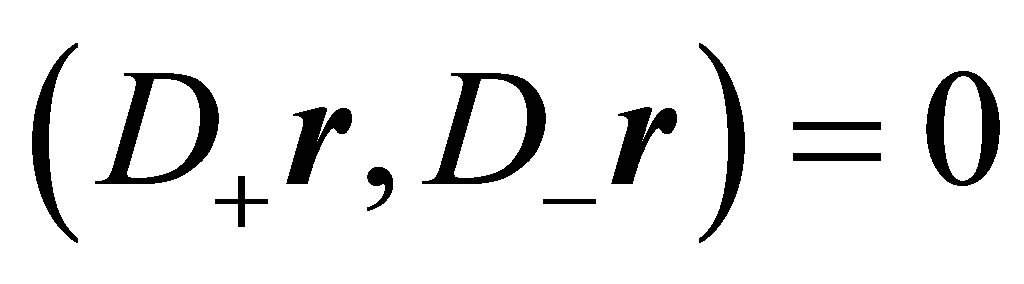 and
and 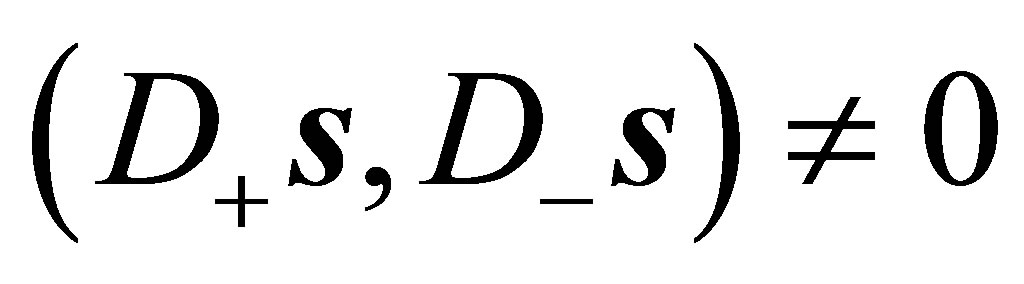 the line of intersection is of the form
the line of intersection is of the form
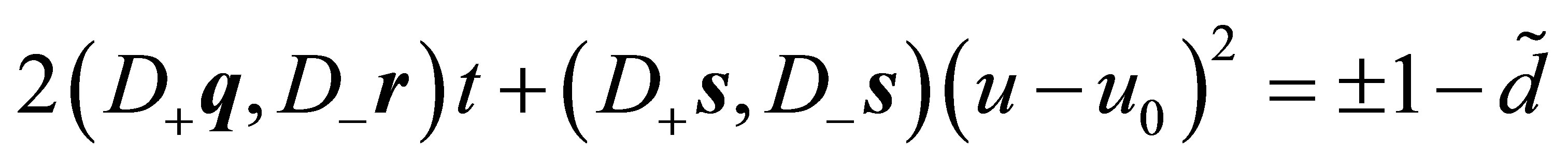 (13)
(13)
with
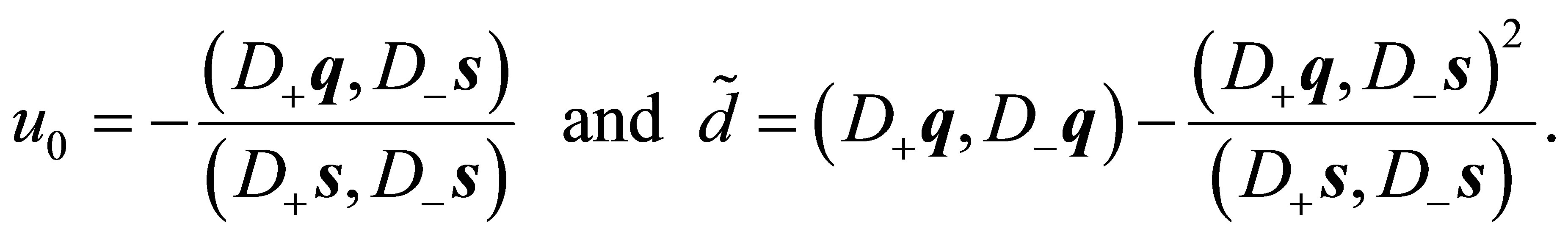
If  holds, (13) represents a parabola in the variables
holds, (13) represents a parabola in the variables 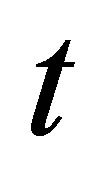 and
and![]() . This will be discussed further in Section 6.
. This will be discussed further in Section 6.
In order to show that the expression ![]() in (10) is independent of the choice of
in (10) is independent of the choice of  this vector may be decomposed orthogonally with respect to
this vector may be decomposed orthogonally with respect to![]() :
:
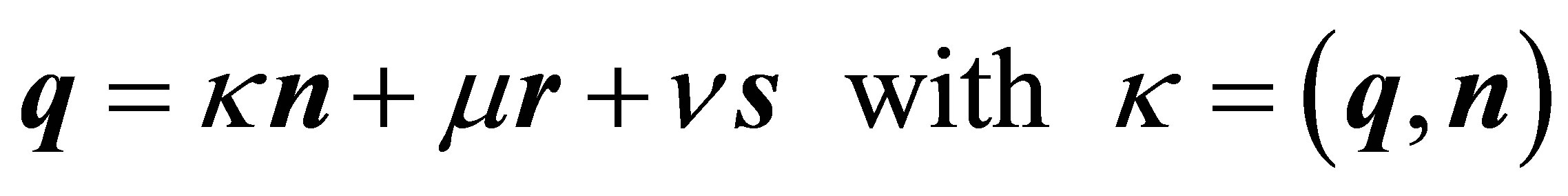 (14)
(14)
where ![]() is the distance of plane (2) from the origin. Substituting
is the distance of plane (2) from the origin. Substituting  into (10) one obtains employing (4), (5), (6) and (7)
into (10) one obtains employing (4), (5), (6) and (7)
 (15)
(15)
The following rules of computation for the cross product in  ([2], p.147) will be applied repeatedly later on. For vectors
([2], p.147) will be applied repeatedly later on. For vectors  of
of  the identity of Lagrange holds
the identity of Lagrange holds
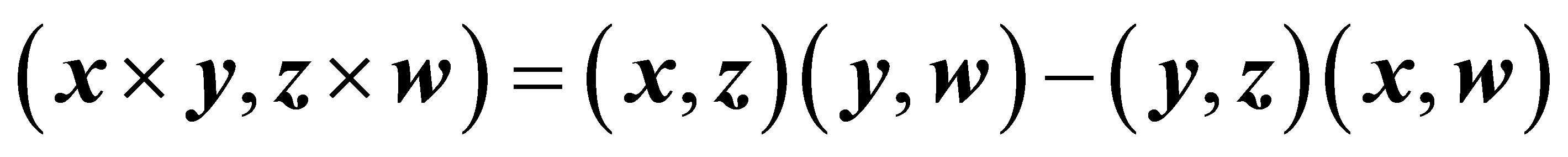 (16)
(16)
and the Grassmann expansion theorem for the double cross product
 (17)
(17)
2. Construction of Vectors ![]() and
and 
Let  be a unit vector orthogonal to the unit normal vector
be a unit vector orthogonal to the unit normal vector ![]() of the plane, so that Equations (4) hold. A suitable vector
of the plane, so that Equations (4) hold. A suitable vector ![]() is obtained as a cross product
is obtained as a cross product
![]()
Then Equations (5) and (6) are fulfilled: ![]() is a unit vector, as can be shown by the identity of Lagrange (16), utilising
is a unit vector, as can be shown by the identity of Lagrange (16), utilising ,
, 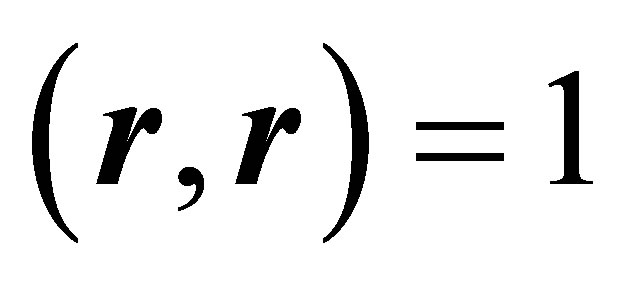 and
and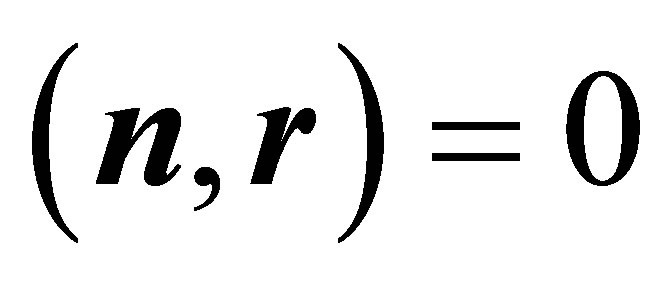 :
:
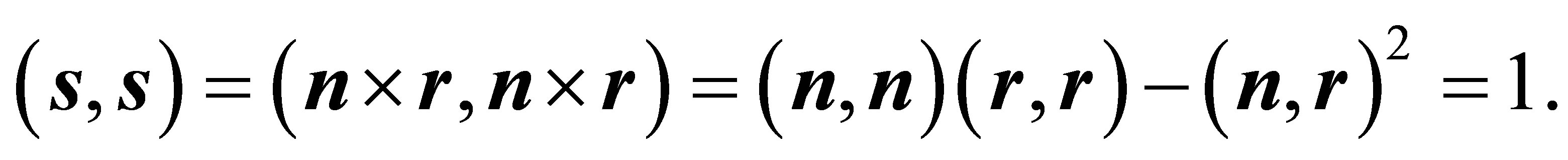
Furthermore one obtains according to the rules applying to the spar product:


In case Equation (7) is not fulfilled for the initially chosen vectors  and
and![]() , i.e.
, i.e.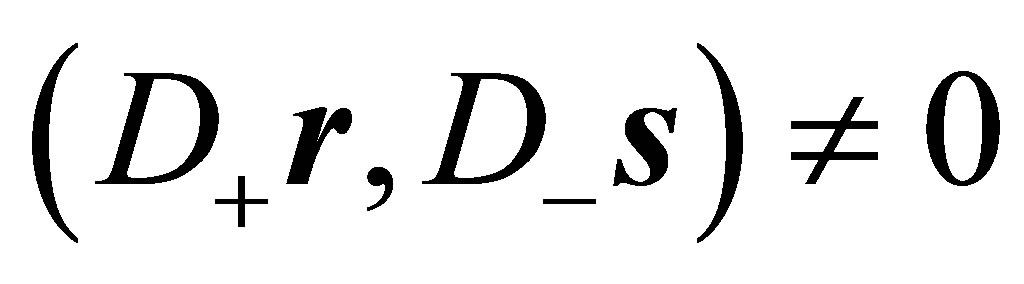 , the following transformation may be performed with
, the following transformation may be performed with 
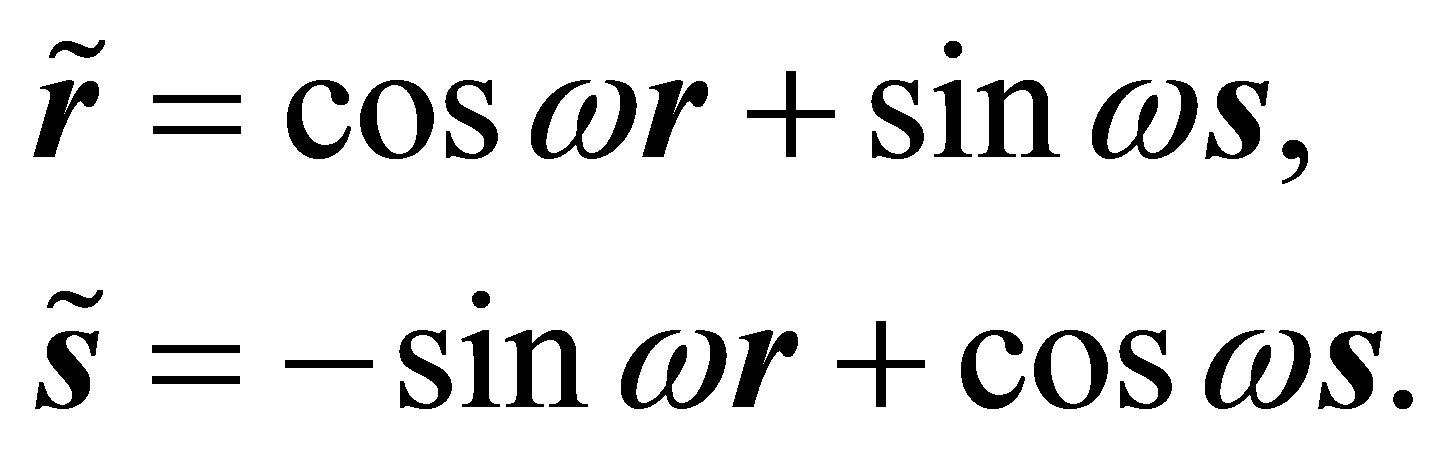
The transformed vectors  and
and  satisfy the following conditions:
satisfy the following conditions: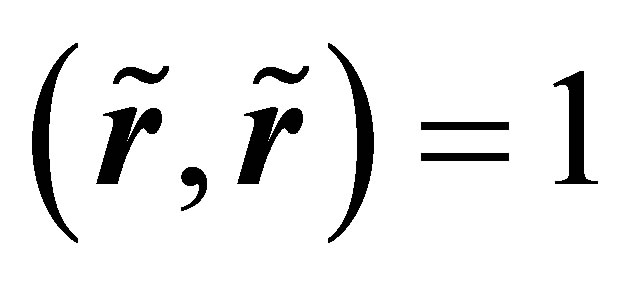 ,
, 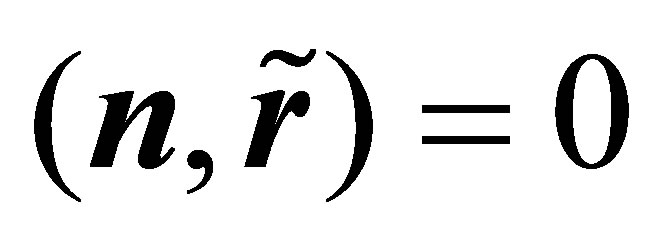 and
and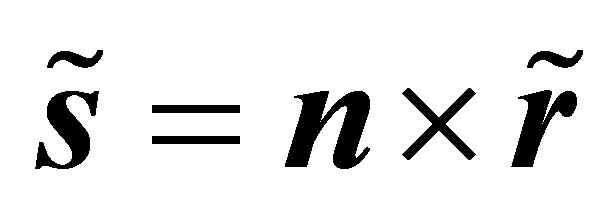 , which imply conditions (4), (5) and (6). The expression
, which imply conditions (4), (5) and (6). The expression
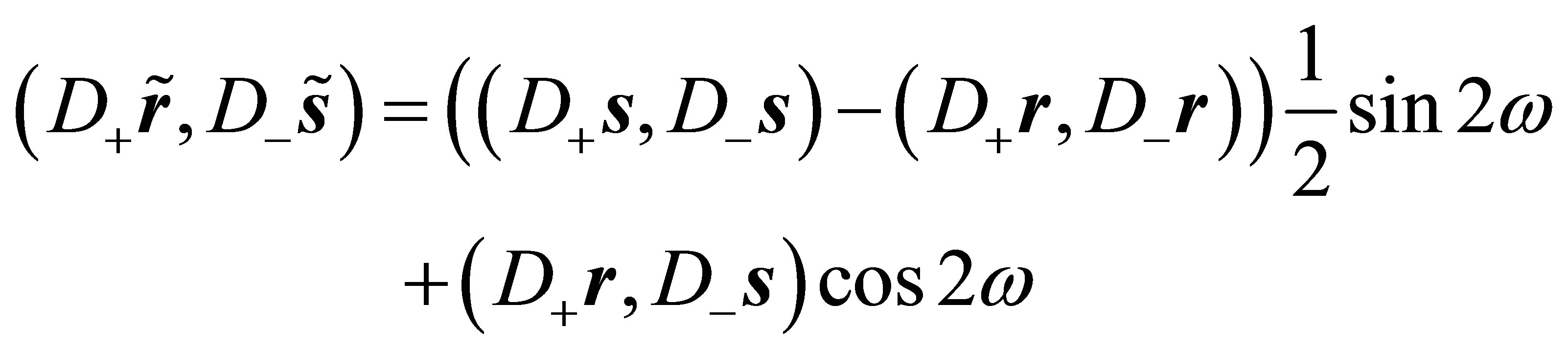
becomes zero, when choosing ![]() such that
such that
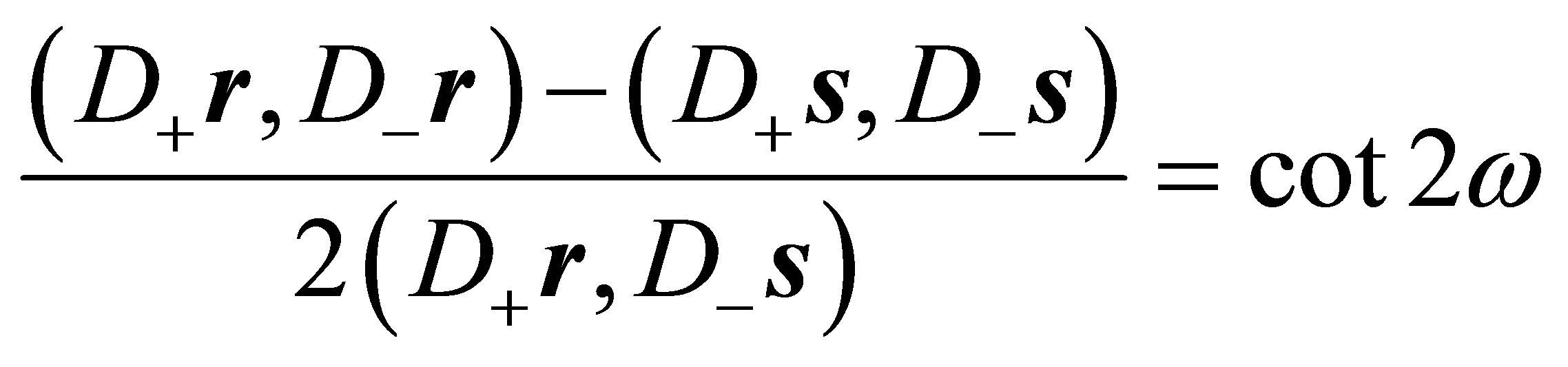
holds.
Corollary 1: For the unit vectors  and
and ![]() orthogonal to each other and
orthogonal to each other and ![]() the following statement holds:
the following statement holds:
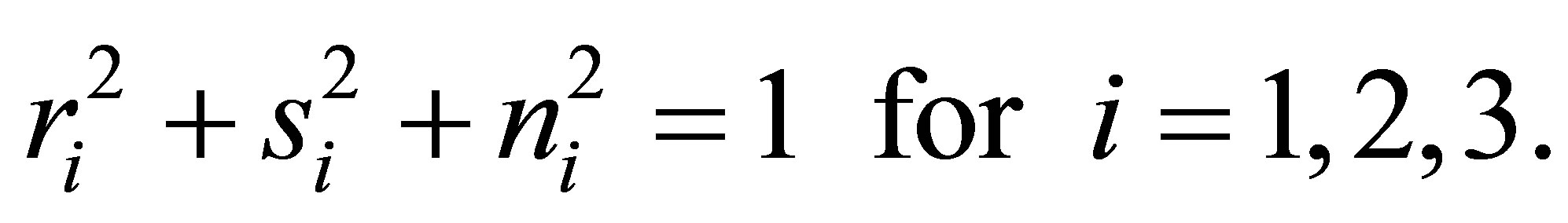
This statement follows by substituting the definition of ![]() and utilising
and utilising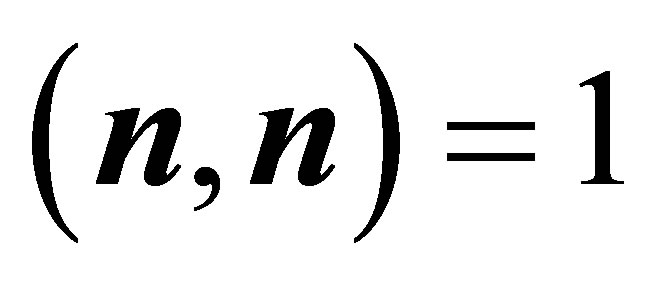 ,
, 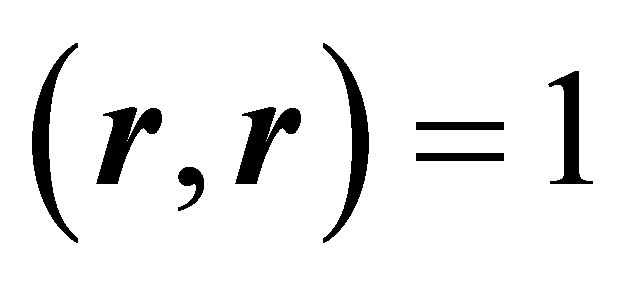 and
and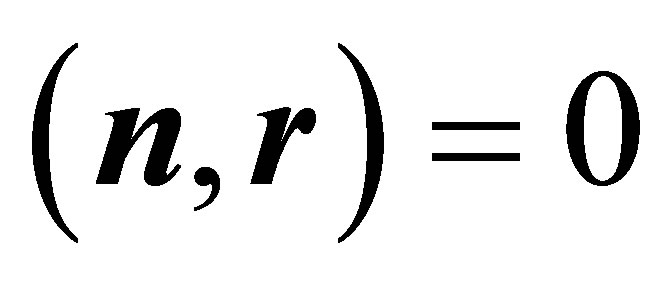 . For
. For 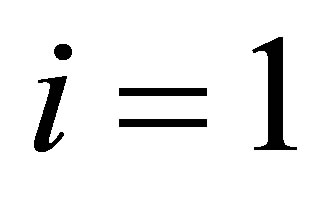 one obtains for instance:
one obtains for instance:

3. A Quadratic Equation
Theorem 1: Let ![]() be the unit normal vector of the plane and let vectors
be the unit normal vector of the plane and let vectors  and
and ![]() satisfy
satisfy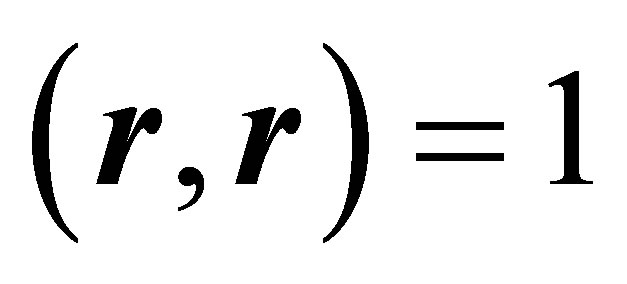 ,
, 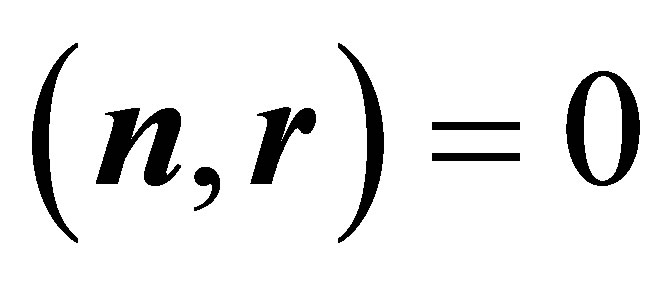 ,
, ![]() and condition (7). Putting
and condition (7). Putting
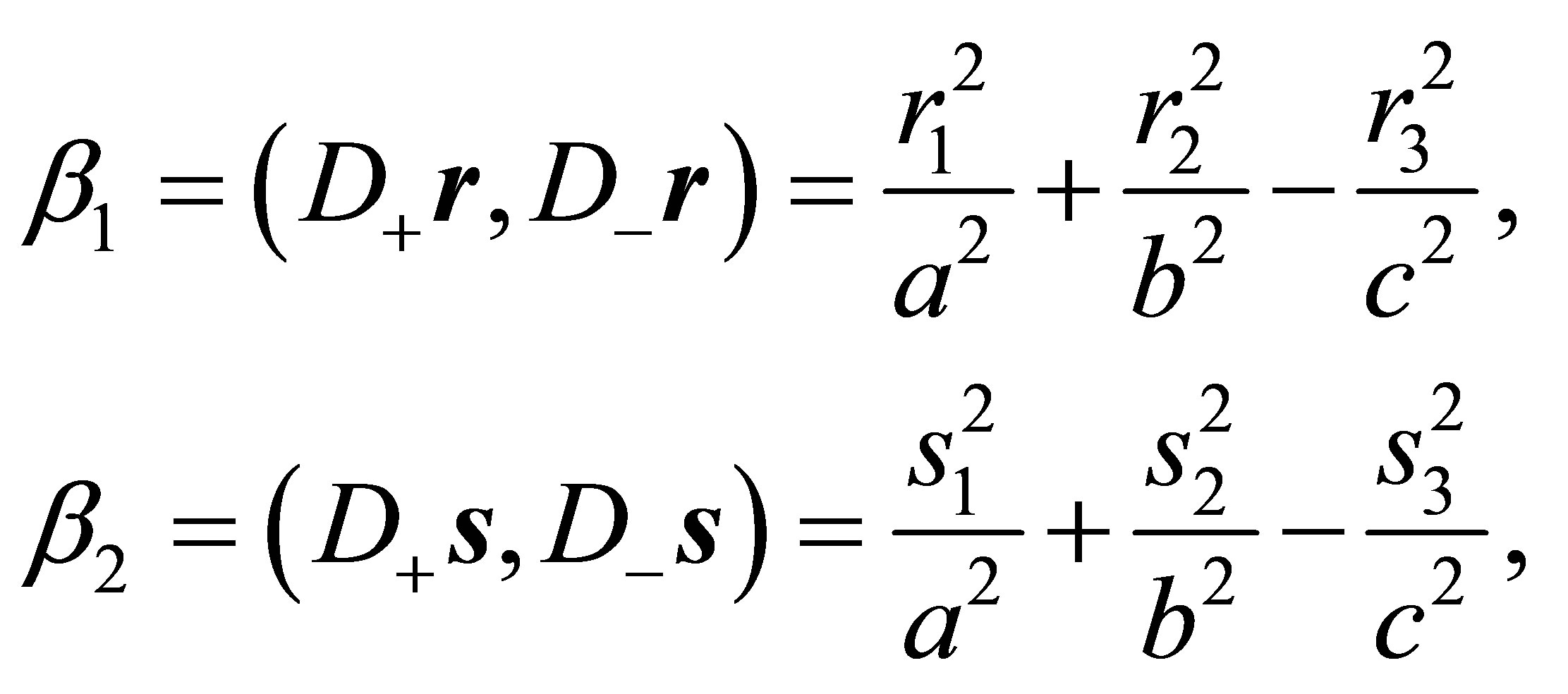 (18)
(18)
 and
and 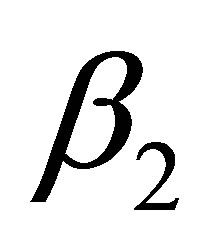 are solutions of the following quadratic Equation:
are solutions of the following quadratic Equation:
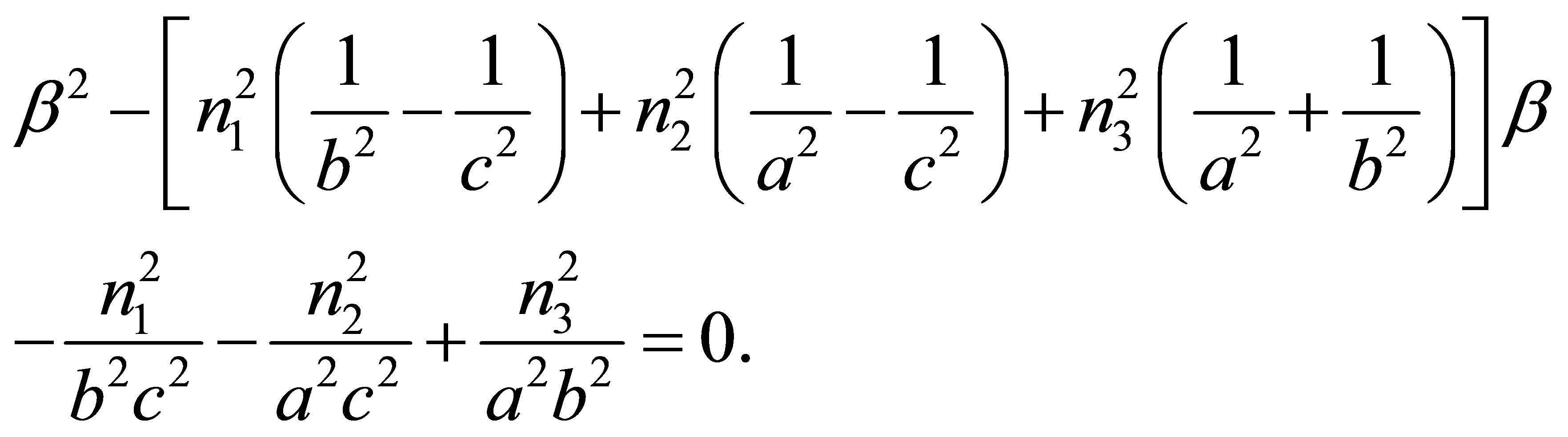 (19)
(19)
Proof: Utilising Corollary 1 one obtains:

Applying diagonality condition (7) and the identity of Lagrange (16) leads to:
 (20)
(20)
For the cross products 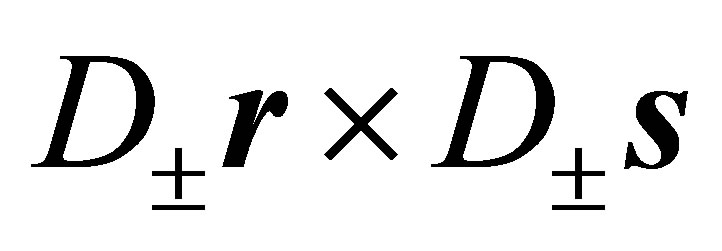 one obtains:
one obtains:
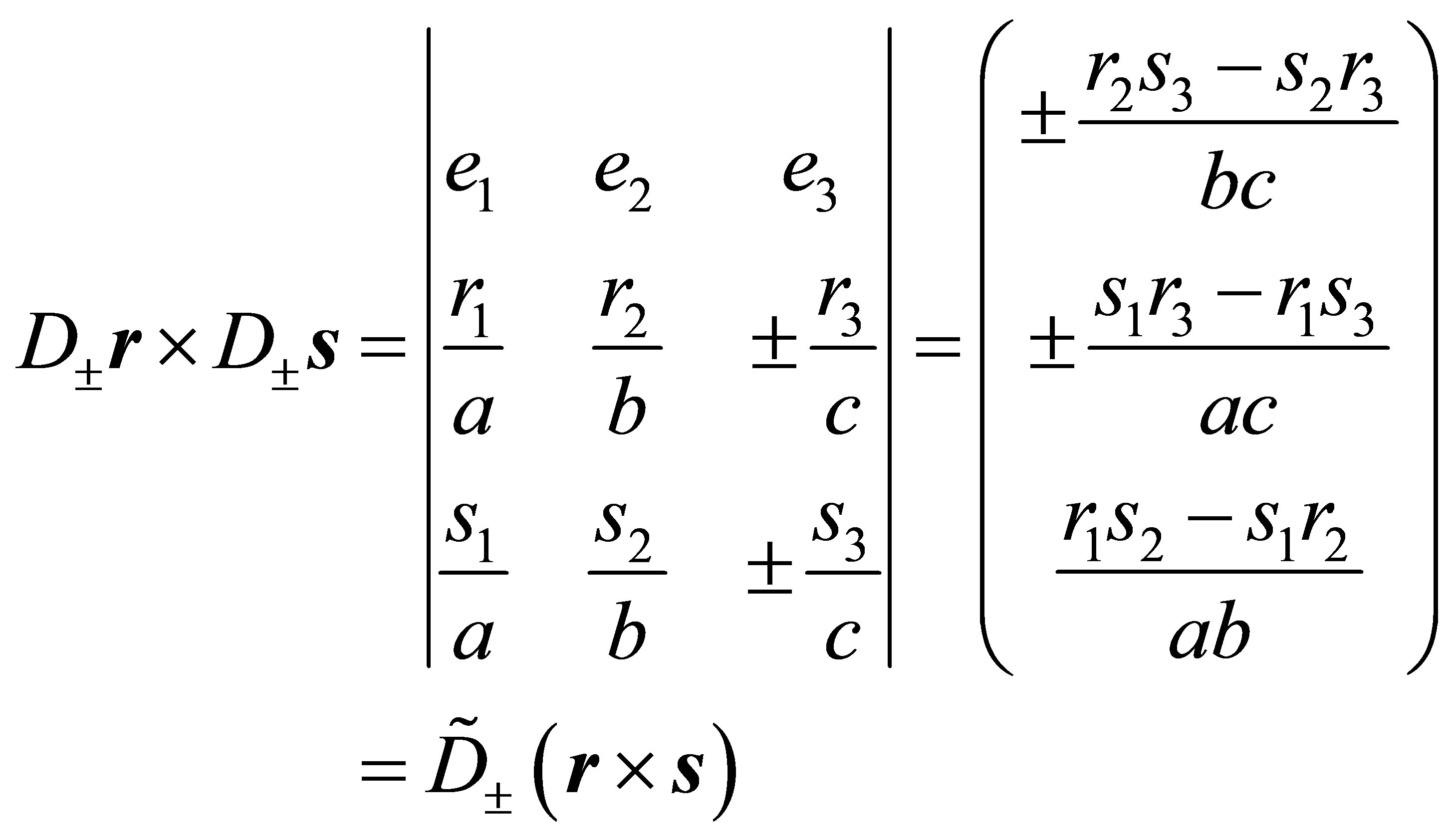 (21)
(21)
with the diagonal matrices
 (22)
(22)
According to Grassmann’s expansion theorem for the double cross product (17)
 (23)
(23)
follows, since 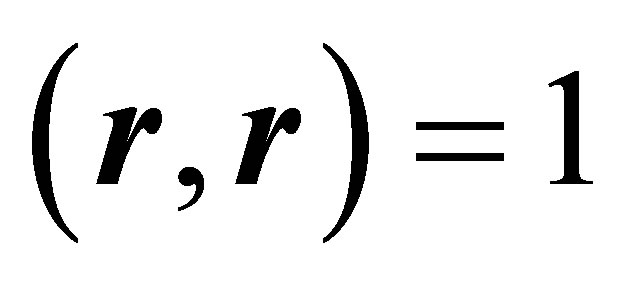 and
and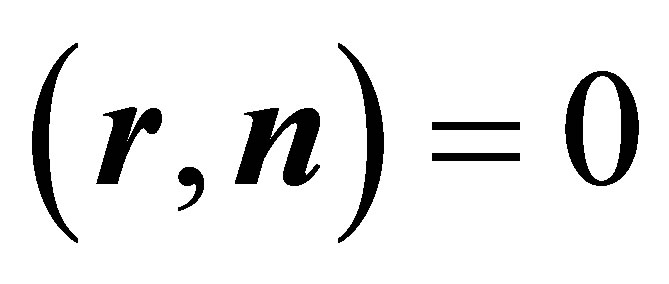 . Applying (20), (21), (23) one obtains:
. Applying (20), (21), (23) one obtains:
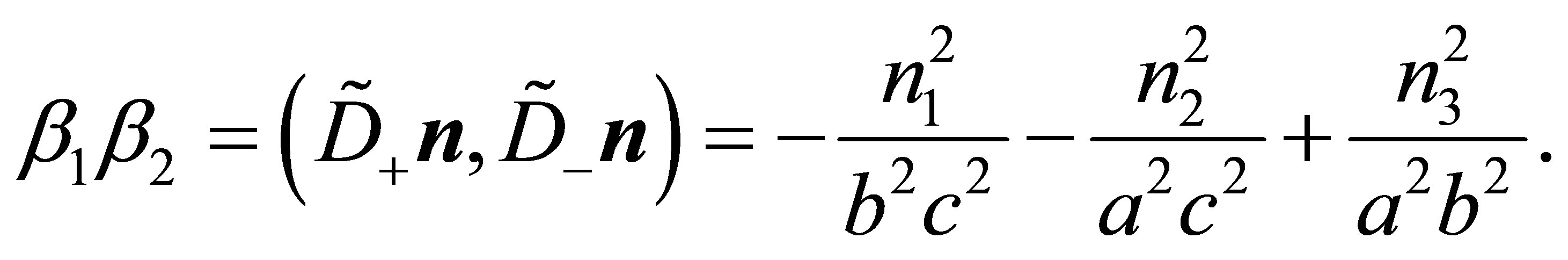 (24)
(24)

Corollary 2: Under the assumptions of Theorem 1 the following three pairs of Equations are valid:
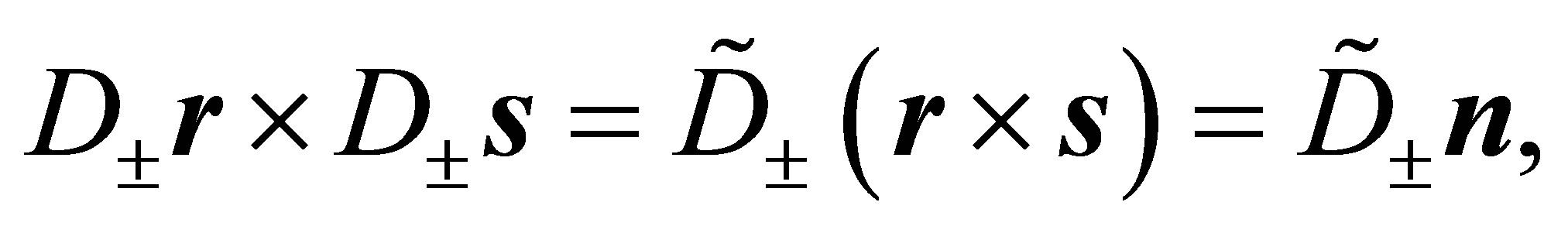
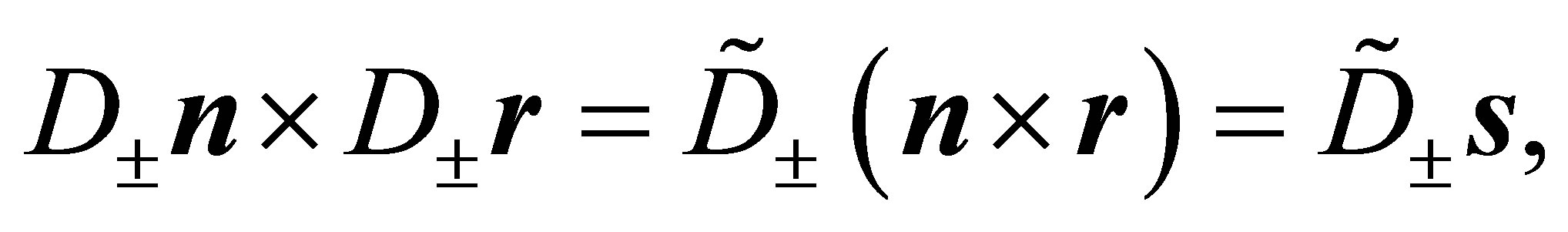

The first pair of Equations was verified in the proof of Theorem 1. The second and the third pair of Equations follow analogously.
4. A Formular for d
Theorem 2: Under the assumptions of Theorem 1 with  and
and  the expression for
the expression for ![]() in (15) is given by:
in (15) is given by:
 (25)
(25)
where ![]() is taken from (14).
is taken from (14).
Proof: The verification of (25) consists of three steps.
Step 1: Applying the identity of Lagrange (16) the following statements hold:
 (26)
(26)
With Corollary 2 and the diagonal matrices
 (27)
(27)
one obtains:
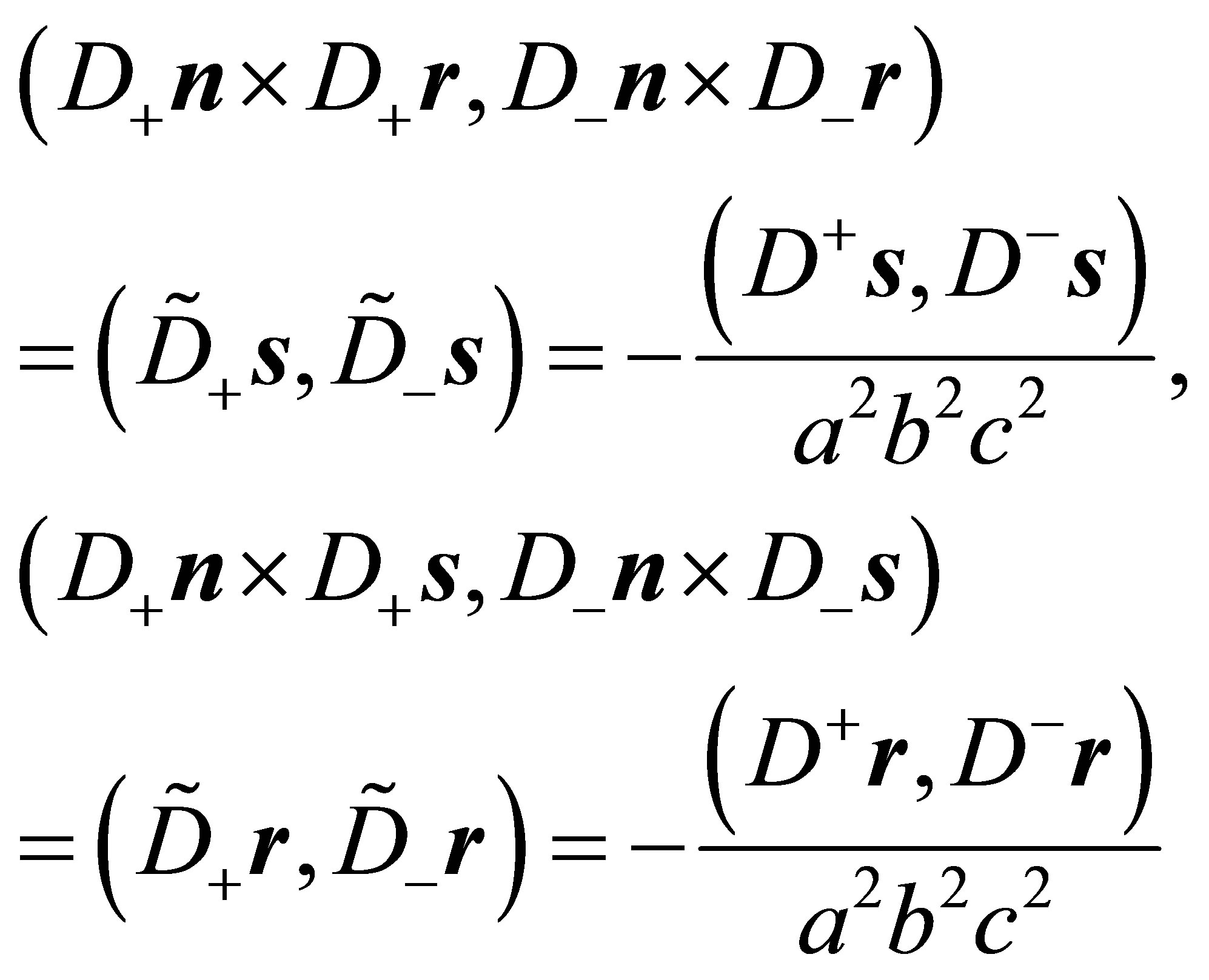 (28)
(28)
and it follows by substituting (28) into (26)
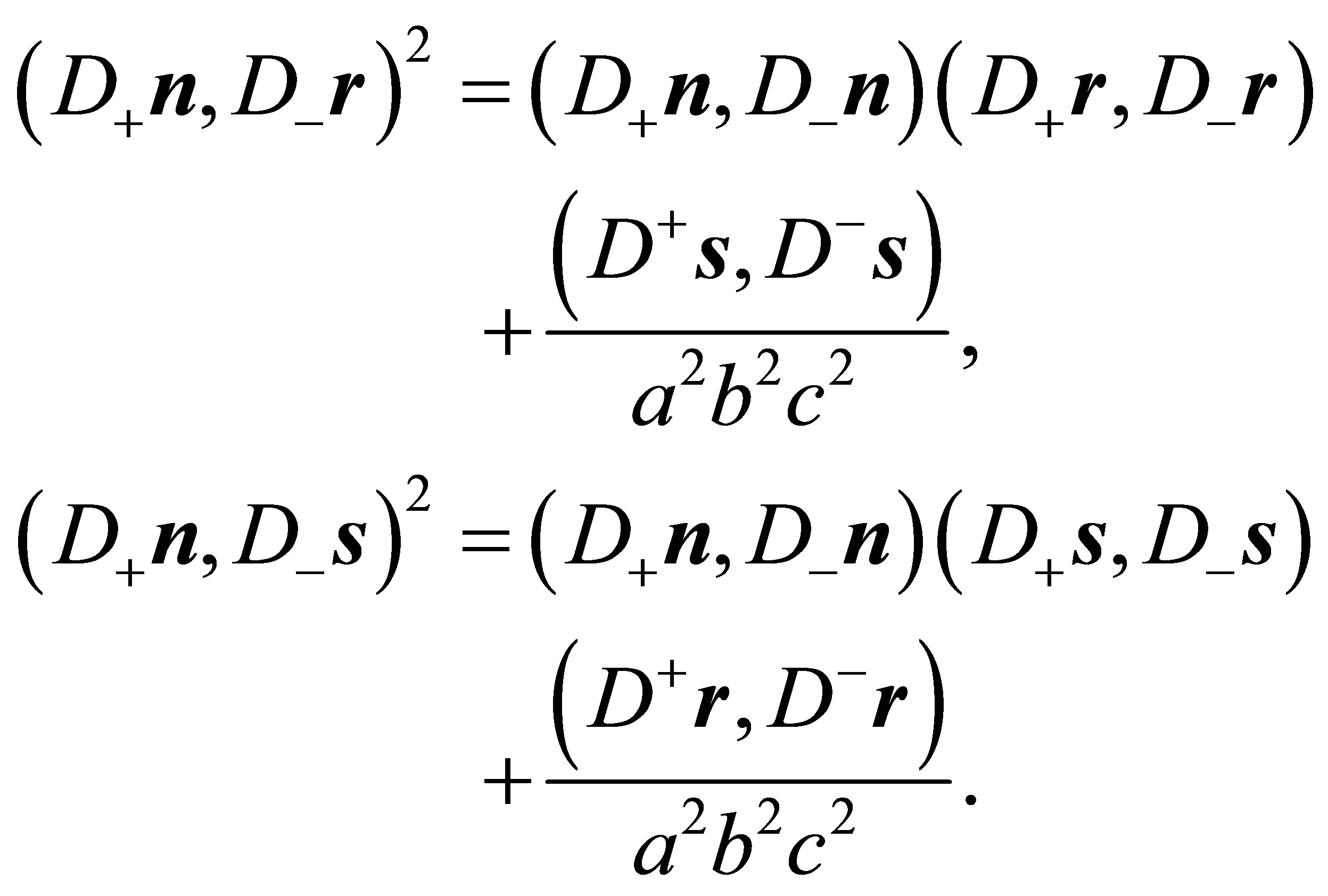 (29)
(29)
Introducing expressions
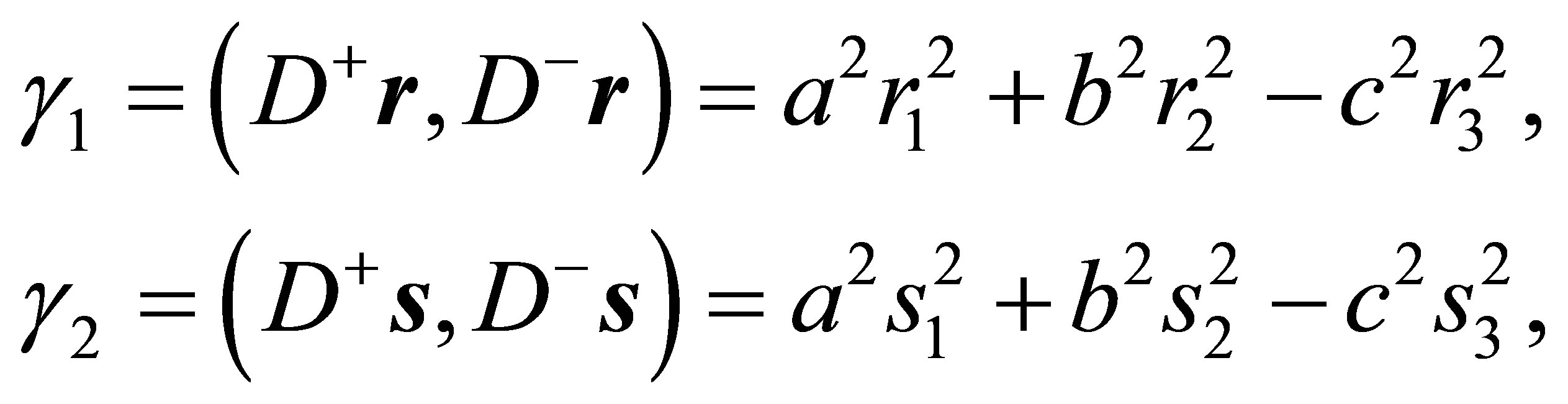 (30)
(30)
one obtains from (29) using (18) and (30)
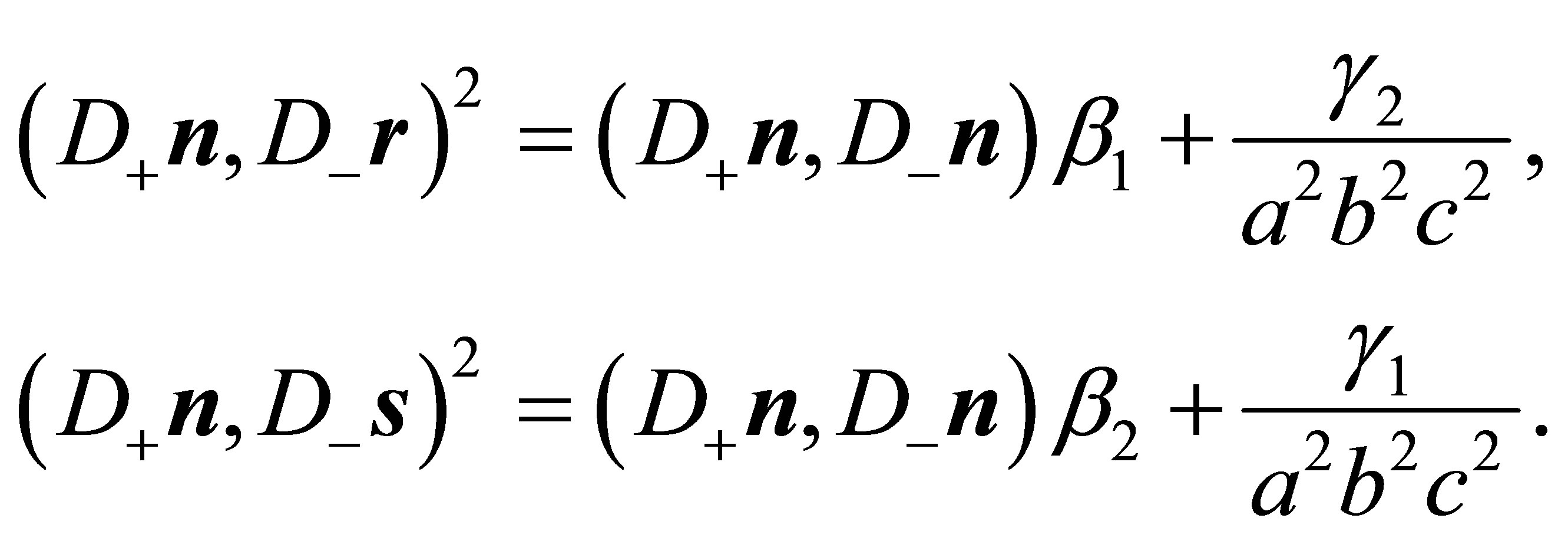 (31)
(31)
Combining both Equations (31) for  and
and  leads to
leads to
 (32)
(32)
Step 2: Analogously to the verification of (24) the application of the identity of Lagrange (16) yields:
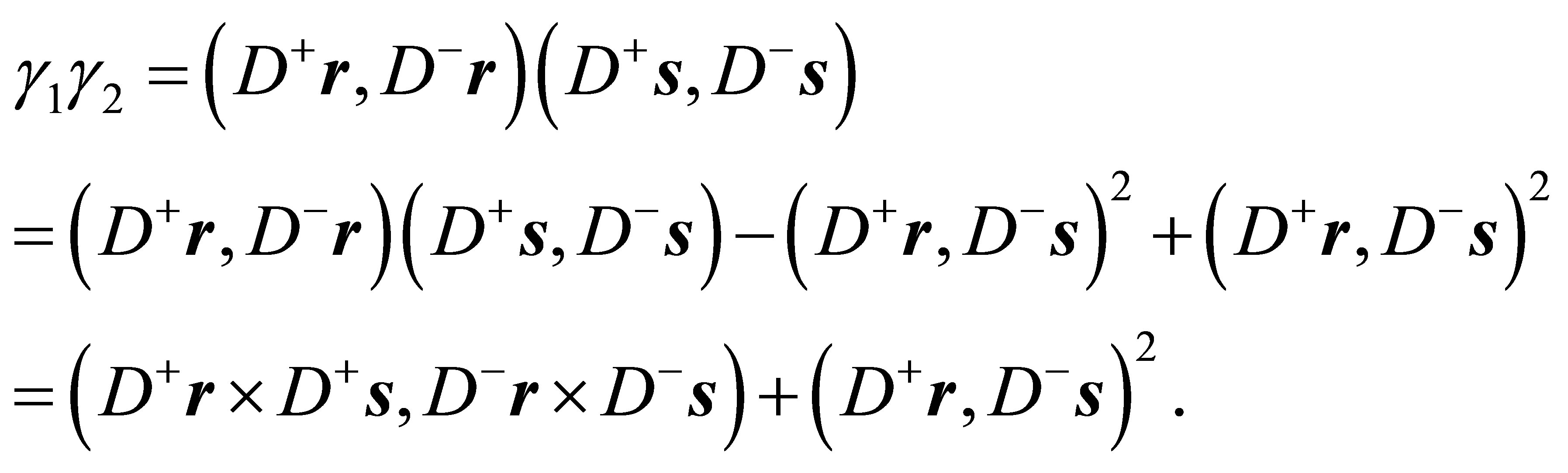
With the diagonal matrices

for the cross products 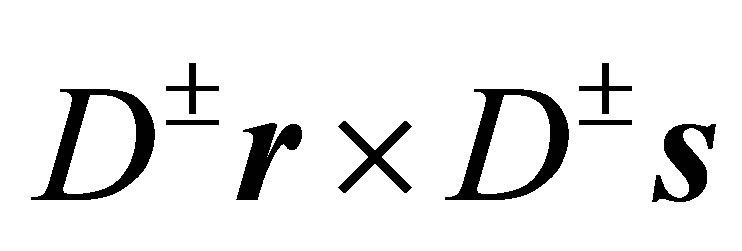 holds:
holds:
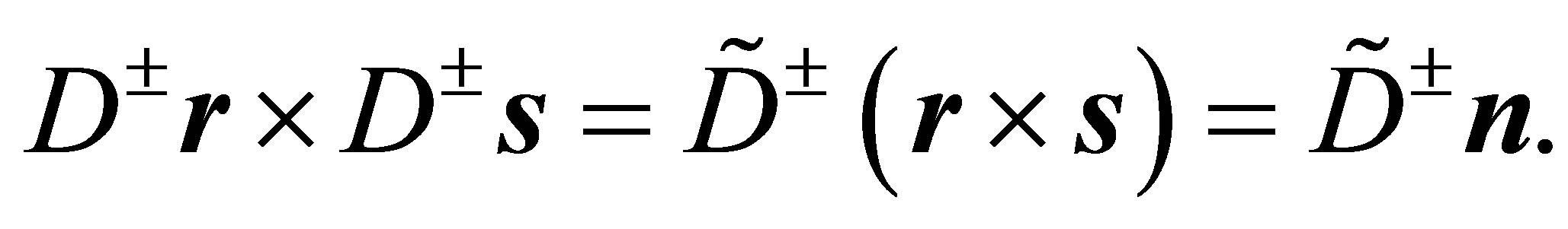
Therefore one obtains
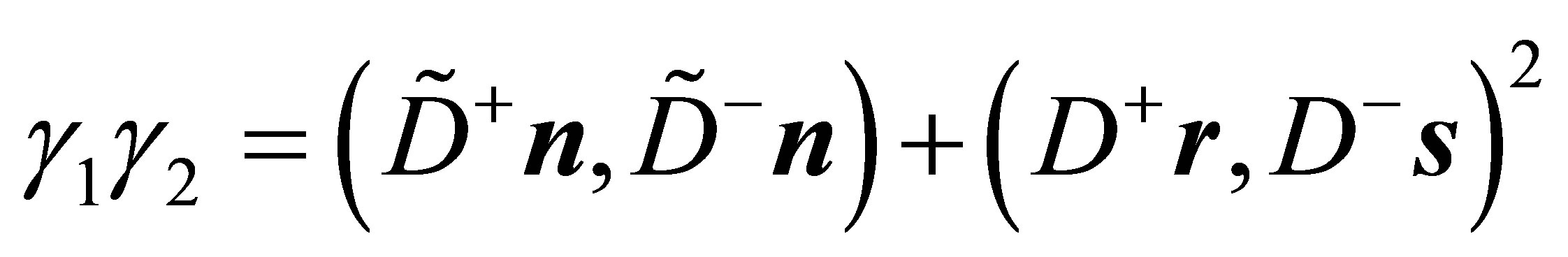
or
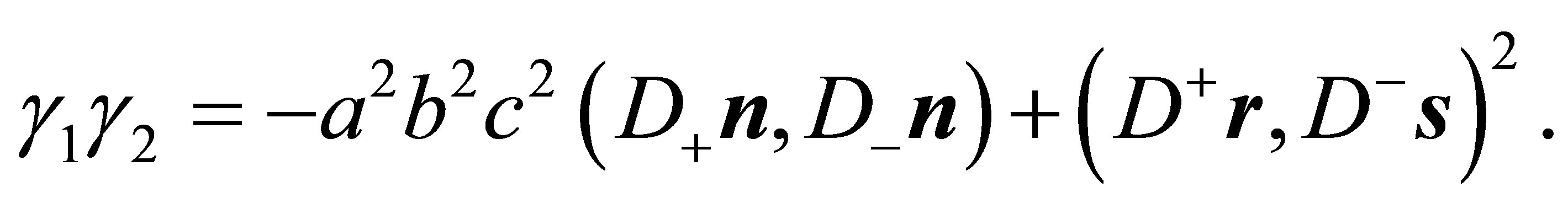 (33)
(33)
In contrast to the verification of (24), where diagonality condition (7) holds, the analogous expression 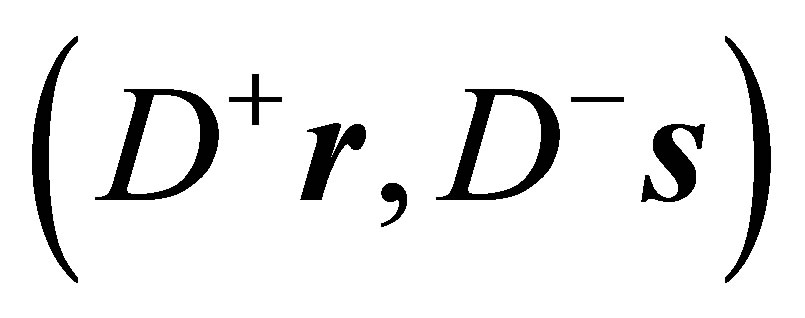 in (33) need not be zero.
in (33) need not be zero.
Step 3: Applying the identity of Lagrange (16) again leads to

Substituting the involved cross products according to Corollary 2 and considering diagonality condition (7) one obtains

or
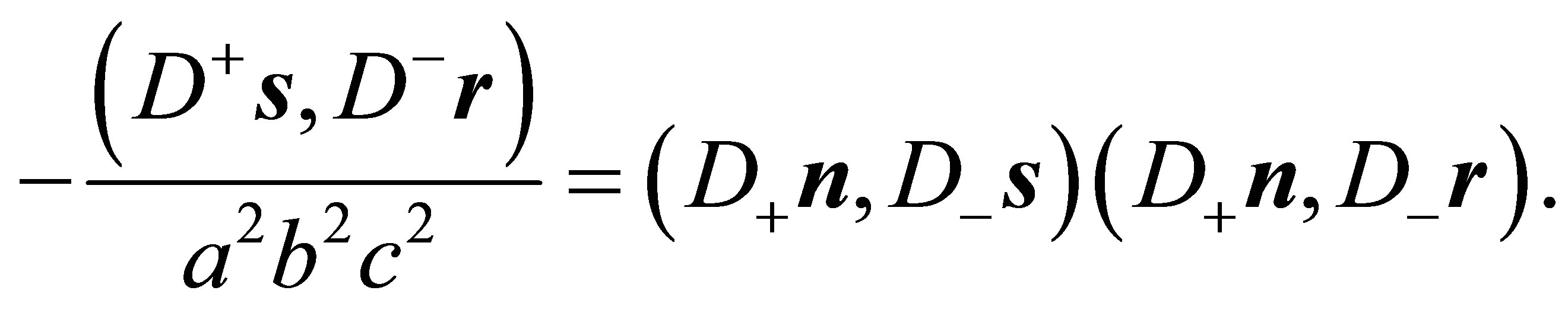 (34)
(34)
Squaring both sides of (34) and substituting the expressions from (31) leads to:

Substitution of (33) results in Equation
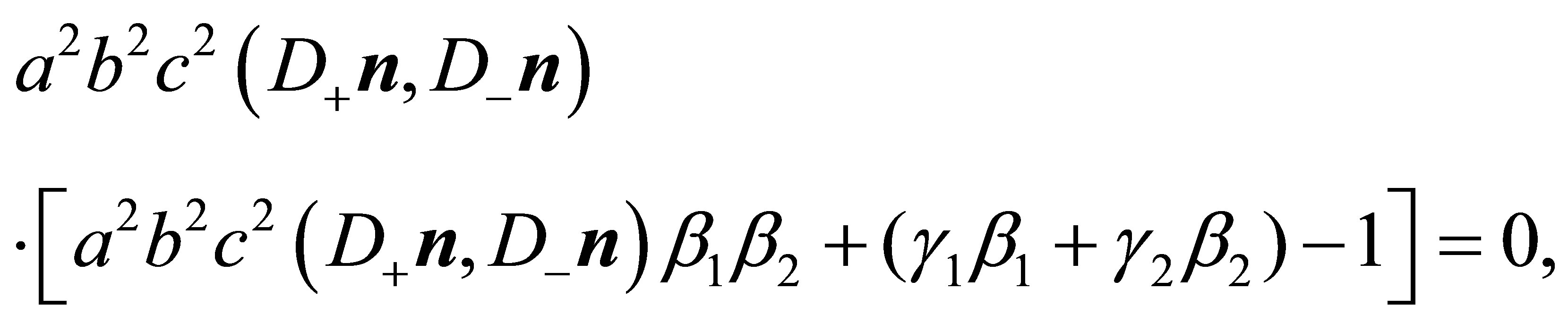
or
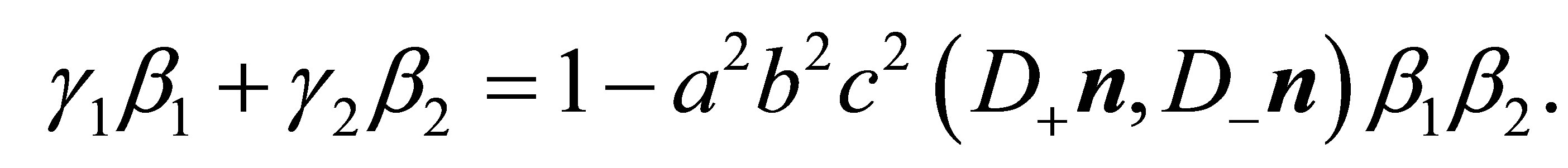 (35)
(35)
Substitution of (35) in (32) leads to:
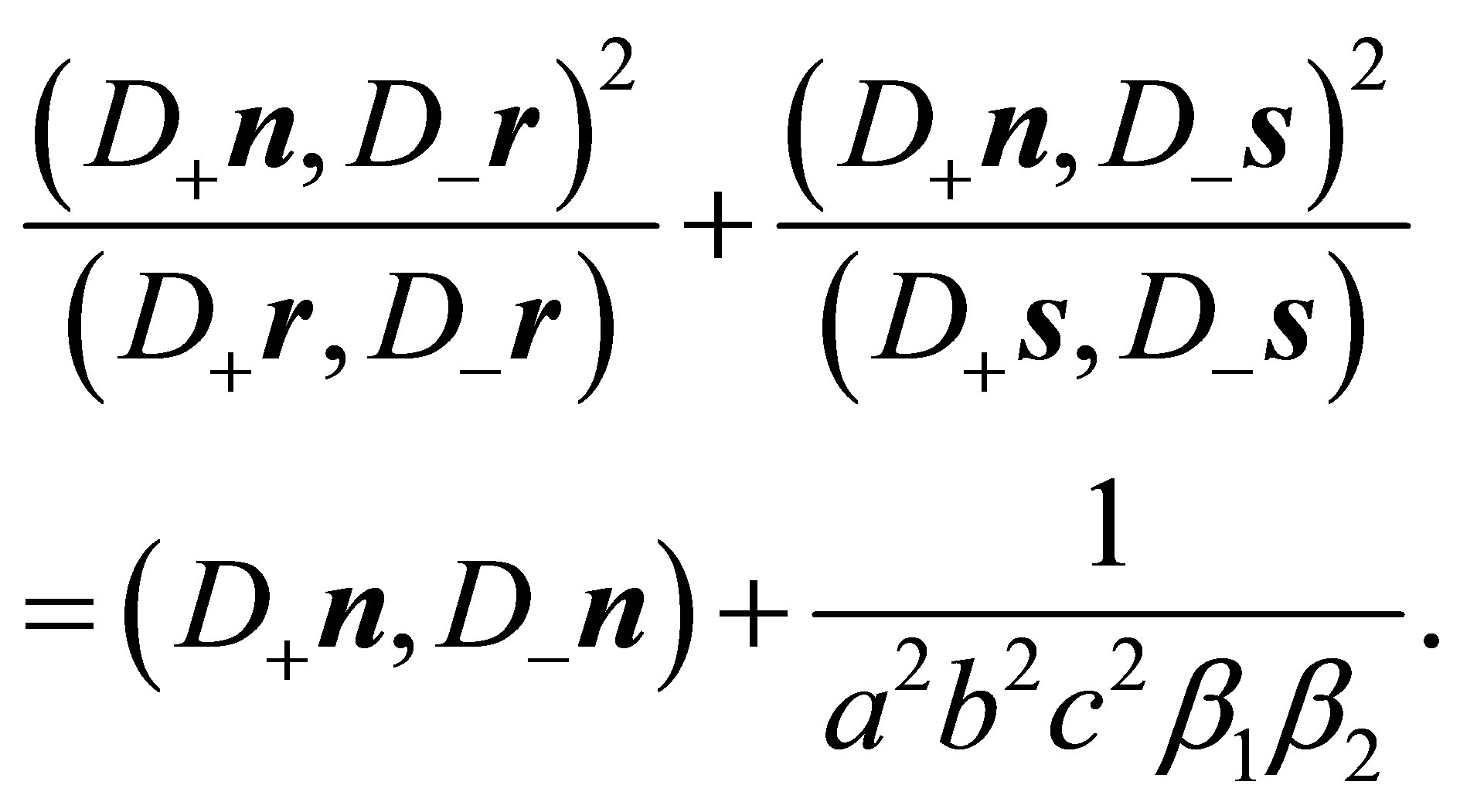 (36)
(36)
Because of (24)
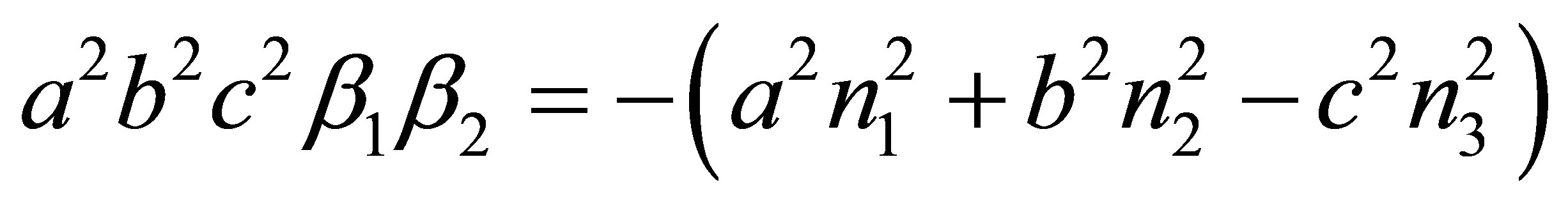 (37)
(37)
holds and with (15) one finally obtains relation (25)
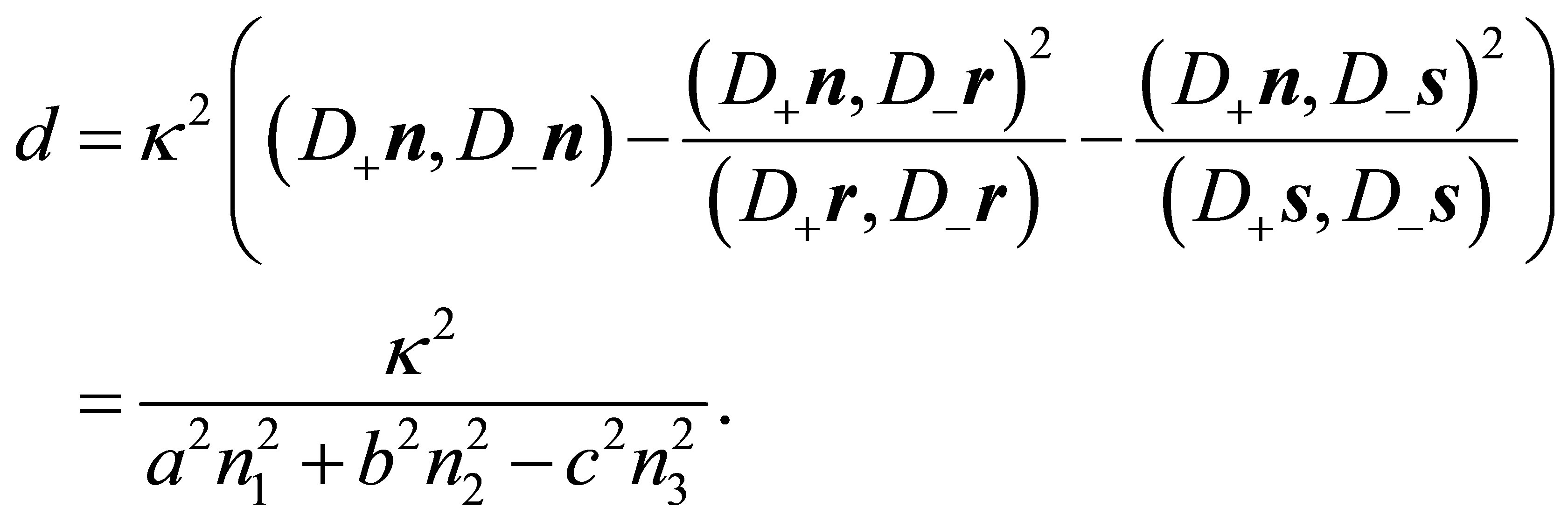

Corollary 3: Under the assumptions of Theorem 1 and in case of a hyperboloid of one sheet assuming  for
for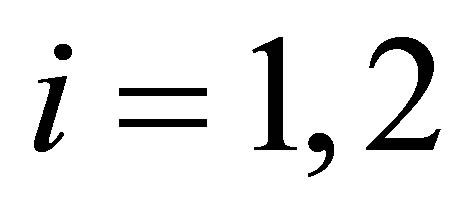 , in case of a hyperboloid of two sheets assuming
, in case of a hyperboloid of two sheets assuming  for
for 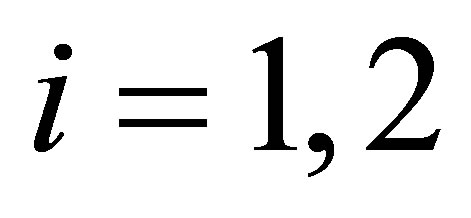 and
and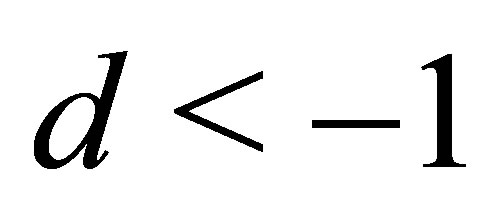 , the intersection of hyperboloid (1) and a plane with unit normal vector
, the intersection of hyperboloid (1) and a plane with unit normal vector ![]() and distance
and distance ![]() from the origin is an ellipse, the area
from the origin is an ellipse, the area  of which is given by:
of which is given by:
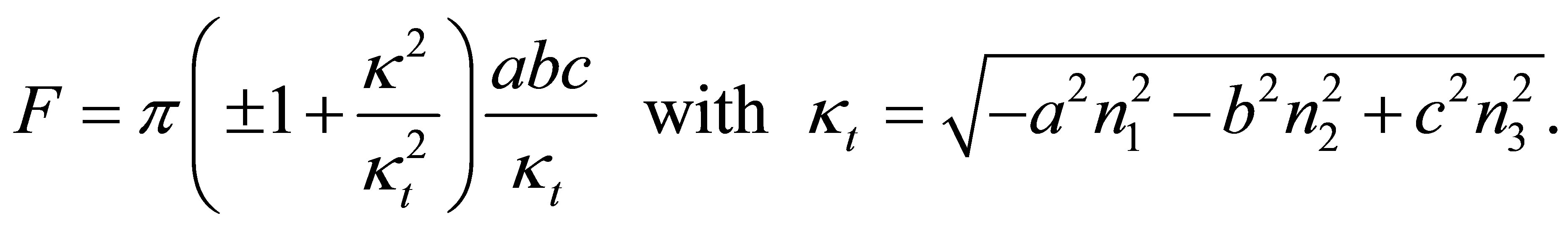
In this formula 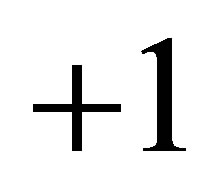 corresponds to a hyperboloid of one sheet,
corresponds to a hyperboloid of one sheet,  to a hyperboloid of two sheets.
to a hyperboloid of two sheets.
Proof: With 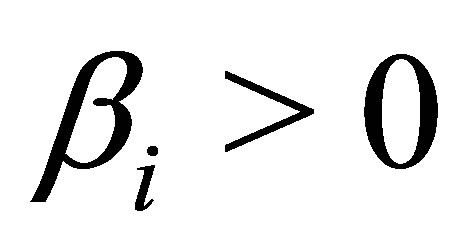 for
for 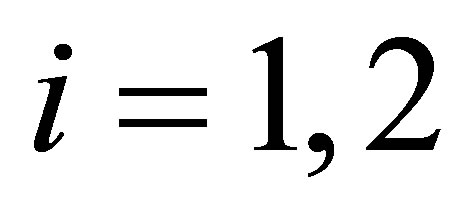 both sides of Equation (37) are positive. Thus
both sides of Equation (37) are positive. Thus ![]() according to (25) is negative for
according to (25) is negative for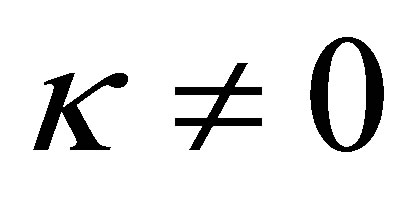 , and zero for
, and zero for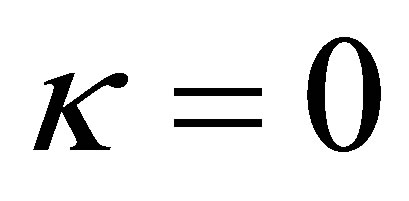 . In case of a hyperboloid of one sheet the numerator
. In case of a hyperboloid of one sheet the numerator 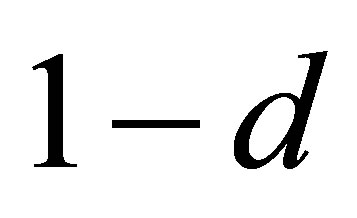 of
of 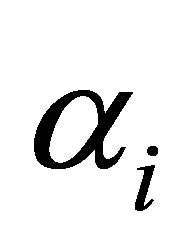 for
for 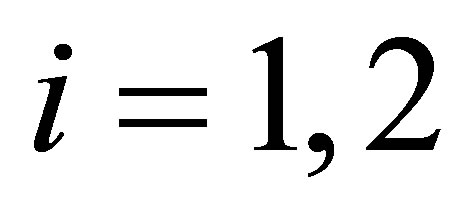 in (12) is positive. In case of a hyperboloid of two sheets the numerator
in (12) is positive. In case of a hyperboloid of two sheets the numerator 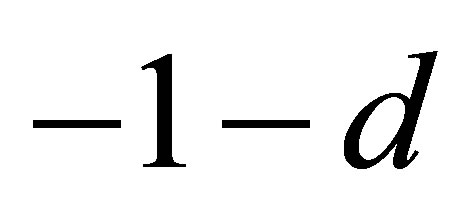 of
of  for
for  in (12) is positive for
in (12) is positive for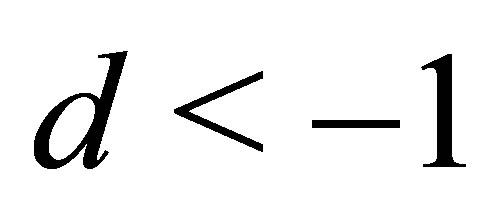 . Substituting
. Substituting 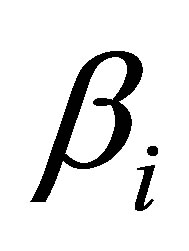 for
for 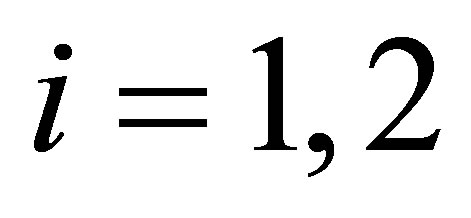 according to (18),
according to (18), 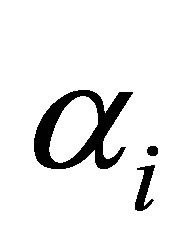 for
for 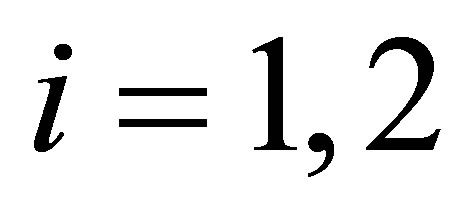 are positive. In both of these cases therefore the curve of intersection (11) is an ellipse with the semi axes
are positive. In both of these cases therefore the curve of intersection (11) is an ellipse with the semi axes
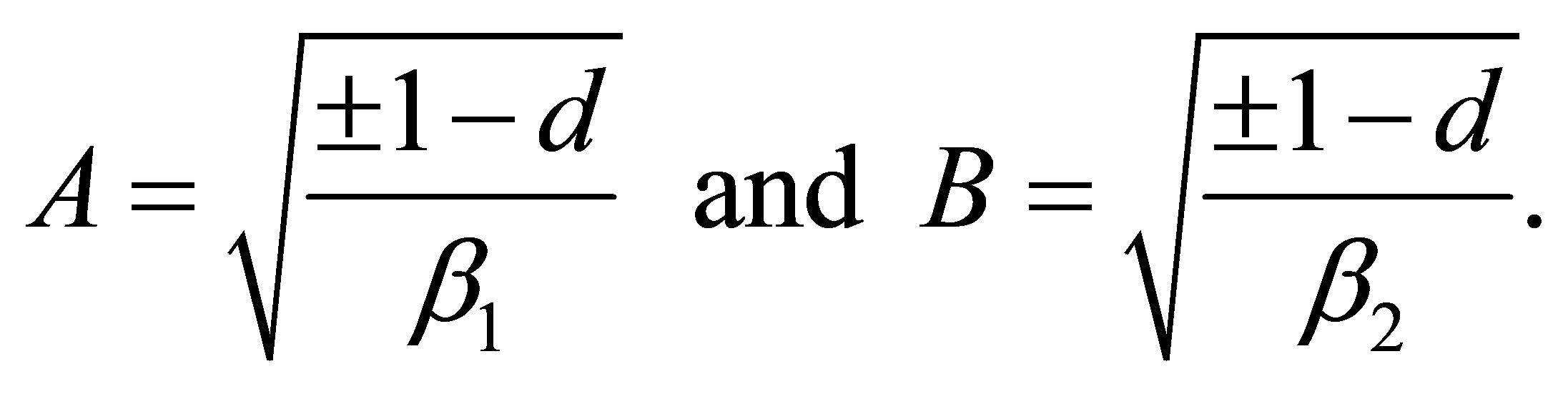
The area of the ellipse is given by:

By applying (25) and (37) one obtains the formula in Corollary 3.
Remark 1: In the special case that the plane of intersection of the hyperboloid is parallel to the x-y-plane, i.e. the normal vector 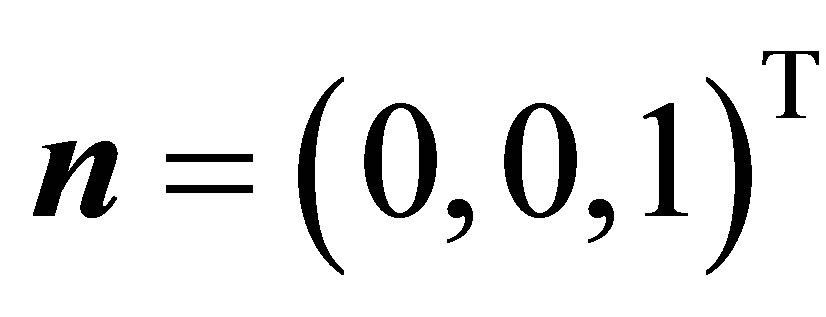 with
with 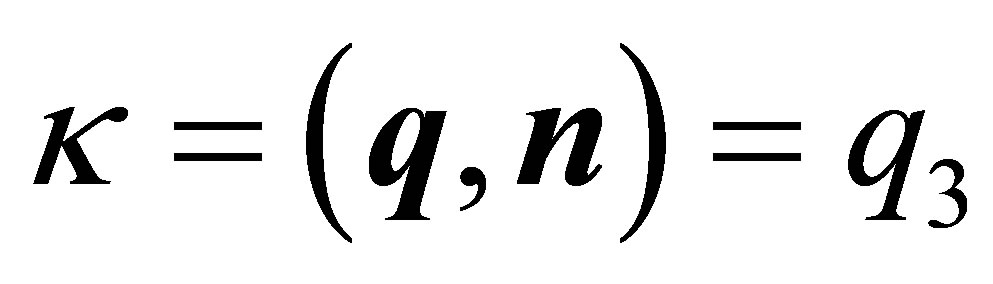 and furthermore
and furthermore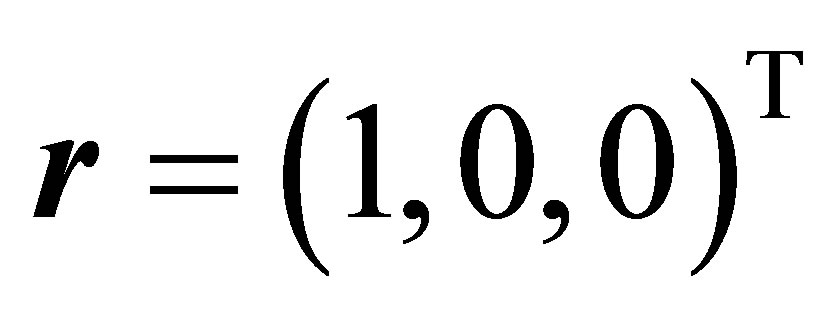 ,
, 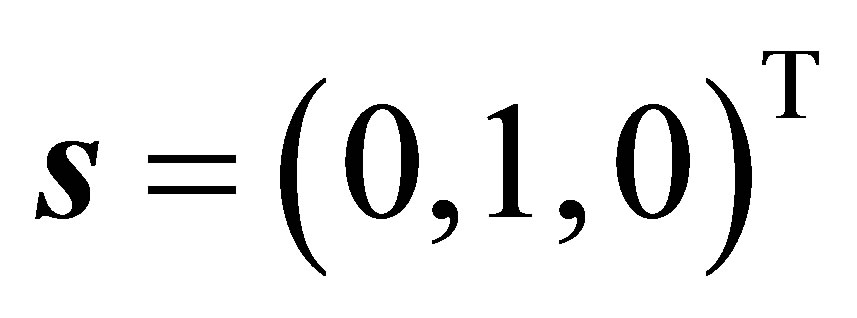 can be chosen satisfying (4), (5), (6), (7) and
can be chosen satisfying (4), (5), (6), (7) and ,
, 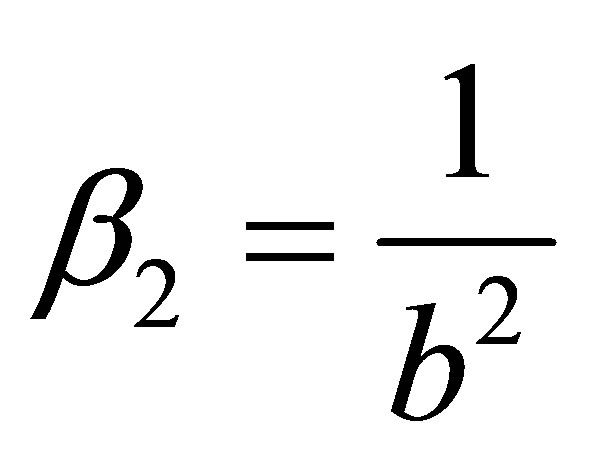 , the formula for the area of the ellipse of intersection reduces to:
, the formula for the area of the ellipse of intersection reduces to:

The same result is obtained from (1) putting  and calculating the area of an ellipse with the semi axes
and calculating the area of an ellipse with the semi axes
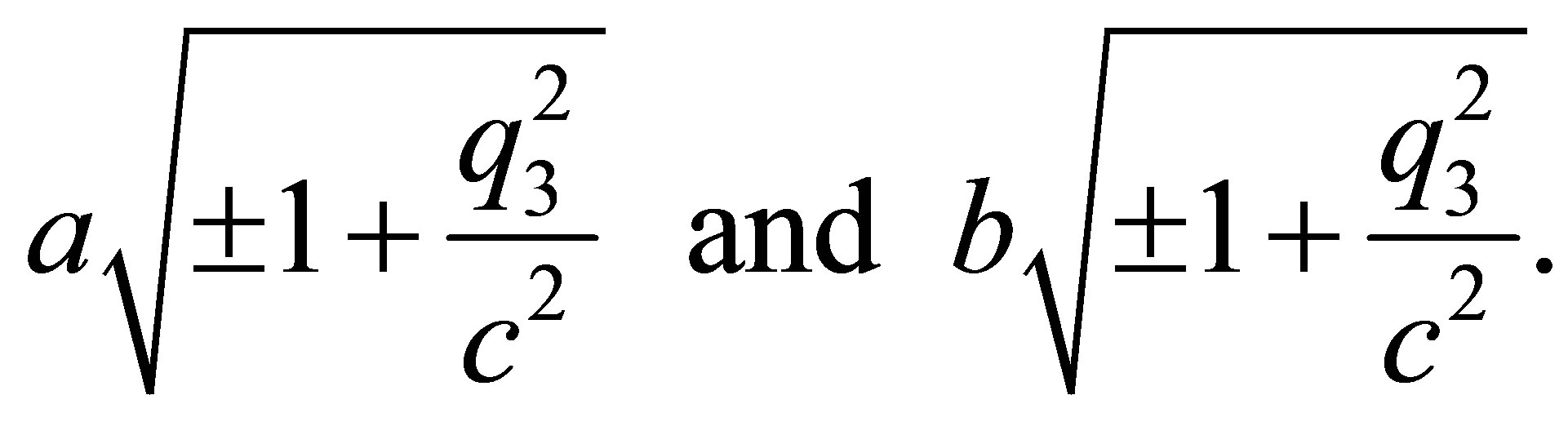
As stated above in case of a hyperboloid of two sheets
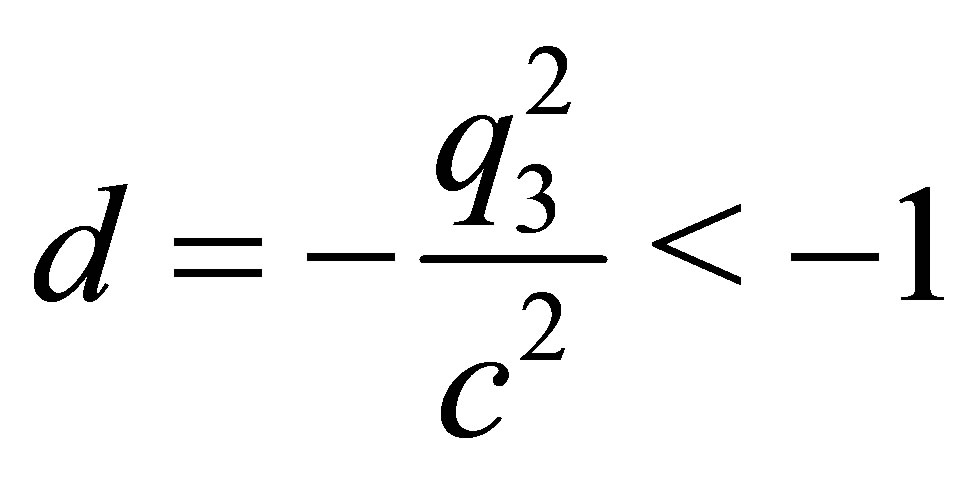 has to be assumed.
has to be assumed.
Remark 2: Assuming 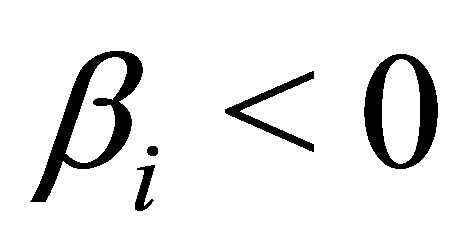 for i = 1, 2 and
for i = 1, 2 and 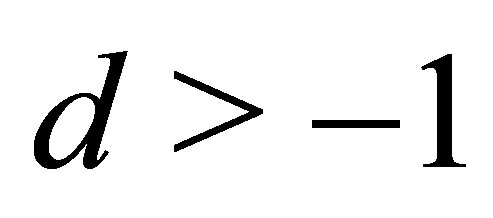 in case of a hyperboloid of two sheets would also result in positive
in case of a hyperboloid of two sheets would also result in positive 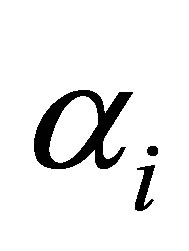 for
for 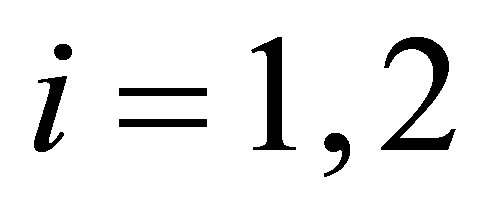 according to (18) and (12). However for two vectors
according to (18) and (12). However for two vectors  and
and ![]() in
in  the conditions
the conditions  for
for  and
and  cannot be fulfilled simultaneously.
cannot be fulfilled simultaneously.
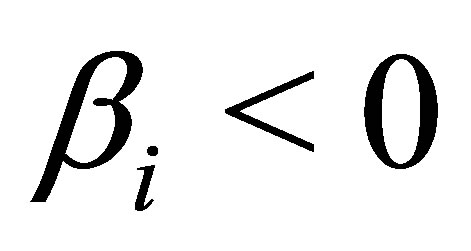 for
for 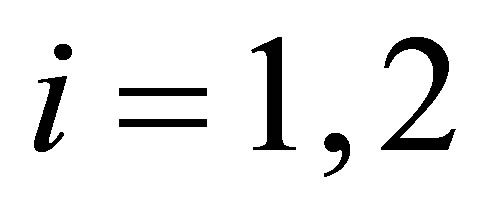 would imply
would imply
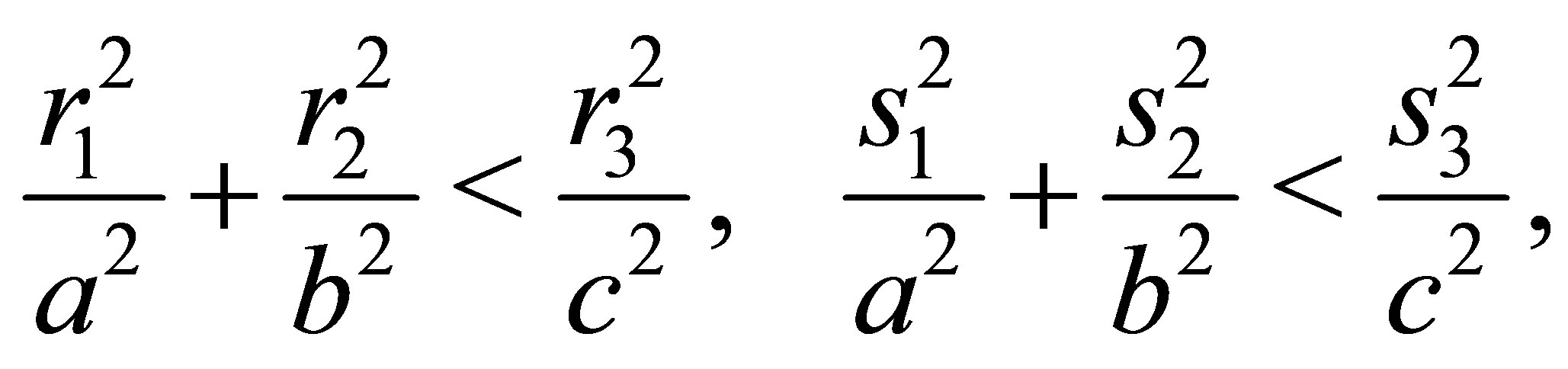
and thus
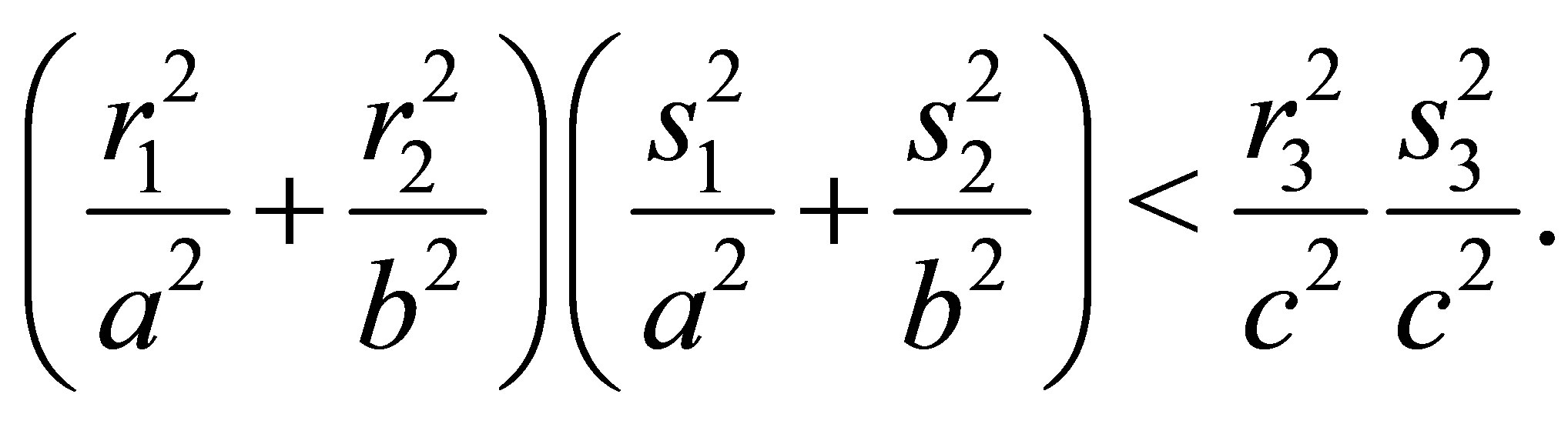
Because of 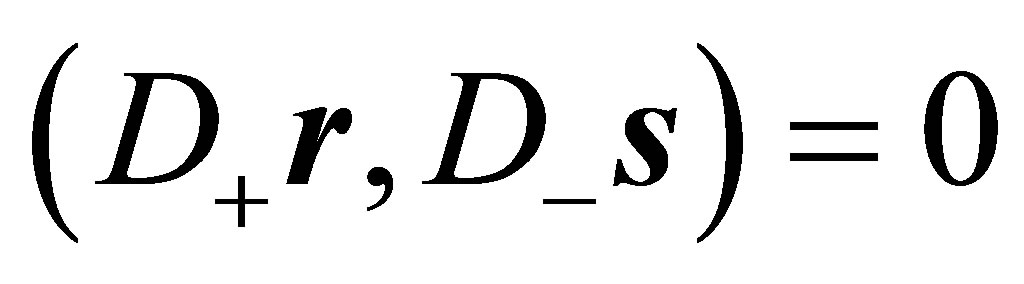

holds. Substituting this Equation into the above inequality gives
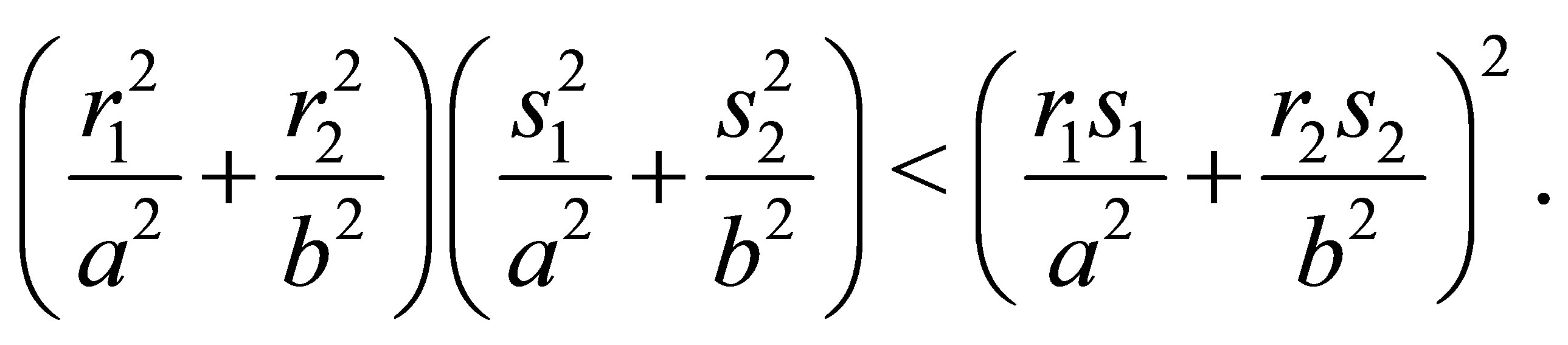
Deleting equal terms on both sides of the inequality finally results in
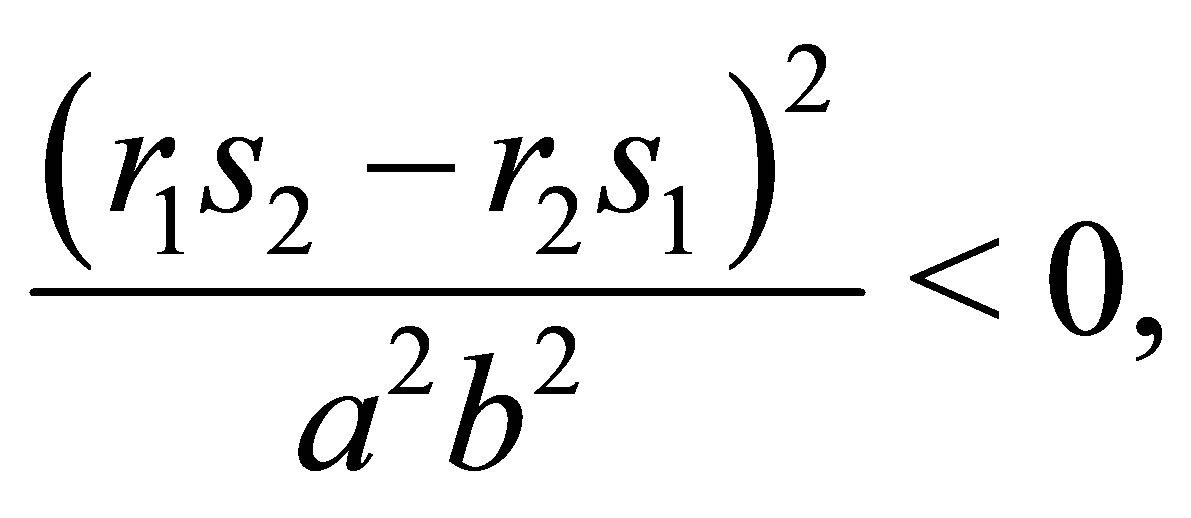
which is impossible for vectors  and
and ![]() with real components.
with real components.
Corollary 4: Under the assumptions of Theorem 1 and assuming  and
and  the intersection of hyperboloid (1) and a plane with unit normal vector
the intersection of hyperboloid (1) and a plane with unit normal vector ![]() and distance
and distance ![]() from the origin is for
from the origin is for 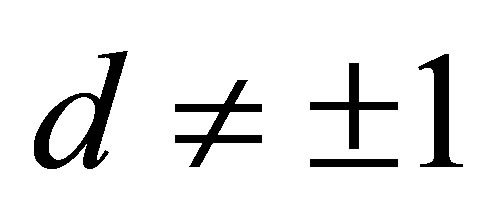 a hyperbola and for
a hyperbola and for  a pair of straight lines.
a pair of straight lines.
Proof: With 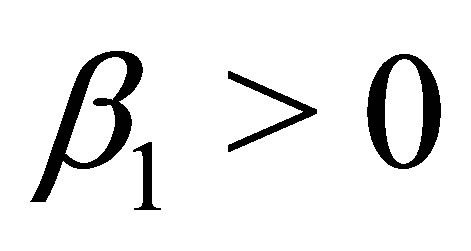 and
and 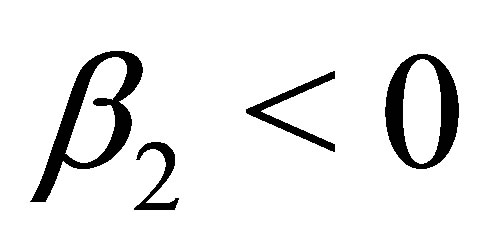 both sides of Equation (37) are negative. Thus
both sides of Equation (37) are negative. Thus ![]() according to (25) is positive or zero. In case
according to (25) is positive or zero. In case 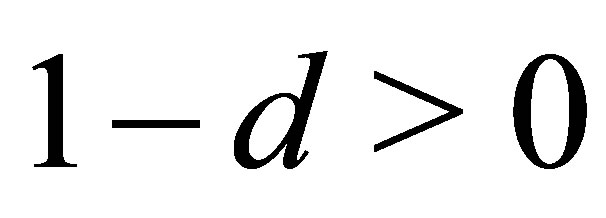 holds for a hyperboloid of one sheet with the semi axes
holds for a hyperboloid of one sheet with the semi axes
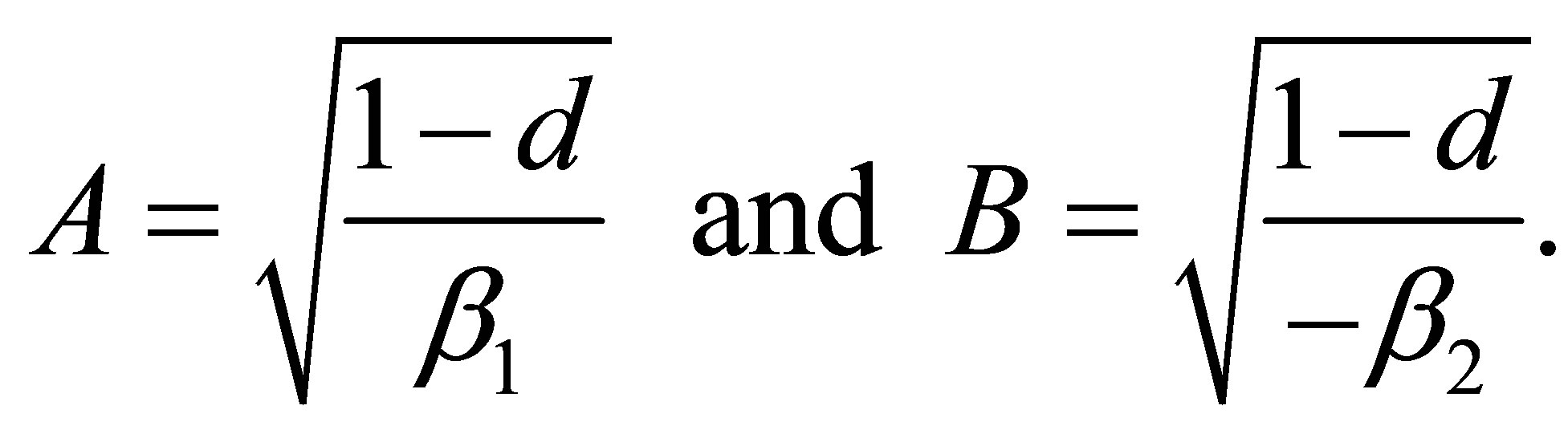
the line of intersection is a hyperbola of the form
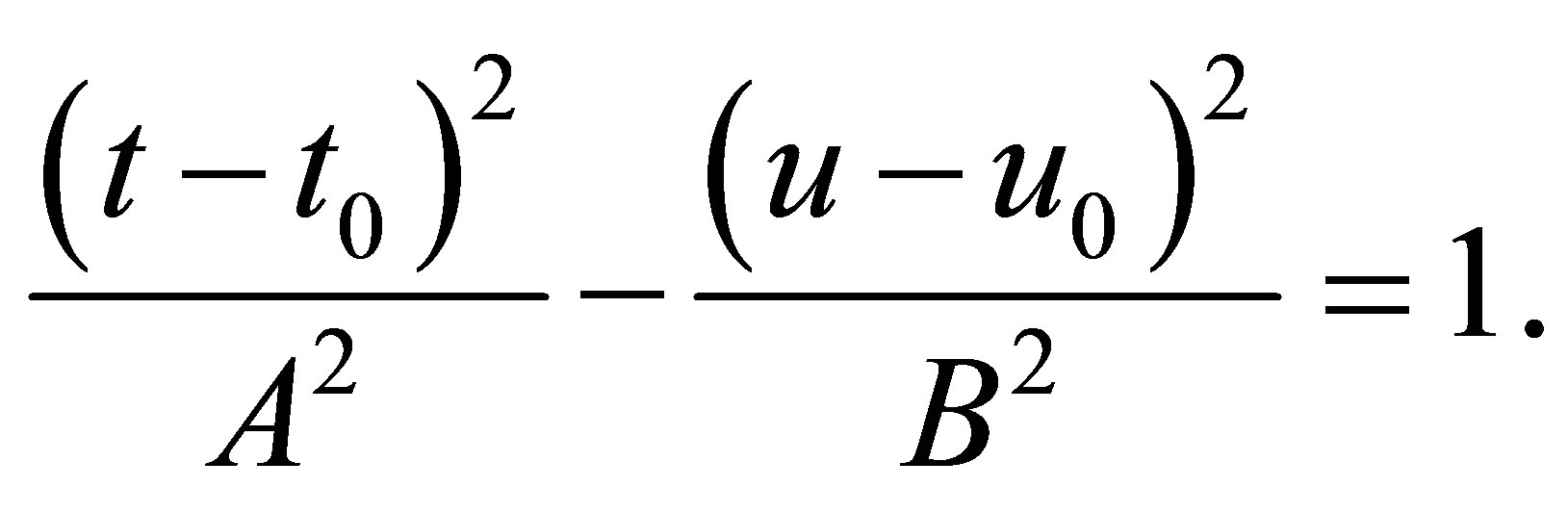
In case 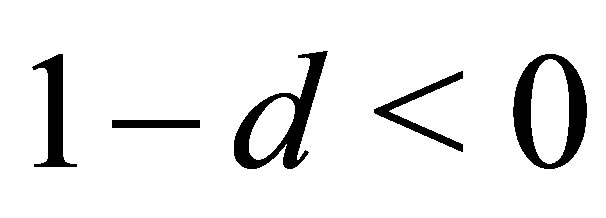 holds for a hyperboloid of one sheet with the semi axes
holds for a hyperboloid of one sheet with the semi axes

the line of intersection is a hyperbola of the form

with the axes interchanged.
Since ![]() is positive or zero,
is positive or zero, 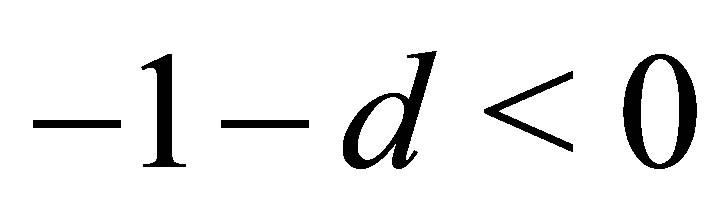 is fulfilled, so that for a hyperboloid of two sheets with the semi axes
is fulfilled, so that for a hyperboloid of two sheets with the semi axes
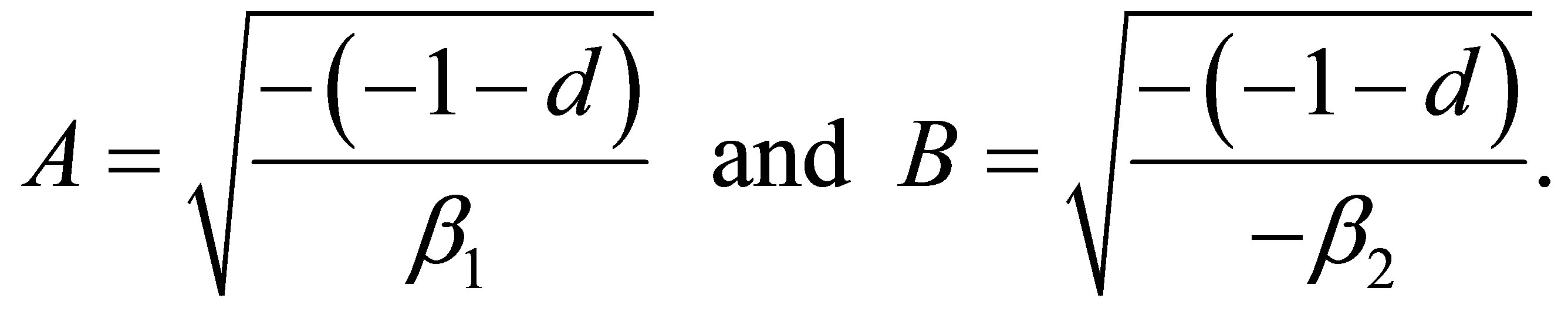
the line of intersection is a hyperbola of the form
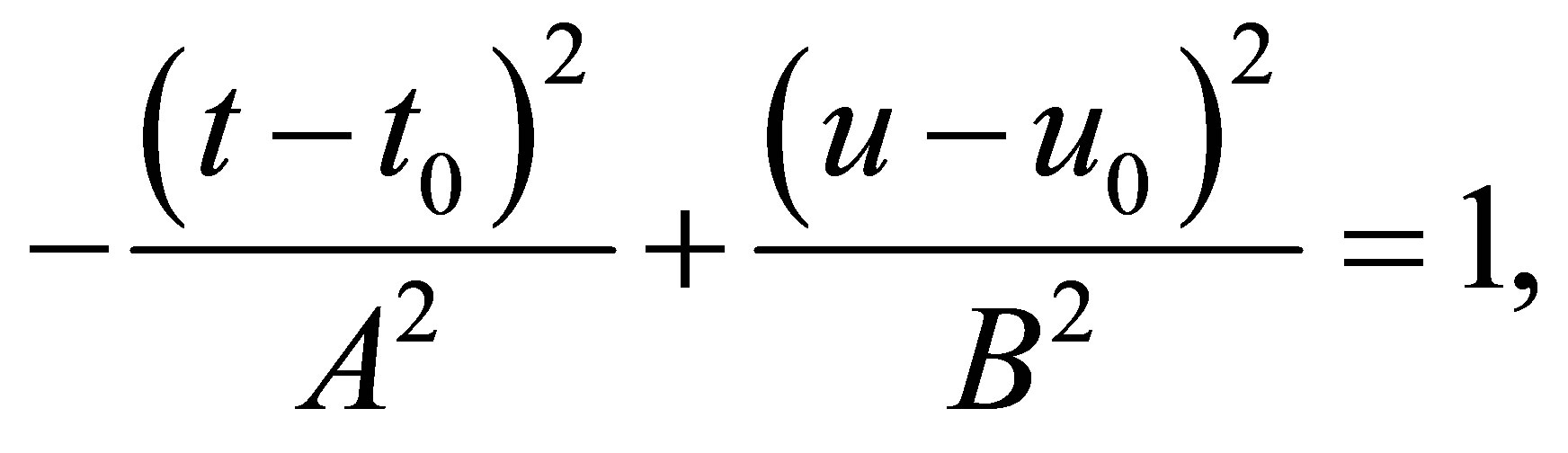
with the axes interchanged, as in the previous case.
In case of 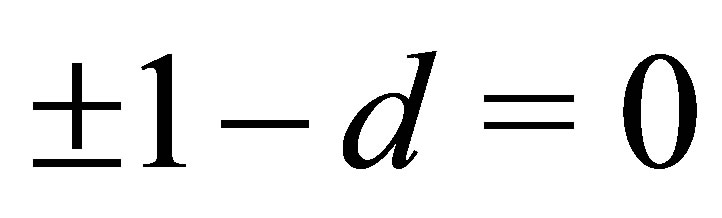 according to (8), after substituting
according to (8), after substituting  and
and  from (18), the line of intersection is a pair of straight lines of the form
from (18), the line of intersection is a pair of straight lines of the form
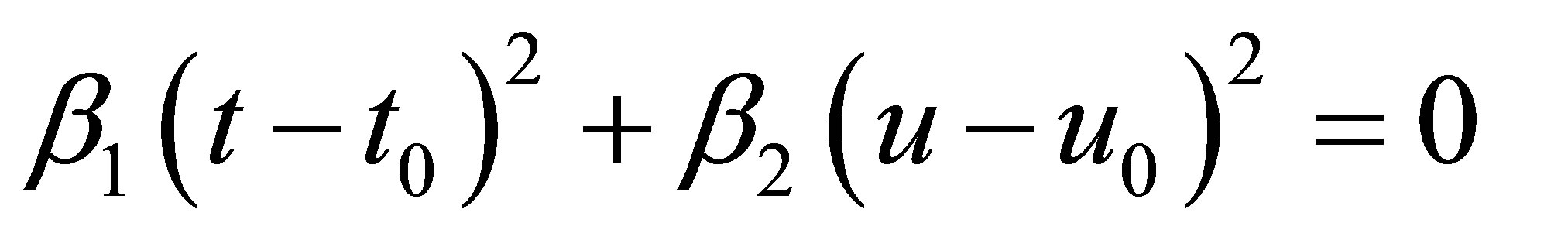
or
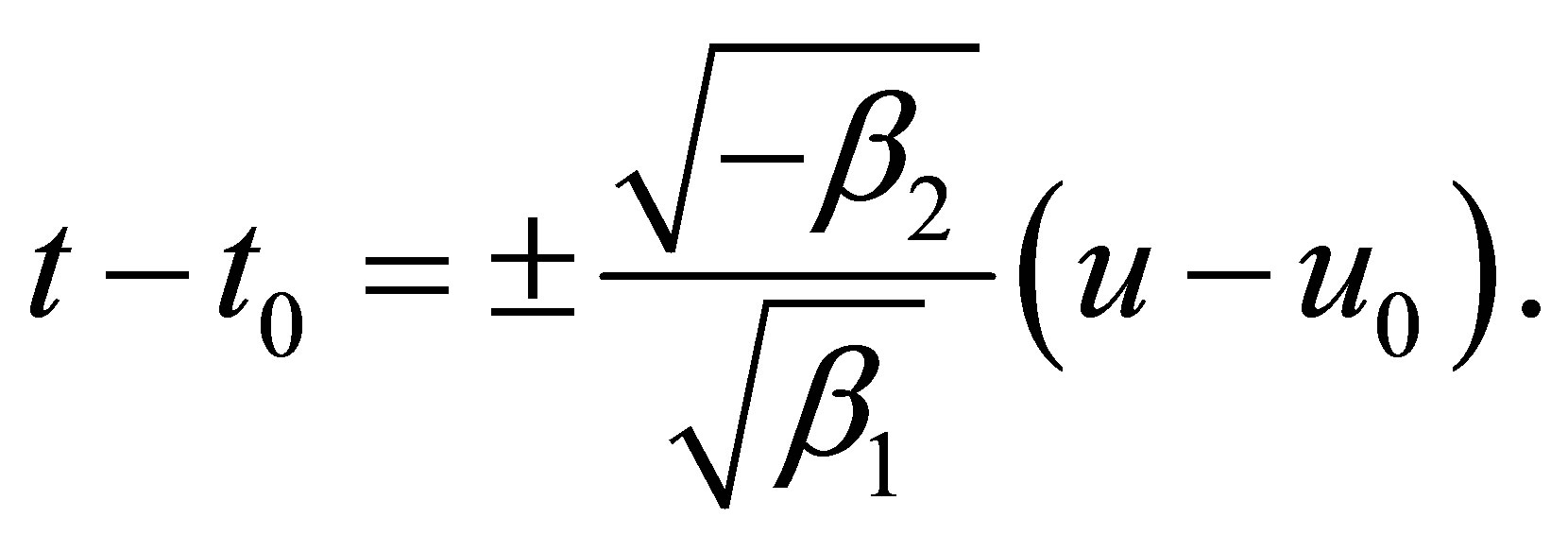

Remark 3: For 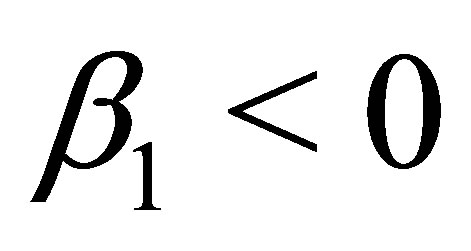 and
and 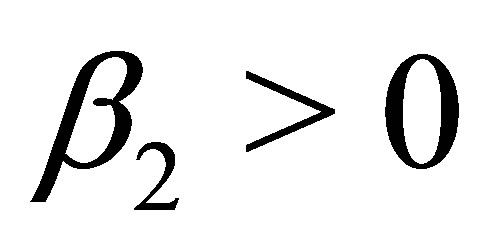 the roles of the variables
the roles of the variables 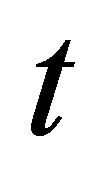 and
and ![]() have to be interchanged.
have to be interchanged.
5. The Center of the Conic
Substituting 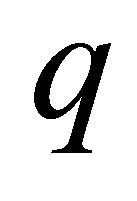 according to (14) in formulars (9) for the coordinates
according to (14) in formulars (9) for the coordinates  of the center of the conic in the plane spanned by
of the center of the conic in the plane spanned by  and
and ![]() one obtains using (7):
one obtains using (7):
 (38)
(38)
The center ![]() of the conic in
of the conic in  is given by:
is given by:
 (39)
(39)
Theorem 3: Let the assumptions of Theorem 1 be fulfilled with  and
and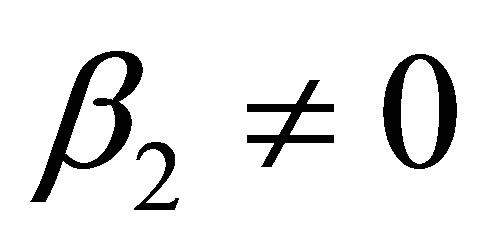 . For the center
. For the center ![]() of the conic of intersection in
of the conic of intersection in  holds:
holds:
 (40)
(40)
Proof: With diagonal matrices 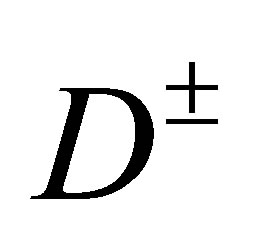 from (27) and
from (27) and  from (22) utilising
from (22) utilising

and (37) one obtains a representation of ![]() equivalent to (40):
equivalent to (40):
 (41)
(41)
It is sufficient to show that for the difference
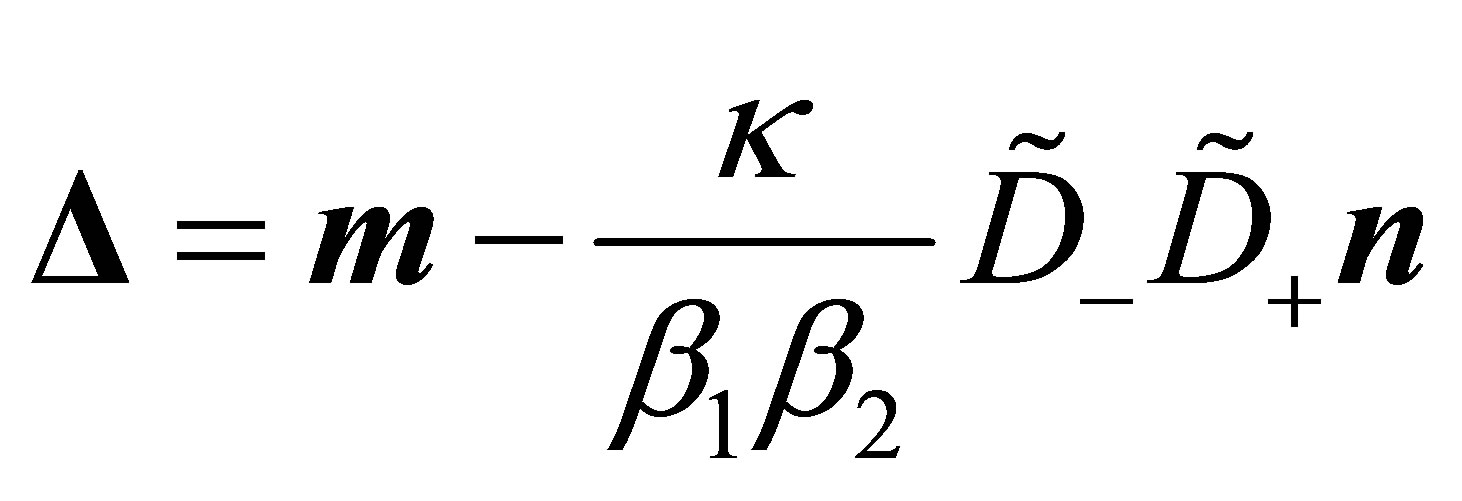
 holds. Thus the coefficients in the expansion of
holds. Thus the coefficients in the expansion of ![]() in
in  with respect to the orthonormal basis
with respect to the orthonormal basis  are zero, i.e.,
are zero, i.e., ![]() is the zero vector.
is the zero vector.
Applying representation (39) and (24) one obtains:
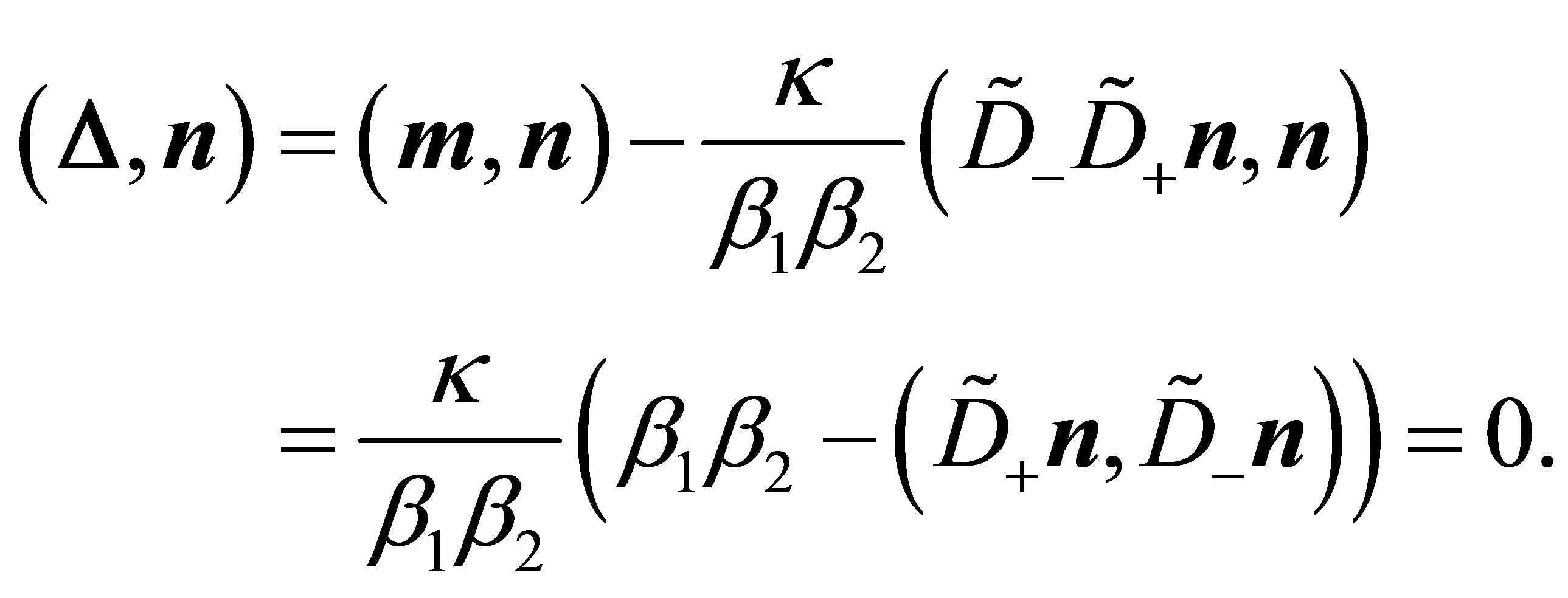
Furthermore one obtains:
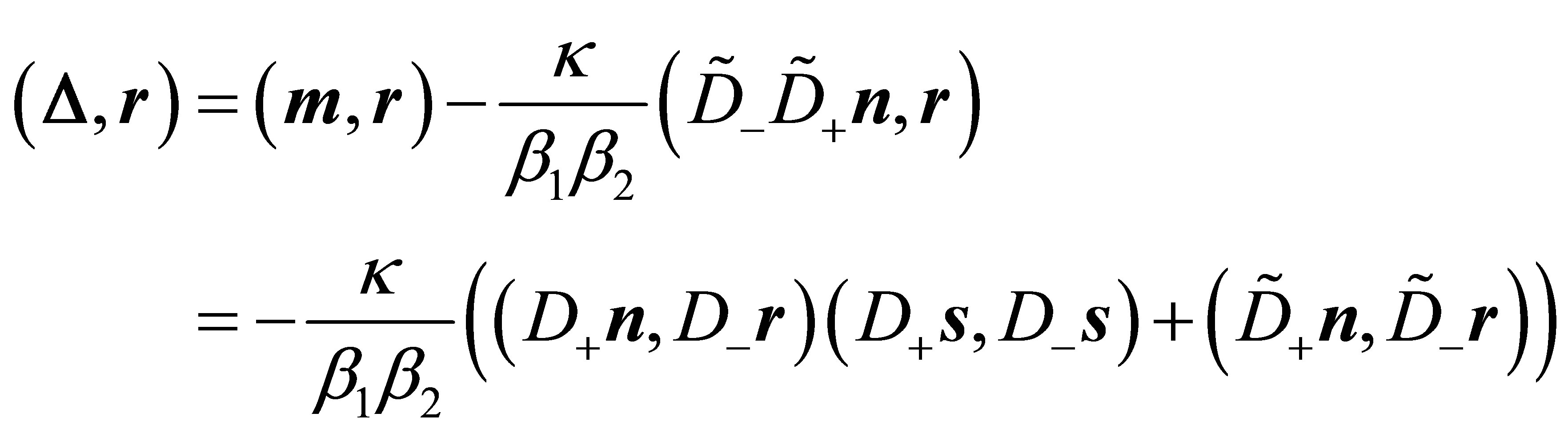
and by interchanging the roles of  and
and![]() :
:
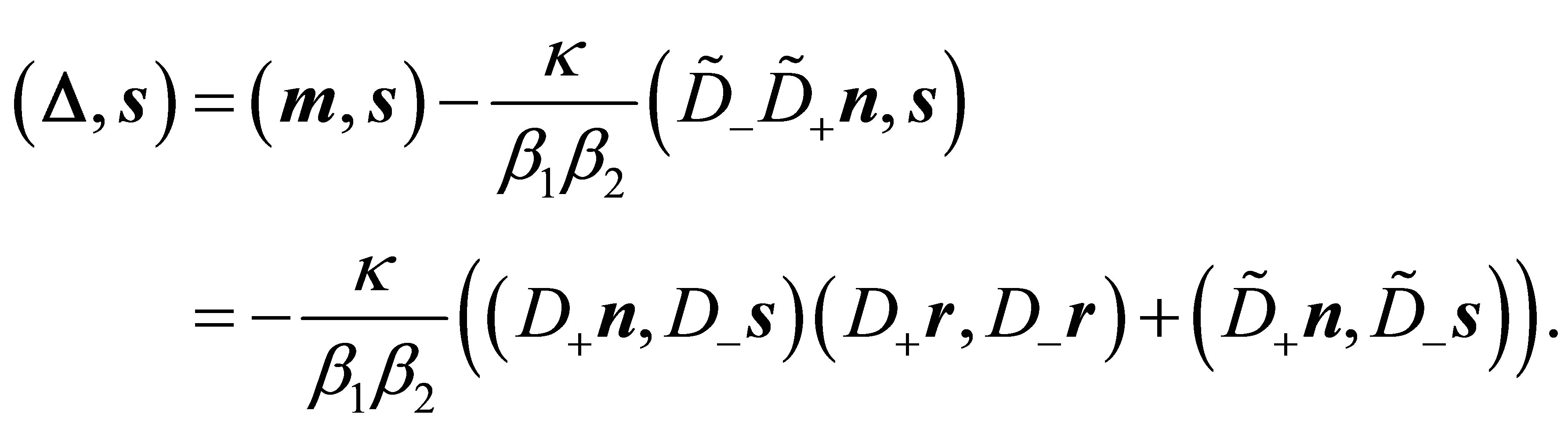
Both previous expressions are zero; this follows by applying diagonality condition (7), the identity of Lagrange (16) and Corollary 2:

Interchanging the roles of  and
and ![]() leads to:
leads to:
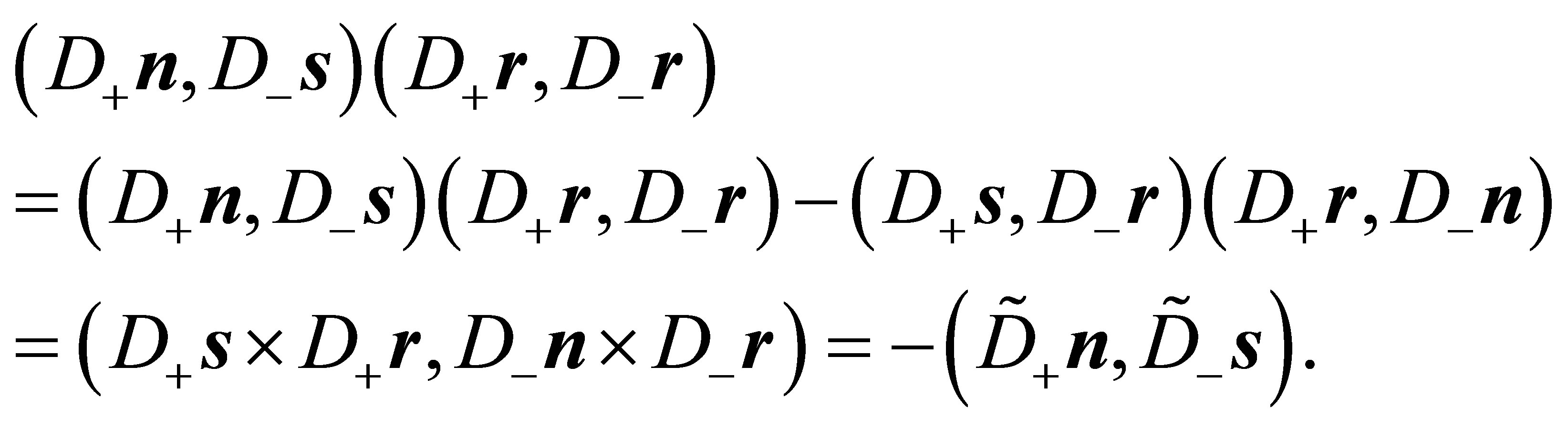

Corollary 5: Under the same assumptions as in Corollary 3 the line of intersection of hyperboloid (1) and a plane is an ellipse with the semi axes 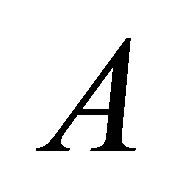 and
and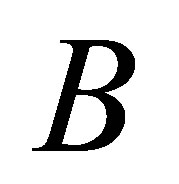 , given in the proof of Corollary 3, and the apexes
, given in the proof of Corollary 3, and the apexes

Proof: Clearly  and
and  are points of the plane cutting the hyperboloid. In order to show that they are belonging to the ellipse of intersection, it has to be verified that they are situated on hyperboloid (1), i.e. the following equalities hold:
are points of the plane cutting the hyperboloid. In order to show that they are belonging to the ellipse of intersection, it has to be verified that they are situated on hyperboloid (1), i.e. the following equalities hold:


This can be verified using ![]() in the form (39) and employing condition (7) and Equation (15).
in the form (39) and employing condition (7) and Equation (15). 
Corollary 6: Under the same assumptions as in Corollary 4 the line of intersection of hyperboloid (1) and a plane is in case of  a hyperbola with the semi axes
a hyperbola with the semi axes  and
and  given in the proof of Corollary 4. The center of the hyperbola given in (9) is equal to the point of intersection of the asymptotes of the hyperbola.
given in the proof of Corollary 4. The center of the hyperbola given in (9) is equal to the point of intersection of the asymptotes of the hyperbola.
Proof: The asymptotes of the hyperbola are given by
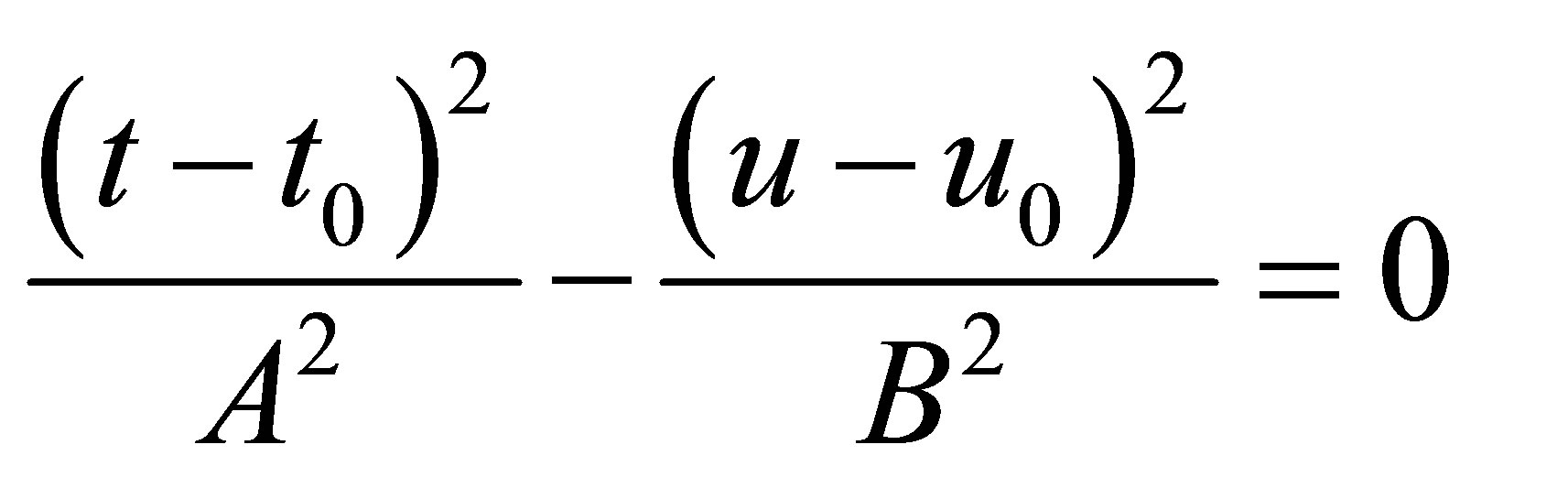
with
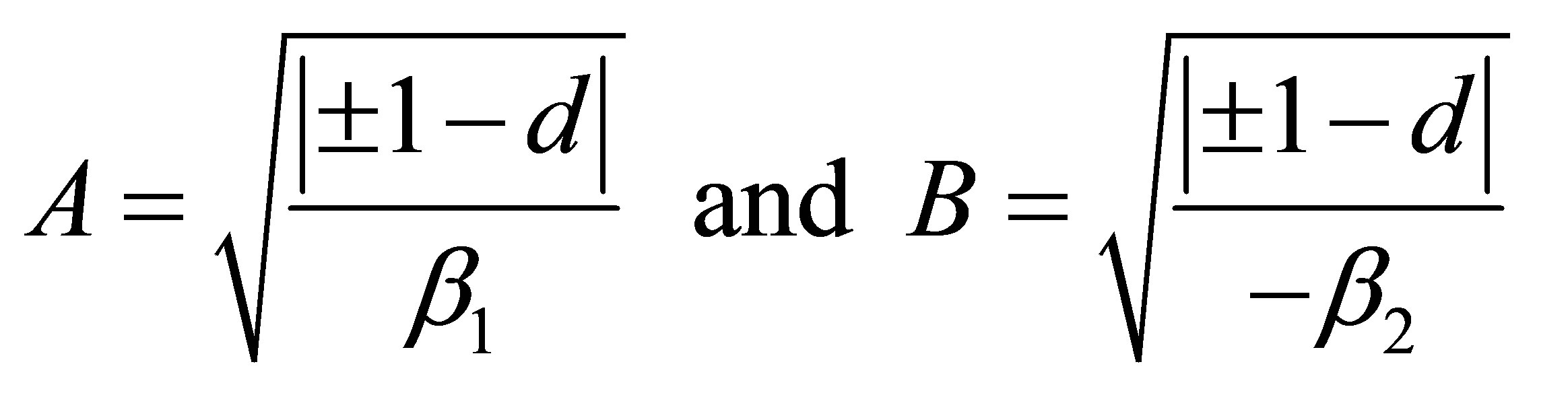
or

The point of intersection of the asymptotes 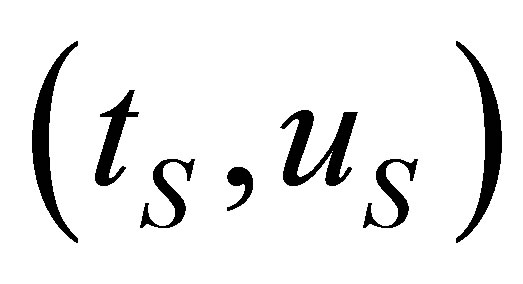 fulfills the following linear system
fulfills the following linear system
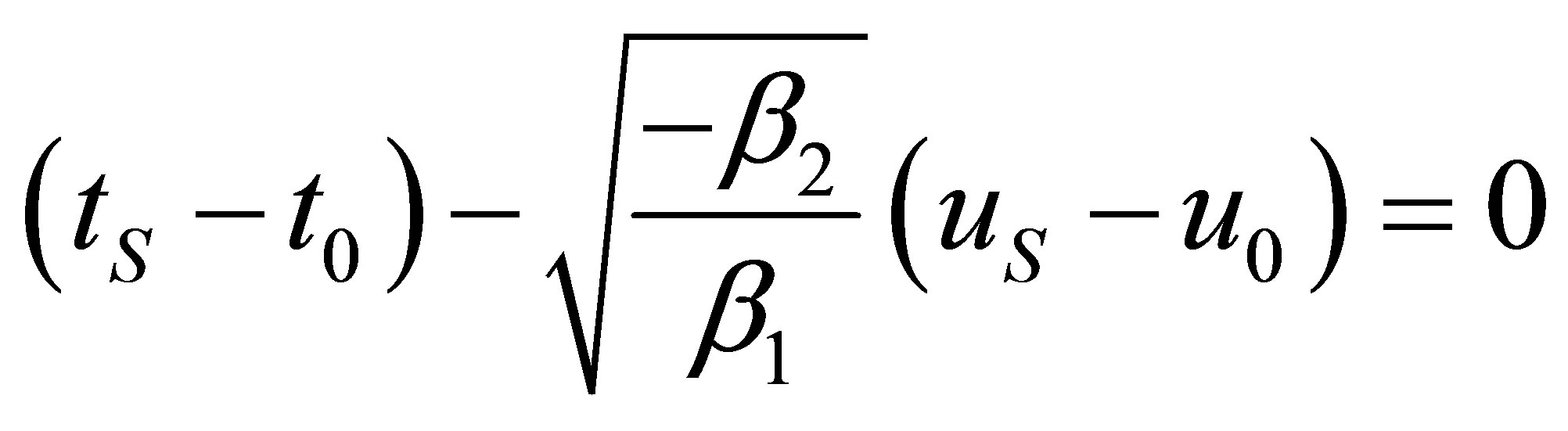
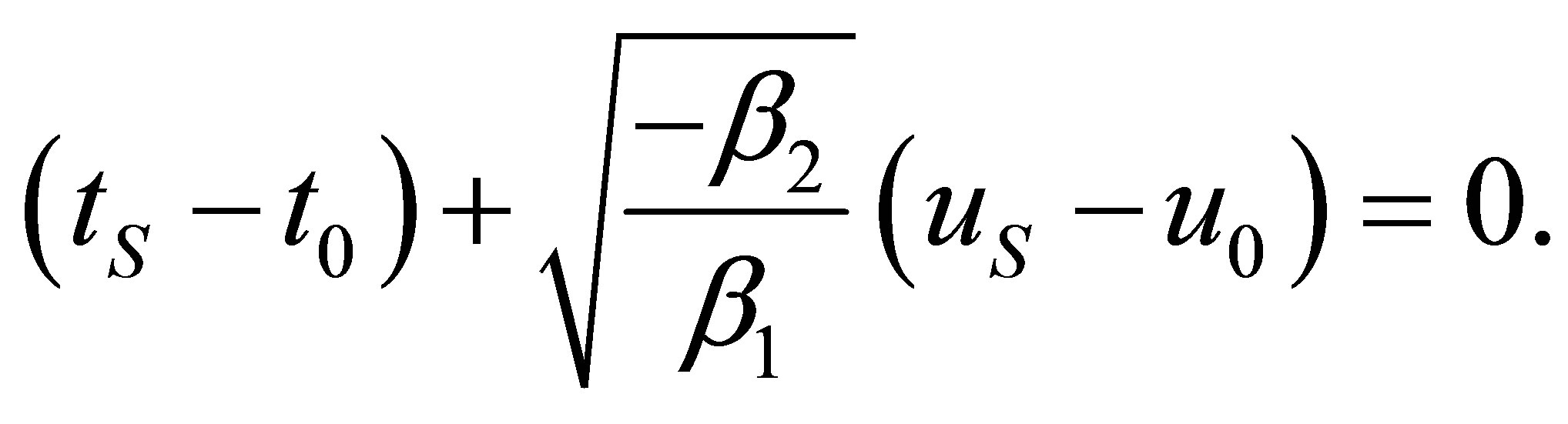
As this homogeneous linear system for the unknowns  and
and  has a nonzero determinant, it can only have the trivial solution, which implies
has a nonzero determinant, it can only have the trivial solution, which implies
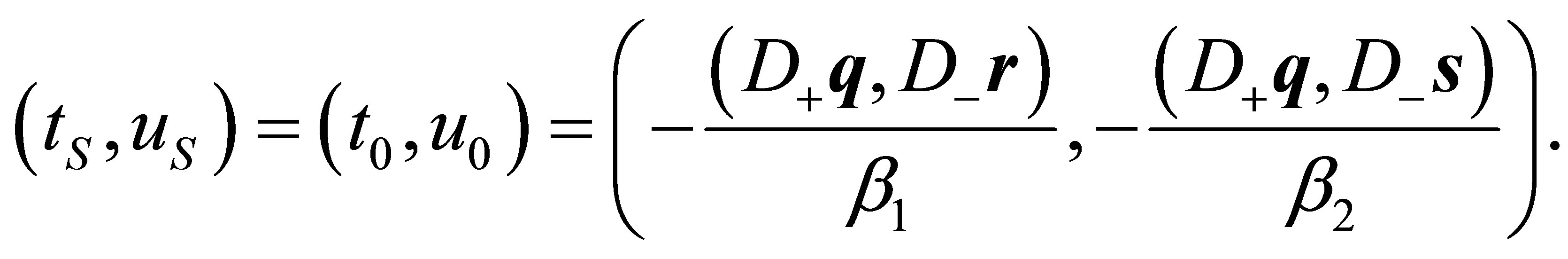

Corollary 7:

Proof: This can be verified, as in the proof of Corollary 5, using ![]() in the form (39) and employing condition (7) and Equation (15).
in the form (39) and employing condition (7) and Equation (15).

Because of Corollary 7
 holds, if and only if
holds, if and only if ![]() is an interior point of a hyperboloid of one sheet,
is an interior point of a hyperboloid of one sheet,
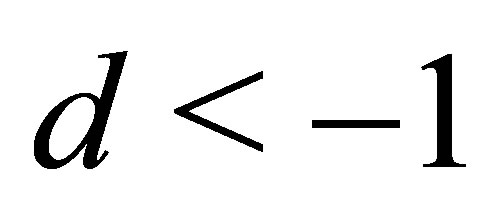 holds, if and only if
holds, if and only if ![]() is an interior point of a hyperboloid of two sheets,
is an interior point of a hyperboloid of two sheets,
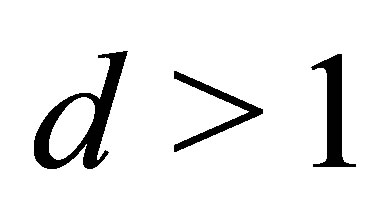 holds, if and only if
holds, if and only if ![]() is an exterior point of a hyperboloid of one sheet,
is an exterior point of a hyperboloid of one sheet,
 holds, if and only if
holds, if and only if ![]() is an exterior point of a hyperboloid of two sheets.
is an exterior point of a hyperboloid of two sheets.
In case of  one obtains from (25)
one obtains from (25)
 .
.
The center (40) of the conic of intersection therefore becomes a tangent contact point
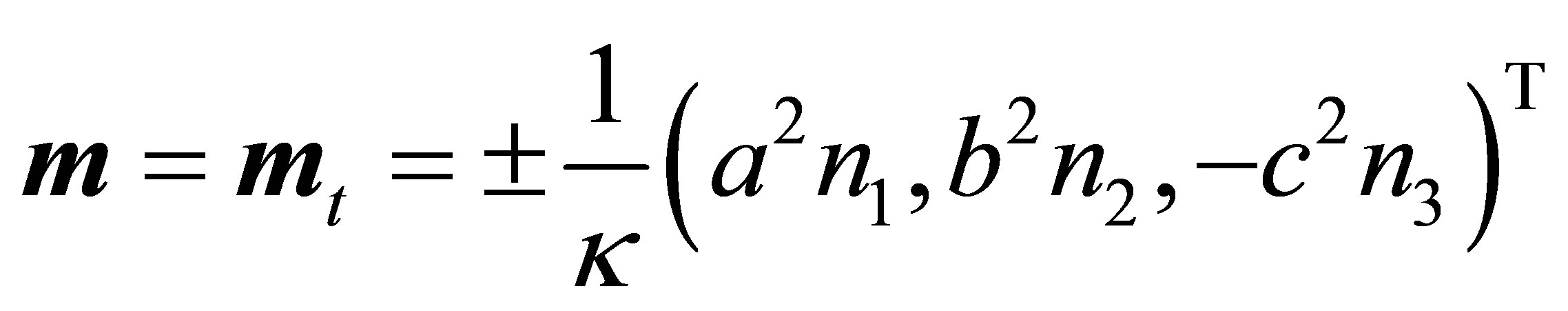
of hyperboloid and plane, where the ![]() -sign corresponds to a hyperboloid of one sheet and the
-sign corresponds to a hyperboloid of one sheet and the  -sign to a hyperboloid of two sheets.
-sign to a hyperboloid of two sheets.
Example: Determine the line of intersection of hyperboloid (1) and a plane, having the normal vector  and containing the point
and containing the point , situated in the interior or on the boundary of (1):
, situated in the interior or on the boundary of (1):
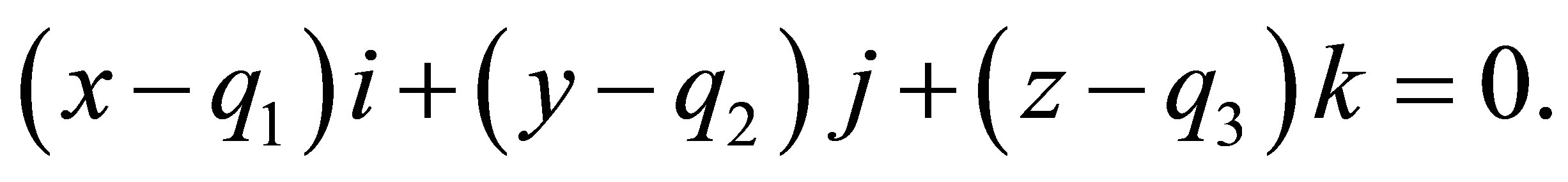
The unit normal vector of the plane has the form:
 (42)
(42)
The distance of the plane from the origin is given by:
 (43)
(43)
According to (25) ![]() can be written as:
can be written as:
 (44)
(44)
Substituting (18) into (12) the expressions of 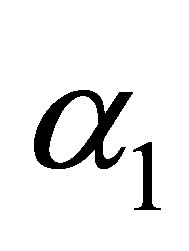 and
and 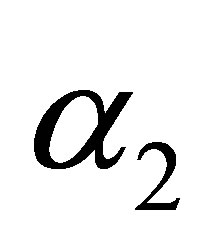 are given by
are given by
 (45)
(45)
where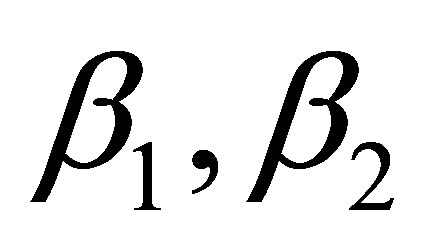 , satisfying
, satisfying 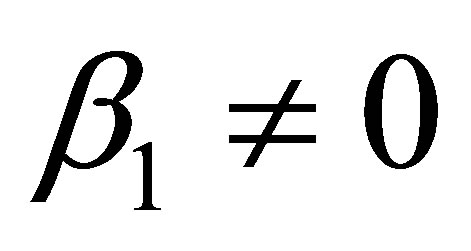 and
and , are solutions of Equation (19) after substituting vector
, are solutions of Equation (19) after substituting vector ![]() from (42):
from (42):
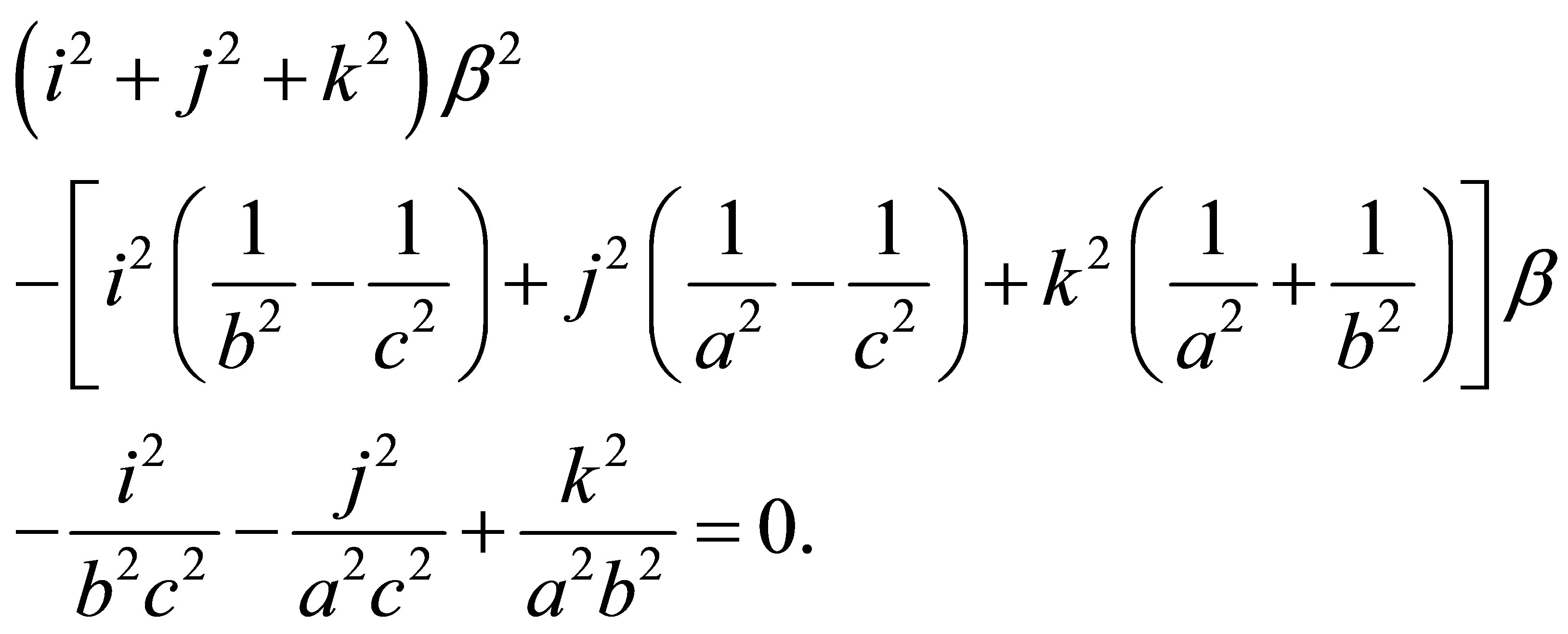 (46)
(46)
With Theorem 3 one obtains by substituting ![]() from (42) and
from (42) and ![]() from (43) the formular for the center
from (43) the formular for the center ![]() of the conic given by:
of the conic given by:
 (47)
(47)
In the special case of a plane containing the origin, i.e.  is the zero vector, it follows by (43), (44) and (47) that
is the zero vector, it follows by (43), (44) and (47) that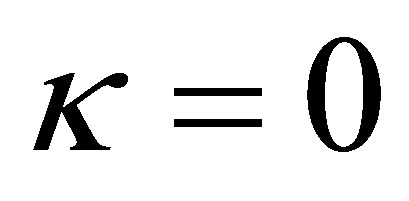 ,
, 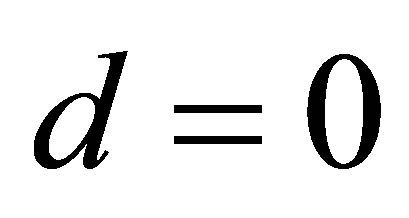 and
and ![]() is the zero vector also. Furthermore the expressions of
is the zero vector also. Furthermore the expressions of 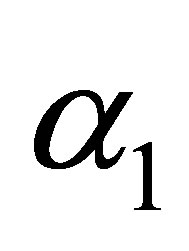 and
and 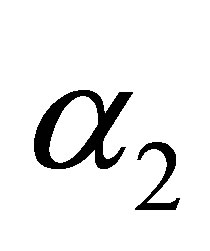 in (45) reduce to
in (45) reduce to

As described in Corollary 3 for a hyperboloid of one sheet and  for
for  one obtains
one obtains 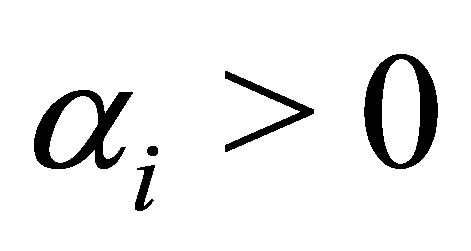 for
for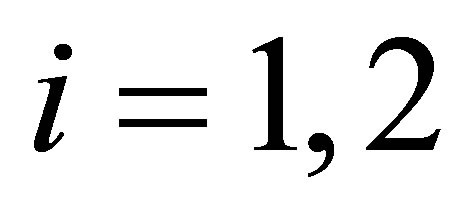 . Then the line of intersection is an ellipse. As stated in Corollary 4 for a hyperboloid of one sheet and
. Then the line of intersection is an ellipse. As stated in Corollary 4 for a hyperboloid of one sheet and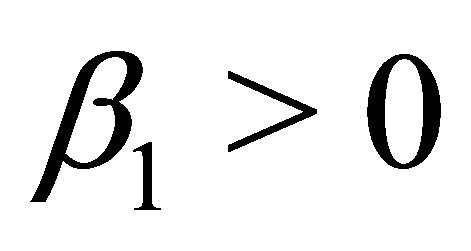 ,
,  one obtains
one obtains ,
,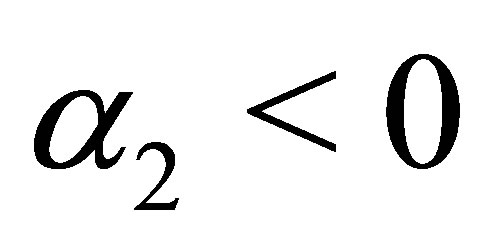 . For a hyperboloid of two sheets and
. For a hyperboloid of two sheets and ,
, 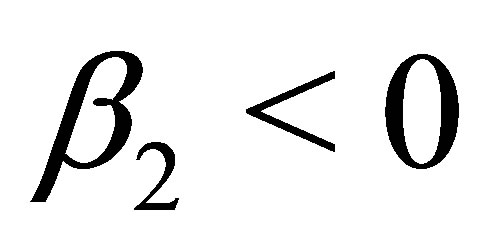 one obtains
one obtains ,
, . In both of these cases the line of intersection is a hyperbola.
. In both of these cases the line of intersection is a hyperbola.
In a second special case with . the above formulas (43), (44) and (47) reduce to:
. the above formulas (43), (44) and (47) reduce to:
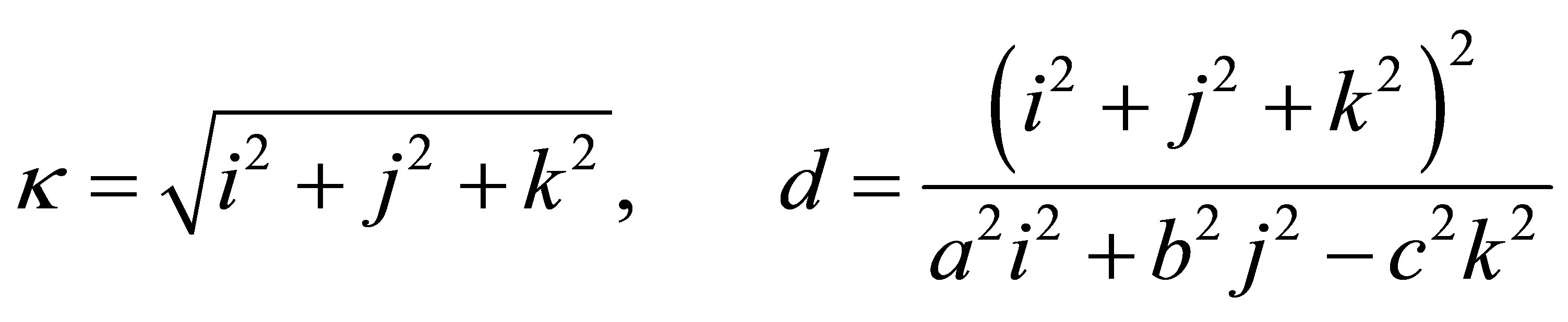
and
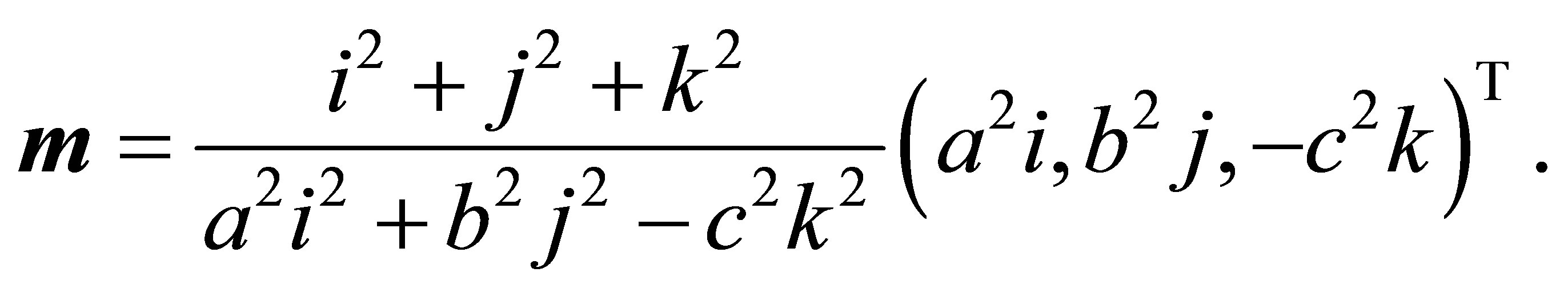
Because of  in (14)
in (14)  holds and (38) reduces to
holds and (38) reduces to
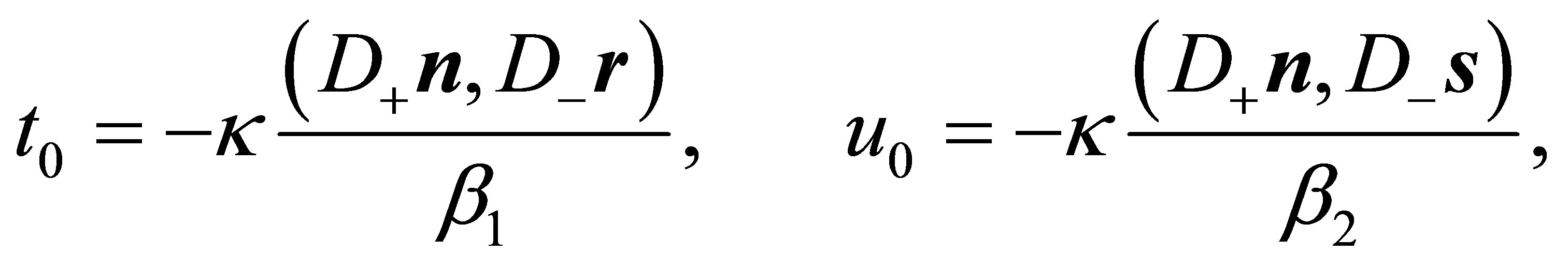
where  and
and  are solutions of the quadratic Equation (46) and vectors
are solutions of the quadratic Equation (46) and vectors  and
and ![]() have to be determined as described above in Section 2. As stated in Corollaries 3 and 4, if
have to be determined as described above in Section 2. As stated in Corollaries 3 and 4, if 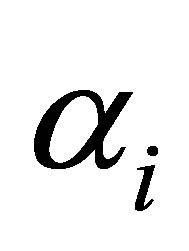 for
for  are both positive, an ellipse as curve of intersection is obtained, and if
are both positive, an ellipse as curve of intersection is obtained, and if  for
for  are of different sign, a hyperbola as curve of intersection results.
are of different sign, a hyperbola as curve of intersection results.
6. Parabola as Curve of Intersection
A parabola (13) as curve of intersection is obtained in case of  and
and . A hyperboloid of one sheet, given in (1), may be factorized in the following form:
. A hyperboloid of one sheet, given in (1), may be factorized in the following form:
 (48)
(48)
With the decomposition
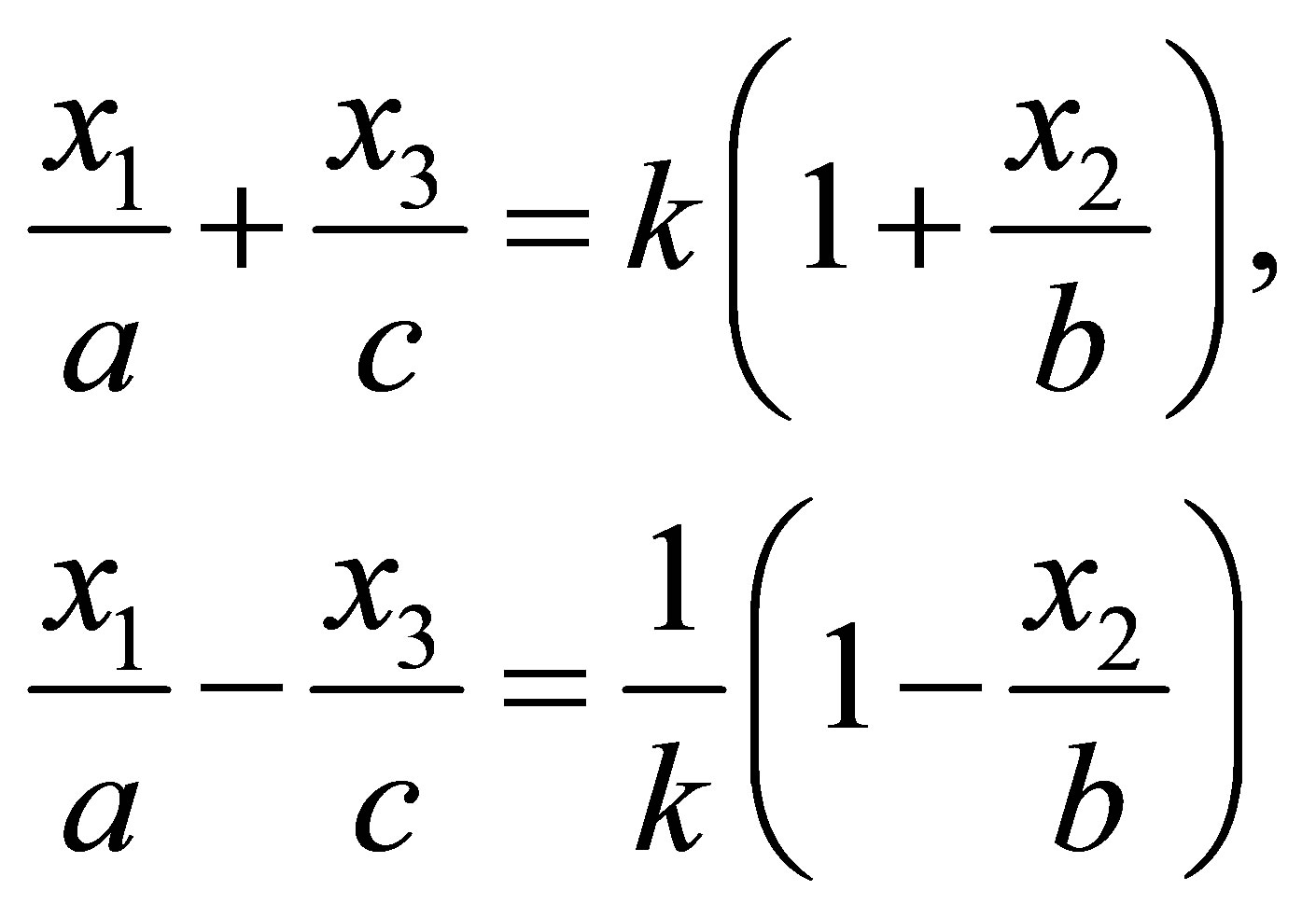 (49)
(49)
for any value of  these Equations represent a straight line, as the intersection of two planes in
these Equations represent a straight line, as the intersection of two planes in . This straight line lies on (48) because, if the members of (49) are multiplied together, (48) results. Rearranging (49) one obtains
. This straight line lies on (48) because, if the members of (49) are multiplied together, (48) results. Rearranging (49) one obtains
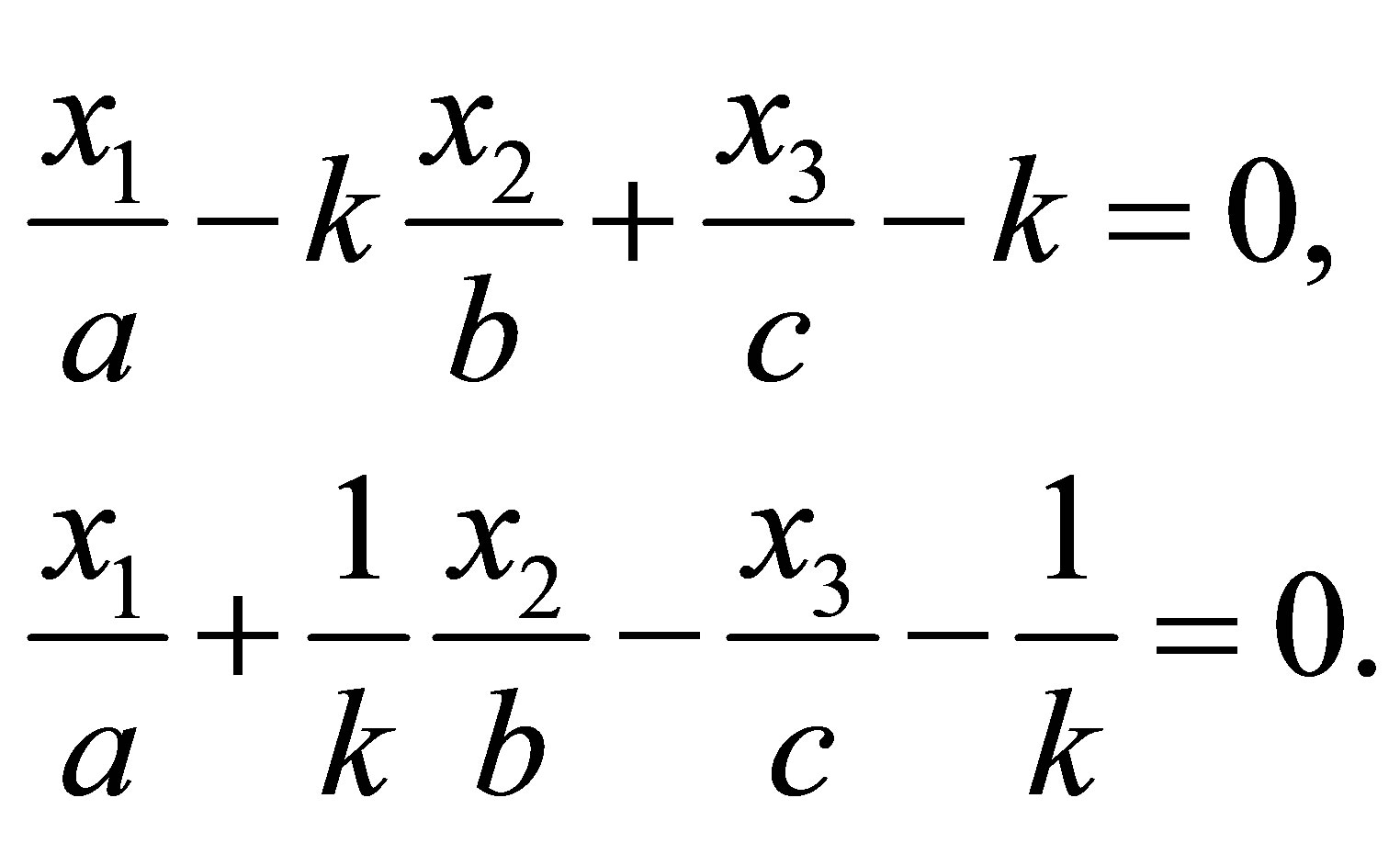 (50)
(50)
With the abbreviations
 (51)
(51)
the straigth line (50) can be equivalently rewritten [3]
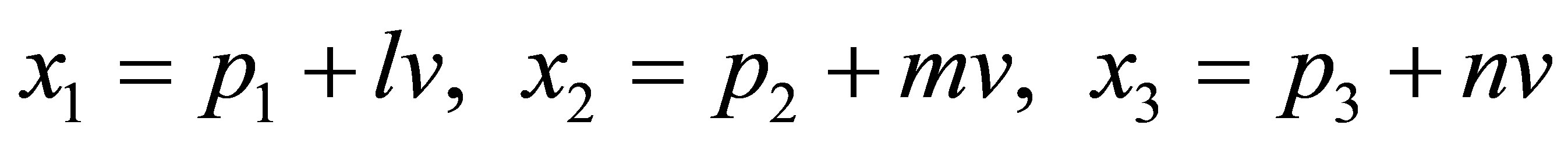 (52)
(52)
with a point 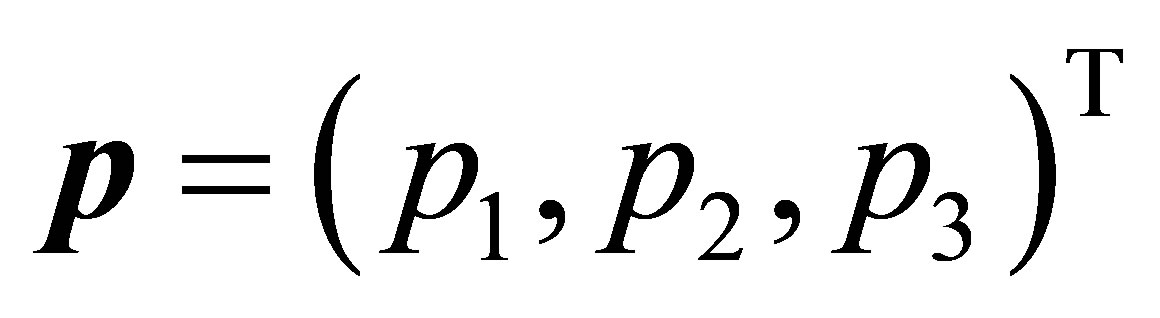 on (50) and
on (50) and .
.
Putting

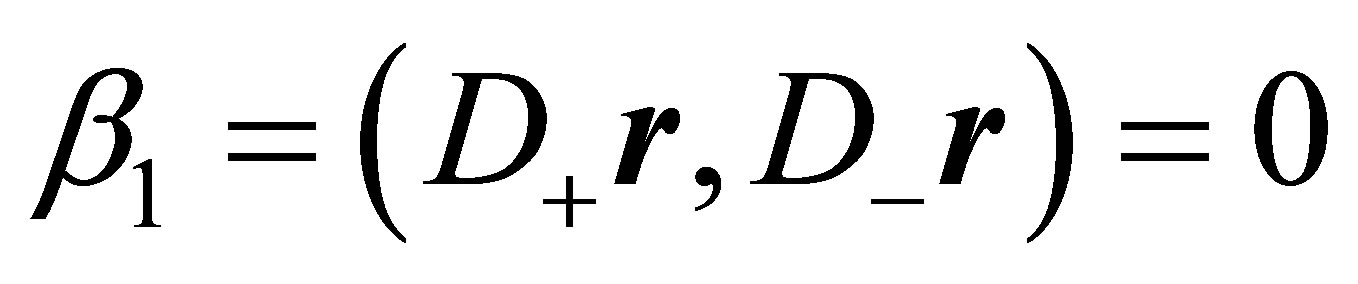 holds, because
holds, because
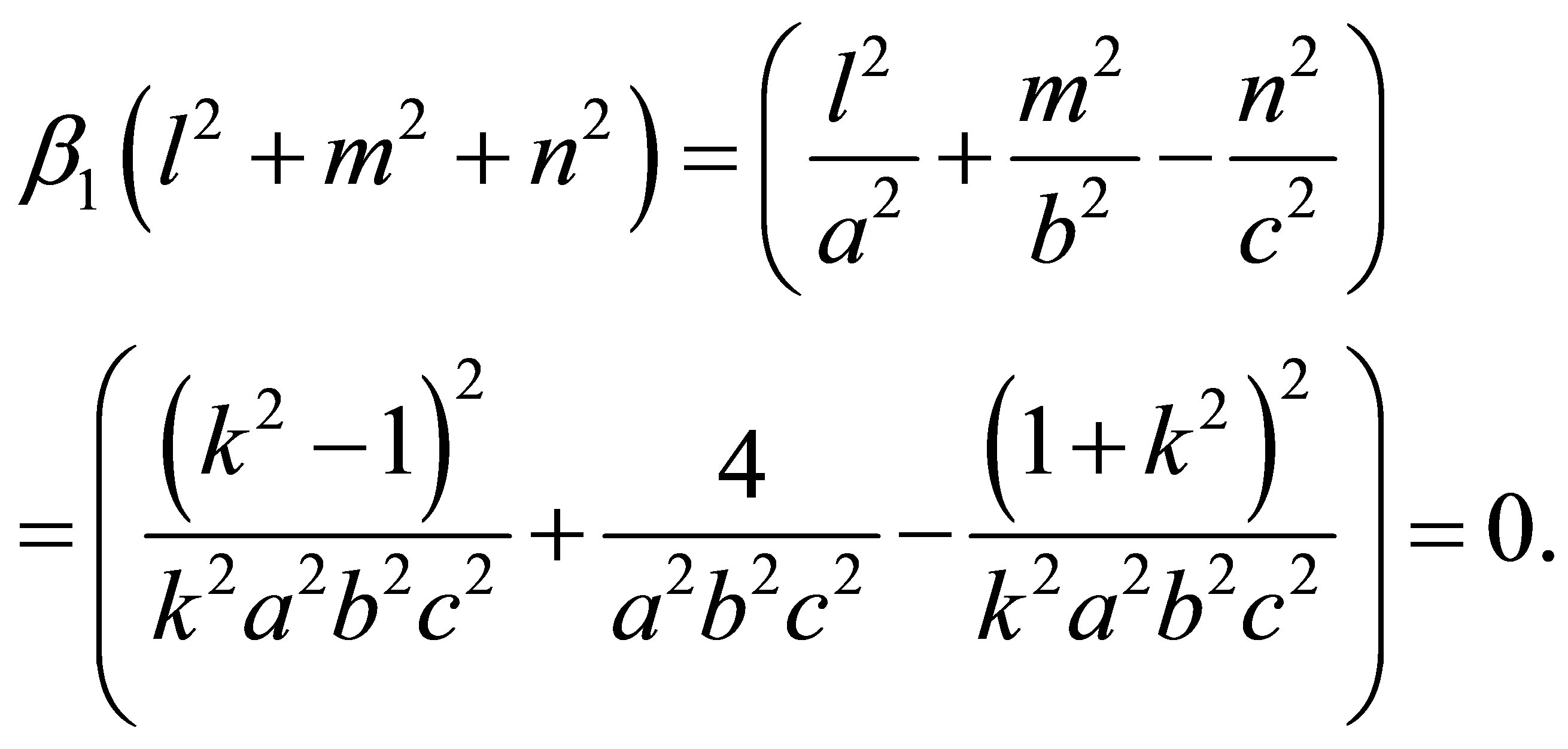
Choosing a vector  on the surface of a hyperboloid of one sheet, as given in (1), for instance
on the surface of a hyperboloid of one sheet, as given in (1), for instance
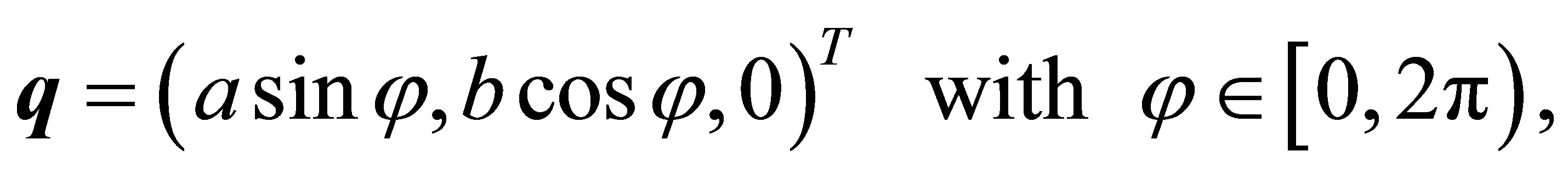 (53)
(53)
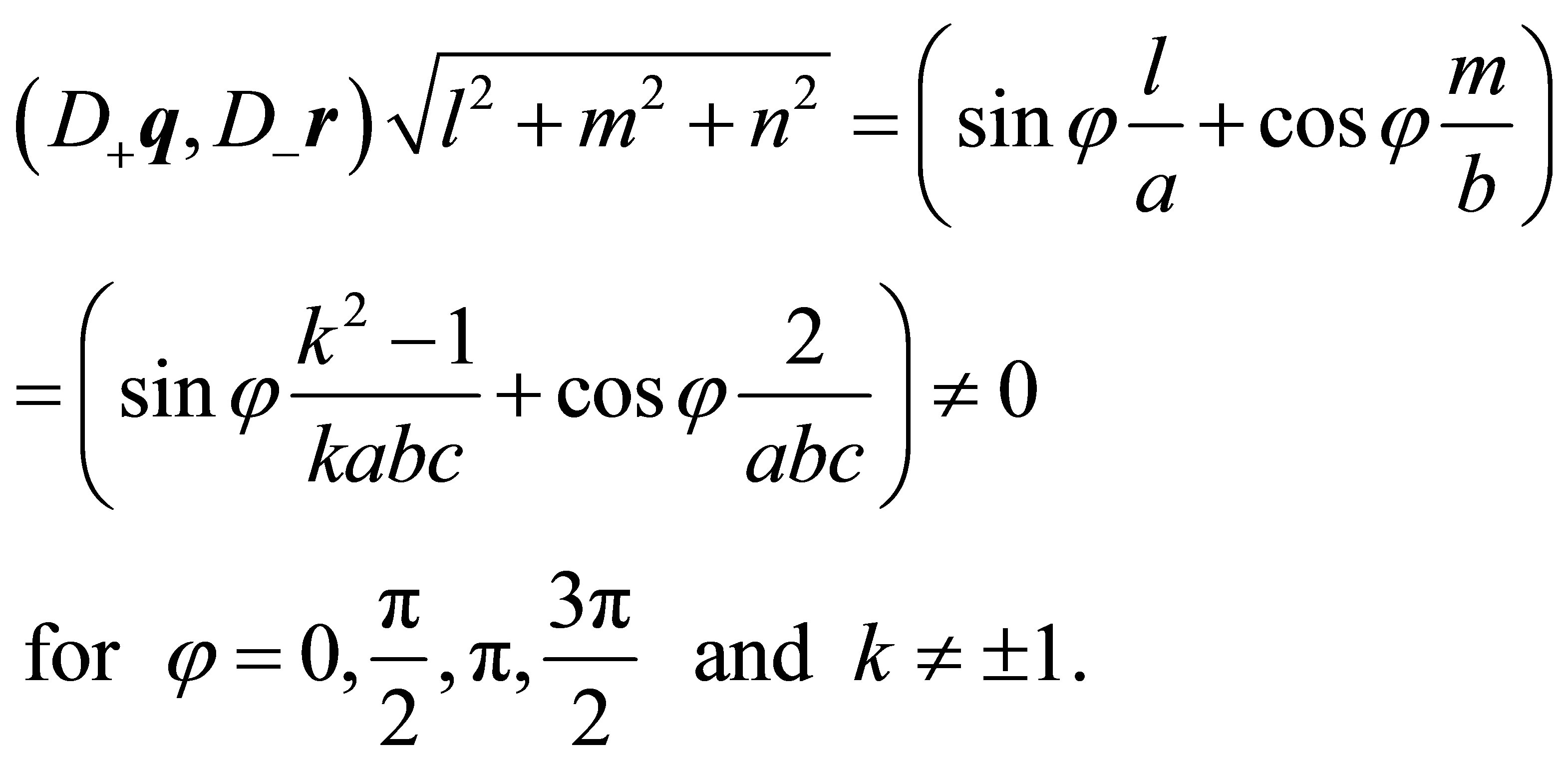
results.
Constructing a vector![]() , fulfilling
, fulfilling
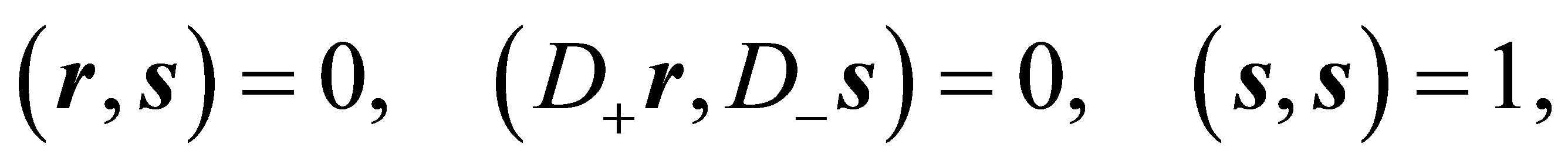 (54)
(54)
a plane spanned by vectors  and
and ![]() is obtained, containing the straight line (52). The two linear Equations in (54) for the components of
is obtained, containing the straight line (52). The two linear Equations in (54) for the components of ![]() can be rewritten:
can be rewritten:
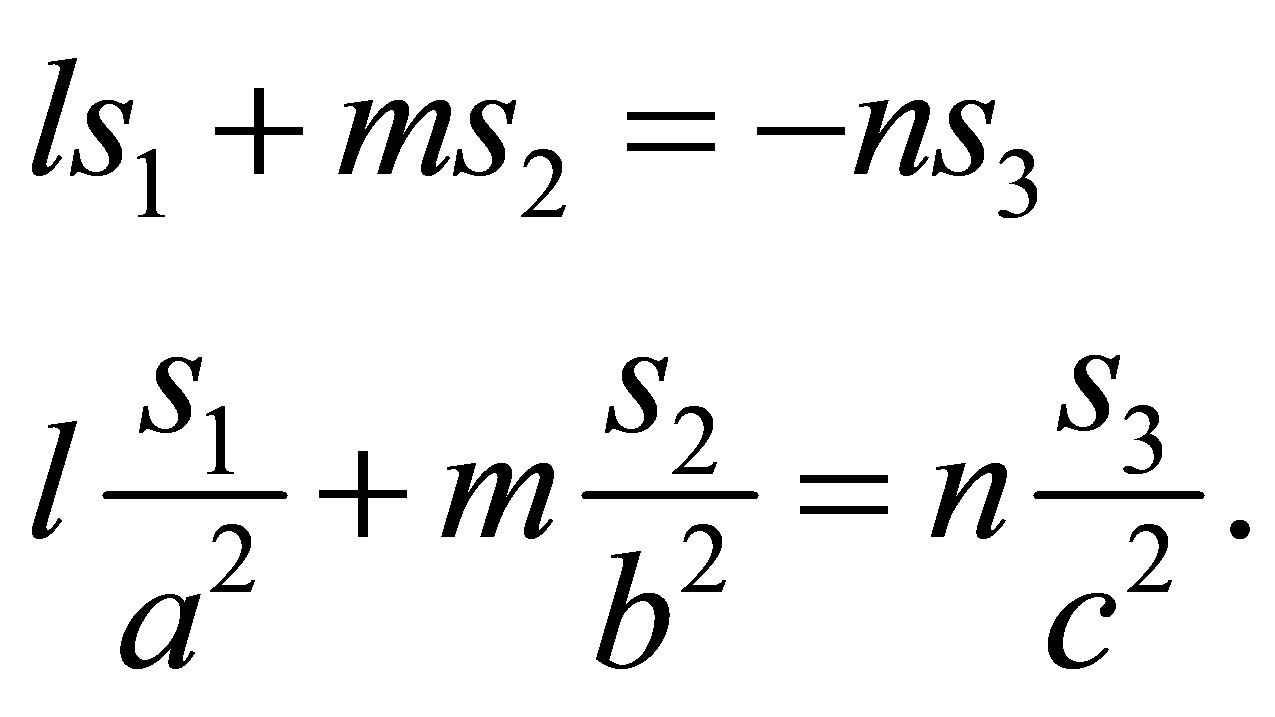 (55)
(55)
Solving for s1 and s2 under the assumptions 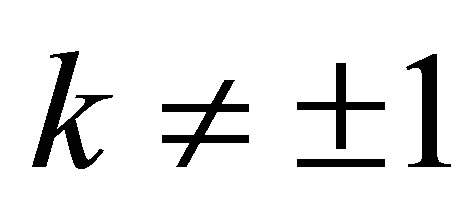 and
and 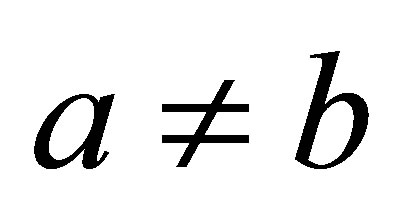 gives:
gives:
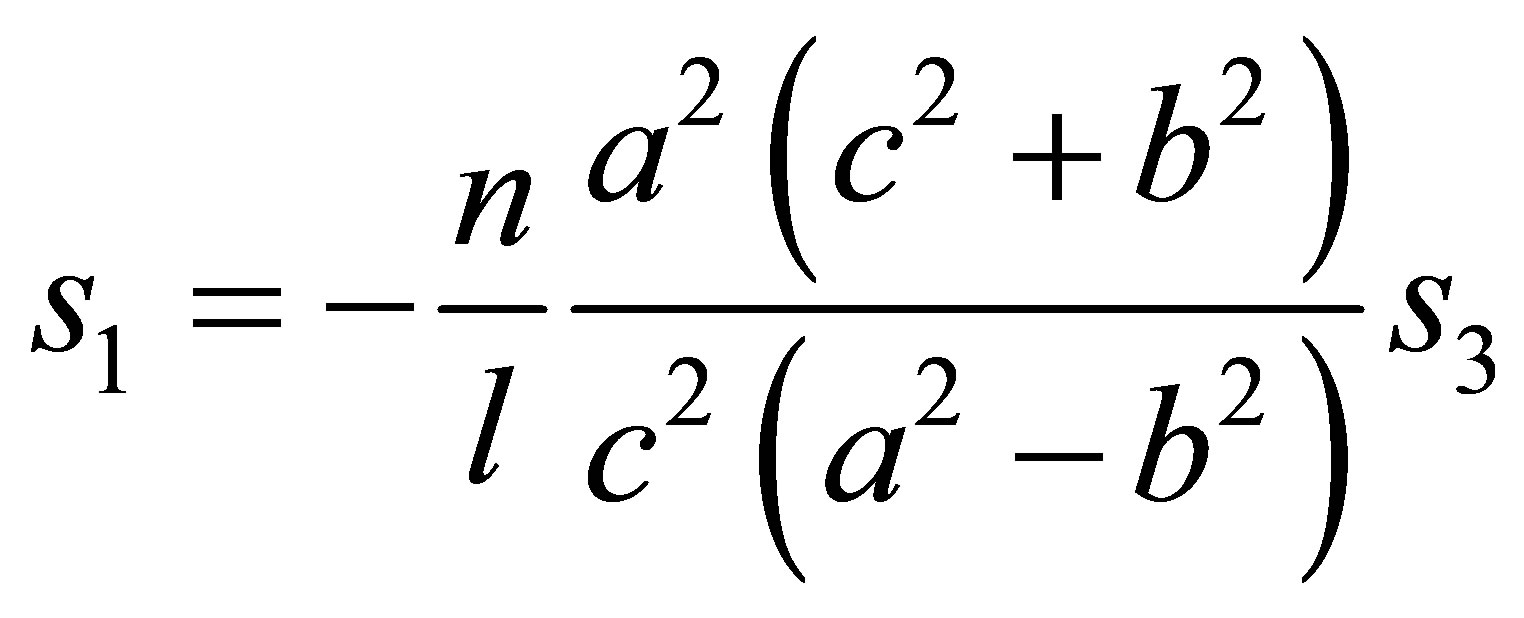
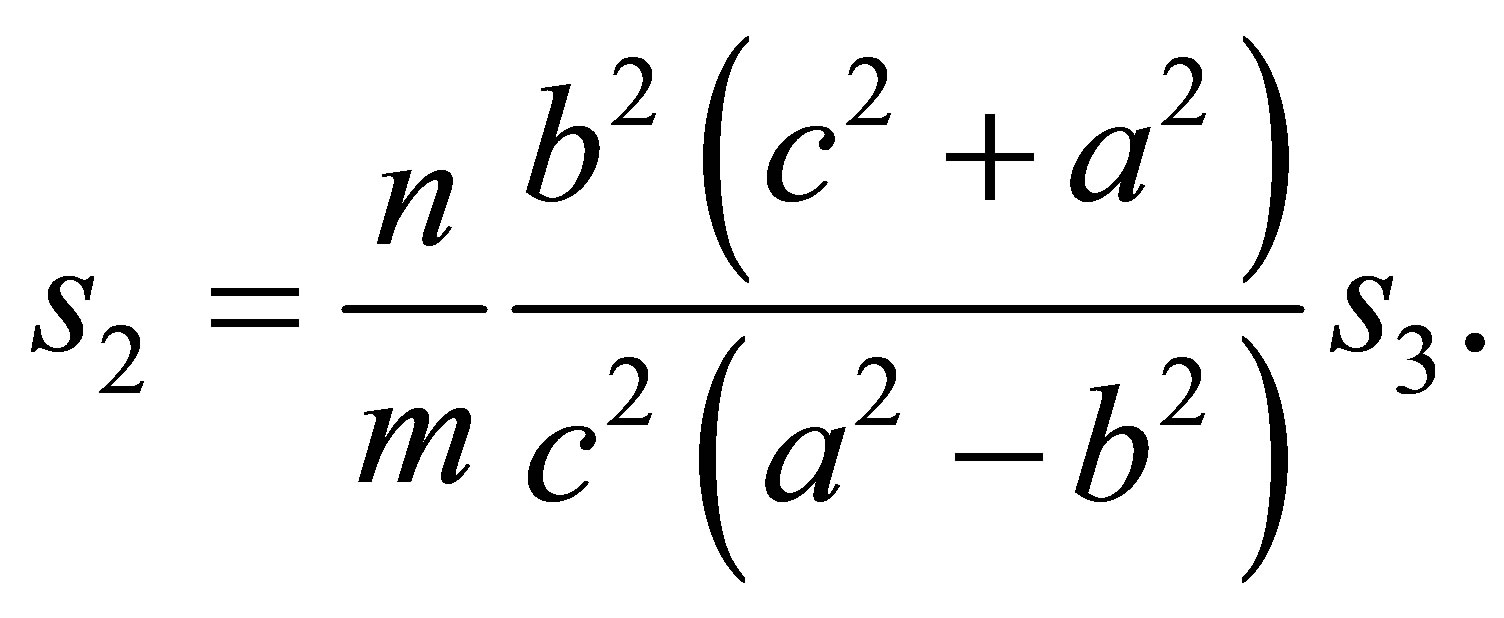
Dividing by  one obtains
one obtains 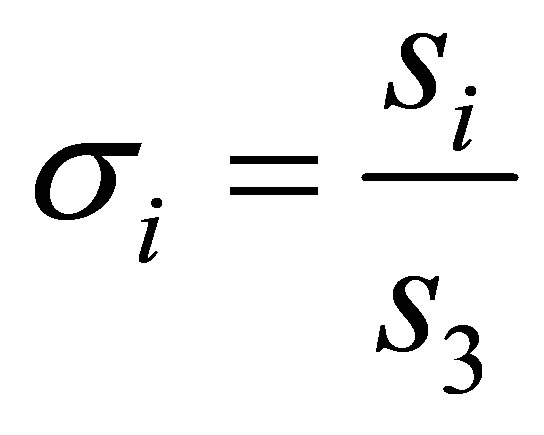 for
for 
and thus the following normalized vector![]() :
:
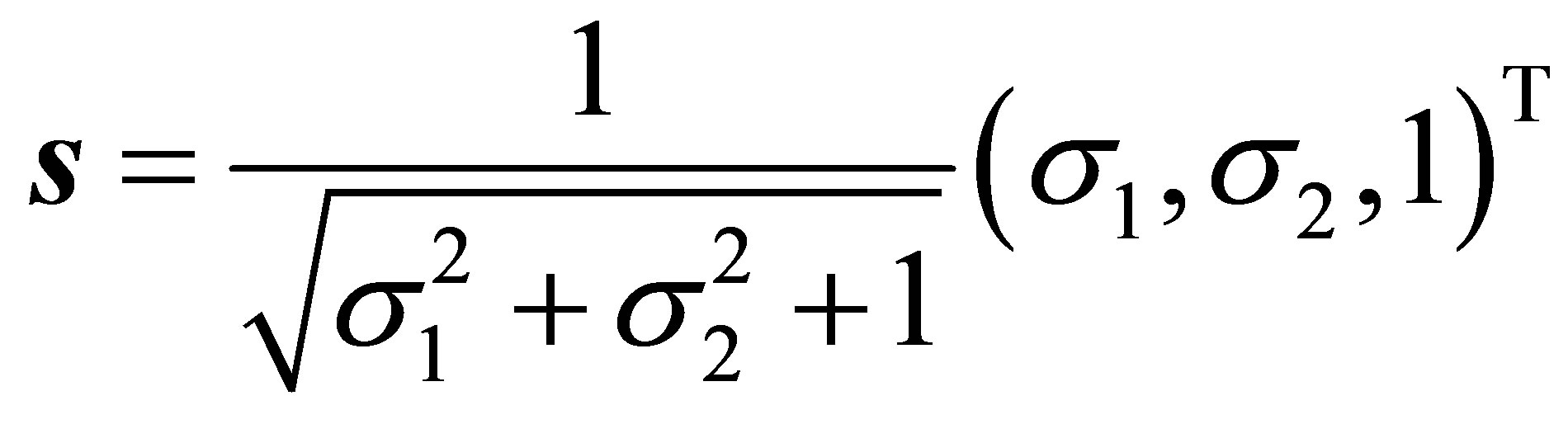
fulfilling (54) and giving
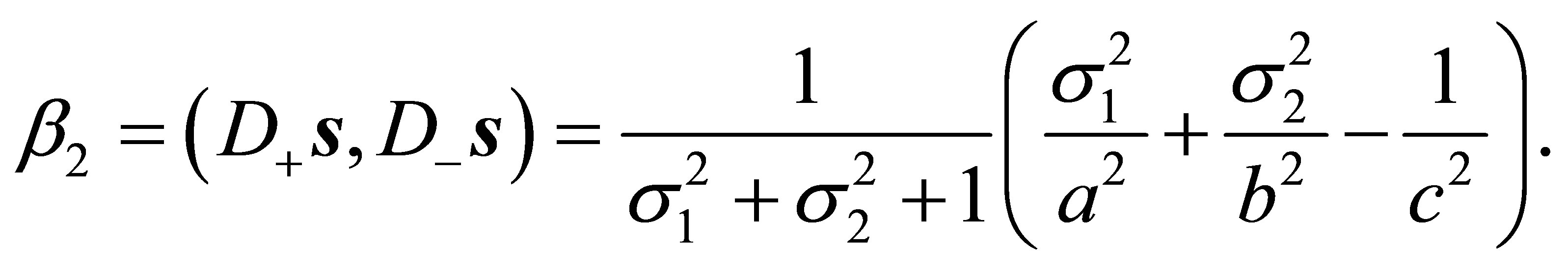
In case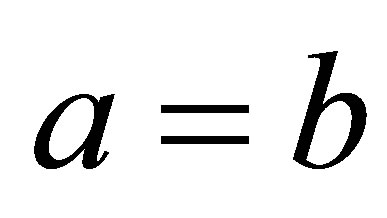 , this signifies rotational symmetry of the hyperboloid with regard to the z-axis, the coefficient matrix of (55) is singular. The condition for solvability of (55) is
, this signifies rotational symmetry of the hyperboloid with regard to the z-axis, the coefficient matrix of (55) is singular. The condition for solvability of (55) is

As 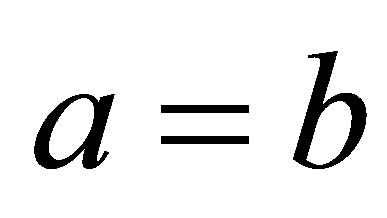 this can be reduced to
this can be reduced to
 (56)
(56)
Both sides of (56) are equal to  only for
only for . A solution vector
. A solution vector ![]() may then be chosen as
may then be chosen as

fulfilling (54). This leads to
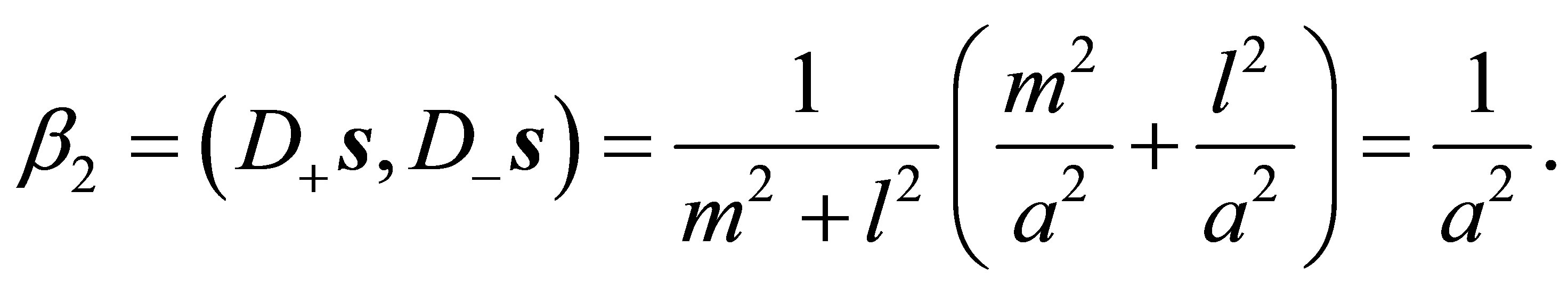
For 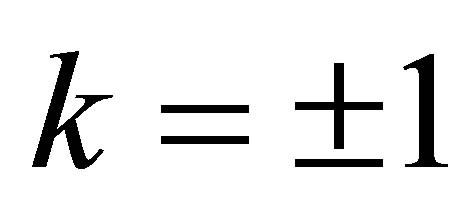 according to (51)
according to (51)  results. Then the linear system (55) is solvable for arbitrary
results. Then the linear system (55) is solvable for arbitrary ![]() and
and
 . Choosing
. Choosing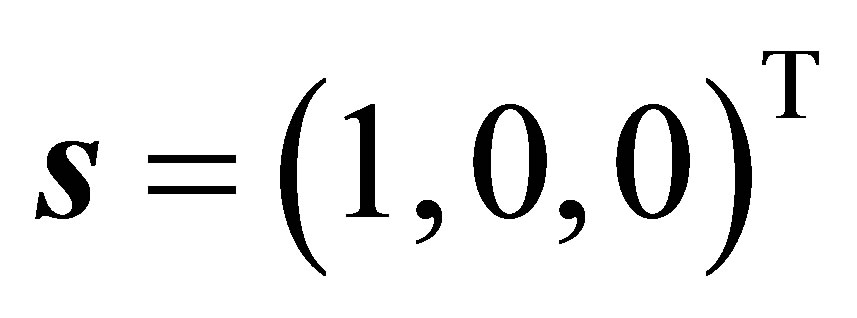 , as above
, as above 
holds.
Using vector  given in (53)
given in (53)
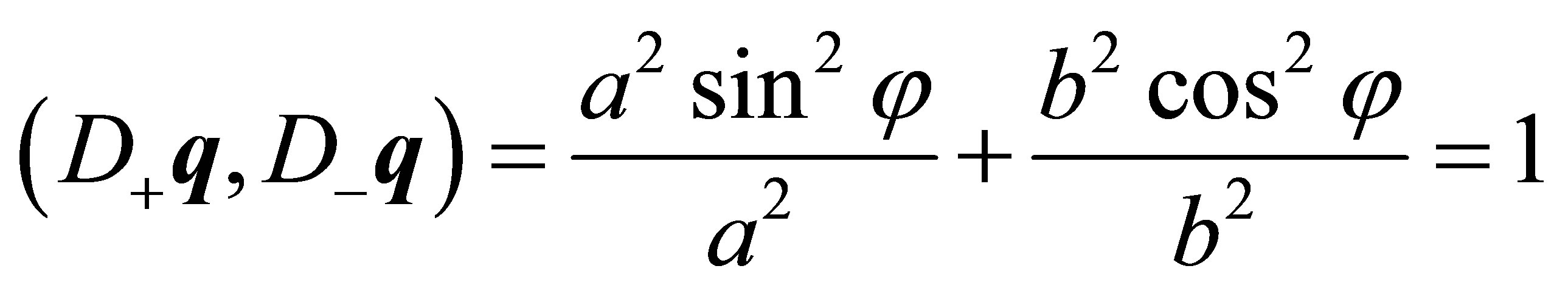
is obtained. Thus parabola (13) has the form
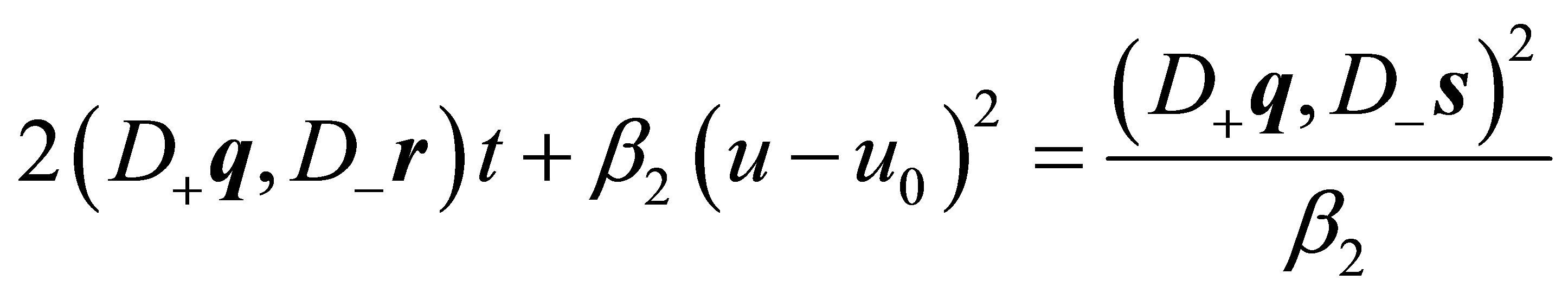 (57)
(57)
with

Instead of (49) the alternative decomposition of (48)
 (58)
(58)
for any value of  may be considered; (58) also describes a straight line as intersection of two planes in
may be considered; (58) also describes a straight line as intersection of two planes in . This straight line as well lies on (48) because, if the members of (58) are multiplied together, (48) results. Rearranging (58) one obtains
. This straight line as well lies on (48) because, if the members of (58) are multiplied together, (48) results. Rearranging (58) one obtains
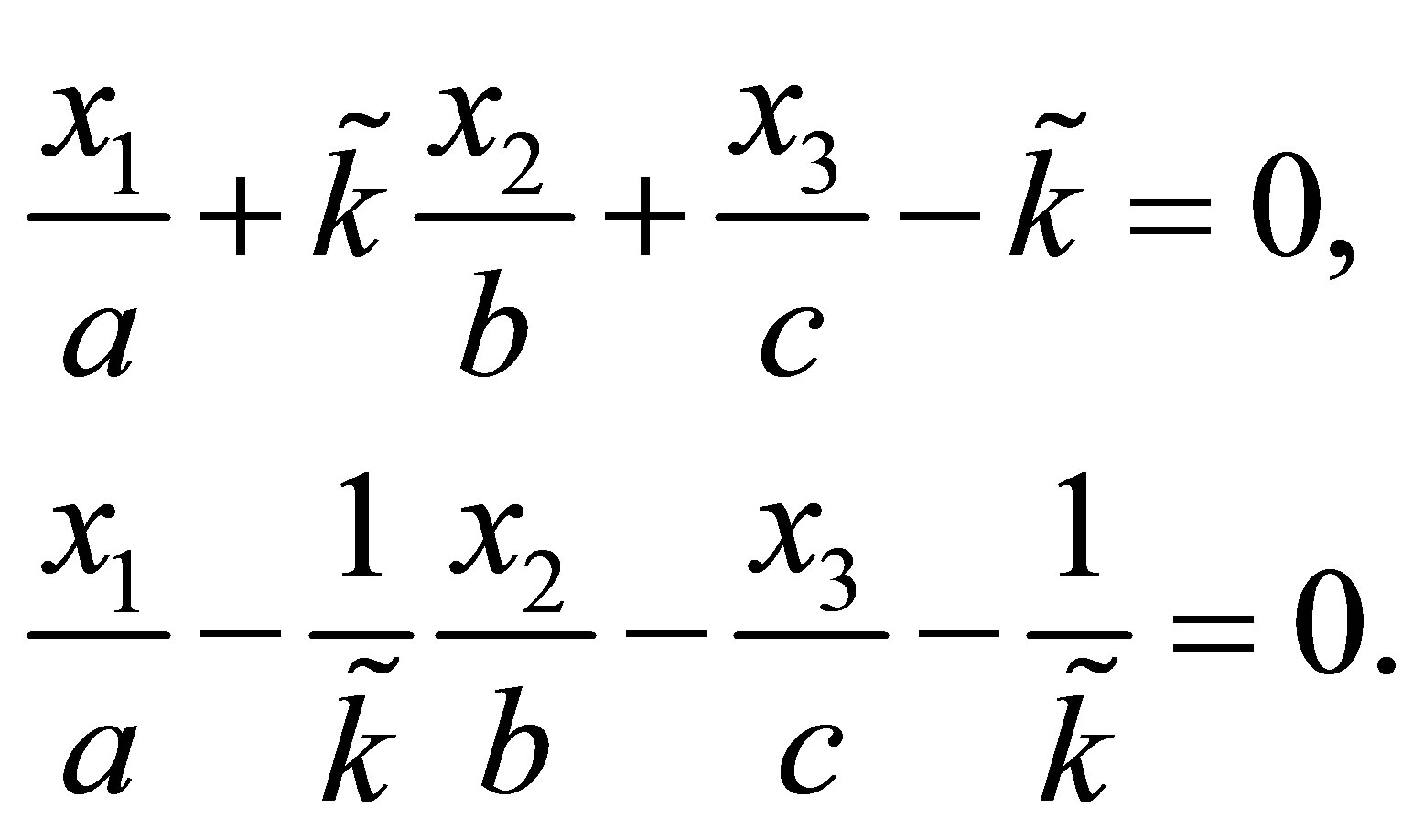 (59)
(59)
With the abbreviations
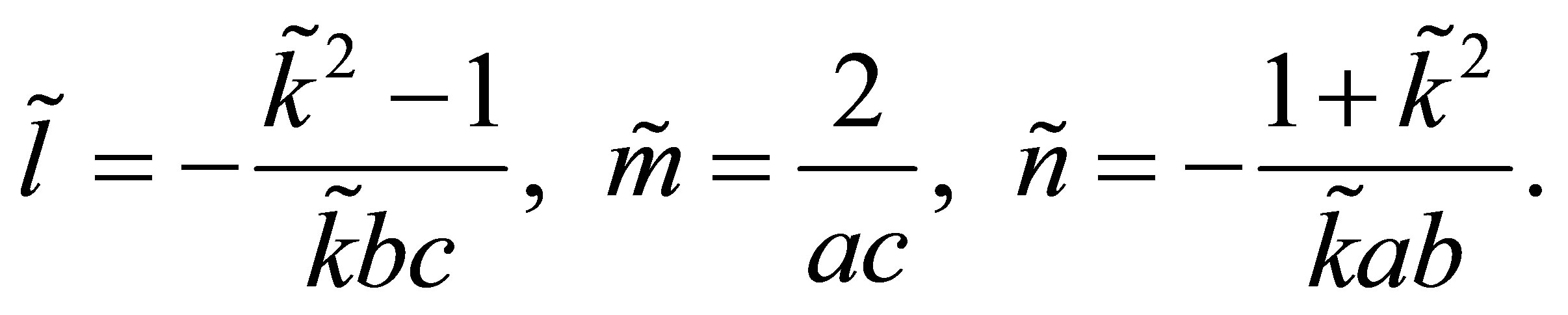 (60)
(60)
the straigth line (59) can be equivalently rewritten [3]
 (61)
(61)
with a point 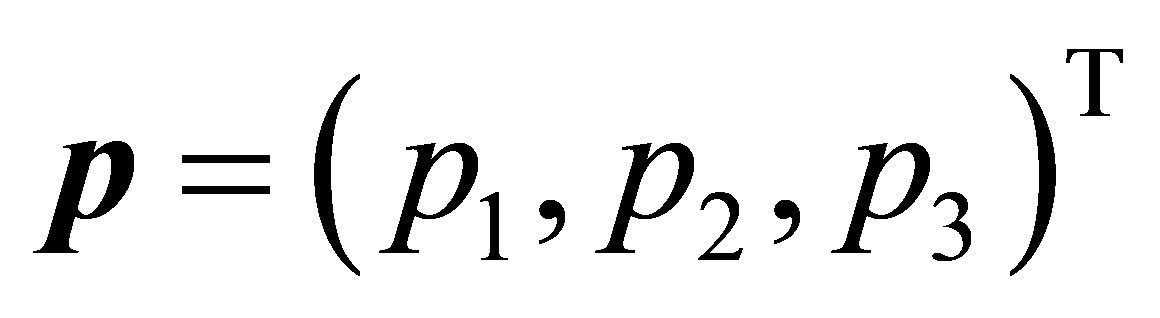 on (59) and
on (59) and .
.
As previously with the terms  now with the terms
now with the terms  vectors
vectors  and
and ![]() can be defined satisfying
can be defined satisfying

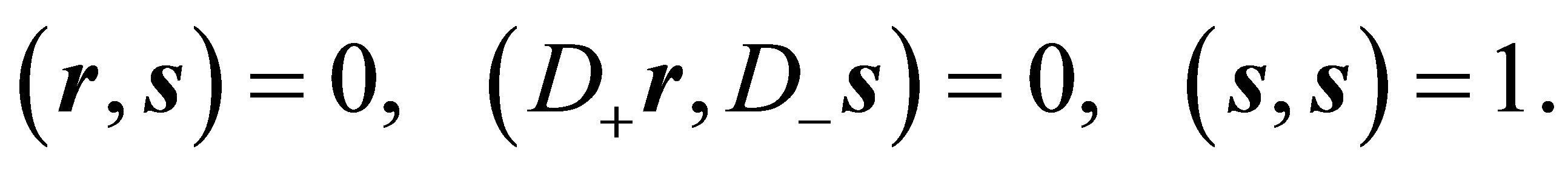
Choosing a vector  as in (53), in the end a parabola of the form (57) is obtained.
as in (53), in the end a parabola of the form (57) is obtained.
Mathematica programs modelling the cases described in Corollaries 3 and 4 and in Section 6 may be obtained from the author upon request.
7. Conclusion
The intention of this paper is to look at cases which are not treated in mathematical textbooks where the plane intersecting a hyperboloid of one sheet or of two sheets is not necessarily parallel to the coordinate planes and thus produces all kinds of conics: ellipses, hyperbolas and parabolas.
REFERENCES
- P. P. Klein, “On the Ellipsoid and Plane Intersection Equation,” Applied Mathematics, Vol. 3, No. 11, 2012, pp. 1634-1640. http://dx.doi.org/10.4236/am.2012.311226
- A. Korn and M. Korn, “Mathematical Handbook for Scientists and Engineers,” Mc Graw-Hill Book Company, Inc., New York, Toronto, London, 1961.
- I. N. Bronshtein, K. A. Semendyayev, G. Musiol, H. Muehlig, “Handbook of Mathematics,” 5th Edition, Springer, Berlin, Heidelberg, New York, 2007.

