Applied Mathematics
Vol.5 No.4(2014), Article ID:43568,14 pages DOI:10.4236/am.2014.54059
Causal Groupoid Symmetries
Sergio Pissanetzky
School of Science, University of Houston, Clear Lake, USA
Email: Sergio@SciControls.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 15 October 2013; revised 15 November 2013; accepted 23 November 2013
ABSTRACT
Proposed here is a new framework for the analysis of complex systems as a non-explicitly programmed mathematical hierarchy of subsystems using only the fundamental principle of causality, the mathematics of groupoid symmetries, and a basic causal metric needed to support measurement in Physics. The complex system is described as a discrete set S of state variables. Causality is described by an acyclic partial order w on S, and is considered as a constraint on the set of allowed state transitions. Causal set (S, w) is the mathematical model of the system. The dynamics it describes is uncertain. Consequently, we focus on invariants, particularly group-theoretical block systems. The symmetry of S by itself is characterized by its symmetric group, which generates a trivial block system over S. The constraint of causality breaks this symmetry and degrades it to that of a groupoid, which may yield a non-trivial block system on S. In addition, partial order w determines a partial order for the blocks, and the set of blocks becomes a causal set with its own, smaller block system. Recursion yields a multilevel hierarchy of invariant blocks over S with the properties of a scale-free mathematical fractal. This is the invariant being sought. The finding hints at a deep connection between the principle of causality and a class of poorly understood phenomena characterized by the formation of hierarchies of patterns, such as emergence, selforganization, adaptation, intelligence, and semantics. The theory and a thought experiment are discussed and previous evidence is referenced. Several predictions in the human brain are confirmed with wide experimental bases. Applications are anticipated in many disciplines, including Biology, Neuroscience, Computation, Artificial Intelligence, and areas of Engineering such as system autonomy, robotics, systems integration, and image and voice recognition.
Keywords: Hierarchies; Groupoids; Symmetry; Causality; Intelligence; Adaptation; Emergence

1. Introduction
Groups and groupoids are very similar, but a critically important case where they behave very differently appears to have remained unnoticed or under-reported. We introduce this case first, and then we review its considerable physical meaning in the context of complex systems. For the present purposes, we are only interested in finite groups and groupoids.
A group is a finite set with a binary function to itself. A groupoid is a finite set with a partial binary function to itself. A block system over some finite set 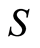 is a partition of
is a partition of 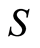 that remains invariant under the action of the group or groupoid. Two trivial partitions of
that remains invariant under the action of the group or groupoid. Two trivial partitions of  that satisfy the invariance requirement always exist, one with
that satisfy the invariance requirement always exist, one with 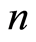 blocks of size 1, the other with 1 block of size
blocks of size 1, the other with 1 block of size , where
, where . Here, we are interested in non-trivial partitions. Computational experiments [1] suggest that non-trivial partitions arise frequently.
. Here, we are interested in non-trivial partitions. Computational experiments [1] suggest that non-trivial partitions arise frequently.
The action of the group or groupoid on 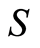 also determines their action on the block system. However, no further structures are generated. The block system is a single-level decomposition of
also determines their action on the block system. However, no further structures are generated. The block system is a single-level decomposition of . It does not generate any hierarchies on
. It does not generate any hierarchies on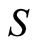 .
.
The case of interest arises when set  is enriched with an acyclic partial order
is enriched with an acyclic partial order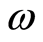 , and a permutation groupoid
, and a permutation groupoid 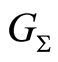 is defined to represent the symmetry of the resulting mathematical object
is defined to represent the symmetry of the resulting mathematical object . Groupoid
. Groupoid 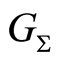 partitions
partitions  into a block system, as before, but now partial order
into a block system, as before, but now partial order 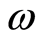 determines a partial order for the blocks themselves. This provides the condition for recurrence: we started from partially ordered set
determines a partial order for the blocks themselves. This provides the condition for recurrence: we started from partially ordered set , and arrived to a new, smaller partially ordered set—the set of blocks. A new permutation groupoid can now be defined, and the entire procedure can be repeated recurrently until a trivial block system is obtained. The result is a hierarchy of invariant block systems on set
, and arrived to a new, smaller partially ordered set—the set of blocks. A new permutation groupoid can now be defined, and the entire procedure can be repeated recurrently until a trivial block system is obtained. The result is a hierarchy of invariant block systems on set 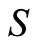 that depends only on
that depends only on  and
and .
.
Without the partial order, the procedure immediately breaks down. The initial permutation groupoid contains all 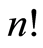 permutations of
permutations of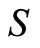 , and is actually the symmetric group of
, and is actually the symmetric group of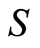 . It generates only a trivial block system over
. It generates only a trivial block system over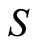 , and there is no recursion. Recall that a permutation of a set
, and there is no recursion. Recall that a permutation of a set 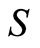 is a bijective map
is a bijective map .
.
In summary, given , there exists a function
, there exists a function  that maps directly from
that maps directly from  to a fractal hierarchy of invariant blocks on set
to a fractal hierarchy of invariant blocks on set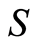 :
:
 (1)
(1)
The partial order is what makes the difference. Function 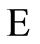 was introduced in [2] . Small examples of non-trivial hierarchies with 5 - 7 levels are published in [1] -[3] .
was introduced in [2] . Small examples of non-trivial hierarchies with 5 - 7 levels are published in [1] -[3] .
So far, we have discussed only pure Mathematics with no physical content. In Mathematics, the groupoid symmetries will work with any partial order, whether it has a physical meaning or not, and the resulting hierarchies will be correct but not necessarily related to the natural hierarchies.
In Physics, instead, we recognize the fundamental principle of causality as the common entity that underlies all complex systems. We choose the partial order to be causal, as dictated by the principle, and we expect the resulting structures to have a physical meaning, to be observable and measurable, and to show a quantitative agreement with those observed. When the partial order is chosen to be causal, the mathematical object 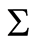 is called a causal set, and the resulting groupoid symmetries are called causal groupoid symmetries.
is called a causal set, and the resulting groupoid symmetries are called causal groupoid symmetries.
Causal set 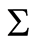 is the mathematical model of the complex system. The complex system is described as a discrete set
is the mathematical model of the complex system. The complex system is described as a discrete set 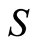 of state variables with only two possible values: past, or future. Initially, most variables are in the future, but some are initialized to past. A state transition takes place every time a variable changes its value from future to past. State transitions can happen in any order that does not violate the partial order. The path followed by the evolution of the system is thus described by any legal permutation of the state variables. There are many possible paths, but the system follows only one, and the principle does not specify which. This is the dynamics of the system, and it is an uncertain dynamics. Hence, we focus on invariants, because invariants are certain and will allow us to make predictions. Function
of state variables with only two possible values: past, or future. Initially, most variables are in the future, but some are initialized to past. A state transition takes place every time a variable changes its value from future to past. State transitions can happen in any order that does not violate the partial order. The path followed by the evolution of the system is thus described by any legal permutation of the state variables. There are many possible paths, but the system follows only one, and the principle does not specify which. This is the dynamics of the system, and it is an uncertain dynamics. Hence, we focus on invariants, because invariants are certain and will allow us to make predictions. Function 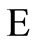 in Equation (1) allows us to calculate the invariants.
in Equation (1) allows us to calculate the invariants.
A basic metric for causal sets is introduced to support measurement. The metric is not needed in Mathematics, but is necessary in Physics because it makes the invariants observable and therefore measurable. A new theory grounded on the principle of causality naturally emerges for a discrete causal space where a dynamics is defined as a process of graph search and invariants with a semantic value are derived directly from the groupoid symmetries without any intervening dynamic law. The findings hint at a deep connection between the principle of causality and a class of little understood phenomena characterized by the formation of hierarchical patterns, including emergence, self-organization, adaptation, intelligence, and semantics. The causal groupoid symmetries of the complex system, described by function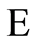 , formalize the connection.
, formalize the connection.
The link between symmetry and invariance is well known in Mathematics and Physics. The theory formalizes this link. Set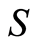 , the set of state variables, has no order when considered by itself. Its symmetry is described by its symmetric group, which induces in it only a trivial block system. Hence, there is a full symmetry, no order, and no structure. When the causal order is introduced, it acts as a constraint, breaks the initial full symmetry, and degrades it to that of the causal permutation groupoid
, the set of state variables, has no order when considered by itself. Its symmetry is described by its symmetric group, which induces in it only a trivial block system. Hence, there is a full symmetry, no order, and no structure. When the causal order is introduced, it acts as a constraint, breaks the initial full symmetry, and degrades it to that of the causal permutation groupoid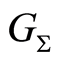 . The invariants are calculated directly from the groupoid, and take the form of a hierarchy of block systems. Hence, a deep connection is revealed between causality and the ubiquitous presence of fractal hierarchies in nature.
. The invariants are calculated directly from the groupoid, and take the form of a hierarchy of block systems. Hence, a deep connection is revealed between causality and the ubiquitous presence of fractal hierarchies in nature.
From the point of view of Mathematical Logic, function 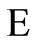 can be regarded as the definition of a process of inference, where meaningful facts are derived directly from observation based on a representation of the world as a collection of cause-effect pairs. This has been examined in more detail in [2] .
can be regarded as the definition of a process of inference, where meaningful facts are derived directly from observation based on a representation of the world as a collection of cause-effect pairs. This has been examined in more detail in [2] .
Causal groupoid symmetries were considered in [1] and applied to the analysis of phenomena of emergence and self-organization, including high cognitive function. A computational study of function 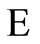 is included. In that work, the terms “groupoid” and “causal set” were not used, but all partially ordered sets reported are causal sets, and all symmetries considered are causal groupoid symmetries. A simple causal model of the brain was proposed, where hierarchies of block systems arise in-situ. The model was used to formulate a prediction for the brain, which was later independently confirmed. Applications to self-programming and object-oriented programming were considered in [2] .
is included. In that work, the terms “groupoid” and “causal set” were not used, but all partially ordered sets reported are causal sets, and all symmetries considered are causal groupoid symmetries. A simple causal model of the brain was proposed, where hierarchies of block systems arise in-situ. The model was used to formulate a prediction for the brain, which was later independently confirmed. Applications to self-programming and object-oriented programming were considered in [2] .
Studies of symmetry, structure and invariance are traditionally carried in the context of groups, but a generalization to groupoids was proposed [4] because groupoids are far less restrictive than groups and can account for many other types of symmetries and invariance observed in nature, even in the absence of geometric automorphisms. However, the critical connection of groupoids with the principle of causality was not made in that work, and, as a consequence, recursion and structural hierarchies were not considered. The notion of symmetry was further extended to directed graphs, and defined as the set of node permutations that preserve the topology of the graph [5] [6] , reporting rhythmic, periodic motion that follows from groupoid symmetries underlying the dynamics. This led to studies of synchrony, phase lock, multirythms, synchronized chaos, and bifurcation, including mammal gait and other examples of repetitive dynamics usually considered as adaptive behavior. In that work, causality was implicitly used, but not formally connected with the principle of causality, and the groupoid formalism was not generalized to all causal dynamical systems.
Studies of adaptive dynamics resulting from the constraint of causality were also conducted in a very different context, that of Cosmology [7] , also reporting periodic behaviors that resemble the human cognitive niche. Several examples were considered, including collaborative behavior, the use of tools, and the evolution of the stock market. An explicit connection with causality was made, and the presence of structures was attributed to the breaking of translational symmetry when a region of space is excluded (see Figure 1(b) ibidem). A deep connection between intelligence and entropy and a general thermodynamic model for adaptive behavior were proposed and illustrated with the examples, but not formalized. No connection with the groupoid symmetry formalism was attempted, no suggestion was made that such basic formalism may underly the much more complex cosmological formalism, and no formal connection with the principle of causality was noted. The formalization remained specific to Cosmology and was not generalized to all complex systems.
In yet another very different context, similar results were derived from Price’s equation of evolutionary biology, suggesting that emergence is a property of causal information [8] . In Computer Science, hierarchies of objects and classes created by human analysts have been used for decades to organize code, but can now be created without human intervention by using causal groupoid symmetries [2] . A quantitative information space as a base for semantics, where life and thought appear as new problems of Mathematics and Physics was proposed [9] . Hierarchies in the brain and mind were extensively discussed [10] .
Our work did not follow any of the paths just reported. It was prompted by the experimental discovery, around 2005, that certain canonical matrices had extraordinary self-organizing properties [1] . Later, the canonical matrices were found to be equivalent to causal sets, and the self-organized patterns were identified as causal groupoid symmetries. The formalization presented here is the result of several years of work that followed the initial discovery.
This is a bottom-up theory that follows directly from the principle of causality and an abstract metric for causal sets that is necessary to support measurement in Physics, and nothing else. There are no heuristics, no arbitrary constants. As such, the theory should be expected to have considerable impact, scope, and unifying power across disciplines.
The next two sections cover the theory. The abstract algebraic aspects of the theory are discussed in Section 2. Physics is discussed on Section 3, where the basic metric and an action functional are introduced. We show that groupoids arise naturally from causal models of complex systems. We also show that fractals and scale invariance are a direct consequence of causality. Block systems and conditions for them to be non-trivial are discussed in Section 4. A thought experiment that serves as a simple example of application of the theory is covered in Section 5. Practical details for constructing causal models of physical systems are covered in Section 6. Practical implementations and predictions are discussed in Sections 7 and 8, respectively.
Supplementary material included with this publication consists of two MS Word files. Other published studies include a study of randomly generated small systems [1] ; an exploratory experiment on Newtonian mechanics intended to discover the fundamentals of CML rather than to be observer-independent or reproducible [1] ; a case study on object-oriented analysis and refactoring of code, based on a published Java program, and another on image recognition, which has not yet been completed due to lack of resources and is still ongoing (see Supplementary material); and the thought experiment reported below in Section 5. The supplementary material is available from http://www.scicontrols.com.
2. Mathematics
In this section, we examine the Mathematics of causal groupoid symmetries in more detail. Let 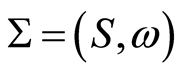 be a causal set, where
be a causal set, where  is a finite set and
is a finite set and  is a partial order on
is a partial order on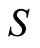 , defined as a collection of ordered pairs of elements of
, defined as a collection of ordered pairs of elements of  that is:
that is:
Ÿ irreflexive: 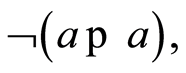
Ÿ acyclic if 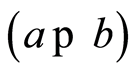 then:
then: , and
, and
Ÿ transitive if 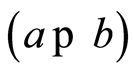 and
and  then
then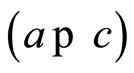 where
where  means “precedes” and
means “precedes” and  are distinct elements of
are distinct elements of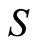 . The nature of the elements of
. The nature of the elements of 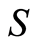 is irrelevant. They have no value and no meaning.
is irrelevant. They have no value and no meaning.
Define now  as the causal space of
as the causal space of , where
, where  is a trajectory in causal space defined as a total order on
is a trajectory in causal space defined as a total order on 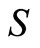 compatible with
compatible with 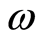 (a linear extension of
(a linear extension of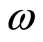 ). Causal space
). Causal space 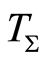 represents the symmetry of
represents the symmetry of . A dynamics in
. A dynamics in 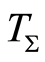 is defined as a graph search process that visits elements of
is defined as a graph search process that visits elements of 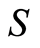 and assigns sequential numbers to them in a causal but otherwise random order. All elements are initially unvisited, and an element can be visited only once. At any step of the search, the past is the set of visited elements, and the future is the set of those unvisited. This dynamics is uncertain. The uncertainty motivates our interest in dynamical invariants.
and assigns sequential numbers to them in a causal but otherwise random order. All elements are initially unvisited, and an element can be visited only once. At any step of the search, the past is the set of visited elements, and the future is the set of those unvisited. This dynamics is uncertain. The uncertainty motivates our interest in dynamical invariants.
To begin our study of dynamical invariants, let now 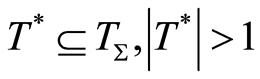 be any subset of
be any subset of  of size 2 or more. We will now show that a groupoid
of size 2 or more. We will now show that a groupoid  and a block system
and a block system , possibly trivial, can be associated with
, possibly trivial, can be associated with , and hence with the symmetry of
, and hence with the symmetry of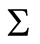 . We are interested in block systems because they are invariant under the action of the groupoid. To define the groupoid, recall that a permutation
. We are interested in block systems because they are invariant under the action of the groupoid. To define the groupoid, recall that a permutation  of
of 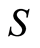 is a map
is a map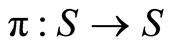 . Arbitrarily choose some reference order
. Arbitrarily choose some reference order  and define the following set of permutations on
and define the following set of permutations on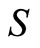 :
:
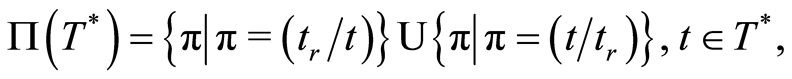 (2)
(2)
where permutations are represented in two-line notation, and 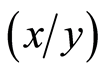 designates
designates 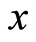 as the top line and
as the top line and 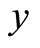 as the bottom line. Then,
as the bottom line. Then,
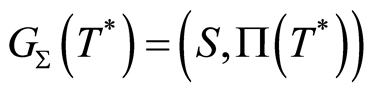 (3)
(3)
is a groupoid, where 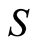 is the set,
is the set, 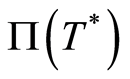 is the partial function, and
is the partial function, and 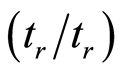 is the identity. A block system
is the identity. A block system  on set
on set 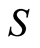 is a partition of
is a partition of  into disjoint subsets called blocks, some or all of which can be trivial, that remains invariant under the action of the groupoid operations
into disjoint subsets called blocks, some or all of which can be trivial, that remains invariant under the action of the groupoid operations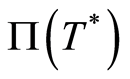 . Block systems are standard in group theory, and procedures for calculating them are readily available.
. Block systems are standard in group theory, and procedures for calculating them are readily available.
A block system is, in turn, a causal set where the blocks are the elements. When blocks are constructed, some of the original ordered pairs become encapsulated in the blocks, and the remaining ones are induced in the block system and form new ordered pairs linking blocks. The new causal set has its own smaller causal space, groupoid, and block system. Repeating the construction, a fractal hierarchy of invariant blocks is obtained, all determined by the original causal set .
.
3. Physics
To study dynamical invariants, we introduce a partial metric and a functional. Both were experimentally observed by the author [1] [2] . For the purpose of the theory, they are introduced by postulate. A metric on a set is a function that defines a distance between elements. A metric is said to be partial if not all distances are defined. For each , define partial metric
, define partial metric 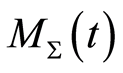 on
on  as follows:
as follows:
 (4)
(4)
where 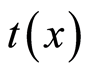 is the ordinal assigned by
is the ordinal assigned by  to element
to element 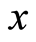 of
of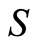 . This is the fundamental metric for the causal space
. This is the fundamental metric for the causal space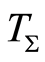 . Since
. Since , then
, then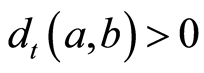 .
.
Functional 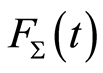 is now defined as twice the sum of the distances of all pairs:
is now defined as twice the sum of the distances of all pairs:
 (5)
(5)
where the factor 2 is included for back-compatibility. This functional is called the action of trajectory  in
in . It is positive definite, and it is the simplest non-constant functional, as it should be by Lee Smolin’s parsimony principle (Occam’s razor). The positive definiteness is key to explain emergent phenomena. It allows a collection of local agents to minimize their respective contributions locally and independently, without any external direction or sense of purpose, and yet achieve an unexpected global effect.
. It is positive definite, and it is the simplest non-constant functional, as it should be by Lee Smolin’s parsimony principle (Occam’s razor). The positive definiteness is key to explain emergent phenomena. It allows a collection of local agents to minimize their respective contributions locally and independently, without any external direction or sense of purpose, and yet achieve an unexpected global effect.
Functional  maps the set of trajectories
maps the set of trajectories 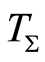 injectively onto a subset of positive integers. By doing so, it partitions
injectively onto a subset of positive integers. By doing so, it partitions  into a collection of disjoint subsets, or macrostates, each containing one or more trajectories with the same value of the action. Figure 1 shows an example of a typical distribution of population per macrostate. Three macrostates are marked on the plot because they are determined by optimization and not by parameter. We want to keep the theory parameter-free. They are: the least-action macrostate
into a collection of disjoint subsets, or macrostates, each containing one or more trajectories with the same value of the action. Figure 1 shows an example of a typical distribution of population per macrostate. Three macrostates are marked on the plot because they are determined by optimization and not by parameter. We want to keep the theory parameter-free. They are: the least-action macrostate , the most-action macrostate
, the most-action macrostate , and the maximum entropy macrostate
, and the maximum entropy macrostate . Both
. Both 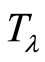 and
and  are found near stationary entropy points, suggesting a reversible physics, but
are found near stationary entropy points, suggesting a reversible physics, but  is not.
is not.
4. Analysis
We now return to our original goal of finding groupoids with non-trivial block systems, while at the same time avoiding introducing any heuristics or adjustable parameters into the theory. We have, however, intentionally left one open parameter: set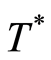 . It is now time to discuss non-heuristic options for
. It is now time to discuss non-heuristic options for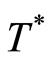 . The preceding analysis is limited to trajectories that connect a given initial state
. The preceding analysis is limited to trajectories that connect a given initial state  with a given final state
with a given final state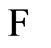 .
.
For example, in the thought experiment of Section 5, the 10 input variables 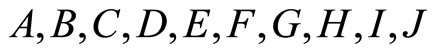 are the initial past, and the 3 output variables
are the initial past, and the 3 output variables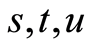 , as well as all the intermediate variables, are the initial future. In the final state
, as well as all the intermediate variables, are the initial future. In the final state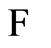 , all variables are past. But this happens only because of the particular way the example causal set
, all variables are past. But this happens only because of the particular way the example causal set 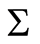 is chosen. In a general case, usually only a few of the future variables are visited and become part of the past.
is chosen. In a general case, usually only a few of the future variables are visited and become part of the past.
Given a causal set  in an initial state
in an initial state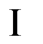 , the selection of a final state is arbitrary. Indeed, any state reachable by the graph search can be considered as the final state, and then used to select a subset of trajectories that lead there, as we did above. Hence, it is reasonable to consider
, the selection of a final state is arbitrary. Indeed, any state reachable by the graph search can be considered as the final state, and then used to select a subset of trajectories that lead there, as we did above. Hence, it is reasonable to consider 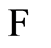 as a goal. Let
as a goal. Let  be the set of all
be the set of all
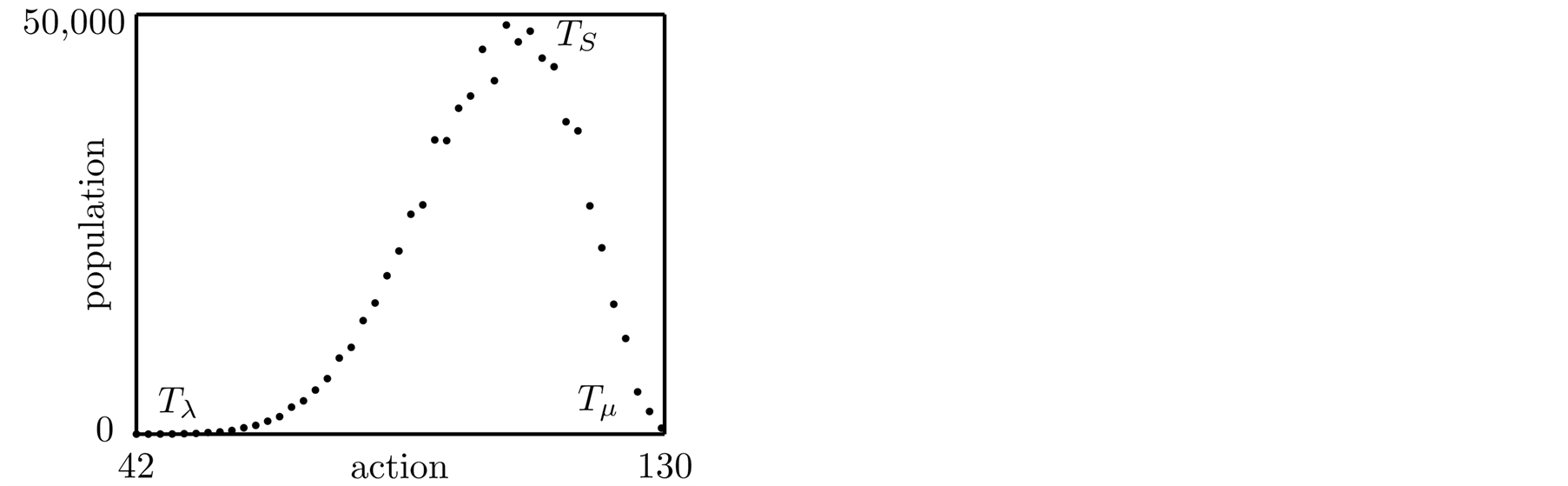
Figure 1. An example of a population vs. action plot for a causal set with 12 elements and 11 ordered pairs, which has a causal space with 954,789 trajectories. The least-action is 42, with a population of 3, and the most-action is 130 with a population of 864.
reachable goals for a given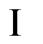 .
.
When a complex system evolves from state  and reaches state
and reaches state , then
, then  becomes the new initial state
becomes the new initial state  and the system continues evolving. It can, in principle, evolve towards any of the goals in
and the system continues evolving. It can, in principle, evolve towards any of the goals in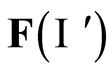 . This is, once more, an uncertain dynamics. Since we are looking for certainty, we raise the following interesting question: Are there any natural processes that favor the selection of some subset of goals from
. This is, once more, an uncertain dynamics. Since we are looking for certainty, we raise the following interesting question: Are there any natural processes that favor the selection of some subset of goals from ?
?
From the two most fundamental principles of Physics, we know of two cases where such processes exist. From the Second Law we know that isolated systems spontaneously evolve towards a state of maximum uncertainty, and from the Principle of Least-Action we know that a system that evolves between two states follows a stationary-action trajectory. Are these two processes appropriately accounted for by the causal theory? Is our assumption that the functional of Equation (5) represents action, justified? Are there or could there be any other processes that favor some form of selection of goals? And if so, what is the connection with emergent phenomena?
The plot in Figure 1 may help us to draw some conjectures directly from the causal theory. Limited evidence indicates that plots with similar features apply to many systems, not just the example case in the figure. If a system evolves in a direction that optimizes some physical quantity, then it has to evolve in that direction until the quantity stabilizes.
We know that any  has a block system, possibly non-trivial, and that
has a block system, possibly non-trivial, and that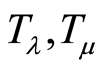 , and
, and  are candidates for a parameter-free theory. A study of many small systems [1] has suggested that non-trivial blocks are more likely to exist in a small
are candidates for a parameter-free theory. A study of many small systems [1] has suggested that non-trivial blocks are more likely to exist in a small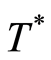 , and that
, and that . Systems can now be loosely classified into three classes, designated as
. Systems can now be loosely classified into three classes, designated as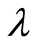 ,
, 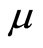 , and
, and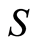 , depending on which one of
, depending on which one of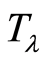 ,
, 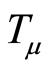 , or
, or  falls in the favorable range and/or has a non-trivial block system.
falls in the favorable range and/or has a non-trivial block system.
The  -class is for relatively unsophisticated systems that spontaneously maximize their entropy by yielding to causal entropic forces, and are causally small enough for
-class is for relatively unsophisticated systems that spontaneously maximize their entropy by yielding to causal entropic forces, and are causally small enough for 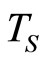 to have invariants. They will exhibit simple, repetitive behavior and support basic adaptive tasks with simple goals, such as gaining an immediate advantage, but their ability for higher cognitive tasks will be limited. These properties are consistent with those anticipated in [6] [7] .
to have invariants. They will exhibit simple, repetitive behavior and support basic adaptive tasks with simple goals, such as gaining an immediate advantage, but their ability for higher cognitive tasks will be limited. These properties are consistent with those anticipated in [6] [7] .
The 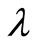 -class is for evolved systems that have developed a mechanism for minimizing their action against causal entropic forces. Such systems can be very large and complex and support higher cognitive and adaptive tasks. In the brain, that mechanism may be provided by resource preservation. Brains grow dendritic trees to store information, and make the trees as short as possible to preserve biological resources. By doing so, as proposed in [1] , they also minimize the action, Equation (5), and cause intelligence to arise as a side effect. In Table 1 in [1] , odd-numbered lines correspond to least-action
-class is for evolved systems that have developed a mechanism for minimizing their action against causal entropic forces. Such systems can be very large and complex and support higher cognitive and adaptive tasks. In the brain, that mechanism may be provided by resource preservation. Brains grow dendritic trees to store information, and make the trees as short as possible to preserve biological resources. By doing so, as proposed in [1] , they also minimize the action, Equation (5), and cause intelligence to arise as a side effect. In Table 1 in [1] , odd-numbered lines correspond to least-action  systems, and the thought experiment of Section 5 and all systems discussed in the Supplementary Material are
systems, and the thought experiment of Section 5 and all systems discussed in the Supplementary Material are 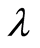 -systems. Optimally short dendritic trees were later independently confirmed [11] .
-systems. Optimally short dendritic trees were later independently confirmed [11] . 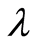 -
-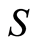 combinations are possible. For example, Nematodes seem to have
combinations are possible. For example, Nematodes seem to have 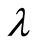 brains, but they have a connectome where neurons communicate by diffusion, which is an
brains, but they have a connectome where neurons communicate by diffusion, which is an 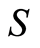 - process.
- process.
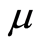 -systems are not well understood. They have been studied in simulations and reported in even-numbered lines in Table 1 in [1] . They have plenty of invariant non-trivial structures, but these differ from those at the
-systems are not well understood. They have been studied in simulations and reported in even-numbered lines in Table 1 in [1] . They have plenty of invariant non-trivial structures, but these differ from those at the  point for a given causal model. They may or may not exist in nature, or may represent a different kind of intelligence.
point for a given causal model. They may or may not exist in nature, or may represent a different kind of intelligence.
When viewed from the graph-theoretical point of view, the behavior of 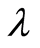 -systems is vastly different from the others. Nature appears to use a three-step divide-and-conquer technique to reduce complexity and find certainty in invariants. Let
-systems is vastly different from the others. Nature appears to use a three-step divide-and-conquer technique to reduce complexity and find certainty in invariants. Let  be the directed graph associated with
be the directed graph associated with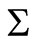 . In the first step, the minimization of the action functional of Equation (5) over
. In the first step, the minimization of the action functional of Equation (5) over  partitions
partitions  into connected components. In step 2, the causal space of each component is partitioned into macrostates, and in step 3, each macrostate is rearranged and partitioned into blocks. The component partition is by far the most significant because the size of the causal space depends exponentially on the size of
into connected components. In step 2, the causal space of each component is partitioned into macrostates, and in step 3, each macrostate is rearranged and partitioned into blocks. The component partition is by far the most significant because the size of the causal space depends exponentially on the size of . Component partitioning has been observed many times in
. Component partitioning has been observed many times in  - systems and is illustrated below in Section 5, but it has not been observed in
- systems and is illustrated below in Section 5, but it has not been observed in  -systems or reported at all for
-systems or reported at all for  -systems. If this were to be the case, then the conjecture could be made that
-systems. If this were to be the case, then the conjecture could be made that 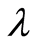 -systems are the most convenient for high cognition because they can grow very complex in causality and still have non-trivial invariants, as the human brain does. Which would then explain why the human brain has evolved to be so large, even at the expense of other evolutionary disadvantages.
-systems are the most convenient for high cognition because they can grow very complex in causality and still have non-trivial invariants, as the human brain does. Which would then explain why the human brain has evolved to be so large, even at the expense of other evolutionary disadvantages.
Causal entropic forces always point in the direction of increasing entropy. An isolated system with a fixed energy will maximize its entropy and become an  system. In the case of
system. In the case of 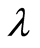 -systems, the present work applies to open systems that: 1) can exchange energy with a reservoir; 2) possess a memory, i.e. a collection of degrees of freedom with states that can be set and “read”, meaning they can interact with other degrees of freedom without changing their states; and 3) possess a mechanism that can oppose causal entropic forces and lower the entropy
-systems, the present work applies to open systems that: 1) can exchange energy with a reservoir; 2) possess a memory, i.e. a collection of degrees of freedom with states that can be set and “read”, meaning they can interact with other degrees of freedom without changing their states; and 3) possess a mechanism that can oppose causal entropic forces and lower the entropy  away from point
away from point 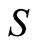 in either direction; Figure 1 in [12] , where
in either direction; Figure 1 in [12] , where 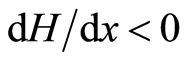 when
when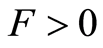 , explains how this can be achieved. Brains satisfy these conditions. Computers can be made to (
, explains how this can be achieved. Brains satisfy these conditions. Computers can be made to (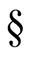 4.3 in [2] ).
4.3 in [2] ).
But we still can’t predict when block systems are non-trivial. There is no known closed-form mathematical answer to that, and there is no proof for the existence of one either. For now, we must be satisfied with construction.
5. Thought Experiment
An imaginary scientist who lived before Newton and knew nothing about Euler’s equations, took measurements at fixed intervals of time using mirrors attached to rotating tops that reflected light onto fixed rulers. She noticed that shorter intervals resulted in better accuracy, but other than that, the measurements had no meaning for her. She measured 10 real-valued variables, named them with generic names: ,
,  ,
,  ,
, 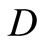 ,
, 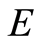 ,
,  ,
, 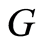 ,
, 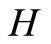 ,
,  ,
,  , except for the time step
, except for the time step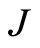 , and obtained the following 21 relations:
, and obtained the following 21 relations:
 (6)
(6)
The 21 lower-case variables become the 21 elements of set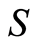 . The ordered pairs are obtained by examining dependencies among elements of
. The ordered pairs are obtained by examining dependencies among elements of 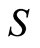 in Equation (6). The resulting causal set
in Equation (6). The resulting causal set 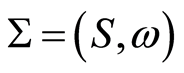 is:
is:
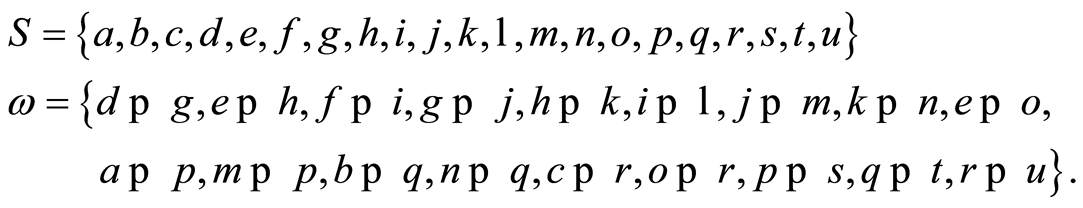 (7)
(7)
The alphabetical order of the elements of  is taken as the reference order
is taken as the reference order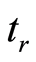 .
.  is very large and has not been calculated. The least-action is 42, and
is very large and has not been calculated. The least-action is 42, and 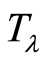 contains 6 trajectories, showed here with their connected components and minimal non-trivial block partitions:
contains 6 trajectories, showed here with their connected components and minimal non-trivial block partitions:
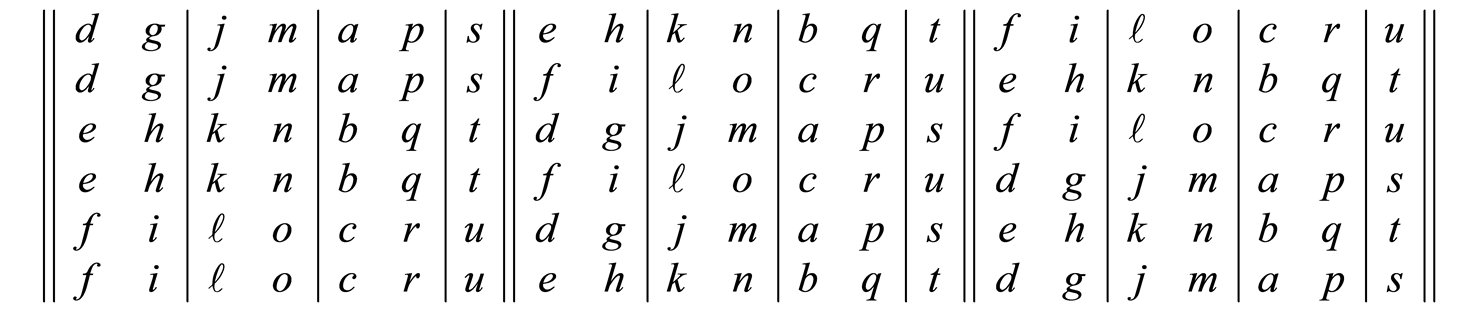 (8)
(8)
There is no need to determine the groupoid explicitly. Set 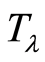 has 3 connected components, identified with double lines, indicating 3 separate equations. Each component has 3 blocks of 2 elements each and 1 block with 1 element. Hence, all 3 components are non-trivial. Further analysis indicates that all 3 block systems are structurally identical. It is now possible to assemble the expressions from Equation (6) into the structure discovered by the group theory, and then rename the variables to make their meaning more obvious. Recall that the original variables had no recognizable meaning. For the first connected component:
has 3 connected components, identified with double lines, indicating 3 separate equations. Each component has 3 blocks of 2 elements each and 1 block with 1 element. Hence, all 3 components are non-trivial. Further analysis indicates that all 3 block systems are structurally identical. It is now possible to assemble the expressions from Equation (6) into the structure discovered by the group theory, and then rename the variables to make their meaning more obvious. Recall that the original variables had no recognizable meaning. For the first connected component:
 (9)
(9)
where we have re-inserted the algebraic signs. When the same step is completed for all 3 components, a pattern becomes apparent. To enhance the effect, we first rename the 10 input and 3 output variables as follows:
 (10)
(10)
After renaming, the 3 final equations are:
 (11)
(11)
The final step is to take the mathematical limit . The limit itself is causal. It means that the rest of each equation becomes independent of
. The limit itself is causal. It means that the rest of each equation becomes independent of  (causal pairs disappear) when
(causal pairs disappear) when 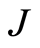 is small enough, thus defining a new function. Using the classical notation
is small enough, thus defining a new function. Using the classical notation 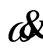 for the time derivative
for the time derivative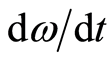 , the Euler equations are obtained in final form:
, the Euler equations are obtained in final form:
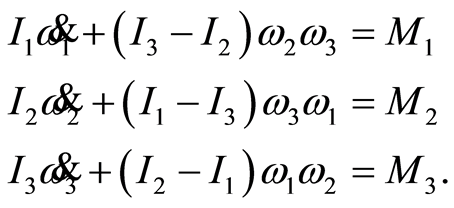 (12)
(12)
The meaning of the variables is now familiar. The scientist’s problem is now solved, and the procedure used to solve it is of a general nature and completely unrelated to the specifics of the problem. The final expressions in Equation (12) are new facts derived directly from facts given in Equation (6). The symbols now have a semantic value because they carry meaning that did not originally exist. These results were not explicitly programmed. They follow directly from the Mathematics of groupoids and the fundamental principles of nature that describe the properties of physical matter.
A person who wanted to solve this problem would need skills possibly comparable to those of a mid-level Physics student. This person would start by examining the sequences in which the variables in Equation (6) are calculated. She would notice that variable , calculated in the first line, is not used before the line that says
, calculated in the first line, is not used before the line that says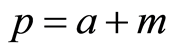 , so it would seem “reasonable” that the two lines should be closer together. However,
, so it would seem “reasonable” that the two lines should be closer together. However,  cannot be calculated unless
cannot be calculated unless  is also available. Continuing this analysis, this person will soon notice that the system splits into 3 components, and would then restart the analysis by rewriting them separately. She would then also notice that the components are identically structured, and that there is more than one way to “organize” each of them. She would soon arrive at one of the orders in Equation (8). The entire process may take a few hours to complete.
is also available. Continuing this analysis, this person will soon notice that the system splits into 3 components, and would then restart the analysis by rewriting them separately. She would then also notice that the components are identically structured, and that there is more than one way to “organize” each of them. She would soon arrive at one of the orders in Equation (8). The entire process may take a few hours to complete.
By contrast, it is possible to imagine an “intelligent machine” that would mechanize the entire process using causal sets and causal groupoid symmetries, and solve the problem without any human intervention. This machine would have no need for any of the skills expected from the Physics student. It would complete execution perhaps in microseconds instead of hours, simply because it will use far less information than the student, and because hardware runs much faster than wetware. Even the mathematical limit, needed to write the final Equation (12), is a simple causal operation in 2nd order causal logic (see Section 2.6 in [2] ).
Furthermore, the positive definite functional of Equation (5) can only be minimized by minimizing the positive contribution from each one of the causal pairs in the causal set. These contributions are only locally interdependent, and can be minimized locally, without the need for any information of a global nature. The property of locality naturally leads to a massively parallel computational architecture. A machine designed along these lines has been proposed in Section 4.3 of [2] and is further discussed in Section 7 below.
What is fascinating about such machine, is that it solves the problem without having been asked to do so. Nothing in the machine is specific to the given problem, nothing has been specifically programmed for any purpose other than minimizing the functional. The machine does not know any Physics, does not know what it is doing or why, and has not been trained with any skills other than the fundamental causal metric. The machine works only from input data containing a causal description of the topology of the problem. It simply decides to do what it does on its own, without any external direction. There is only one machine of this kind for all problems.
To the best of our knowledge, this is the first time that high cognitive behavior has been quantitatively shown to emerge from a non-explicitly programmed model.
Of course, the thought experiment is very small, and does not sufficiently represent the power of the ideas being exposed. In 1985, on page 633 of Metamagical Themas, and in his familiar style, Douglas Hofstadter asked: “The major question of AI is this: What in the world is going on to enable you to convert 100,000,000 retinal dots into one single word ‘mother’ in one tenth of a second?” Each retinal dot generates a causal pair, of which the cause is the beam of light, and the effect is the signal the dot sends to the brain. There is going to be a causal set with 100 million pairs (additional geometric information is necessary but is ignored here for simplicity). The causal set will likely partition into many components, each representing features of the image. But the question of which features and how to represent them and inter-relate them, is decided by the process itself. There is no need to prescribe any “feature vectors” specific to the problem at hand. There is also going to be a groupoid and symmetries and a hierarchy of structures for each component. Will those structures be sufficient to identify the image? Will the machine solve the recognition problem in microseconds? Will the theory scale appropriately to such a large problem? We believe it will. We know it will scale because the fractal property of the invariants guarantees a constant execution time, independent of the size of the problem. We believe it will solve the recognition problem in microseconds. But the only way to know for sure is to try. Pronouncing the word “mother” would be a little beyond scope here, but it can be reduced to groupoids as well.
6. Causal Models
As usual, the first step for the analysis of a complex system is to prepare a mathematical model of it. In the causal theory, this model is a causal set. Causal set models are ubiquitous. They can be found everywhere, and are part of our daily life and of all our scientific activities. But their direct use is relatively new in Science. To dispel concerns, we open the section with the following rules of thumb:
1. If you can write a computer program about it, then you can also write a causal set about it.
2. The output of any sensor is a causal set.
3. The input to any actuator is a causal set.
In fact, a computer program is a causal set written in a condensed human-readable notation. Everything in the program is finite, even “real” numbers. Everything in the program is causal and deterministic, even “random” numbers. The principle of causality posits that effects follow their causes, but does not require that causes be known for every effect or that “all” causal pairs for a given effect be known. The typical situation is one where we know some cause-effect pairs for some effects and want to test what we know, compare with observation, and eventually seek to obtain more information and repeat the process. Conversions from software notation to causal set notation are admittedly cumbersome, but will not be once they are automated for the most important programming languages. They have been discussed in Section III in [13] .
The same considerations apply to algorithms, sets of equations, either algebraic or differential, theories, and many other forms of expression. This is a causal world, and causality underlies everything. The rules of thumb above provide some idea of how to go from underlying causality to a causal set model.
The entire body of Science is a constant quest for causes. We use them to create mental models that allow us to predict, and we constantly refine them by searching for more detail. We find these activities natural.
At this point, it is important to compare the causal theory with the methods of statistical physics. In statistical physics, we deal with complex systems where it would be too difficult to gather enough information to directly apply the laws of Physics to every interaction. We are forced to disregard details that appear to be irrelevant, and to apply probabilistic methods trying to approximately explain the properties of matter in aggregate. Once disregarded, we do not have a direct mechanism to evaluate the relevance of a particular detail without significant changes to the model.
In causal physics, particularly when we deal with a complex system, we may again run into a situation where information is limited and incomplete, and it may be difficult or unfeasible to gather more detail. We start with a coarse model, and we still want to test what we have and compare with observations in the hope that the test will either be satisfactory or at least tell us where more detail may be necessary. When more detail becomes available, then that detail itself is a causal set, and we simply merge it with the original causal set and re-calculate the invariants. This is the causal version of the procedure known as machine learning in Artificial Intelligence. See Sections IV and V.F in [13] for more detail.
The critical difference between causal analysis and statistical analysis is that statistical methods discard detail, while causal methods preserve detail, and in fact there is no limit to the degree of detail they can carry. And because adding detail is a simple merge, it can be mechanized, with the additional detail obtained either by experiments carried by human scientists or directly by sensors. Permanent causal models can be created that evolve automatically by learning from their environments.
In such sense, it can be said that the causal theory offers an alternative to Statistical Physics, with very different features.
The most interesting application of the causal theory to complex systems is expected to be the brain. It is our working hypothesis that the brain acquires causal information directly from the sensory organs and transforms it through a causal process. Other applications will include Artificial Intelligence and Computer Science.
The Supplementary Material contains examples of causal sets and of the procedures used to obtain them. Additional literature includes [1] [14] -[20] .
7. Practical Implementation
In this Section we review some practical details for a prototype computer implementation of causal groupoid symmetries and the causal theory that needs them. The host-guest process described above is a system with various basic components. It needs an input module that can receive causal data from a variety of sources such as sensors, computer files, existing algorithms and computer programs optionally in various languages, etc., and deliver the corresponding causal set. It also needs an output module with presentation capabilities and support for the user to view and use the results. And it needs a central processing unit that can find the least-action or maximum entropy groupoid symmetries and corresponding structural hierarchies for the given causal set. The core unit consists of a linear array of simple computational units, called neurons, each of which can communicate only with its two nearest neighbors, but which are otherwise completely independent. All neurons work at the same time, each minimizing its own contribution, and resulting in massive parallelism. The execution time for a given problem is constant and independent of the size of the problem provided the number of neurons equals or exceeds the number of elements in the causal set.
This machine is not specific to any particular problem. It is general, the same machine for all problems. There is only one such machine, although many different implementations on the same or different substrates are possible. The difference will be in the kind of training it receives and in the size and computational power needed to address that kind of training. Once a machine is trained in some specific area, then copies can be made and individual machines created that specialize in subareas, as needed. Except for the “copies” part, the reader may have noticed that the present paragraph would apply to humans almost without change.
The functional in Equation (5) is positive definite, defined as the sum of positive contributions from each one of the causal pairs. It can only be minimized by minimizing each one of the contributions. The positive definiteness property connects local to global and is essential for emergence because it allows a collection of independent agents to achieve a global effect that exceeds the sum of their individual contributions. This positive definiteness is also critically necessary to allow the massively parallel implementation of the action minimization algorithm. Based on the independence of the agents, the functional is minimized when each agent locally minimizes its own contribution without the need for any global information or sense of purpose.
These elements of design have been discussed in Section 4 of [2] , where, particularly in subsection 4.3, a prototype has been proposed that can be implemented on an FPGA or GPGPU processor. This design can be considered as a neural network where nodes correspond to elements of the causal set, and commutation of adjacent pairs is used to systematically create permutations with progressively lower values of the action. The “differential pulls” described in that subsection correspond to (the negatives of) causal entropic forces, that try to increase the entropy of the system. By forcibly opposing these forces, the entropy and action are minimized, and a  -type system is obtained.
-type system is obtained.
This design uses a large number of very simple processors, each with only a tiny amount of memory. The number of processors is required to be at least as large as the number of elements of the causal set to be processed, and the total execution time is constant, independent of the number of elements, provided the condition is satisfied that each processor can minimize its local contribution in a period of time that does not exceed a certain constant value. These conditions are strongly reminiscent of the proverbial massive parallelism of the human brain and of its apparently very fast response time even to the largest of problems. In fact, they suggest an explanation for the large size of the human brain. However, the hardware prototype would be expected to run perhaps 106 times faster than the brain just because electronics is much faster than wetware. In time, we expect that microchips with millions, perhaps billions of processors will be built.
No unit of the type proposed here has yet been build, at least not in our knowledge. All computational work and examples discussed in this paper were performed on a personal computer.
8. Predictions
In [1] , we proposed a working hypothesis that the brain is a complex system where intelligence is an emergent process, and that the internal representations that our brains make, such as the representation of a face or smell we have recognized and which needs to be invariant under transformations of many types, do indeed arise from groupoid symmetries and are to be considered invariants as rightfully as those we consider in Physics. There immediate follows from our assumption that there exists a very large number of invariants, possibly infinite, of which only a very small number has been discovered so far.
Based on the working hypothesis, a causal set model of the brain was proposed. The model is a network where nodes correspond to elements and links to relations in the causal set. The physical length of the connections corresponds to the abstract measures 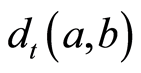 in Equation (4). The model was used to formulate some predictions and obtain verifications of the theory.
in Equation (4). The model was used to formulate some predictions and obtain verifications of the theory.
One of the predictions states that, if the brain does have the ability to minimize action, then dendritic trees must be as short as possible. At that time, the belief in Neuroscience was that the total length of dendritic trees followed a 4/3 power law, which is not optimally short. Later, however, a team of neuroscientists working independently from us proposed an optimally short 2/3 power law with a wide experimental base including the human brain and even across species [11] , thus confirming our prediction.
Another prediction was also made in [1] that the theoretical study of macrostate population, an example of which is shown in Figure 1, should apply to the human brain. This was independently confirmed by comparing the theoretical curve, appropriately rescaled and horizontally inverted, with the measured EEG intensities in Figure 6 left of [21] , which shows the initial ascent from least-entropy up to the entropy peak followed by a slow decay towards minimum entropy as the action decreases. This prediction serves as a verification of the theory.
Still in the same working hypothesis, we predicted that the brain should operate like a host-guest dynamical system, where the host is unconscious and of a thermodynamic nature, while the guest is conscious and algorithmic. We predicted this independently, from the model, and later found out that in mid 19th century, in his studies of the visual system in humans, Physicist and Physiologist Hermann von Helmholtz had predicted that a process of inference should exist in order to complete the processing of an image. He named this process “Unconscious Inference”, because we weren’t aware it was taking place. We also learned of the Dual Process theory in Psychology, which proposes an implicit, unconscious process, which is automatic and we can’t control, and an explicit conscious process that we control. This convergence of concepts from three very different sources is remarkable, but even more in particular because the causal theory is not a theory of the brain and contains nothing indicating that brains even exist.
The European Example in the Supplemental Material is a black-box brain experiment, where the results from a task usually performed only by humans and considered as high brain function, are compared with results directly predicted by the causal theory. The task in question is object-oriented design—the design of the class and inheritance structure for the architecture of a computer program, usually done by a human analyst from a given problem statement. To do the experiment, we start from the finished product, an OO design and program developed by human analysts. We remove all structure and order, leaving only the causal relationships in the program, but no information at all about the classes. This step leaves only a causal set, nothing else. Then, we apply the usual causal theory, which has not been explicitly programmed to do OO design and knows nothing about computers or programs, and certainly not about software engineering. The result is a class structure nearly identical to the original man-made one.
Another example in the Supplementary Material, the Point Separation example, is concerned with the problem of image recognition, and corresponds to Figure 4 of [1] . The size of the corresponding causal sets—1433 elements—far exceeds our current resources (about 12 to 15 elements). We carried the calculations out to the point where the 167 points are effectively separated into 3 groups, but were unable to proceed any further (such as an identification of the letter “C” in the figure). The example is temporarily paused, but even the very preliminary result that the points are separated is of value because the system does that on its own. Again, the system knows nothing about points or even about geometry, and it is certainly not aware that it is separating points or recognizing an image.
It should be noted at this point that the limitation is one of architecture, and would not be solved by a supercomputer. The correct architecture is discussed in Section 4.3 of [2] . This architecture is a neural network where each “neuron” is a very simple processor to which only local near-neighbor information is available. Neurons correspond to elements in the causal set, and all work simultaneously in steps. Assuming that the maximum number of steps per neuron is limited, this architecture has the property that the total execution time is constant and independent of the size of the problem, under the condition that the number of neurons equals or exceeds the number of elements. The reader should recognize the proverbial “massive parallelism” usually attributed to the brain.
Finally, the thought experiment in Section 5 starts from (imaginary) experimental information supposedly measured for a rotating top, and leads to the Euler equations for rotating bodies obtained directly from the causal theory and the notion of mathematical limit. Once more, the causal theory knows nothing about tops or theories of Physics and has not been told to derive any equations.
The value of these predictions and verifications stems from the fact that the same non explicitly-programmed system was used for all cases, without any modifications and without any programming specific to any particular problem.
9. Conclusions
A causal theory of Physics is proposed where a causal set is considered as a mathematical model of a complex system and groupoid symmetries existing in the causal set are applied directly to derive a hierarchy of invariants for that system. The theory is fundamental because it follows directly from the principle of causality and a basic causal metric, and does not include any heuristics or adjustable parameters. It applies to all causal systems, even under conditions where only partial information is available, because any model can always be refined by adding more information as it becomes available. As such, it provides an alternative to traditional statistical methods.
A discrete causal space independent of traditional space and time is introduced, where states, trajectories and invariants exist, and invariance is proposed as the base for semantics. Groupoid symmetries with invariant hierarchies of block systems naturally exist in causal space as a consequence of the partial order of trajectories, and many of them may be imprimitive, meaning their invariant hierarchies are non-trivial. These hierarchies are the invariants being sought.
The metric naturally partitions the causal space first into connected components, then into macrostates, and finally into block systems that are invariant under the action of the groupoid. The partition gives rise to exactly three types of macrostates that can be specified by optimization and are therefore fundamental. Any of the other macrostates would have to be specified by parameter and would not be fundamental. In correspondence with the fundamental macrostates, three very different classes of physical systems can be identified, designated as  -,
-,  -, and
-, and 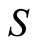 -systems. Limited experimental information suggests that the conditions for a system to be imprimitive depend on the class.
-systems. Limited experimental information suggests that the conditions for a system to be imprimitive depend on the class.  -systems appear to be more likely to be imprimitive when they are small and simple. They give rise to basic, repetitive behaviors with a basic goal, such as gaining an immediate advantage or increasing the number of options. These properties match the properties reported in [6] [7] .
-systems appear to be more likely to be imprimitive when they are small and simple. They give rise to basic, repetitive behaviors with a basic goal, such as gaining an immediate advantage or increasing the number of options. These properties match the properties reported in [6] [7] .  -systems, instead, may be imprimitive even if they are very large. They would be evolved and sophisticated systems, possibly with a connectome, and would exhibit complex cognitive behaviors with abstract goals. The brain seems to be a
-systems, instead, may be imprimitive even if they are very large. They would be evolved and sophisticated systems, possibly with a connectome, and would exhibit complex cognitive behaviors with abstract goals. The brain seems to be a 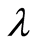 -system. Both
-system. Both 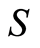 -systems and
-systems and  -systems exist in nature. It is not known whether
-systems exist in nature. It is not known whether 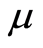 -systems exist in nature, but they can be created artificially. Imprimitive
-systems exist in nature, but they can be created artificially. Imprimitive 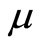 -systems would be similar but less sophisticated than
-systems would be similar but less sophisticated than  -systems. Imprimitive systems are the ones that exhibit adaptive behavior.
-systems. Imprimitive systems are the ones that exhibit adaptive behavior.
These considerations hint at a deep connection between causality and invariance with self-organization, emergence, semantics, and, ultimately, intelligence and adaptation. The theory is proposed as a formalization of this connection. Preliminary computational experiments and predictions made for the brain, both quantitative and qualitative, some already confirmed, suggest a correlation with observed cognitive structures.
To the best of our knowledge, this is the first time that high cognitive behavior has been quantitatively shown to emerge from a non-explicitly programmed model. The results are remarkable because the software has never been told to do what it did, and was never given any problem-specific goals. It simply decided to do it. We said in the Introduction that our focus was on groupoids with non-trivial block systems. That’s our focus, but our vision goes much farther: it is to make intelligence a problem of Physics and Applied Mathematics.
References
- Pissanetzky, S. (2011) Emergence and Self-Organization in Partially Ordered Sets. Complexity, 17, 19-38. http://onlinelibrary.wiley.com/doi/10.1002/cplx.20389/abstract http://dx.doi.org/10.1002/cplx.20389
- Pissanetzky, S. (2012) Reasoning with Computer Code: A New Mathematical Logic. Journal of Artificial General Intelligence, 3, 11-42. http://www.degruyter.com/view/j/jagi.2012.3.issue-3/issue-files/jagi.2012.3.issue-3.xml
- Pissanetzky, S. (2011) Structural Emergence in Partially Ordered Sets Is the Key to Intelligence. Lecture Notes in Computer Science. Artificial General Intelligence, 6830, 92-101. http://dl.acm.org/citation.cfm?id=2032884
- Weinstein, A. (1996) Groupoids: Unifying Internal and External Symmetry. Notices of the AMS, 43, 744-752. http://www.ams.org/notices/199607/weinstein.pdf
- Stewart, I., Golubitsky, M. and Pivato, M. (2003) Symmetry Groupoids and Patterns of Synchrony in Coupled Cell Networks. SIAM Journal of Applied Dynamical Systems, 2, 609-646. http://epubs.siam.org/doi/abs/10.1137/S1111111103419896 http://dx.doi.org/10.1137/S1111111103419896
- Golubitsky, M. and Stewart, I. (2006) Nonlinear Dynamics of Networks: The Groupoid Formalism. Bulletin of the American Mathematical Society, 43, 305-364. http://www.ams.org/journals/bull/2006-43-03/S0273-0979-06-01108-6/ http://dx.doi.org/10.1090/S0273-0979-06-01108-6
- Wissner-Gross, A.D. and Freer, C.E. (2013) Causal Entropic Forces. Physical Review Letters, 110, 168702. http://link.aps.org/doi/10.1103/PhysRevLett.110.168702 http://dx.doi.org/10.1103/PhysRevLett.110.168702
- Gardner, A. and Conlon, J.P. (2013) Cosmological Natural Selection and the Purpose of the Universe. Complexity, 18, 48-56. http://onlinelibrary.wiley.com/doi/10.1002/cplx.21446/abstract http://dx.doi.org/10.1002/cplx.21446
- Eigen, M. (2013) From Strange Simplicity to Complex Familiarity. Oxford University Press, New York. http://dx.doi.org/10.1093/acprof:oso/9780198570219.001.0001
- Fuster, J.M. (2005) Cortex and Mind. Unifying Cognition. Oxford University Press, New York. http://dx.doi.org/10.1093/acprof:oso/9780195300840.001.0001
- Cuntz, H., Mathy, A. and Häusser, M. (2012) A Scaling Law Derived from Optimal Dendritic Wiring. Proceedings of the National Academy of Sciences USA, 109, 11014. http://www.pnas.org/content/early/2012/06/19/1200430109.full.pdf http://dx.doi.org/10.1073/pnas.1200430109
- Verlinde, E. (2011) On the Origin of Gravity and the Laws of Newton. Journal of High Energy Physics, 4, 1-26. http://arxiv.org/pdf/1001.0785.pdf
- Pissanetzky, S. (2009) A New Universal Model of Computation and Its Contribution to Learning, Intelligence, Parallelism, Ontologies, Refactoring, and the Sharing of Resources. International Journal of Information and Mathematical Sciences, 5, 952-982. http://www.scicontrols.com/Publications/ANewUniversalModel.pdf
- Bolognesi, T. (2010) Causal Sets from Simple Models of Computation. arXiv:1004.3128. http://arxiv.org/abs/1004.3128
- Carlson, C.R. (2010) Causal Set Theory and the Origin of Mass-Ratio. viXra:1006.0070. http://vixra.org/abs/1006.0070
- Pissanetzky, S. and Lanzalaco, F. (2013) Black-Box Brain Experiments, Causal Mathematical Logic, and the Thermodynamics of Intelligence. Koene, R., Sandberg, A. and Deca, D., Eds., Journal of Artificial General Intelligence, Special Issue on Brain Emulation and Connectomics, to be published.
- Mason, J.W.D. (2013) Consciousness and the Structuring Property of Typical Data. Complexity, 18, 28-37. http://onlinelibrary.wiley.com/doi/10.1002/cplx.21431/full http://dx.doi.org/10.1002/cplx.21431
- Pearl, J. (2009) Causality. Models, Reasoning, and Inference. 2nd Edition, Cambridge University Press, New York. http://dx.doi.org/10.1017/CBO9780511803161
- Neural Information Processing Foundation (2013) http://nips.cc/Conferences/2013/
- Stephan, K.E., Penny, W.D., Moran, R.J., den Ouden, H.E., Daunizeau, J. and Friston, K.J. (2010) Ten Simple Rules for Dynamic Causal Modeling. Neuroimage, 49, 3099-3109. http://www.ncbi.nlm.nih.gov/pubmed/19914382 http://dx.doi.org/10.1016/j.neuroimage.2009.11.015
- Kawamata, M., Kirino, E., Inoue, R. and Arai, H. (2007) Event-Related Desynchronization of Frontal-Midline Theta Rhythm during Preconscious Auditory Oddball Processing. Clinical EEG and Neuroscience, 38, 193. http://www.ncbi.nlm.nih.gov/pubmed/17993201 http://dx.doi.org/10.1177/155005940703800403

