Applied Mathematics
Vol.4 No.11A(2013), Article ID:38844,11 pages DOI:10.4236/am.2013.411A1005
Solution of Laplace’s Differential Equation and Fractional Differential Equation of That Type
1Tohoku University, Sendai, Japan
2College of Engineering, Nihon University, Koriyama, Japan
Email: senmm@jcom.home.ne.jp
Copyright © 2013 Tohru Morita, Ken-ichi Sato. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received August 19, 2013; revised September 19, 2013; accepted September 26, 2013
Keywords: Laplace’s Differential Equation; Kummer’s Differential Equation; Fractional Differential Equation; Distribution Theory; Operational Calculus; Inhomogeneous Equation; Polynomial Solution
ABSTRACT
In a preceding paper, we discussed the solution of Laplace’s differential equation by using operational calculus in the framework of distribution theory. We there studied the solution of that differential equation with an inhomogeneous term, and also a fractional differential equation of the type of Laplace’s differential equation. We there considered derivatives of a function 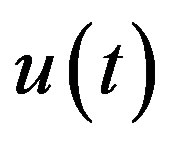 on
on , when
, when 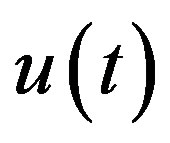 is locally integrable on
is locally integrable on , and the integral
, and the integral  converges. We now discard the last condition that
converges. We now discard the last condition that 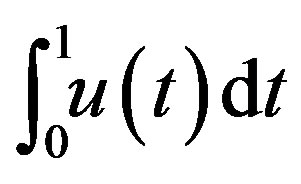 should converge, and discuss the same problem. In Appendices, polynomial form of particular solutions are given for the differential equations studied and Hermite’s differential equation with special inhomogeneous terms.
should converge, and discuss the same problem. In Appendices, polynomial form of particular solutions are given for the differential equations studied and Hermite’s differential equation with special inhomogeneous terms.
1. Introduction
Yosida [1,2] discussed the solution of Laplace’s differential equation (DE), which is a linear DE, with coefficients which are linear functions of the variable. The DE which he takes up is
 (1.1)
(1.1)
where  and
and  for
for  are constants. His discussion is based on Mikusiński’s operational calculus [3]. Yosida [1,2] gave there only one of the solutions of the DE (1.1).
are constants. His discussion is based on Mikusiński’s operational calculus [3]. Yosida [1,2] gave there only one of the solutions of the DE (1.1).
In the preceding paper [4], we discussed the solution of an fractional differential equation (fDE) of the type of DE (1.1), that is given by
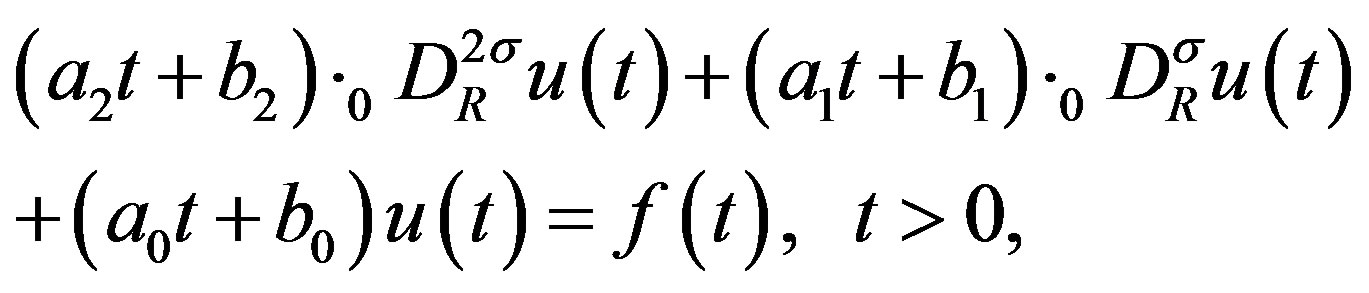 (1.2)
(1.2)
for 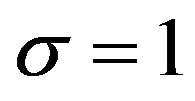 and
and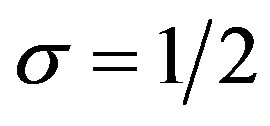 . Here
. Here  for
for 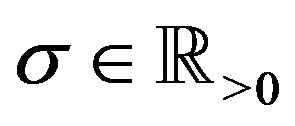 is the Riemann-Liouville fractional derivative (fD) defined in Section 2. We use
is the Riemann-Liouville fractional derivative (fD) defined in Section 2. We use  to denote the set of all real numbers, and
to denote the set of all real numbers, and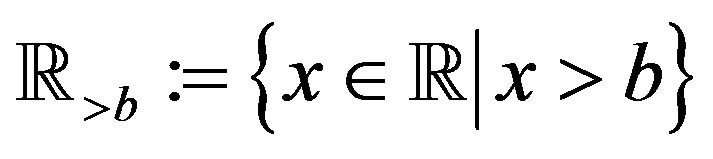 . When
. When  is equal to an integer
is equal to an integer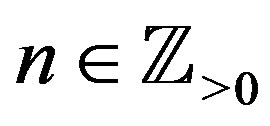 ,
,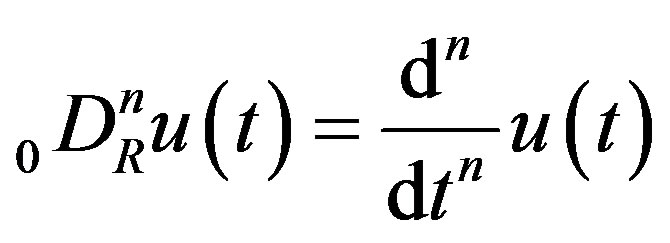 . When
. When
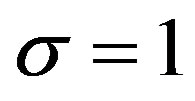 , (1.2) is the inhomogeneous DE for (1.1). We use
, (1.2) is the inhomogeneous DE for (1.1). We use 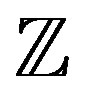 to denote the set of all integers, and
to denote the set of all integers, and ,
, 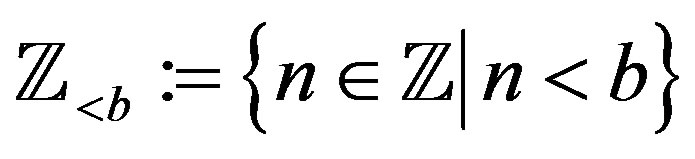 and
and
 for
for 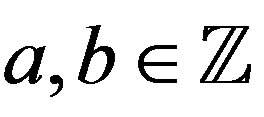 satisfying
satisfying .
.
We use  for
for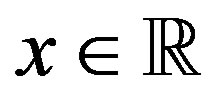 , to denote the least integer that is not less than
, to denote the least integer that is not less than .
.
In [4], we adopt operational calculus in the framework of distribution theory developed for the solution of the fDE with constant coefficients in [5,6]. In [4], we give the recipe of obtaining the solution of the inhomogeneous equation as well as the homogeneous one, and we show how the set of two solutions of the homogeneous equation is attained.
In [4], we adopt the usual definition of the Riemann-Liouville fD, which defines 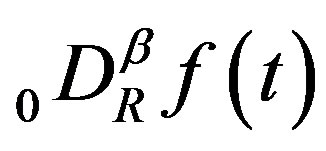 only for such a locally integrable function
only for such a locally integrable function 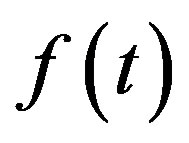 on
on 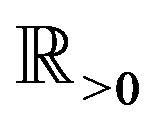 that
that
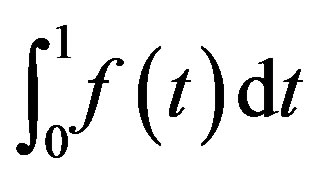 is finite. Practically, we adopt Condition B in
is finite. Practically, we adopt Condition B in
[4], which is Condition IB  and
and  are expressed as a linear combination of
are expressed as a linear combination of 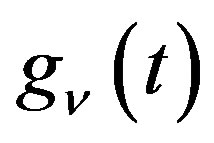 for
for .
.
Here 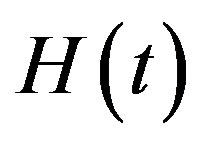 is Heaviside’s step function, and when
is Heaviside’s step function, and when 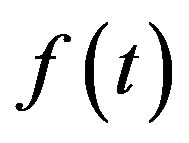 is defined on
is defined on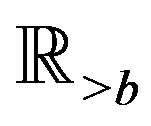 ,
, 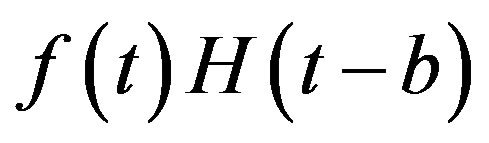 is assumed to be equal to
is assumed to be equal to 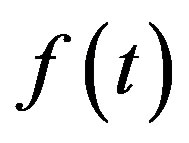 when
when 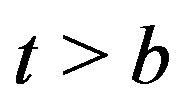 and to
and to  when
when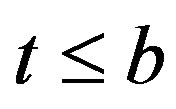 .
. 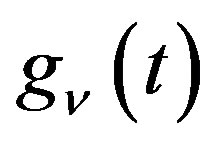 is defined by
is defined by
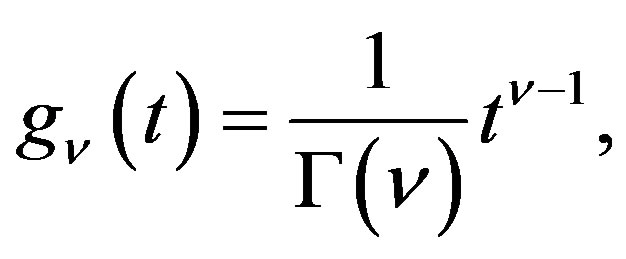 (1.3)
(1.3)
for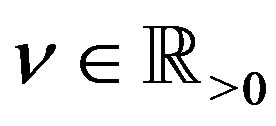 , where
, where 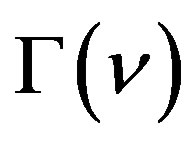 is the gamma function.
is the gamma function.
In [4], we take up Kummer’s DE as an example, which is
 (1.4)
(1.4)
where 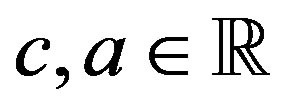 are constants. If
are constants. If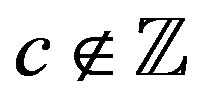 , one of the solutions given in [7,8] is
, one of the solutions given in [7,8] is
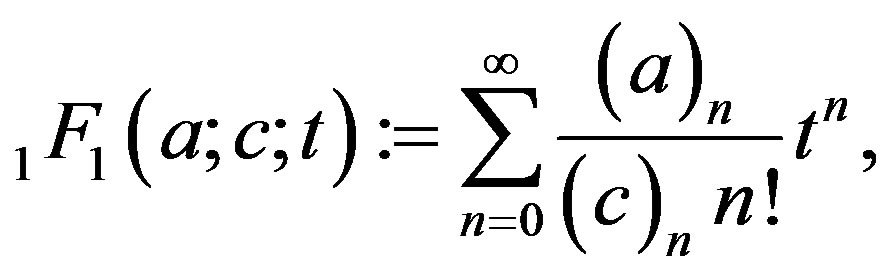 (1.5)
(1.5)
where  for
for  and
and and
and . The other solution is
. The other solution is
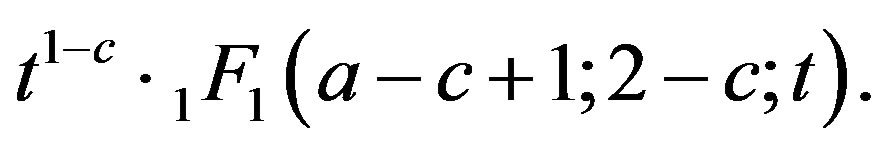 (1.6)
(1.6)
In [4], if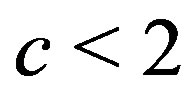 , we obtain both of the solutions. But when
, we obtain both of the solutions. But when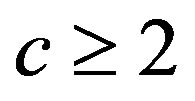 , (1.6) does not satisfy Condition IB and we could not get it.
, (1.6) does not satisfy Condition IB and we could not get it.
In a recent review [9], we discussed the analytic continuations of fD, where an analytic continuation of Riemann-Liouville fD,  , is such that the fD exists even for such a locally integrable function
, is such that the fD exists even for such a locally integrable function 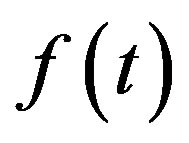 on
on
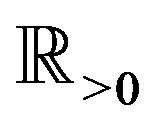 that
that 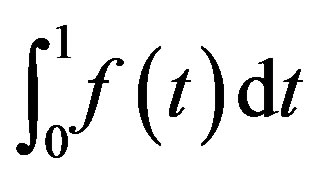 diverges. In the present paper, we adopt this analytic continuation of
diverges. In the present paper, we adopt this analytic continuation of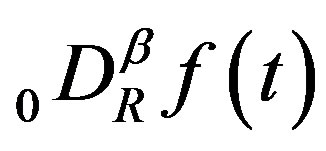 .
.
In place of the above Condition IB, we now adopt the following condition.
Condition A  and
and 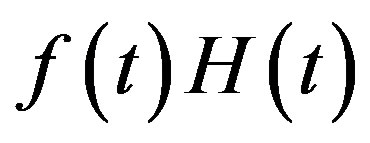 are expressed as a linear combination of
are expressed as a linear combination of  for
for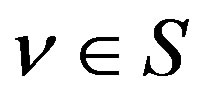 , where
, where  is a set of
is a set of  for some
for some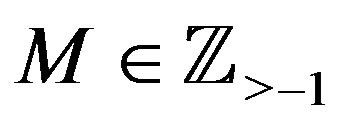 .
.
As a consequence, we can now achieve ordinary solutions for (1.2) of . For (1.4), we obtain both solutions (1.5) and (1.6) if
. For (1.4), we obtain both solutions (1.5) and (1.6) if .
.
It is the purpose this paper to show how the presentation in [4] should be revised, with the change of definition of fD and the replacement of Condition IB with Condition A.
In Section 2, we prepare the definition of RiemannLiouville fD and then explain how the function 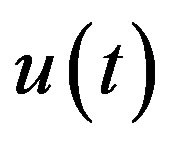 and its fD in (1.2) are converted into the corresponding distribution
and its fD in (1.2) are converted into the corresponding distribution 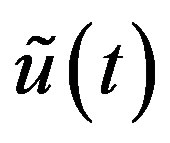 and its fD in distribution theory, and also how
and its fD in distribution theory, and also how 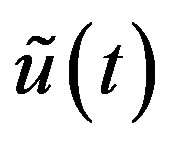 is converted back into
is converted back into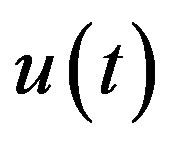 . After these preparation, a recipe is given to be used in solving the fDE (1.2) with the aid of operational culculus in Section 3. In this recipe, the solution is obtained only when
. After these preparation, a recipe is given to be used in solving the fDE (1.2) with the aid of operational culculus in Section 3. In this recipe, the solution is obtained only when
 and
and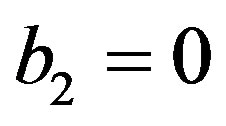 . When
. When ,
,  is also required. An explanation of this fact is given in Appendices C and D of [4]. In Section 4, we apply the recipe to (1.2) where
is also required. An explanation of this fact is given in Appendices C and D of [4]. In Section 4, we apply the recipe to (1.2) where 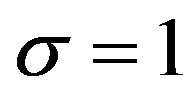 and
and , of which special one is Kummer’s DE. This is an example which Yosida [1,2] takes up. In Section 5, we apply the recipe to the fDE with
, of which special one is Kummer’s DE. This is an example which Yosida [1,2] takes up. In Section 5, we apply the recipe to the fDE with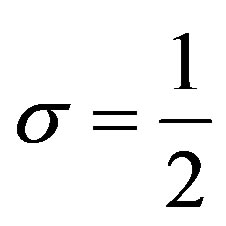 , assuming
, assuming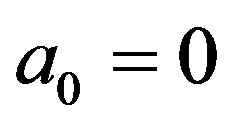 .
.
For the Hermite DE with inhomogeneous term, Levine and Malek [10] showed that there exist particular solutions in the form of polynomial. In Appendices A and C, we show that such a solution exists for the DE and fDE studied in Sections 4 and 5, respectively. In Appendix B, we show how the results presented in [10] are derived from those in Appendix A.
2. Formulas
We now adopt Condition A. We then express  as follows;
as follows;
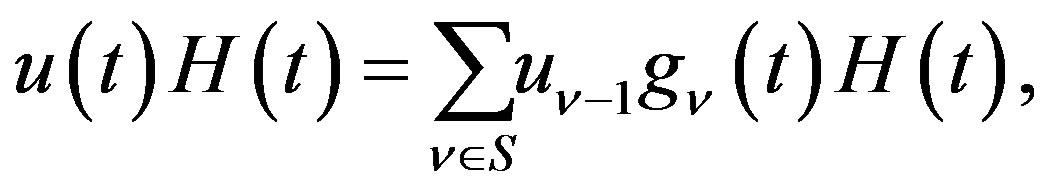 (2.1)
(2.1)
where 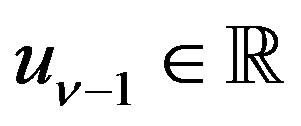 are constants.
are constants.
Lemma 1 For ,
,
 (2.2)
(2.2)
Proof By (1.3), for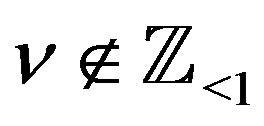 , we have
, we have
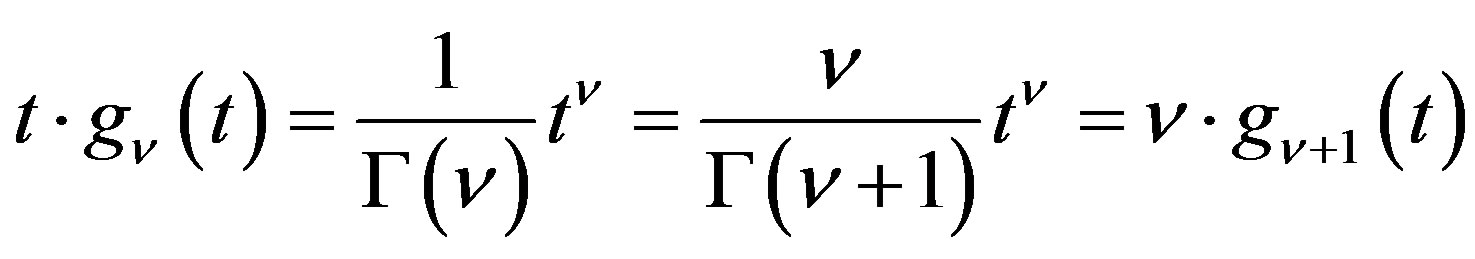 .
. 
2.1. Riemann-Liouville Fractional Integral and Derivative
Let 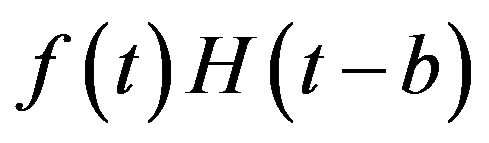 be locally integrable on
be locally integrable on . We then define the Riemann-Liouville fractional integral,
. We then define the Riemann-Liouville fractional integral,  , of order
, of order  by
by
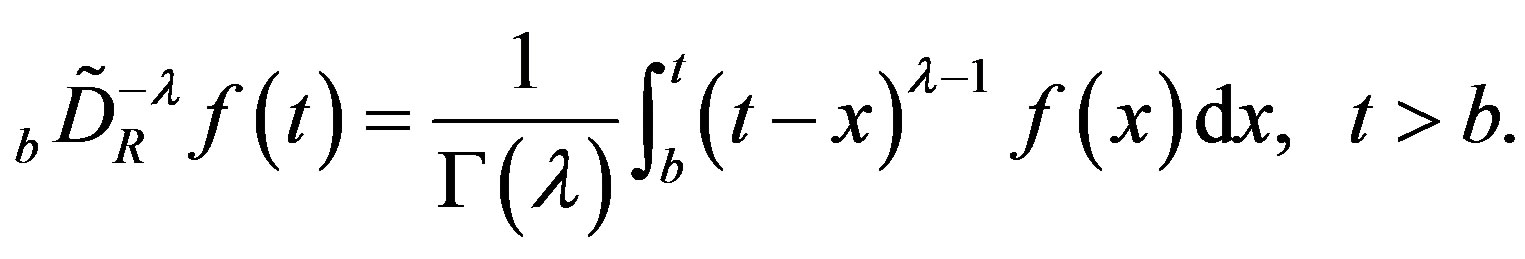 (2.3)
(2.3)
We then define the Riemann-Liouville fD,  , of order
, of order , by
, by
 (2.4)
(2.4)
if it exists, where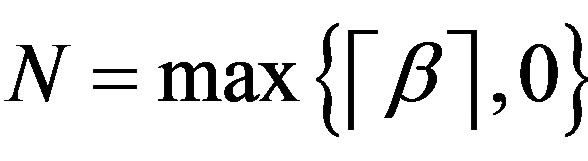 , and
, and 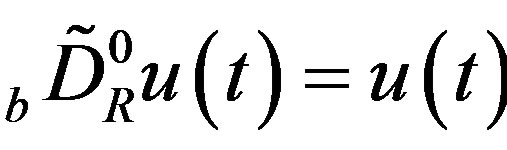 for
for .
.
For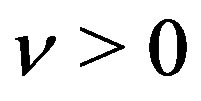 , we have
, we have
 (2.5)
(2.5)
If we assume that 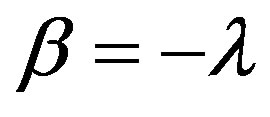 takes a complex value,
takes a complex value,  by definition (2.3) is analytic function of
by definition (2.3) is analytic function of  in the domain
in the domain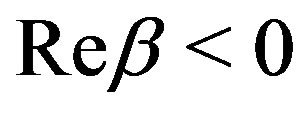 , and
, and  defined by (2.4) is its analytic continuation to the whole complex plane. If we assume that
defined by (2.4) is its analytic continuation to the whole complex plane. If we assume that 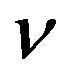 also takes a complex value,
also takes a complex value, 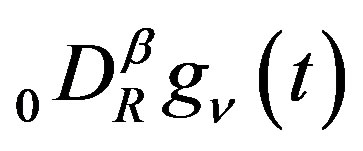 defined by (2.4) is an analytic function of
defined by (2.4) is an analytic function of 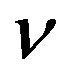 in the domain
in the domain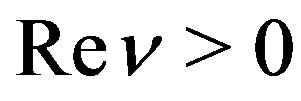 . The analytic continuation as a function of
. The analytic continuation as a function of  was also studied. The argument is naturally concluded that (2.5) should apply for the analytic continuation, even in
was also studied. The argument is naturally concluded that (2.5) should apply for the analytic continuation, even in  except at the points where
except at the points where ; see [9].
; see [9].
We now adopt this analytic continuation of 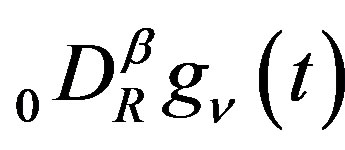 to represent
to represent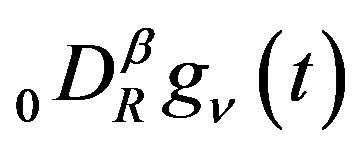 , and hence we accept the following lemma.
, and hence we accept the following lemma.
Lemma 2 (2.5) holds for every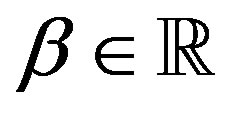 ,
, .
.
By (2.1) and (2.5), we have
 . (2.6)
. (2.6)
For 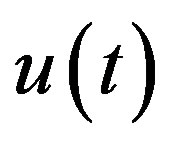 defined by (2.1), we note that
defined by (2.1), we note that
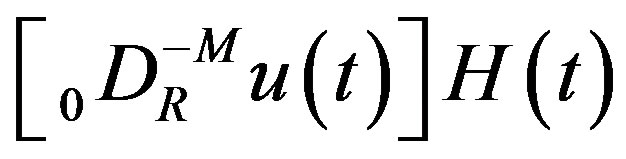
is locally integrable on .
.
2.2. Fractional Integral and Derivative of a Distribution
We consider distributions belonging to . When a function
. When a function 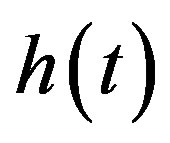 is locally integrable on
is locally integrable on  and has a support bounded on the left, it belongs to
and has a support bounded on the left, it belongs to  and is called a regular distribution. The distributions in
and is called a regular distribution. The distributions in  are called right-sided distributions.
are called right-sided distributions.
A compact formal definition of a distribution in 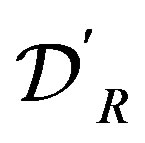 and its fractional integral and derivative is given in Appendix A of [4].
and its fractional integral and derivative is given in Appendix A of [4].
Let 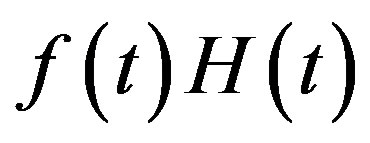 be a regular distribution. Then
be a regular distribution. Then
 for
for  is also a regular distribution, and distribution
is also a regular distribution, and distribution  is defined by
is defined by
 (2.7)
(2.7)
Let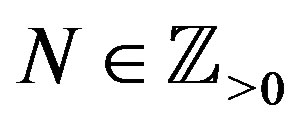 , and let
, and let  be such a regular distribution that
be such a regular distribution that 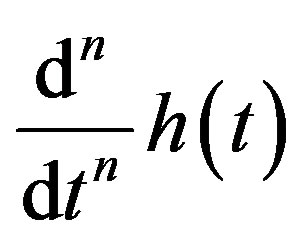 is continuous and differentiable on
is continuous and differentiable on
 , for every
, for every . Then
. Then  is defined by
is defined by
 (2.8)
(2.8)
Let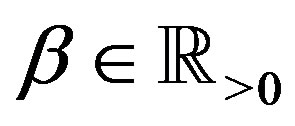 ,
, 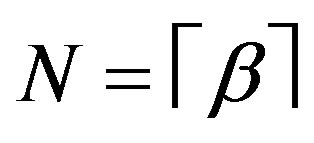 , and let
, and let

be continuous and differentiable on  for every
for every . Then
. Then
 (2.9)
(2.9)
When  is a regular distribution,
is a regular distribution,  is defined for all
is defined for all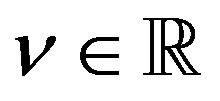 .
.
Lemma 3 For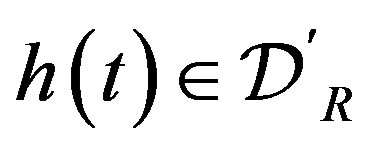 , the index law:
, the index law:
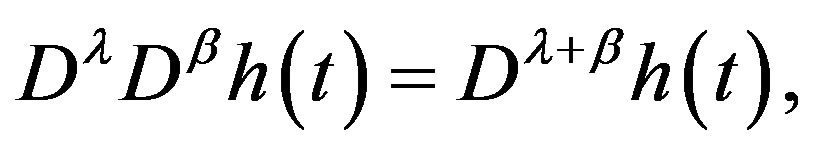 (2.10)
(2.10)
is valid for every .
.
Dirac’s delta function  is the distribution defined by
is the distribution defined by .
.
Let 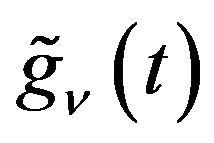 for
for  be defined by
be defined by
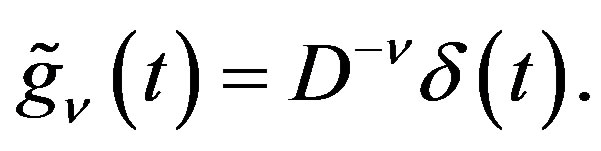 (2.11)
(2.11)
Lemma 4 If ,
,
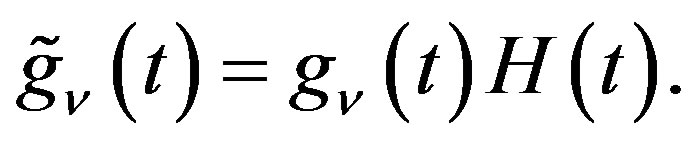 (2.12)
(2.12)
Proof By putting  in (2.7) and using (2.11) and (2.5), we obtain
in (2.7) and using (2.11) and (2.5), we obtain
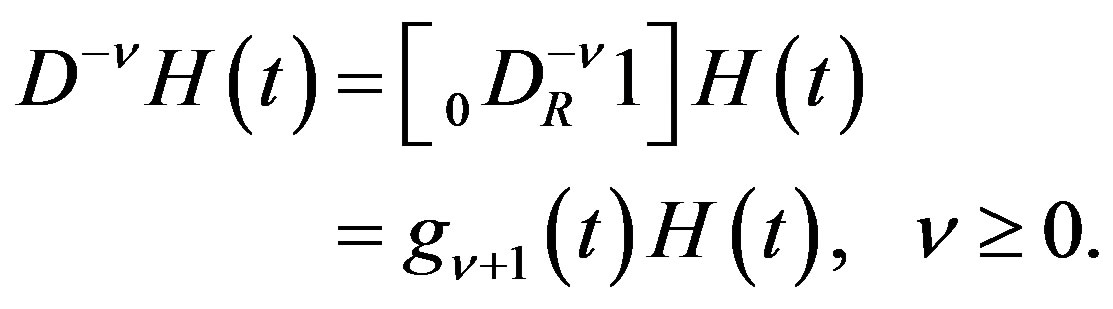
By operating  to this and using (2.9) and (2.5), we obtain (2.12).
to this and using (2.9) and (2.5), we obtain (2.12). 
Corresponding to  expressed by (2.1), we define
expressed by (2.1), we define 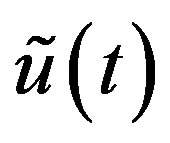 by
by
 (2.13)
(2.13)
Then 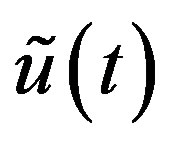 and
and 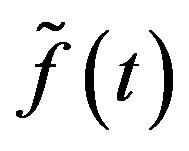 are expressed as
are expressed as
 (2.14)
(2.14)
where
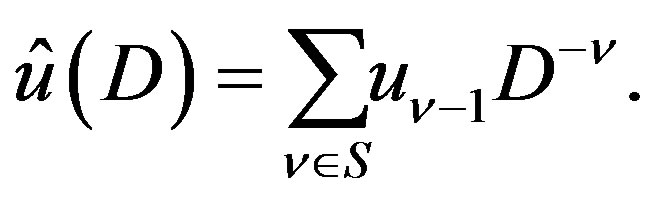 (2.15)
(2.15)
Because of (2.11), we have
 (2.16)
(2.16)
Lemma 5 Let . Then
. Then
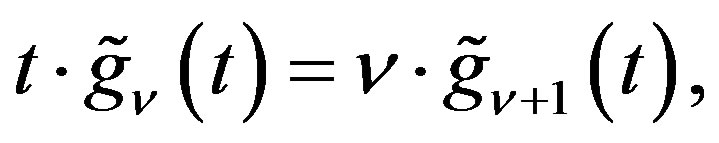 (2.17)
(2.17)
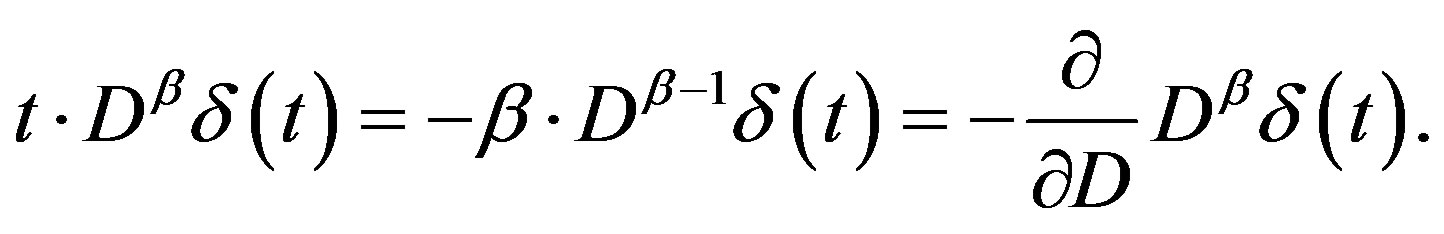 (2.18)
(2.18)
The last derivative with respect to  is taken regarding
is taken regarding  as a variable.
as a variable.
A proof of (2.17) for  is given in Appendix B of [4].
is given in Appendix B of [4].
Proof When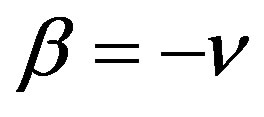 ,
,  , by Lemmas 4 and 1,
, by Lemmas 4 and 1,
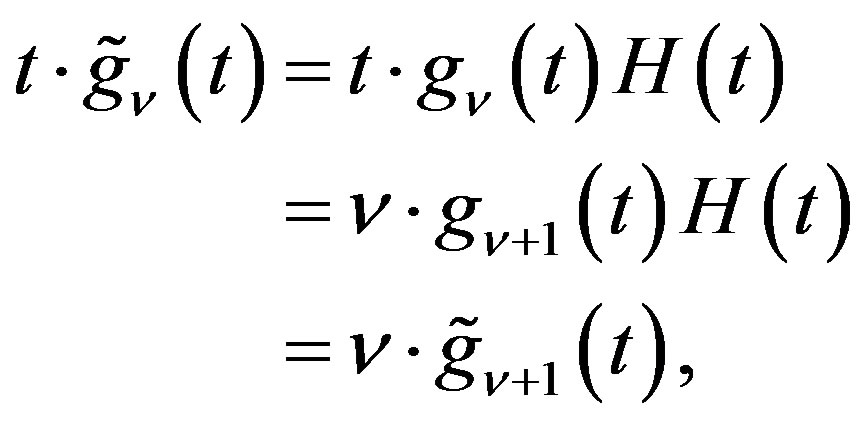
The first equality in (2.18) is obtained from (2.17) and vice versa, by using (2.11). 
The following lemma is a consequence of this lemma.
Lemma 6 Let 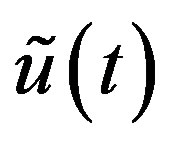 be expressed as a linear combination of
be expressed as a linear combination of 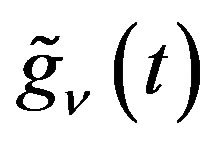 for
for . Then
. Then
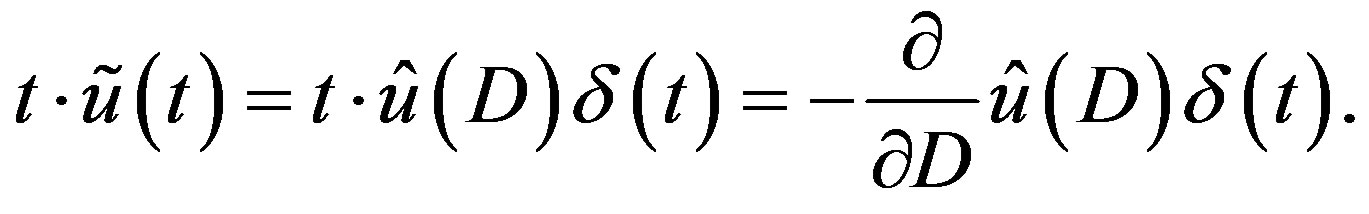 (2.19)
(2.19)
2.3. From  to
to  and Vice Versa
and Vice Versa
Lemma 7 Let ,
, 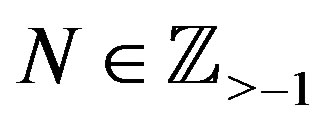 satisfy
satisfy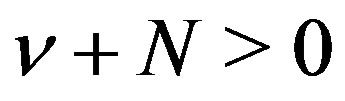 . Then
. Then
 (2.20)
(2.20)
 (2.21)
(2.21)
Proof Formula (2.20) is derived by applying (2.3), (2.12) and (2.16) to the righthand. Formula (2.21) follows from (2.20) by replacing 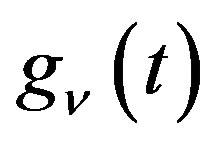 and
and  by
by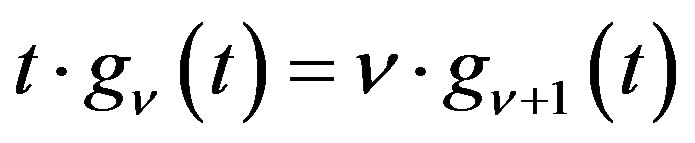 , and
, and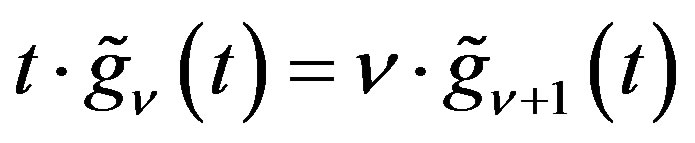 , respectively, by using (2.2) and (2.17).
, respectively, by using (2.2) and (2.17). 
By using Lemma 7 to (2.6), we obtain
 (2.22)
(2.22)
 (2.23)
(2.23)
Lemma 8 Let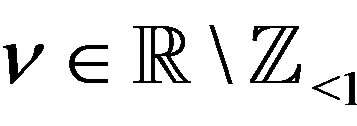 ,
,  satisfy
satisfy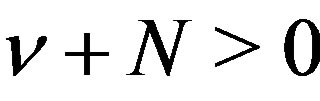 . Then
. Then
 (2.24)
(2.24)
This follows from (2.20).
Condition B  is expressed as a linear combination of
is expressed as a linear combination of 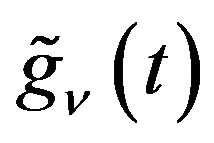 for
for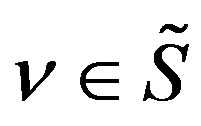 , where
, where 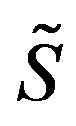 is a set of
is a set of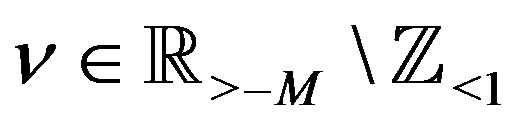 , for some
, for some .
.
When this condition is satisfied,  is expressed as (2.13) with
is expressed as (2.13) with 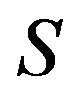 replaced by
replaced by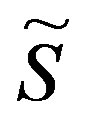 .
.
Lemma 9 Let 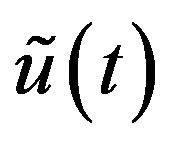 satisfy Condition B. Then the corresponding
satisfy Condition B. Then the corresponding 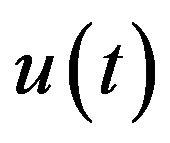 is obtained from
is obtained from , by
, by
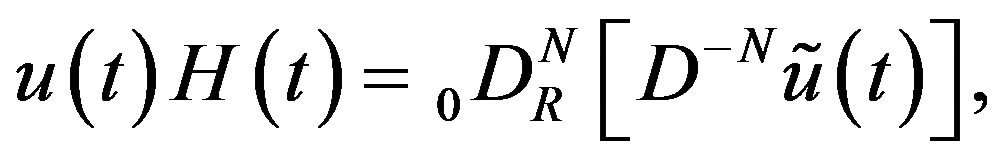 (2.25)
(2.25)
and is expressed by (2.1) with  replaced by
replaced by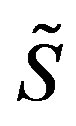 .
.
Lemma 10 Let 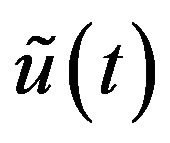 and
and 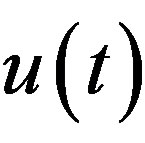 be given by (2.13) and (2.1), respectively. Then
be given by (2.13) and (2.1), respectively. Then  and
and  are related by
are related by
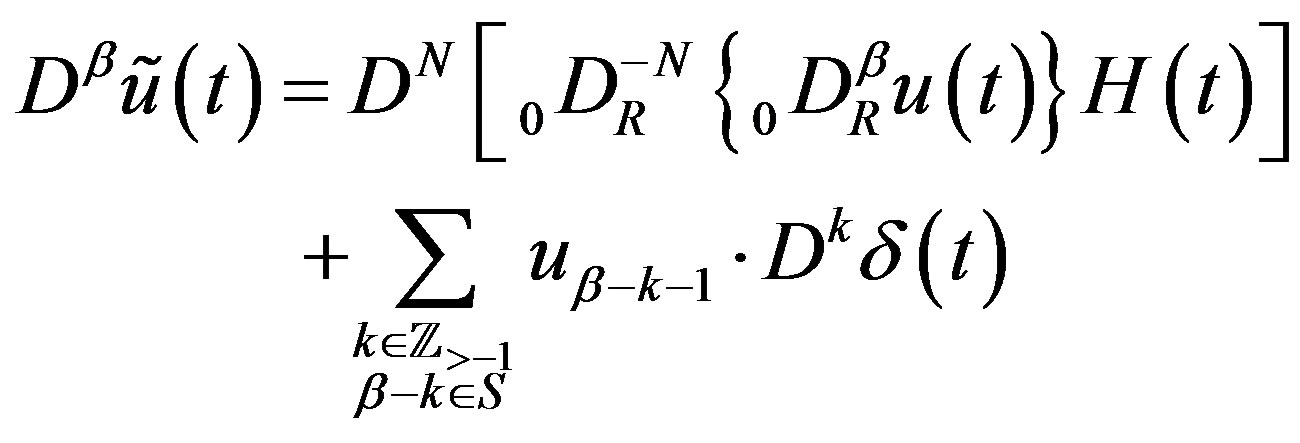 (2.26)
(2.26)
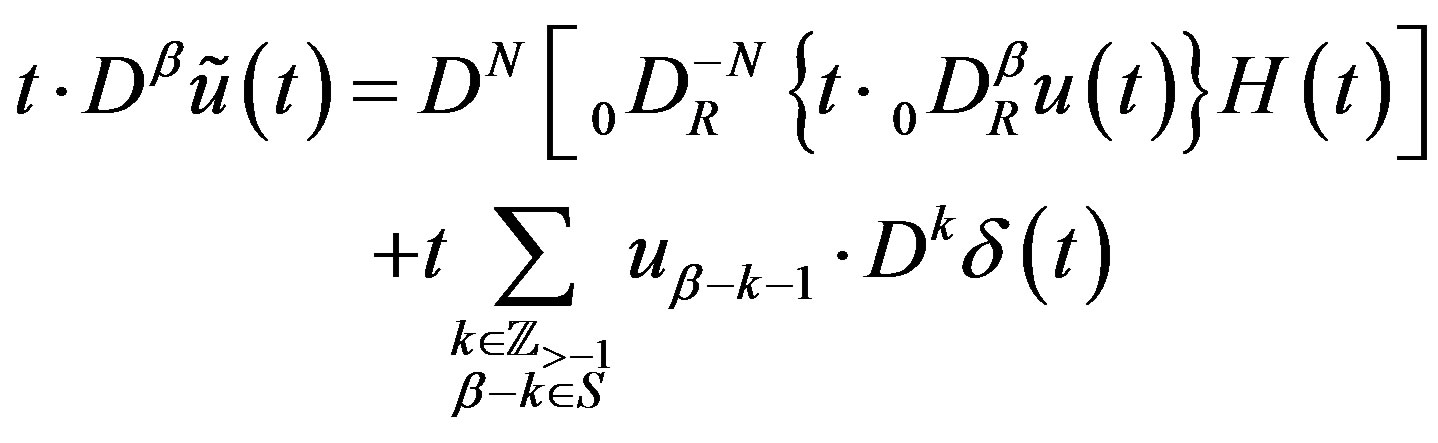 (2.27)
(2.27)
if  satisfies
satisfies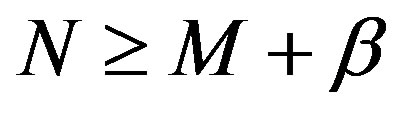 .
.
Proof By (2.13) and (2.16), we have
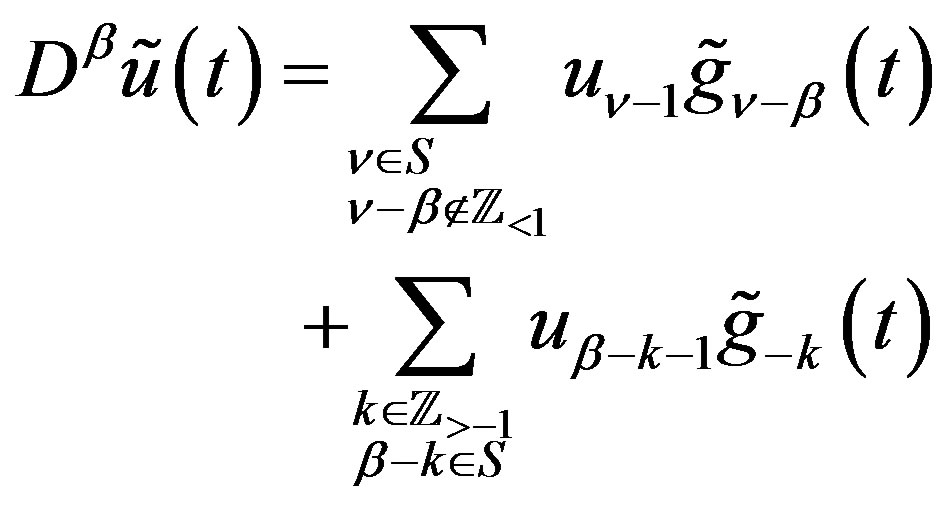 (2.28)
(2.28)
Using (2.22) in the first term on the righthand side, we obtain (2.26). Multiplying (2.28) by  and noting that the first term on the righthand side is then equal to (2.23), we obtain (2.27).
and noting that the first term on the righthand side is then equal to (2.23), we obtain (2.27). 
3. Recipe of Solving Laplace’s DE and fDE of That Type
We now express the DE/fDE (1.2) to be solved, as follows:
 (3.1)
(3.1)
where 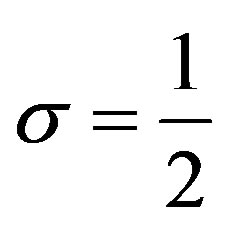 or
or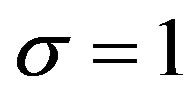 , and
, and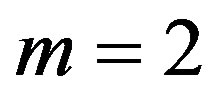 . In Sections 4 and 5, we study this DE for
. In Sections 4 and 5, we study this DE for  and this fDE for
and this fDE for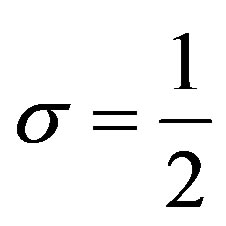 , respectively.
, respectively.
3.1. Deform to DE/fDE for Distribution
Using Lemma 10, we express (3.1) as
 (3.2)
(3.2)
where
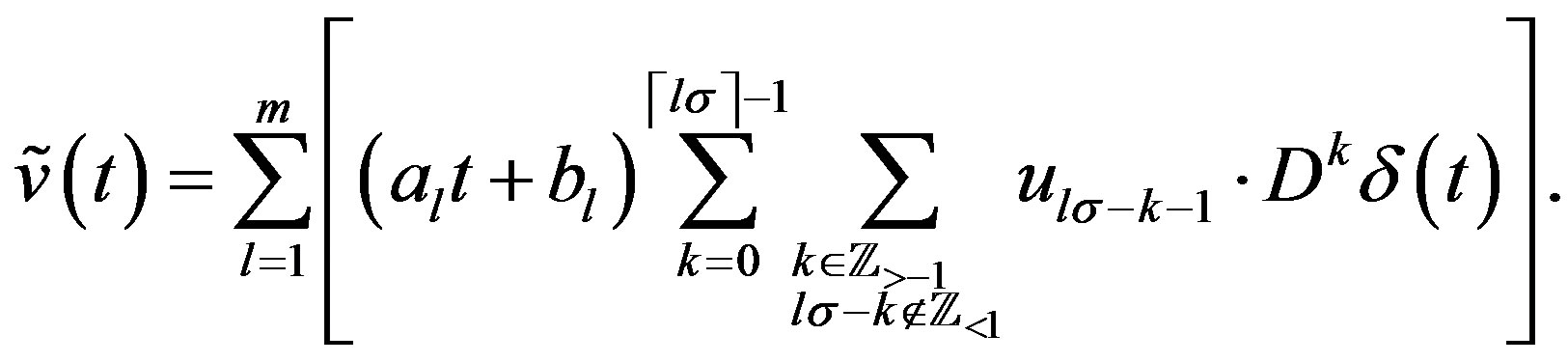 (3.3)
(3.3)
3.2. Solution Via Operational Calculus
By using (2.14) and (2.19), we express (3.2) as
 (3.4)
(3.4)
where
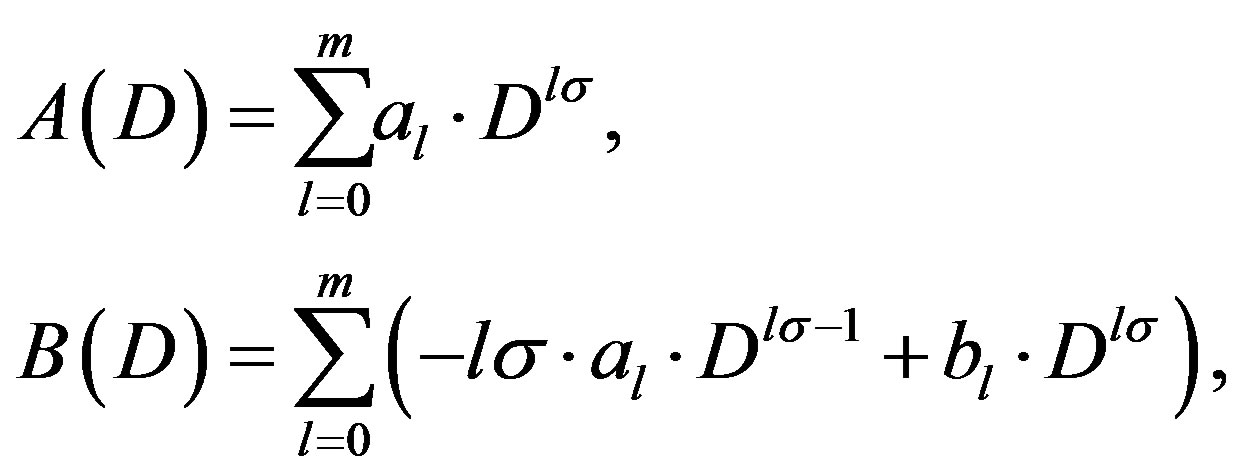 (3.5)
(3.5)
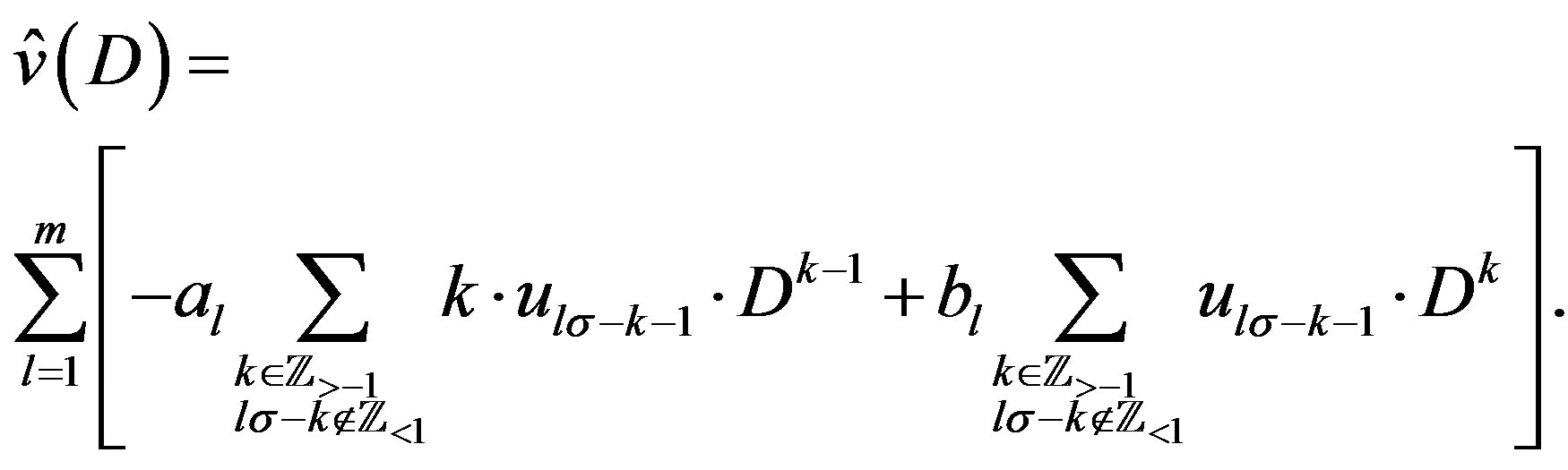 (3.6)
(3.6)
In order to solve the Equation (3.4) for
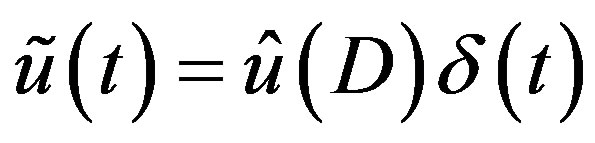 we solve the following equation for function
we solve the following equation for function 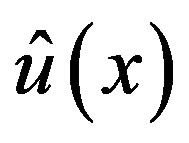 of real variable
of real variable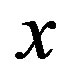 :
:
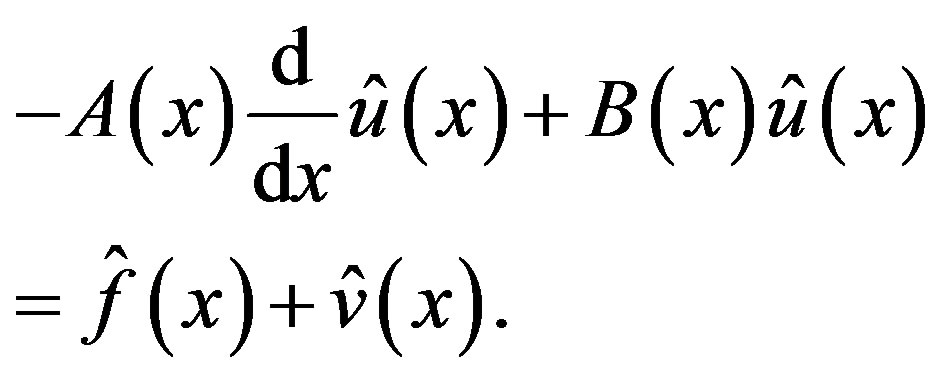 (3.7)
(3.7)
Lemma 11 The complementary solution (C-solution) of equation (3.7) is given by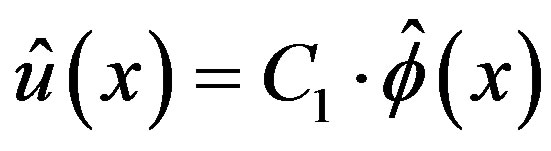 , where
, where  is an arbitrary constant and
is an arbitrary constant and
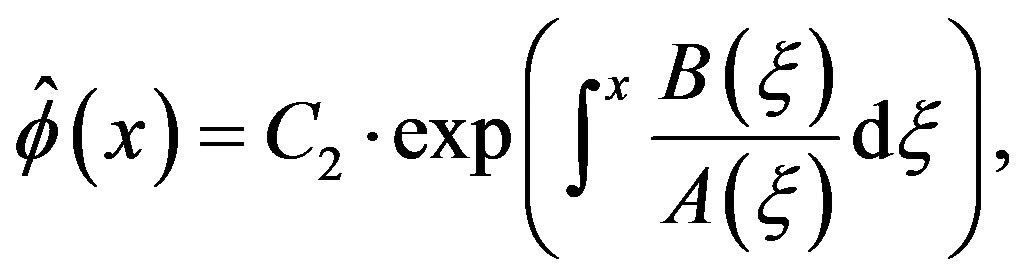 (3.8)
(3.8)
where the integral is the indefinite integral and 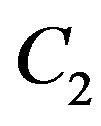 is any constant.
is any constant.
Lemma 12 Let 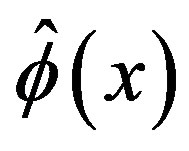 be the C-solution of (3.7), and
be the C-solution of (3.7), and  be the particular solution (P-solution) of (3.7), when the inhomogeneous term is
be the particular solution (P-solution) of (3.7), when the inhomogeneous term is 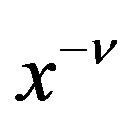 for
for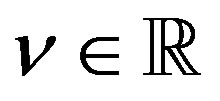 . Then
. Then
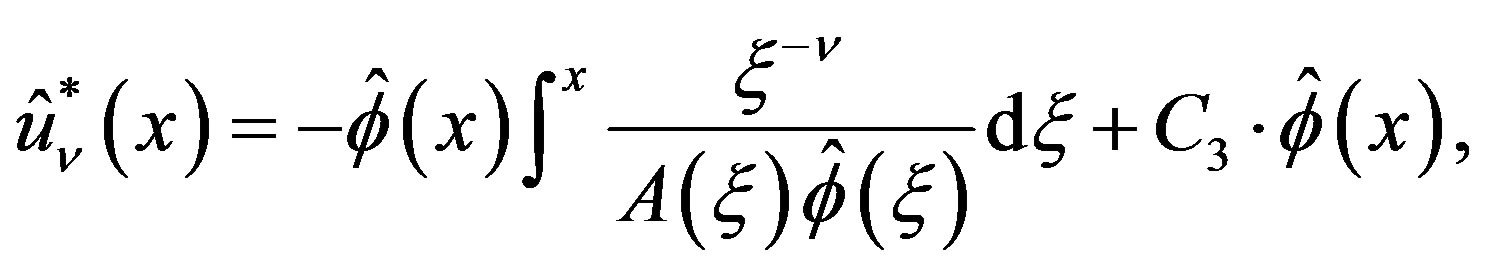 (3.9)
(3.9)
where  is any constant.
is any constant.
Since 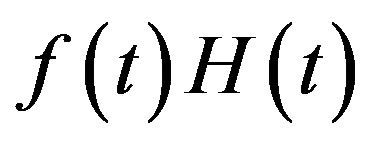 satisfies Condition A and
satisfies Condition A and 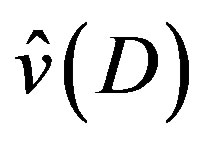 is given by (3.6), the P-solution
is given by (3.6), the P-solution 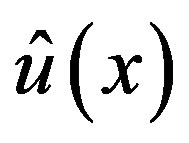 of (3.7) is expressed as a linear combination of
of (3.7) is expressed as a linear combination of 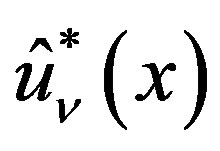 for
for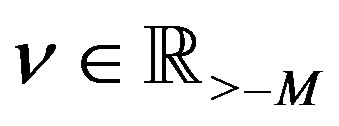 , and of
, and of  for
for , respectively.
, respectively.
From the solution  of (3.7),
of (3.7), 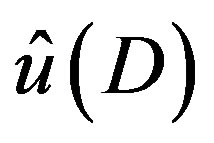 is obtained by substituting
is obtained by substituting  by
by . Then we confirm that (3.4) is satisfied by that
. Then we confirm that (3.4) is satisfied by that  operated to
operated to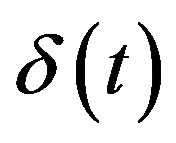 .
.
3.3. Neumann Series Expansion
Finally the obtained expression of  is expanded into Neumann series [11]. Practically we expand it into the sum of terms of negative powers of D, and then we obtain the solution
is expanded into Neumann series [11]. Practically we expand it into the sum of terms of negative powers of D, and then we obtain the solution  of (3.4). If the obtained
of (3.4). If the obtained 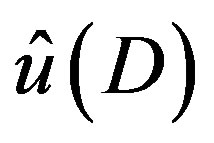 is a linear combination of
is a linear combination of 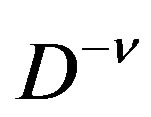 for
for  with some
with some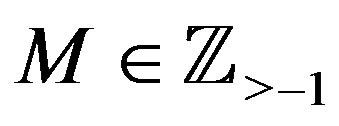 , then
, then 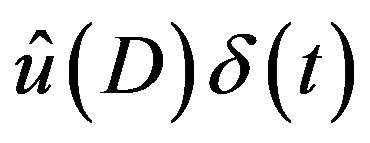 is the solution
is the solution 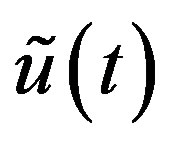 of (3.2). If it satisfies Condition B, it is converted to a solution
of (3.2). If it satisfies Condition B, it is converted to a solution 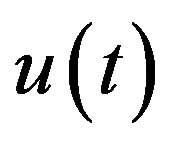 of (3.1) for
of (3.1) for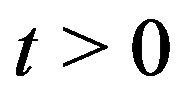 , with the aid of Lemma 9.
, with the aid of Lemma 9.
3.4. Recipe of Obtaining the Solution of (3.1)
1) We prepare the data: 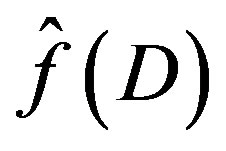 by (2.14), and
by (2.14), and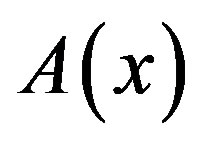 ,
,  and
and 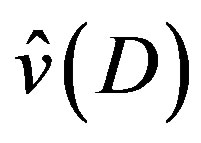 by (3.5) and (3.6).
by (3.5) and (3.6).
2) We obtain 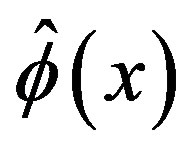 by (3.8). The C-solution of (3.2) is given by
by (3.8). The C-solution of (3.2) is given by
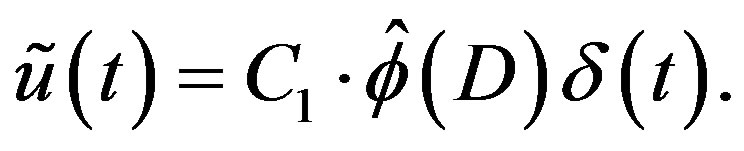
If , the C-solution of (3.1) is obtained from this with the aid of Lemma 9.
, the C-solution of (3.1) is obtained from this with the aid of Lemma 9.
3) If 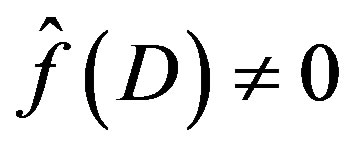 or
or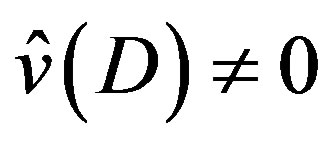 , we obtain
, we obtain  given by (3.9).
given by (3.9).
4) If 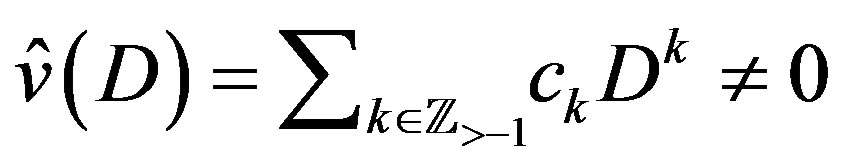 and
and , the solution of (3.2) is given by
, the solution of (3.2) is given by
 (3.10)
(3.10)
where  are constants. The C-solution of (3.1) is then obtained from this with the aid of Lemma 9.
are constants. The C-solution of (3.1) is then obtained from this with the aid of Lemma 9.
5) If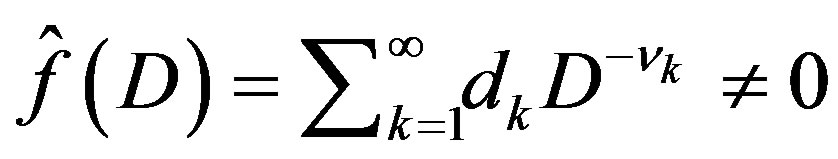 , the P-solution of (3.2)
, the P-solution of (3.2)
is given by
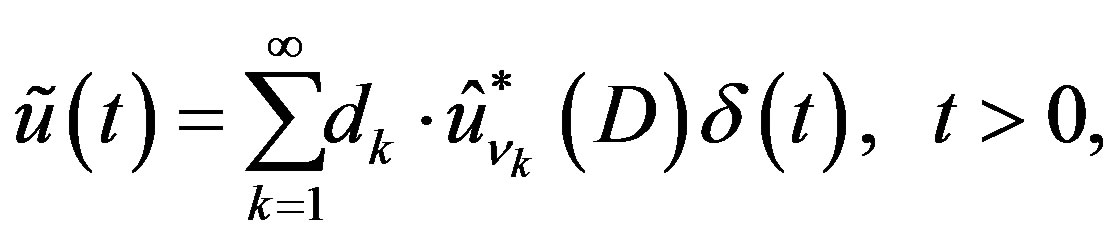
where  and
and  are constants. The P-solution of (3.1) with inhomogeneous term
are constants. The P-solution of (3.1) with inhomogeneous term
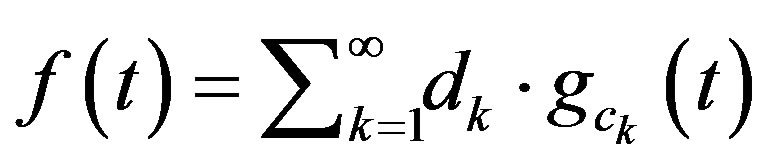
is obtained from this with the aid of Lemma 9.
3.5. Comments on the Recipe
In the above recipe, we first obtain the C-solution of (3.7), that is . It gives the C-solution
. It gives the C-solution 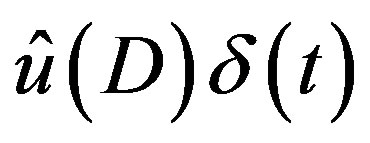 of (3.4) and hence the C-solutions
of (3.4) and hence the C-solutions 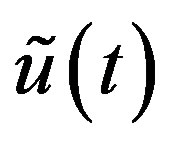 of (3.2). A C-solution
of (3.2). A C-solution 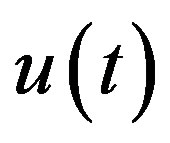 of (3.1) is then obtained with the aid of Lemma 9.
of (3.1) is then obtained with the aid of Lemma 9.
We next obtain the P-solution 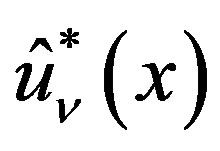 of (3.7), when the inhomogeneous part is
of (3.7), when the inhomogeneous part is 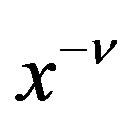 for
for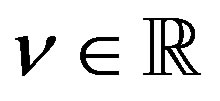 . As noted above, the P-solutions
. As noted above, the P-solutions 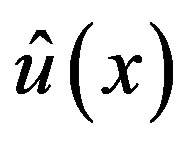 of (3.7) for
of (3.7) for  and for
and for , are expressed as a linear combination of
, are expressed as a linear combination of 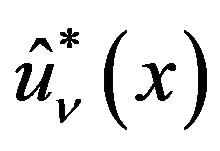 for
for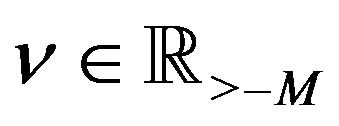 , and of
, and of  for
for , respectively. The sum of the P-solutions
, respectively. The sum of the P-solutions 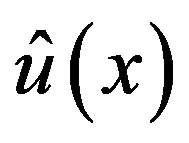 of (3.7) for
of (3.7) for 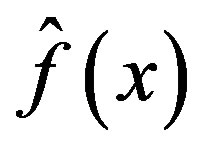 and for
and for  gives the P-solution
gives the P-solution 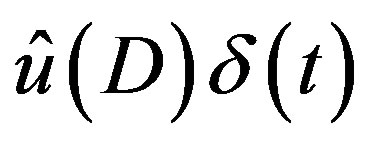 of (3.4) and hence the P-solution
of (3.4) and hence the P-solution  of (3.2). The C-solution
of (3.2). The C-solution  of (3.1) comes from the C-solution of (3.7) and the P-solution of (3.7) for
of (3.1) comes from the C-solution of (3.7) and the P-solution of (3.7) for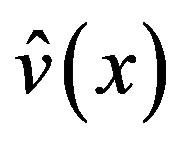 .
.
3.6. Remarks
When we obtain  at the end of Section 3.2, we must examine whether it is compatible with Condition B. We will find that if
at the end of Section 3.2, we must examine whether it is compatible with Condition B. We will find that if 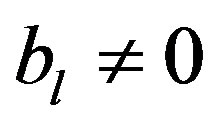 for
for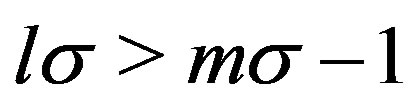 , the obtained
, the obtained 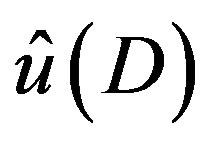 is not acceptable. Hence we have to solve the problem, assuming that
is not acceptable. Hence we have to solve the problem, assuming that  for all
for all .
.
When  and
and , we put
, we put . When
. When
 and
and , we put
, we put . Discussion of this problem is given in Appendices C and D of [4]. In the present case, the discussion must be read taking Condition B there to represent the present Condition B.
. Discussion of this problem is given in Appendices C and D of [4]. In the present case, the discussion must be read taking Condition B there to represent the present Condition B.
4. Laplace’s and Kummer’s DE
We now consider the case of σ = 1, m = 2,  , and
, and . Then (3.1) reduces to
. Then (3.1) reduces to
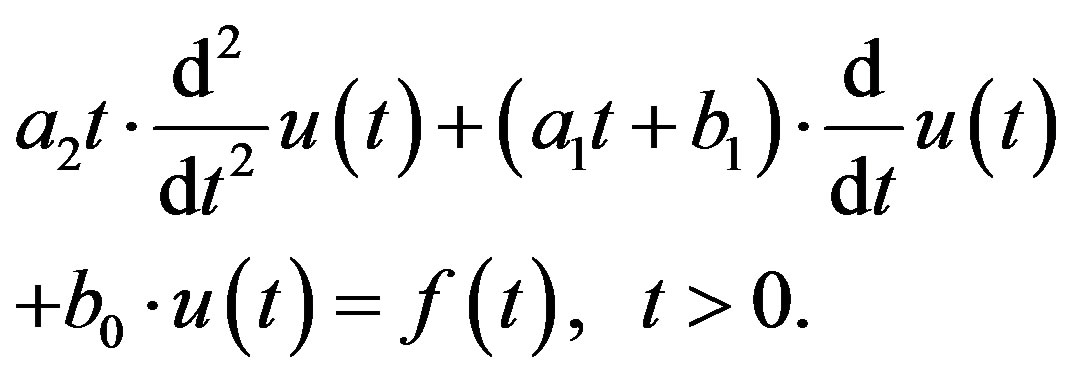 (4.1)
(4.1)
By (3.5) and (3.6), 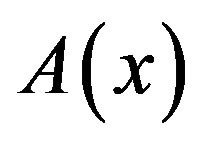 ,
, 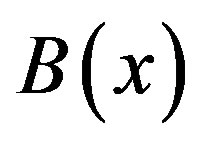 and
and  are
are
 (4.2)
(4.2)
 (4.3)
(4.3)
where .
.
4.1. Complementary Solution of (3.7), (3.2) and (4.1)
In order to obtain the C-solution  of (3.7) by using (3.8), we express
of (3.7) by using (3.8), we express 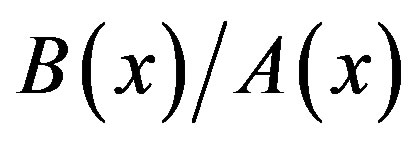 as follows:
as follows:
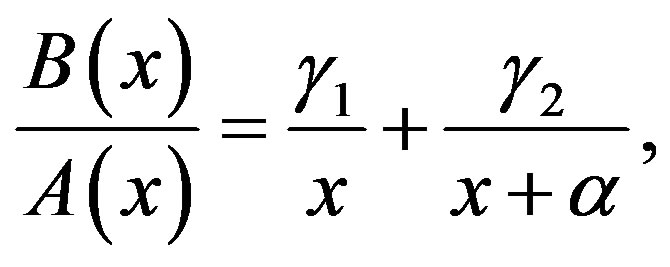 (4.4)
(4.4)
where
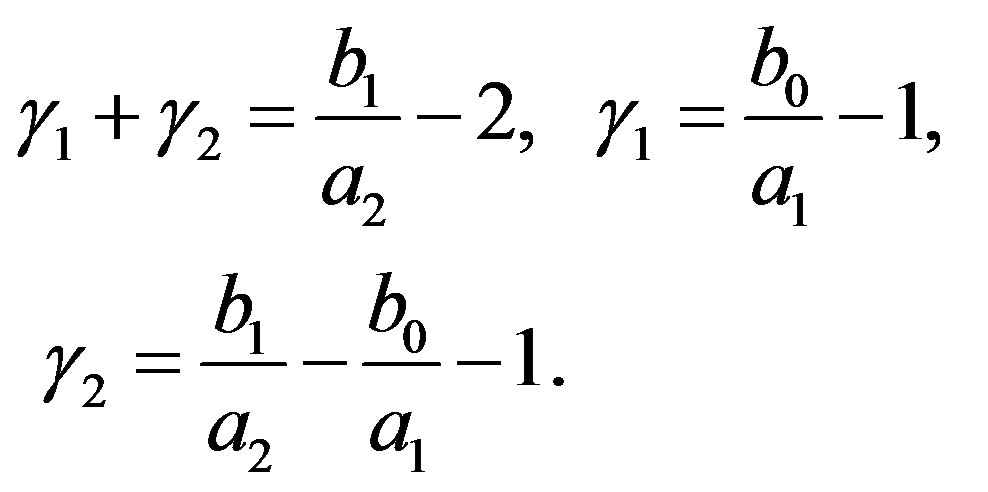 (4.5)
(4.5)
B(x) is now expressed as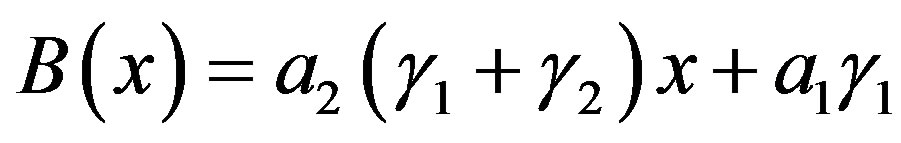 .
.
By using (3.8), we obtain
 (4.6)
(4.6)
where 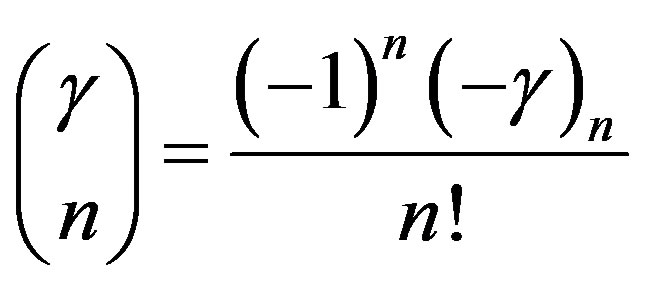 for
for 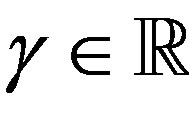 and
and  are the binomial coefficients.
are the binomial coefficients.
The C-solution of (3.2) is given by
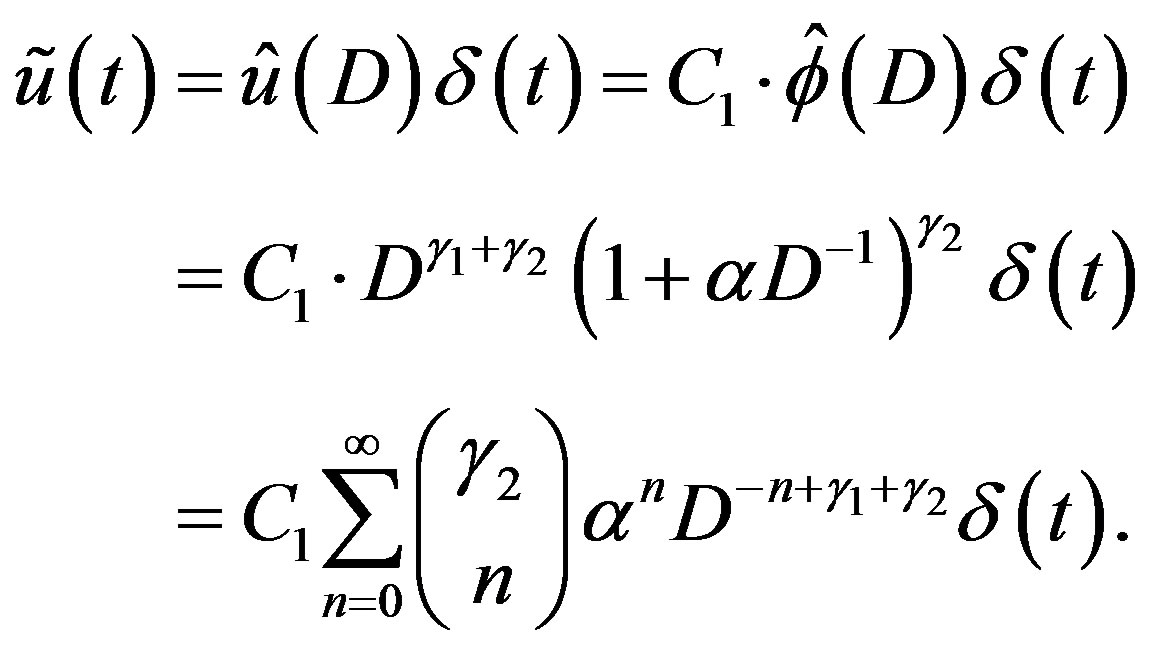 (4.7)
(4.7)
If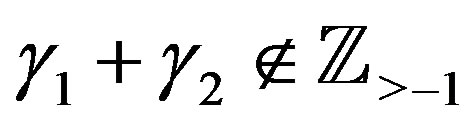 , we obtain a C-solution of (4.1), by using Lemma 9:
, we obtain a C-solution of (4.1), by using Lemma 9:
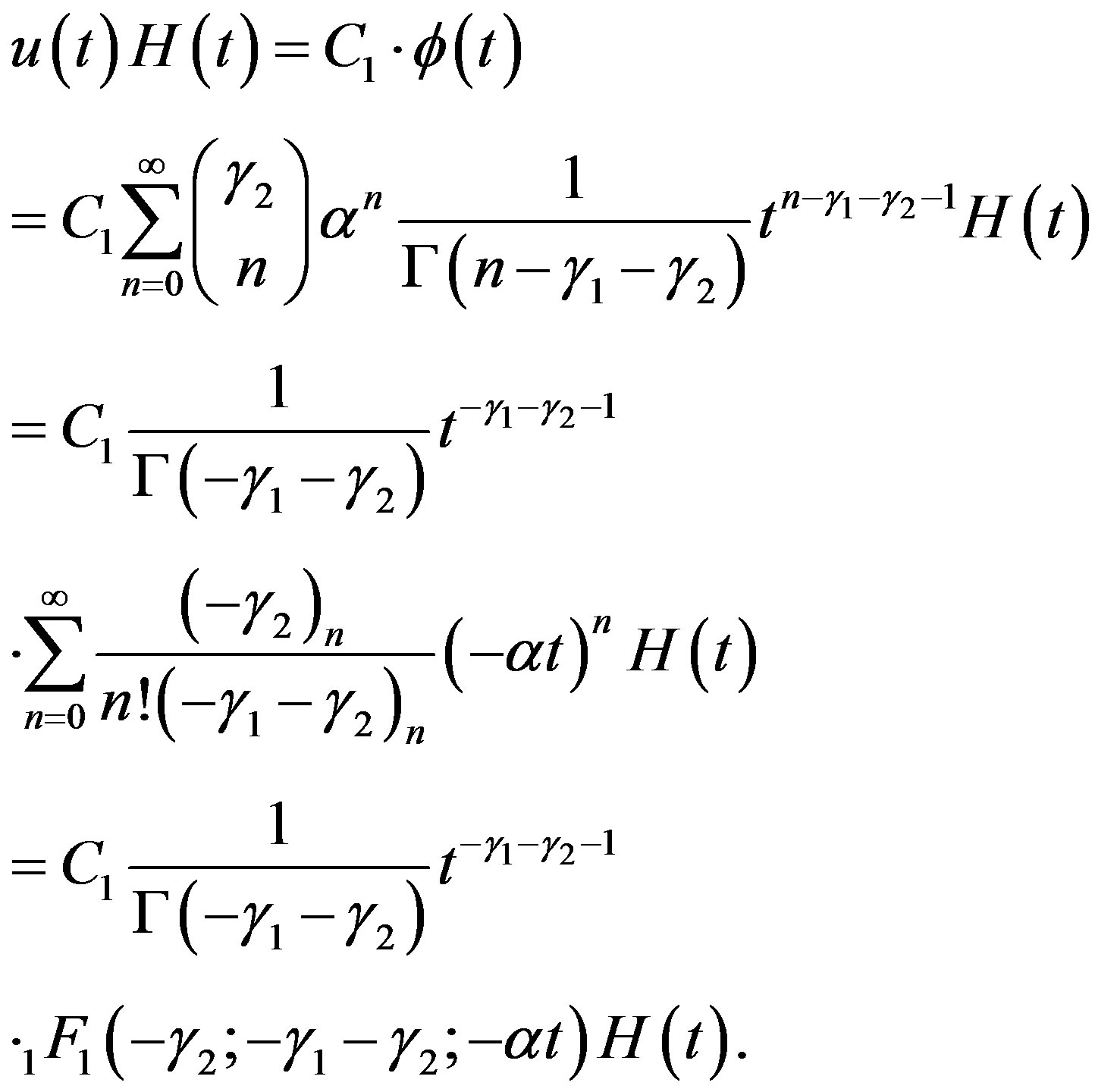 (4.8)
(4.8)
Remark 1 In Introduction, Kummer’s DE is given by (1.4). It is equal to (4.1) for ,
, 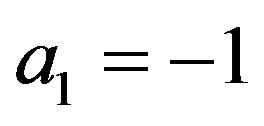 ,
, 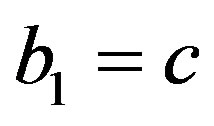 and
and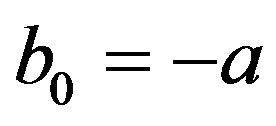 . In this case,
. In this case,
 (4.9)
(4.9)
We then confirm that the expression (4.8) for  agrees with (1.6), which is one of the C-solutions of Kummer’s DE given in [7,8].
agrees with (1.6), which is one of the C-solutions of Kummer’s DE given in [7,8].
4.2. Particular Solution of (3.7)
We now obtain the P-solution of (3.7), when the inhomogeneous term is equal to  for
for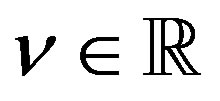 .
.
When the C-solution of (3.7) is , the P-solution of (3.7) is given by (3.9). By using (4.2) and (4.6), the following result is obtained in [4]:
, the P-solution of (3.7) is given by (3.9). By using (4.2) and (4.6), the following result is obtained in [4]:
 (4.10)
(4.10)
where
 (4.11)
(4.11)
Lemma 13 When ,
,  defined by (4.11) is expressed as
defined by (4.11) is expressed as
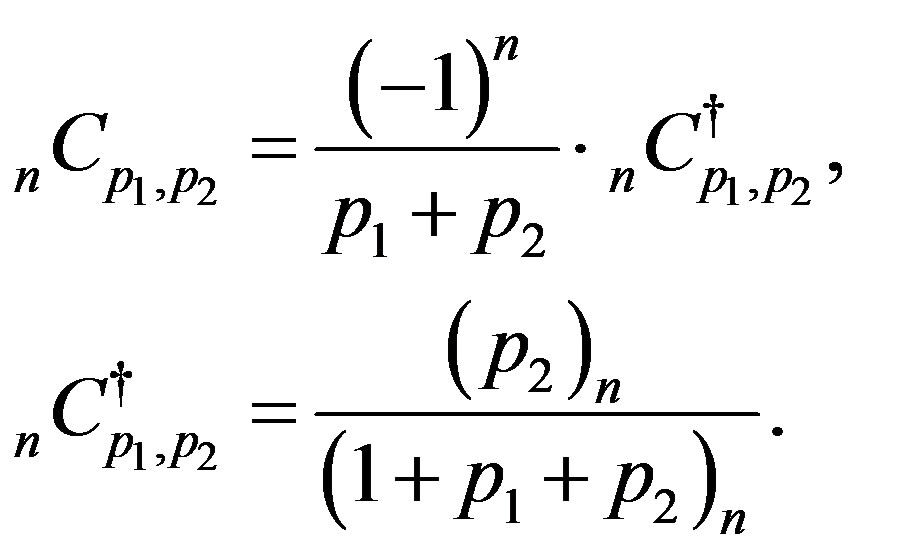 (4.12)
(4.12)
This lemma is proved in [4].
4.3. Particular Solutions of (3.2) and (4.1)
Equation (4.10) shows that if the inhomogeneous term is  for
for , the P-solution of (3.2) is given by
, the P-solution of (3.2) is given by
 (4.13)
(4.13)
Theorem 1 Let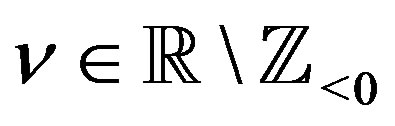 ,
,  , and
, and . Then we have a P-solution
. Then we have a P-solution  of (4.1), given by
of (4.1), given by
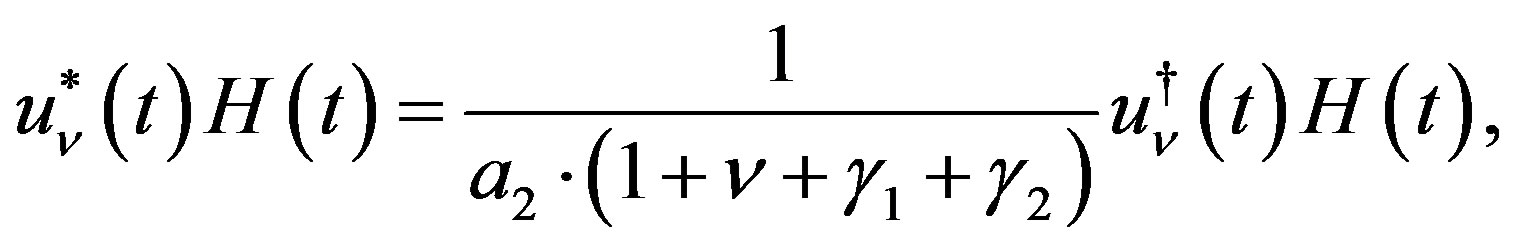 (4.14)
(4.14)
where
 (4.15)
(4.15)
Proof Applying Lemma 9 to (4.13), we obtain
 (4.16)
(4.16)
By using (4.12) in (4.16), we obtain (4.14) with (4.15). 
We note that 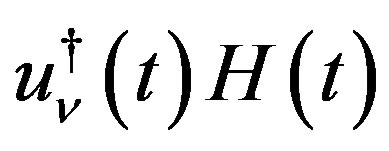 is expressed as
is expressed as
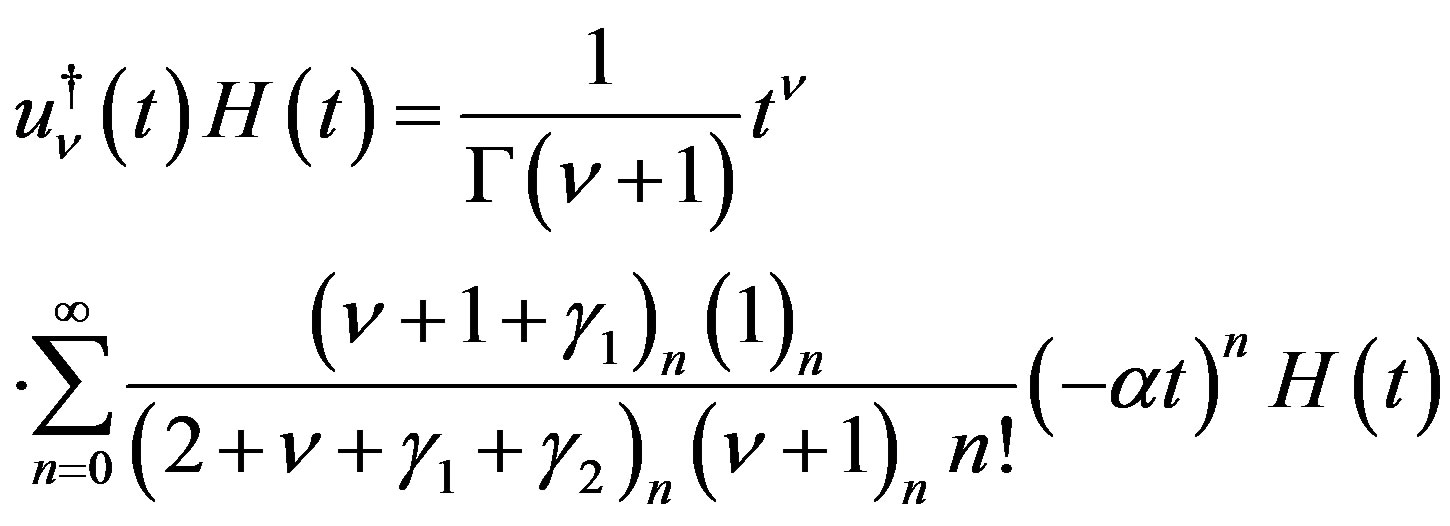 (4.17)
(4.17)
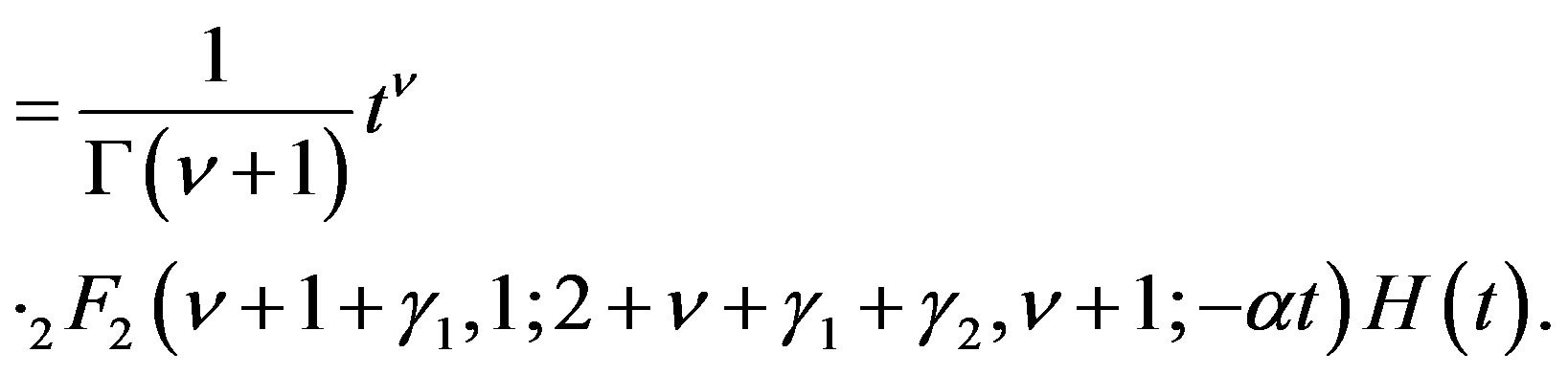 (4.18)
(4.18)
4.4. Complementary Solution of (4.1)
By (4.3) and (4.5), . When
. When
 and
and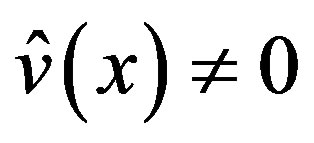 , the P-solution of (4.7) is given by
, the P-solution of (4.7) is given by
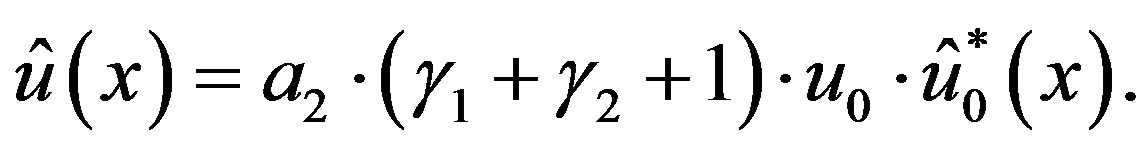 (4.19)
(4.19)
By using (4.14) for , if
, if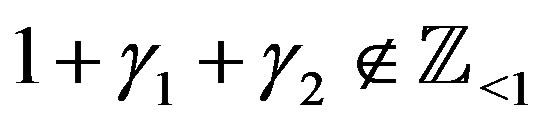 , we obtain a C-solution of (4.1):
, we obtain a C-solution of (4.1):
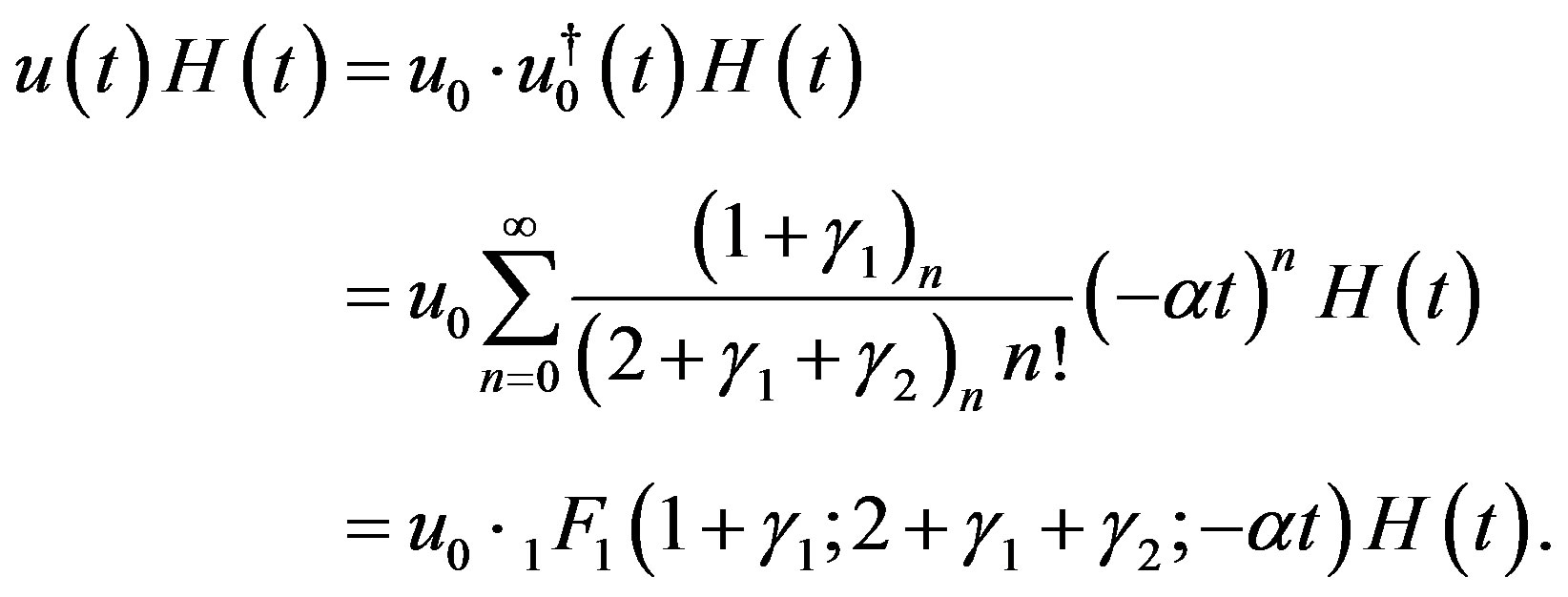 (4.20)
(4.20)
In Section 4.1, we have (4.8), that is another C-solution of (4.1). If we compare (4.8) with (4.15), when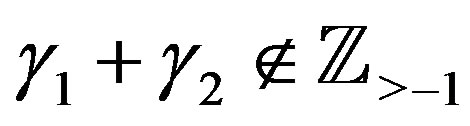 , it can be expressed as
, it can be expressed as
 (4.21)
(4.21)
Proposition 1 When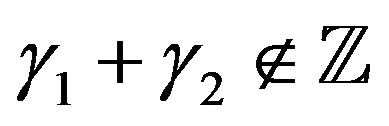 , the complementary solution of (4.1), multiplied by
, the complementary solution of (4.1), multiplied by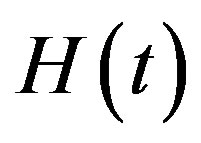 , is given by the sum of the righthand sides of (4.8) and of (4.20), which are equal to
, is given by the sum of the righthand sides of (4.8) and of (4.20), which are equal to 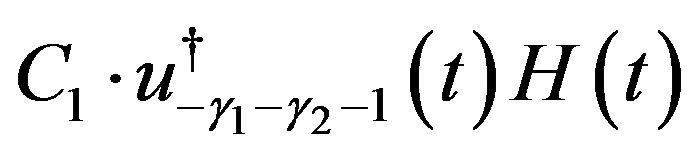 and
and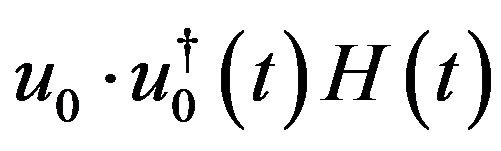 respectively.
respectively.
Remark 2 As stated in Remark 1, for Kummer’s DE,  and
and 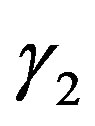 are given in (4.9), and
are given in (4.9), and
 (4.22)
(4.22)
We then confirm that if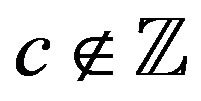 , the set of (4.8) and (4.20) agrees with the set of (4.5) and (4.6).
, the set of (4.8) and (4.20) agrees with the set of (4.5) and (4.6).
4.5. Remarks
In [10], it was shown that there exist P-solutions expressed by a polynomial for inhomogeneous Hermite’s DE, et al. We can obtain the corresponding result for Laplace’s DE. We discuss this problem in Appendix A, and then discuss the P-solution of inhomogeneous Hermite’s DE in the present formulation in Appendix B.
5. Solution of fDE (3.1) for 
In this section, we consider the case of ,
, 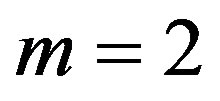 ,
,
 , and
, and Then the Equation (3.1) to be solved is
Then the Equation (3.1) to be solved is
 (5.1)
(5.1)
Now (3.5) and (3.6) are expressed as
 (5.2)
(5.2)
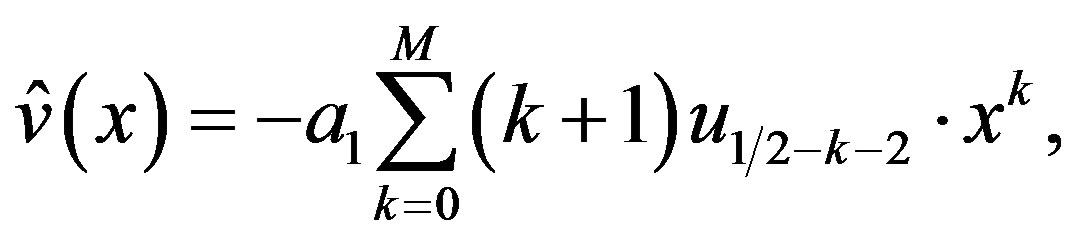 (5.3)
(5.3)
where .
.
5.1. Complementary Solution of (3.7)
By using (5.2),  is expressed as
is expressed as
 (5.4)
(5.4)
where
 (5.5)
(5.5)
By (3.8), the C-solution  of (3.7) is given by
of (3.7) is given by
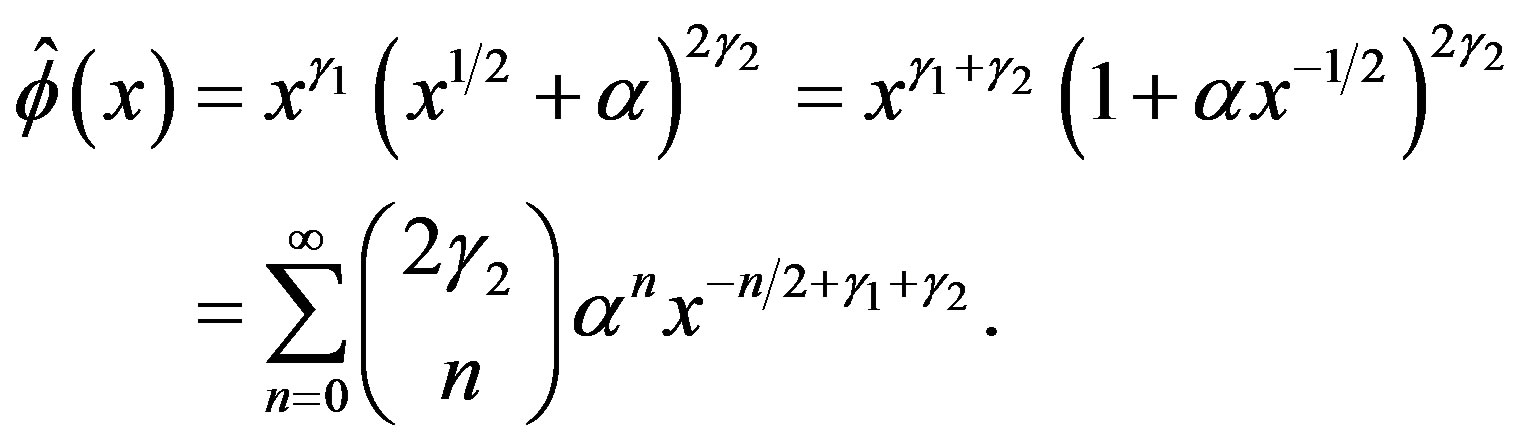 (5.6)
(5.6)
5.2. Complementary Solution of (3.2) and (5.1)
The C-solution of (3.2) is given by
 (5.7)
(5.7)
If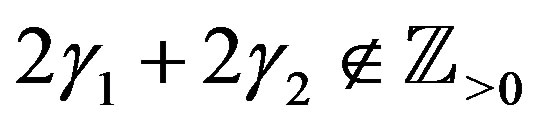 , by applying Lemma 9 to this, we obtain the C-solution of (5.1):
, by applying Lemma 9 to this, we obtain the C-solution of (5.1):
 (5.8)
(5.8)
5.3. Particular Solution of (3.2) and (5.1)
By using the expressions of 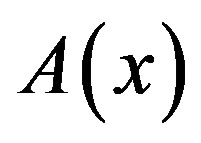 and
and 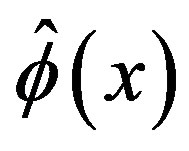 given by (5.2) and (5.6) in (3.9), we obtain the P-solution of (3.7), when the inhomogeneous term is
given by (5.2) and (5.6) in (3.9), we obtain the P-solution of (3.7), when the inhomogeneous term is 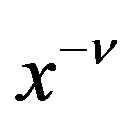 for
for :
:
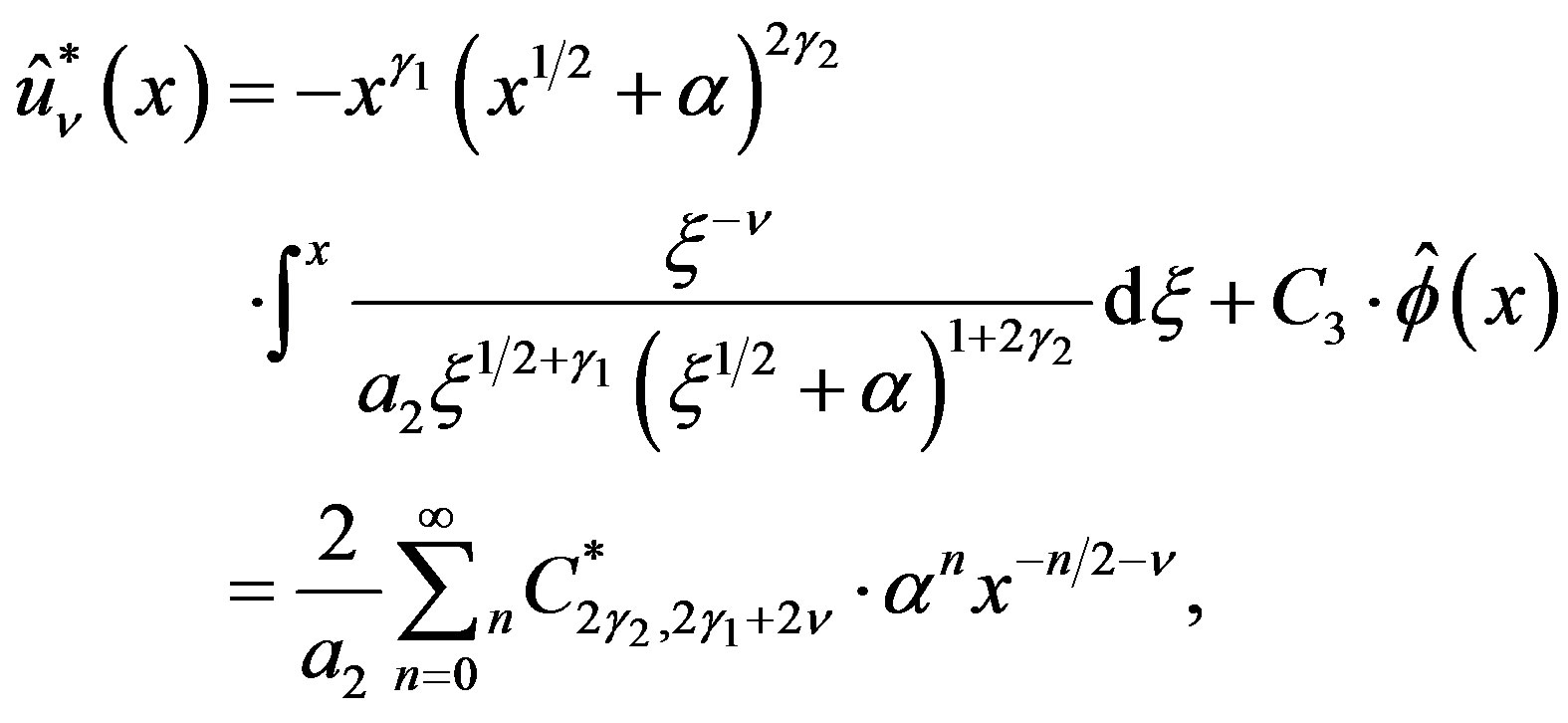 (5.9)
(5.9)
where 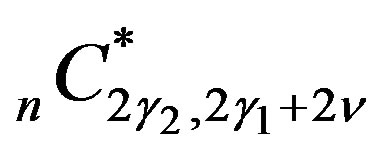 is defined by (4.11) and is given by
is defined by (4.11) and is given by
(4.12), if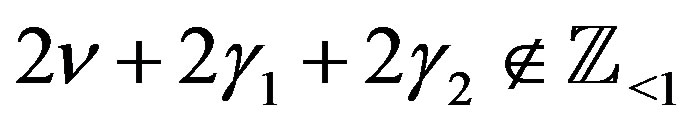 .
.
By using (4.12) in (5.9), we can show that if the inhomogeneous term is  for
for , the P-solution of (3.2) is
, the P-solution of (3.2) is . By applying Lemma 9 to this, we obtain the following theorem.
. By applying Lemma 9 to this, we obtain the following theorem.
Theorem 2 Let ,
, 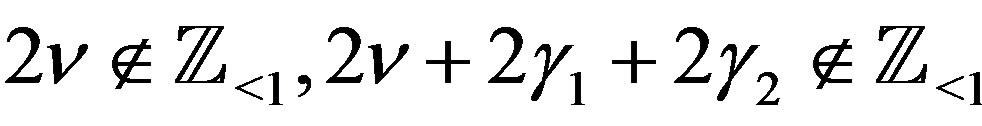 and
and  . Then we have a P-solution
. Then we have a P-solution 
of (5.1), given by

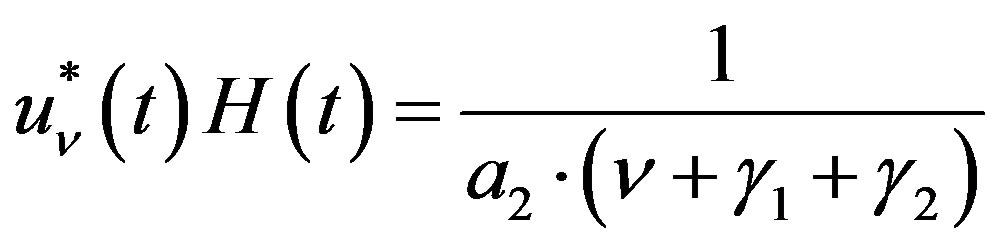 (5.10)
(5.10)
where
 (5.11)
(5.11)
In Appendix C, discussion is given to show that there exist P-solutions in the form of polynomial for (5.1).
5.4. Complementary Solution of (5.1)
We obtain the solution  only for
only for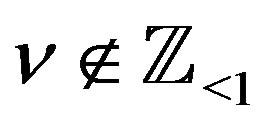 . Even though we have P-solutions of (3.2) for
. Even though we have P-solutions of (3.2) for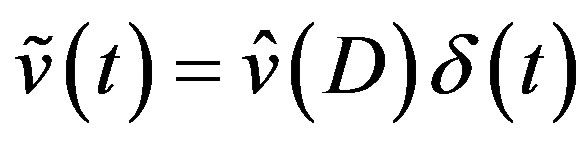 , when
, when  is given by (5.3) with nonzero values of
is given by (5.3) with nonzero values of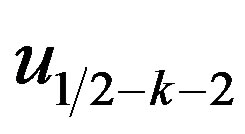 , it does not satisfy Condition B, and does not give a solution of (5.1). Hence
, it does not satisfy Condition B, and does not give a solution of (5.1). Hence 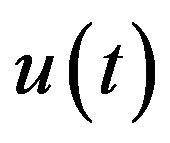 given by (5.8) is the only C-solution of (5.1).
given by (5.8) is the only C-solution of (5.1).
If we compare (5.8) with (5.11), we obtain the following proposition.
Proposition 2 Let . Then the C-solution of (5.1) is given by
. Then the C-solution of (5.1) is given by
 (5.12)
(5.12)
REFERENCES
- K. Yosida, “The Algebraic Derivative and Laplace’s Differential Equation,” Proceedings of the Japan Academy, Vol. 59, Ser. A, 1983, pp. 1-4.
- K. Yosida, “Operational Calculus,” Springer-Verlag, New York, 1982, Chapter VII.
- J. Mikusiński, “Operational Calculus,” Pergamon Press, London, 1959.
- T. Morita and K. Sato, “Remarks on the Solution of Laplace’s Differential Equation and Fractional Differential Equation of That Type,” Applied Mathematics, Vol. 4, No. 11A, 2013, pp. 13-21.
- T. Morita and K. Sato, “Solution of Fractional Differential Equation in Terms of Distribution Theory,” Interdisciplinary Information Sciences, Vol. 12, No. 2, 2006, pp. 71-83.
- T. Morita and K. Sato, “Neumann-Series Solution of Fractional Differential Equation,” Interdisciplinary Information Sciences, Vol. 16, No. 1, 2010, pp. 127-137.
- M. Abramowitz and I. A. Stegun, “Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables,” Dover Publ., Inc., New York, 1972, Chapter 13.
- M. Magnus and F. Oberhettinger, “Formulas and Theorems for the Functions of Mathematical Physics,” Chelsea Publ. Co., New York, 1949, Chapter VI.
- T. Morita and K. Sato, “Liouville and Riemann-Liouville Fractional Derivatives via Contour Integrals,” Fractional Calculus and Applied Analysis, Vol. 16, No. 3, 2013, pp. 630-653.
- L. Levine and R. Maleh, “Polynomial Solutions of the Classical Equations of Hermite, Legendre and Chebyshev,” International Journal of Mathematical Education in Science and Technology, Vol. 34, 2003, pp. 95-103.
- F. Riesz and B. Sz.-Nagy, “Functional Analysis,” Dover Publ., Inc., New York, 1990, p. 146.
Appendix A: Polynomial Form of P-Solution of (4.1)
Let  and
and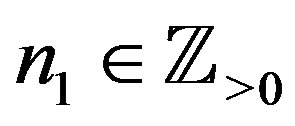 . Then (4.15) gives
. Then (4.15) gives
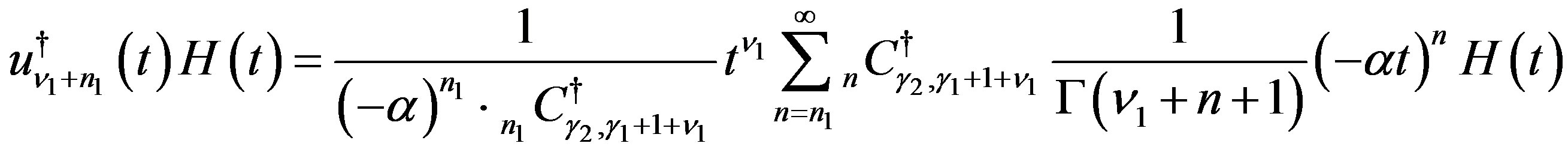 (A.1)
(A.1)
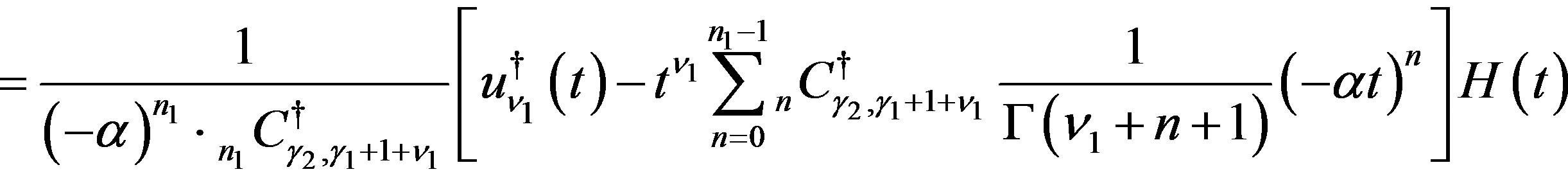 (A.2)
(A.2)
where
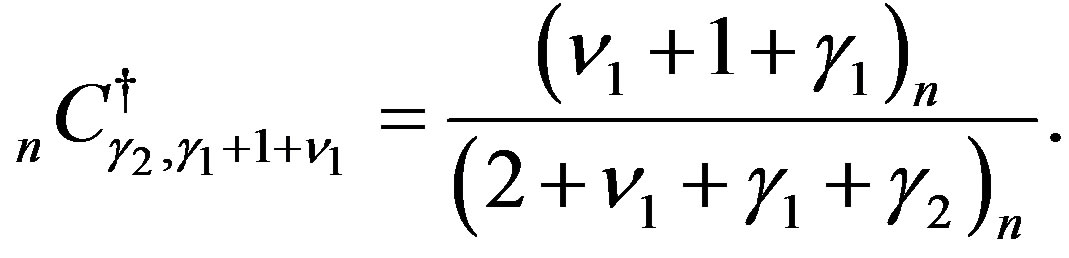 (A.3)
(A.3)
We obtain the following theorems from (A.2) with the aid of Proposition 1.
Theorem 3 Let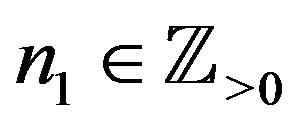 ,
, 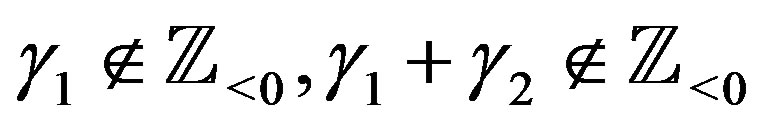 , and
, and . Then we have the polynomial form of P-solution of (4.1):
. Then we have the polynomial form of P-solution of (4.1):
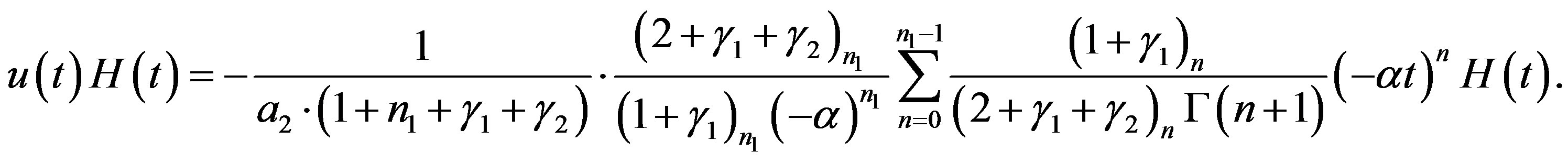 (A.4)
(A.4)
Theorem 4 Let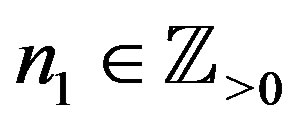 ,
, 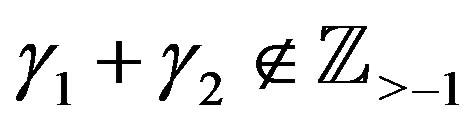 ,
, 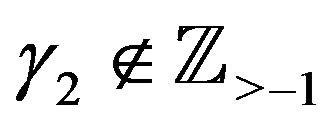 and
and  for
for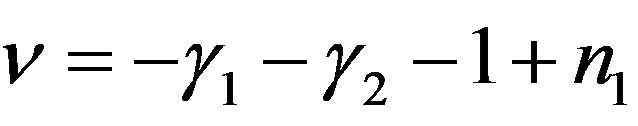 . Then we have the polynomial form of P-solution of (4.1):
. Then we have the polynomial form of P-solution of (4.1):
 (A.5)
(A.5)
Appendix B: Polynomial Form of P-Solution of Hermite DE
We now consider the inhomogeneous Hermite DE given by
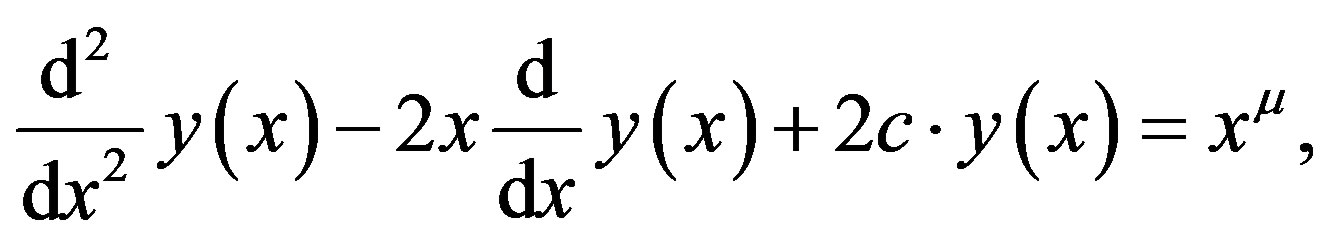 (B.1)
(B.1)
for 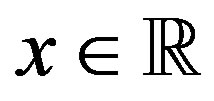 and
and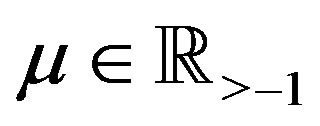 . We put
. We put  and
and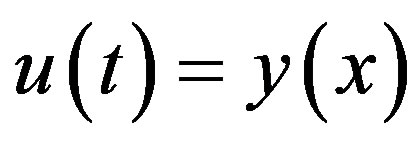 . Then the equation for
. Then the equation for 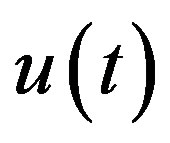 is given by
is given by
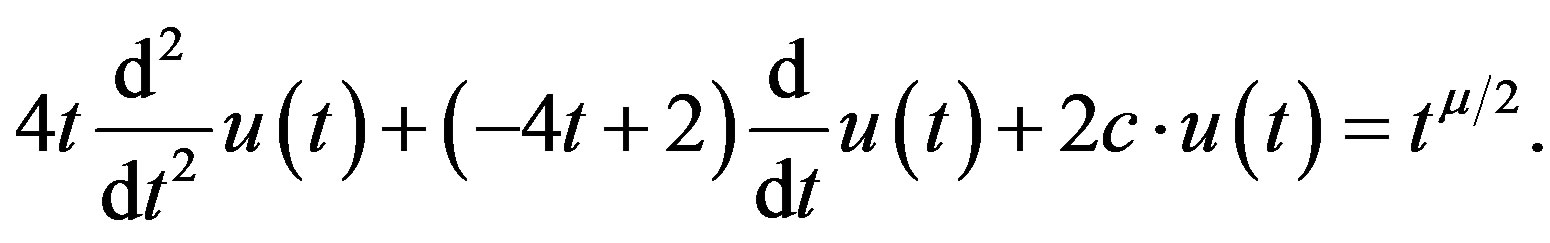 (B.2)
(B.2)
This is Laplace’s DE (4.1) with parameters
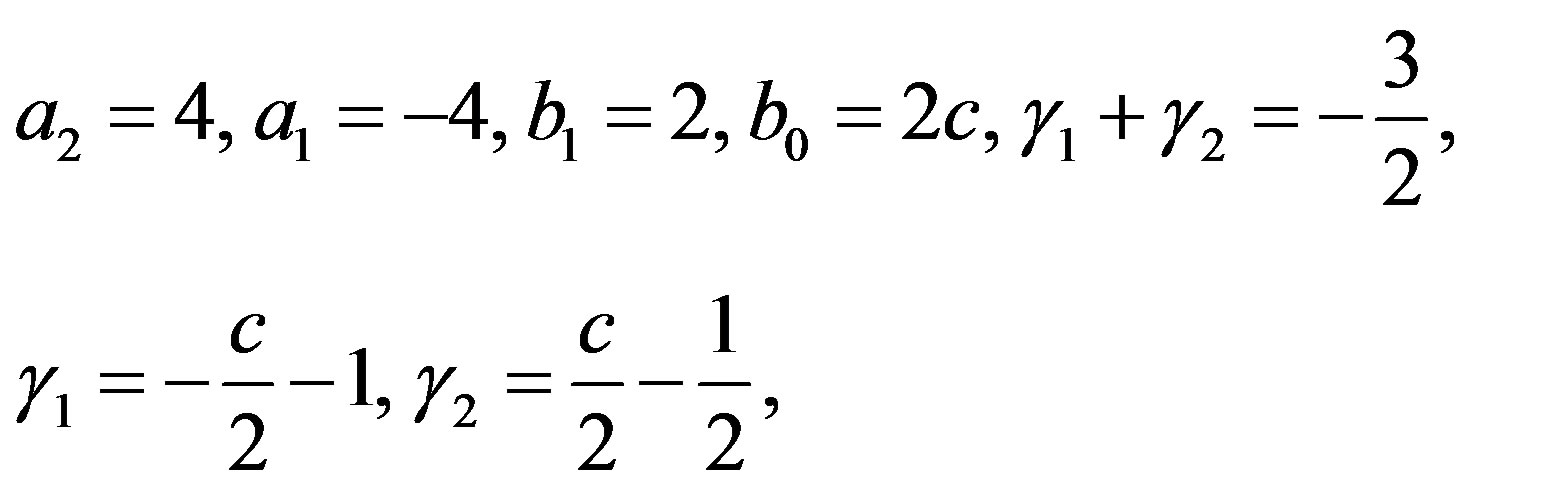 (B.3)
(B.3)
and the inhomogeneous term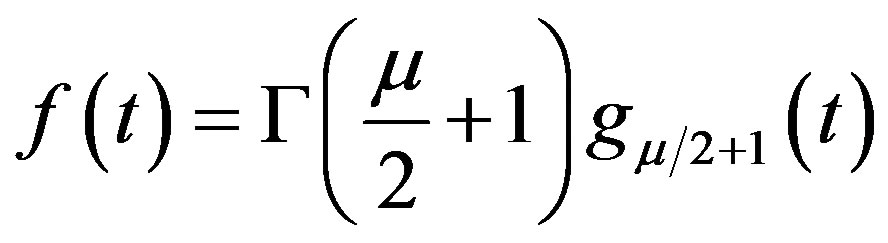 .
.
Theorem 5 Let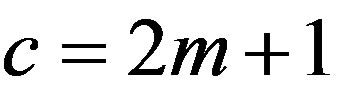 ,
,  , and
, and ,
,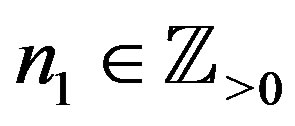 . Then we have the polynomial form of Psolution of (B.2):
. Then we have the polynomial form of Psolution of (B.2):
 (B.4)
(B.4)
Proof In this case,  ,
,  , and
, and
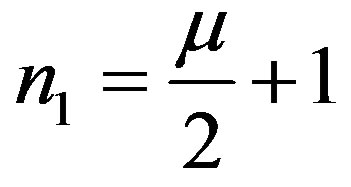 . By Theorem 3, we obtain this result.
. By Theorem 3, we obtain this result. 
Theorem 6 Let ,
, 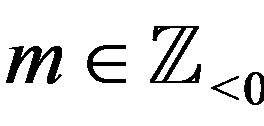 , and
, and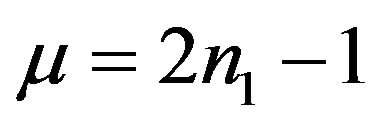 ,
, . Then we have the polynomial form of Psolution of (B.2):
. Then we have the polynomial form of Psolution of (B.2):
 (B.5)
(B.5)
Proof In this case, 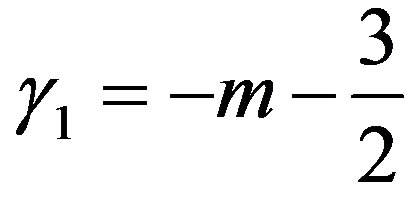 ,
, 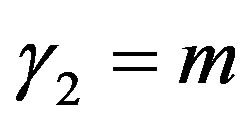 , and
, and . By Theorem 4, we obtain this result.
. By Theorem 4, we obtain this result. 
Theorem 7 Let ,
,  , and
, and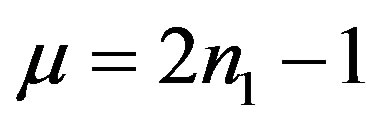 ,
,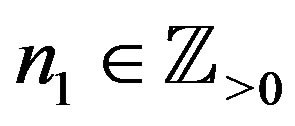 . Then we have the polynomial form of Psolution of (B.2):
. Then we have the polynomial form of Psolution of (B.2):
 (B.6)
(B.6)
Proof In this case,  ,
, 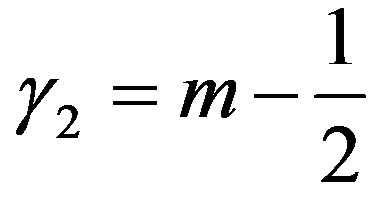 , and
, and . By Theorem 4, we obtain this result.
. By Theorem 4, we obtain this result. 
Theorem 8 Let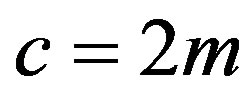 ,
,  , and
, and ,
, . Then we have the polynomial form of Psolution of (B.2):
. Then we have the polynomial form of Psolution of (B.2):
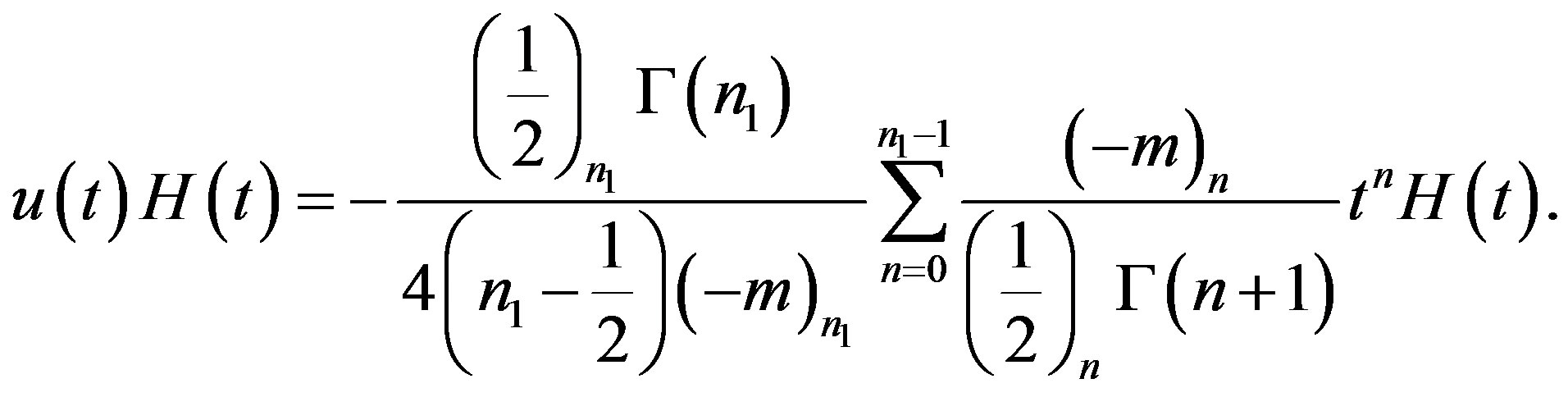 (B.7)
(B.7)
Proof In this case, 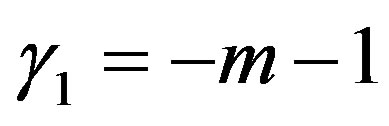 ,
, 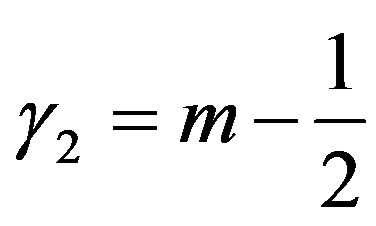 , and
, and . By Theorem 3, we obtain this result.
. By Theorem 3, we obtain this result. 
Remark 3 We confirm that Theorems 7 and 5, respectively, agree with Theorems 1 and 2 in [10].
Appendix C: Polynomial Form of P-Solution of (5.1)
Let  and
and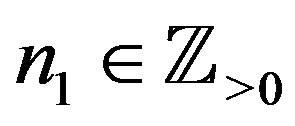 . Then (5.11) gives
. Then (5.11) gives
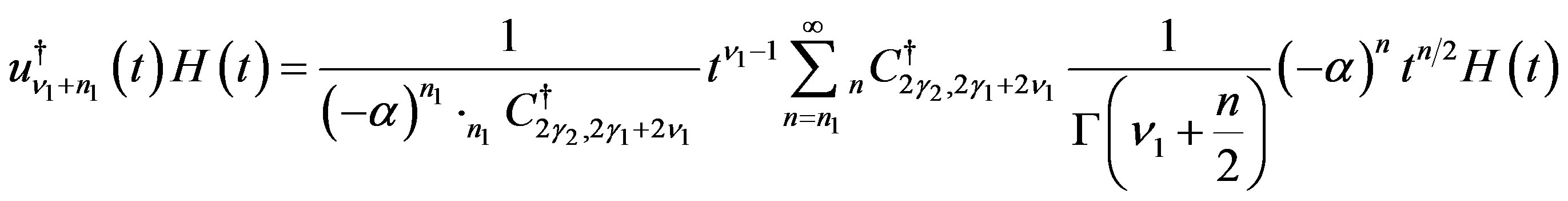 (C.1)
(C.1)
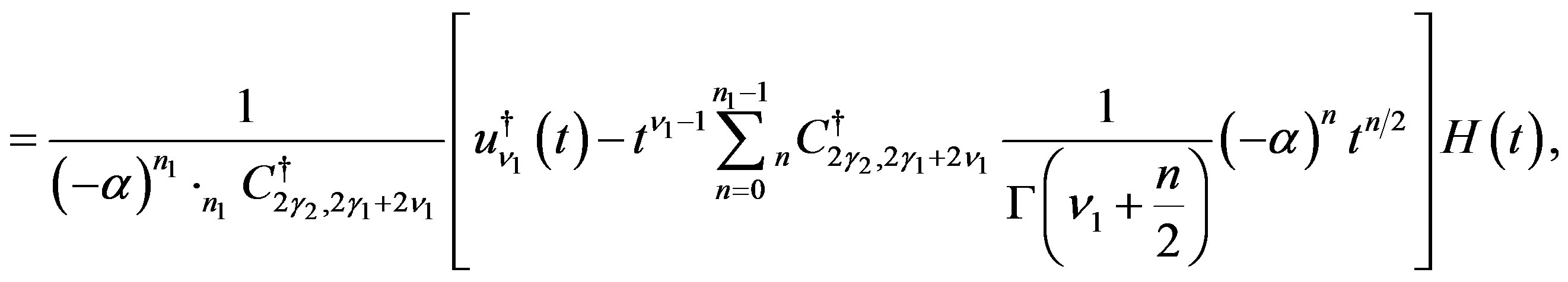 (C.2)
(C.2)
where
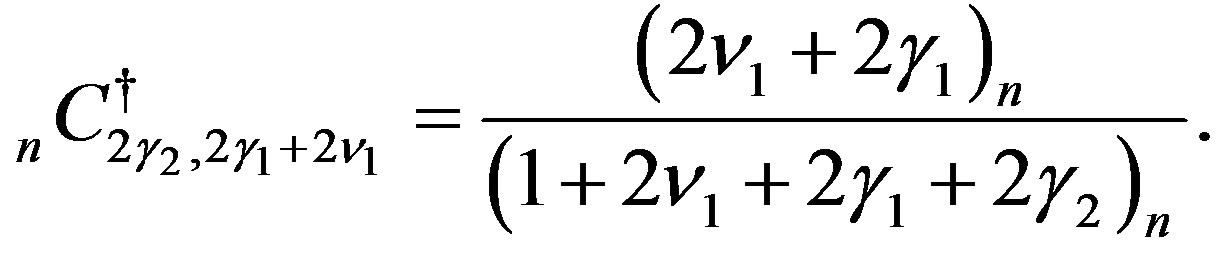 (C.3)
(C.3)
We obtain the following theorem from (C.2) with the aid of Proposition 2.
Theorem 9 Let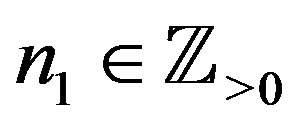 ,
, 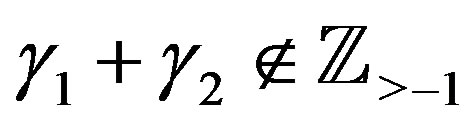 ,
, 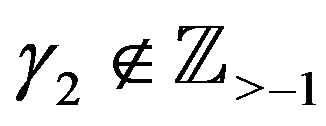 and
and 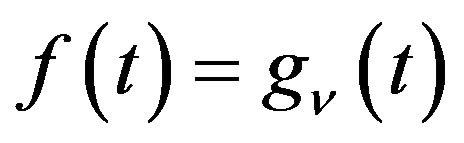 for
for . Then we have the polynomial form of P-solution of (5.1):
. Then we have the polynomial form of P-solution of (5.1):
 (C.4)
(C.4)

