Applied Mathematics
Vol.4 No.10B(2013), Article ID:37458,6 pages DOI:10.4236/am.2013.410A2005
Invasive Species Control Based on a Cooperative Game
1Department of Industrial and Manufacturing Engineering, Wichita State University, Wichita, USA
2Computer Science and Engineering, Arizona State University, Tempe, USA
3Department of Agricultural and Resource Economics, University of Arizona, Tucson, USA
4Department of Applied Mathematics, University of Pécs, Pécs, Hungary
Email: esra.b@wichita.edu
Copyright © 2013 İsmet Esra Büyüktahtakın et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received August 7, 2013; revised September 7, 2013; accepted September 14, 2013
Keywords: Non-Native Invasive Species; Buffelgrass; Optimal Control; Integer Programming; Cooperative Games; Shapley Value
ABSTRACT
We develop a long-term dynamic model for controlling invasive species using the theory of cooperative games. The model is applied to control of invasive buffelgrass in the Arizona desert, which directly competes with indigenous species and can increase wildfire risk. Interest groups care about damages to three threatened resources: saguaro, cactus, riparian vegetation, and buildings. The model optimally allocates labor and a budget to protect these resources by controlling the buffelgrass population over a multi-period planning horizon. The solution is based on computing the Shapley values for the interest groups. A homeowner strategy of creating defensible space around structures to protect against wildfire affords less protection to the other resources. A similar result holds for protection of saguaros, which are also spatially concentrated. Under the optimal solution, groups caring about spatially-dispersed, riparian vegetation would compensate homeowners and groups caring about saguaros for a reallocation of resources toward greater protection of dispersed vegetation. Results highlight the importance of the spatial configuration of players and the resources they wish to protect in invasive species control problems.
1. Introduction
The invasion of non-native species may lead to significant ecological and economic damages. When non-native species occupy new areas, they can eradicate native plants and animals as they compete for ground surface, sunlight, moisture, and nutrients. The invasion of nonnative species can cause drastic changes to an ecosystem [1-3]. Invasive species provide fuel for fires, which could destroy native habitats and man-made structures. While humans introduce some invasive species intentionally, for instance to serve as food crops, many are introduced accidentally or they escape from confinement and spread through ecosystems [1]. About 50,000 non-native species in the United States cause $115 billion in damages and losses annually, and that around $21 billion is spent on controlling non-native species population each year [4]. Naturally, there is an extensive literature for the control of invasive species. Epanchin-Niell and Hastings [1] provide a detailed review of the studies on the economically optimal control of some established invasive species.
Moody and Mack [5] and Martin et al. [6] perform a comparative study of the efficiency of different treatment variants on invasive species, while Wadsworth et al. [7] compare alternative strategies based on proximity for human settlements, weed population size, age and spatial distribution. Jetter et al. [8] study and provide a review for the benefits and costs of biological control programs. Olson [9] gives a review of a variety of optimization methods to solve the invasive species management problem including dynamic programming [10], optimal control theory [1,10] and genetic algorithms [11]. Burnett et al. [12] study the problem of determining the optimal amount of resources that should be applied for controlling specific invasions including estimates of real costs, damages and spread patterns into an optimization framework. Epanchin-Niell and Hastings [1] and Olson and Roy [13] investigate the optimal control principles for invasive species management and corresponding influencing factors through theoretical models.
In this paper, we consider a long-term dynamic model for controlling invasive species using cooperative game theory with the application to buffelgrass control in the Arizona desert. Buffelgrass is an invasive bunchgrass that was introduced to Arizona from Africa for cattle forage. Established buffelgrass forms large and dense colonies that exclude other species and is difficult to eradicate. The plants reduce the space available for the native species and compete with them for scarce water and nutrients. Furthermore, buffelgrass can easily lead to big fires. Büyüktahtakın et al. [14] study the spread and control of buffelgrass in Arizona as a spatial-dynamic problem. The authors provide two heuristic strategies: potential damage weighting and consecutive year treatment to solve the problem with some computational results to demonstrate the performance of these heuristics in terms of the relative damage reduction to no treatment and to static optimization. In another study, Büyüktahtakın et al. [15] provide a large scale, nonlinear 0 - 1 integer programming model for the dynamic control of invasive weeds while they introduce a multi-objective optimization model in [16]. In another study, the authors consider three different valued and threatened resources including saguaros, buildings and vegetation as players of the game, and provide optimal control strategies based on conflict resolution [17]. In this paper, we propose a model, which decides the optimal allocation of labor and budget to these resources to control the population of the species in a multi-period planning horizon based on the theory of cooperative games.
If no cooperation is assumed between the decision makers, then each of them wants to maximize its own benefit without any consideration to the others. The Nash equilibrium is the most common solution concept for such cases [18,19]. In this paper, we consider a cooperative case and aim to find out what payoff will be awarded to each decision maker in the cooperation given the sets of feasible payoffs to each coalition. We aim to answer this question by using cooperative game theoretical methodology. There are several different ways to model the cooperation of the decision makers including conflict resolution [20,21], multi-objective optimization [22], partial cooperation [23], and solution concepts based on characteristic functions [18]. In this paper, this last approach is selected and the Shapley values [24,25] of the three-person cooperative game are determined.
The invaded area is modeled as a gridded landscape, where each cell of the grid represents one acre of land. The potential for an invasive weed to become established as well as damages and the cost of control are defined by the carrying capacity, which varies across the landscape. The damage in any cell depends on the buffelgrass population density in the cell and the location of the valued, threatened resources with respect to the cell and its close neighborhood. We define the decision variables to represent the management decision, which is to treat or not to treat a cell in a given period. If it is treated, then the population decreases immediately depending on the kill rate of the herbicide treatment, otherwise its population grows according to the natural growth model. We have limited treatment resources including labor and budget, which drastically can change the optimal control strategy compared to the unconstrained optimal policy [11,26]. Given labor and budget constraints, our goal is to minimize the total discounted damage during the entire considered time interval subject to competing resources.
This paper is organized as follows: In Section 2, we present the formulation of the 0 - 1 dynamic model forcontrolling invasive species. The applied game theoreticcal solution methodology is described in Section 3. Experimental results and their analysis are provided in Section 4. In Section 5, conclusions and future research directions are outlined.
2. Mathematical Model
In this section, we provide a model with the objective of minimizing the total damage caused by the invasion, which is the present value of the sum of costs corresponding to total damages across space and time. The notations are as follows:
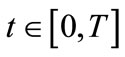 denotes any year of the time horizon T;
denotes any year of the time horizon T;
 indicates cells of the grid by row i and column j in the landscape;
indicates cells of the grid by row i and column j in the landscape;
 is the decision variable of cell
is the decision variable of cell 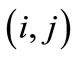 at time t, where
at time t, where 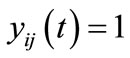 if the cell is treated and
if the cell is treated and  otherwise;
otherwise;
 represents the population volume of cell
represents the population volume of cell  at time t;
at time t;
 is the carrying capacity of cell
is the carrying capacity of cell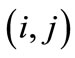 ;
;
 is the vector of buffelgrass population volumes in the eight cells surrounding cell
is the vector of buffelgrass population volumes in the eight cells surrounding cell 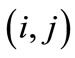 at time t.
at time t.
Let g be the logistic growth function such that the population grows fast at the beginning and then at a decreasing rate when the population approaches the carrying capacity. The state transition relations without treatment are formulated as
 (1)
(1)
However, if possible treatment is considered, the new state can be stated as follows:
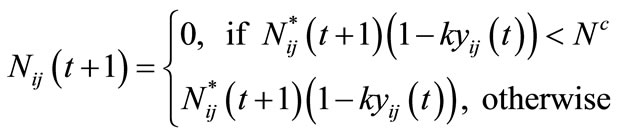 (2)
(2)
since if the cell is treated, then the population becomes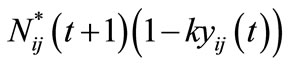 , and if this volume is below a given threshold
, and if this volume is below a given threshold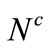 , then the treatment eradicates buffelgrass completely from the cell.
, then the treatment eradicates buffelgrass completely from the cell.
Let 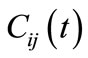 denote the cost of treating cell
denote the cost of treating cell  in year t:
in year t:
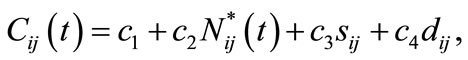
where 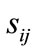 is the average cell slope,
is the average cell slope, 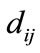 is the distance of the cell from the closest road, and the coefficients
is the distance of the cell from the closest road, and the coefficients  are estimated by the least squares method based on recent treatment records [28].
are estimated by the least squares method based on recent treatment records [28].
The labor requirement 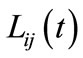 is also assumed to have a linear form,
is also assumed to have a linear form,
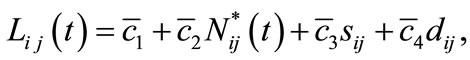
where the coefficients  are also obtained by the least squares method using actual recent treatment data [28].
are also obtained by the least squares method using actual recent treatment data [28].
Finally, let  represent the damage to resource r in cell
represent the damage to resource r in cell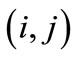 , which depends on the buffelgrass population
, which depends on the buffelgrass population  and the proportion of resource r at risk in cell
and the proportion of resource r at risk in cell 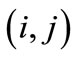 and in the surrounding cells,
and in the surrounding cells, 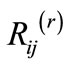 , and the management priority for resource r,
, and the management priority for resource r, 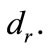 We then give its formulation as:
We then give its formulation as:
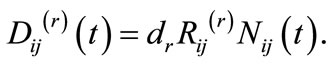
We then formulate the optimization problem for resource r as a nonlinear 0 - 1 integer programming problem as follows:
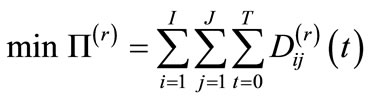 (3)
(3)
subject to:
Constraints (1) & (2)
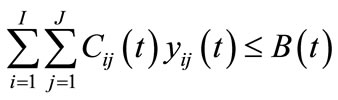 (4)
(4)
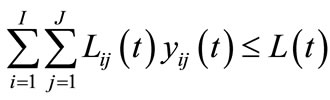 (5)
(5)
The objective function (3) defines the total damage caused by the weed population over all cells and all years during the given time period of T + 1 years. Given that 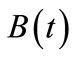 and
and 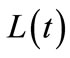 are the annual budget and available labor in year t, constraints (4) and (5) guarantee that both the budget and labor restrictions are satisfied.
are the annual budget and available labor in year t, constraints (4) and (5) guarantee that both the budget and labor restrictions are satisfied.
3. Solution Methodology
Let 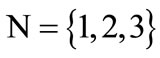 denote the set of the three interest groups, each of them wants to control the buffelgrass population considering only one resource j: riparian vegetation, houses and other building structures, and saguaros. The characteristic function of the three-person cooperative game is a real-valued function v defined on all possible coalitions. Function v is defined as follows: Let
denote the set of the three interest groups, each of them wants to control the buffelgrass population considering only one resource j: riparian vegetation, houses and other building structures, and saguaros. The characteristic function of the three-person cooperative game is a real-valued function v defined on all possible coalitions. Function v is defined as follows: Let 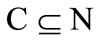 be any coalition. Then
be any coalition. Then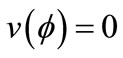 , and if
, and if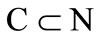 , then
, then
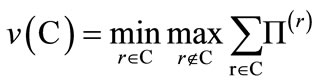 (6)
(6)
In the special case of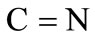 ,
,
 (7)
(7)
The Shapley value of the interest groups can be computed from the values of the characteristic function. Let 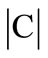 denote the number of members of the coalition
denote the number of members of the coalition ; then the Shapley value for interest group r is given as
; then the Shapley value for interest group r is given as
 (8)
(8)
Notice that if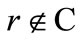 , then the corresponding term of the summation is zero, so we have to consider only those coalitions that contain interest group r. It can be proved that
, then the corresponding term of the summation is zero, so we have to consider only those coalitions that contain interest group r. It can be proved that
 (9)
(9)
That is, in implementing the Shapley value, minimizing the overall damage is the best possibility for all interest groups. That is, the sum of the three damages is minimized. However, the actual damages for the individual interest groups are not necessarily equal the Shapley values. In such cases side payments have to be used to compensate interest groups that have larger actual damages than the Shapley values. This can be either direct financial compensation or compensation can be made by providing more labor for additional treatments. Under side payment compensation, every player receives their Shapley value. So, if a player’s payoff exceeds this value, the player must compensate other players. Otherwise, the player should receive compensation from others.
4. Numerical Results
The feasible decision space is determined by the model constraints as well as by the recommendation of the Buffelgrass Working Group [27] that treatments have to be continued at least for a consecutive three-year period. The logic of this strategy derives from the logistic growth process of the buffelgrass population. If buffelgrass population of treated cell is close to its carrying capacity, a single year of treatment will push that population back the fast-growing part of its growth curve. The population quickly rebounds in subsequent years, so that a single year of treatment has little long-term effect. Earlier research has verified that the three-year treatment strategy is highly effective [14,15].
The area is divided into cells, a 40 × 50 rectangular array of cells is considered. The buffelgrass population has a 12-year history in Arizona, so the current year is set to 12. We consider treatment until year 30. We calibrate the parameters of the numerical buffelgrass spread model to replicate actual, historic spread behavior of buffelgrass based on recent treatment records in and around the Desert Lab and the exotic plant surveys performed since 1983 at Tumamoc Hill [28].
The future damages for each resource after this period are taken into account by computing the maximum possible damage value 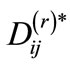 for each cell if the cell is left untreated from the current period to the end of the planning horizon and consider the weighted averages:
for each cell if the cell is left untreated from the current period to the end of the planning horizon and consider the weighted averages:
 (10)
(10)
with w = 0.5 coefficient value.
Because side payments are considered among the interest groups, all damages were computed with their dollar values. The estimated values of houses and replacement costs for saguaros and other important desert plants were obtained from the Office of Arid Land Studies of the University of Arizona. We solve the resulting linear binary integer program by a branch and bound algorithm [29]. In our computations, we used a state of art integer programming solver ILOG CPLEX (2010) [30].
In computing the characteristic function values as shown in Equation (6), notice that the maximum damage with 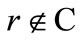 occurs if the cells controlled by the groups outside coalition
occurs if the cells controlled by the groups outside coalition 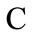 are not treated at all. So
are not treated at all. So 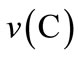 is obtained by minimizing the overall damage for the coalition under this additional constraint. Figure 1 shows the cell grid with the indication of each interest group and the grid cells which are controlled by that interest group.
is obtained by minimizing the overall damage for the coalition under this additional constraint. Figure 1 shows the cell grid with the indication of each interest group and the grid cells which are controlled by that interest group.
For the experimentation, we assume that each own

Figure 1. Cell grid with controlling interest groups: riparian (1), houses (2), and saguaros (3).
group has their own budget allotted based on the area of the land they had and only control their own land. Even though a grid cell is controlled by only one interest group shown in Figure 1, a grid cell may have all three valuable resources. Once the interest groups join the coalition, their objective is to minimize the damage to all the resources that are concerned by the coalition. Since minimizing the damage is equivalent to maximizing damage reduction, in the numerical part, we simply considered damage reduction, which is actually the difference between possible largest damage and the actual damage. Table 1 shows the characteristic function values with actual damage reductions in million $ for the  possible coalitions of the three interest groups.
possible coalitions of the three interest groups.
Utilizing Equation (8) the Shapley value with for interest group 1, 2 and 3 can be computed as follows:

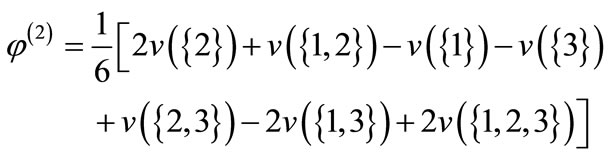
and

Based on the values shown in Table 1, we have
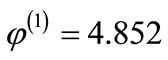
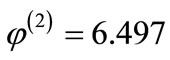


Table 1. Characteristic function values with actual damage reductions.
The values of  and
and 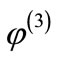 indicate that the interest group of homeowners and saguaros should be compensated by the riparian group for their controlling efforts. Figure 1 provides some intuition for this result. Most structures are concentrated on the fringe of the study area. Acting alone, an optimal strategy for homeowners is to create “defensible space” around structures, reducing buffelgrass populations to protect against wildfire risk. Likewise, saguaro populations are less scattered throughout the study area than riparian vegetation. Creating defensible space around saguaros provides fewer benefits to other, dispersed vegetation. Thus, the interest group that cares about dispersed resources will have to compensate those groups wanting to protect more spatially concentrated resources. The actual treatment strategies are obtained from the optimization problem (7). The three damage trajectories when all the parties are in coalition are shown in Figure 2. The damage values are obtained by solving the optimization problem (1), (2), (4) and (5) with objective (10) when considering all parties are in coalition. In Figure 2, we observe that the damage reduction trajectory is almost linear for houses. On the other hand, we observe that the damage reduction function trend is exactly same for riparian and saguaros. Therefore blue and green trajectories are identical in Figure 2.
indicate that the interest group of homeowners and saguaros should be compensated by the riparian group for their controlling efforts. Figure 1 provides some intuition for this result. Most structures are concentrated on the fringe of the study area. Acting alone, an optimal strategy for homeowners is to create “defensible space” around structures, reducing buffelgrass populations to protect against wildfire risk. Likewise, saguaro populations are less scattered throughout the study area than riparian vegetation. Creating defensible space around saguaros provides fewer benefits to other, dispersed vegetation. Thus, the interest group that cares about dispersed resources will have to compensate those groups wanting to protect more spatially concentrated resources. The actual treatment strategies are obtained from the optimization problem (7). The three damage trajectories when all the parties are in coalition are shown in Figure 2. The damage values are obtained by solving the optimization problem (1), (2), (4) and (5) with objective (10) when considering all parties are in coalition. In Figure 2, we observe that the damage reduction trajectory is almost linear for houses. On the other hand, we observe that the damage reduction function trend is exactly same for riparian and saguaros. Therefore blue and green trajectories are identical in Figure 2.
5. Conclusions
In this paper, a dynamic model was introduced for controlling invasive species. The case study used data for the increasing ecological problem caused by the buffelgrass population in the Southern Arizona Desert. We considered three interest groups. The first group’s interest is to minimize damage to riparian vegetation; the second group represents the interest of homeowners; while the third group wants to preserve the famous saguaros of the Arizona desert. Because all groups have the common

Figure 2. Damage reduction trajectories for years 12 through 30.
interest of preserving the environment and man-made structures, they must cooperate to gain the maximum benefits of damage reduction.
This study used cooperative game theory, the solution concept of Shapley, which is based on the characteristic function values for all possible coalitions of the three interest groups. Our numerical results indicate that in order to have the optimal cooperation of the homeowner’s as well as saguaro protection groups in controlling the buffelgrass population, they have to be compensated for their efforts. Results highlight the importance of the spatial configuration of players and the resources they wish to protect. An important subject for future research is to apply other cooperative game-theoretic concepts and methods to this spatial invasive species control problem to compare solution results to those obtained in this paper.
6. Acknowledgements
This research is based upon work supported by the National Science Foundation under grant No. EPS-0903806 and the state of Kansas through the Kansas Board of Regents.
REFERENCES
- R. Epanchin-Niell and A. Hastings, “Controlling Established Invaders: Integrating Economics and Spread Dynamics to Determine Optimal Management,” Ecology Letters, Vol. 13, No. 4, 2010, pp. 528-541. http://dx.doi.org/10.1111/j.1461-0248.2010.01440.x
- J. Luken and J. Thieret, “Assessment and Management of Plant Invasions,” Springer-Verlag, New York, 1997. http://dx.doi.org/10.1007/978-1-4612-1926-2
- R. Sheley and J. Clark, “Biology and Management of Noxious Rangeland Weeds,” Oregon State University Press, Oregon, 1999.
- D. Pimentel, L. Lach, R. Zuniga and D. Morrison, “Environmental and Economic Costs of Nonindigenous Species in the United States,” BioScience, Vol. 50, No. 1, 2000, pp. 53-65. http://dx.doi.org/10.1641/0006-3568(2000)050[0053:EAECON]2.3.CO;2
- M. Moody and R. Mack, “Controlling the Spread of Plant Invasions: The Importance of Nascent Foci,” Journal of Applied Ecology, Vol. 25, No. 3, 1988, pp. 1009-1021. http://dx.doi.org/10.2307/2403762
- B. Martin, D. Hanna, N. Korb and L. Frid, “Decision Analysis of Alternative Invasive Weed Management Strategies for Three Montana Landscapes,” The Nature Conservancy of Montana, Helena, MT and ESSA Technologies Ltd., Vancouver, 2007.
- R. Wadsworth, Y. Collingham, S. Willis, B. Huntley and P. Hulme, “Simulating the Spread and Management of Alien Riparian Weeds: Are They out of Control?” Journal of Applied Ecology, Vol. 37, Suppl. s1, 2000, pp. 28- 38. http://dx.doi.org/10.1046/j.1365-2664.2000.00551.x
- K. Jetter, J. DiTomaso, D. Drake, K. Klonsky, M. Pitcairn and D. Sumner, “Biological Control of Yellow Starthistle,” In: D. A. Sumner, Ed., Exotic Pests and Diseases: Biology and Economics for Biosecurity, Iowa State University Press, Ames, 2003, pp. 121-150.
- L. Olson, “The Economics of Terrestrial Invasive Species: A Review of the Literature,” Agricultural and Resource Economics Review, Vol. 35, No. 1, 2006, p. 178.
- C. Clark, “Mathematical Bioeconomics: The Optimal Management of Renewable Resources,” 2nd Edition, Wiley, New York, 1990.
- C. Taylor and A. Hastings, “Finding Optimal Control Strategies for Invasive Species: A Density Structured Model for Spartina Alterniflora,” Journal of Applied Ecology, Vol. 41, No. 6, 2004, pp. 1049-1057. http://dx.doi.org/10.1111/j.0021-8901.2004.00979.x
- K. Burnett, B. Kaiser and J. Roumasset, “Economic Lessons from Control Efforts for an Invasive Species: Miconia Calvescens in Hawaii,” Journal of Forest Economics, Vol. 13, No. 2-3, 2007, pp. 151-167. http://dx.doi.org/10.1016/j.jfe.2007.02.007
- L. Olson and S. Roy, “The Economics of Invasive Species Management: The Economics of Controlling a Stochastic Biological Invasion,” American Journal of Agricultural Economics, Vol. 84, No. 5, 2002, pp. 1311-1316. http://dx.doi.org/10.1111/1467-8276.00395
- İ. E. Büyüktahtakın, F. Zhuo, A. Olsson, G. Frisvold and F. Szidarovszky, “Positive Analysis of Invasive Species Control as a Dynamic Spatial Process,” 2010 Annual Meeting, Denver, 25-27 July 2010, pp. 1-33.
- İ. E. Büyüktahtakın, F. Zhuo, G. Frisvold and F. Szidarovszky and A. Olsson, “A Dynamic Model of Controlling Invasive Species,” Computers and Mathematics with Applications, Vol. 62, No. 9, 2011, pp. 3326-3333. http://dx.doi.org/10.1016/j.camwa.2011.08.037
- İ. E. Büyüktahtakın, F. Zhuo and F. Szidarovszky, “A Multi-Objective Optimization Model for Invasive Species Control,” Journal of Operational Research Society, 2013, in Press.
- İ. E. Büyüktahtakın, F. Zhuo, G. Frisvold and F. Szidarovszky, “A Game Theoretical Approach to Invasive Species Management,” Proceedings of the 2011 Industrial Engineering Research Conference, Reno, 20-22 May 2011.
- F. Forgó, J. Szép and F. Szidarovszky, “Introduction to the Theory of Games: Concepts, Methods, Applications,” Kluwer Academic Publishers, Dordrecht, 1999.
- M. Osborne, “An Introduction to Game Theory,” Oxford University Press, New York, 2004.
- J. Nash, “The Bargaining Problem,” Econometrica, Vol. 18, No. 2, 1950, pp. 155-162. http://dx.doi.org/10.2307/1907266
- A. Roth, “Axiomatic Models of Margaining,” SpringerVerlag, New York, 1979. http://dx.doi.org/10.1007/978-3-642-51570-5
- F. Szidarovszky, M. Gershon and L. Duckstein, “Techniques for Multiobjective Decision Making in Systems Management,” Elsevier, Amsterdam, 1986.
- R. Cyert and M. DeGroot, “An Analysis of Cooperation and Learning in a Duopoly Context,” The American Economic Review, Vol. 63, No. 1, 1973, pp. 24-37.
- S. S. Lloyd, “A Value for N-Person Games,” In: H. W. Kuhn and A. W. Tucker, Eds., Contributions to the Theory of Games, Volume II, Annals of Mathematical Studies, Princeton University Press, Princeton, 1953, pp. 307-317.
- A. Roth, “Axiomatic Models of Margaining,” SpringerVerlag, New York, 1979. http://dx.doi.org/10.1007/978-3-642-51570-5
- O. Cacho, R. Wise, S. Hester and J. Sinned, “Bioeconomic Modeling for Control of Weeds in Natural Environments,” Ecological Economics, Vol. 65, No. 3, 2008, pp. 559-568. http://dx.doi.org/10.1016/j.ecolecon.2007.08.006
- A. Rogstad, “Southern Arizona Buffelgrass Strategic Plan: A Regional Guide for Control, Mitigation, and Restoration,” U. B. W. Group, Tucson, 2008.
- J. E. Bowers, T. M. Bean and R. M. Turner, “Twodecades of Change and Distribution of Exotic Plants at the Desert Laboratory, Tucson, Arizona,” Madroño, Vol. 53, No. 3, 2006, pp. 252-263. http://dx.doi.org/10.3120/0024-9637(2006)53[252:TDOCID]2.0.CO;2
- G. L. Nemhauser and L. A. Wolsey, “Integer and Combinatorial Optimization,” John Wiley & Sons, New York, 1988.
- ILOG CPLEX, “IBM ILOG CPLEX: High-Performance Mathematical Programming Engine,” 2013. http://www-01.ibm.com/software/integration/optimization/cplex

