Applied Mathematics
Vol.4 No.7(2013), Article ID:33958,8 pages DOI:10.4236/am.2013.47137
Hyers-Ulam-Rassias Stability for the Heat Equation
Department of Mathematics, AlQuds Open University, Salfit, Palestine
Email: mkerawani@qou.edu
Copyright © 2013 Maher Nazmi Qarawani. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 26, 2013; revised May 27, 2013; accepted June 5, 2013
Keywords: Hyers-Ulam-Rassias Stability; Heat Equation; Fourier Transform; Laplace Transform
ABSTRACT
In this paper we apply the Fourier transform to prove the Hyers-Ulam-Rassias stability for one dimensional heat equation on an infinite rod. Further, the paper investigates the stability of heat equation in 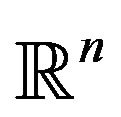 with initial condition, in the sense of Hyers-Ulam-Rassias. We have also used Laplace transform to establish the modified Hyers-Ulam-Rassias stability of initial-boundary value problem for heat equation on a finite rod. Some illustrative examples are given.
with initial condition, in the sense of Hyers-Ulam-Rassias. We have also used Laplace transform to establish the modified Hyers-Ulam-Rassias stability of initial-boundary value problem for heat equation on a finite rod. Some illustrative examples are given.
1. Introduction and Preliminaries
The study of stability problems for various functional equations originated from a famous talk given by Ulam in 1940. In the talk, Ulam discussed a problem concerning the stability of homomorphisms. A significant breakthrough came in 1941, when Hyers [1] gave a partial solution to Ulam’s problem. Afterthen and during the last two decades a great number of papers have been extensively published concerning the various generalizations of Hyers result (see [2-10]).
Alsina and Ger [11] were the first mathematicians who investigated the Hyers-Ulam stability of the differential equation 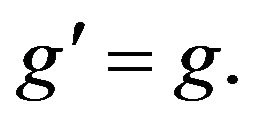 They
They proved that if a differentiable function
proved that if a differentiable function 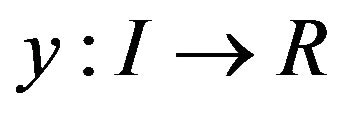 satisfies
satisfies 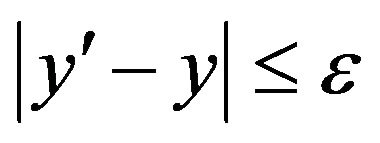 for all
for all 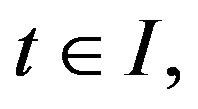 then there exists a differentiable function
then there exists a differentiable function 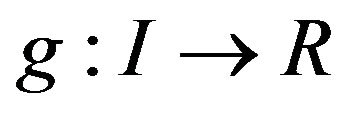 satisfying
satisfying  for any
for any 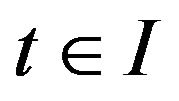 such that
such that 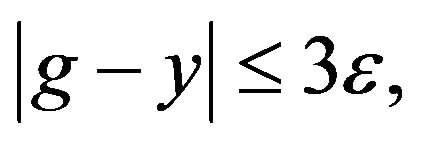 for all
for all 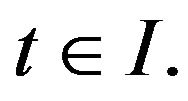 This result of alsina and Ger has been generalized by Takahasi et al. [12] to the case of the complex Banach space valued differential equation
This result of alsina and Ger has been generalized by Takahasi et al. [12] to the case of the complex Banach space valued differential equation 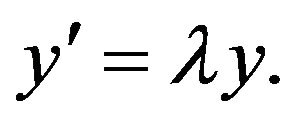
Furthermore, the results of Hyers-Ulam stability of differential equations of first order were also generalized by Miura et al. [13], Jung [14] and Wang et al. [15].
Li [16] established the stability of linear differential equation of second order in the sense of the Hyers and Ulam 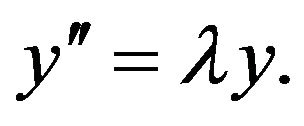 Li and Shen [17] proved the stability of nonhomogeneous linear differential equation of second order in the sense of the Hyers and Ulam
Li and Shen [17] proved the stability of nonhomogeneous linear differential equation of second order in the sense of the Hyers and Ulam 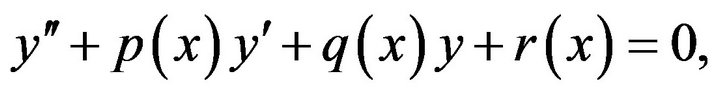 while Gavruta et al. [18] proved the Hyers-Ulam stability of the equation
while Gavruta et al. [18] proved the Hyers-Ulam stability of the equation  with boundary and initial conditions. Jung [19] proved the Hyers-Ulam stability of first-order linear partial differential equations. Gordji et al. [20] generalized Jung’s result to first order and second order Nonlinear partial differential equations. Lungu and Craciun [21] established results on the Ulam-Hyers stability and the generalized Ulam-HyersRassias stability of nonlinear hyperbolic partial differential equations.
with boundary and initial conditions. Jung [19] proved the Hyers-Ulam stability of first-order linear partial differential equations. Gordji et al. [20] generalized Jung’s result to first order and second order Nonlinear partial differential equations. Lungu and Craciun [21] established results on the Ulam-Hyers stability and the generalized Ulam-HyersRassias stability of nonlinear hyperbolic partial differential equations.
In this paper we consider the Hyers-Ulam-Rassias stability of the heat equation
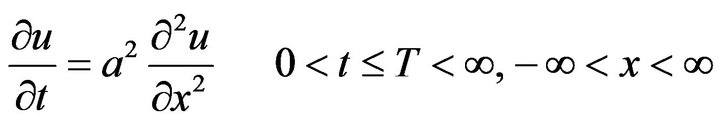 (1)
(1)
with the initial condition
 (2)
(2)
where  and
and
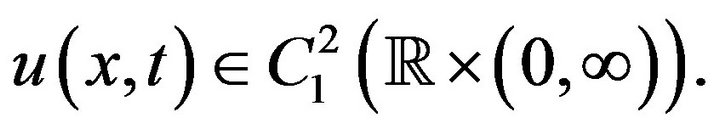
We also use a similar argument to establish the HyersUlam-Rassias for the heat equation in higher dimension
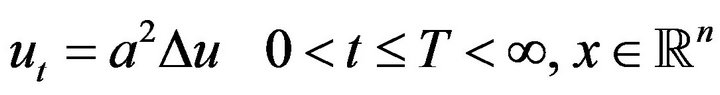 (3)
(3)
with the initial condition
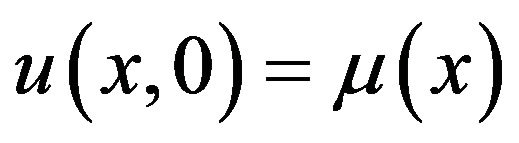 (4)
(4)
where 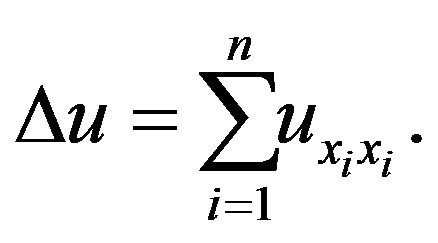
Moreover we have proved theorems on Hyers-UlamRassias-Gavruta stability for the heat equation in a finite rod.
Definition 1 We will say that the Equation (1) has the Hyers-Ulam-Rassias stability with respect to 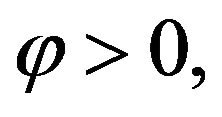 if there exists K > 0 such that for each
if there exists K > 0 such that for each 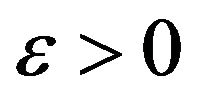 and for each solution
and for each solution 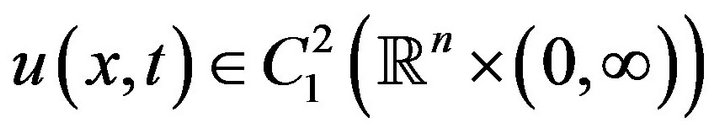 of the inequality
of the inequality 
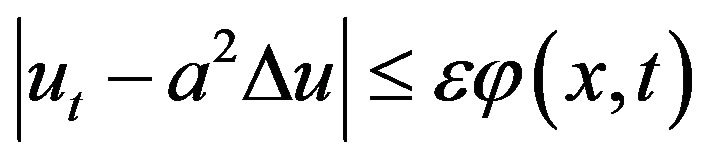 (5)
(5)
with the initial condition (2) then there exists a solution
then there exists a solution 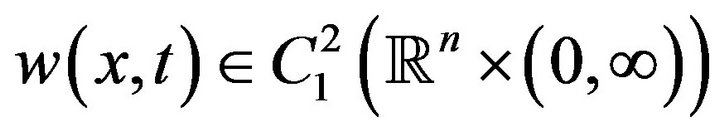 of the Equation (1), such that
of the Equation (1), such that
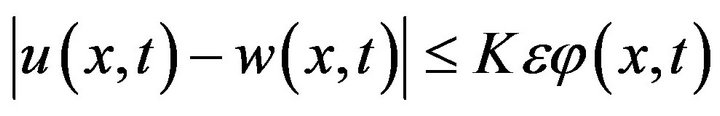 ,
,
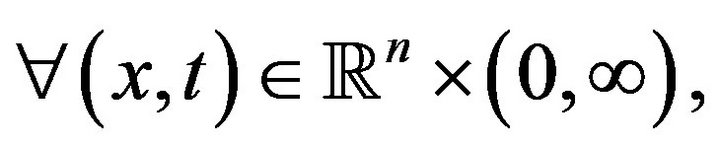
where 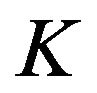 is a constant that does not depend on
is a constant that does not depend on 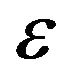 nor on
nor on 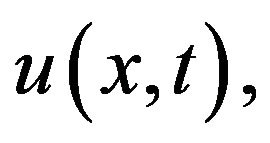 and
and 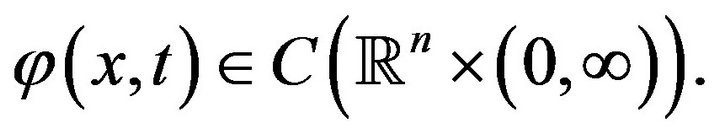
Definition 2 We will say that the equation (1) has the Hyers-Ulam-Rassias-Gavruta (HURG) stability with respect to 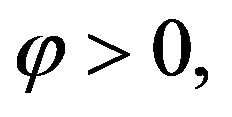 if there exists K > 0 such that for each
if there exists K > 0 such that for each 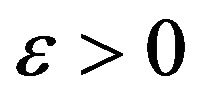 and for each solution
and for each solution 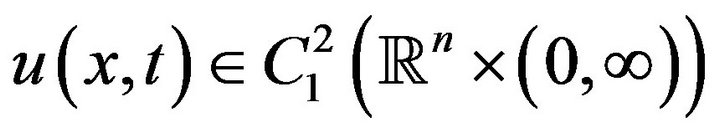 of the inequality
of the inequality 
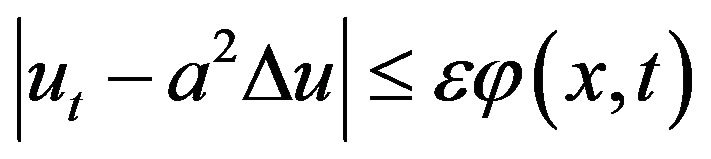 (6)
(6)
with the initial condition (2), then there exists a solution  of the Equation (1), such that
of the Equation (1), such that
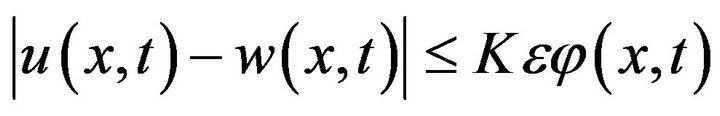 ,
,
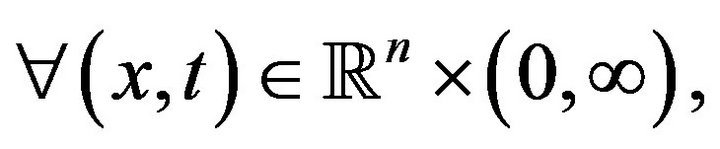
where 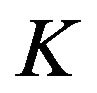 is a constant that does not depend on
is a constant that does not depend on 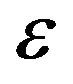 nor on
nor on 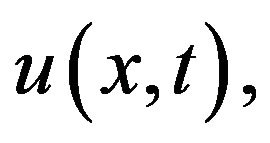 and
and 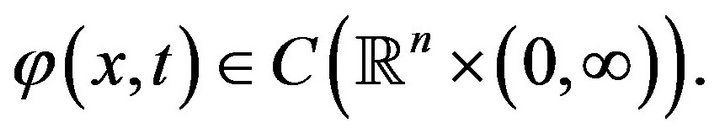
Definition 3 We will say that the solution of the initial value problem (1), (2) has the Hyers-Ulam-Rassias asymptotic stability with respect to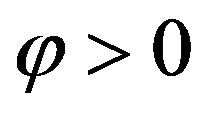 , if it is stable in the sense of Hyers and Ulam with respect to
, if it is stable in the sense of Hyers and Ulam with respect to  and
and
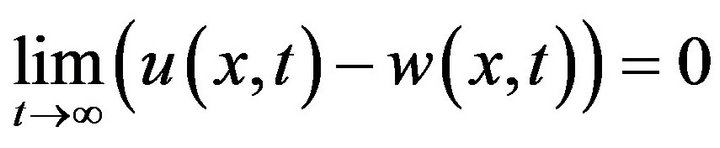
Definition 4 Assume the functions 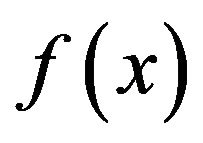 and
and 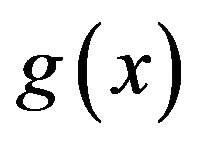 defined on
defined on 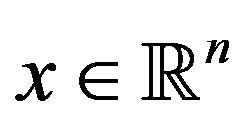 are continuously differentiable and absolutely integrable, then the Fourier transform of
are continuously differentiable and absolutely integrable, then the Fourier transform of 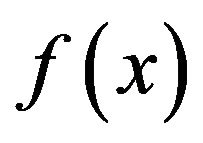 is defined as
is defined as
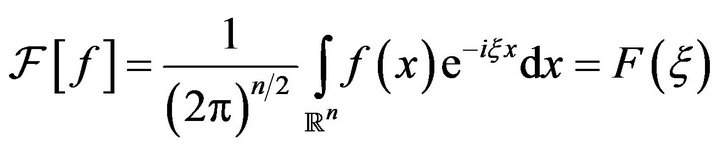
and the inverse Fourier transform of 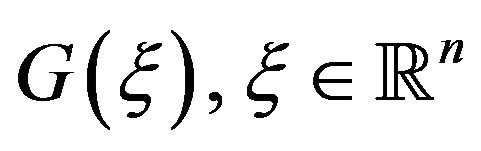 is
is
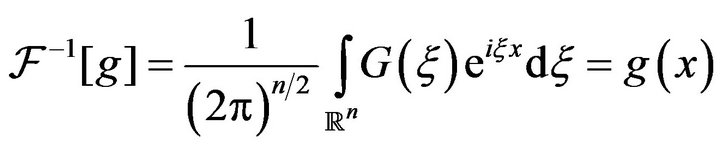
Example 1 Let
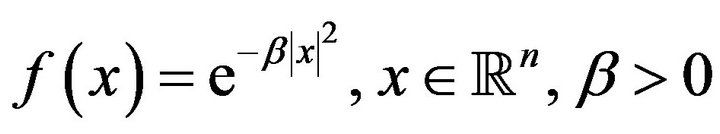
We find the Fourier transform of the function.
Since
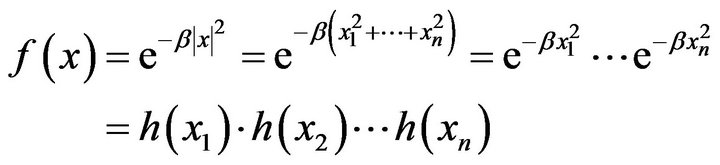
Then
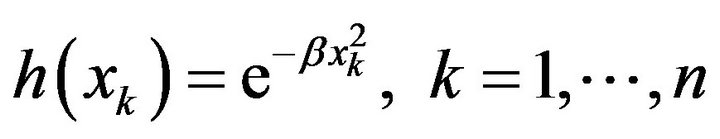
and by defintion 4 we have
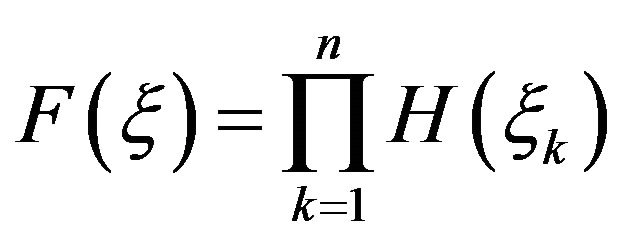 (7)
(7)
where
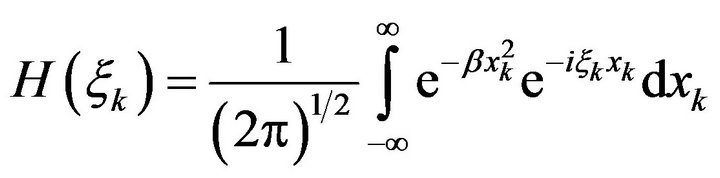 (8)
(8)
Differentiating 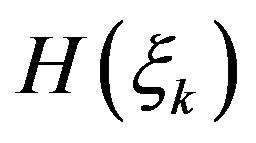 with respect to
with respect to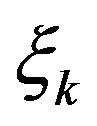 , we get
, we get 
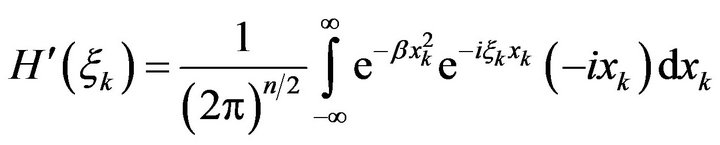
Integrating by parts gives
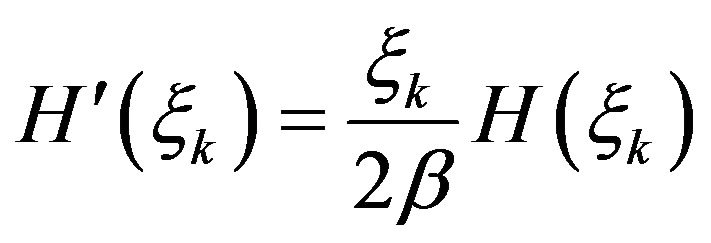
Hence
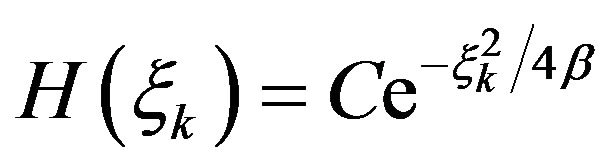
Putting 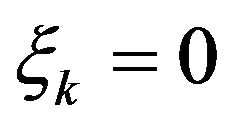 gives
gives 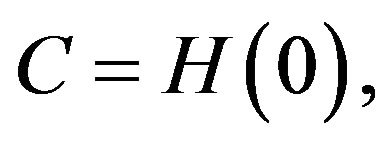 and from (8) one has
and from (8) one has
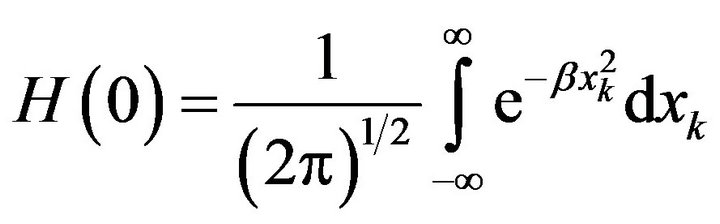
Using that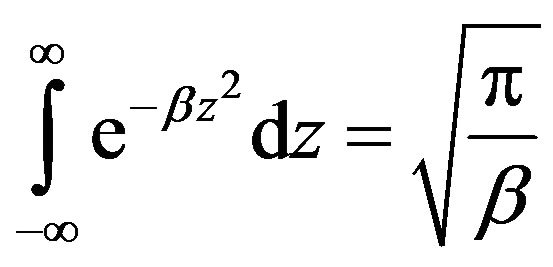 ,
, we have
we have
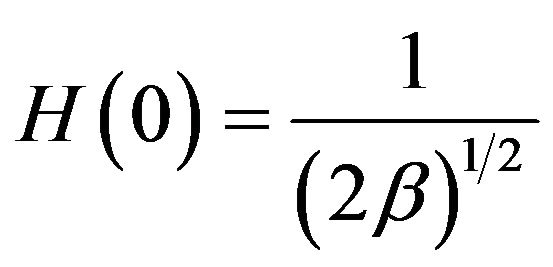
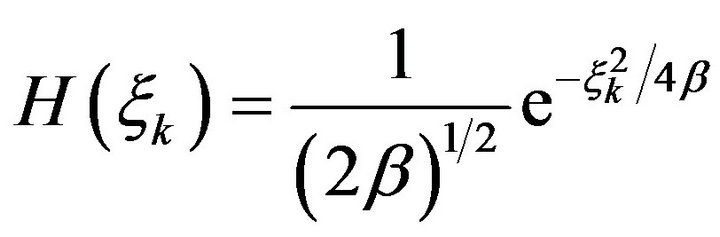 (9)
(9)
Therefore, from (7), (9) we obtain
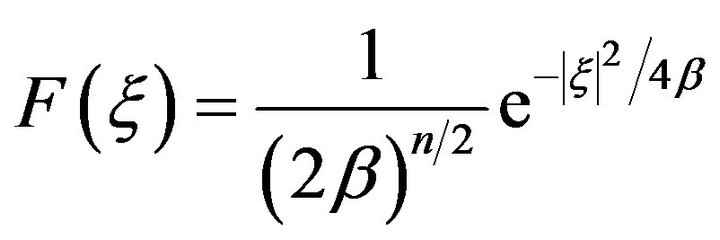
Theorem 1 (See Evans [22]) Assume that 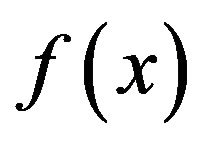 and
and 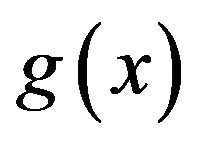 are continuously differentiable and absolutely integrable on
are continuously differentiable and absolutely integrable on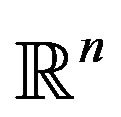 . Then 1) for each
. Then 1) for each  such that
such that 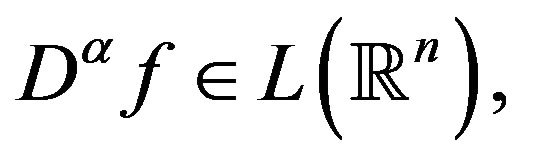

2) 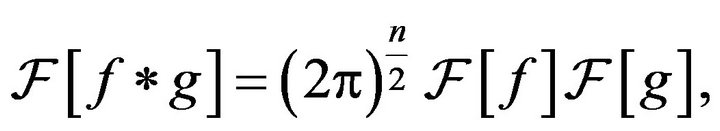 where
where
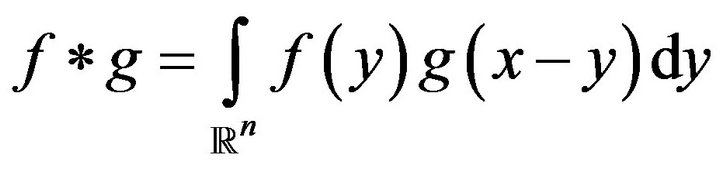 is the convolution of
is the convolution of 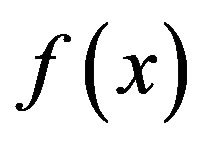 and
and 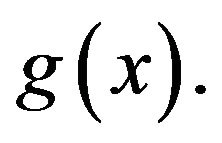
2. On Hyers-Ulam-Rassias Stability for Heat Equation on an Infinite Rod
Theorem 2 If 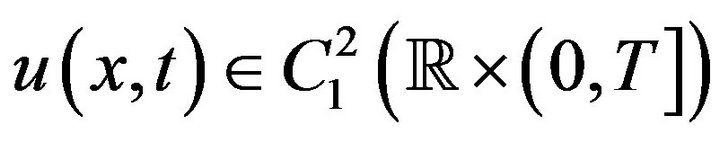 then the initial value problem (1), (2) is stable in the sense of HyersUlam-Rassias.
then the initial value problem (1), (2) is stable in the sense of HyersUlam-Rassias.
Proof. Let 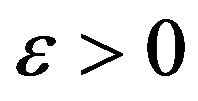 and
and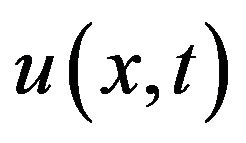 be an approximate solution of the initial value problem (1), (2). We will show that there exists a function
be an approximate solution of the initial value problem (1), (2). We will show that there exists a function  satisfying the Equation (1) and the initial condition (2) such that
satisfying the Equation (1) and the initial condition (2) such that
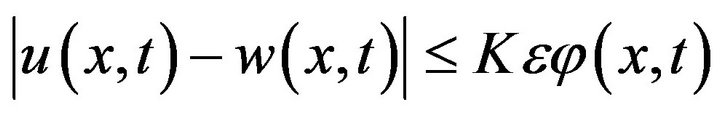
If we take 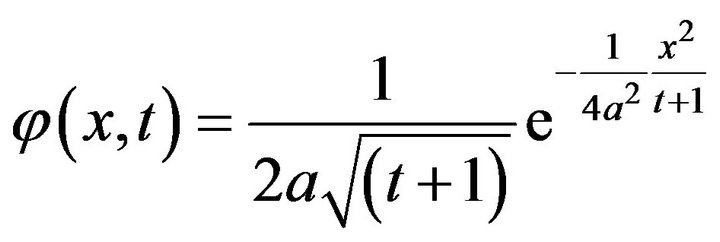 then from inequality (5), we have
then from inequality (5), we have
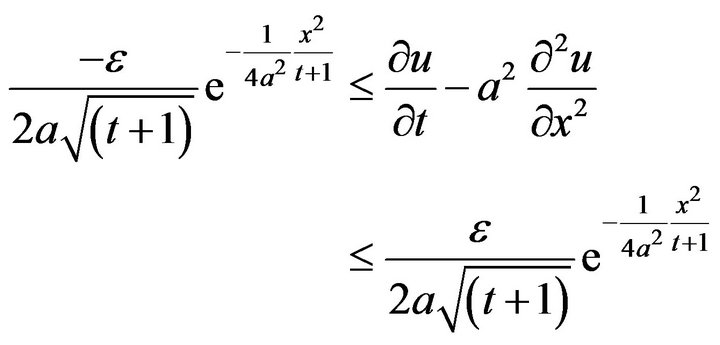 (10)
(10)
Applying Fourier Transform to inequality (10), we get
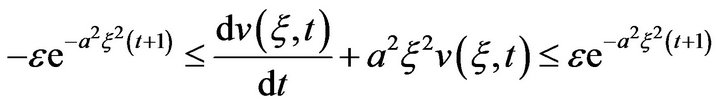 (11)
(11)
Or, equivalently
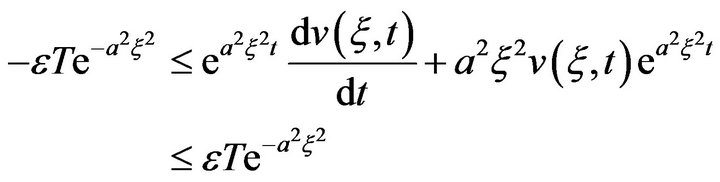
Integrating the inequality from 0 to 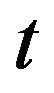 we obtain
we obtain
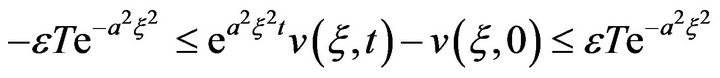
From which it follows
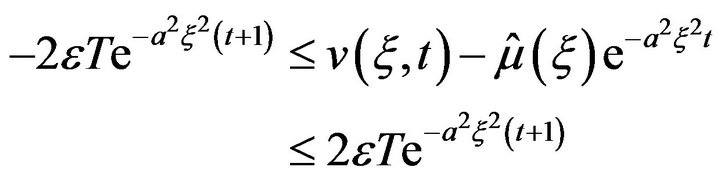 (12)
(12)
where 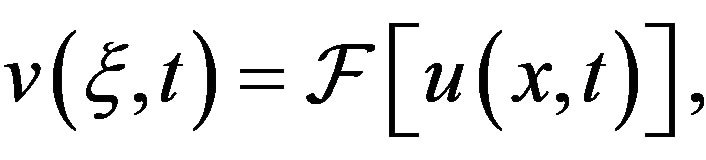 and
and  In Example 1, we have established
In Example 1, we have established
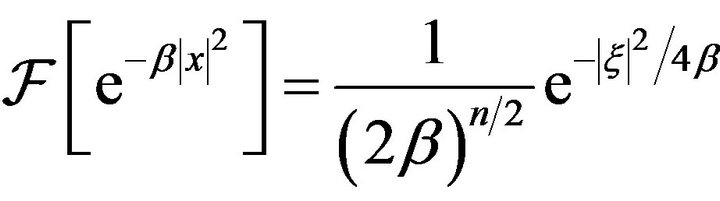 . Putting n = 1, and
. Putting n = 1, and , we obtain
, we obtain 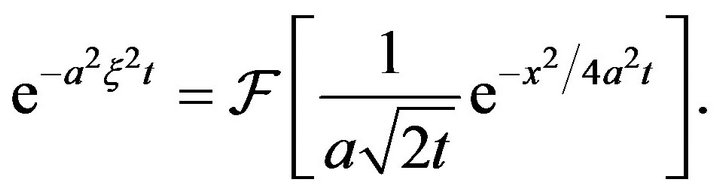
Now, Using the convolution theorem, from inequality (12) one has
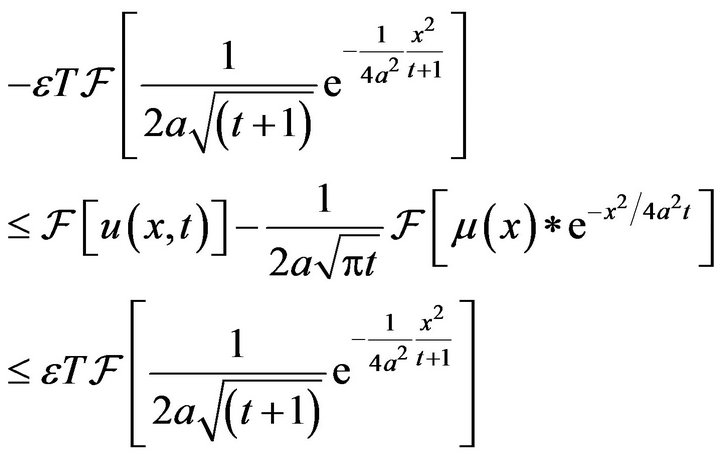
Applying inverse Fourier transform to the last inequality and using convolution theorem we have
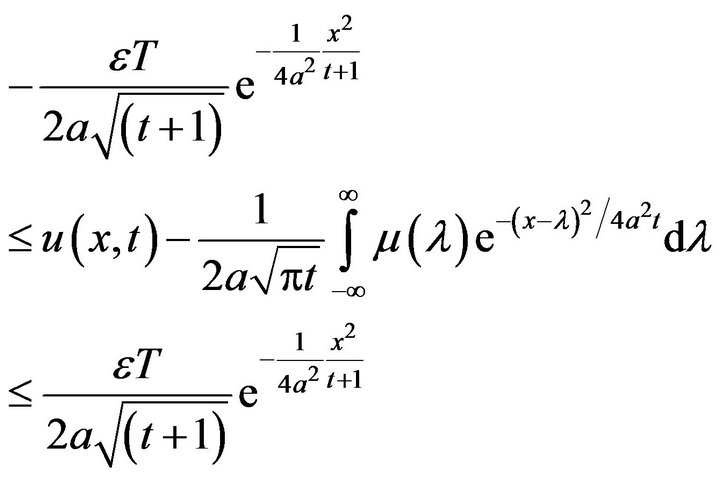
Let us take
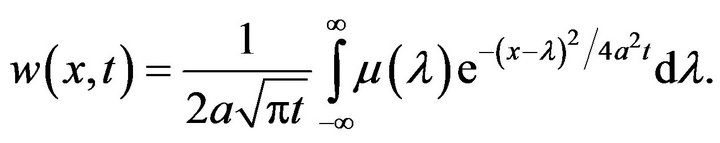 (13)
(13)
Applying arguments shown above to initial-value problem (1), (2), one can show that (13) is an exact solution of Equation (1).
To show that 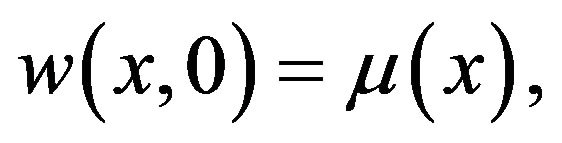 we put
we put 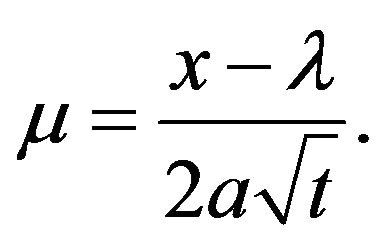 Then
Then 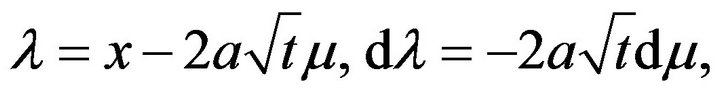 so that
so that
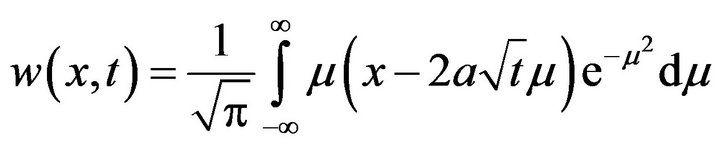
Hence, as  we find
we find
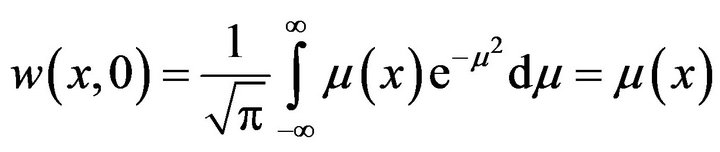
Therefore the initial value problem (1), (2) is stable in the sense of Hyers-Ulam-Rassias.
More generally, the following Theorem was established for the Hyers-Ulam-Rassias stability of heat equation in 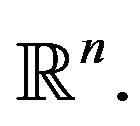
Theorem 3 If  then the initial value problem (3), (4) is stable in the sense of Hyers-Ulam-Rassias.
then the initial value problem (3), (4) is stable in the sense of Hyers-Ulam-Rassias.
Proof. Let
Let 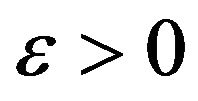 and
and 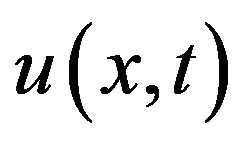 be an approximate solution of the initial value problem (3), (4). We will show that there exists a function
be an approximate solution of the initial value problem (3), (4). We will show that there exists a function 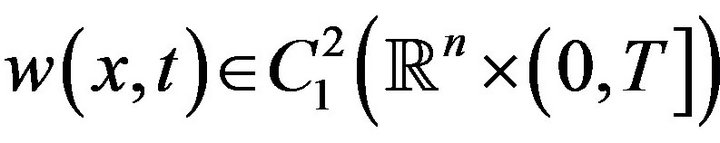 satisfying the Equation (3) and the initial condition (4) such that
satisfying the Equation (3) and the initial condition (4) such that
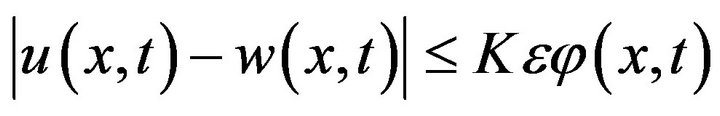
Taking 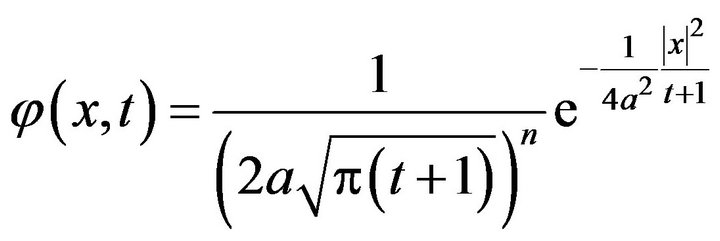 then from the inequality (5), we have
then from the inequality (5), we have
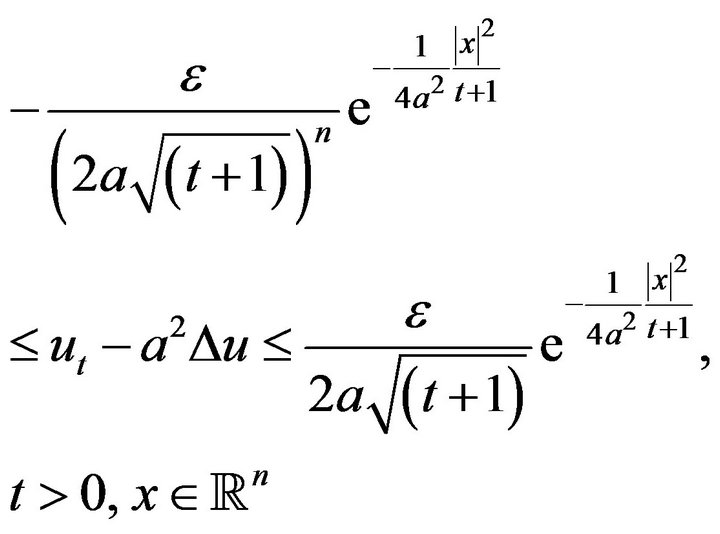 (14)
(14)
Applying Fourier Transform to inequality (14), we get
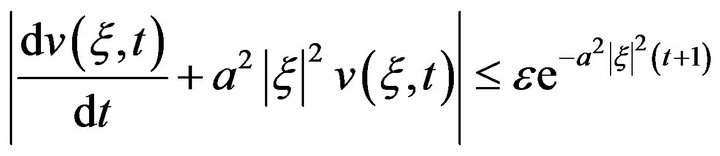
Or, equivalently
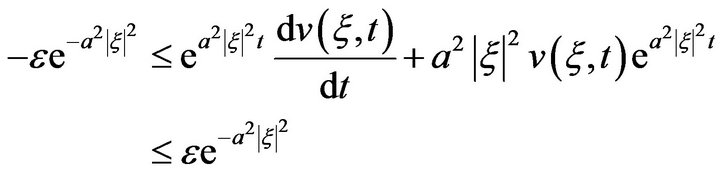
Integrating the inequality from 0 to 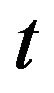 we obtain
we obtain
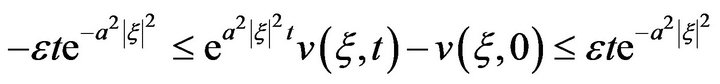
From which it follows
 (15)
(15)
where 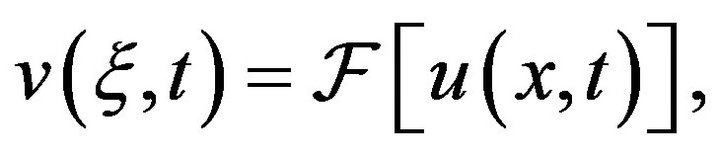 and
and 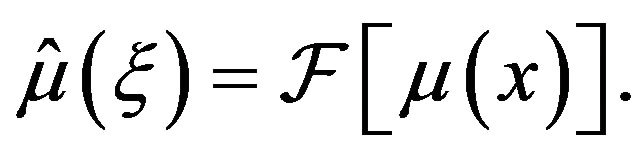
Using Example 1, we find that
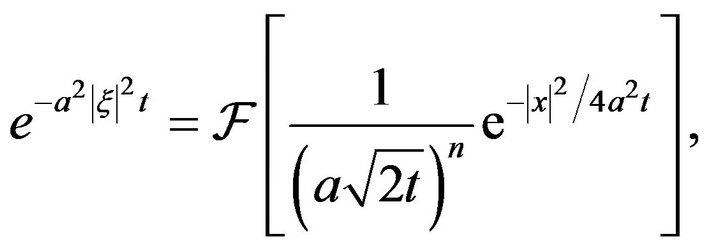
and applying the convolution theorem, from inequality (15) one has

By applying the inverse Fourier transform to the last inequality, and then using convolution theorem we get
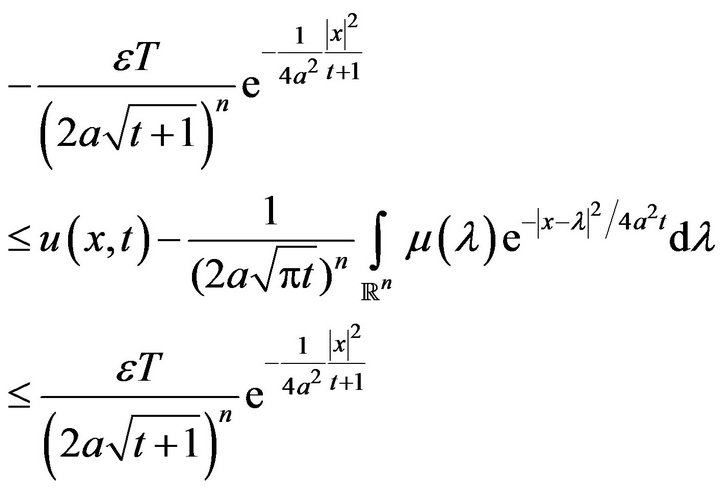
Now, let us take
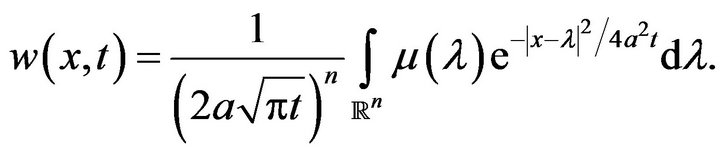 (16)
(16)
One can find that (16) is a solution of Equation (3).
To show that 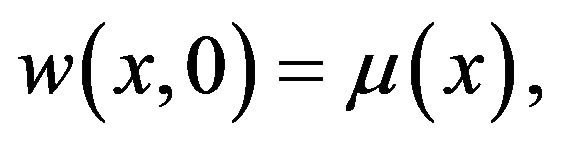 we put
we put  Then
Then 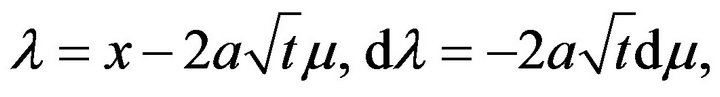 so that
so that
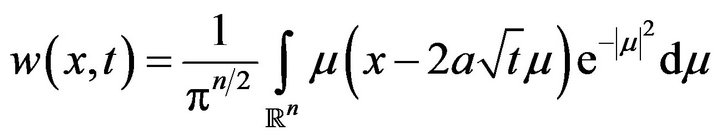
Hence as  we obtain
we obtain
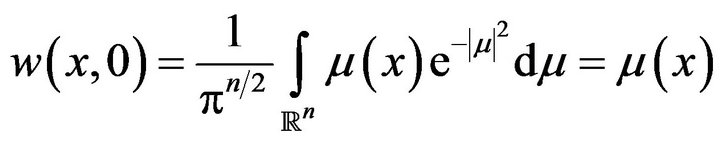
since 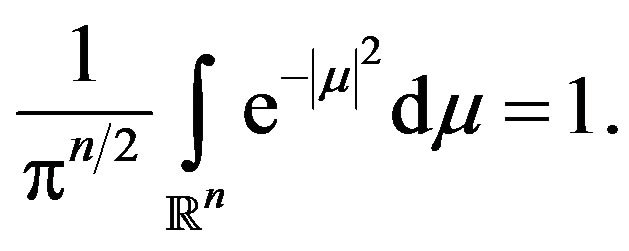
Hence the initial value problem (3), (4) is stable in the sense of Hyers-Ulam-Rassias.
Theorem 4 Suppose that 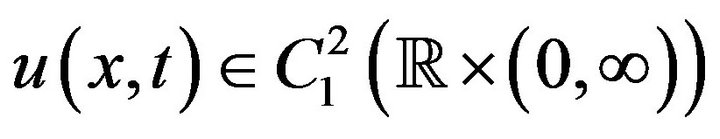 satisfies the inequality (5) with the initial condition
satisfies the inequality (5) with the initial condition 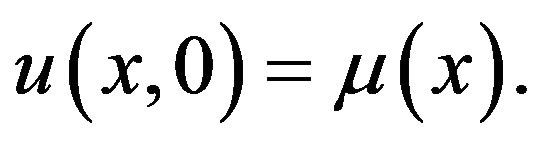 Then the the initial-value problem (1), (2) is stable in the sense of HURG.
Then the the initial-value problem (1), (2) is stable in the sense of HURG.
Proof. Indeed, if we take 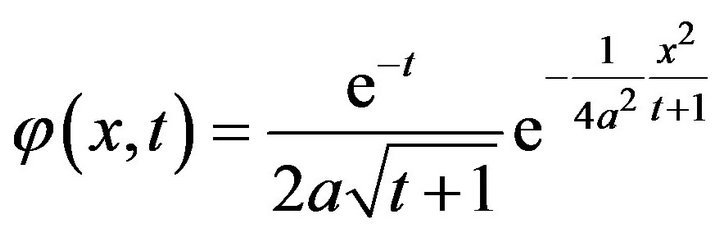 then from the inequality (5), we have
then from the inequality (5), we have
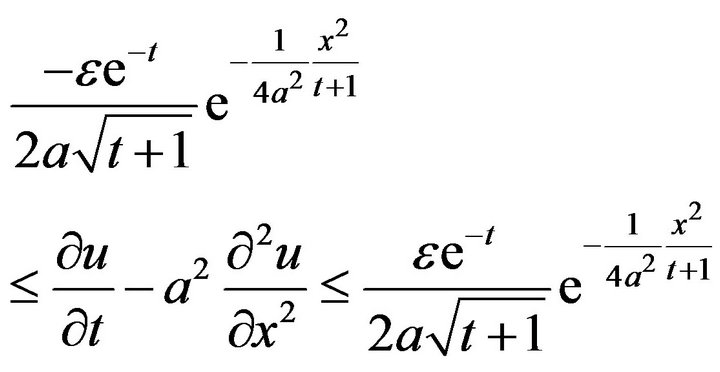 (17)
(17)
Applying Fourier Transform to inequality (17), we get
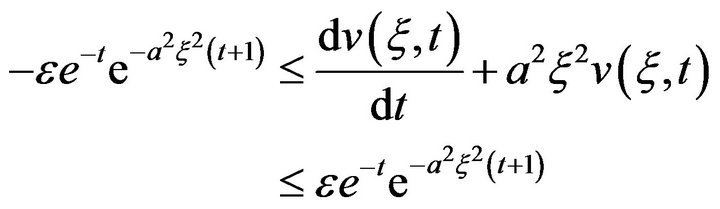
Now, by applying the same argument used above, we obtain
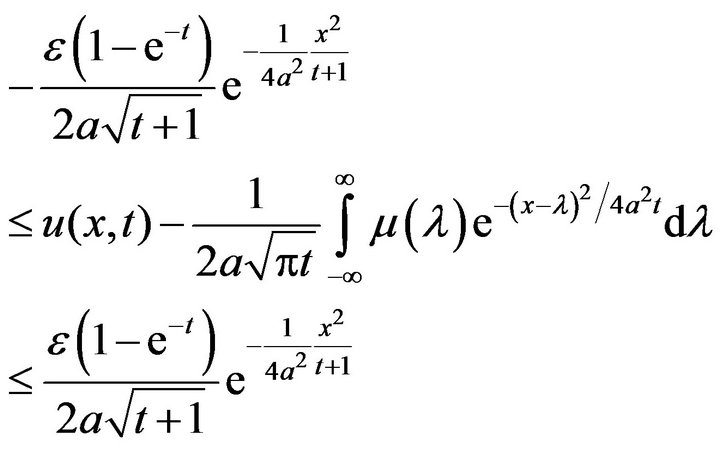 (18)
(18)
One takes
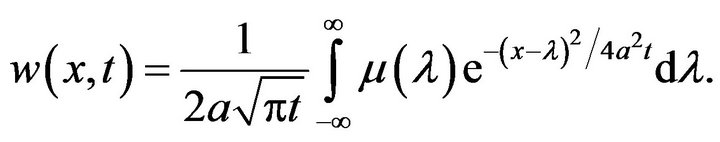
as a solution of initial-value problem (1), (2).
Therefore the initial value problem (1), (2) is stable in the sense of HURG.
Corollary 1 Suppose that 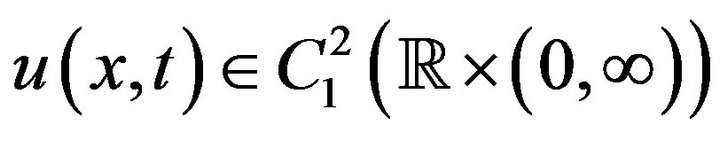 satisfies the inequality (5) with the initial condition (2). Then the the initial-value problem (1), (2) is asymptotically stable in the sense of Hyers-Ulam-Rassias.
satisfies the inequality (5) with the initial condition (2). Then the the initial-value problem (1), (2) is asymptotically stable in the sense of Hyers-Ulam-Rassias.
Proof. It follows from Theorem 4, and letting  in (18), we infer that
in (18), we infer that 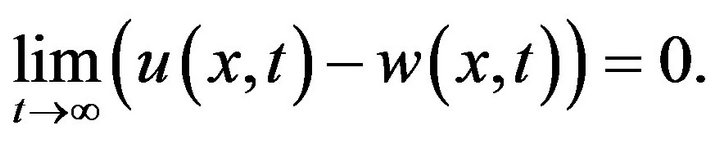
Remark Using similar arguments it can be shown that the initial-value problem (3), (4) is asymptotically stable in the sense of HURG.
Example 2 We find the solution of the Cauchy problem
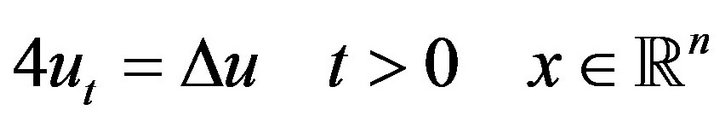 (19)
(19)
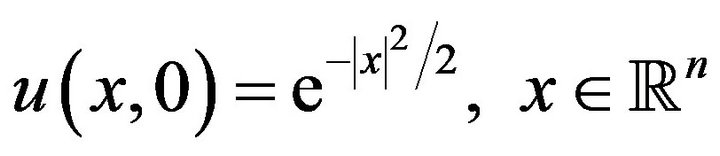 (20)
(20)
Applying the same argument used in the proof of the Theorem 4 to the inequality
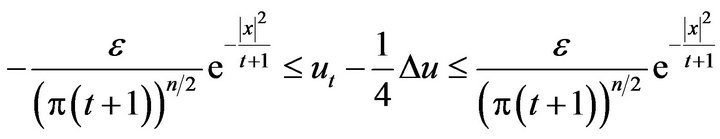
we get
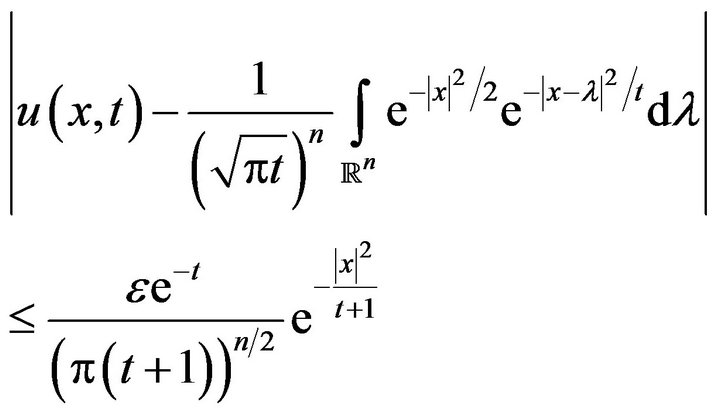 (21)
(21)
One can show that the function
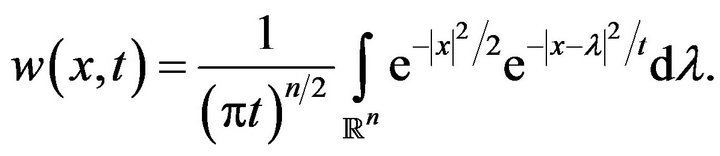 (22)
(22)
is a solution of the problem (19), (20).
Or, equivalently
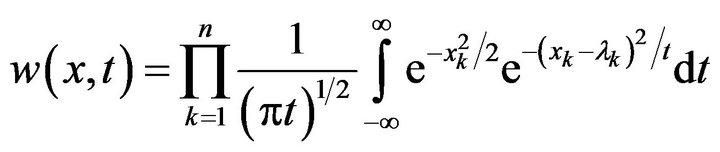
Now, using the change of variables
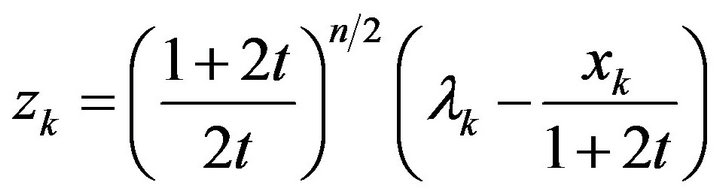 in the integral
in the integral
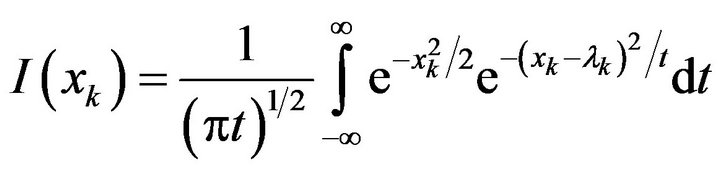
we obtain the integral
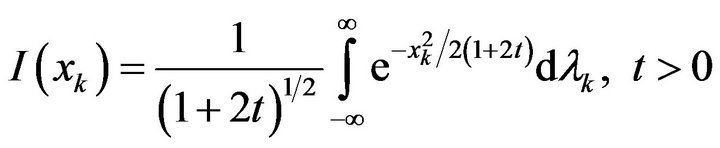
Therefore we have
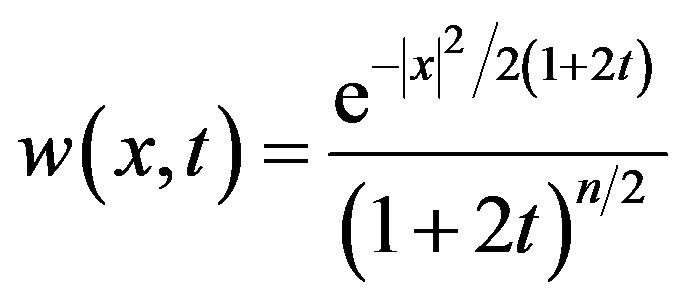 (23)
(23)
It is clear that 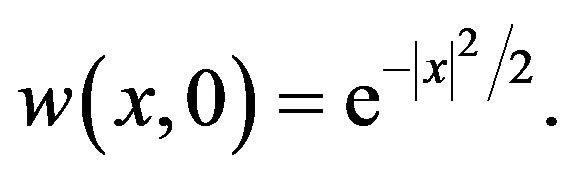
Hence, from (21) and (23) we get
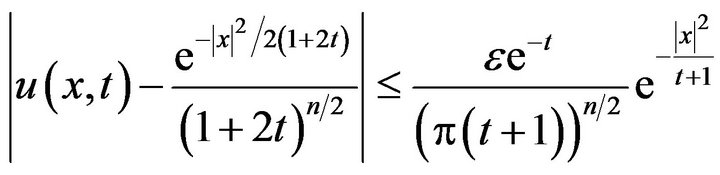
Hence the initial value problem (19), (20) is stable in the sense of HURG. Moreover, since
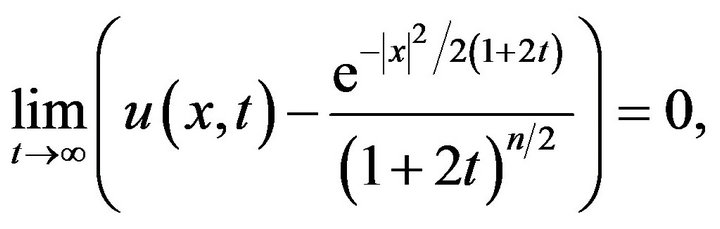 then problem (19), (20) is asymptotically stable in the sense of HURG.
then problem (19), (20) is asymptotically stable in the sense of HURG.
3. A Modified Hyers-Ulam-Rassias Stability for Problem of Heat Propagation in a Finite Rod
In this section we show how Laplace transform method can be used to esatblish the Hyers-Ulam-Rassias-Gavruta (HURG) stability of solution for heat equation
 (24)
(24)
with the initial condition
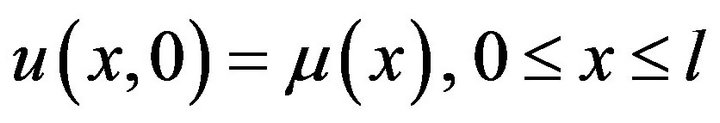 (25)
(25)
and the boundary conditions
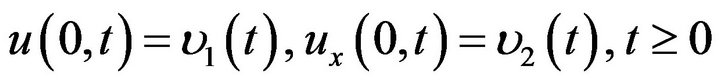 (26)
(26)
where 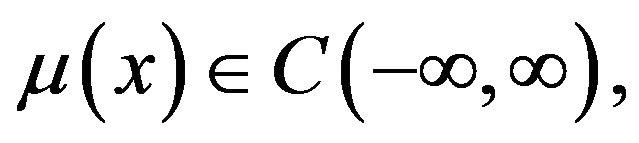 and
and
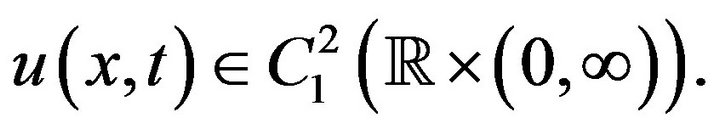
We introduce the notation
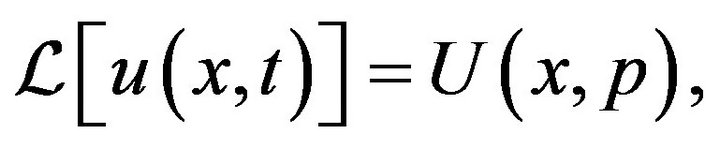
where 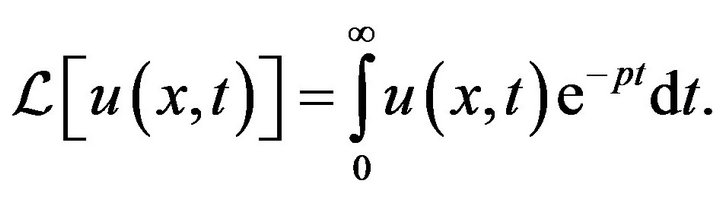
Theorem 5 If 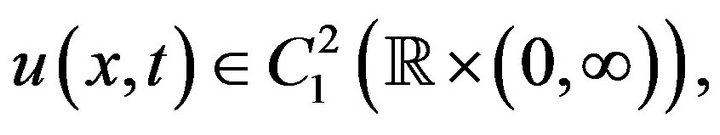 then the initial-boundary value problem (24-26) is stable in the sense of Hyers-Ulam-Rassias.
then the initial-boundary value problem (24-26) is stable in the sense of Hyers-Ulam-Rassias.
Proof. Given 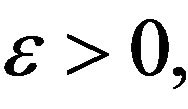 Suppose
Suppose 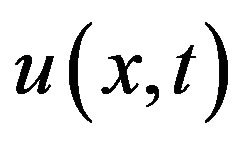 is an approximate solution of the initial value problem (24)-(26). We show that there exists an exact solution
is an approximate solution of the initial value problem (24)-(26). We show that there exists an exact solution 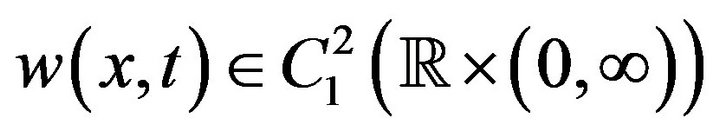 satisfying the Equation (24) such that
satisfying the Equation (24) such that
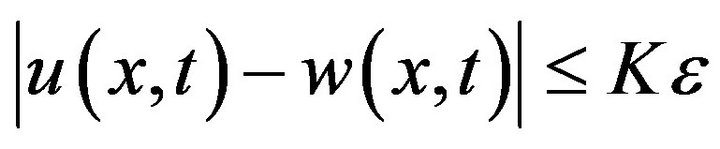
where 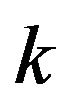 is a constant that does not explicitly depend on
is a constant that does not explicitly depend on 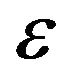 nor on
nor on 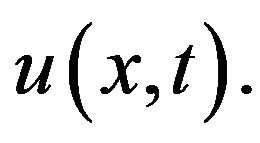
From the definition of Hyers-Ulam stability we have
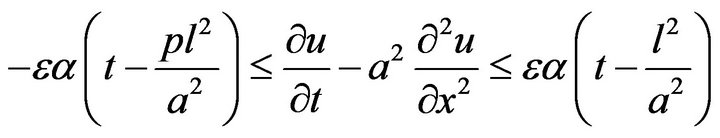 (27)
(27)
where 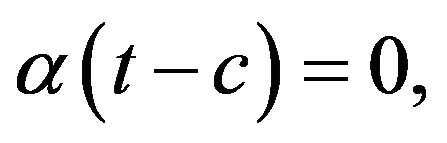 for t < c and
for t < c and 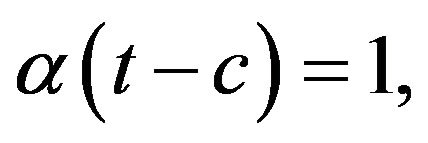 for t > c,
for t > c,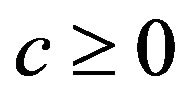 .
.
By applying the Laplace transform to (26), (27) we obtain
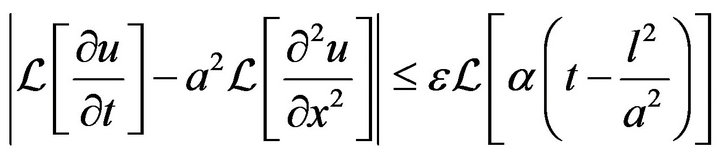 (28)
(28)
and
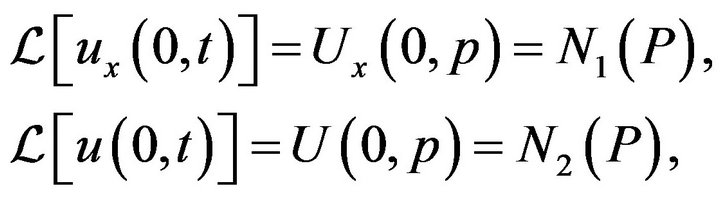
Assuming the operation of differentiation with respect to 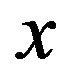 is interchangeable with integration with respect to
is interchangeable with integration with respect to 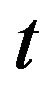 in Laplace transform, we will get
in Laplace transform, we will get
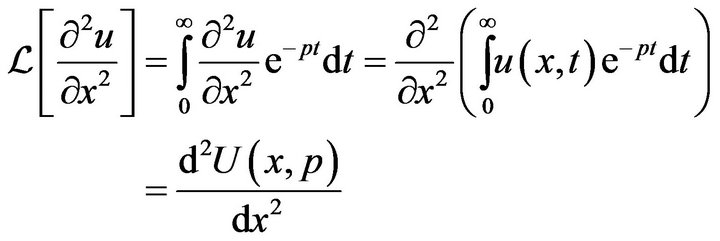 (29)
(29)
We also have
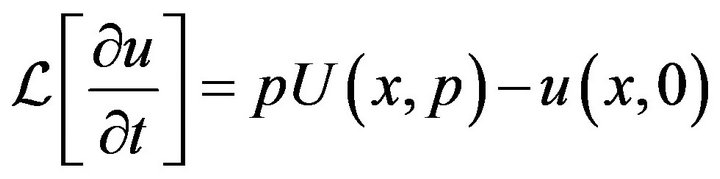 (30)
(30)
From the inequality (28), and using (29), (30) it follows that
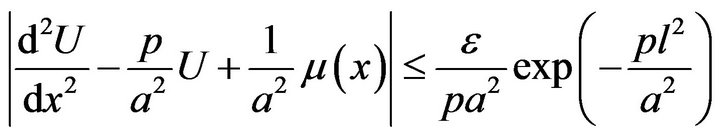 (31)
(31)
Integrating twice inequality (31) from 0 to x, we have
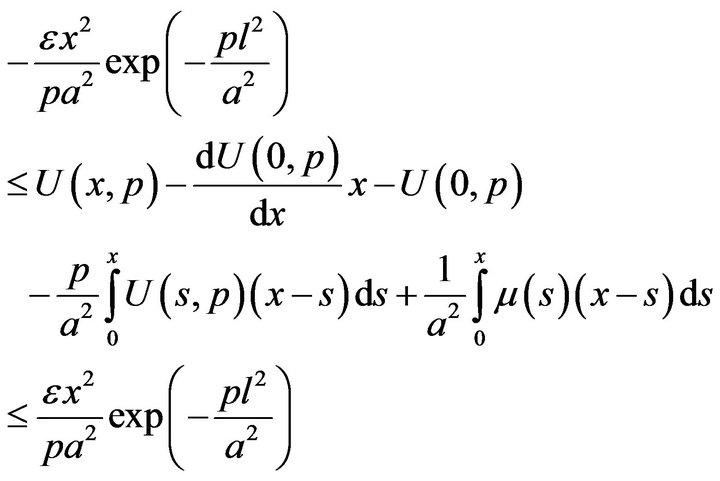
with the boundary conditions
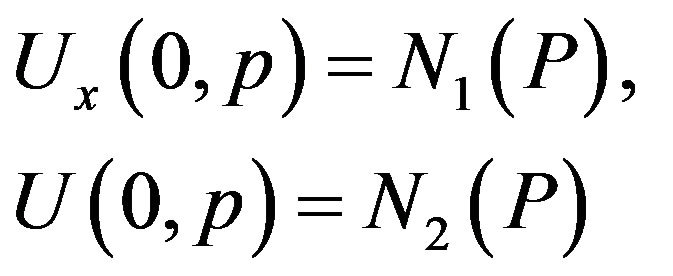 (32)
(32)
One can easily verify that the function 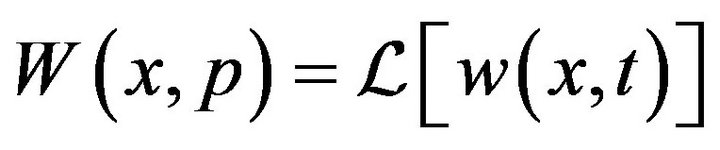 which is given by
which is given by
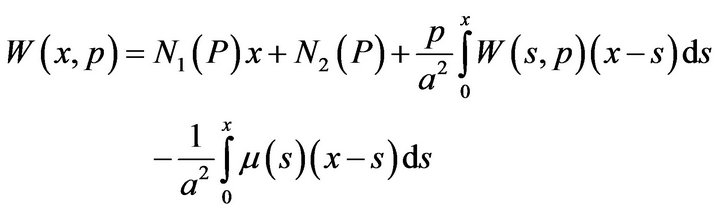
has to satisfy the the equation
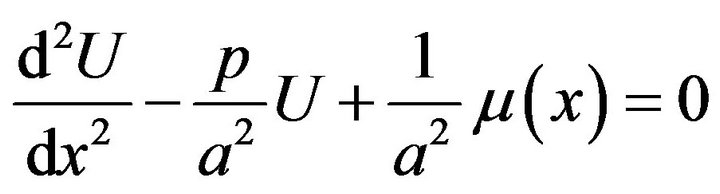
with boundary condition (32).
Now consider the difference 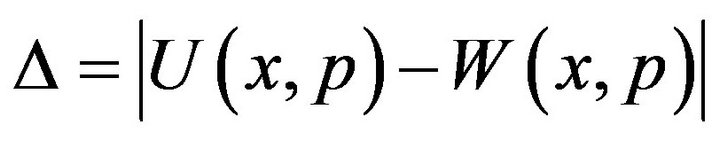
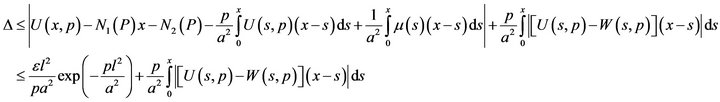
Using Gronwall’s inequality, we get the estimation
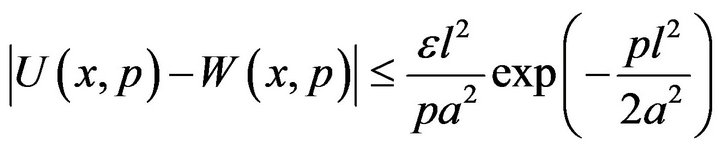
Or, equivalently
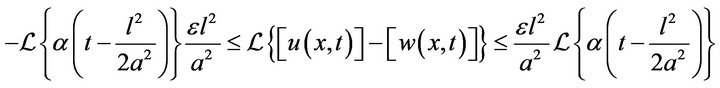
Consequently, we have
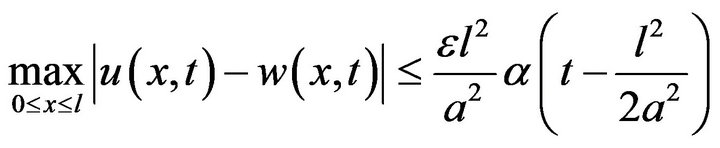
Hence the initial-boundary value problem (24)-(26) is stable in the sense of HURG.
Example 3 Consider the problem
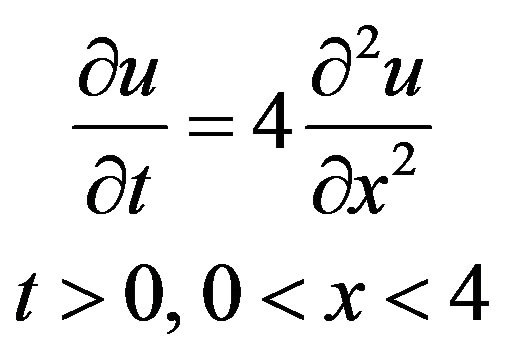 (33)
(33)
with the initial condition
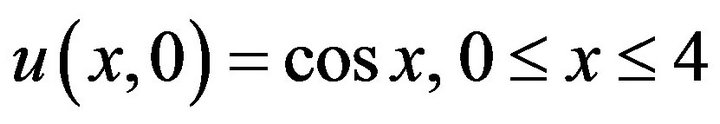 (34)
(34)
with the boundary conditions
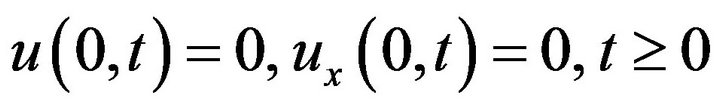 (35)
(35)
By the definition of HURG stability we have
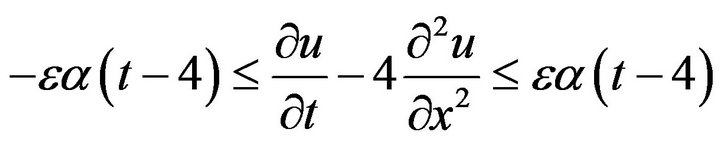 (36)
(36)
By applying the Laplace transform to ( 36) we obtain
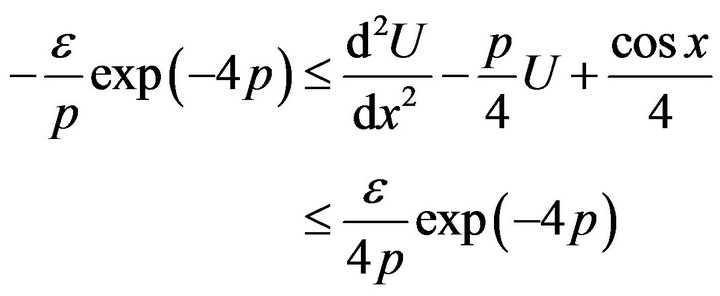 (37)
(37)
Integrating twice inequality (37) from 0 to x, we have

with the boundary conditions
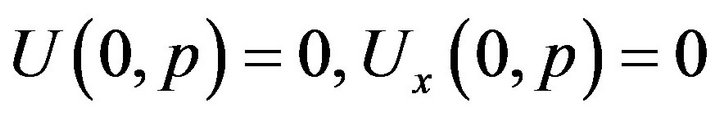
It is easily to verify that the function
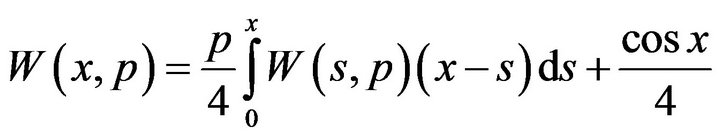
satisfies the boundary value problem
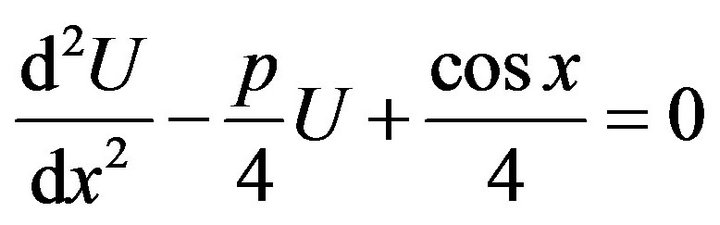
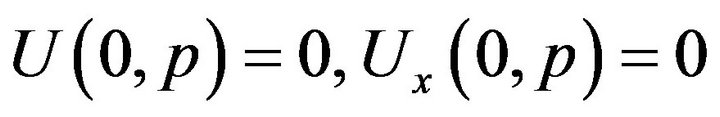
Now consider the difference

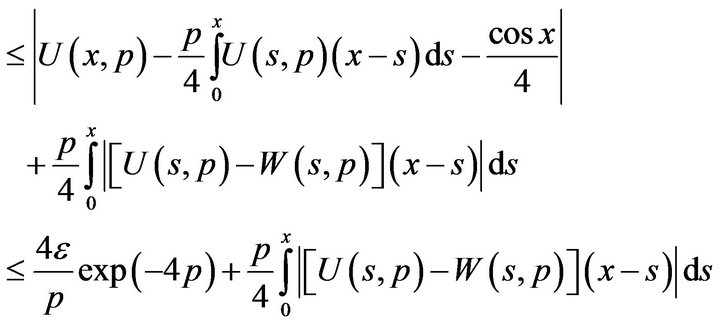
Hence, we get the estimation
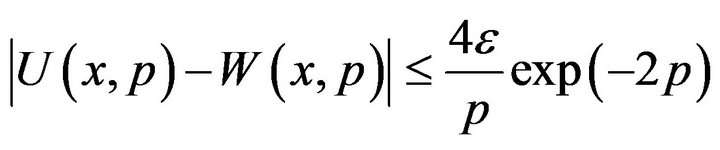
Or, equivalently
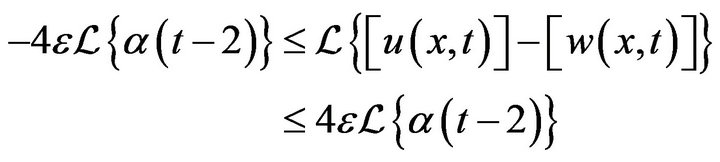
Consequently, we have
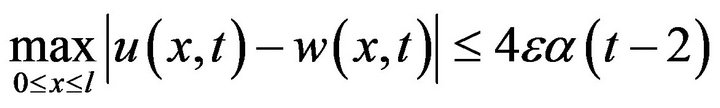
Hence the initial-boundary value problem (33)-(35) is stable in the sense of HURG.
REFERENCES
- D. H. Hyers, “On the Stability of the Linear Functional Equation,” Proceedings of the National Academy of Sciences of the United States of America, Vol. 27, No. 4, 1941, pp. 222-224. doi:10.1073/pnas.27.4.222
- T. M. Rassias, “On the Stability of the Linear Mapping in Banach Spaces,” Proceedings of the American Mathematical Society, Vol. 72, No. 2, 1978, pp. 297-300. doi:10.1090/S0002-9939-1978-0507327-1
- P. Gavruta, “A Generalization of the Hyers-Ulam-Rassias Stability of Approximately Additive Mappings,” Journal of Mathematical Analysis and Applications, Vol. 184, No. 3, 1994, pp. 431-436. doi:10.1006/jmaa.1994.1211
- S. M. Jung, “On the Hyers-Ulam-Rassias Stability of Approximately Additive Mappings,” Journal of Mathematical Analysis and Applications, Vol. 204, No. 1, 1996, pp. 221-226. doi:10.1006/jmaa.1996.0433
- S. M. Jung, “Hyers-Ulam-Rassias Stability of Functional Equations in Mathematical Analysis,” Hadronic Press, Palm Harbor, 2001.
- T. Miura, S.-E. Takahasi and H. Choda, “On the HyersUlam Stability of Real Continuous Function Valued Differentiable Map,” Tokyo Journal of Mathematics, Vol. 24, No. 2, 2001, pp. 467-476. doi:10.3836/tjm/1255958187
- C. G. Park, “On the Stability of the Linear Mapping in Banach Modules,” Journal of Mathematical Analysis and Applications, Vol. 275, 2002, pp. 711-720. doi:10.1016/S0022-247X(02)00386-4
- C. G. Park, “Homomorphisms between Poisson JC*-Algebras,” Bulletin of the Brazilian Mathematical Society, Vol. 36, No. 1, 2005, pp. 79-97. doi:10.1007/s00574-005-0029-z
- C. G. Park, Y.-S. Cho and M. Han, “Functional Inequalities Associated with Jordan-Von Neumanntype Additive Functional Equations,” Journal of Inequalities and Applications, Vol. 2007, 2007, Article ID: 41820.
- K.-W. Jun and Y.-H. Lee, “A Generalization of the HyersUlam-Rassias Stability of the Pexiderized Quadratice Quations,” Journal of Mathematical Analysis and Applications, Vol. 297, No. 1, 2004, pp. 70-86. doi:10.1016/j.jmaa.2004.04.009
- C. Alsina and R. Ger, “On Some Inequalities and Stability Results Related to the Exponential Function,” Journal of Inequalities and Applications, Vol. 2, No. 4, 1998, pp. 373-380.
- E. Takahasi, T. Miura and S. Miyajima, “On the HyersUlam Stability of the Banach Space-Valued Differential Equation
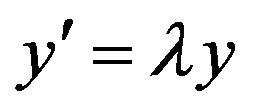 ,” Bulletin of the Korean Mathematical Society, Vol. 39, No. 2, 2002, pp. 309-315. doi:10.4134/BKMS.2002.39.2.309
,” Bulletin of the Korean Mathematical Society, Vol. 39, No. 2, 2002, pp. 309-315. doi:10.4134/BKMS.2002.39.2.309 - T. Miura, S. Miyajima and S.-E. Takahasi, “A Characterization of Hyers-Ulam Stability of First Order Linear Differential Operators,” Journal of Mathematical Analysis and Applications, Vol. 286, No. 1, 2007, pp. 136-146. doi:10.1016/S0022-247X(03)00458-X
- S. M. Jung, “Hyers-Ulam Stability of Linear Differential Equations of First Order,” Journal of Mathematical Analysis and Applications, Vol. 311, No. 1, 2005, pp. 139- 146. doi:10.1016/j.jmaa.2005.02.025
- G. Wang, M. Zhou and L. Sun, “Hyers-Ulam Stability of Linear Differential Equations of First Order,” Applied Mathematics Letters, Vol. 21, No. 10, 2008, pp. 1024- 1028. doi:10.1016/j.aml.2007.10.020
- Y. Li, “Hyers-Ulam Stability of Linear Differential Equations,” Thai Journal of Mathematics, Vol. 8, No. 2, 2010, pp. 215-219.
- Y. Li and Y. Shen, “Hyers-Ulam Stability of Nonhomogeneous Linear Differential Equations of Second Order, Internat,” Journal of Mathematical Sciences, Vol. 2009, 2009, Article ID: 576852.
- P. Gavruta, S. Jung and Y. Li, “Hyers-Ulam Stability for Second-Order Linear Differential Equations with Boundary Conditions,” Electron Journal of Differential Equations, Vol. 2011, No. 80, 2011, pp. 1-7.
- S. M. Jung, “Hyers-Ulam Stability of Linear Partial Differential Equations of First Order,” Applied Mathematics Letters, Vol. 22, No. 1, 2009, pp. 70-74. doi:10.1016/j.aml.2008.02.006
- M. E. Gordji, Y. J. Cho, M. B. Ghaemi and B. Alizadeh, “Stability of the Exact Second Order Partial Differential Equations,” Journal of Inequalities and Applications, Vol. 2011, 2011, Article ID: 306275. doi:10.1186/1029-242X-2011-81
- N. Lungu and C. Craciun, “Ulam-Hyers-Rassias Stability of a Hyperbolic Partial Differential Equation,” ISRN Mathematical Analysis, Vol. 2012, 2012, Article ID: 609754.
- L. C. Evans, “Partial Differential Equations,” 2nd Edition, Graduate Studies in Mathematics, V19 AMS, 2010.

