ABSTRACT

In this paper, three types of modeling of diffusion equations for price changing of commodity are studied. In which, the partial derivatives of price of commodity respected to time on the left hand side are integer-derivative, fractal derivative, and fractional derivative respectively; while just a second order derivative respected to space is considered on the right hand side. The solutions of these diffusion equations are obtained by method of departing variables and initial boundary conditions, by translation of variables, and by translation of operators. The definitions of order of commodity x and the distance between commodity x_i and x_j are defined as [1]. Examples of calculation of price of pork, beef and mutton mainly due to price raising of pork in 2007-07 to 2008-02 in China are given with same market data as [1]. Conclusion is made.

1. Introduction

Control and preventing inflation is a focus goal in the world. It is also an important task of macro-control in China in 2008 and 2011. Now, the price problem is widely concerned in China. However, the solutions of the problem are more on practice monitoring and control (investigation, statistics, monitoring, etc.), rather than on theoretical study. As the theoretical research, focuses are more on qualitative analysis, or on statistic probability rather than on quantitative analysis. The core of solutions is on policy making, price reform, price system, and price forming, so far no paper on price diffusion is found in literature. This paper extends the author’s paper [1], in which the diffusion of price changing is quantitatively analyzed by a partial differential equation based on analogy of heat diffusion equation explained by Newton’s second law via “time-space exchanging”, to a fractal and fractional diffusion equations.

Fractal or fractional calculus is a branch of mathematical analysis that studies differential operators or integral operators with real number power (or order) or complex number of power. Which have been used to improve the modeling accuracy of phenomena in many fields like heat conduction, fluid flow in discontinuous porous media, relaxation in viscoelastic materials, diffusion of drug molecules in living tissues, dynamics of seismic waves, automatic control, and finance, etc. (p.1 of [2]).

As for the diffusion equation modeling by fractal and fractional derivatives, it has been studied in field of visco-elasticity [3], however, no paper concerned diffusion equation modeling with fractal and fractional derivative used in price changing of commodity has been found. This paper, we extend the study of heat diffusion equation for price changing of commodity [1] to modeling with fractal and fractional derivative form. In Section 2, definitions of fractal and fractional derivative are given. In Section 3, three types of diffusion equation with integer-derivatives, fractal derivative and fractional derivative are given, and the corresponding solutions haven been found by method of departing variables, by transform of variables, and by transform of operators respectively. In Section 4, for convenience to readers, the definition of spatial 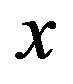-axes of commodity and the distance between commodity 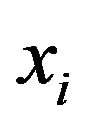and commodity stated in [1] are repeated. And a correction of (Equation (12) of [1], miss-typed as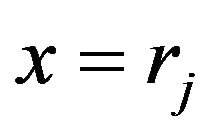) is made. In Section 5, examples of calculation of price of pork, beef and mutton mainly due to price raising of pork in 2007-07 to 2008-02 in China are given with same data as

[1]. Finally, Conclusion is made.

2. Definition of Fractal Derivative and Fractional Derivative

Definition of fractal derivative (same as Ref. [3]):

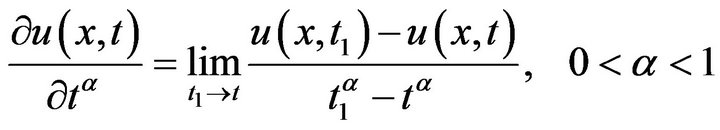, (2-1)

And the definition of fractional derivative (same as (3.10) of Ref. [2])

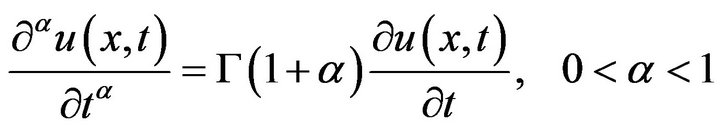, (2-2)

(2-2) is called “fractional derivative of order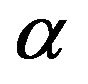”, where is Gamma function.

3. Three Types of Modeling on Diffusion Equation for Price Changing of Commodity with Integer-Derivatives, Fractal Derivative, and Fractional Derivative, and Their Solutions

For simplicity, three types of modeling on diffusion equation for price changing of commodity with integer-derivatives, with fractal derivative and with fractional derivative are studied herein, i.e.,

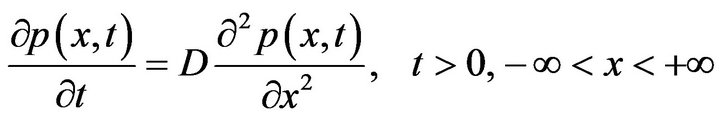, (3-1)

, (3-2)

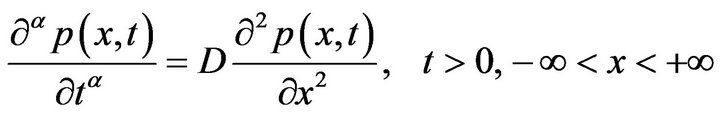, (3-3)

where, is a diffusion coefficient, and denotes the price of commodity located on at time.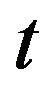

3.1. The Solution of (3-1)

Equation (3-1) is exactly the form of one-dimensional heat diffusion equation:

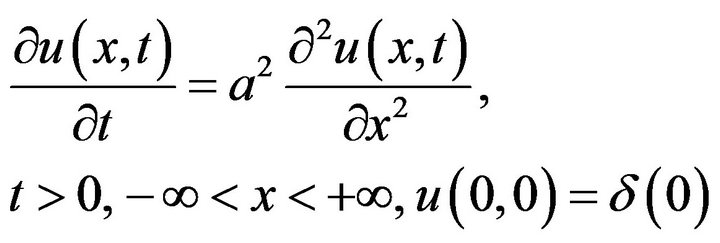(3-4)

Problem (3-4) is called Cauchy problem, its fundamental solution is well-known [4]. However, the boundary condition of (3-1) is herein somewhat deferent from (3-4), e.g., , while 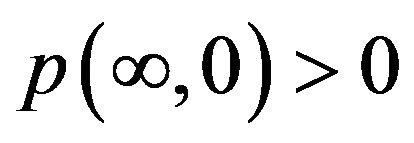since the price of any commodity always greater than zero. So that for convenience in calculation, we prefer employ the solution of (3-1) found in [1] by method of departing variables and is shown in following:

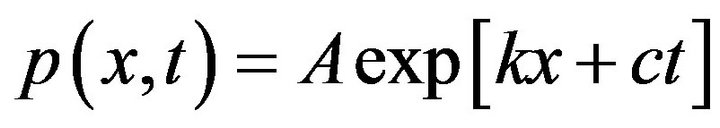, (3-5)

where, , 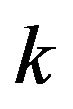are constants, and are determined by initial boundary conditions, i.e.1) (3-6)

(3-7)

For practical calculation, the market data provided is announced per month, so that the unit time used for price changing is 1.

3)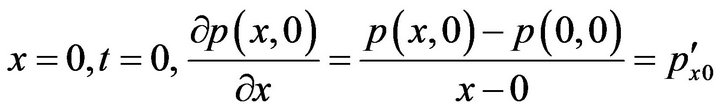 (3-8)

Substituting (3-6)-(3-8), into (3-5), we have

, (3-9)

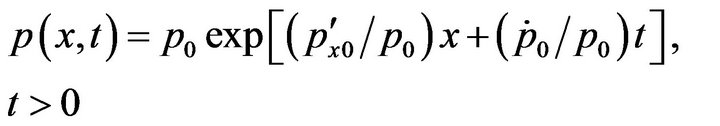(3-10)

Substituting (3-5) into (3-1), we have

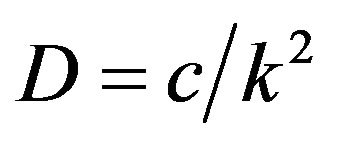, (3-11)

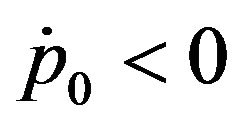Note that the constant is positive. If, i.e., the changing rate of price changing is negative (price falling down), then, the last term of (3-5) should be changed to.

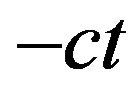3.2. The Solution of (3-2)

Translation of variables, let

, (3-12)

Then, (3-2) becomes to the form of (3-1), and the solution of (3-1) is (3-10), so that substituting (3-12) into the corresponding term of (3-10), we get the solution of (3-2) as

(3-13)

3.3. The Solution of (3-3)

Translation of operators, according to Equation (3.10) of [2], we have

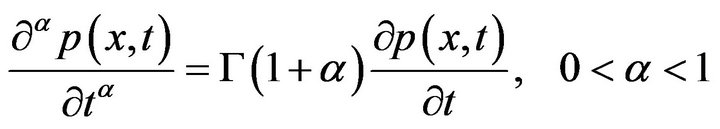, (3-14)

where is Gamma function. Substituting (3-14) into (3-3), then (3-3) reduces to

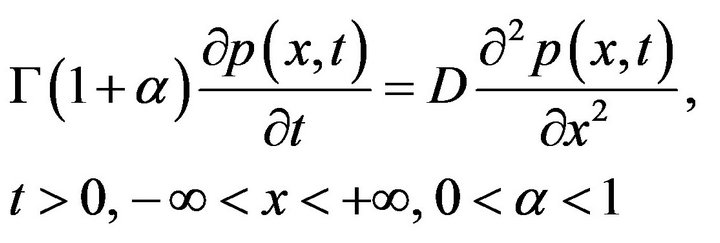(3-15)

(3-15) differs from (3-1) just a constant term, so the solution of (3-15) can be obtained from (3-10) by instead of by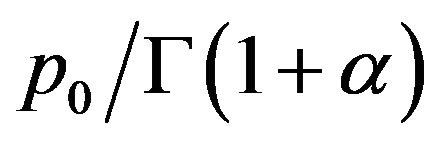, i.e.,

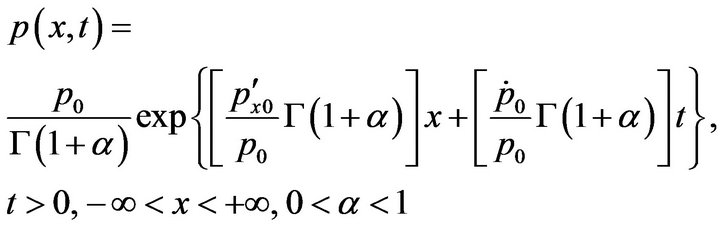(3-16)

3.4. Comparing Solutions (3-13), (3-16) with (3-10)

As a standard, the solution (3-10) of diffusion equation with integer-derivatives (3-1) is used for comparing. The following results are obvious.

1) The difference between (3-13) and (3-10) is just on time 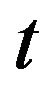instead of;

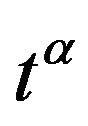2) The difference between (3-16) and (3-10) is just on the parameter instead of.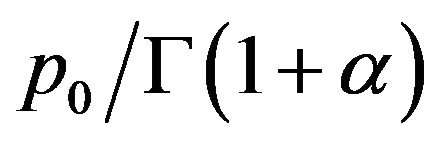

The partial derivative is viewed as a ratio, in which the dimension of denominator is viewed as “time”; the dimension of numerator is viewed as “space”, then the above results show that the fractal derivative changes the ratio of space/time of the standard case; while the fractional derivative does not change the ratio space/time of the standard case, but enlarging or reducing the scale of the space/time ratio of the standard case. So that if the market data does not suited for description by standard modeling, then, using a fractional modeling is no use for improving the accuracy.

4. Definition of Order of Commodities and Distance between Commodities

For the convenience to readers, we repeat the definition of order of commodities stated in [1].

Definition

Let

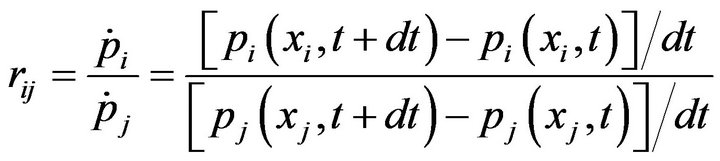, (4-1)

be the price relation degree (or dependent degree) of commodity 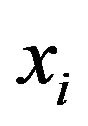on commodity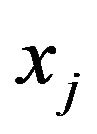. Note that 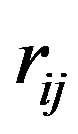is defined to be determined just by the property of commodity and shown to be fixed in a relative equilibrium state, so that it is independent of time, or it is independent at least in a time interval. For convenience of practical calculation, differential calculation is replaced by difference calculation, so (4-1) is rewritten as

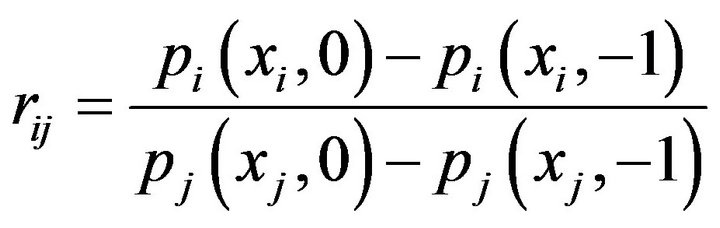, (4-2)

where the time 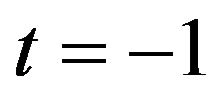and represent the time before and at (or after) the price changing due to a source at respectively.

If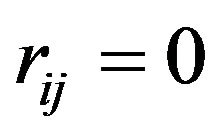, i.e., the price of commodity 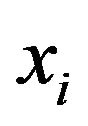does not changed due to the source of price changing at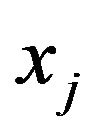, which means that is no related to.

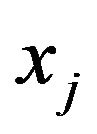From (4-2), we have

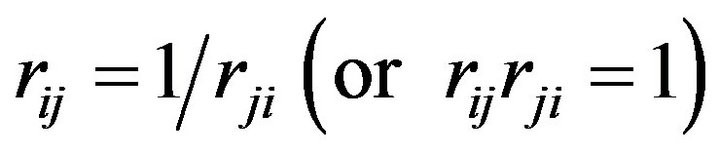(4-3)

(4-4)

Now, we define the order of commodity 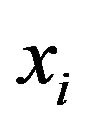by price relation degree.

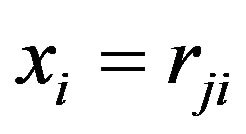, (4-5)

No loss of generality, we let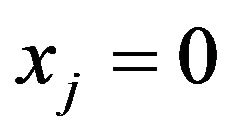, i.e., let the source of price changing 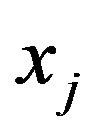be located at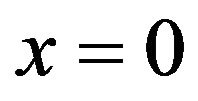. Since 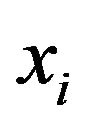is determined by one parameter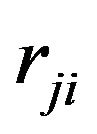, and 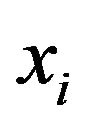can be any commodity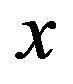, i.e., the subscript 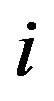can be removed, so the 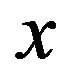coordinate is one-dimensional.

Now we make a correction of [1], where Equation (12) of [1] is mistyped, it should be stated as (4-5), i.e.,

,        (4-5)’

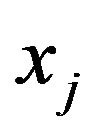We also define the “distance” between commodity and commodity by

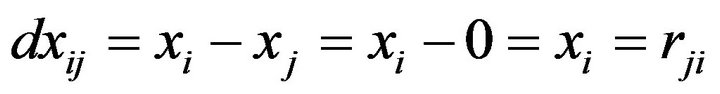, (4-6)

Here, we use the price relation degree to define the distance between two commodities and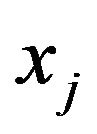. Original commodity and commodity 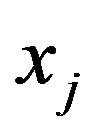are signs of commodity, they have no order. However, once we have introduced the concept of price relation degree to define the order of commodity and set up the definition of distance, then we can make use of calculus for our calculation.

5. Examples of Calculation of Price of Pork, Beef and Mutton Mainly Due to Price Raising of Pork in 2007-07 to 2008-02 in China Are Given with Same Data as [1]

The typical example of one source of diffusion is the food price rising mainly due to the price of pork from 2007-07 to 2008-02 in China. According to www.chinesenews.com.cn 2008-02-05 reported data from www. sdpc.gov.cn: The average price of pork is 14.31 (unit 1 Yuan/500g of RMB, same in the following) in 2008-01, with a 4.53% increase in price of 2007-12 (simplifying as 4.53% increase 2007-12, same in following); beef 14.85 (2008-01) a 9.51% increase (2007-12); mutton 16.26 (2008-01), a 4.36% increase (2007-12).

The above price rising is mainly caused by pork and transmitted to beef, mutton, etc.

5.1. Calculation by (3-10)

Pork,

Let 2008-01 be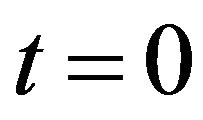, 2007-12 be, 2008-02 be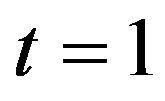. From the data, we have

,

,

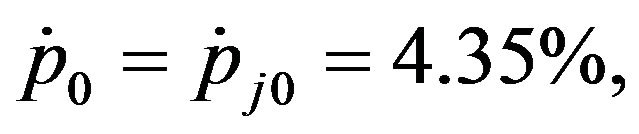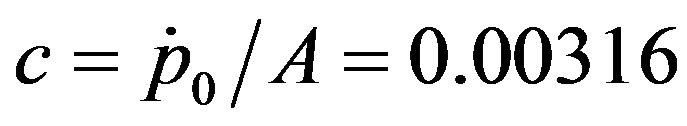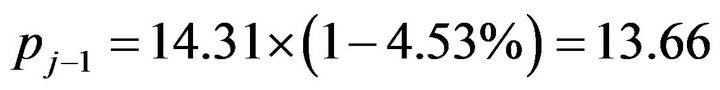
Substituting the above values into (3-10), we have

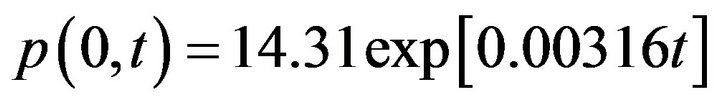, (5-1)

The prediction of price of pork in 2008-02 shall be (substituting 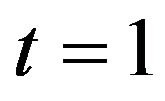into (5-1))

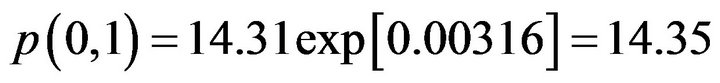, (5-2)

Beef: (without bone)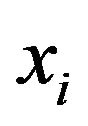

The price of 2007-12 is

the price ratio of beef to pork is

,

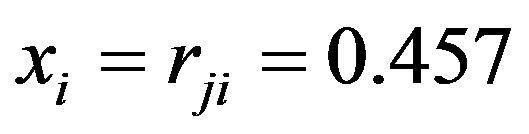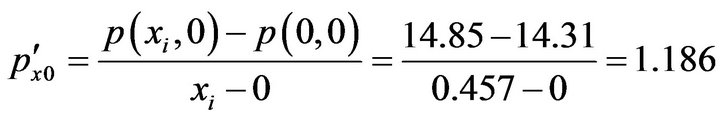, (5-3)

Substituting these values into (3-10), we have

Comparing with the data 14.85, the error is

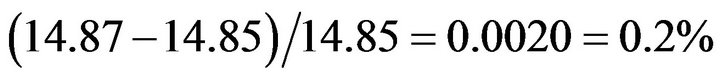
The predict price of beef in 2008-02 is

Mutton

The price of mutton in 2007-12 is

.

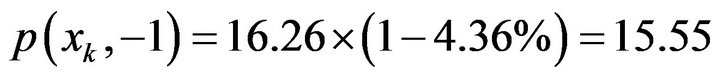The price of ratio of pork to mutton is

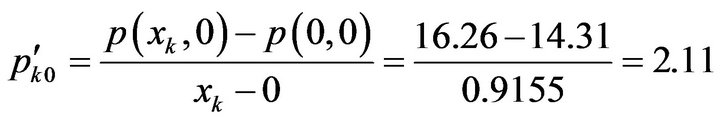, (5-4)

Substituting these values into (3-10), we get the predict price of mutton in 2008-01 is

(5-5)

Comparing with the price of mutton 16.26 in 2008-01, the error is

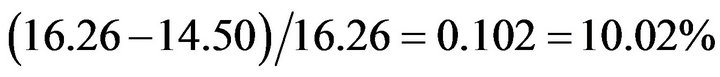
It is regretted that no statistic data of the same form of prices of pork, beef, and mutton as shown in 2008-02-05 can be found in China’s Official Net (the samples of statistic are changed from 36 cities to 70 cities since 2008- 03) so the above predictions of price can not be checked. However, the calculating price of beef in 2008-01 is checked to be accurate, and the price of mutton needs to improve.

5.2. Calculation by (3-13)

There is no more data can be used to improve the accuracy of calculation in (5-5). Perhaps (3-13) may be useful. By (3-13),

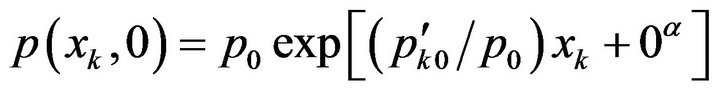, (5-6)

If we choose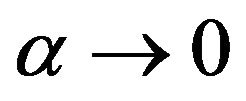, then 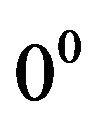is undetermined, it can be used to improve the difference calculation. Now 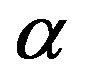is so chosen, such that, by (5-6).

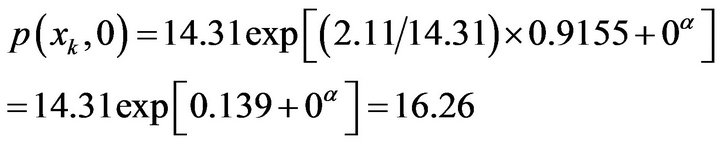(5-7)

i.e.,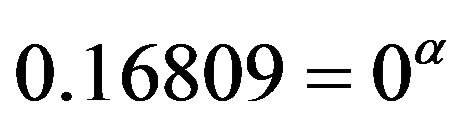. From a 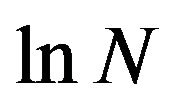table [4], we get.

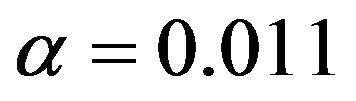6. Conclusions

Fractal derivative can be used to improve the accuracy of some calculation based on integer derivative model, while the fractional derivative model can not improve the accuracy of the integer derivative model.

Furthermore, on heat diffusion equation and diffusion with multiple source on shares may referred to [5,6].

REFERENCES