Applied Mathematics
Vol.4 No.8A(2013), Article ID:35080,7 pages DOI:10.4236/am.2013.48A005
Mathematical Modeling of the Efficiency Gadolinium Based Neutron Converters
Physical Technical Institute, Academy of Science of Republic of Tajikistan, Dushanbe, Tajikistan
Email: abdush_dj@mail.ru
Copyright © 2013 Djamshed Alievich Abdushukurov. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 8, 2013; revised May 8, 2013; accepted May 15, 2013
Keywords: Mathematic Modeling; Neutron Converter; Gadolinium
ABSTRACT
Procedures of mathematical modeling of thin solid-state converters of neutrons are described and converters a foil from natural gadolinium and its 157 isotopes are viewed. Algorithms of calculation of absorption of neutrons in a material of converters, probabilities formation of secondary electrons, probability of an exit of electrons from a material of the converter and efficiency of converters are given. Calculation is made for various thicknesses of converters, and various wavelengths of neutrons. The optimal converter thicknesses are chosen.
1. Introduction
Mechanisms for detecting neutrons in matter are based on indirect methods. Neutrons are neutral; they do not interact directly with the electrons in matter. The neutrons can cause a nuclear reaction. The process of neutron detection begins when neutrons, interacting with various nuclei, initiate the release of one or more charged particles. The products from these reactions, such as protons, alpha particles, gamma rays, electrons and fission fragments, can initiate the detection process. For detection of neutrally charged neutrons, it is necessary to use converters of neutron radiation. These converters will converse radiations of neutrons to the charged radiation, which can be in further detected with various detectors.
For an optimal choice of the converter foil material, the following properties should consider:
• A large neutron capture-cross section needed in order to achieve high detection efficiency with minimum foil thickness.
• The range of the neutron-induced charged primary particles should be large compared with the converter foil thickness.
• The converter material should possess small crosssection of activation. Daughter isotopes occurring as result of activation should not create the significant background.
• The γ-ray sensitivity of the detector material should be low.
Converters of neutron radiation play a determining role at designing detectors of neutron radiation. They define the key parameters of detectors, such as the efficiency, the spatial resolution and so on. Among the solid-state converters of thermal neutrons the highest efficiency of registration has received using the Gadolinium based converters, and especially, its 157 isotope. As a result of radiating capture of thermal neutrons by nucleus of Gadolinium the internal conversion and Auger electrons are radiated.
Idea of using thin Gadolinium foils to convert neutrons radiation into charged particles and count the conversion products in a solid-state detector was originally proposed by Feigl and Rauch [1,2]. They used natural Gd and pure l57Gd convertor foils and measured the exit probabilities and the energy distributions of the escaping electrons with Si surface barrier detectors.
Mathematical modeling allows to prospect, without special material cost, to carry out search the most suitable configuration of converters and the optimum geometrical ratio. It in turn allows refusing from realization of superfluous development and researches.
2. Model Calculation
Efficiency of the Gadolinium based neutron converters is the ration of the electrons which have depart from converters, to total number of falling on the converter neutrons. The efficiency of converters is the product of three variables. These are the followings:
• Probabilities of thermal neutrons capture by nucleus of the converter, which depends on its thickness, and the cross-section of interaction. The cross-section of interaction in turn depends on isotope composition of the converter and energy or wavelength of neutron.
• Probabilities of creation of the secondary charged particles, in our case of internal conversion and Auger electrons.
• Probabilities of exit of the created electrons from the substance of the converter, which depends on, free path length of electrons in a converter substance and thickness of converter.
Energies of the secondary electrons are discrete values and are formed with the certain probability. At calculation of probability of exit it is necessary to take into account emission of each electron with its characteristic energy and its weight factor (probability of formation). In that specific case efficiency can be described by the following expression [3,4]
 (1)
(1)
where Wi is the efficiency of registration of the absorbed with the probability Pn(σLj) neutron absorption, which caused formation of electrons De(EiNi) with the discrete energies and probability of formation, probability of escape of electrons from a material of converter He(ReiLi) in view of the maximal free path length of electrons in a substance of the converter and its thickness. Generally probabilities are necessary for summarizing, so calculations are made for 446 discrete energies of electrons with the energies in the range from 0.9 up to 1000 keV.
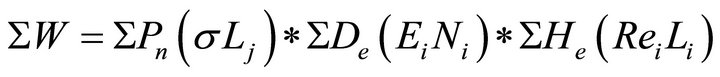 (2)
(2)
Modeling was realized by examining the simple geometrical model, the plane-parallel foils. The calculations for thermal neutrons with fixed energies, which correspond to the neutron wavelength of 1, 1.8, 3 and 4 Å were carried out; also both the thickness of converters from 1 µm to 40 µm, and isotopic composition of converter (for natural Gd and 157Gd) were varied. In the calculation all electrons (appeared as a result of neutron capture act) are taken into account which are able to exit an infinite plane-parallel plate of the converter. The ratio of the number of electrons exiting from the foil to the number of incident neutrons is referred to as the efficiency of the converter.
Conventionally we divide the thickness of a foil into more thin components. For each elementary layer we count the probability of neutrons absorption with the fixed energy. Efficiency of the converter will be determined by the multiplication of probabilities of neutron absorption and probability of the electron exit from the converter. The choice of the model was made from the following assumptions: all electron emissions are isotropic, the length of free path for any fixed energy of electrons (Rei) is constant (fluctuation of power losses in the end of path is neglected). Then the density of probability to find electrons in the material forms is a sphere with radius equal to Rei (for each fixed energy). If the center of the sphere is crossed by the plane, two identical hemispheres are formed, which correspond to the electron escape to the forward and backward hemisphere, thus the volume of hemispheres could be considered as the probability of an electron output. In this case total probability is 100%, and exit to the one of hemispheres is 50%. If we begin to cross a sphere with a step much less than Rei, segments will be formed whose volume will be equal to probability of the electron presence. The step of iterations should be less than Rei. The volume of a segment and accordingly probability of the electron escape becomes equal to zero in the intersection of a sphere by the plane at the distance Rei. The sum of probabilities of electron escapes for all energies, taking into account their weight contribution will determine the total electron escape probability [5,6].
Probability of neutron absorption Pn(σLj). In calculations, of the probability of neutron absorption for each elementary layer, as a result of reaction of inelastic interaction (n, γ), it is necessary using database on crosssection of neutron interaction [7] for each fixed energies. In the Figure 1 the dependence of cross-section (barn) of

Figure 1. Cross-section of thermal neutrons capture, for the reaction (n, g), depending on energy of neutrons for natural Gadolinium and its 157 isotope (input date).
neutron radiation capture on the energy of incident neutrons (eV), for natural Gadolinium and the same dependence for its 157 isotope are shown. Arrows indicate energy of neutrons for which we will carry out our calculations. As one can see, with the reduction of energy of neutrons the cross-section of interaction strongly increases. Especially it increases in the region of cold and ultra cold neutrons.
The scheme of algorithms calculation of neutron absorption in a converter material is shown in Figure 2. In the beginning the select of a material of the converter (natural Gadolinium or its 157 isotope), and a neutron wavelength is necessary. In calculations we are use four fixed neutron energies; these are conform for neutrons with wavelengths of 1, 1.8, 3 and 4 Å. After a select of parameters from a database data about cross section of neutron interaction with materials [7] retrieved.
Calculation of neutron absorption is made for each selected layers. The attenuation of the narrow collimated neutron beam in thin layer materials is governed by the exponential law
 (3)
(3)
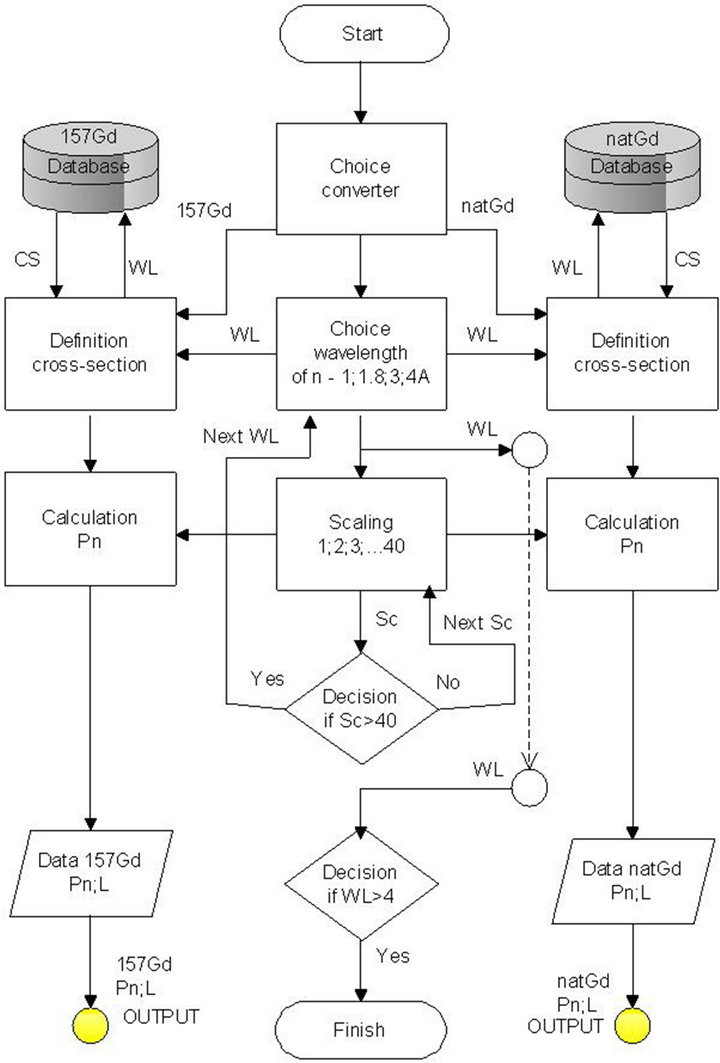
Figure 2. Calculation algorithm diagram of absorption path of neutrons in substance.
where Fx and F0 are the neutron flux density after and before its passage through the layer of the material with the thickness L, correspondingly, NA is the number of nucleus in the volume of 1 cm3, σ- is full microscopic cross-section of neutron interaction with the nuclei of material.
Results of calculations of neutron absorption in converters made from natural Gadolinium and its 157 isotope are shown in the Figure 3. Figure show that at 30 microns thickness of the natural Gadolinium converter the neutrons with the wave length above 1.8 Å are absorbed completely. For its 157 isotope for neutrons with the wave lengths >1.8 Å the same absorption happens at 8 microns thickness of the converter.
Probability of electrons formation De(EiNi). In the reaction of 157Gd neutron capture, 7937.33 keV energy is emitted. In total 390 gamma lines with energy ranges from 79.5 up to 7857.670 keV with line intensity of 2 × 10−8 up to 139 gamma-quanta on 100 captured neutrons are emitted. In Figure 4, the histogram showing dependence of gamma quantum intensity on the energy is presented [8].
The low-energy gamma quanta are present at the spectrum and during their emission electrons from atomic subshells (so-called internal conversion electrons) are radiated with a high probability. The nuclear removes its
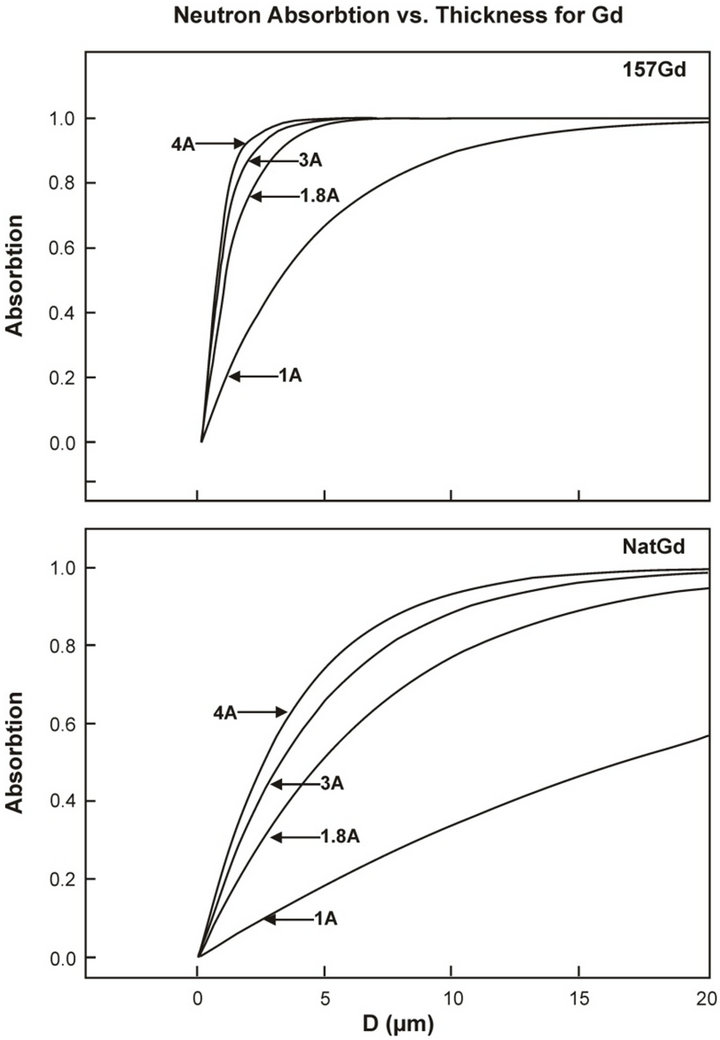
Figure 3. Curve absorption path of neutrons for lengths of waves 1, 1.8, 3 and 4 Å for natural Gadolinium and it 157 isotopes (output data).
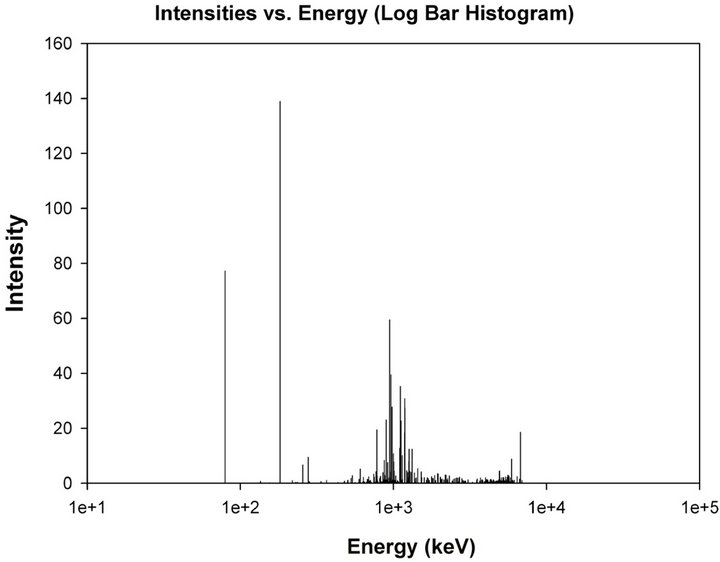
Figure 4. Histogram of dependence of intensity of gammaquanta with energy for the reaction of 157Gd (n, γ) 158Gd by 100 neutrons (input data).
excitation by radiating a gamma-quantum, but also a close located electron can be irradiated too. Usually K-electron (electron from K-subshell) is emitted, but also electrons from the higher subshells (like L, M, N and so on) can be emitted too. Vacancy of electrons (an electronic hole), formed as a result of this process, is filled by another electron from a higher level. This process is accompanied by radiation of X-ray quantum, or radiation of Augerelectron.
In Figure 5, scheme of algorithms for calculation of the internal conversion electrons are show. First of all it’s necessary to define energies and quantity of gammas quanta’s emitted in the reaction of radiation capture of neutrons by Gadolinium nuclear (Figure 4). This data can obtain from the data-base [9]. Energy of internal conversion electrons equal to energy of gammas minus of binding electrons energies of atomic subshells (K, L, M...). For calculation of quantity of internal conversion electrons it’s necessary to define of internal conversion coefficients for Gadolinium for each atomic subshells.
In Figure 6, result of calculation of energy and quantity of internal conversion electrons shown.
Probability exit of electrons from a converter De(EiNi)*He(ReiLi). The probability of exit of electrons from a converter substance can be considered on the basis of Bethe-Bloch theory. For realization of calculations it is important to have exact data on brake ability of various substances for the charged particles. Brake ability is average speed of lose of energy by charged particles in any point along their tracks.
Calculations of exit probability of isotropic emitting electrons, originated in the 157Gd (n, γ) 158Gd radiation capture reaction, are conducted. In Figure 6 one can see contributions of electrons of different energetic groups. Calculations were made for conditionally fixed point of
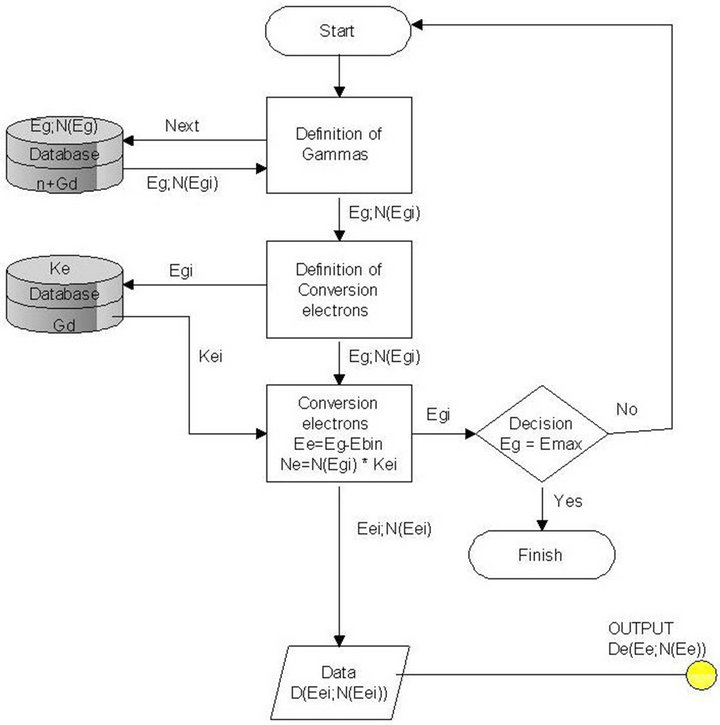
Figure 5. Diagram of algorithms for calculation of internal conversion electrons.
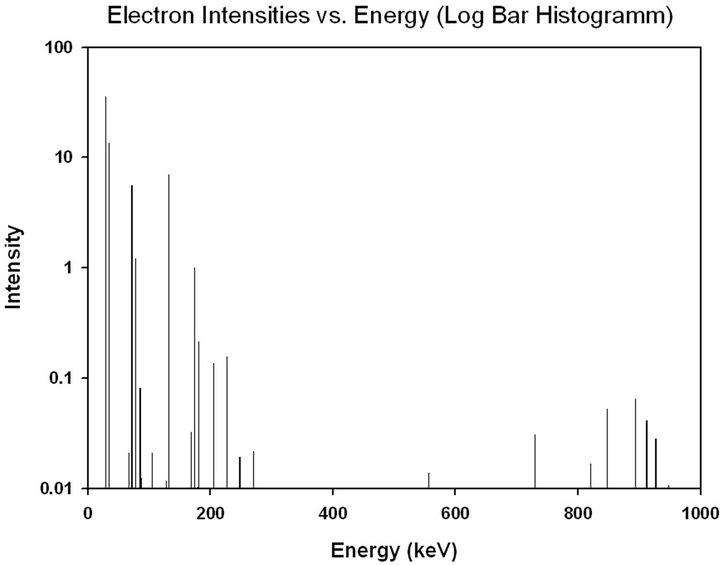
Figure 6. Intensity of internal conversion electrons emitted in the reaction 157Gd (n, γ) 158Gd depending on their energy by 100 neutrons (output data).
conversion of neutrons having coordinate (X = 0, Y = 0).
The scheme of algorithm calculation of ability an electrons exit from the converter is shown in Figure 7. For calculations of probabilities of electrons output from substance the data about internal conversion and Auger (Figure 6) downloaded. For each discrete energy of an electron the database [10] about of free length (Re) electron in substance were used. For each elemental stratum probability of an exit of electrons is yielded, for calculation the data on Re and intensity of electrons used.
In the Figure 8 contribution of 4 groups of electrons with different energies is well seen. Separated energies of electrons could be divided into 4 groups (Figure 6). In the
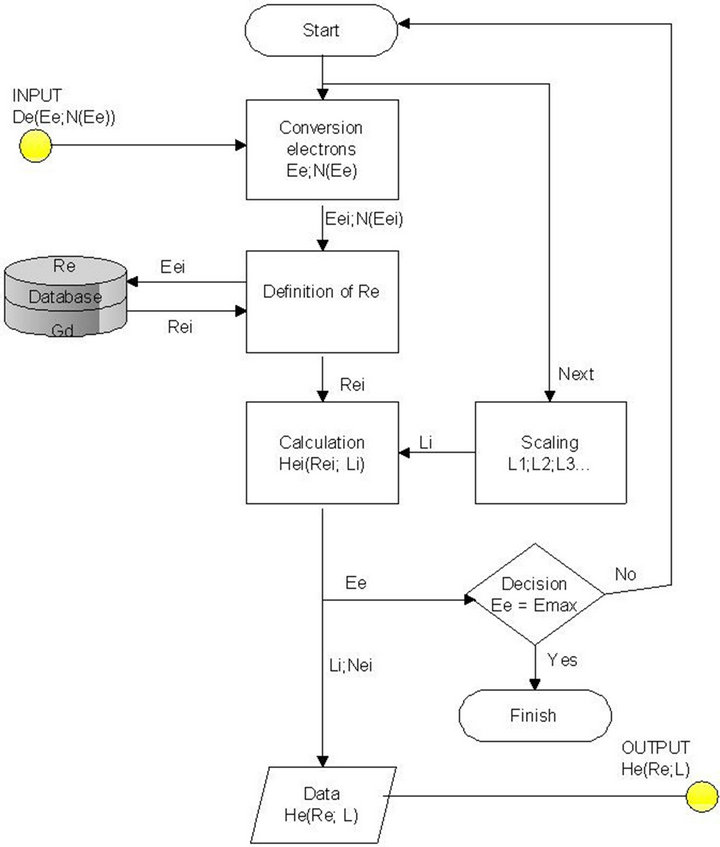
Figure 7. Scheme of algorithm calculation of ability an electrons exit from the converter body.
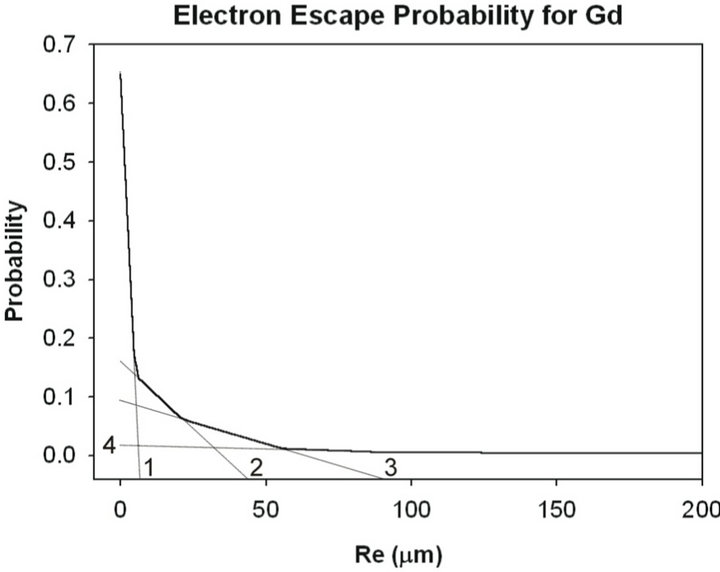
Figure 8. Probability of exit of isotropic emitting secondary electrons from Gadolinium foils of various thicknesses, in view of their intensity (output data).
first group the least energetic and therefore having small ranges in the substance, and in the fourth one the most energetic electrons are placed.
Efficiency of converter W. Calculations of converters efficiency have been executed for the foils makes of natural Gadolinium and it 157 isotopes, for four fixed wavelengths of neutrons 1, 1.8, 3 and 4 Å. Calculation were performs for geometry of an exit of electrons in a back, forward hemisphere and their sum for different thickness of the converter.
The scheme of algorithms of calculation is given in Figure 9. In the beginning the select of the type of converter and a neutron wavelength was made. The thickness of the converter is divided into thin elemental stratums. For each stratum the corresponding data on absorption of neutrons (Pn, L) download. During calculation to each stratum conventionally co-ordinates X0, Y0 appropriated, the data on probability of an exit of electrons (He(Re)) is download. The data gained on each stratum tots. At modeling efficiency calculations separately for geometry of an exit of electrons in a forward and back hemisphere and their sum were made.
Results of calculations of neutron absorption in converters made from natural Gadolinium and its 157 isotope are shown in the Figures 10 and 11. Figures show that at 30 microns thickness of the natural Gadolinium converter the neutrons with the wave length above 1.8 Å are absorbed completely. For its 157 isotope for neutrons with the wave lengths >1.8 Å the same absorption happens at 8 microns thickness of the converter.
In order to detect thermal neutrons by the 157Gd converters we could limit by the thickness of 5 microns of
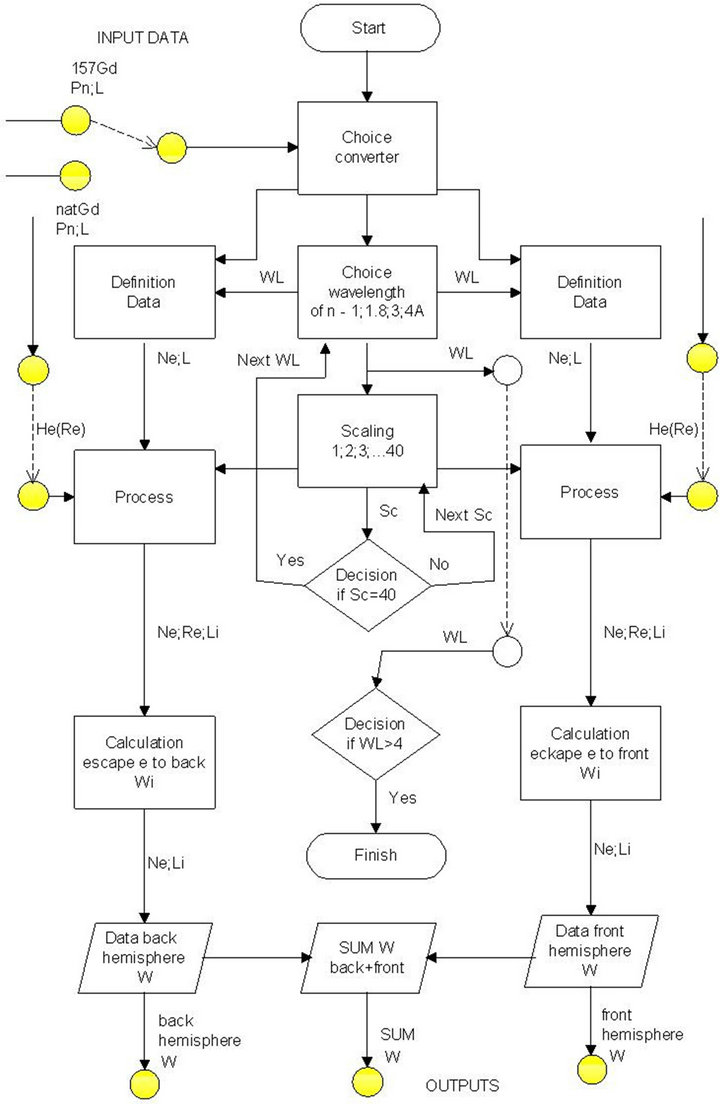
Figure 9. Scheme algorithm calculation of the efficiency of converters.
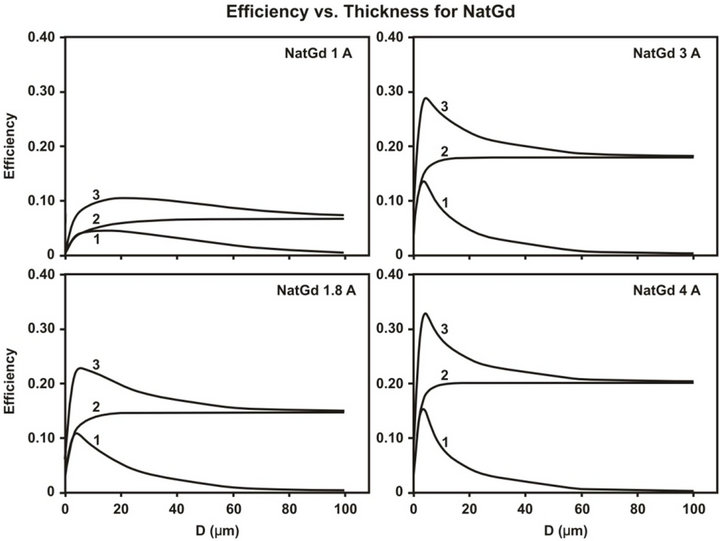
Figure 10. Dependence of the neutron registration efficiency of the natural Gadolinium converter on its thickness. Curves 1 and 2 correspond to emission of electrons into the front and back hemisphere, respectively, curve 3 is their sum.
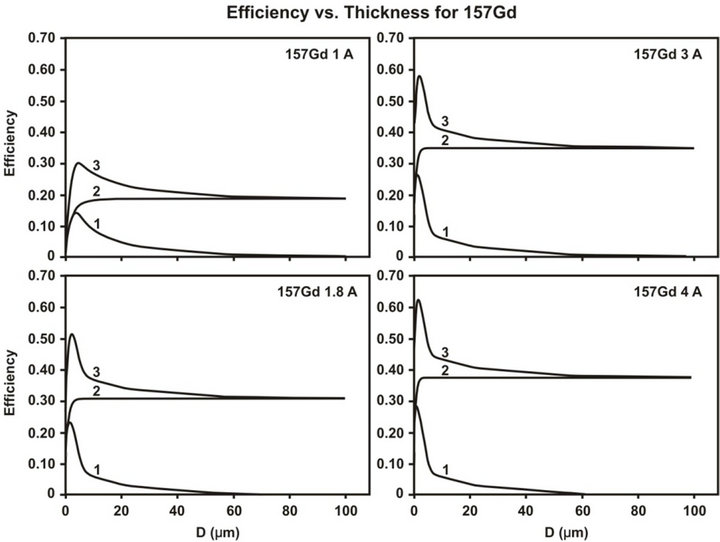
Figure 11. Dependence of the neutron registration efficiency of the 157 isotope of Gadolinium converter on its thickness. Curves 1 and 2 correspond to emission of electrons into the front and back hemisphere, respectively, curve 3 is their sum.
the converter, if there no technological restrictions. It should be taken into account that the majority of electrons emitted in the reaction of radiating capture of neutrons have ranges less than 5 microns. When using natural Gadolinium the situation is more complex, since low absorption requires converter to be thicker than 20 - 40 micron.
3. Conclusions
Mathematical modeling of efficiency of registration of thermal neutrons by the foil converters made from natural Gadolinium and its 157 isotope carried out. Algorithms of calculations of absorption of neutrons in substance of the converter, probability of formation of secondary electrons and probability of an exit of electrons from the substance of converter are described.
Processes of neutron absorption in the material of a converter and the probability of secondary electron escapes were examined. Calculation was made for converters with the various thicknesses. We have chosen the most optimal converter thicknesses, both from natural Gadolinium and from its 157 isotopes. While using converters from natural Gadolinium, it is possible to obtain total efficiency of 10%, 21%, 26%, 30%, correspondingly for the neutrons with wavelengths of 1, 1.8, 3 and 4 Å with converter thickness of 24, 7, 5, 4 microns. For the converters with 157 isotopes, it is possible to reach total efficiency of registration up to 27%, 45%, 49%, 52% for the neutrons with the wavelengths 1, 1.8, 3 and 4 Å with the thickness of converter 5, 3, 2, 2 microns, respectively. The received results are in good agreement with the experimental data [3].
REFERENCES
- H. Rauch, F. Grass and B. Feigl, “Ein Neuartiger fur Langsame Neutronen,” Nuclear Instruments and Methods, Vol. 46, 1967, pp. 150-153.
- B. Feigl and H. Rauch, “Der Gd-Neutronenzahler,” Nuclear Instruments and Methods, Vol. 61, No. 3, 1968, pp. 349-356. doi:10.1016/0029-554X(68)90250-4
- D. A. Abdushukurov, “Gadolinium Foils as Converters of Thermal Neutrons in Detectors of Nuclear Radiation,” In: Physics Research and Technology, Nova Science Publishers Inc., New York, 2010, pp. 1-124.
- D. A. Abdushukurov, “Application of the Gadolinium Foils as Converters of Thermal Neutrons in Detectors of Nuclear Radiation,” In: C. C. Tompson, Ed., Gadolinium: Compounds, Production and Application, Chapter 2, Series: Chemical Engineering Methods and Technology, Nova Science Publishers Inc., New York, 2010, pp. 53- 141.
- D. A. Abdushukurov, A. A. Djuraev, S. S. Evteeva et al., “Model Calculation of GadoliniumBased Converters of Thermal Neutrons,” Nuclear Instruments and Methods in Physics, Vol. 84B, 1994, p. 400.
- D. A. Abdushukurov, M. A. Abduvokhidov, D. V. Bondarenko, et al., “Modeling the Registration Efficiency of Thermal Neutrons by Gadolinium Foils,” Journal of Instrumentation, Institute of Physics Publishing and SISSA. Archives of Los Alamos National Laboratory USA, 2007, 2007, pp. 1-19. http://arxiv.org/ftp/physics/papers/0611/0611225.pdf
- Evaluated Nuclear Data File, “IAEA-NDS,” ENDF. http://www.nndc.bnl.gov/exfor3/endf00.htm
- “Thermal Neutron Capture Gammas by Target, NDS, IA EA.” http://www-nds.iaea.org/oldwallet/tnc/ngtblcontentbyn.shtml
- Bricc 2.0a, “Band-Raman International Conversion Coefficients,” BNL. http://www.nndc.bnl.gov/bricc/
- International Commission on Radiation Units and Measurements, “Stopping Powers for Electrons and Positrons,” International Commission on Radiation Units and Measurements, ICRU Rep. 37, No. 1, 1984, pp. 123-125.

