Applied Mathematics
Vol.4 No.1A(2013), Article ID:27493,6 pages DOI:10.4236/am.2013.41A031
Numerical Solution of Freholm-Volterra Integral Equations by Using Scaling Function Interpolation Method
Department of Mathematics, Central Michigan University, Mt. Pleasant, USA
Email: enbing.lin@cmich.edu
Received October 15, 2012; revised November 15, 2012; accepted November 23, 2012
Keywords: Wavelets; Coiflets; Scaling Function Interpolation; Volterra Integral Equation; Fredholm-Volterra Integral Equation
ABSTRACT
Wavelet methods are a very useful tool in solving integral equations. Both scaling functions and wavelet functions are the key elements of wavelet methods. In this article, we use scaling function interpolation method to solve Volterra integral equations of the first kind, and Fredholm-Volterra integral equations. Moreover, we prove convergence theorem for the numerical solution of Volterra integral equations and Freholm-Volterra integral equations. We also present three examples of solving Volterra integral equation and one example of solving Fredholm-Volterra integral equation. Comparisons of the results with other methods are included in the examples.
1. Introduction
The study of finite-dimensional linear systems is well developed. As an infinite-dimensional counter part of finite-dimensional linear systems, one can view integral equations as extensions of linear systems of algebraic equations. An integral equation maybe interpreted as an analogue of a matrix equation which is easier to solve. There are many different ways to transform integral equations to linear systems. Many different methods have been used for solving Volterra integral equations and Freholm-Velterra integral equations numerically.
In this paper, we first recall the method of scaling function interpolation. Then we solve linear Volterra integral equation of the form:
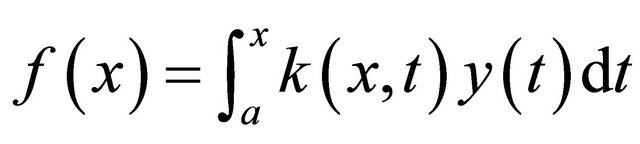 (1)
(1)
and Fredholm-Volterra integral equations of the form:
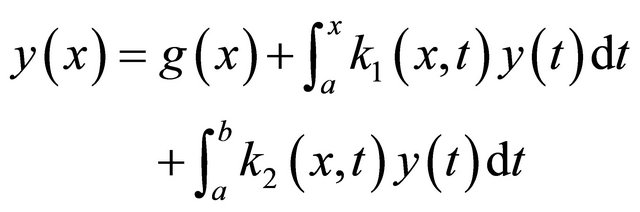 (2)
(2)
where the functions 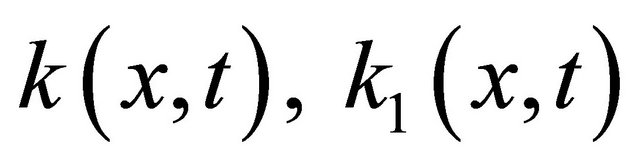 and
and 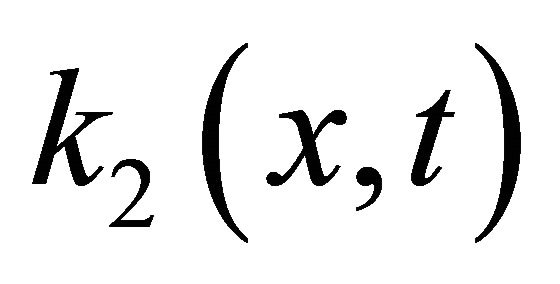 are known functions and called kernels. The function
are known functions and called kernels. The function 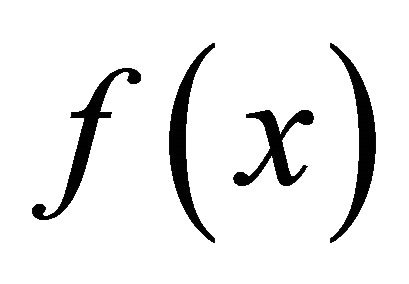 is known, and the function
is known, and the function 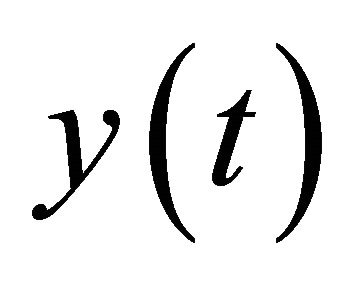 is to be determined. One of the motivations in this study arose from equations in theoretical physics. In fact, there are many applications in several disciplines as well. We will use scaling function interpolation method to solve integral equations. As a natural question, one would wonder any possible convergence properties and how this method would compare with other methods. We will prove two convergence theorems and present several examples.
is to be determined. One of the motivations in this study arose from equations in theoretical physics. In fact, there are many applications in several disciplines as well. We will use scaling function interpolation method to solve integral equations. As a natural question, one would wonder any possible convergence properties and how this method would compare with other methods. We will prove two convergence theorems and present several examples.
2. Approximation
Wavelets and scaling functions are a useful tool in approximation methods of solutions of differential and integral equations [1]. We first recall Multiresolution analysis (MRA) [2]. We assume the scaling function and wavelet function f, Ψ are sufficiently smooth and satisfy MRA with compact support and Ψ has N vanishing moments (defined below). The scaling function 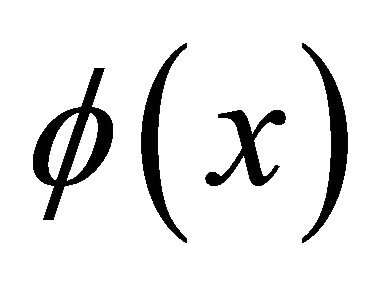 is defined as
is defined as
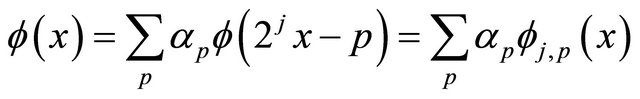 (3)
(3)
for some coefficients . By using this dilation and translation we defined a nested of sequence spaces
. By using this dilation and translation we defined a nested of sequence spaces 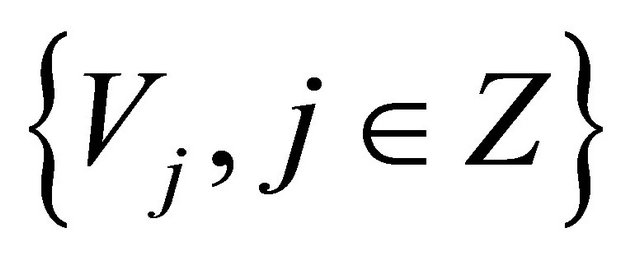 which is called MRA of
which is called MRA of 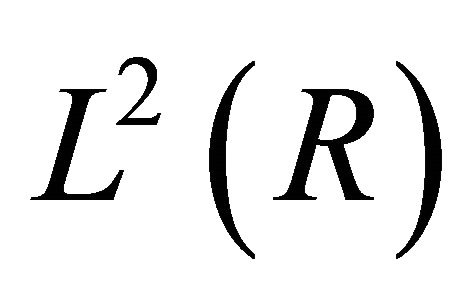 with the following properties:
with the following properties:
 (4)
(4)
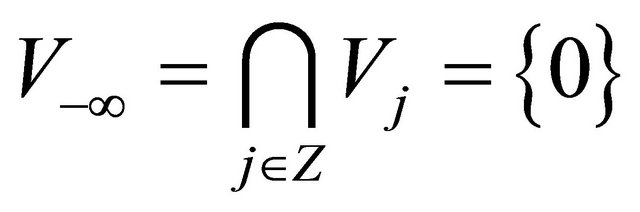 (5)
(5)
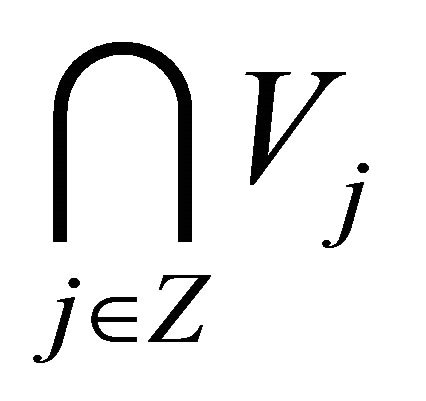 is dense in
is dense in 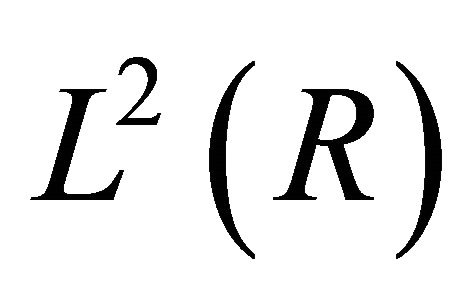 (6)
(6)
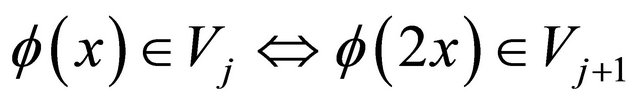 . (7)
. (7)
For the subspace  is built by
is built by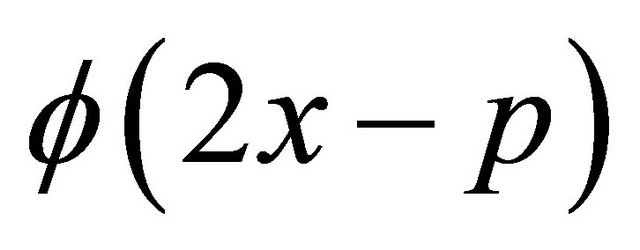 ,
, 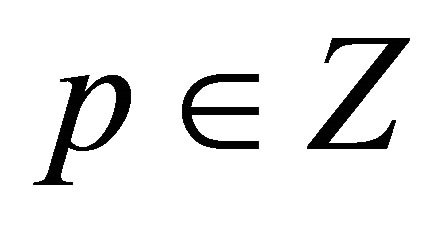
then 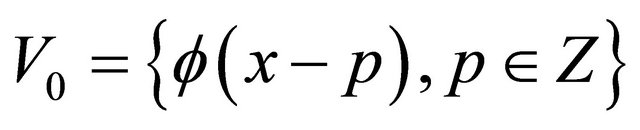 and
and  we can write
we can write
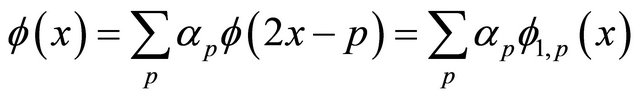 . In general,
. In general,
 . (8)
. (8)
In fact, for each j we define the orthogonal subspace 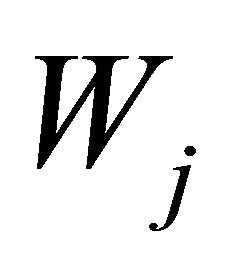 of
of 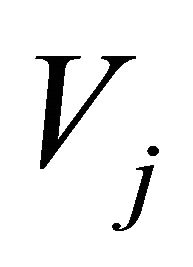 in the subspace
in the subspace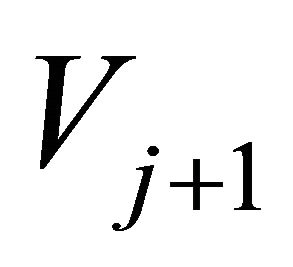 , the or thogonal basis of
, the or thogonal basis of  is denoted by
is denoted by
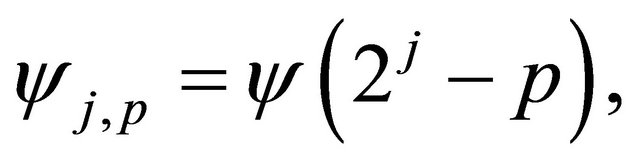 (9)
(9)
and the wavelet function can be obtained by
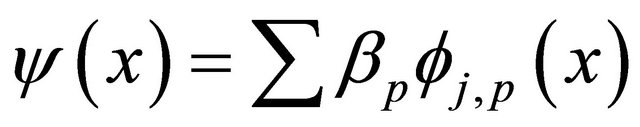 . (10)
. (10)
for some coefficients . Some interesting properties of scaling and wavelet functions make wavelet method more efficiently than other methods such as spline approximations in solving an equation. A lot of computational time and storage capacity can be saved since we do not require a huge number of arithmetic operations partly due to the following properties.
. Some interesting properties of scaling and wavelet functions make wavelet method more efficiently than other methods such as spline approximations in solving an equation. A lot of computational time and storage capacity can be saved since we do not require a huge number of arithmetic operations partly due to the following properties.
Vanishing moments:
 (11)
(11)
and in this case the wavelet is said to have a vanishing moment of order k.
Semiorthogonality:
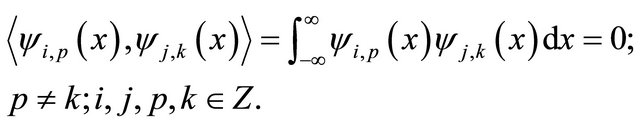 (12)
(12)
The set of scaling functions 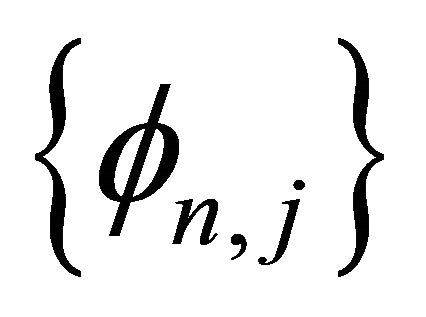 is orthogonal at the same level n, which means:
is orthogonal at the same level n, which means:
 (13)
(13)
Coiflet (of order L) has more symmetries and it is an orthogonal multiresolution wavelet system with,
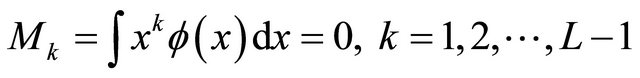 . (14)
. (14)
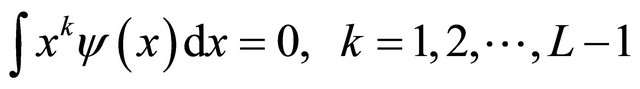 . (15)
. (15)
where  is the moment of scaling functions.
is the moment of scaling functions.
3. Scaling Function Interpolation
In MRA, any given function 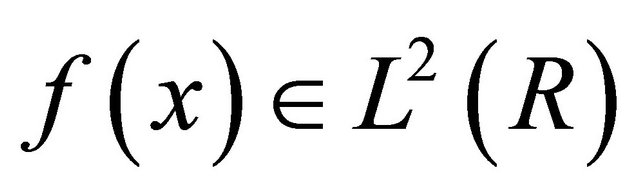 can be interpolated by using the basis functions in the subspace
can be interpolated by using the basis functions in the subspace 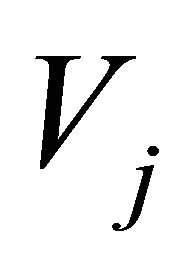 as follows:
as follows:
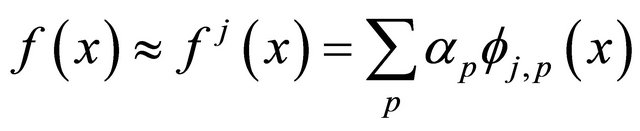 (16)
(16)
where the coefficientsv 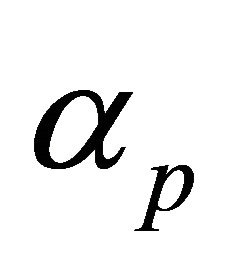 are evaluated by using the semiorthogonality of the scaling functions (12) such that
are evaluated by using the semiorthogonality of the scaling functions (12) such that
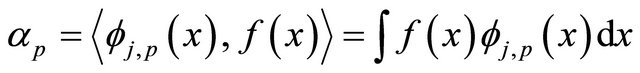 . (17)
. (17)
Hence the Equation (16) becomes as follows:

To approximate a given function f, one can use sampling values of f at certain points. It is proved in [3], namely, an interpolation theorem using coiflet, namely, if 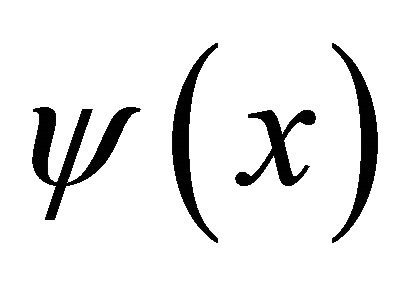 and
and  are sufficiently smooth and satisfy the Equations (10)-(15) and the function
are sufficiently smooth and satisfy the Equations (10)-(15) and the function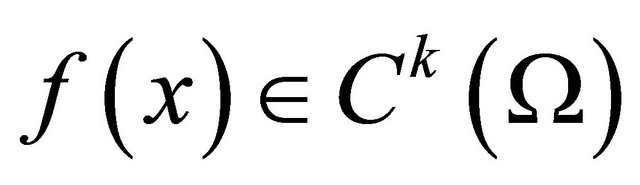 , where Ω is a bounded open set in R2,
, where Ω is a bounded open set in R2, 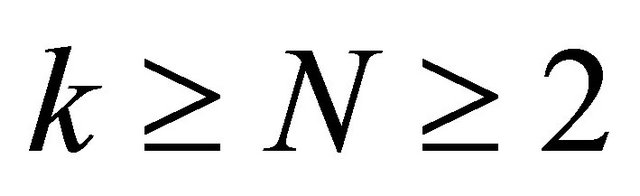 ,
, 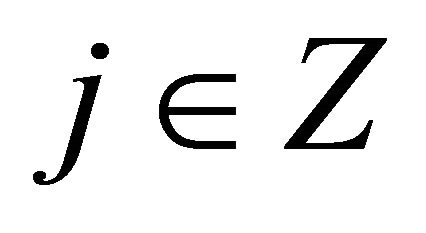 then,
then,
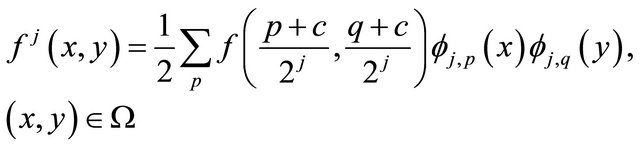 (18)
(18)
where the index set is
 .
.
In addition, the moment 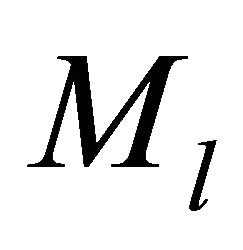 satisfies
satisfies
 .
.
Then 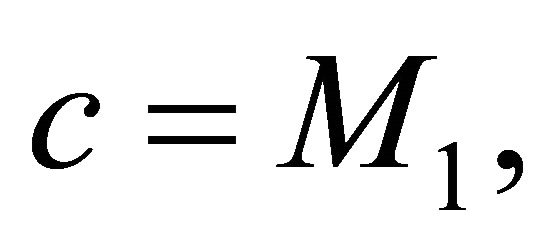 and
and
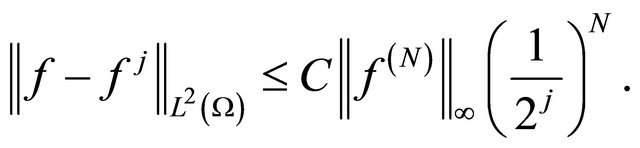
where C is a constant depending only on N, diameter of Ω and
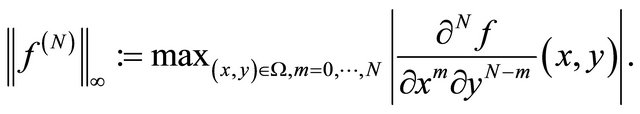
For one-dimensional analogue, we have
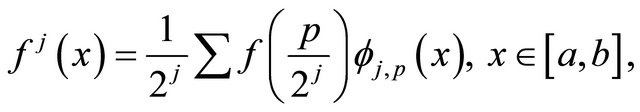 (19)
(19)
and
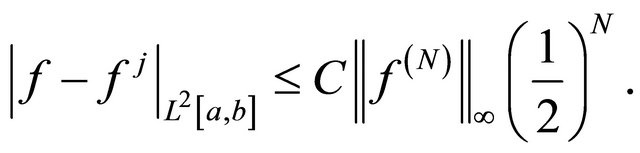 (20)
(20)
where
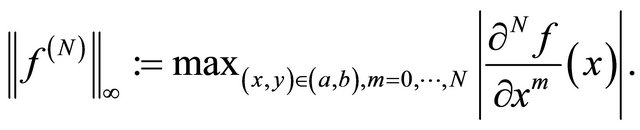
4. Solutions of Linear Integral Equation
In this section, Coiflet is used to solve linear integral Equations (1) and (2), where we will explain the method in terms of matrix notation.
4.1. Linear Volterra Integral Equation
In this subsection we will use the interpolation Formula (19) to solve Volterra integral Equation (1). The unknown function  in Equation (1) can be expressed in term of scaling functions
in Equation (1) can be expressed in term of scaling functions  in the subspace
in the subspace 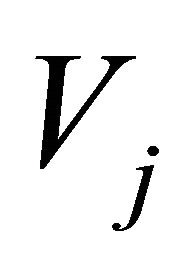 such that
such that
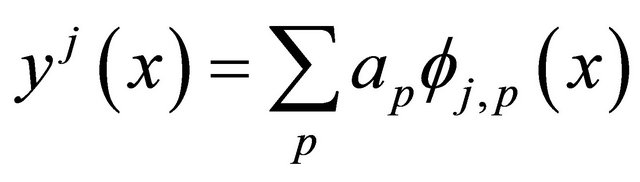 . (21)
. (21)
By substituting Equation (21) into the Equation (1), we have the following system,
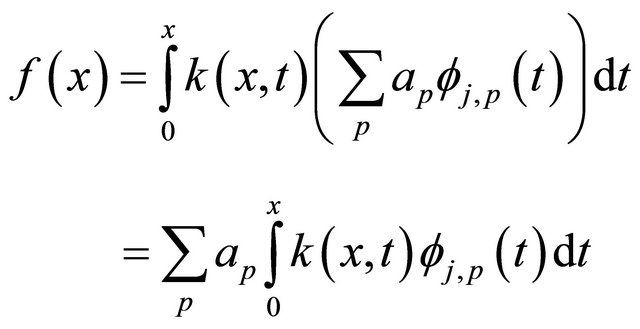 (22)
(22)
To simplify the system, let
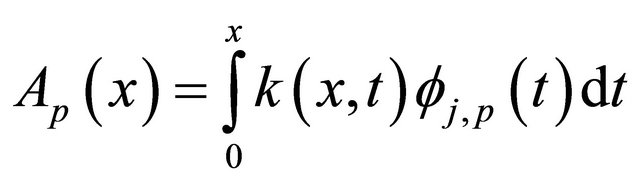
Then the system (22) becomes
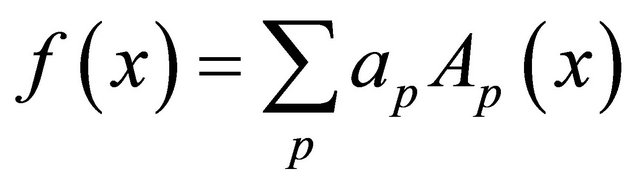 . (23)
. (23)
The coefficients 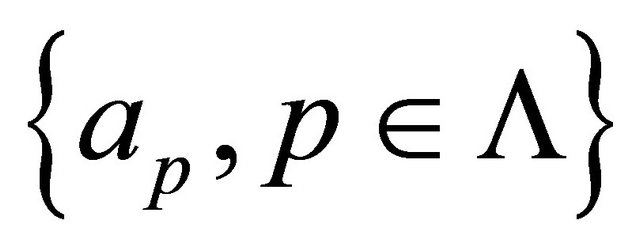 can be evaluated by substituting the set of real numbers
can be evaluated by substituting the set of real numbers

into the system (23), let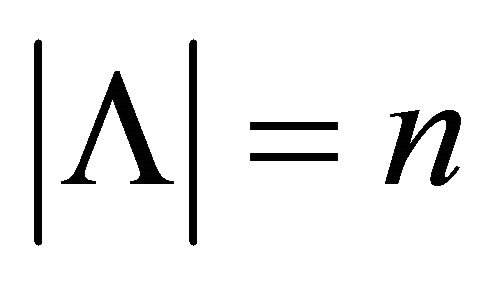 , then the system (23) can be written in the form
, then the system (23) can be written in the form
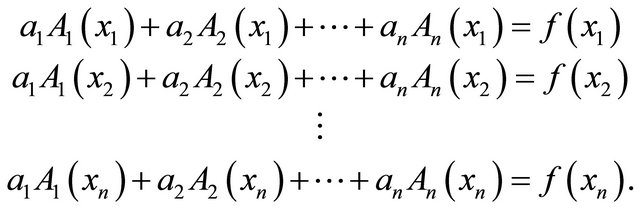
If we use the notation 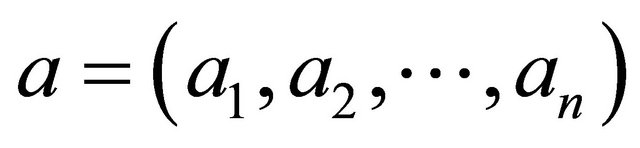 and
and
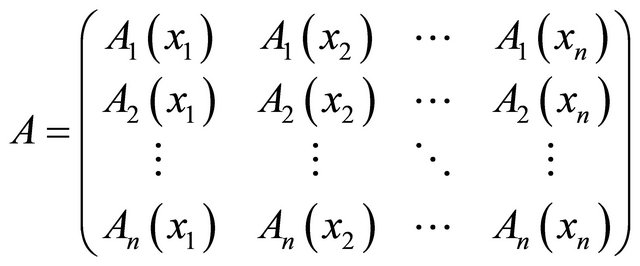
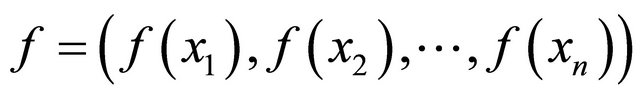 , then the system (23) is equivalent to the system
, then the system (23) is equivalent to the system , and the solution is
, and the solution is
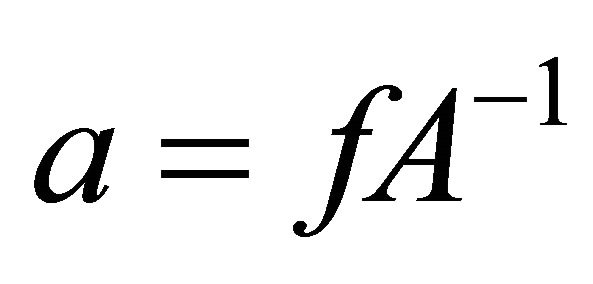 . (24)
. (24)
This gives raise to coefficients in (23) and we obtained a numerical solution to Equation (1).
4.2. Linear Fredholm-Volterra Integral Equation
To solve the Fredholm-Volterra integral Equation (2), we use a similar algorithm as we use in 4.1. The unknown function can be approximated by using Equation (1) and one can have the system of linear equations;
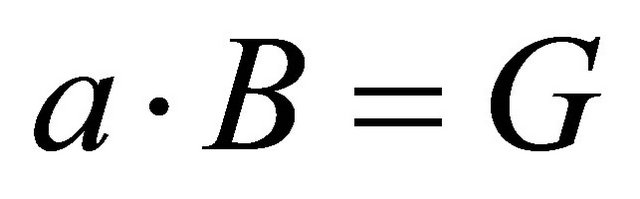
where a is the vector of unknowns as we introduce in Equation (21),
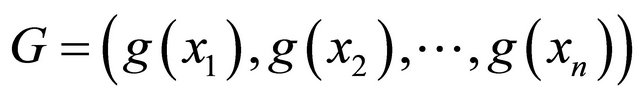
and
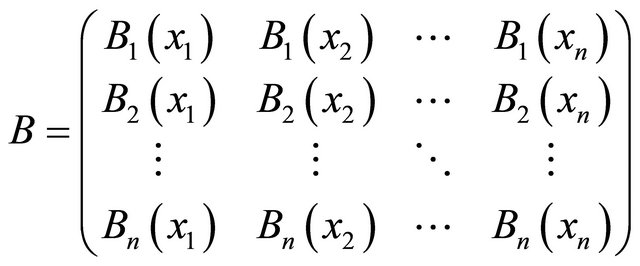
with
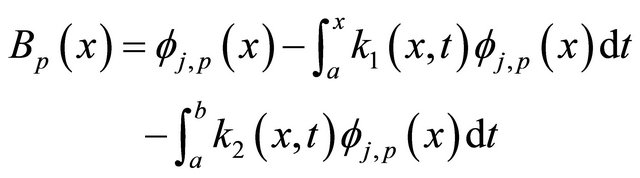
and the set of 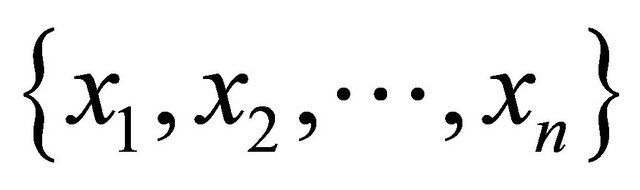 is in the interval
is in the interval 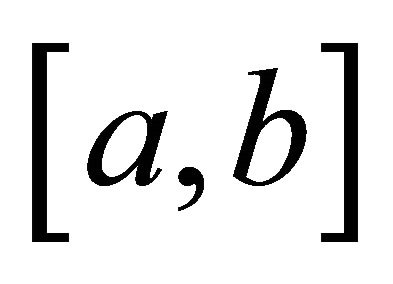 which one can be choose equally spaced. In the next section we will discuss the convergence for the method by deriving a convergence theorem of this numerical solution.
which one can be choose equally spaced. In the next section we will discuss the convergence for the method by deriving a convergence theorem of this numerical solution.
5. Error Analysis
In this section, we provide with the convergence rate of our method for the numerical solution of solving linear Volterra integral equations and Freholm-Volterra integral equation respectively. We will explain the necessary conditions for the convergence.
Theorem 5.1
In Equation (1), suppose that the functions
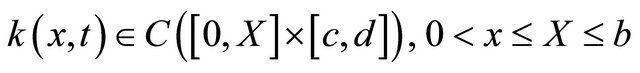 ,
,
 and the two functions
and the two functions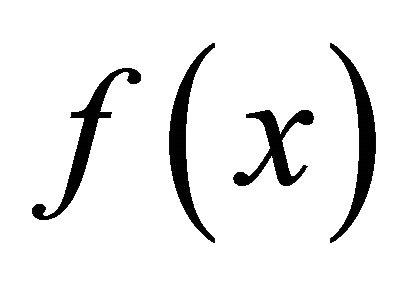 ,
, 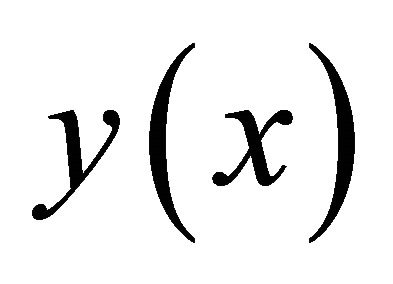 are in
are in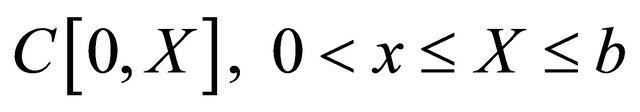 , for
, for 
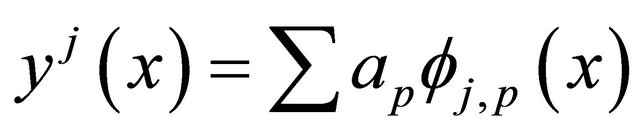 .
.
If an approximate solution of the Equation (1) with coefficients obtained in (24), and the error at the point
 is
is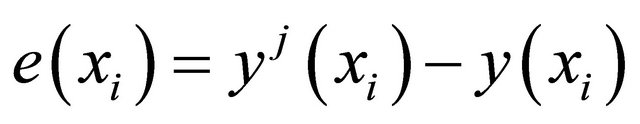 . Then
. Then where c is a constant.
where c is a constant.
wang#title3_4:spProof:
We begin with the following equation.
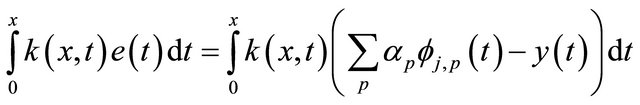 . (25)
. (25)
At any point  Equation (25) becomes:
Equation (25) becomes:
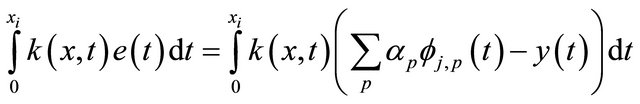 then
then
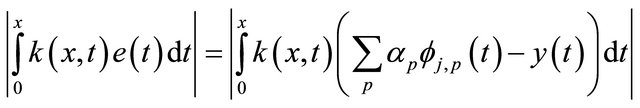 . (26)
. (26)
For
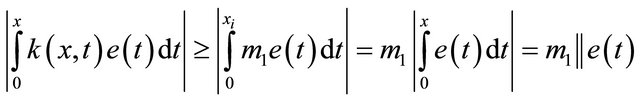
Then,
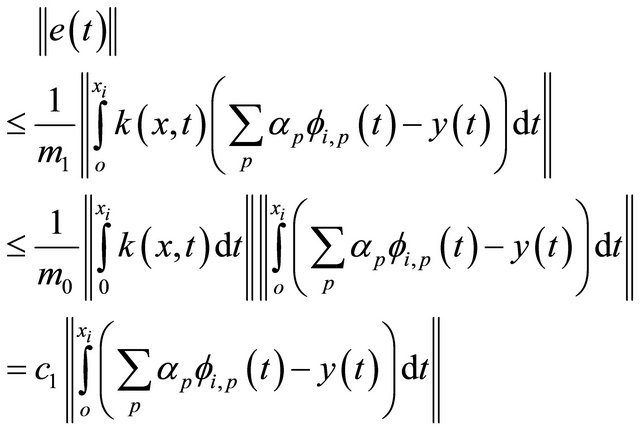 (27)
(27)
Such that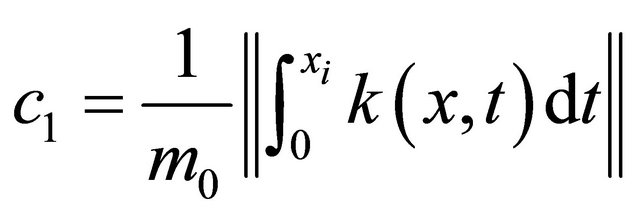 .
.
By (19), the unknown function  can be interpolated by using the coiflet such that:
can be interpolated by using the coiflet such that:
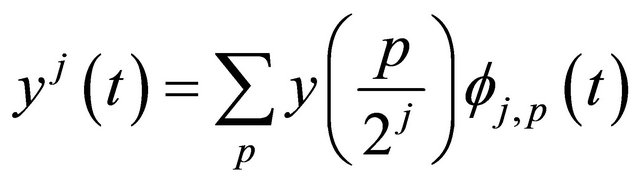 (28)
(28)
If we add and subtract Equation (28) in Equation (27), we get the following inequality:
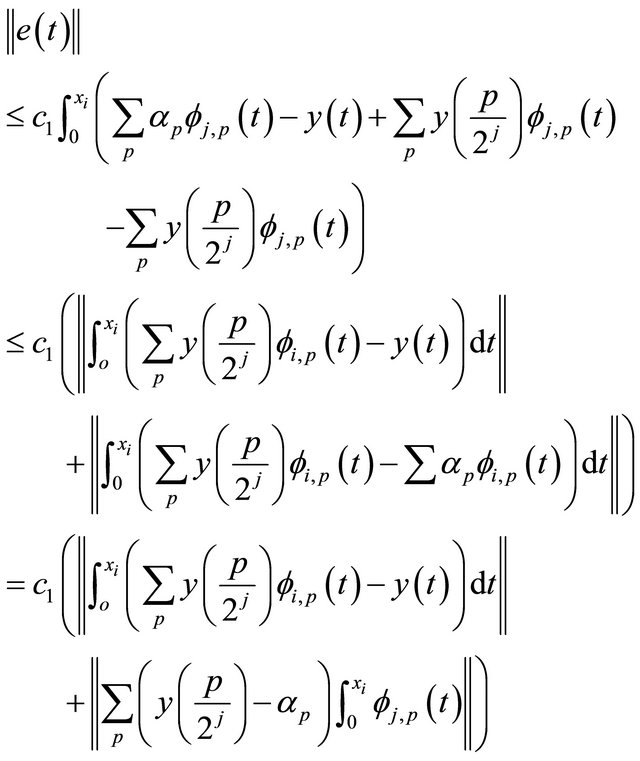
But by (20), we have that;
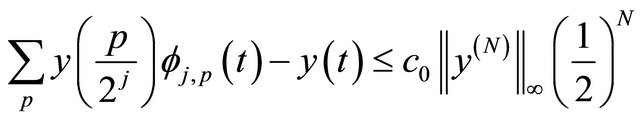 And since
And since 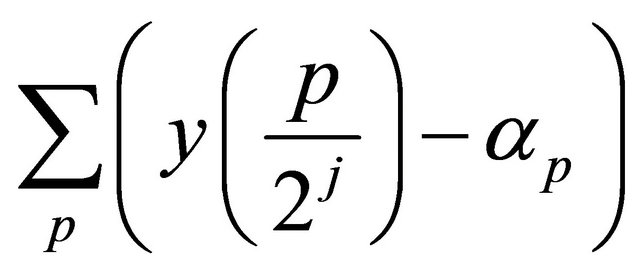 is finite then denote it as
is finite then denote it as

By using the above results and the orthonomality of the scaling functions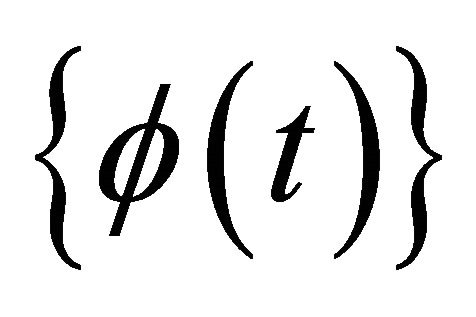 , we conclude that
, we conclude that
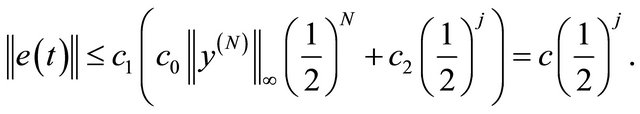
Theorem 5.2
In Equation (2), suppose that the functions
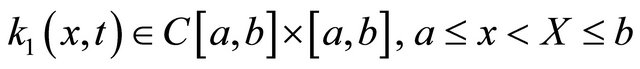 ,
,
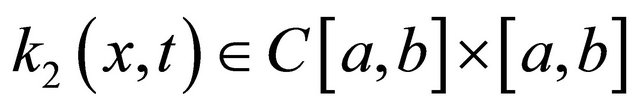 , and
, and 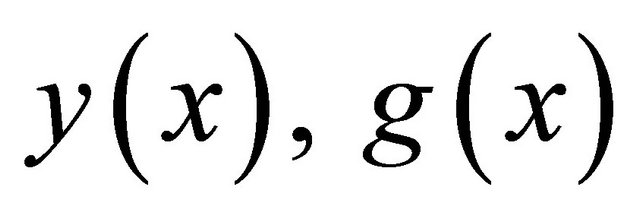 are in
are in
 , for
, for 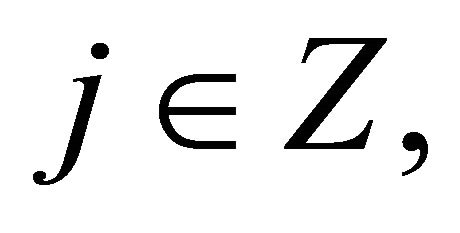
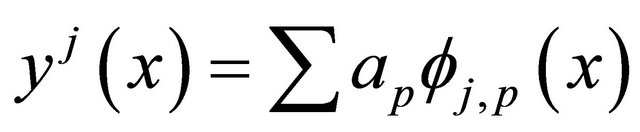
If an approximate solution of the Equation (2) with coefficients obtained in (24), and the error at the point 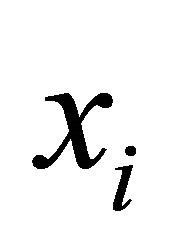 is
is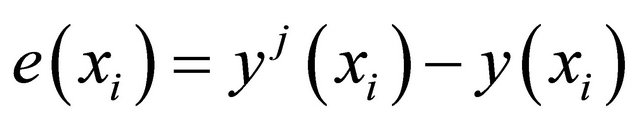 . Then
. Then
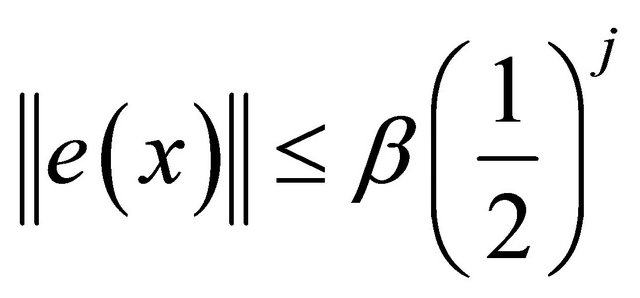 , where β is a constant
, where β is a constant
wang#title3_4:spProof:
Substitute (21) into Equation (2), we get the following integral equation
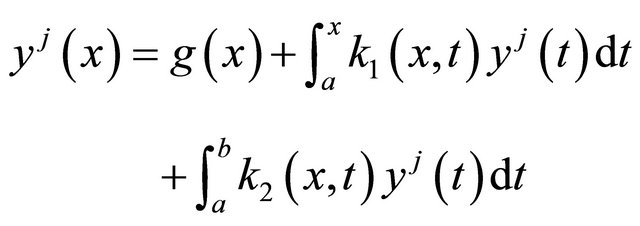 (29)
(29)
Subtracts Equation (27) from (1) and substitute x by xi to get;
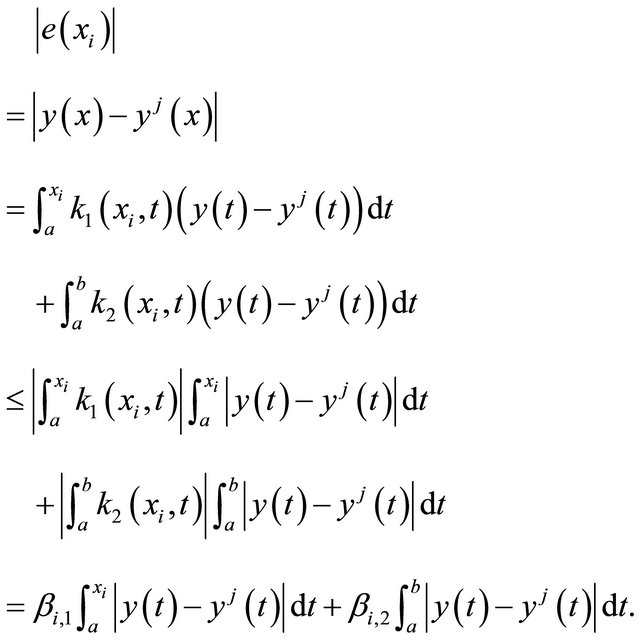 (30)
(30)
Add and subtract Equation (28) for absolute value in the previous equation, we get the following equation.
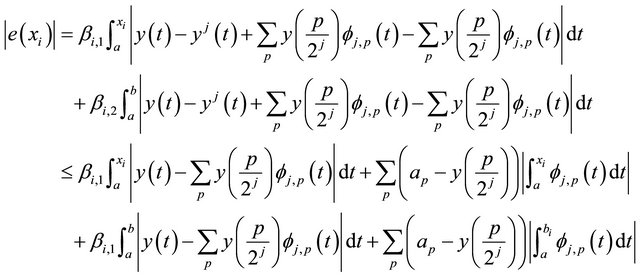 (31)
(31)
We use the same idea in the proof of 5.1, and obtain the following error estimate.
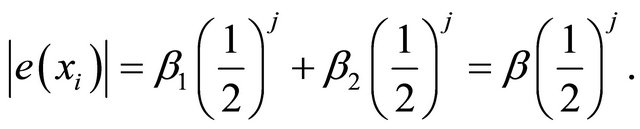
Remark
Here we discuss only the case when the kernel function 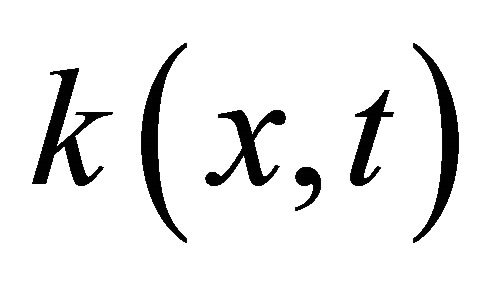 is positive. We can generalize our method for any given continuous function
is positive. We can generalize our method for any given continuous function  in Equation (1);
in Equation (1);
1) If  is positive, we have obtained the convergence theorem.
is positive, we have obtained the convergence theorem.
2) If  is negative then let
is negative then let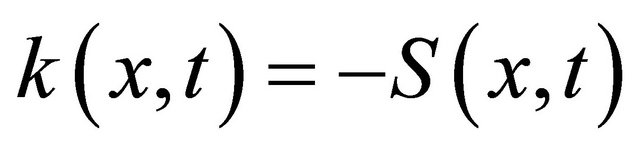 , then the function
, then the function  is positive and we can apply our method for the equation
is positive and we can apply our method for the equation  which has the same solution as the Equation (1).
which has the same solution as the Equation (1).
3) If the function 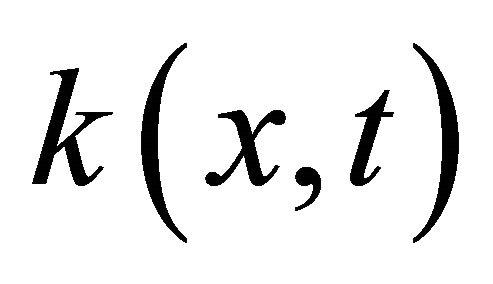 is neither of the above two cases, the function
is neither of the above two cases, the function 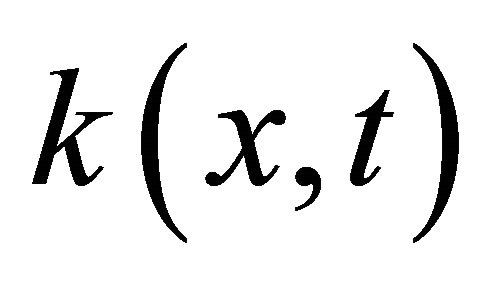 can be written as a sum of two positive functions where
can be written as a sum of two positive functions where
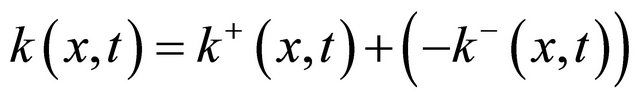
Then Equation (1) becomes
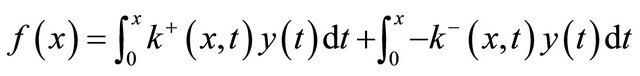
And hence the result is concluded in a similar fashion.
6. Numerical Examples
In the following examples, we will solve several linear Volterra integral equations of the first kind and Fredholme-Volterra integral equations using coiflet of order 5 and provide the absolute errors. The examples (1-3) are also shown in [4] and the example 4 is presented in [5]. We will compare our results with others and show that our method has better approximations than other methods.
Example 1
Consider the integral Equation (1) with;
 and the exact solution is
and the exact solution is
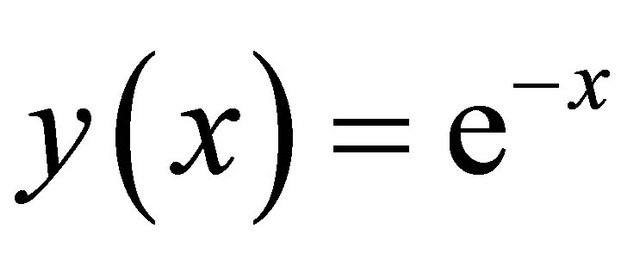 . The numerical results are presented in Table 1.
. The numerical results are presented in Table 1.
Example 2
Consider the integral Equation (1) with;
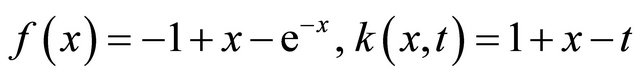 and b = 1, and the exact solution is
and b = 1, and the exact solution is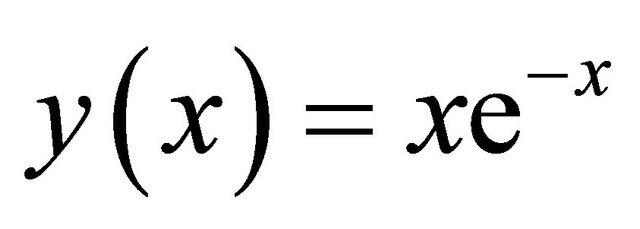 . The numerical results are presented in Table 2.
. The numerical results are presented in Table 2.
Example 3
Consider the integral Equation (1) with;
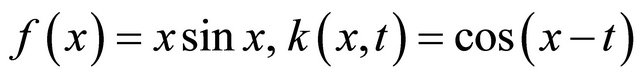 and the exact solution is
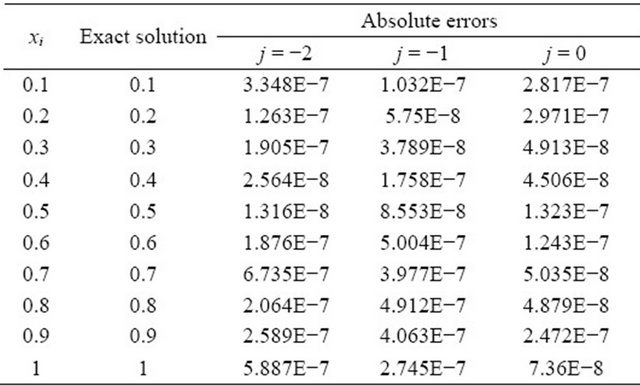
and the exact solution is . The numerical result are presented in Table 3.
. The numerical result are presented in Table 3.
Example 4
Consider the integral Equation (2) with;
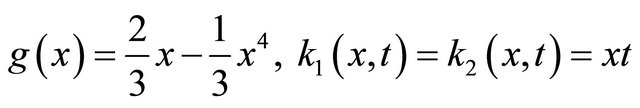 and the exact solution is
and the exact solution is 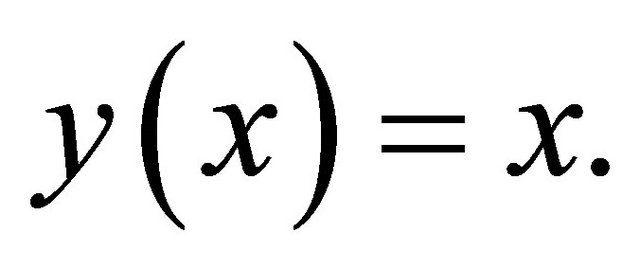 The numerical results are presented in Table 4.
The numerical results are presented in Table 4.
Table 1. The absolute errors for example 1.
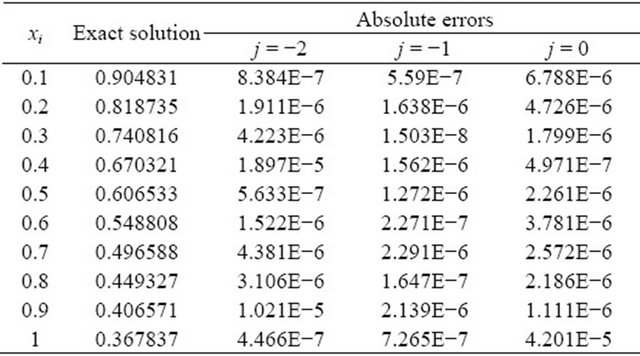
Table 2. The absolute errors for example 2.
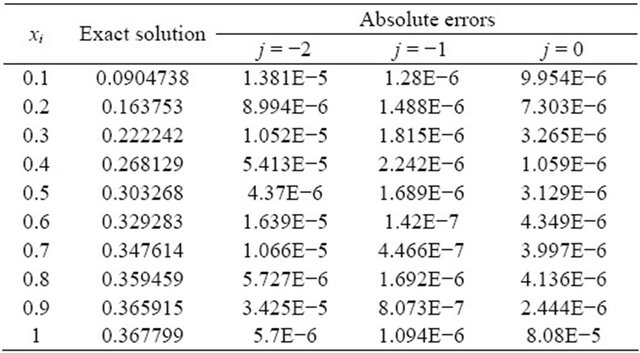
Table 3. The absolute errors for example 3.
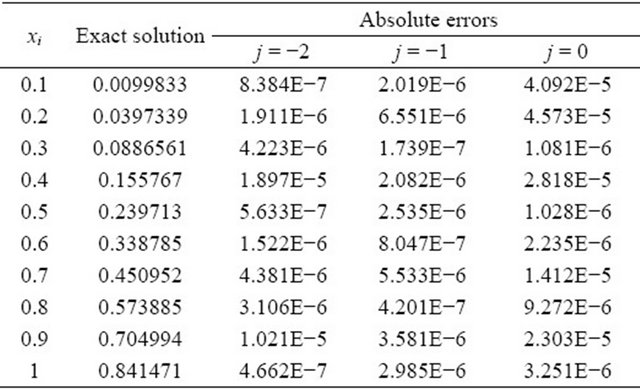
Table 4. The absolute errors for example 4.
In the above tables, we use the notation E − n which denotes ![]() and j denotes the level of MRA.
and j denotes the level of MRA.
7. Concluding Remark
In this paper we have shown a better method in solving Volterra integral equations of the first kind, and Fredholm-Volterra integral equations. We also prove convergence theorem for the numerical solution of Volterra integral equations and Freholm-Volterra integral equations respectively. It would be interesting to extend the results to two-dimensional case for the above mentioned equations and apply to some imaging problems.
REFERENCES
- E. B. Lin and N. Liu, “Legendre Wavelet Method for Numerical Solutions of Partial Differential Equations,” Numerical Methods of Partial Differential Equation, Vol. 26, No. 1, 2010, pp. 81-94. doi:10.1002/num.20417
- C. K. Chui, “In Introduction to Wavelets,” Academic Press, Boston, 1992.
- E. B. Lin and X. Zhou, “Coiflet Interpolation and Approximate Solutions of Elliptic Partial Differential Equations,” Methods for Partial Differential Equations, Vol. 13, No. 4, 1997, pp. 302-320.
- M. T. Rashad, “Numerical Solution of the Integral Equations of the First Kind,” Applied Mathematics and Computation, Vol. 145, No. 2-3, 2003, pp. 413-420. doi:10.1016/S0096-3003(02)00497-6
- A. S. Shamloo, S. Shaker and A. Madadi, “Numerical Solution of Fredholm-Volterra Integral Equation by the Sunc Function,” American Journal Computation Mathematics, Vol. 2, No. 2, 2012, pp. 136-142. doi:10.4236/ajcm.2012.22019

