Applied Mathematics
Vol.3 No.12(2012), Article ID:25347,3 pages DOI:10.4236/am.2012.312255
Some Results on (1,2n – 1)-Odd Factors
1Department of Basic Course, Air Force Logistics College, Xuzhou, China
2Aerial Four Station Department, Air Force Logistics College, Xuzhou, China
Email: liuman8866@163.com
Received September 4, 2012; revised November 1, 2012; accepted November 8, 2012
Keywords: Claw Free Graphs; 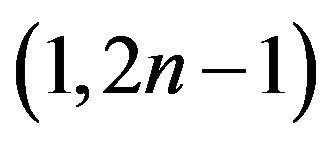 -Odd Factor; Factor-Criticality
-Odd Factor; Factor-Criticality
ABSTRACT
Let 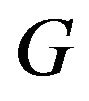 be a graph. If there exists a spanning subgraph
be a graph. If there exists a spanning subgraph 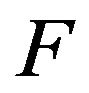 such that
such that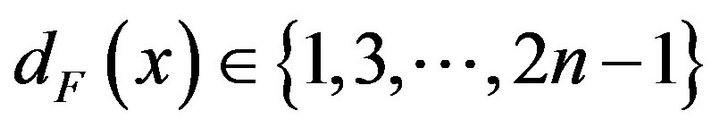 , then
, then 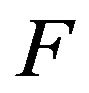 is called to be
is called to be 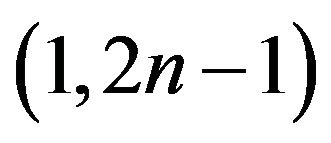 -odd factor of
-odd factor of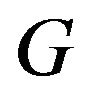 . Some sufficient and necessary conditions are given for
. Some sufficient and necessary conditions are given for  to have
to have  -odd factor where
-odd factor where  is any subset of
is any subset of 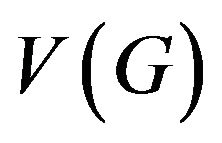 such that
such that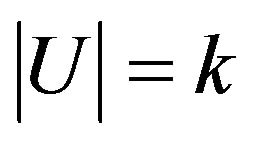 .
.
1. Introduction
We consider finite undirected graph without loops and multiple edges .Let 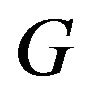 be a graph with vertex set
be a graph with vertex set 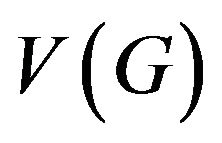 and edge set
and edge set 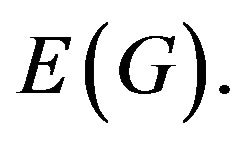 Given
Given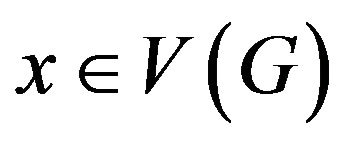 , the set of vertexes adjacent to
, the set of vertexes adjacent to ![]() is said to be the neighborhood of
is said to be the neighborhood of![]() , denoted by
, denoted by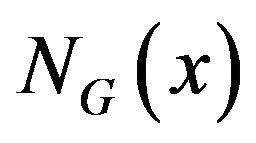 , and
, and  is called the degree of
is called the degree of![]() , If there exists a spanning subgraph
, If there exists a spanning subgraph 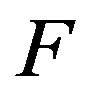 such that
such that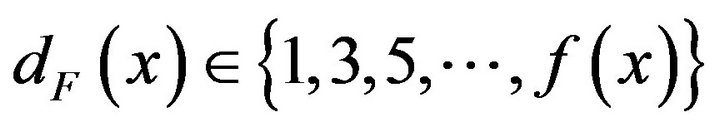 , then
, then 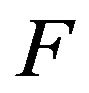 is called a
is called a 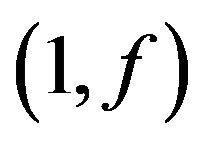 -odd factor of
-odd factor of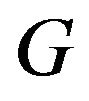 , especially, if for every
, especially, if for every  such that
such that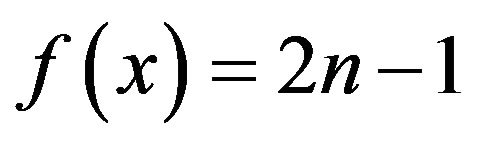 , then it is called
, then it is called 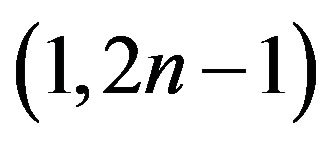 -odd factor. especially,
-odd factor. especially, 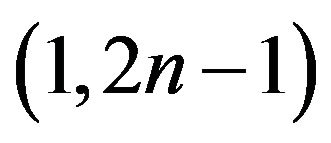 -odd factor is 1-factor when n = 1. For a subset
-odd factor is 1-factor when n = 1. For a subset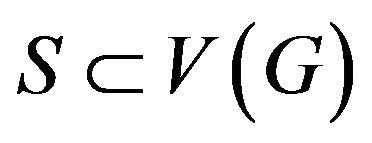 , let
, let  denote the subgraph obtained from
denote the subgraph obtained from  by deleting all the vertexes of
by deleting all the vertexes of ![]() together with the edges incident with the vertexes of
together with the edges incident with the vertexes of 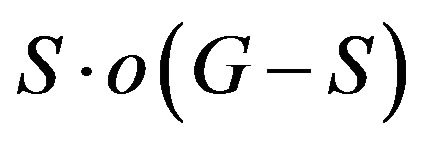 denotes the number of odd components of
denotes the number of odd components of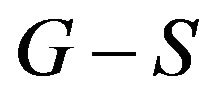 . The sufficient and necessary condition for graph to have
. The sufficient and necessary condition for graph to have 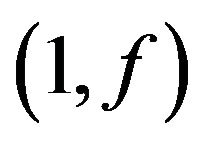 -odd factor was given in paper [1] Ryjacek [2] introduced one kind of new closure operation: let
-odd factor was given in paper [1] Ryjacek [2] introduced one kind of new closure operation: let  be a graph,
be a graph, 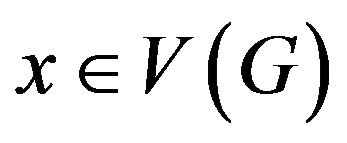 , if the subgraph induced by
, if the subgraph induced by 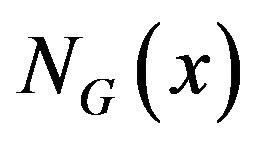 is not complete graph, we consider the following operation: jointing every pair of nonadjacent vertex in
is not complete graph, we consider the following operation: jointing every pair of nonadjacent vertex in 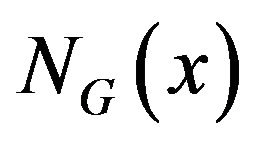 makes
makes 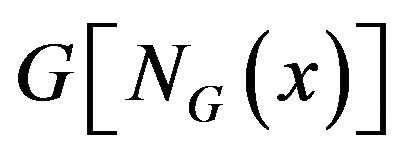 to be a complete graph. The operation is called local completely at point
to be a complete graph. The operation is called local completely at point![]() . If the subgraph induced by
. If the subgraph induced by  is k-vertex connected, then vertex
is k-vertex connected, then vertex ![]() is called local
is called local 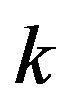 -vertex connected graph
-vertex connected graph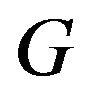 .
.
Favaron gave the concept of k-factor critical in paper [3]. If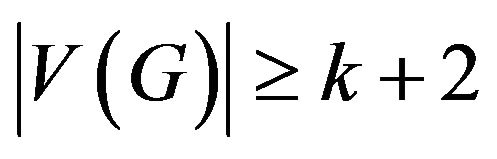 , and for any
, and for any 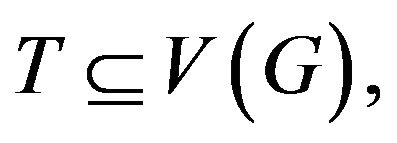
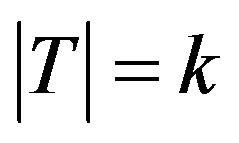 ,
, 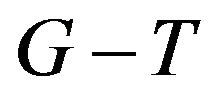 is perfect matching ,then we call the graph
is perfect matching ,then we call the graph 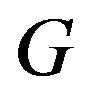 to be k-factor critical. Of course, 0-factor critical graph is perfect matching. Favaron popularized a series of the properties of perfect matching to k-factor critical, at the same time the sufficient and necessary conditions were given for the graph to be k-factor critical, more results in factor critical graphs were referred to [4,5].
to be k-factor critical. Of course, 0-factor critical graph is perfect matching. Favaron popularized a series of the properties of perfect matching to k-factor critical, at the same time the sufficient and necessary conditions were given for the graph to be k-factor critical, more results in factor critical graphs were referred to [4,5].
For  -odd factor, Chen Ci-ping [6] gave a sufficient condition for a matching with exactly
-odd factor, Chen Ci-ping [6] gave a sufficient condition for a matching with exactly 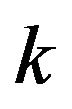 edges extended to
edges extended to  -odd factor. Teng Cong generalized some results on kto
-odd factor. Teng Cong generalized some results on kto  -odd factor, and proved that the connected graph
-odd factor, and proved that the connected graph  exists
exists 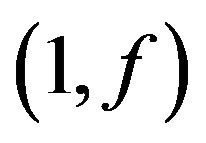 -odd factor with k-extended, then for the any edge
-odd factor with k-extended, then for the any edge ![]() of
of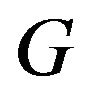 ,
, 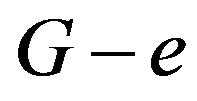 exists
exists -odd factor [7] with
-odd factor [7] with 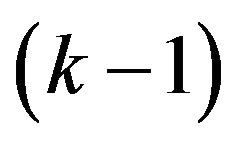 -extended. If there exists
-extended. If there exists 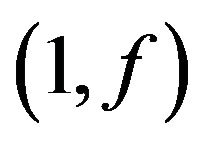 -odd factor of
-odd factor of 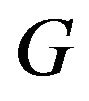 with k-extended, then there exists
with k-extended, then there exists  -odd factor with
-odd factor with 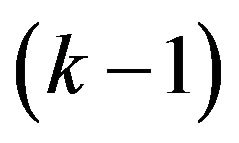 -extended, and
-extended, and  is
is 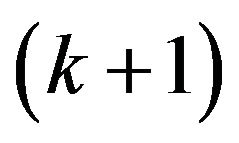 -connected [8]. We will popularize some results of k-factor critical to
-connected [8]. We will popularize some results of k-factor critical to 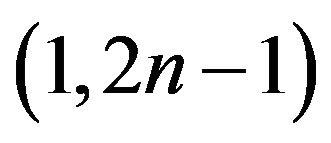 -odd factor, and gain several sufficient and necessary conditions for
-odd factor, and gain several sufficient and necessary conditions for 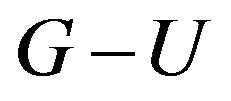 to have
to have  -odd factor for any subset
-odd factor for any subset  of
of 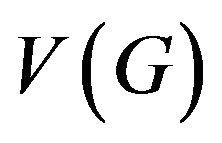 such that
such that .
.
2. Main Results
We start with some lemmas as following.
Lemma 1 The sufficient and necessary condition for a graph 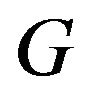 to have
to have  -odd factor after cutting off any
-odd factor after cutting off any 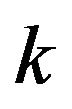 vertexes is
vertexes is
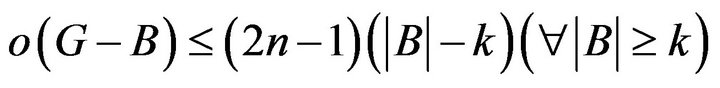
Proof For set 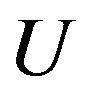 with any
with any 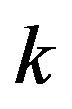 vertexes,
vertexes, 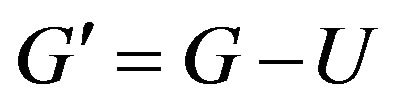 has
has 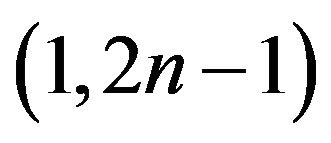 -odd factor, next we will prove
-odd factor, next we will prove
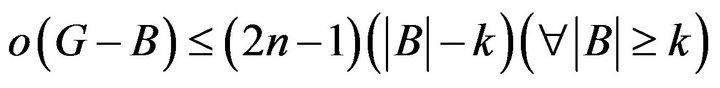
For any 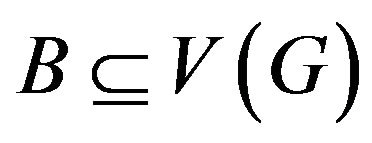 and
and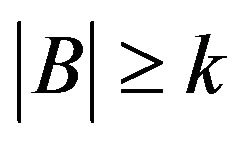 , let
, let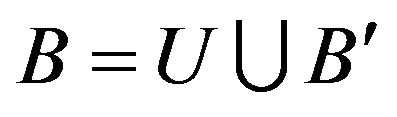 , where
, where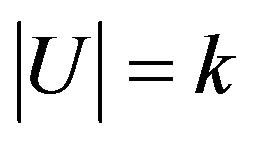 . Since
. Since 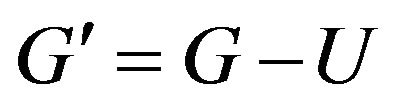 has a
has a 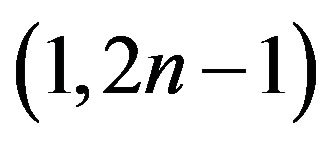 -odd factor, by the sufficient and necessary condition for graph with
-odd factor, by the sufficient and necessary condition for graph with  -odd factor we have
-odd factor we have
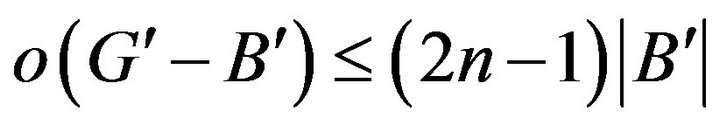 .
.
Noting that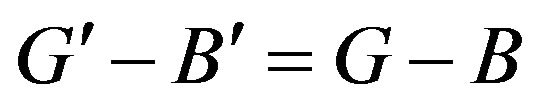 Therefore
Therefore
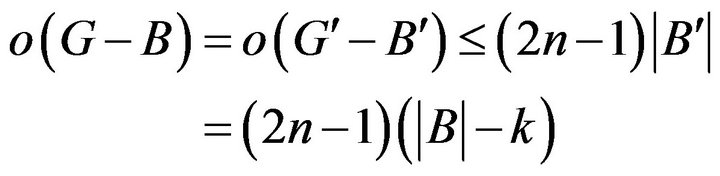
For any 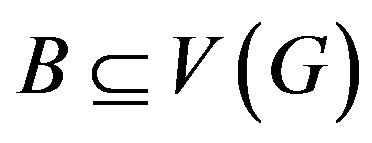 and
and 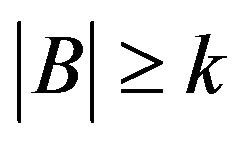 we have
we have
 the following that the set
the following that the set 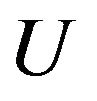 with any
with any 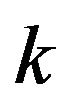 vertexes,
vertexes, 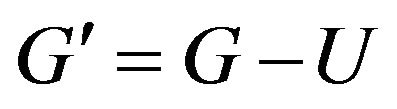 has
has 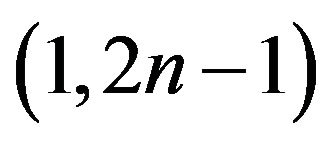 -odd factor, i.e., for any
-odd factor, i.e., for any , there
, there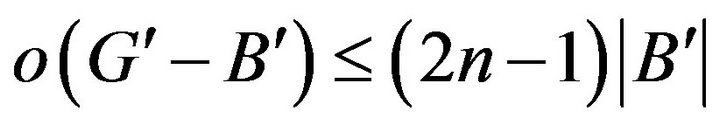 .
.
Noting that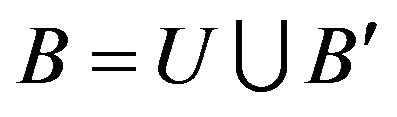 , of course
, of course .
.
By
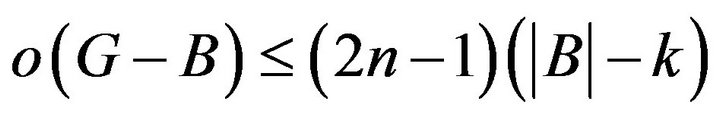 and
and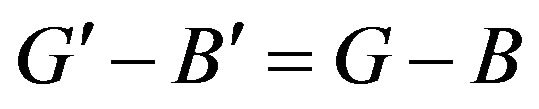 , we have
, we have
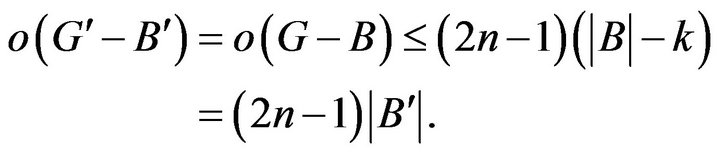
Lemma 2 [9] Connected claw free graphs of even order have 1-factor.
Lemma 3 Connected claw free graphs of even order have 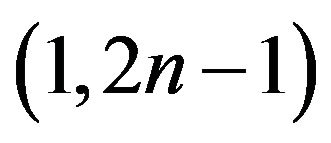 -odd factor.
-odd factor.
Proof If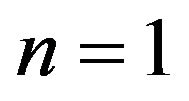 , by lemma 2, the conclusion is proved. Assume that
, by lemma 2, the conclusion is proved. Assume that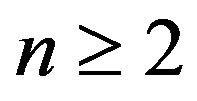 .
.
By contradiction, we assume that 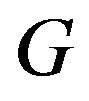 has no
has no  -odd factor, i.e.,
-odd factor, i.e., 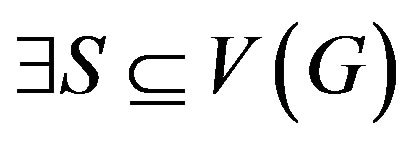 such that
such that
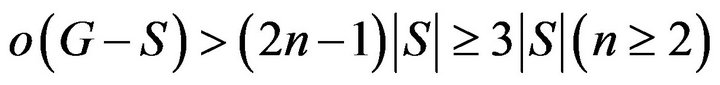 .
.
then there exists 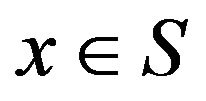 such that
such that ![]() connecting with three components of
connecting with three components of  at least. If not, for
at least. If not, for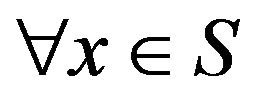 ,
, ![]() connects with two components of
connects with two components of 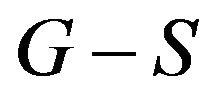 at most, consequently
at most, consequently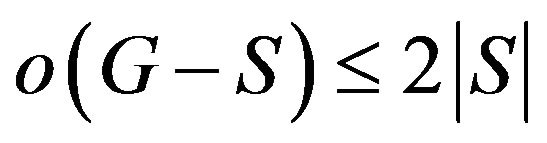 , contradiction.
, contradiction.
Theorem 1 Let 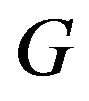 be graph with
be graph with ![]() order,
order, 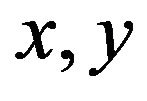 are a couple of nonadjacent vertexes and satisfy
are a couple of nonadjacent vertexes and satisfy
 then the sufficient and necessary condition for
then the sufficient and necessary condition for 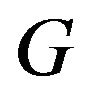 removing any
removing any 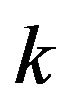 vertexes with
vertexes with  -odd factor is that
-odd factor is that 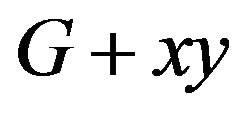 getting rid of any
getting rid of any 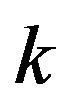 vertexes with
vertexes with  -odd factor.
-odd factor.
Proof The necessary condition is obvious, next we prove the sufficient condition.
By contradiction, let 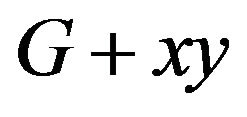 remove any
remove any 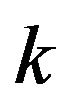 vertexes with
vertexes with 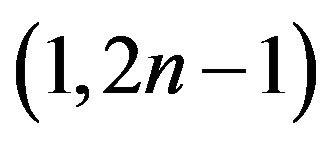 -odd factor, but there exist
-odd factor, but there exist 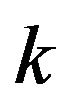 vertexes after getting rid of the
vertexes after getting rid of the  vertexes of
vertexes of 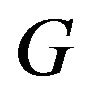 without
without  -odd factor. By lemma 1, there exists
-odd factor. By lemma 1, there exists

such that
 and
and
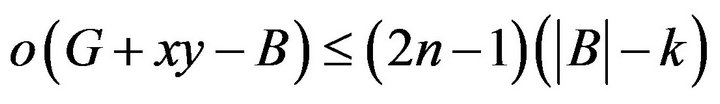 .
.
at the same time, by  and
and
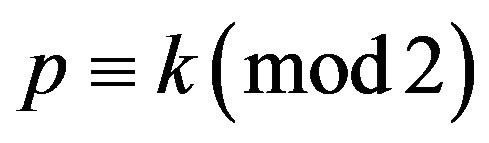 Thereby
Thereby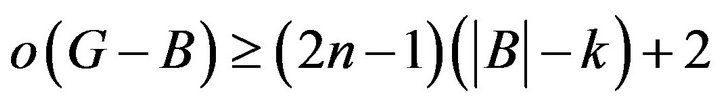 .
.
Furthermore, by Consequently
Consequently

Accordingly
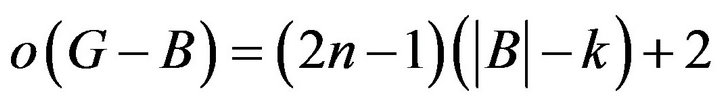
and
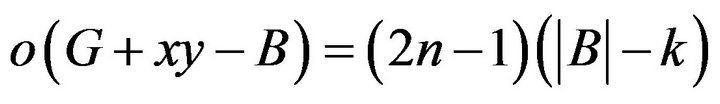 .
.
It shows that 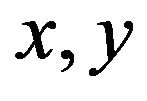 are part of two odd components
are part of two odd components  of
of  respectively.
respectively.
Thus
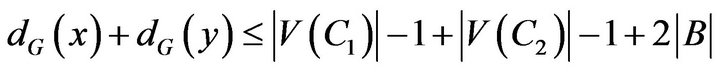 .
.
On the other hand, by hypothesis
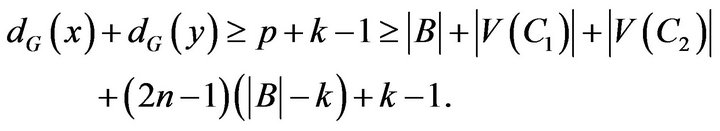
But
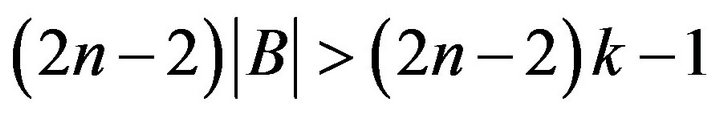 .
.
Contradiction.
Theorem 2 Let 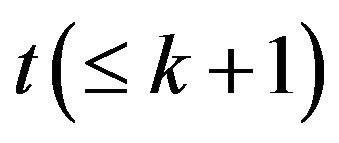 connected graph
connected graph 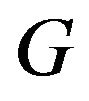 be
be ![]() order,
order,  are a couple of any nonadjacent vertexes of
are a couple of any nonadjacent vertexes of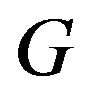 , and satisfy
, and satisfy
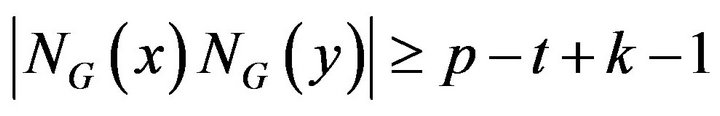 then the sufficient and necessary condition for
then the sufficient and necessary condition for  removing any
removing any 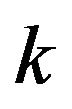 vertexes with
vertexes with 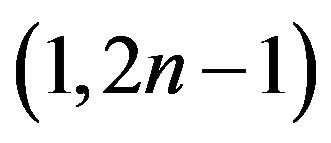 -odd factor is
-odd factor is 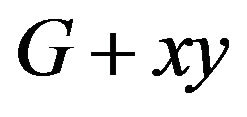 getting rid of any
getting rid of any  vertexes with
vertexes with
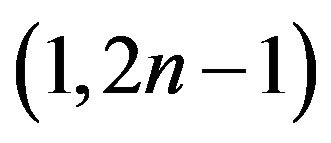 -odd factor.
-odd factor.
Proof 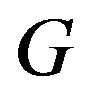 is a spanning subgraph of
is a spanning subgraph of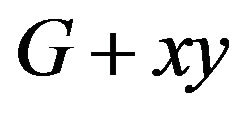 , so the necessary condition is obvious.
, so the necessary condition is obvious.
Next we prove the sufficient condition. We suppose 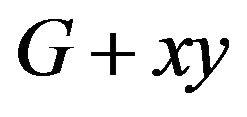 getting rid of any
getting rid of any 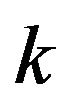 vertexes with
vertexes with 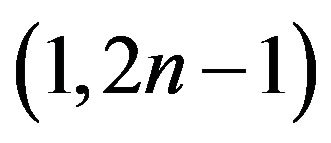 - odd factor, but
- odd factor, but 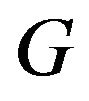 is not, i.e. there exist
is not, i.e. there exist
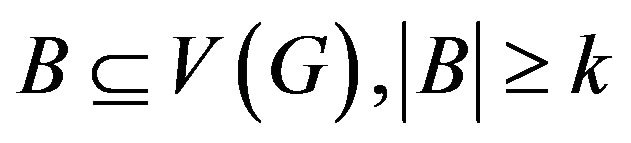
such that
 .
.
Be similar to the discussion of theorem 1
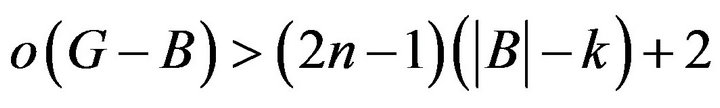
and
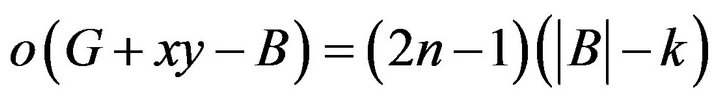 .
.
thereby  are part of two odd components
are part of two odd components 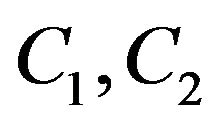 of
of  respectively.
respectively.
Noting that
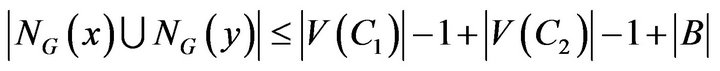 (1)
(1)
By hypothesis
 (2)
(2)
Combining (1) with (2)
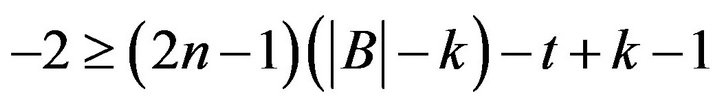
Consequently
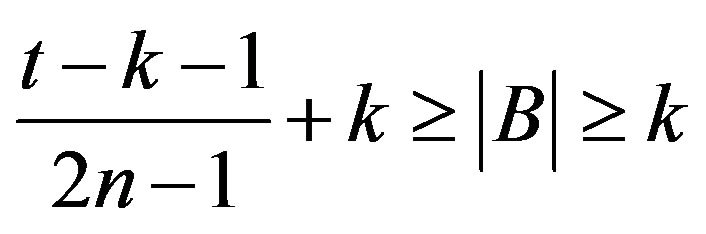 but
but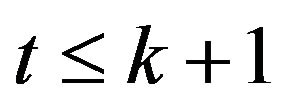 .
.
Contradiction.
Theorem 3 Let  be claw free graphs,
be claw free graphs, ![]() be partial
be partial 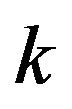 connection point.
connection point. 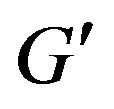 be graph obtained by locally fully on
be graph obtained by locally fully on 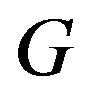 in
in ![]() point, then for
point, then for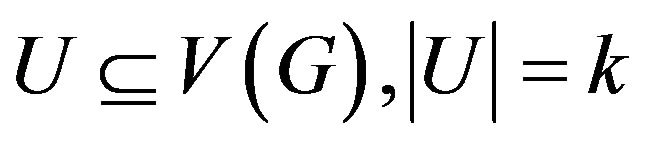 , the sufficient and necessary condition for
, the sufficient and necessary condition for 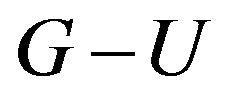 with
with  -odd factor is
-odd factor is 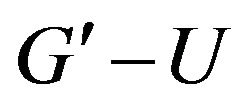 with
with  -odd factor.
-odd factor.
Proof 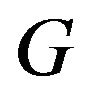 is a spanning subgraph of
is a spanning subgraph of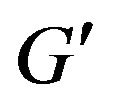 , so the necessary condition is obvious.
, so the necessary condition is obvious.
Next we prove the sufficient condition. Let 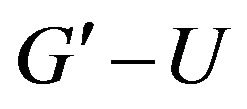 have
have  -odd factor,
-odd factor,  have no
have no 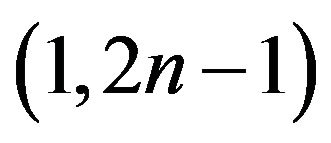 - odd factor.
- odd factor. 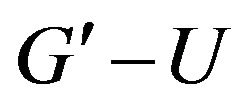 has
has 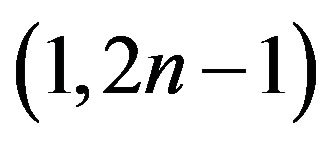 -odd factor,
-odd factor, 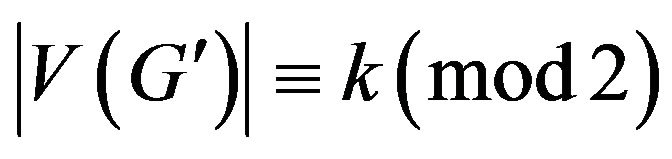 , so
, so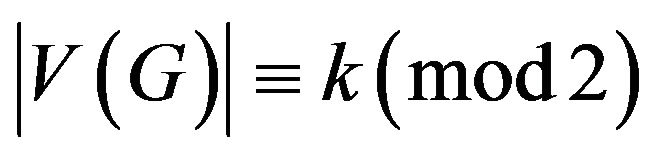 .
.
On the other hand, 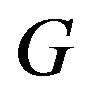 is claw free, so
is claw free, so 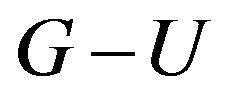 is claw free.
is claw free.
By lemma 2, lemma 3, 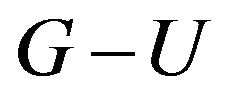 has two odd components at least.
has two odd components at least.
If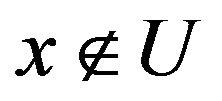 , let
, let 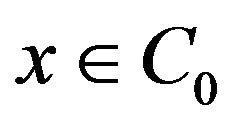 (
(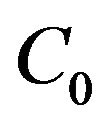 is branch of
is branch of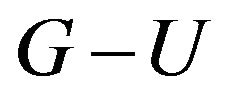 ). Now,
). Now, 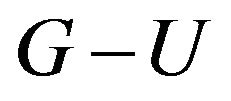 has the same odd components as
has the same odd components as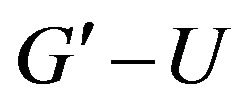 , therefore,
, therefore, 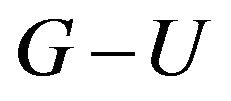 has
has 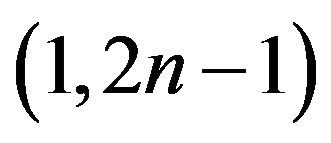 -odd factor. which is contradiction.
-odd factor. which is contradiction.
Next let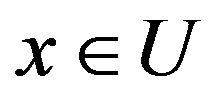 , since
, since 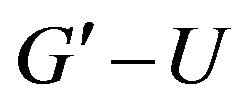 has not odd components, for any odd components of
has not odd components, for any odd components of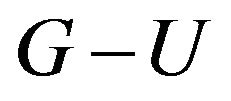 ,
,

is complete.
Let 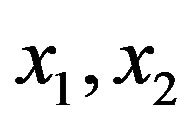 be adjacent vertexes of
be adjacent vertexes of ![]() in two odd components of
in two odd components of 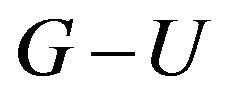 respectively.
respectively.
Then 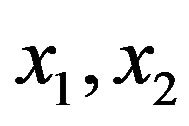 is nonadjacent in the induced subgraph of
is nonadjacent in the induced subgraph of
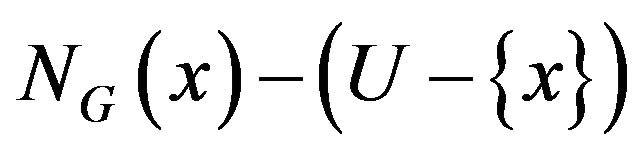 , which is contradiction to the fact that
, which is contradiction to the fact that
![]() is a locally
is a locally 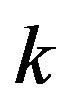 connected vertex, since
connected vertex, since
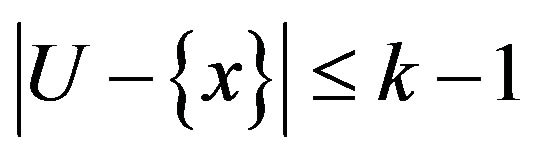
The proof is complete.
REFERENCES
- Y. Cui and M Cano, “Some Results on Odd Factors of Graphs,” Journal of Graph Theory, Vol. 12, No. 3, 1988, pp. 327-333. doi:10.1002/jgt.3190120305
- Z. Ryjáček, “On a Closure Concept in Claw-Free Graphs,” Journal of Combinatorial Theory, Series B, Vol. 70, No. 2, 1997, pp. 217-224.
- O. Favaron, “On n-Factor-Critical Graphs,” Discussiones Mathematicae Graph Theory, Vol. 16, 1996, pp. 41-51.
- N. Ananchuen and A. Daito, “Factor Criticality and Complete Closure of Graphs,” Discrete Mathematics, Vol. 265, No. 1-3, 2003, pp. 13-21.
- G. Z. Liu and Q. L. Yu, “Toughness and Perfect Matchings in Graphs,” Ars combinatorial, Vol. 48, 1998, pp. 129-134.
- C. P. Chen, “The Extendability of Matchings,” Journal of Beijing Agricultural Engineering University, Vol. 12, No. 4, 1992, pp. 36-39.
- C. Teng, “Some New Results on
 -Odd Factor of Graphs,” Journal of Shandong University, Vol. 31, No. 2, 1996, pp. 160-163.
-Odd Factor of Graphs,” Journal of Shandong University, Vol. 31, No. 2, 1996, pp. 160-163. - C. Teng, “Some New Results on
 -Odd Factor of Graphs,” Pure and Applied Mathematics, Vol. 10, 1994, pp. 188-192.
-Odd Factor of Graphs,” Pure and Applied Mathematics, Vol. 10, 1994, pp. 188-192. - D. P. Sumner, “Graphs with 1-Factors,” Proceedings of the American Mathematical Society, Vol. 42, No. 1, 1974, pp. 8-12.

