Applied Mathematics
Vol. 3 No. 11 (2012) , Article ID: 24377 , 7 pages DOI:10.4236/am.2012.311222
Limit Theorems for a Storage Process with a Random Release Rule
Department of Mathematics, Faculty of Science, King Abdulaziz University, Jeddah, Saudi Arabia
Email: mezianilakhdar@hotmail.com
Received August 29, 2012; revised October 8, 2012; accepted October 15, 2012
Keywords: Storage Process; Random Walk; Strong Law of Large Numbers; Central Limit Theorem
ABSTRACT
We consider a discrete time Storage Process 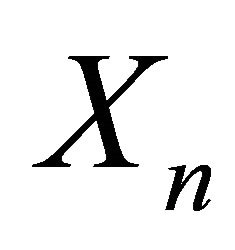 with a simple random walk input
with a simple random walk input 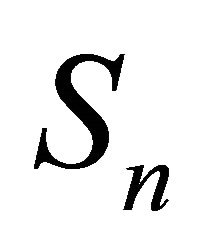 and a random release rule given by a family
and a random release rule given by a family 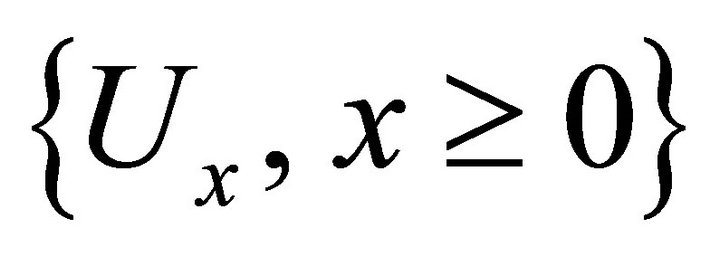 of random variables whose probability laws
of random variables whose probability laws 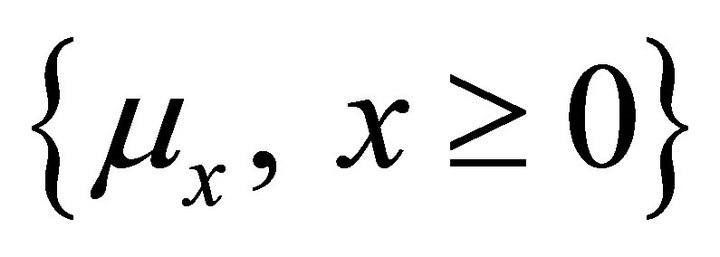 form a convolution semigroup of measures, that is,
form a convolution semigroup of measures, that is, 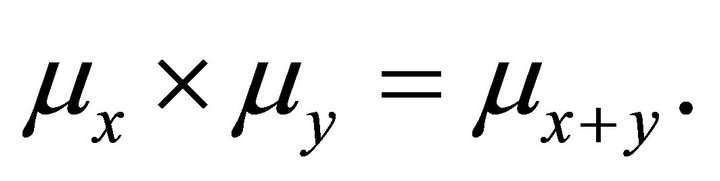 The process
The process 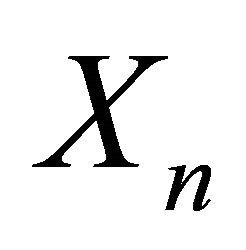 obeys the equation:
obeys the equation: 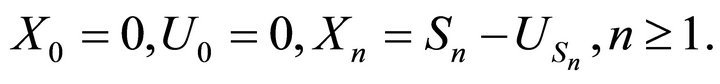 Under mild assumptions, we prove that the processes
Under mild assumptions, we prove that the processes  and
and 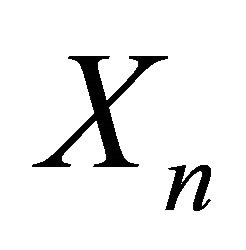 are simple random walks and derive a SLLN and a CLT for each of them.
are simple random walks and derive a SLLN and a CLT for each of them.
1. Introduction and Assumptions
The formal structure of a general storage process displays two main parts: the input process and the release rule. The input process, mostly a compound Poisson process , describes the material entering in the system during the interval
, describes the material entering in the system during the interval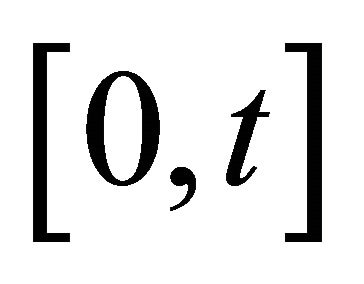 . The release rule is usually given by a function
. The release rule is usually given by a function 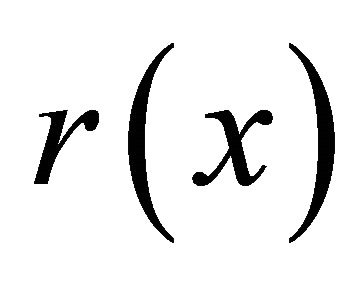 representing the rate at which material flows out of the system when its content is
representing the rate at which material flows out of the system when its content is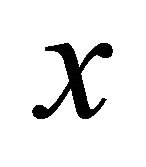 . So the state
. So the state 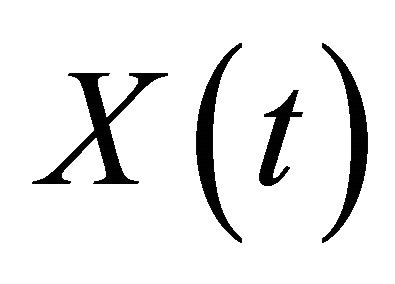 of the system at time
of the system at time  obeys the well known equation:
obeys the well known equation:
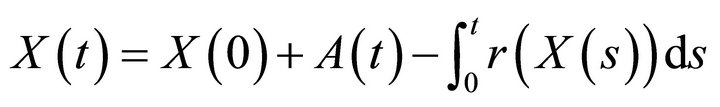 .
.
Limit theorems and approximation results have been obtained for the process 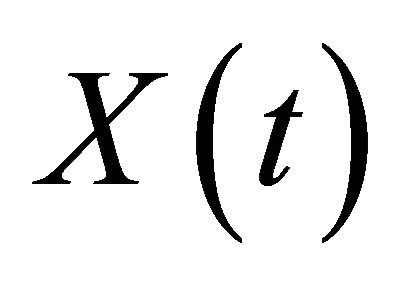 by several authors, see [1-5] and the references therein. In this paper we study a discrete time new storage process with a simple random walk input
by several authors, see [1-5] and the references therein. In this paper we study a discrete time new storage process with a simple random walk input 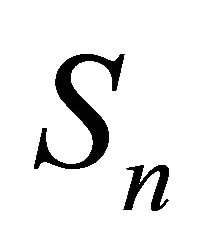 and a random release rule given by a family of random variables
and a random release rule given by a family of random variables 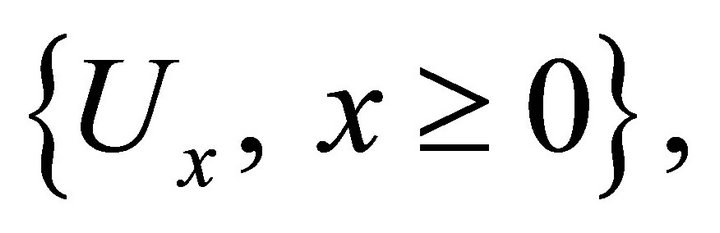 where
where 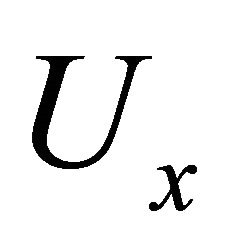 has to be interpreted as the amount of material removed when the state of the system is
has to be interpreted as the amount of material removed when the state of the system is  Hence the evolution of the system obeys the following equation:
Hence the evolution of the system obeys the following equation: 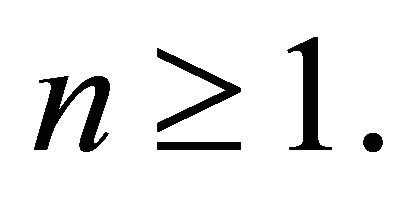
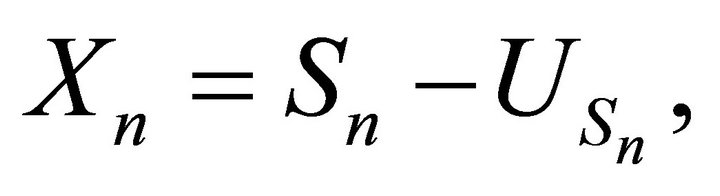
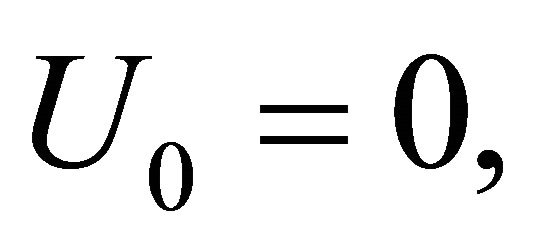
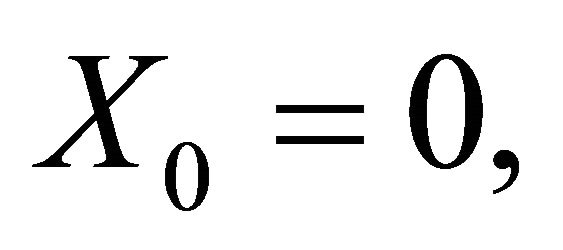 where
where ,
, 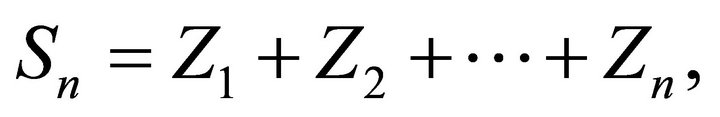 for i.i.d. positive random variables
for i.i.d. positive random variables 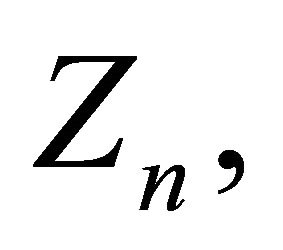 with
with  and
and 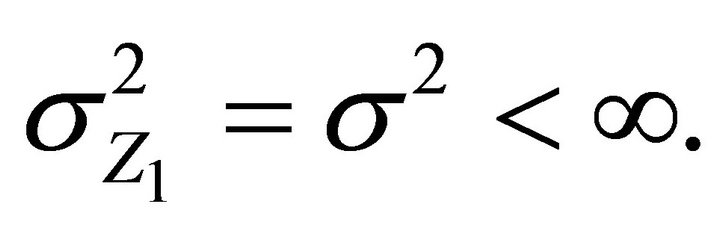
We will make the following assumptions:
1.1. The probability distributions  of the random variables
of the random variables  form a convolution semigroup of measures:
form a convolution semigroup of measures:
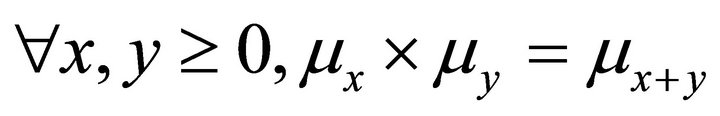 , (1.1)
, (1.1)
We will assume that for each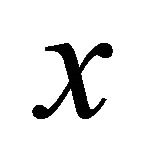 ,
, 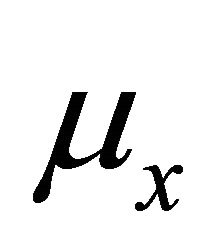 is supported by the interval
is supported by the interval  that is,
that is, 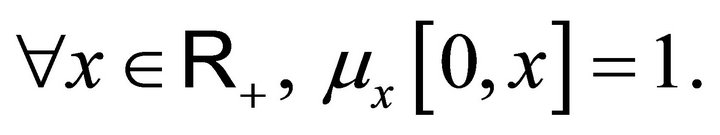 Consequently, for
Consequently, for 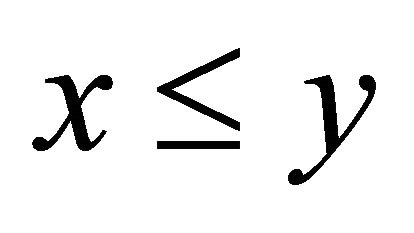 the distribution of
the distribution of 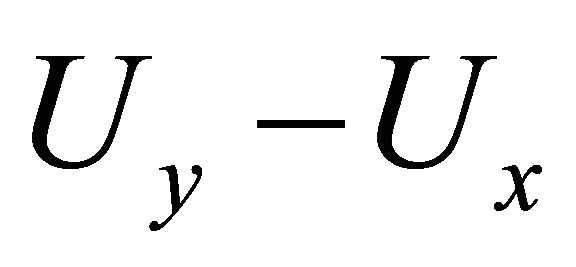 is the same as that of
is the same as that of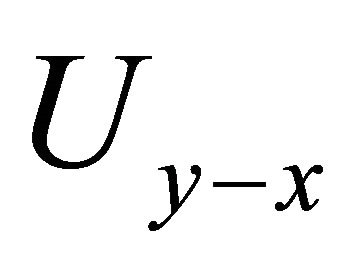 , (see 2.2
, (see 2.2 ).
).
1.2. Also we will need some smoothness properties for the stochastic process  These will be achieved if we impose the following continuity condition:
These will be achieved if we impose the following continuity condition:
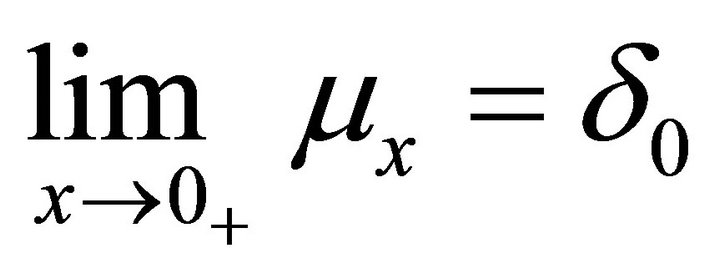 (1.2)
(1.2)
where 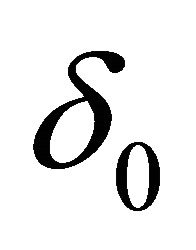 is the unit mass at 0 and the limit is in the sense of the weak convergence of measures.
is the unit mass at 0 and the limit is in the sense of the weak convergence of measures.
1.3. The two families of random variables  and
and  are independent.
are independent.
2. Construction of the Processes  and
and 
2.1. Let 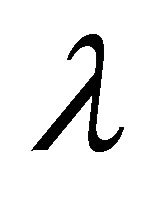 be a probability measure on the Borel sets
be a probability measure on the Borel sets 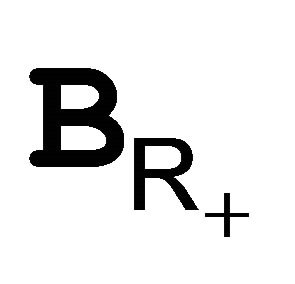 of the positive real line
of the positive real line 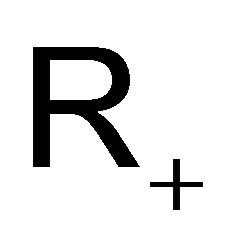 and form the infinite product space
and form the infinite product space 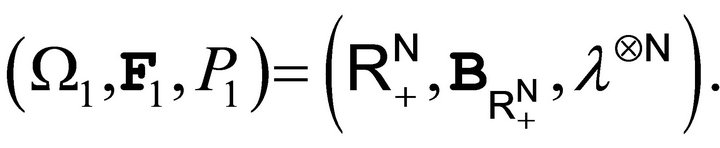 Now, as usual define random variables
Now, as usual define random variables 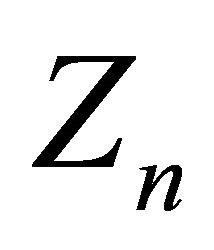 on
on  by:
by:
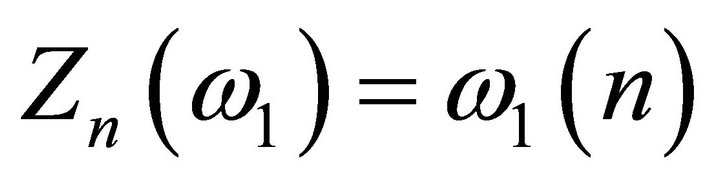 , if
, if 
Then the 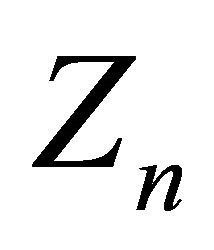 are independent identically distributed with common distribution
are independent identically distributed with common distribution  We will assume that
We will assume that 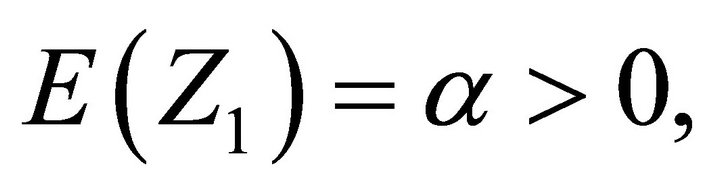 and
and 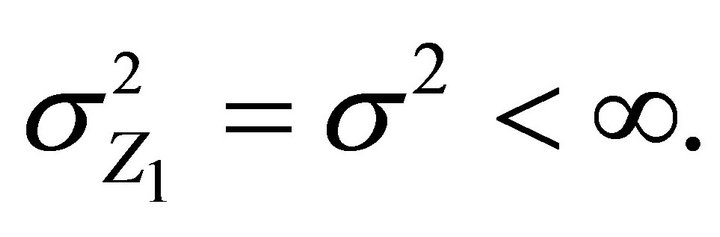
2.2. Let 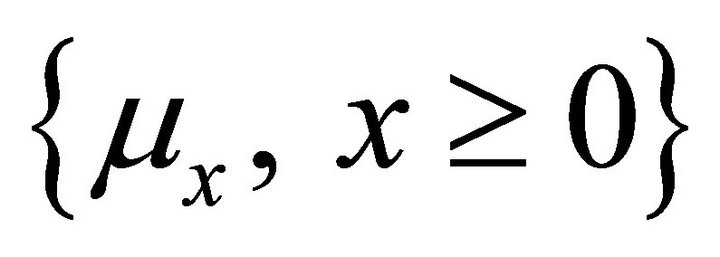 be a semigroup of convolution of probability measures on
be a semigroup of convolution of probability measures on 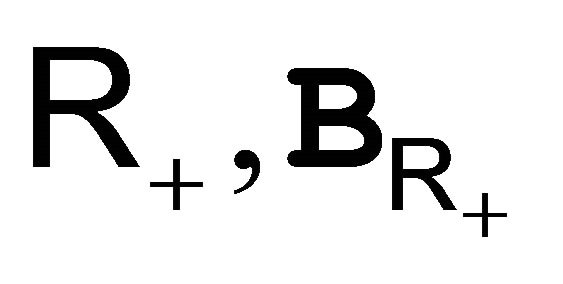 with
with 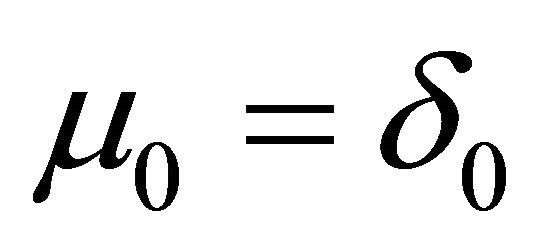 and satisfying (1.2) then, it is well known, that there is a probability space
and satisfying (1.2) then, it is well known, that there is a probability space  and a family
and a family 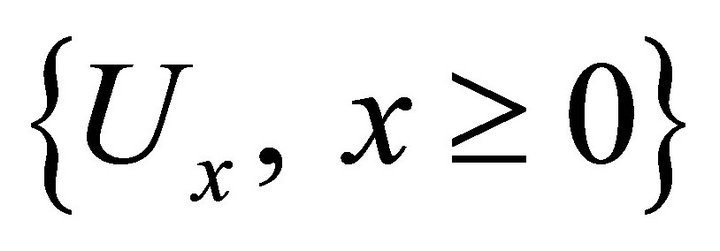 of positive random variables defined on this space such that the following properties hold:
of positive random variables defined on this space such that the following properties hold:
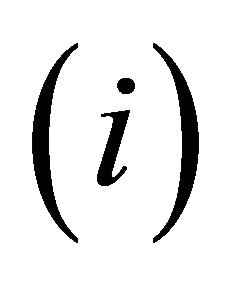 . Under
. Under  the distribution of
the distribution of  is
is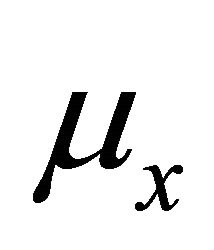 ,
, 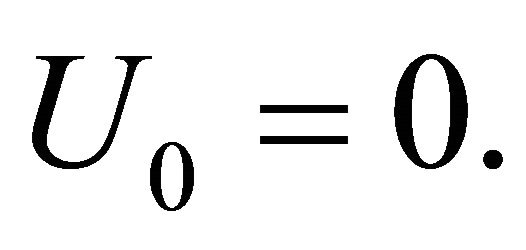
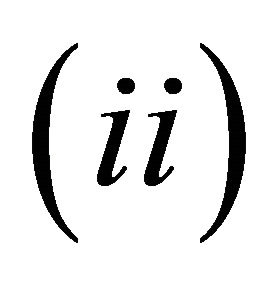 . For
. For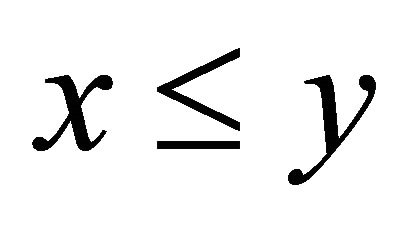 , the random variables
, the random variables 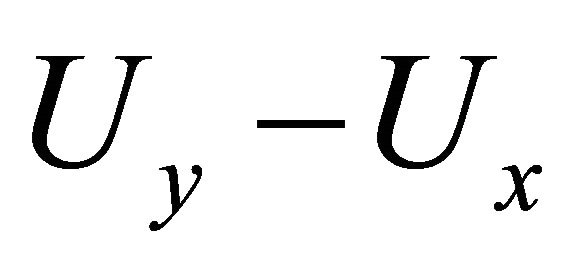 and
and 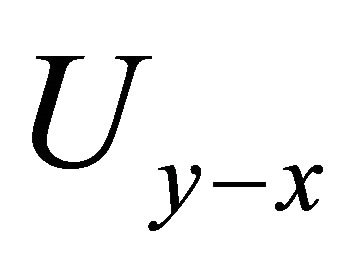 have under
have under 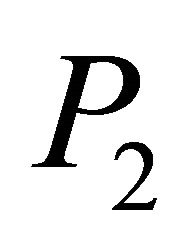 the same distribution
the same distribution 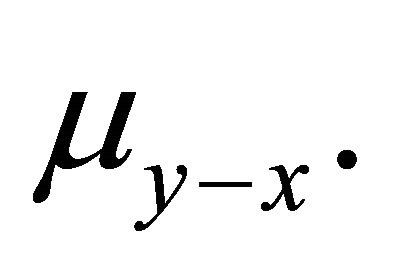
 . For every
. For every 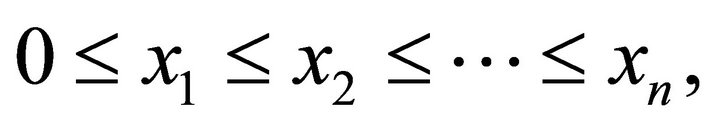 the increments
the increments  are independent.
are independent.
 . For almost all
. For almost all 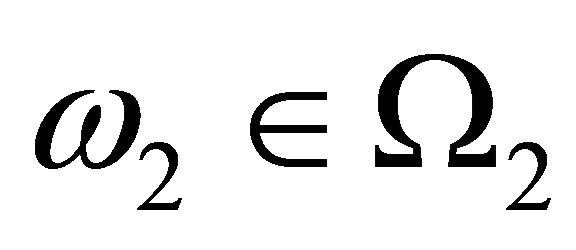 the function
the function
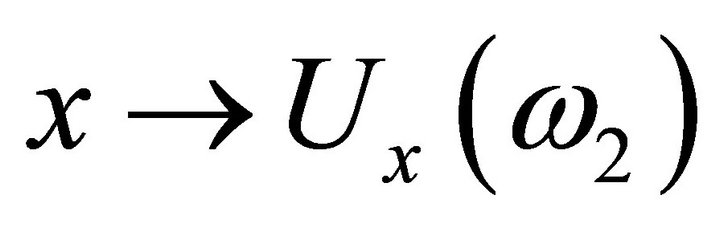 is right continuous with left hand limit (cadlag).
is right continuous with left hand limit (cadlag).
From  we deduce:
we deduce:
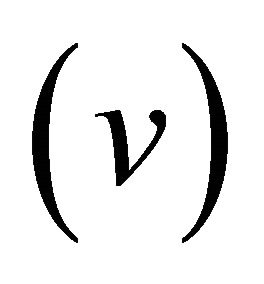 . The function
. The function 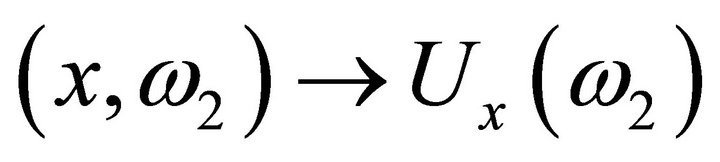 is measurable on the product space
is measurable on the product space 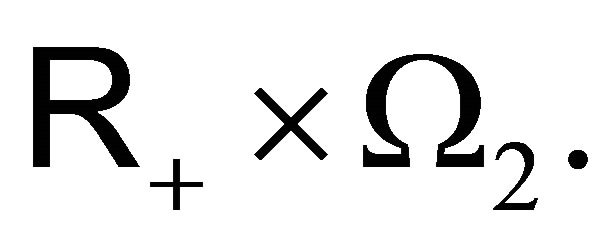
2.3. The basic probability space for the storage process  will be the product
will be the product 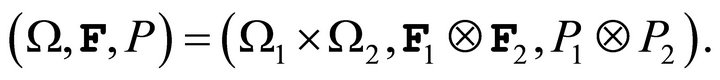 Then we define
Then we define  by the following recipe:
by the following recipe:
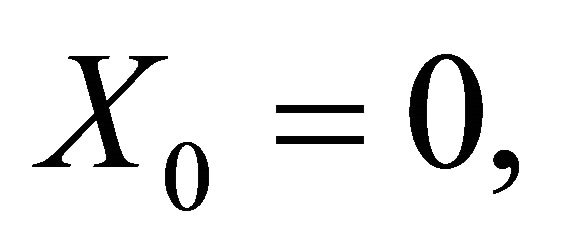 (2.3)
(2.3)
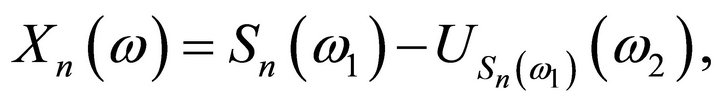 if
if 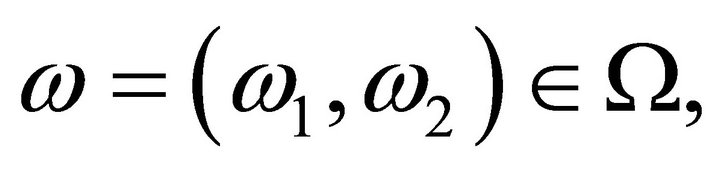
 where
where 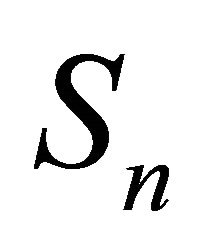 is the simple random walk with:
is the simple random walk with: 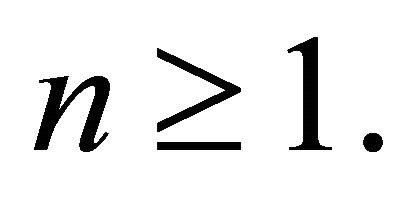

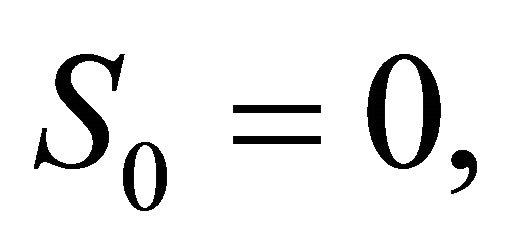
2.4. Since 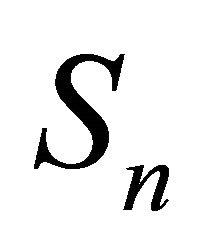 is a simple random walk, the random variables
is a simple random walk, the random variables 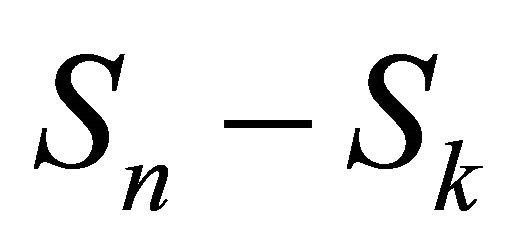 and
and 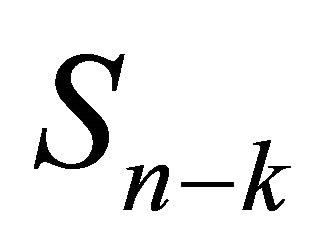 have the same distribution for
have the same distribution for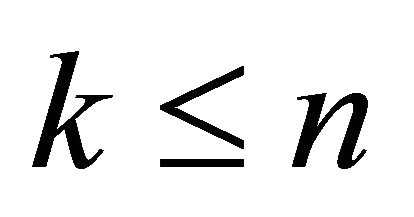 .
.
3. The Main Results
The main objective is to establish limit theorems for the processes 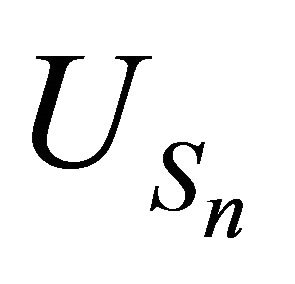 and
and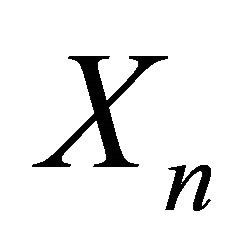 . Since the behavior of
. Since the behavior of  is well understood, we will focus attention on the structure of the process
is well understood, we will focus attention on the structure of the process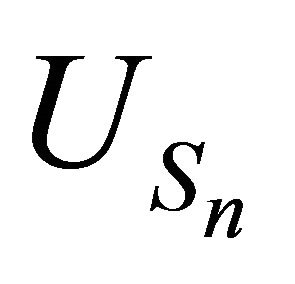 . The outstanding fact is that
. The outstanding fact is that 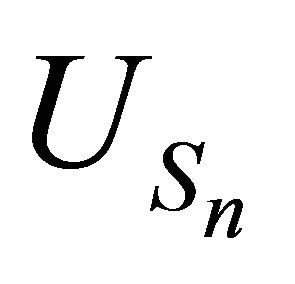 itself is a simple random walk. First we need some preparation.
itself is a simple random walk. First we need some preparation.
3.1. Proposition: For every measurable bounded function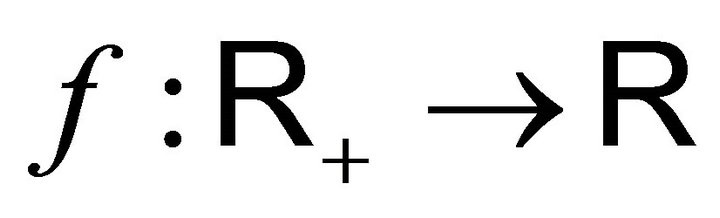 , the function
, the function
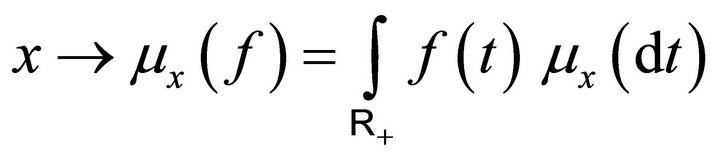 is measurable. Thus for any Borel set
is measurable. Thus for any Borel set  of
of  the function
the function 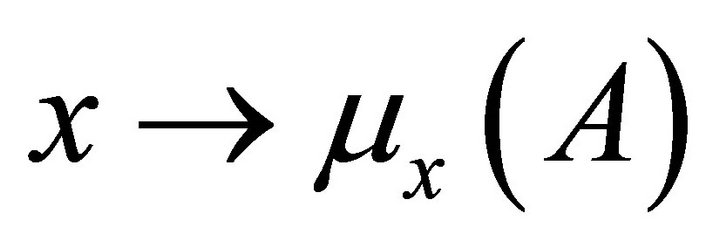 is measurable.
is measurable.
Proof: Assume first  continuous and bounded, then from (1.2) we have
continuous and bounded, then from (1.2) we have
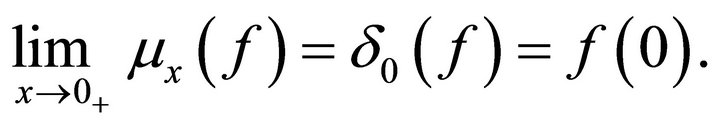
Now by (1.1) we have
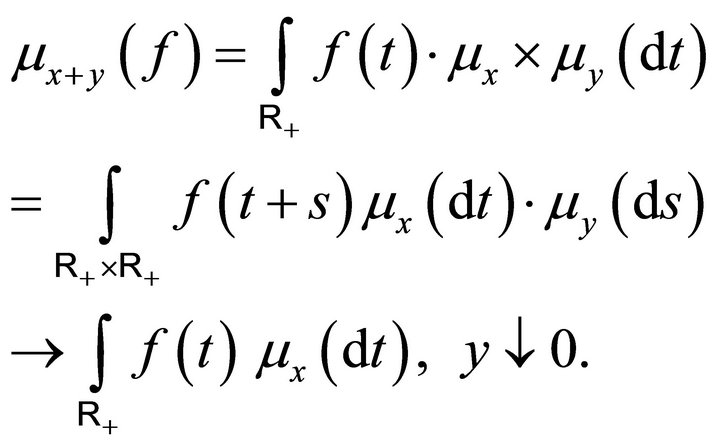
by (1.2) and the bounded convergence theorem. Consequently the function 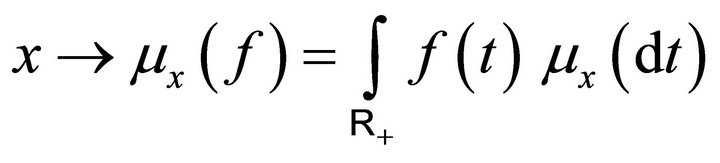 is right continuous for all
is right continuous for all  hence it is measurable if
hence it is measurable if 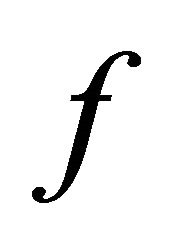 is continuous and bounded. Next consider the class of functions:
is continuous and bounded. Next consider the class of functions:

then  is a vector space satisfying the conditions of Theorem I,T20 in [6]. Moreover, by what just proved,
is a vector space satisfying the conditions of Theorem I,T20 in [6]. Moreover, by what just proved,  contains the continuous bounded functions
contains the continuous bounded functions 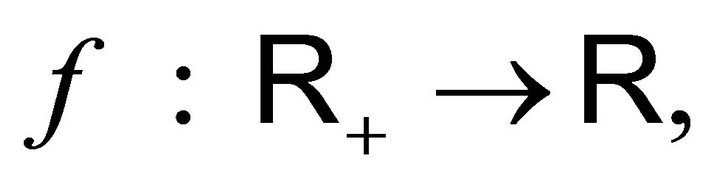 therefore
therefore  contains every measurable bounded function
contains every measurable bounded function 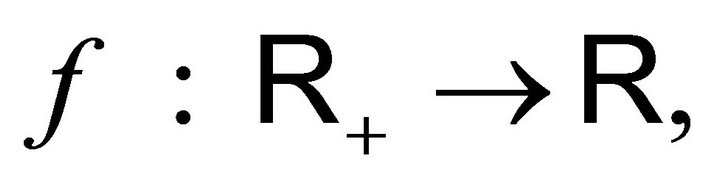 ■
■
3.2. Remark: Let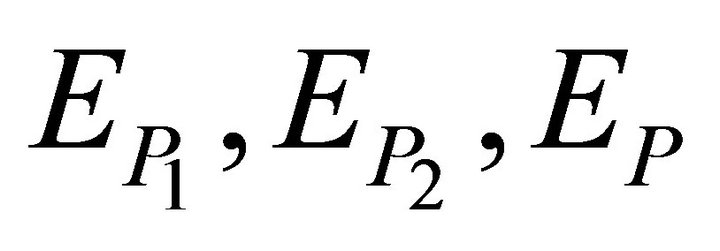 , be the expectation operators with respect to
, be the expectation operators with respect to 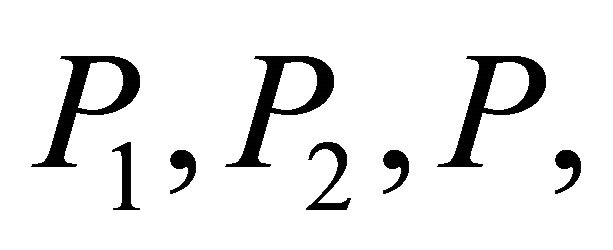 respectively. Since
respectively. Since 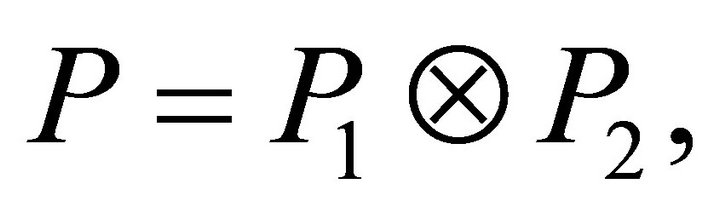 we have
we have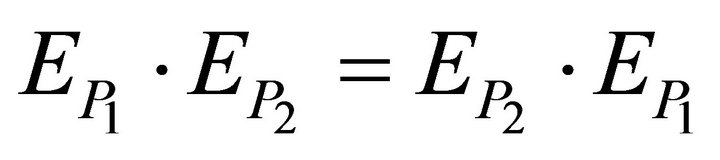 , by Fubini theorem. ■
, by Fubini theorem. ■
3.3. Proposition: Let 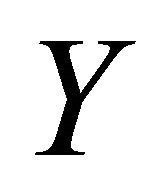 be a positive random variable on
be a positive random variable on 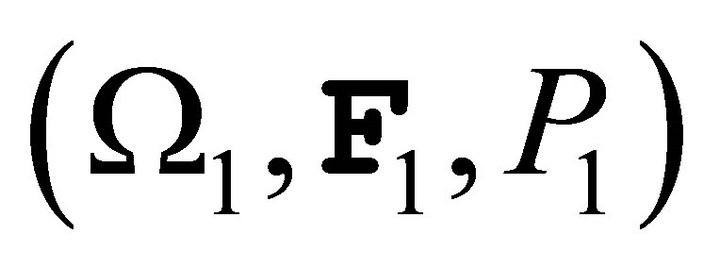 with probability distribution
with probability distribution 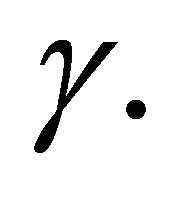 Then the function
Then the function 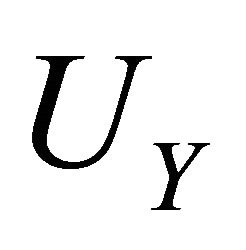 defined on
defined on  by:
by:
 (3.3)
(3.3)
is a random variable such that
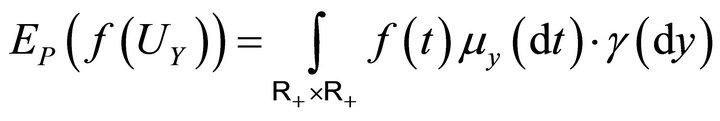
for every measurable positive function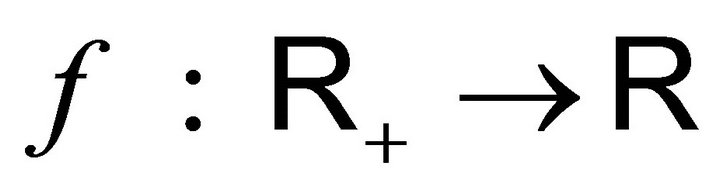 . In particular the probability distribution of
. In particular the probability distribution of 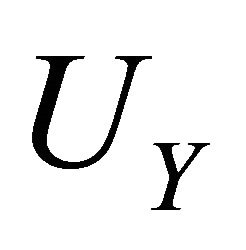 is given by:
is given by:
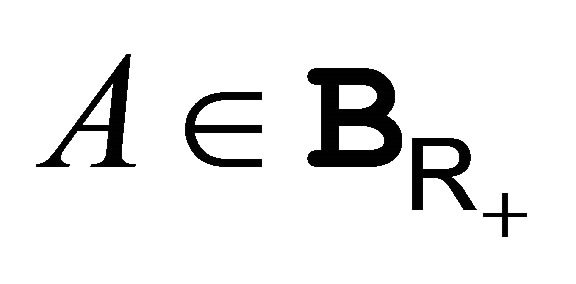 (3.5)
(3.5)
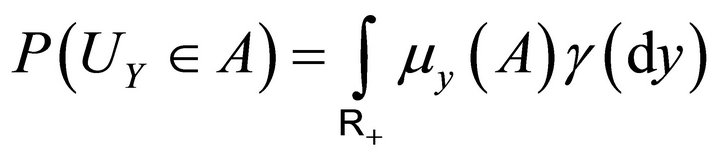
and its expectation is equal to
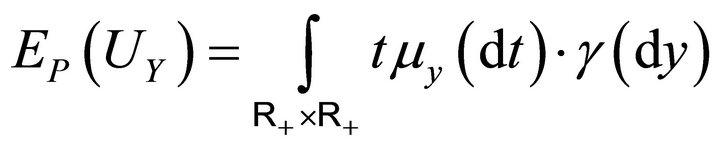 (3.6)
(3.6)
Proof: Define 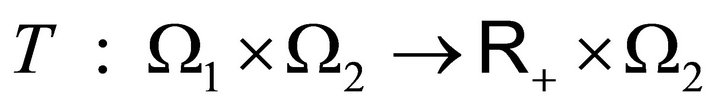 by
by
 and
and 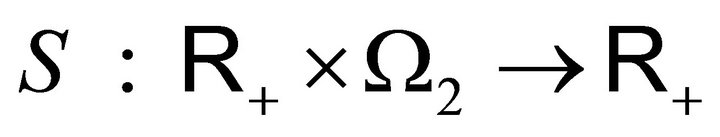 by
by
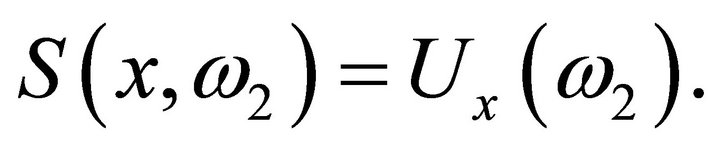 It is clear that
It is clear that 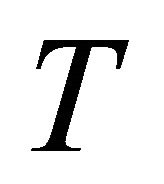 is measurable. Also
is measurable. Also  is measurable by 2.2
is measurable by 2.2 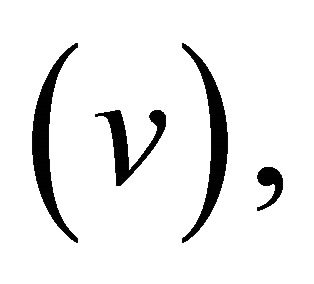 so
so 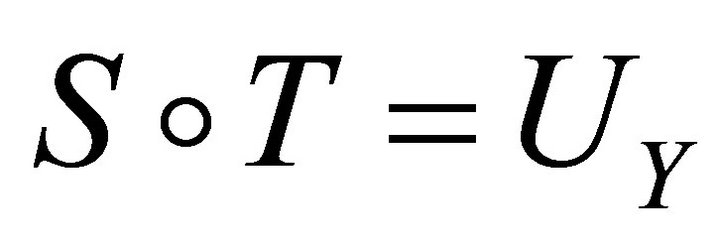 is measurable.
is measurable.
(3.4) is a simple change of variable formula since 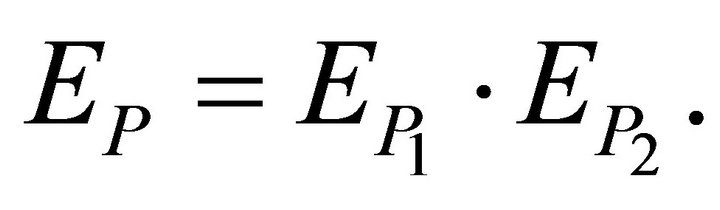 ■
■
3.7. Proposition: For all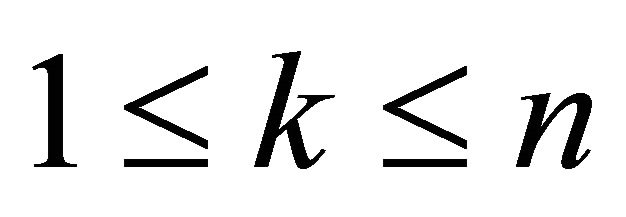 , the random variables
, the random variables 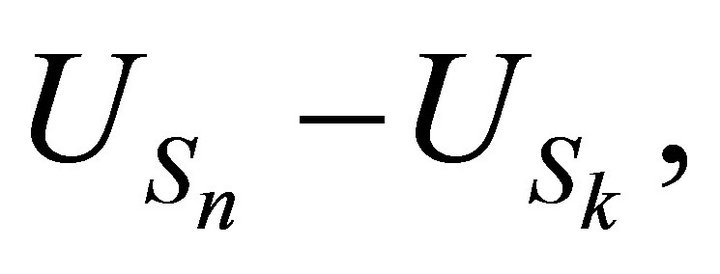
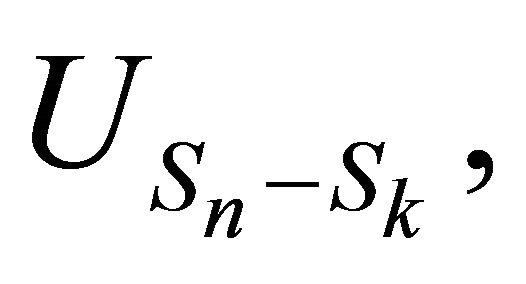
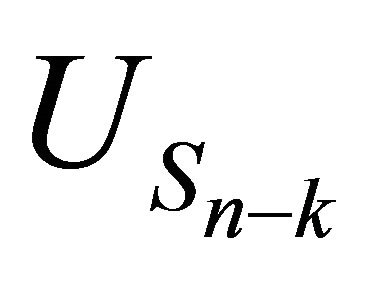 have the same probability distribution.
have the same probability distribution.
Proof: It is enough to show that for every positive measurable function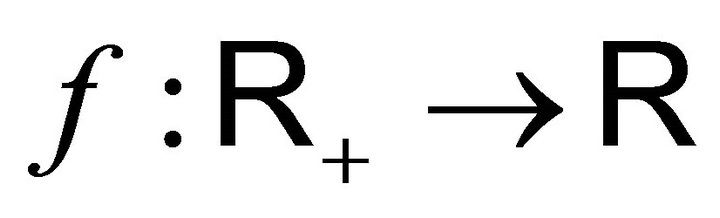 , we have:
, we have:
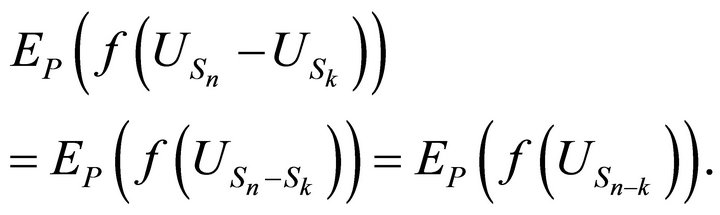 (3.4)
(3.4)
Since 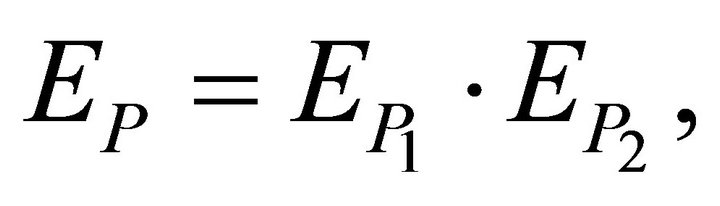 we can write:
we can write:
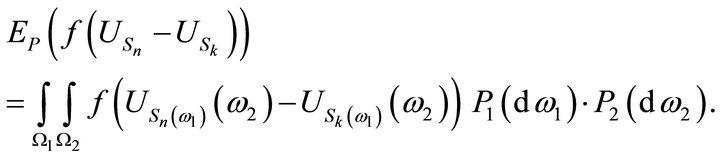
But for each fixed 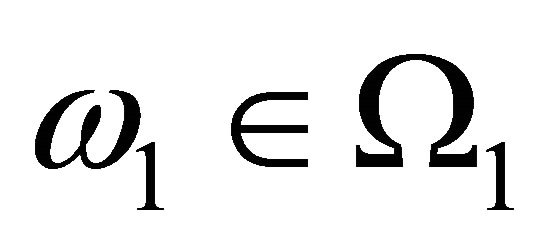 we get from 2.2
we get from 2.2
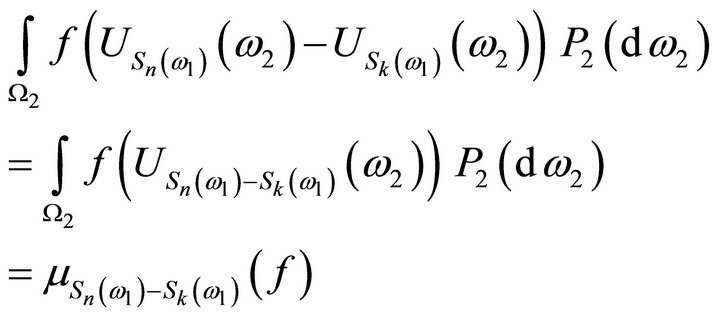
Applying  to both sides of this formula we get the first equality of (3.7). To get the second one, observe that the function
to both sides of this formula we get the first equality of (3.7). To get the second one, observe that the function 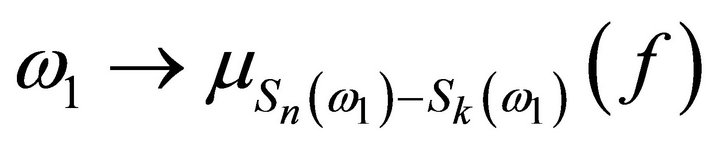 is measurable (Proposition 3.1) and use the fact that under
is measurable (Proposition 3.1) and use the fact that under , the random variables
, the random variables 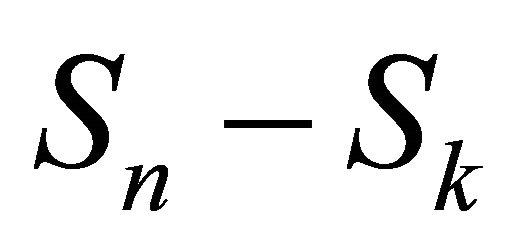 and
and  have the same probability distribution by 2.4. ■
have the same probability distribution by 2.4. ■
3.8. Theorem: The process 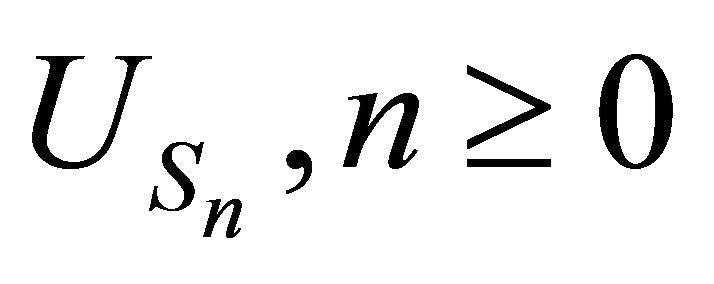 is a simple random walk with:
is a simple random walk with:

and 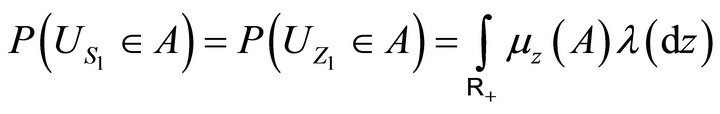
Proof: We prove that for all integers 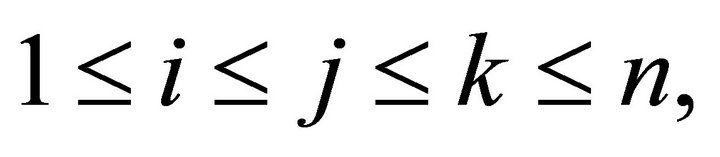 and all positive measurable functions
and all positive measurable functions 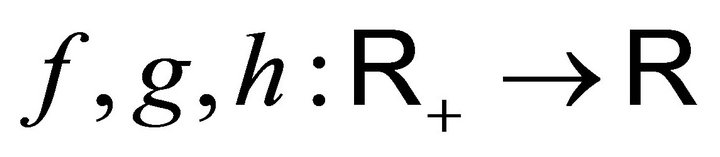 we have:
we have:
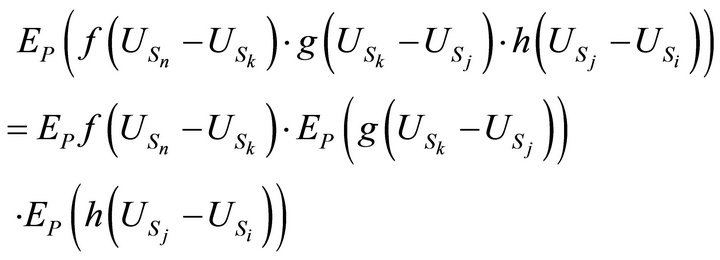 (3.8)
(3.8)
Let  be fixed in
be fixed in . By 2.2
. By 2.2  under
under 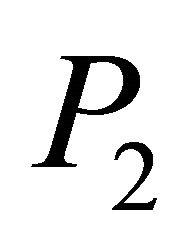 the random variables
the random variables
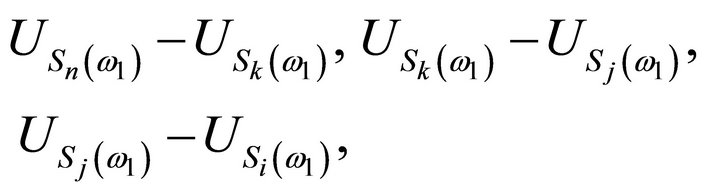
are independent. Therefore, applying first 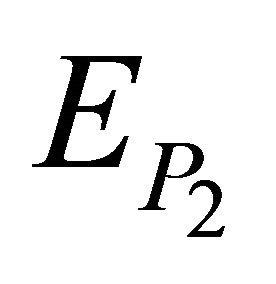 in the L.H.S of (3.8), we get the formula:
in the L.H.S of (3.8), we get the formula:
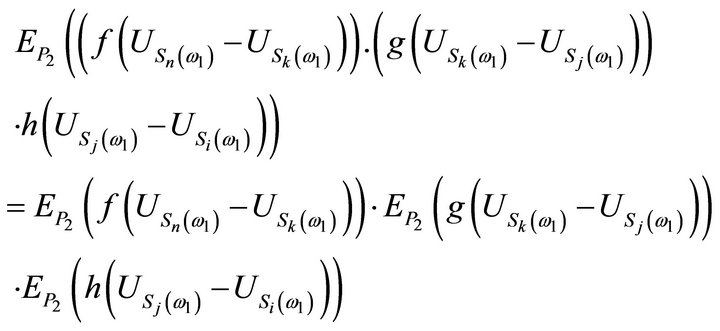 (*)
(*)
But 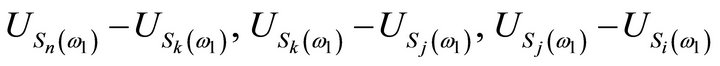 have distributions
have distributions 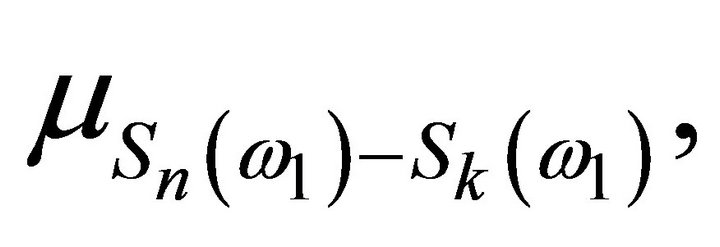
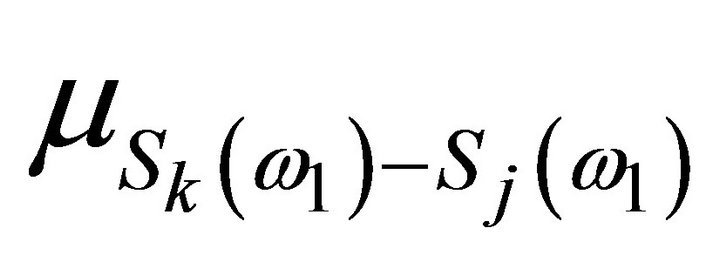 ,
,  , respectively. Thus:
, respectively. Thus:
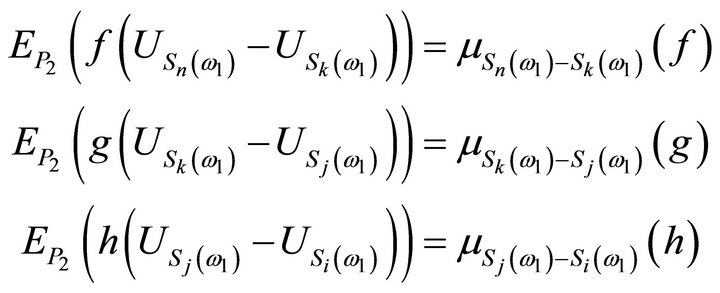
By Proposition 3.1, the R.H.S of these equalities are random variables of , independent under
, independent under  since they are measurable functions of the independent random variables
since they are measurable functions of the independent random variables 

 Therefore, applying
Therefore, applying  to both sides of formula (*) we get the proof of (3.8):
to both sides of formula (*) we get the proof of (3.8):
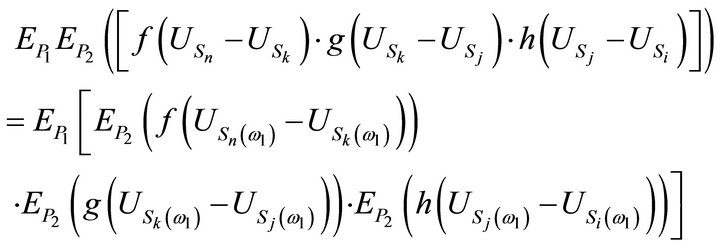
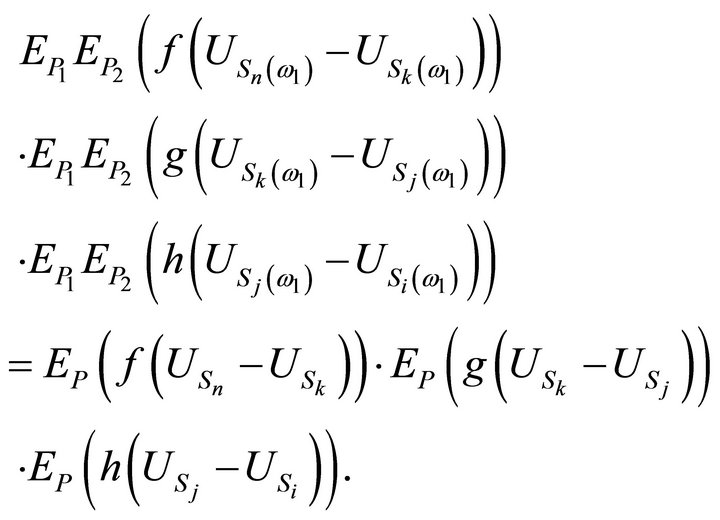
To achieve the proof, write 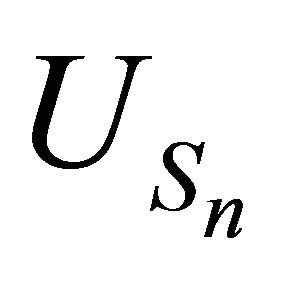 as follows:
as follows:
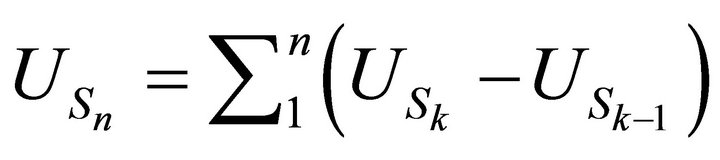 , where the
, where the  are independent with the same distribution given by
are independent with the same distribution given by
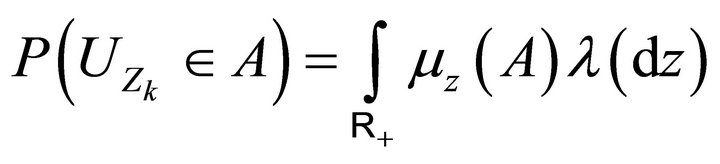
according to (3.5). ■
3.9. Proposition: For every positive measurable function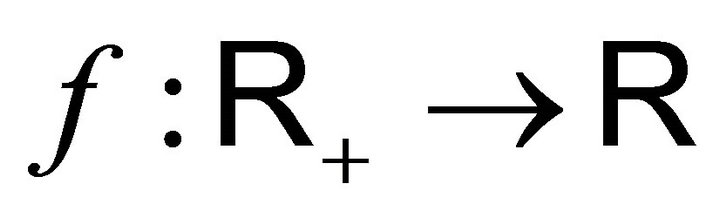 , we have:
, we have:
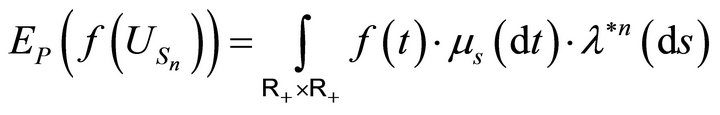 (3.9)
(3.9)
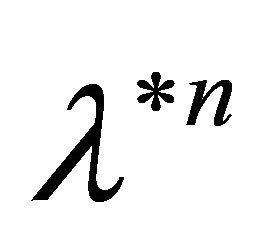 being the n-fold convolution of the probability
being the n-fold convolution of the probability  In particular the distribution law of the process
In particular the distribution law of the process  is given by:
is given by:
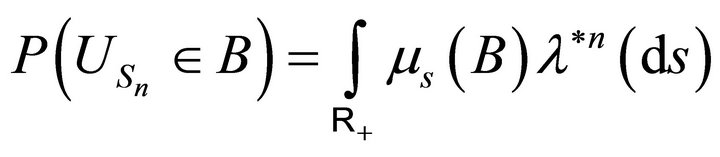
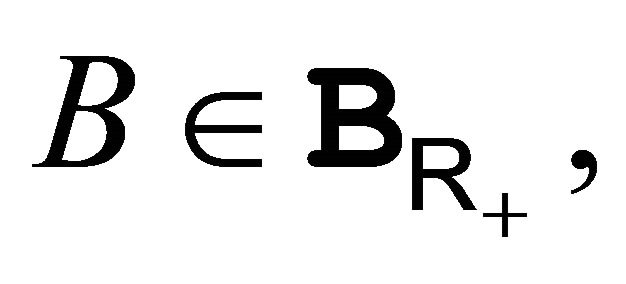
and its expectation is:

Proof: We have:
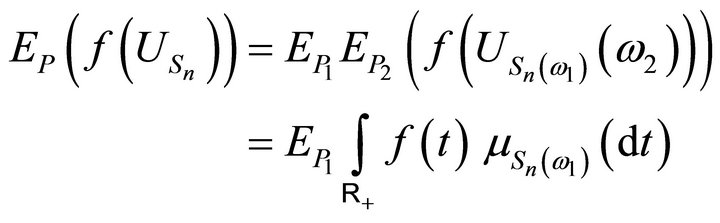
and, by Proposition 3.1, the function
 is a measurable function of
is a measurable function of
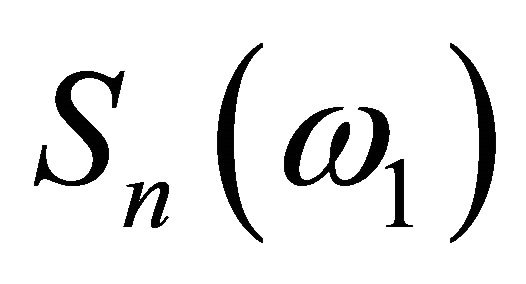 . Since
. Since 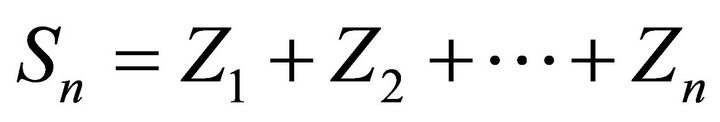 is a simple random walk with the
is a simple random walk with the 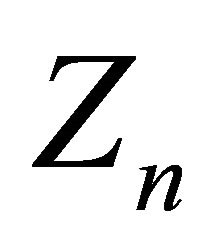 having distribution
having distribution 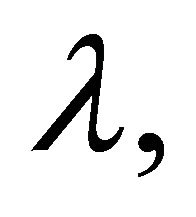 the random variable
the random variable 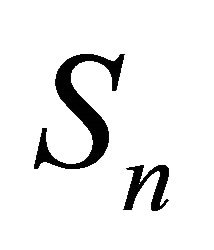 has the distribution
has the distribution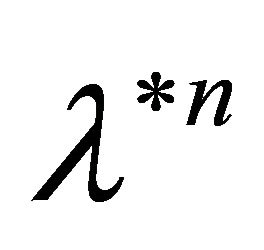 . So, by a simple change of variable we get:
. So, by a simple change of variable we get:
 . So formula (3.9) is proved. To get the distribution law of the process
. So formula (3.9) is proved. To get the distribution law of the process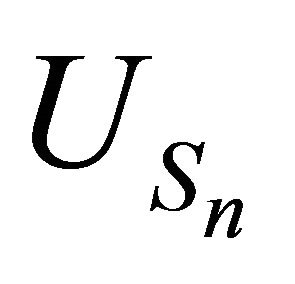 , take
, take 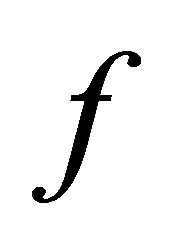 equal to the characteristic function of some Borel set B. ■
equal to the characteristic function of some Borel set B. ■
3.10. Remark: Let 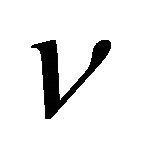 be the distribution of
be the distribution of that is
that is  and let
and let
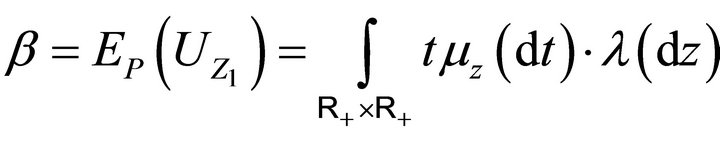 , then as a direct consequence of theorem 3.8,
, then as a direct consequence of theorem 3.8,

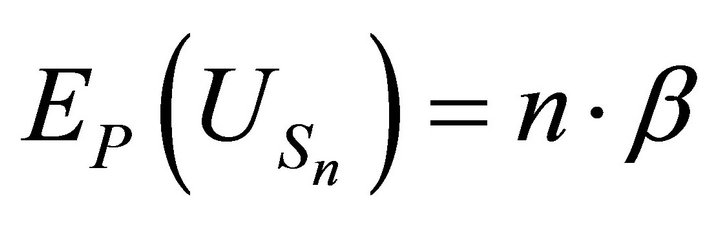 ■
■
Now we turn to the structure of the process . We need the following technical lemma:
. We need the following technical lemma:
3.11. Lemma: For every Borel positive function
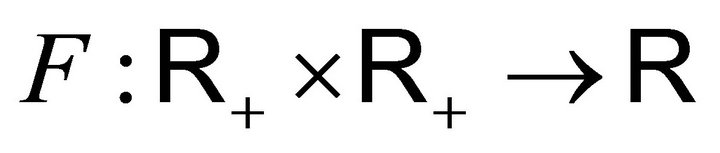 , the function
, the function 
is measurable.
Proof: Start with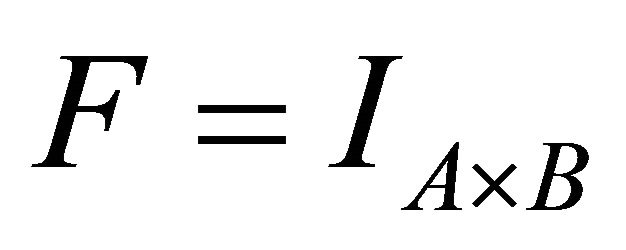 , the characteristic function of the measurable rectangle
, the characteristic function of the measurable rectangle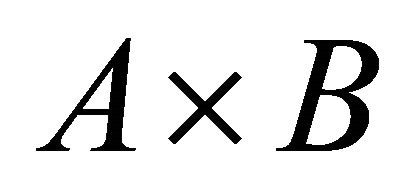 , in which case we have
, in which case we have 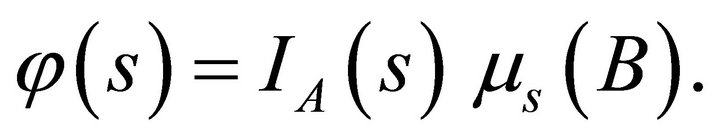 Since by proposition 3.1, the function
Since by proposition 3.1, the function 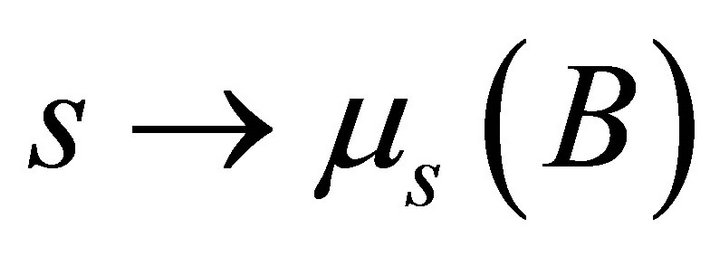 is measurable we deduce that
is measurable we deduce that  is measurable in this case. Next consider the family
is measurable in this case. Next consider the family
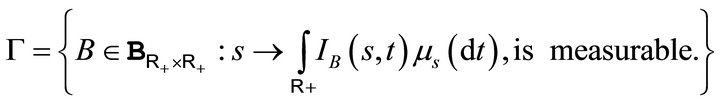
It is easy to check that  is a monotone class closed under finite disjoint unions. Since it contains the measurable rectangles, we deduce that
is a monotone class closed under finite disjoint unions. Since it contains the measurable rectangles, we deduce that 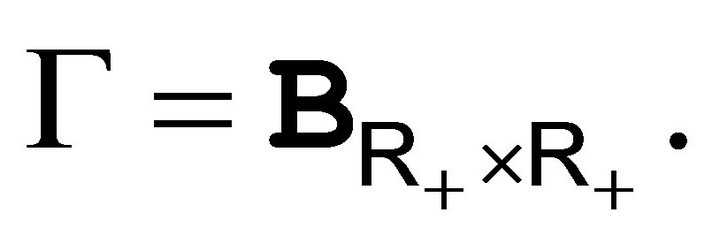 Finally consider the following class of Borel positive functions
Finally consider the following class of Borel positive functions
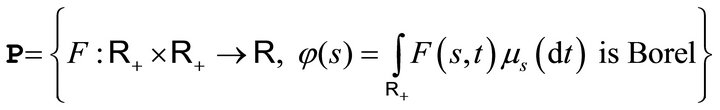
It is clear that  is closed under addition and, by the step above, it contains the simple Borel positive functions. By the monotone convergence theorem,
is closed under addition and, by the step above, it contains the simple Borel positive functions. By the monotone convergence theorem,  is exactly the class of all Borel positive functions. ■
is exactly the class of all Borel positive functions. ■
3.12. Theorem: The random variables 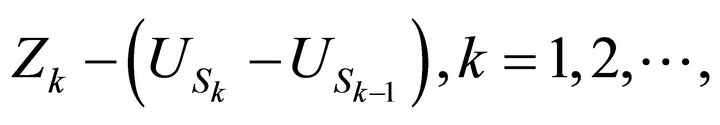 are independent with the same distribution given by: for
are independent with the same distribution given by: for 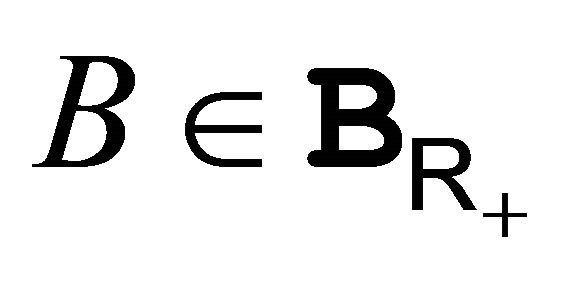
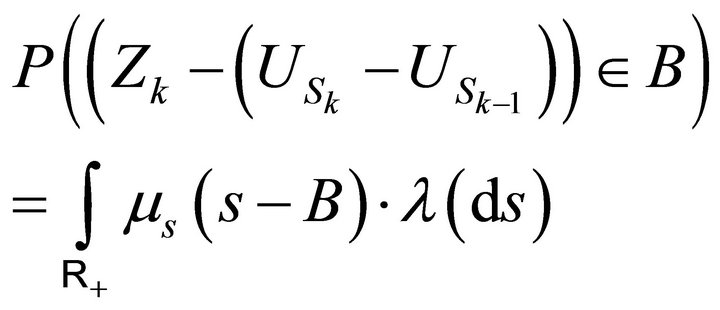 (3.12)
(3.12)
Consequently the storage process
 , is a simple random walk with the basic distribution (3.12).
, is a simple random walk with the basic distribution (3.12).
Proof: For each integer , and each
, and each  put:
put:
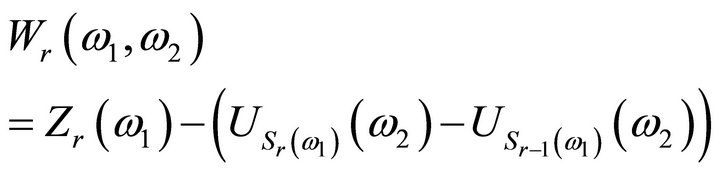
So it is enough to prove that for all 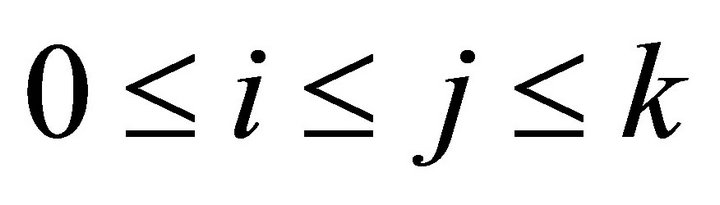 and all Borel positive functions
and all Borel positive functions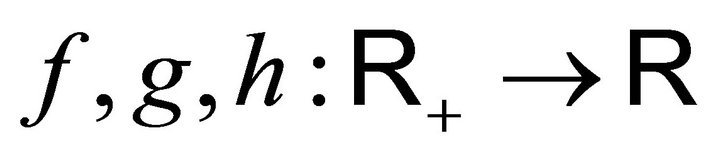 , we have:
, we have:
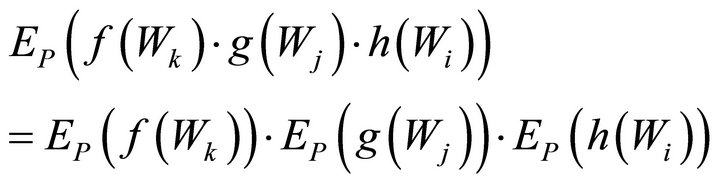 (3.13)
(3.13)
From the construction of the process 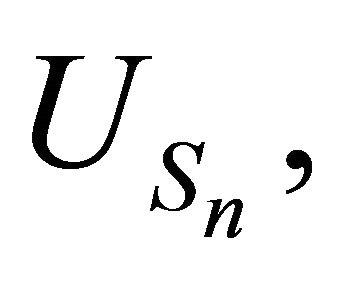 we know that for
we know that for  fixed, the random variables
fixed, the random variables 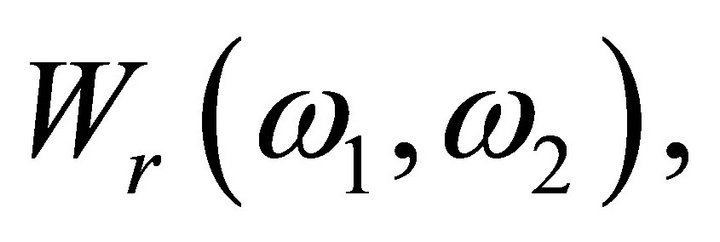
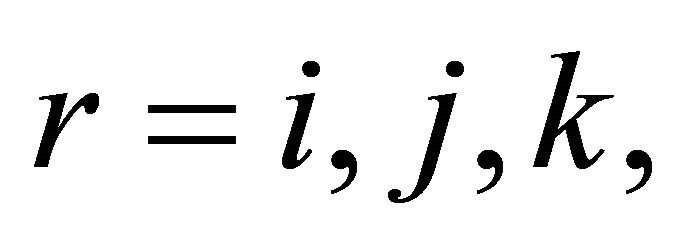 are independent under
are independent under 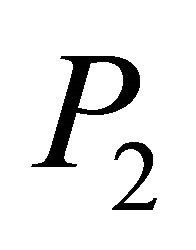 (see 2.2 (iii)). So, applying
(see 2.2 (iii)). So, applying 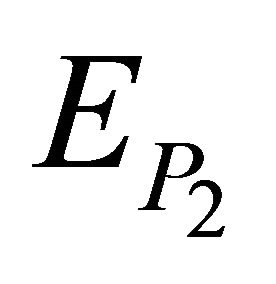 to
to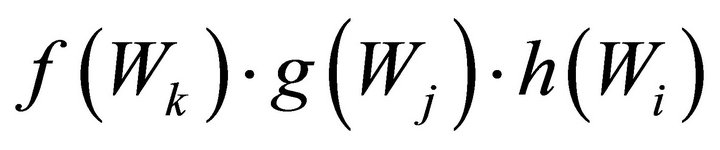 , we get:
, we get:
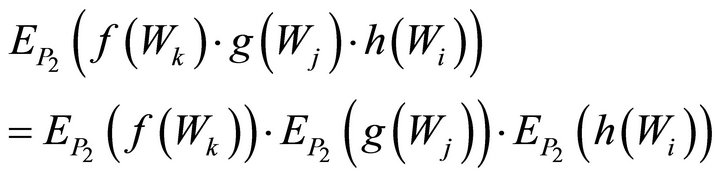 (3.14)
(3.14)
Now, since under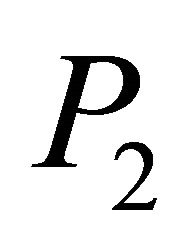 , the distribution of
, the distribution of
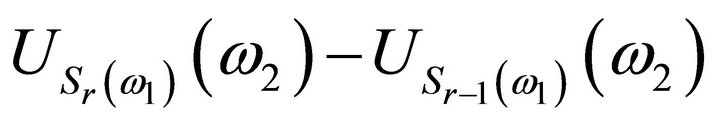 is the same as that of
is the same as that of
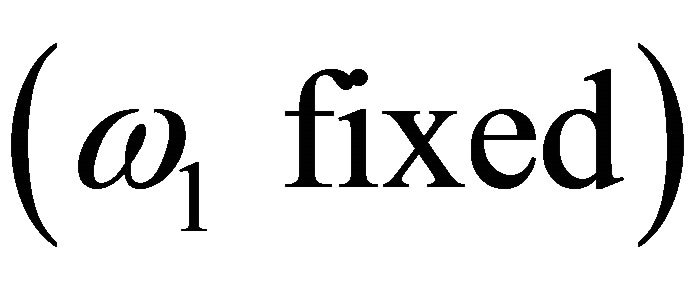
 , we have for each Borel positive function
, we have for each Borel positive function 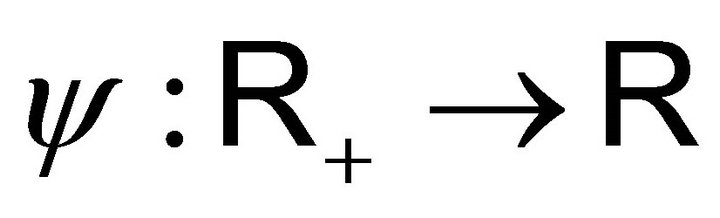
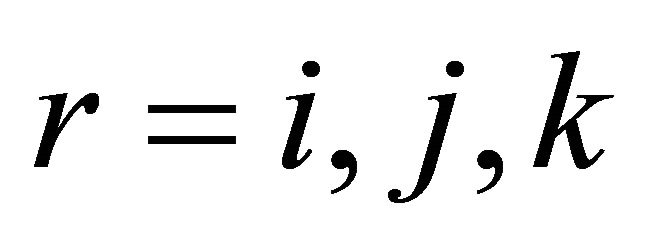

From lemma 3.11, the functions
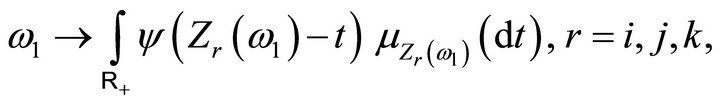 are Borel functions of the random variables
are Borel functions of the random variables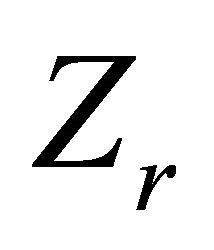 , thus they are independent under the probability
, thus they are independent under the probability 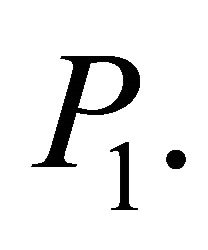 Therefore, applying
Therefore, applying  to both sides of (3.14) we get (3.13). ■
to both sides of (3.14) we get (3.13). ■
As for the process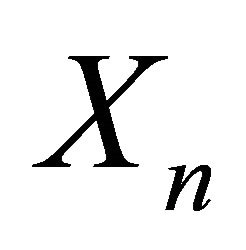 , the counterpart of proposition 3.9 is the following:
, the counterpart of proposition 3.9 is the following:
3.15. Proposition: If 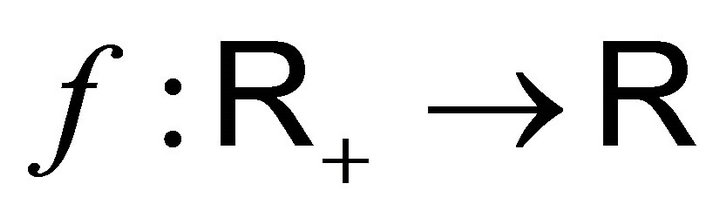 is positive measurable and if
is positive measurable and if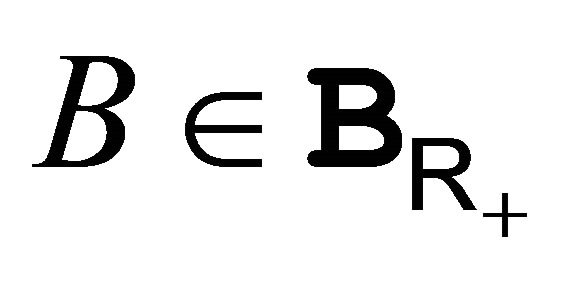 , then we have:
, then we have:
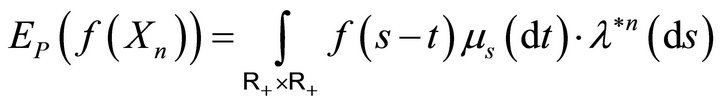
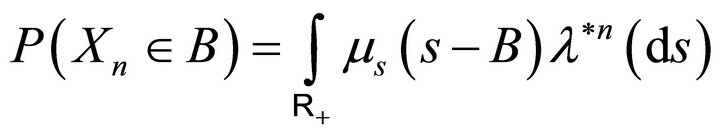
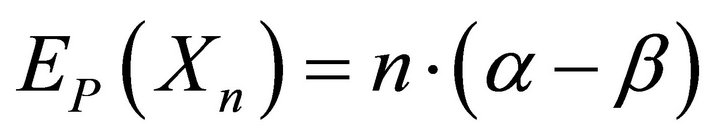
For the proof, use the formula 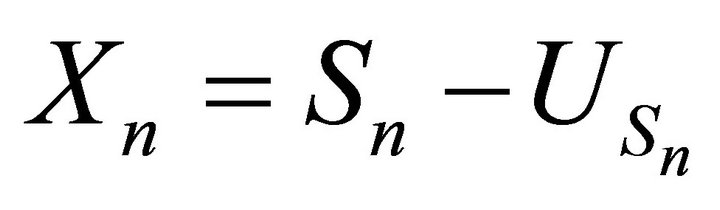 and routine integration.
and routine integration.
3.16. Example: Let  and let us take as measure
and let us take as measure 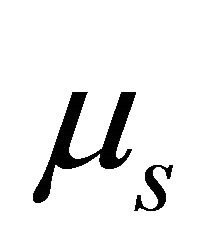 the unit mass at the point
the unit mass at the point , that is, the Dirac measure
, that is, the Dirac measure 
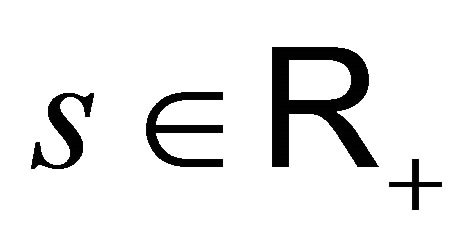 . It easy to check that
. It easy to check that 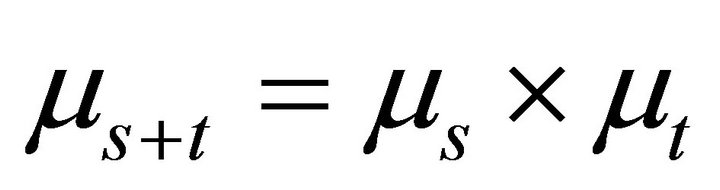 for all
for all 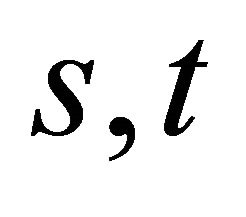 in
in 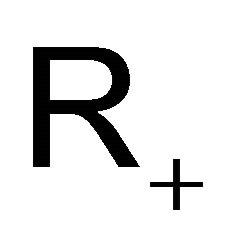 Then for every probability measure
Then for every probability measure 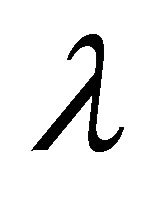 on
on 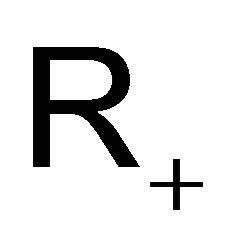
we have: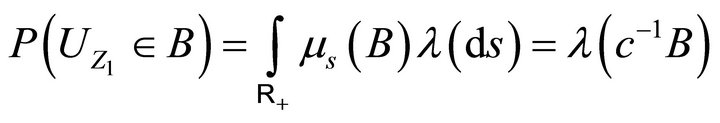 . This gives the distribution of the release process in this case:
. This gives the distribution of the release process in this case:
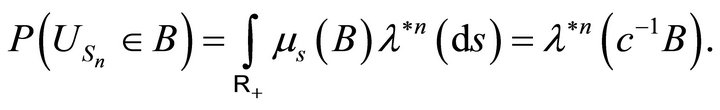
Since we have , we deduce that the release rule consists in removing from
, we deduce that the release rule consists in removing from 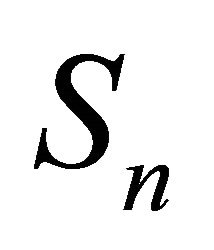 the quantity
the quantity 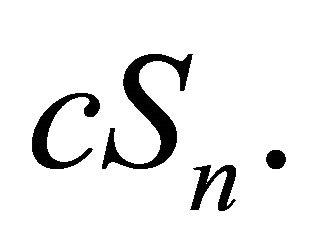
Likewise it is straightforward, from Proposition 3.14, that

from which we deduce that the distribution of the storage process is
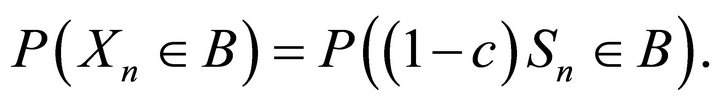
One can give more examples in this way by choosing the distribution  or/and the semigoup
or/and the semigoup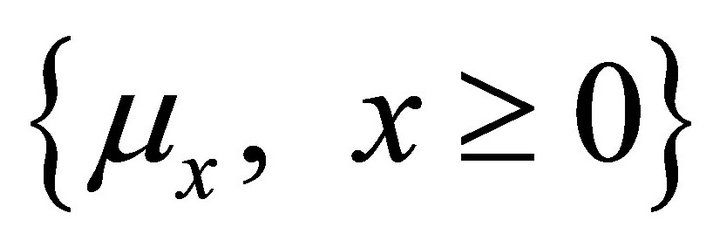 . Consider the following simple example:
. Consider the following simple example:
3.17. Example: Take 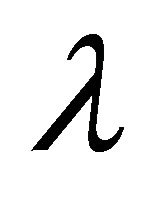 the 0 - 1 Bernoulli distribution with probability of success
the 0 - 1 Bernoulli distribution with probability of success 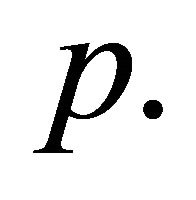 In this case the semigroup
In this case the semigroup  is a sequence
is a sequence 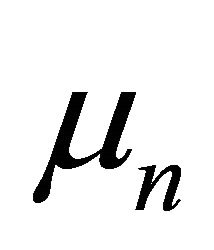 of probabilities with
of probabilities with  supported by
supported by 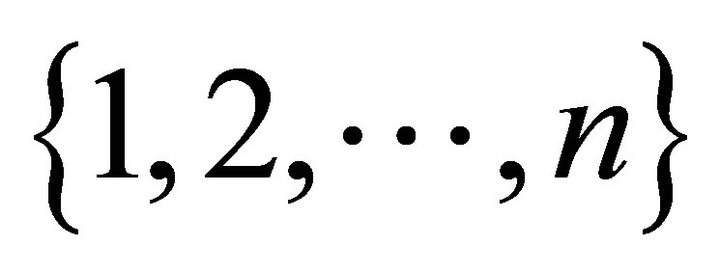 for
for 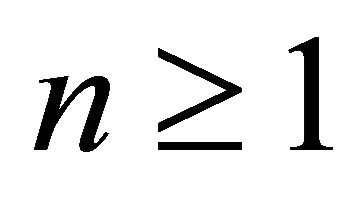 and
and 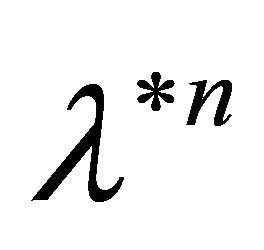 is the Binomial distribution. So we get from proposition 3.9
is the Binomial distribution. So we get from proposition 3.9
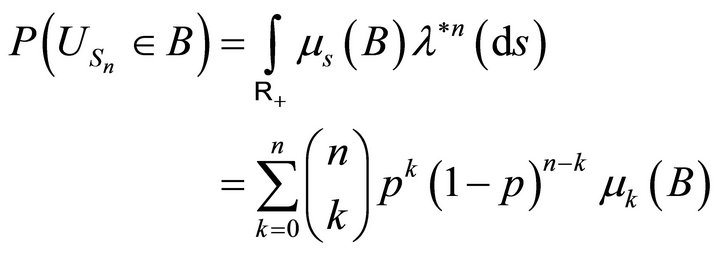
Likewise we get the distribution of 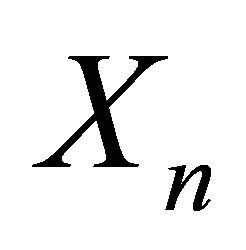 from proposition 3.15 as :
from proposition 3.15 as :
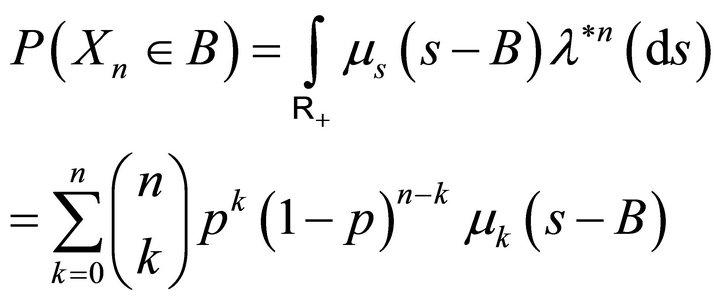 . ■
. ■
4. Limit Theorems
Due to the simple structure of the processes 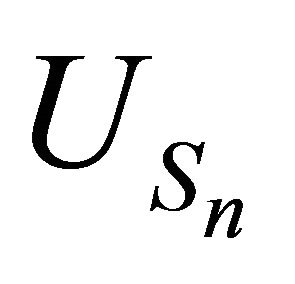 and
and 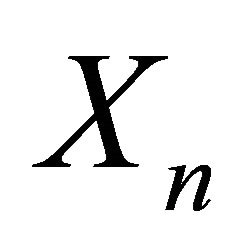 (Theorems 3.8, 3.12), it is not difficult to establish a SLLN and a CLT for them.
(Theorems 3.8, 3.12), it is not difficult to establish a SLLN and a CLT for them.
4.1. Theorem: For the storage process 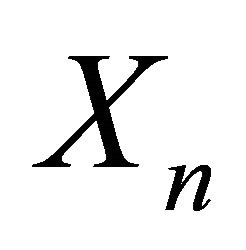 and the release rule process
and the release rule process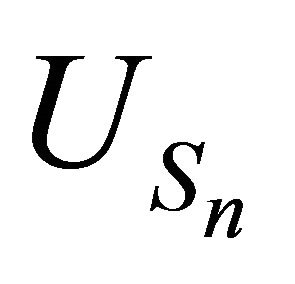 , we have:
, we have:

and
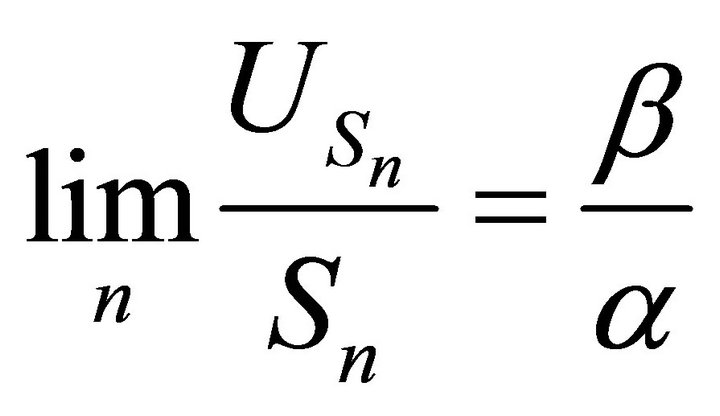
Proof: Since 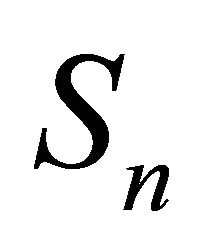 and
and 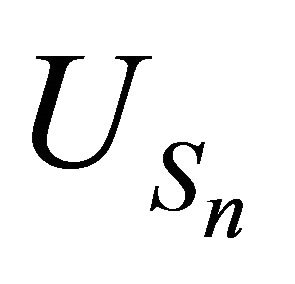 are simple random walks with
are simple random walks with 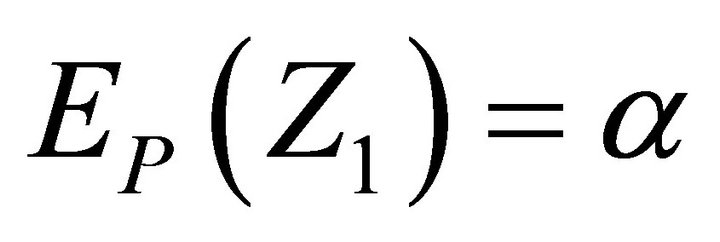 and
and  we have:
we have:
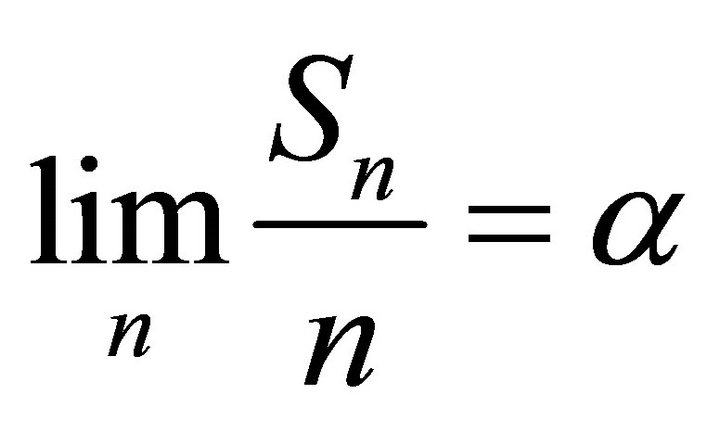 and
and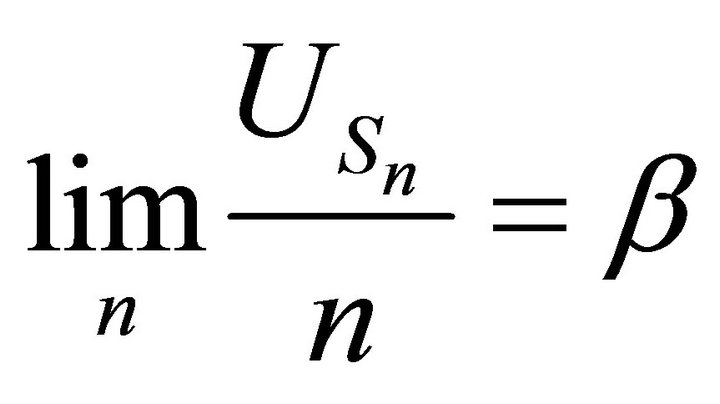 , by the classical S.L.L.N.
, by the classical S.L.L.N.
So we deduce:
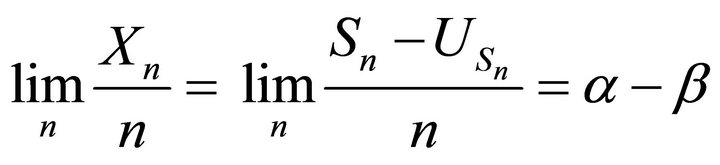
and

4.2. Proposition: Under the conditions:
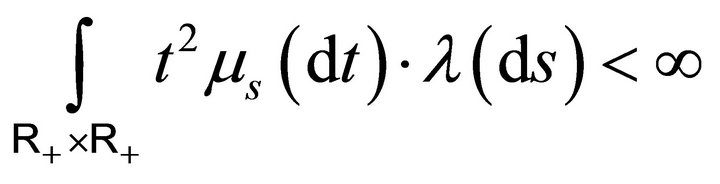 and
and
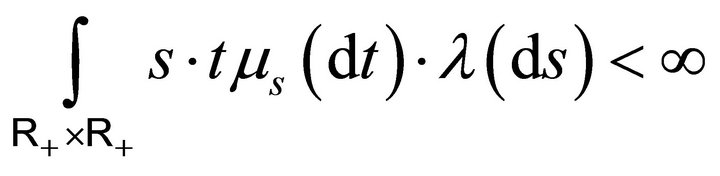 , the variances
, the variances 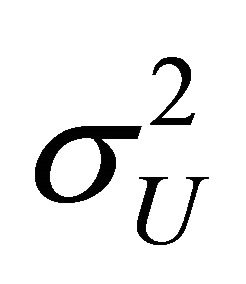 and
and 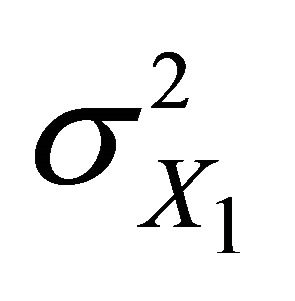
of the random variables 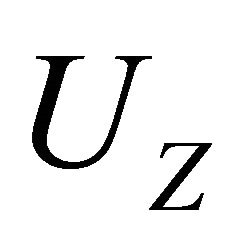 and
and 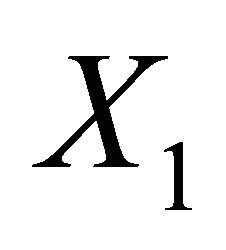 are finite. The conditions can respectively be written as
are finite. The conditions can respectively be written as
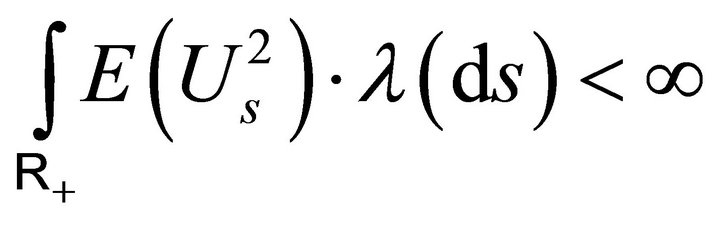
and
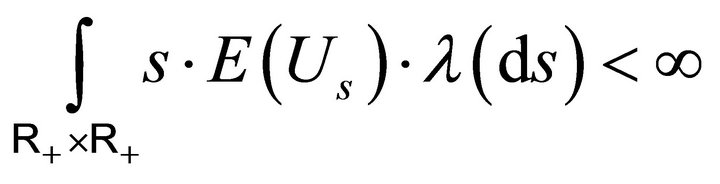 .
.
Proof: We have
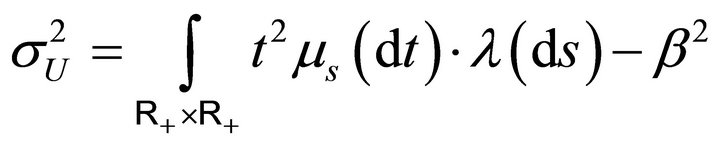 , so the first condition gives
, so the first condition gives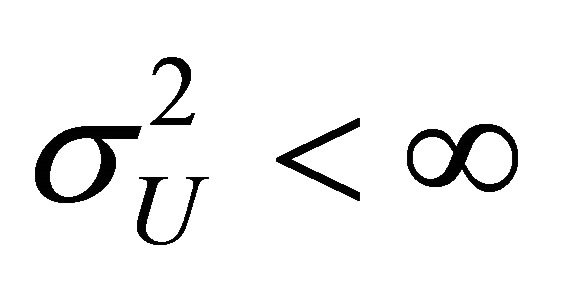 . On the other hand we have
. On the other hand we have
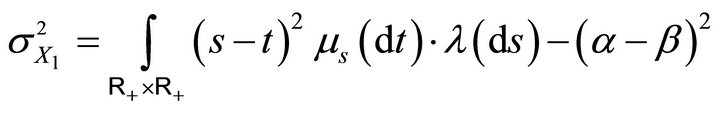
and
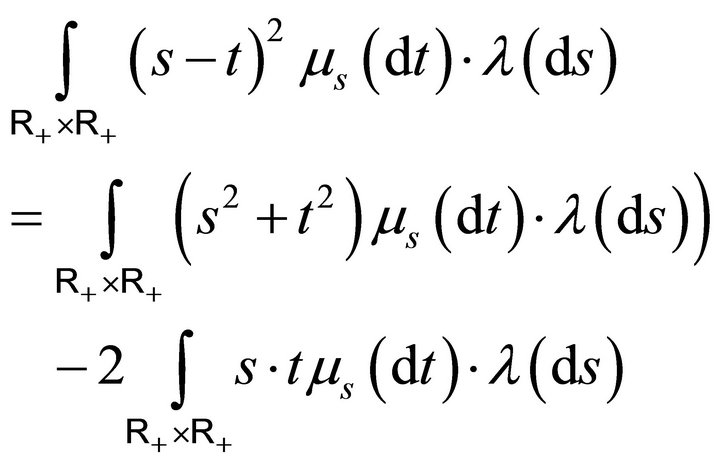
Since the variance 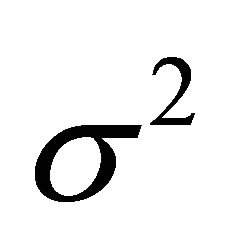 of
of 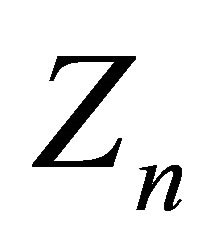 is finite we have
is finite we have
 , so the conclusion follows. ■
, so the conclusion follows. ■
Finally we get under the conditions of proposition 4.2:
4.3. Theorem: Assume the conditions of proposition 4.2. Then the normalized sequences of random variables:
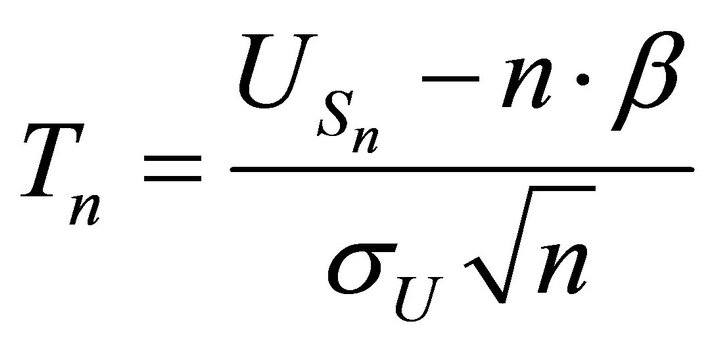 and
and 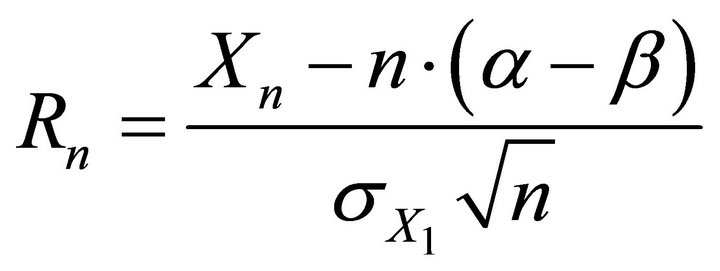
both converge in distribution to the Normal law 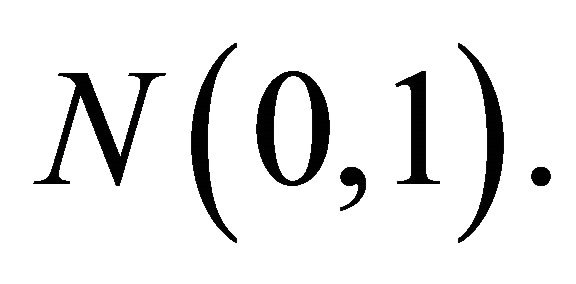
Proof: The condition of the theorem insures the finiteness of the variances 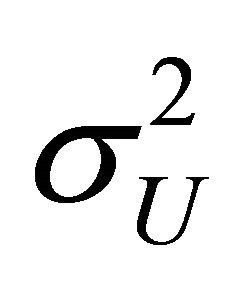 and
and 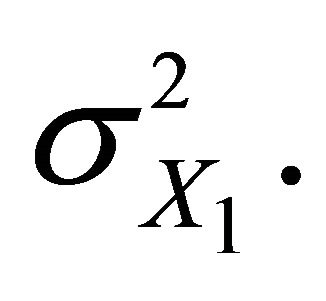 Now the conclusion results from the fact that
Now the conclusion results from the fact that 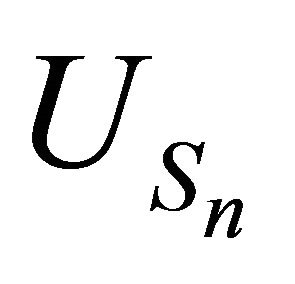 and
and 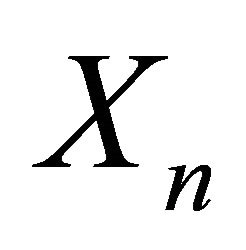 are simple random walks and the Lindberg Central Limit Theorem. To see this, we use the method of characteristic functions. Let us denote by
are simple random walks and the Lindberg Central Limit Theorem. To see this, we use the method of characteristic functions. Let us denote by 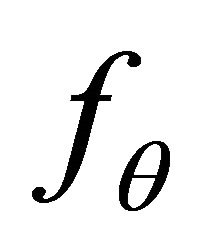 the characteristic function of the random variable
the characteristic function of the random variable . Since by Theorem 3.8 the components
. Since by Theorem 3.8 the components  of
of 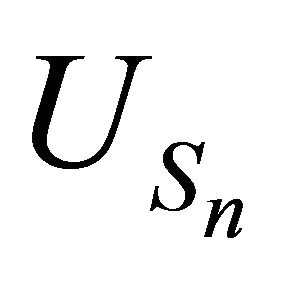 have the same distribution as
have the same distribution as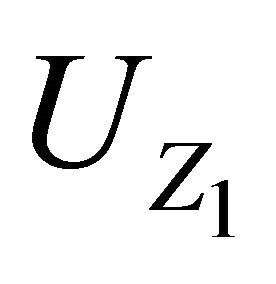 , we have
, we have

where the second equality comes from the Taylor expansion of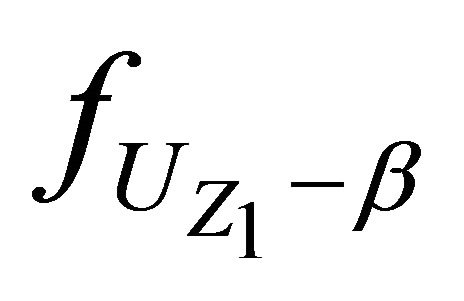 . It is well known that this limit is the characteristic function of the random variable
. It is well known that this limit is the characteristic function of the random variable  The same proof works for
The same proof works for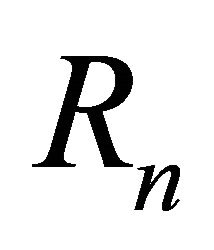 , using the components of the process
, using the components of the process 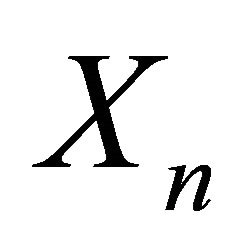 as given in Theorem 3.12. ■
as given in Theorem 3.12. ■
In some storage systems, the changes due to supply and release do not take place regularly in time. So it would be more realistic to consider the time parameter 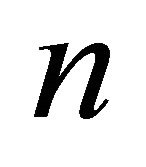 as random. We will do so in what follows and will consider the asymptotic distributions of the processes
as random. We will do so in what follows and will consider the asymptotic distributions of the processes , and
, and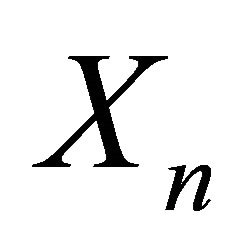 , when properly normalized and randomized. First let us put for each
, when properly normalized and randomized. First let us put for each 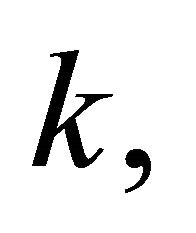
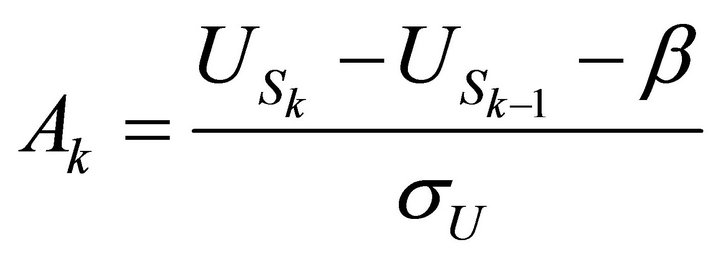 , and
, and
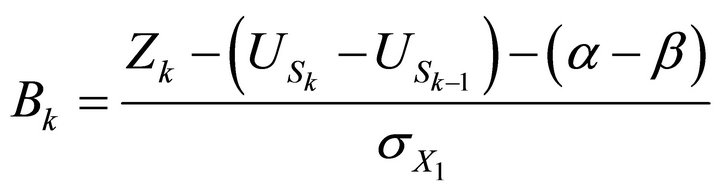 .
.
Then we have:
4.4. Theorem: Let 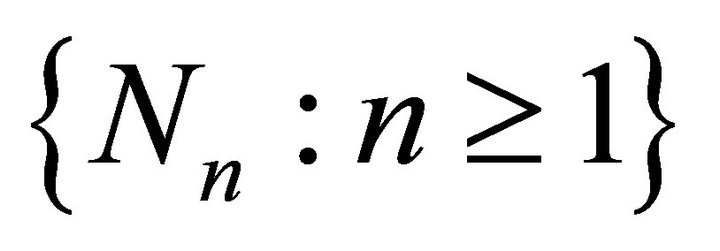 be a sequence of integral valued random variables, independent of the
be a sequence of integral valued random variables, independent of the 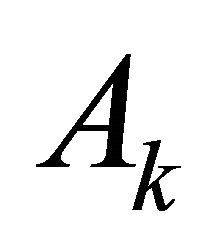 and
and .
.
If 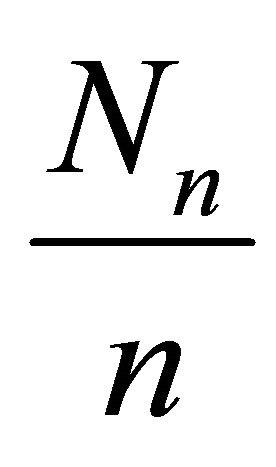 converges in probability to 1, as
converges in probability to 1, as , then the randomized processes:
, then the randomized processes:
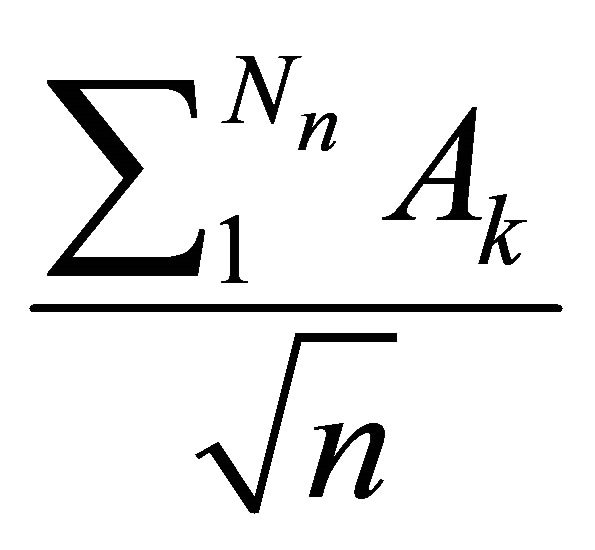 and
and 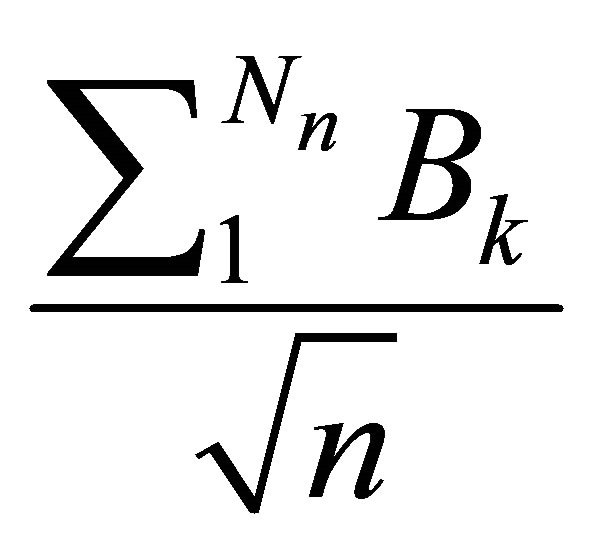
both converge in distribution to the Normal law 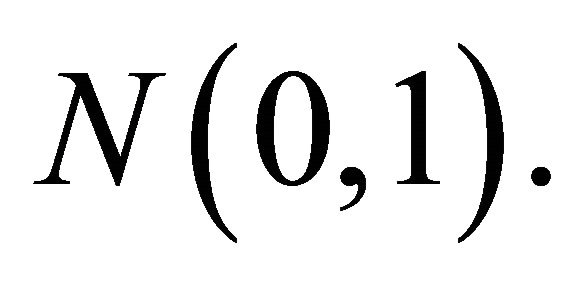
Proof: It is a simple adaptation of [7], VIII.4, Theorem 4, p. 265. ■
5. Conclusion
In this paper, we presented a simple stochastic storage process 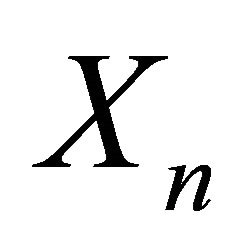 with a random walk input
with a random walk input 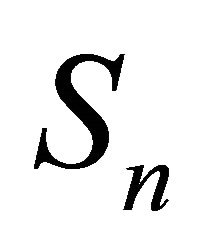 and a natural release rule
and a natural release rule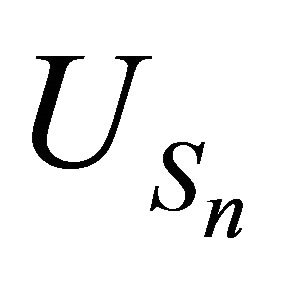 . Realistic conditions are prescribed which make this process more tractable when compared to those models studied elsewhere (see Introduction). In particular the conditions led to a simple structure of random walk for the processes
. Realistic conditions are prescribed which make this process more tractable when compared to those models studied elsewhere (see Introduction). In particular the conditions led to a simple structure of random walk for the processes  and
and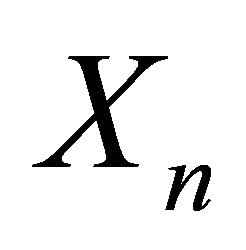 , which has given explicitly their distributions, and a rather good insight on their asymptotic behavior since a SLLN and a CLT has been easily established for each of them. Moreover, a slightly more general limit theorem has been obtained when time is adequately randomized and both processes
, which has given explicitly their distributions, and a rather good insight on their asymptotic behavior since a SLLN and a CLT has been easily established for each of them. Moreover, a slightly more general limit theorem has been obtained when time is adequately randomized and both processes 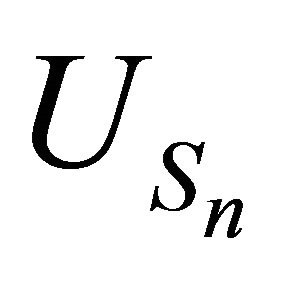 and
and 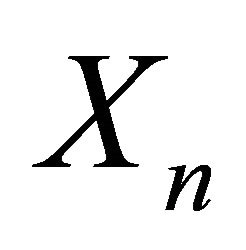 properly normalized.
properly normalized.
6. Acknowledgements
I gratefully would like to thank the Referee for his appropriate comments which help to improve the paper.
REFERENCES
- E. Cinlar and M. Pinsky, “On Dams with Additive Inputs and a General Release Rule,” Journal of Applied Probability, Vol. 9, No. 2, 1972, pp. 422-429. doi:10.2307/3212811
- E. Cinlar and M. Pinsky, “A Stochastic Integral in Storage Theory,” Probability Theory and Related Fields, Vol. 17, No. 3, 1971, pp. 227-240. doi:10.1007/BF00536759
- J. M. Harrison and S. I. Resnick, “The Stationary Distribution and First Exit Probabilities of a Storage Process with General Release Rule,” Mathematics of Operations Research, Vol. 1, No. 4, 1976, pp. 347-358. doi:10.1287/moor.1.4.347
- J. M. Harrison and S. I. Resnick, “The Recurrence Classification of Risk and Storage Processes,” Mathematics of Operations Research, Vol. 3, No. 1, 1978, pp. 57-66. doi:10.1287/moor.3.1.57
- K. Yamada, “Diffusion Approximations for Storage Processes with General Release Rules,” Mathematics of Operations Research, Vol. 9, No. 3, 1984, pp. 459-470. doi:10.1287/moor.9.3.459
- P. A. Meyer, “Probability and Potential,” Hermann, Paris, 1975.
- W. Feller, “An Introduction to Probability Theory and Its Applications,” 2nd Edition, Wiley, Hoboken, 1970.

