Applied Mathematics
Vol.3 No.11A(2012), Article ID:24756,8 pages DOI:10.4236/am.2012.331244
A Novel Voronoi Based Particle Filter for Multi-Sensor Data Fusion
Mathematics and Statistics, Electrical Engineering and Computer Science, University of Toledo, Toledo, USA
Email: Vani.Cheruvu@utoledo.edu, Priyanka.Aggarwal@utoledo.edu, Vijay.Devabhaktuni@utoledo.edu
Received July 30, 2012; revised September 2, 2012; accepted September 9, 2012
Keywords: Sensor Fusion; Global Positioning System; Inertial Navigation System; Voronoi Tessellations; Particle Filter
ABSTRACT
Seamless and reliable navigation for civilian/military application is possible by fusing prominent Global Positioning System (GPS) with Inertial Navigation System (INS). This integrated GPS/INS unit exhibits a continuous navigation solution with increased accuracy and reduced uncertainty or ambiguity. In this paper, we propose a novel approach of dynamically creating a Voronoi based Particle Filter (VPF) for integrating INS and GPS data. This filter is based on redistribution of the proposal distribution such that the redistributed particles lie in high likelihood region; thereby increasing the filter accuracy. The usual limitations like degeneracy, sample impoverishment that are seen in conventional particle filter are overcome using our VPF with minimum feasible particles. The small particle size in our methodology reduces the computational load of the filter and makes real-time implementation feasible. Our field test results clearly indicate that the proposed VPF algorithm effectively compensated and reduced positional inaccuracies when GPS data is available. We also present the preliminary results for cases with short GPS outages that occur for low-cost inertial sensors.
1. Introduction
Development of a reliable, risk-free course in a complex and dynamic environment for military or civilian applications requires a sense of positioning, tracking and navigation (constituting of position, velocity and attitude parameters). Global Positioning System (GPS) has been the prominent technology to fulfill the demands for reliable navigation, over extended periods of time, covering any part of the world during day or night [1]. However, standalone GPS signals may be completely lost for short durations when, for example, a vehicle goes through a tunnel or passes under a bridge or dense foliage [2] or can be deliberately jammed. Under these circumstances, alternate information sources need to be employed like Inertial Navigation System (INS), to bridge the non-GPS signal reception periods [3]. INS overcomes the shortcomings of GPS by providing continuous navigation data based on the self-contained measurements derived from inertial sensors (accelerometers and gyroscopes) [4]. INS can bridge GPS signal gaps, assist in signal reacquisition after an outage and reduce the search domain for detecting and correcting GPS cycle slips [3,4]. However, its solution accuracy decreases with time because of inherent sensor errors (biases, scale-factor errors, noises and drifts) that may render the uncorrected measurements useless, especially for low-cost sensors [5]. The INS error growth can be limited by utilizing external aiding sources like GPS derived position and velocity data, with bounded errors [2-5]. Therefore, to provide continuous, accurate and affordable navigation solution under all environmental scenarios, information coming from these multiple sensors (like GPS and INS) need to be fused or integrated together by accurate, robust and reliable algorithms/integration platforms [6]. Motivated by this scenario, this paper strives to develop a novel and reliable multi-sensor fusion algorithm based on integrating Particle filter with Voronoi tessellations called Voronoi based Particle Filter (VPF).
Generally, Kalman Filter (KF) and its modifications are the most widely used methods for integrating INS and GPS system because of their simplicity and ability to estimate past, current and even future states [7]. KF is an optimal filter for linear systems with Gaussian noise but is not applicable to non-linear systems. For non-linear models, Extended Kalman Filter (EKF) can be implemented, which is based on linearization of the non-linear models. Kalman filters and its variant assume the Gaussian distribution to obtain a closed form solution for the nonlinear model and propagate only mean and covariance of the state vector through approximate models (in case of EKF). However, the linearization process in EKF is often complicated, time consuming and may cause filter divergence [3,8]. To overcome these current limitations, other types of Bayesian filters like Unscented Kalman Filter (UKF) were developed [8]. UKF is based on the principle that it is easier to approximate a Gaussian distribution by fixed number of sigma points, than to approximate an arbitrary nonlinear function. However, when the nonlinearity is highly pronounced, even the best fitting Gaussian distribution becomes a poor approximation to the posterior distribution [9,10] as illustrated in Figure 1. As observed, neither an exact nor a finite-dimensional solution can be obtained for nonlinear filtering problem [10]. Hence, various numerical approximation methods (like sequential Monte Carlo or particle filters) are developed to address the intractability which will be discussed in Section 2.
This paper has been divided into 5 sections. Section 2 describes the various particles filters while Section 3 describes our proposed Voronoi based particle filter. Section 4 illustrates the results obtained with and without GPS outages and conclusions are drawn in Section 5.
2. Types of Particle Filters
Particle Filter (PF) was implemented in order to overcome the current limitations of EKF and UKF by various researchers [4,7,9-16]. The PF can deal with nonlinearities and does not require any assumption about the form of the posterior distributions. In PF the posterior distribution is represented by a cluster of random particles rather than a linearized function (EKF) or deterministically chosen few points around the mean value (UKF) [10]. According to the law of large numbers, larger the number of particles, closer is the distribution to the true posterior function. In PF, to avoid intractable integrals, the desired posterior density  is represented by N independent, random samples
is represented by N independent, random samples 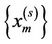 with equal weights
with equal weights 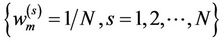 drawn from the distribution according to the Monte Carlo principle as given by Equation (1).
drawn from the distribution according to the Monte Carlo principle as given by Equation (1).
 (1)
(1)
where  represents the Dirac delta function. Since, it is not always feasible to sample from the true posterior distribution, it is common to sample from an easy to implement distribution called the proposal distribution
represents the Dirac delta function. Since, it is not always feasible to sample from the true posterior distribution, it is common to sample from an easy to implement distribution called the proposal distribution  , as per the Importance Sampling (IS) algorithm [4,7,10-16]. The importance weights are then given by Equation (2).
, as per the Importance Sampling (IS) algorithm [4,7,10-16]. The importance weights are then given by Equation (2).
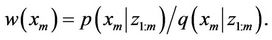 (2)
(2)
Based on the choice of this proposal density, different types of particle filters have emerged. In the simplistic Sequential Importance Sampling (SIS) Particle filter, the prior density  function is selected as the importance or proposal density, so as to simplify the particle selection and weight calculations [10-12]. Consequently after a few iterations dispersion occurs, i.e., most of the samples exhibit negligible weights as information coming from the latest measurement is completely ignored while drawing out particles from the prior density [13-16]. The most common ways to avoid this problem is to use larger number of particles or to use Resampling method [10,11], leading to Sequential Importance Resampling (SIR) Particle filter. SIR filter constitutes of SIS + Resampling method at every time instant, which
function is selected as the importance or proposal density, so as to simplify the particle selection and weight calculations [10-12]. Consequently after a few iterations dispersion occurs, i.e., most of the samples exhibit negligible weights as information coming from the latest measurement is completely ignored while drawing out particles from the prior density [13-16]. The most common ways to avoid this problem is to use larger number of particles or to use Resampling method [10,11], leading to Sequential Importance Resampling (SIR) Particle filter. SIR filter constitutes of SIS + Resampling method at every time instant, which

Figure 1. Sensor fusion algorithms (including proposed VPF).
eliminates particles with lower weights and multiplies particles with higher weights. Introducing resampling at every time step leads to sample impoverishment as similar particles will be repeated number of times [12]. An ad-hoc approach called jittering was suggested to alleviate the sample impoverishment issue [17]. This approach added a small amount of Gaussian noise to each resampled particles so as to increase their diversity. However, this comes at the cost of immediately introducing some additional variance [12]. The performance of the SIS or SIR PF is limited because of the choice of the proposal distribution, especially when the likelihood is too narrow in comparison to the transition prior density function [4, 7,10].
To overcome these issues, a better proposal distribution is desired, which is conditioned on the latest measurement [11-14]. Kalman based filters incorporate the latest measurement into the updated posterior state. Therefore, if EKF or UKF is used to generate the importance distribution, latest measurement can be incorporated into the distribution through the local linearization around each particle [15,16]. This is the principle behind the Extended particle filter (EPF) [15,18] and the Unscented particle filter (UPF). The UPF is based on the UKF, an attractive alternative to EKF for highly nonlinear problems. However, the computational cost per particle is higher as each particle is individually propagated through EKF or UKF to form the proposal distribution. To overcome these limitations, a hybrid extended particle filter (HEPF) was proposed [19]. HEPF combines the advantages of EKF (less computational load) and EPF (more accuracy during highly nonlinear regions) by alternating between the two filters, based on system dynamic. Another option to alternating between two different filters is to marginalize out the linear states of the model from the nonlinear states as introduced in the RaoBlackwellized particle filter (RBPF) [20,21]. In RBPF the linear states are estimated by the KF while the nonlinear states by the PF portion of the algorithm. These strategies reduce the filter divergence issue and require less number of particles for outputting adequate navigation solution. However, since the EPF or classic PF are still used by the HEPF or RBPF for the non-linear state estimation, their respective problems remain associated with the filter design [22].
Another approach to alleviate sample impoverishment problem in SIS/SIR filter is addressed by Pitt and Shepard in the form of the Auxiliary particle filter (APF) [23]. APF enhances the effectiveness of the importance sampling step by augmenting the existing good particles
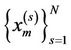 such that their predictive likelihood
such that their predictive likelihood 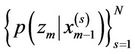 is high. Hence, the selected proposal density is a mixture of past states and the most recent observations. As long as the process noise is small, the performance of APF is superior to SIR PF. However, the moment the process noise increases, its accuracy decreases because of poor approximation of the
is high. Hence, the selected proposal density is a mixture of past states and the most recent observations. As long as the process noise is small, the performance of APF is superior to SIR PF. However, the moment the process noise increases, its accuracy decreases because of poor approximation of the 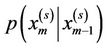 [21].
[21].
Further, APF is computationally slower since the proposal is used twice in the implementation. In likelihood PF (LPF), the likelihood function 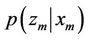 is selected to be the proposal density based on the assumption that particles drawn from the likelihood function will be closer to the true posterior density in comparison to particles drawn from the state transition density [10,11]. This is effective only when the likelihood function is highly peaked and transition density is broad [21]. To combine the advantages of LPF and SIR filters, mixture particle filters (MPF) were developed. These MPF can be based on mixture posterior; where posterior is a weighted Gaussian mixture of parallel EKF or mixture proposal distributions [24], where distribution is based on mixture transition and likelihood functions. However, there are number of practical implementation limitations of these filters, for eg. the selection of Gaussian distribution parameters or decision about the number of samples to be used from the transition and likelihood function etc.
is selected to be the proposal density based on the assumption that particles drawn from the likelihood function will be closer to the true posterior density in comparison to particles drawn from the state transition density [10,11]. This is effective only when the likelihood function is highly peaked and transition density is broad [21]. To combine the advantages of LPF and SIR filters, mixture particle filters (MPF) were developed. These MPF can be based on mixture posterior; where posterior is a weighted Gaussian mixture of parallel EKF or mixture proposal distributions [24], where distribution is based on mixture transition and likelihood functions. However, there are number of practical implementation limitations of these filters, for eg. the selection of Gaussian distribution parameters or decision about the number of samples to be used from the transition and likelihood function etc.
From all these methodologies discussed in literature, couple of prominent limitations like dispersion and sample impoverishment, are being addressed by our methodology. For a given finite set of generators, a Voronoi tessellation for each of these generators consists of all particles whose distance to a generator is not greater than to any other generator [25]. Motivated by this advantage of Voronoi tessellations, in this paper we have developed VPF method. In our methodology, Voronoi are created dynamically as and when new generators become available.
3. Methodology of Voronoi Particle Filter
At previous epoch, N particles are generated from the prior distribution 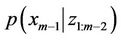 and assigned equal weights. Now each of these particles is passed through the developed system model as given by Equation (3).
and assigned equal weights. Now each of these particles is passed through the developed system model as given by Equation (3).
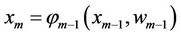 (3)
(3)
where at time ,
, 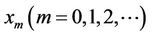 is the state vector of dimension
is the state vector of dimension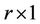 ,
, 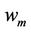 is the independent dynamic noise
is the independent dynamic noise 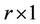 vector, and the nonlinear function
vector, and the nonlinear function , of dimension
, of dimension , describes the state transition from discrete time
, describes the state transition from discrete time 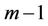 to time m to get predicted state vector
to time m to get predicted state vector . The particles are now ready to be used for the creation of a dynamic Voronoi. This procedure follows different path for different scenarios which are explained below.
. The particles are now ready to be used for the creation of a dynamic Voronoi. This procedure follows different path for different scenarios which are explained below.
3.1. Situation I: GPS Data Is Available
3.1.1. Voronoi Gets Filled with the Maximum Capacity
These set of particles in storage , are subdivided into tessellations
, are subdivided into tessellations 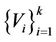 if
if 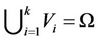 and
and ,
, 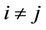 , where k is the number of tessellations. Each such tessellation
, where k is the number of tessellations. Each such tessellation  is constructed using a data point called generator
is constructed using a data point called generator . The Voronoi tessellation
. The Voronoi tessellation 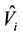 for each
for each 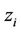 is the set of all points closer to
is the set of all points closer to 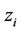 than
than 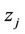 for
for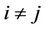 , as defined by Equation (4).
, as defined by Equation (4).
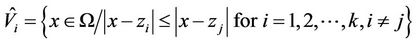 (4)
(4)
Let 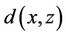 denote a distance function induced by a norm that is equivalent to the
denote a distance function induced by a norm that is equivalent to the 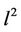 norm on
norm on . Then Voronoi tessellation of
. Then Voronoi tessellation of , with respect to this metric, is defined by Equation (5).
, with respect to this metric, is defined by Equation (5).
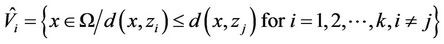 (5)
(5)
Dynamic creation of a Voronoi is withheld until the GPS data is available, as GPS is the Voronoi generator 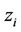 (illustrated by Figure 2). Till the arrival of GPS, the incoming INS particles are stored in
(illustrated by Figure 2). Till the arrival of GPS, the incoming INS particles are stored in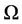 . Bythe time GPS data becomes available, storage
. Bythe time GPS data becomes available, storage 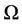 might have none, some or huge set of INS particles. The decision to cluster an INS particle into the Voronoi is based on Equation (5). If the criterion is met, the INS particle joins with that Voronoi otherwise the INS particles are stored in
might have none, some or huge set of INS particles. The decision to cluster an INS particle into the Voronoi is based on Equation (5). If the criterion is met, the INS particle joins with that Voronoi otherwise the INS particles are stored in 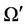 for the next Voronoi. This procedure is continued till the Voronoi gets the set number (N) of INS particles. With this, Voronoi is closed and the algorithm looks for the dynamic creation of next Voronoi. Thus theVoronoi tessellations
for the next Voronoi. This procedure is continued till the Voronoi gets the set number (N) of INS particles. With this, Voronoi is closed and the algorithm looks for the dynamic creation of next Voronoi. Thus theVoronoi tessellations  are formed such that particles with similar weights that satisfy Equation (5) are grouped together in a tessellation
are formed such that particles with similar weights that satisfy Equation (5) are grouped together in a tessellation .
.
3.1.2. Voronoi Gets Partially Filled
If sufficient number of particles did not satisfy Equation (5) then Voronoi gets partially filled. In this case, the data in storage 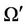 is redistributed depending on the distance function (Equation (8)) and thus results in a dynamic Voronoi. Given a tessellation
is redistributed depending on the distance function (Equation (8)) and thus results in a dynamic Voronoi. Given a tessellation 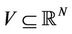 and a density function
and a density function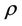 , defined in V, the mass centroid
, defined in V, the mass centroid 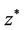 of V is defined by Equation (6).
of V is defined by Equation (6).
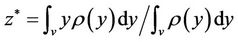 (6)
(6)
In our case, the arithmetic mean (Equation (7)) corresponds to the mass centroid of V, where n is the number of particles in the tessellation V
 (7)
(7)
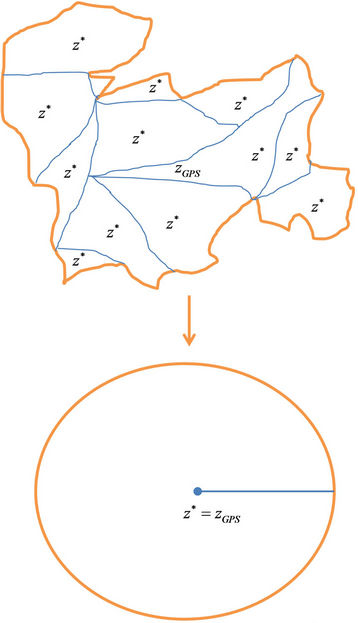
Figure 2. Voronoi with center as z* = zGPS.
Given a set of k particles which are generators, 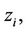 where
where ; we can define their associated Voronoi tessellations
; we can define their associated Voronoi tessellations . On the other hand, given the tessellation
. On the other hand, given the tessellation  we can define their mass centroids
we can define their mass centroids  as illustrated by Figure 2. Here, we are interested in the situation where
as illustrated by Figure 2. Here, we are interested in the situation where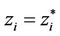 , i.e., the particles zi, that serve as generators for the Voronoi tessellations
, i.e., the particles zi, that serve as generators for the Voronoi tessellations 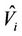 are themselves the mass centroids of those tessellations. We call such a tessellation Centroidal Voronoi tessellation [25]. Partially filled Voronoi has the generator zi and one can compute the mass centroid
are themselves the mass centroids of those tessellations. We call such a tessellation Centroidal Voronoi tessellation [25]. Partially filled Voronoi has the generator zi and one can compute the mass centroid 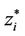 for the data in storage
for the data in storage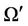 . Now the process of simultaneously redistributing the particles in the storage
. Now the process of simultaneously redistributing the particles in the storage  and checking distance function (Equation (8)) between the new mass centroid and zi is iterated till convergence
and checking distance function (Equation (8)) between the new mass centroid and zi is iterated till convergence 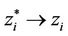 is achieved. These iterations guarantee that the Voronoi gets filled to the maximum capacity with
is achieved. These iterations guarantee that the Voronoi gets filled to the maximum capacity with .
.
 (8)
(8)
Once the dynamic Voronoi is filled with the given GPS measurement as the center zi, weights 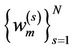 of the particles are updated according to Equation (9) where h is the measurement model.
of the particles are updated according to Equation (9) where h is the measurement model.
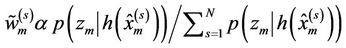 (9)
(9)
The posterior density function (required density) will be represented by a collection of these predicted particles along with their updated weight as given in Equation (10). The complete Voronoi based particle filter algorithm is illustrated in Figure 3.
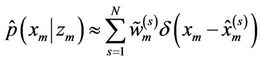 (10)
(10)
3.2. Situation II: GPS Data Is Unavailable
In case of non-availability of GPS, the previous GPS data point acts as the starting point for zi. The INS data that is already collected is divided into arbitrary number of balls and their mass centroids 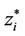 are computed. They then follow a sequence of iterations to simultaneously correct the centers
are computed. They then follow a sequence of iterations to simultaneously correct the centers  and redistributing the arbitrary balls with reference to
and redistributing the arbitrary balls with reference to 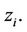 The resulting balls are ordered in an increasing error threshold (i.e.,
The resulting balls are ordered in an increasing error threshold (i.e.,  is more closer to
is more closer to 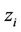 than
than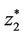 ) and the Voronoi starts getting filled with the first ball and incase it is not filled to its maximum capacity, second ball in row is used. This ensures creation of an appropriate Voronoi with propagated GPS (
) and the Voronoi starts getting filled with the first ball and incase it is not filled to its maximum capacity, second ball in row is used. This ensures creation of an appropriate Voronoi with propagated GPS ( ) as the center. Further, incorporation of the non-holonomic conditions, given by Equation (11) guarantees the vehicle progresses in the correct path.
) as the center. Further, incorporation of the non-holonomic conditions, given by Equation (11) guarantees the vehicle progresses in the correct path.
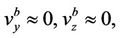 (11)
(11)
where  and
and  denote the body frame velocities in Y and Z directions respectively. The created Voronoi has all the particles with equal weights, which are later updated according to the new GPS center. The posterior density function (required density) will be represented by a collection of these predicted particles along with their updated weights.
denote the body frame velocities in Y and Z directions respectively. The created Voronoi has all the particles with equal weights, which are later updated according to the new GPS center. The posterior density function (required density) will be represented by a collection of these predicted particles along with their updated weights.
4. Results
The field test data was collected by installing various equipments in a test vehicle [24]. These include a Crossbow IMU 300CC-100, reference high grade Honeywell IMU-HG1700, Novatel OEM GPS receivers and computer. The test trajectory covered a number of vehicle dynamics. Throughout the test, a minimum of seven satellites were visible, except for several short natural GPS signal outages. For testing purposes, we carried out many experiments (without GPS outage) and here we report a couple of cases with N = 15 (Figure 5) and N = 45 particles (Figure 6). We established the performance of the VPF algorithm by plotting the least square error (Figure 7) of the calculated trajectories (for N = 15 to 55) with respect to their reference solution. We also introduced several short GPS outages at various locations that are intentionally picked under diverse conditions. The position predicted by the VPF approach during one such

Figure 3. Voronoi based particle filter.

Figure 4. VPF with 15 particles.
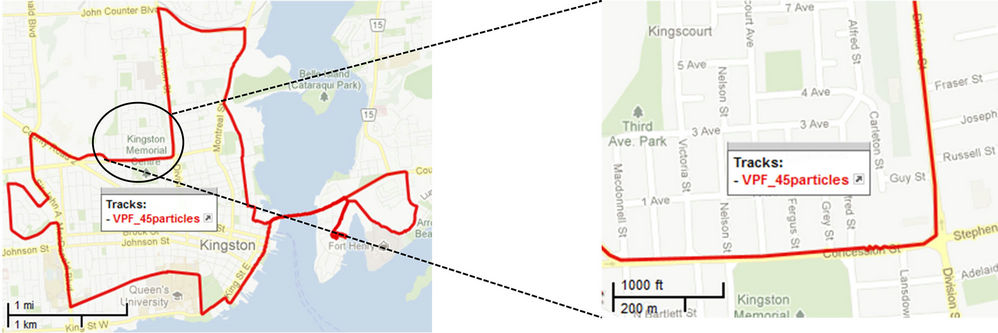
Figure 5. VPF with 45 particles.

Figure 6. Least square errors vs particles.
outage is compared with the reference differential GPS for N = 15 and N = 45 particles (Figure 7).
4.1. Without GPS Outage
In this section we demonstrate the successful completion of the 52 minute trajectory with as small as 15 particles by our proposed Voronoi based particle filter. The trajectory data is shown using the GPS Visualizer toolbox. We observe that as the number of particles increases, the trajectory becomes smoother and smoother. Figures 4 and 5 illustrate the complete trajectories with N = 15 and N = 45 particles. We observe that trajectory with 45 particles has lesser error and is smoother than the trajectory with 15 particles. We have highlighted a section of the trajectory to illustrate this observation. Figure 6 illustrates the performance of the VPF with different number of particles ranging from 15 to 55. The least square error is calculated by comparing each trajectory with the reference solution. We observe that as the number of particles increases, the error decreases.
4.2. With GPS Outage
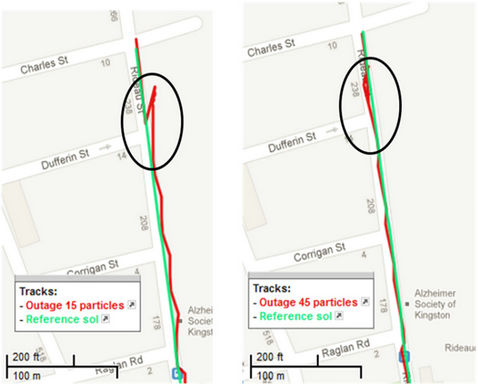
We carried out some initial experiments with GPS outages at various intentionally chosen locations. We could successfully bridge the GPS gap with as small as 15 particles. This shows that our algorithm works in the GPS outage scenario as well. We report here the preliminarily
 (a) (b)
(a) (b)
Figure 7. Performance of VPF with (a) 15 and (b) 45 particles during GPS outage.
results for 15 and 45 particles as given in Figure 7, where GPS gap is highlighted. We can clearly see that the error with 45 particles (circled region in Figure 7(b)) is less than the error with 15 particles (circled region in Figure 7(a)). More work will be put in this scenario with longer GPS outages under diverse conditions in our future publications.
5. Conclusion
We have developed a Voronoi based particle filter to integrate GPS and INS data for the navigation purpose. In some scenarios creation of Voronoi involves redistribution of the particles indicating the modification of the proposal distribution. Using the concept of dynamic Voronoi, we made more particles to fall into the high likelihood region; thereby increasing the reliability of our proposed VPF algorithm. The robustness of the algorithm is illustrated by completing the whole trajectory with as minimum as fifteen particles with acceptable error. On increasing the number of particles to 45, we were able to achieve a smoother trajectory with less error compared to 15 particles case. Due to the redistribution principle, we are able to overcome the drawbacks of dispersion (maximum number of particles ending up with negligible weights) and sample impoverishment (many identical particles found in the posterior distribution), inherent in conventional particle filters. In case of GPS outages, we incorporated non-holonomic constraints to create dynamic Voronoi with virtual GPS center. Based on this method, we have obtained initial results and demonstrated the performance of the VPF algorithm. Future work will include larger GPS outages at various locations in the trajectory and this will be reported in later publication.
REFERENCES
- P. Misra and P. Enge, “Global Positioning System: Signals, Measurements and Performance,” Ganga-Jamuna Press, Massachusetts, 2010.
- M. Grewal, L. Weill and A. Andrews, “Global Positioning Systems Inertial Navigation, and Integration,” 2nd Edition, Wiley-Interscience, New Jersey, 2007. doi:10.1002/0470099720
- N. El-Sheimy, “Inertial Techniques and INS/DGPS Integration,” ENGO 623-Course Notes, University of Calgary, Calgary, 2006.
- P. Aggarwal, Z. Syed, A. Noureldin and N. El-Sheimy, “Integrated MEMS Based Navigation Systems,” Artech House, Norwood, 2010.
- P. Aggarwal, Z. Syed, X. Niu and N. El-Sheimy, “A Standard Testing and Calibration Procedure for Low Cost MEMS Inertial Sensors and Units,” Journal of Navigation, Vol. 61, No. 2, 2007, pp. 323-336.
- C. Hide, “Integration of GPS and Low-Cost INS Measurements,” Ph.D. Thesis, University of Nottingham, Nottingham, 2003.
- B. Ristic, S. Arulampalan and N. Gordon, “Beyond the Kalman Filter: Particle Filters for Tracking Applications,” Artech House, 2004.
- S. Julier, J. Uhlmann and H. Durrant, “A New Approach for Nonlinear Transformations of Means and Covariances in Filters and Estimators,” IEEE Transactions on Automatic Control, Vol. 45, No. 3, 2000, pp. 477-482. doi:10.1109/9.847726
- N. Bergman, “Recursive Bayesian Estimation: Navigation and Tracking Applications,” Ph.D. Thesis, Linköping University, Linköping, 1999.
- A. Doucet, N. Freitas and N. Gordon, “Sequential Monte Carlo Methods in Practice,” Springer, New York, 2001.
- M. Arulampalam, S. Maskell, N. Gordon and T. Clapp, “A Tutorial on Particle Filters for Online Nonlinear/NonGaussian Bayesian Tracking,” IEEE Transactions on Signal Processing, Vol. 50, No. 2, 2002, pp. 174-188. doi:10.1109/78.978374
- A. Doucet and A. Johansen, “A Tutorial on Particle Filtering and Smoothing: Fifteen Years Later,” In: D. Crisan and B. Rozovsky, Eds., Handbook of Nonlinear Filtering, Oxford University Press, Oxford, 2011.
- F. Gustafsson, F. Gunnarsson, N. Bergman, U. Forssell, J. Jansson, R. Karlsson and P. Nordlund, “Particle Filters for Positioning, Navigation and Tracking,” IEEE Transactions on Signal Processing, Vol. 50, No. 2, 2002, pp. 425-437. doi:10.1109/78.978396
- G. Kitagawa, “Monte Carlo Filter and Smoother for NonGaussian Nonlinear State Space Models,” Journal of Computational and Graphical Statistics, Vol. 5, No. 1, 1996, pp. 1-25.
- R. Merwe, A. Doucet, J. Freitas and E. Wan, “The Unscented Particle Filter,” University of Cambridge, Cambridge, 2000.
- A. Haug, “A Tutorial on Bayesian Estimation and Tracking Techniques Applicable to Nonlinear and Non-Gaussian Processes,” MITRE Technical Report, MTR 05W- 0000004, MITRE Corporation, 2005.
- N. Gordon, D. Salmond and A. Smith, “Novel Approach to Nonlinear and Non-Gaussian Bayesian State Estimation,” Proceedings of the IEEE, Vol. 140, 1993, pp. 107- 113.
- P. Aggarwal, D. Gu and N. El-Sheimy, “Extended Particle Filter (EPF) for Land Vehicle Navigation Applications,” International Global Navigation Satellite Systems (IGNSS), Sydney, 4-6 December 2007.
- P. Aggarwal, Z. Syed and N. El-Sheimy, “Hybrid Extended Particle Filter for Integrated Navigation and Global Positioning System,” Measurement Science and Technology, Vol. 20, No. 5, 2009.
- A. Doucet, N. Freitas, K. Murphy and S. Russell, “RaoBlackwellised Particle Filtering for Dynamic Bayesian Networks,” Proceedings of the 16th Conference on Uncertainty in Artificial Intelligence, Stanford, 30 June-3 July 2000, pp. 176-183.
- Z. Chen, “Bayesian Filtering: From Kalman Filters to Particle Filters, and Beyond,” Adaptive Systems Laboratory Technical Report, McMaster University, Hamilton.
- Y. Jianjun, Z. Jianqiu and M. Klaas, “The Marginal RaoBlackwellized Particle Filter for Mixed Linear/Nonlinear State Space Models,” Chinese Journal of Aeronautics, Vol. 20, No. 4, 2007, pp. 346-352. doi:10.1016/S1000-9361(07)60054-5
- M. Pitt and N. Shephard, “Filtering via Simulation: Auxiliary Particle Filters,” Journal of the American Statistical Association, Vol. 94, No. 446, 1999, pp. 590-599. doi:10.1080/01621459.1999.10474153
- J. Georgy, A. Noureldin, M. Korenberg and M. Bayoumi, “Low Cost 3-D Navigation Solution for RISS/GPS Integration Using Mixture Particle Filter,” IEEE Transactions on Vehicular Technology, Vol. 59, No. 2, 2010, pp. 599- 615. doi:10.1109/TVT.2009.2034267
- Q. Du, V. Faber and M. Gunzburger, “Centroidal Voronoi Tesselations: Applications and Algorithms”, SIAM Review, Vol. 41, No. 4, 1999, pp. 637-676. doi:10.1137/S0036144599352836
NOTES
*Both authors contributed equally.

