Applied Mathematics
Vol. 3 No. 5 (2012) , Article ID: 19052 , 12 pages DOI:10.4236/am.2012.35065
Non-Newtonian Power-Law Fluid Flow and Heat Transfer over a Non-Linearly Stretching Surface
1Department of Mathematics, Central College Campus, Bangalore University, Bangalore, India
2Tata Institute of Fundamental Research, Centre for Applicable Mathematics, Bangalore, India
Email: *prasadkv2000@yahoo.co.in
Received March 15, 2012; revised April 5, 2012; accepted April 12, 2012
Keywords: Boundary Layer Flow; Magneto-Hydrodynamic Flow; Power-Law Fluid; Stretching Sheet; Modified Prandtl Number; Heat Source/Sink Parameter
ABSTRACT
The problem of magneto-hydrodynamic flow and heat transfer of an electrically conducting non-Newtonian power-law fluid past a non-linearly stretching surface in the presence of a transverse magnetic field is considered. The stretching velocity, the temperature and the transverse magnetic field are assumed to vary in a power-law with the distance from the origin. The flow is induced due to an infinite elastic sheet which is stretched in its own plane. The governing equations are reduced to non-linear ordinary differential equations by means of similarity transformations. These equations are then solved numerically by an implicit finite-difference scheme known as Keller-Box method. The numerical solution is found to be dependent on several governing parameters, including the magnetic field parameter, power-law index, velocity exponent parameter, temperature exponent parameter, Modified Prandtl number and heat source/sink parameter. A systematic study is carried out to illustrate the effects of these parameters on the fluid velocity and the temperature distribution in the boundary layer. The results for the local skin-friction coefficient and the local Nusselt number are tabulated and discussed. The results obtained reveal many interesting behaviors that warrant further study on the equations related to non-Newtonian fluid phenomena.
1. Introduction
During the past four decades the study of non-Newtonian fluids has gained interest because of their numerous technological applications, including manufacturing of plastic sheets, performance of lubricants, and movement of biological fluids. In particular, the flow of an incompressible non-Newtonian fluid over a stretching sheet has several industrial applications in, for example, extrusion of a polymer sheet from a dye or in the drawing of plastic films. In view of their differences with Newtonian fluids, several models of non-Newtonian fluids have been proposed. Amongst these the simplest and the most common model is the power-law fluid, which has received special attraction from the researchers in the field. The rheological equation of the state for the power-law fluid, which is the relationship between the stress components  and strain components
and strain components 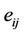 as proposed by [1], reads:
as proposed by [1], reads:
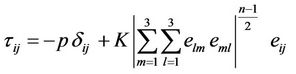
where  is the pressure,
is the pressure, 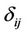 is the Kroneckar delta and
is the Kroneckar delta and 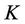 and
and  are the consistency coefficient and the power-law index of the fluid, respectively. When
are the consistency coefficient and the power-law index of the fluid, respectively. When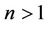 , the fluid is said to be dilatant or shear thickening; for
, the fluid is said to be dilatant or shear thickening; for , the fluid is called shear thinning or pseudo plastic and for
, the fluid is called shear thinning or pseudo plastic and for  the fluid is simply the Newtonian fluid. Several studies in the literature suggest the range
the fluid is simply the Newtonian fluid. Several studies in the literature suggest the range  for the power-law index
for the power-law index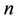 . Since the pioneering work of [2] various aspects of the stretching sheet problem involving Newtonian/non-Newtonian fluids have been extensively studied by several authors. Some recent papers in this direction may be found in the references ([3-5]). These research works do not however consider the situation where hydromagnetic effects arise. The study of hydrodynamic flow and heat transfer over a stretching sheet may find its applications in polymer technology related to the stretching of plastic sheets. Also, many metallurgical processes involve the cooling of continuous strips or filaments by drawing them through a quiescent fluid and while drawing these strips are sometimes stretched. The rate of cooling can be controlled by drawing such strips in an electrically conducting fluid subjected to a magnetic field in order to get the final products of desired characteristics; as such a process greatly depends on the rate of cooling. In view of this, the study of MHD flow of Newtonian/non-Newtonian flow over a stretching sheet was carried out by many researchers ([6-10]).
. Since the pioneering work of [2] various aspects of the stretching sheet problem involving Newtonian/non-Newtonian fluids have been extensively studied by several authors. Some recent papers in this direction may be found in the references ([3-5]). These research works do not however consider the situation where hydromagnetic effects arise. The study of hydrodynamic flow and heat transfer over a stretching sheet may find its applications in polymer technology related to the stretching of plastic sheets. Also, many metallurgical processes involve the cooling of continuous strips or filaments by drawing them through a quiescent fluid and while drawing these strips are sometimes stretched. The rate of cooling can be controlled by drawing such strips in an electrically conducting fluid subjected to a magnetic field in order to get the final products of desired characteristics; as such a process greatly depends on the rate of cooling. In view of this, the study of MHD flow of Newtonian/non-Newtonian flow over a stretching sheet was carried out by many researchers ([6-10]).
All the above mentioned investigators confined their analyses to MHD flow and heat transfer over a linear stretching sheet. However, the intricate flow and heat transfer problem over a non-linearly stretching sheet with the effects of internal heat generation/absorption is yet to be studied. This has applications to several industrial problems such as engineering processes involving nuclear power plants, gas turbines and many others [11-13]). Reference [14] studied viscous flow and heat transfer over a nonlinearly stretching sheet.
Motivated by these analyses and practical applications, the main concern of the present paper is to study the effect of variable thermal conductivity on the power-law fluid flow and heat transfer over a non-linearly stretching sheet in the presence of a transverse magnetic field. This extends the work in [14], to the case of MHD non-Newtonian power-law fluid flow and heat transfer by considering the contribution of internal heat generation/absorption. Because of the intricacy, the influence of power-law index parameter, magnetic parameter, non-linear velocity and temperature exponent and heat source/sink parameter make the momentum and energy equations coupled and highly non-linear partial differential equations. To reduce the number of independent variables, these partial differential equations are simplified to coupled non-linear ordinary differential equations by suitable similarity transformations. These equations are in turn solved numerically by an implicit finite-difference scheme known as Keller-box method. Thus, for the solution of highly non-linear boundary value problem, computer simulation is a powerful technique to predict the flow behavior.
2. Mathematical Formulation
In view of the present physical situation we have considered steady laminar two-dimensional boundary layer flow due to a stretching sheet in a quiescent viscous incompressible and electrically conducting fluid obeying power-law model in the presence of a transverse magnetic field . The flow is generated as a consequence of non-linear stretching of the boundary sheet, caused by simultaneous application of two equal and opposite forces along
. The flow is generated as a consequence of non-linear stretching of the boundary sheet, caused by simultaneous application of two equal and opposite forces along 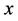 -axis, while keeping the origin fixed in the fluid of the ambient temperature
-axis, while keeping the origin fixed in the fluid of the ambient temperature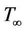 . The positive
. The positive  -coordinate is measured along the direction of the motion, with the slot at the origin, and the positive
-coordinate is measured along the direction of the motion, with the slot at the origin, and the positive 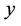 -coordinate is measured normal to the surface of the sheet and is positive from the sheet to the fluid. The continuous stretching sheet is assumed to have a non-linear velocity and prescribed temperature of the form
-coordinate is measured normal to the surface of the sheet and is positive from the sheet to the fluid. The continuous stretching sheet is assumed to have a non-linear velocity and prescribed temperature of the form 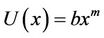 and
and 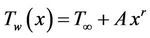 respectively, where
respectively, where  is the stretching constant,
is the stretching constant, 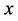 is the distance from the slot;
is the distance from the slot; 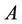 is a constant whose value depends upon the properties of the fluid. Here,
is a constant whose value depends upon the properties of the fluid. Here, 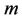 and
and  are the velocity and temperature exponents, respectively. It is also assumed that the magnetic Reynolds number
are the velocity and temperature exponents, respectively. It is also assumed that the magnetic Reynolds number  is very small; i.e.
is very small; i.e.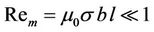 , where
, where 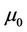 is the magnetic permeability and
is the magnetic permeability and  is the electric conductivity. We neglect the induced magnetic field, which is small in comparison with the applied magnetic field. Further, the external electrical field is assumed to be zero and the electric field due to polarization of charges is also negligible. Under these assumptions, the basic equations governing the flow and heat transfer in usual notation are:
is the electric conductivity. We neglect the induced magnetic field, which is small in comparison with the applied magnetic field. Further, the external electrical field is assumed to be zero and the electric field due to polarization of charges is also negligible. Under these assumptions, the basic equations governing the flow and heat transfer in usual notation are:
 (2.1)
(2.1)
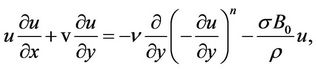 (2.2)
(2.2)
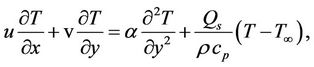 (2.3)
(2.3)
where  and
and  are the flow velocity components along the
are the flow velocity components along the  and
and  -axes respectively,
-axes respectively, 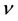 is the kinematic viscosity of the fluid,
is the kinematic viscosity of the fluid, 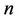 is the power-law index,
is the power-law index, 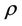 is the fluid density and
is the fluid density and  is the specific heat at constant pressure. The first term in the right hand side of the Equation (2.2), is the shear rate
is the specific heat at constant pressure. The first term in the right hand side of the Equation (2.2), is the shear rate 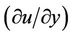 has been assumed to be negative throughout the boundary layer since the stream wise velocity component
has been assumed to be negative throughout the boundary layer since the stream wise velocity component 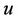 decreases monotonically with the distance
decreases monotonically with the distance  from the moving surface (for continuous stretching surface). A rigorous derivation and subsequent analysis of the boundary layer equations, for power-law fluids, were recently provided by [15]. They focused on boundary layer flow driven by free stream
from the moving surface (for continuous stretching surface). A rigorous derivation and subsequent analysis of the boundary layer equations, for power-law fluids, were recently provided by [15]. They focused on boundary layer flow driven by free stream 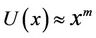 i.e., of Falkner-Skan type. Such boundary layer flows are driven by a stream wise pressure gradient
i.e., of Falkner-Skan type. Such boundary layer flows are driven by a stream wise pressure gradient  set up by the external free stream outside the viscous boundary layer. In the present context no driving pressure gradient is present. Instead the flow is driven solely by the stretching surface, which moves with a prescribed velocity
set up by the external free stream outside the viscous boundary layer. In the present context no driving pressure gradient is present. Instead the flow is driven solely by the stretching surface, which moves with a prescribed velocity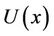 . T is the temperature of the fluid and
. T is the temperature of the fluid and 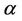 is the thermal diffusivity of the fluid. The last term containing
is the thermal diffusivity of the fluid. The last term containing  in Equation (2.3) represents the temperature-dependent volumetric rate of heat source when
in Equation (2.3) represents the temperature-dependent volumetric rate of heat source when  and heat sink when
and heat sink when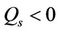 . These deal with the situation of exothermic and endothermic chemical reactions respectively. Thus the relevant boundary conditions applicable to the flow are:
. These deal with the situation of exothermic and endothermic chemical reactions respectively. Thus the relevant boundary conditions applicable to the flow are:
 (2.4)
(2.4)
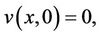 (2.5)
(2.5)
 (2.6)
(2.6)
 (2.7)
(2.7)
Here, boundary condition (2.7) means that the streamwise velocity and the temperature vanish outside the boundary layer. Equation (2.6) is the variable prescribed surface temperature at the wall whereas the Equation (2.5) signifies the importance of impermeability of the stretching surface and the Equation (2.4) assures no slip at the surface. In order to obtain the similarity solutions of Equations (2.1)-(2.7), we assume that the variable magnetic field 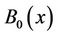 is of the form
is of the form . This form of
. This form of  has also been considered by [11-13] in the study of MHD flow problems past moving or fixed flat plate. The momentum and energy equations can be transformed to the corresponding ordinary differential equations by the following transformation ([8])
has also been considered by [11-13] in the study of MHD flow problems past moving or fixed flat plate. The momentum and energy equations can be transformed to the corresponding ordinary differential equations by the following transformation ([8])
 (2.8)
(2.8)
where 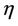 is the similarity variable,
is the similarity variable,  is the stream function
is the stream function  and
and  are the dimensionless similarity function and temperature, respectively. The velocity components
are the dimensionless similarity function and temperature, respectively. The velocity components 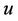 and v are given by
and v are given by
 ,
, (2.9)
(2.9)
The local Reynolds number is defined by
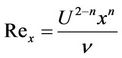 (2.10)
(2.10)
The mass conservation Equation (2.1) is automatically satisfied by Equation (2.9). By assuming the similarity function  to depend on the similarity variable
to depend on the similarity variable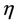 , the momentum Equation (2.2) and the heat Equation (2.3) transform into the coupled non-linear ordinary differential equations of the form
, the momentum Equation (2.2) and the heat Equation (2.3) transform into the coupled non-linear ordinary differential equations of the form
 (2.11)
(2.11)
 (2.12)
(2.12)
The boundary conditions (2.4)-(2.7) now become
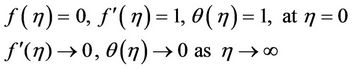 (2.13)
(2.13)
where 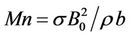 is the magnetic parameter,
is the magnetic parameter,
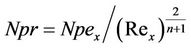 is the modified Prandtl number for power-law fluids,
is the modified Prandtl number for power-law fluids,  is the convectional Peclet number ([16] and [17]),
is the convectional Peclet number ([16] and [17]), 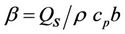 is the heat source/sink parameter. Here, primes and subscript
is the heat source/sink parameter. Here, primes and subscript  denote the differentiation with respect to
denote the differentiation with respect to . Equations (2.11) and (2.12) are solved numerically subject to the boundary conditions (2.13).
. Equations (2.11) and (2.12) are solved numerically subject to the boundary conditions (2.13).
We notice that in the case of linear stretching  and in the absence of magnetic parameter, Equations (2.11) and (2.12) reduce to those of [18], while in the case of linear stretching
and in the absence of magnetic parameter, Equations (2.11) and (2.12) reduce to those of [18], while in the case of linear stretching 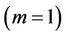 and in the absence of heat source/sink, Equations (2.11) and (2.12) reduce to those of [19] and in the presence of magnetic field parameter these equations reduce to those of [8] and [10]. Further, for linear stretching
and in the absence of heat source/sink, Equations (2.11) and (2.12) reduce to those of [19] and in the presence of magnetic field parameter these equations reduce to those of [8] and [10]. Further, for linear stretching  the analytical solution of the Equations (2.11) and (2.12) with the corresponding boundary conditions (2.13) is obtained for Newtonian fluid
the analytical solution of the Equations (2.11) and (2.12) with the corresponding boundary conditions (2.13) is obtained for Newtonian fluid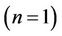 . This agrees well with the results of [3] and [20]. It should be noted that the velocity
. This agrees well with the results of [3] and [20]. It should be noted that the velocity 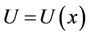 is used to define the dimensionless stream function
is used to define the dimensionless stream function 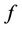 in the Equation (2.11). The local Reynolds number in Equation (2.10) describes the velocity of the moving surface that drives the flow. This choice contrasts with the conventional boundary layer analysis, in which the free stream velocity is taken as the velocity scale. Although the transformation defined in Equation (2.8) and (2.10) can be used for arbitrary variation of
in the Equation (2.11). The local Reynolds number in Equation (2.10) describes the velocity of the moving surface that drives the flow. This choice contrasts with the conventional boundary layer analysis, in which the free stream velocity is taken as the velocity scale. Although the transformation defined in Equation (2.8) and (2.10) can be used for arbitrary variation of , the transformation results in a true similarity problem only if
, the transformation results in a true similarity problem only if 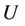 varies as
varies as . Such surface velocity variations are therefore required for the ordinary differential Equation (2.11) to be valid.
. Such surface velocity variations are therefore required for the ordinary differential Equation (2.11) to be valid.
The physical quantities of interest are the skin-friction coefficient 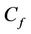 and the local Nusselt number
and the local Nusselt number , which are defined as
, which are defined as
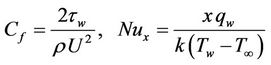 (2.14)
(2.14)
respectively, where the wall shear stress 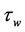 and heat transfer from the sheet
and heat transfer from the sheet  are given by
are given by
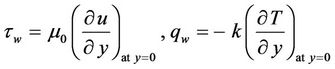 (2.15)
(2.15)
with 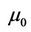 and
and 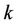 being the dynamic viscosity and thermal conductivity, respectively. Using the non-dimensional variables (2.7), we obtain
being the dynamic viscosity and thermal conductivity, respectively. Using the non-dimensional variables (2.7), we obtain

 (2.16)
(2.16)
where 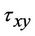 is the shear stress and
is the shear stress and 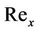 is the local Reynolds number.
is the local Reynolds number.
3. Numerical Procedure
The system of transformed governing non-linear coupled differential Equations (2.11) and (2.12) with the boundary conditions (2.13) is solved numerically using the finite-difference scheme known as Keller-Box scheme as described in [21] and [22]. This method is unconditionally stable and has second-order accuracy with arbitrary spacing. The transformed differential equations and the boundary conditions are first written as a first-order system, which are then converted to a set of finite-difference equations using central differences. Then the non-linear algebraic equations are linearised by Newton’s method and the resulting system of linear equations is then solved by block tri-diagonal elimination technique. For the sake of brevity, the details of the numerical solution procedure are not presented here. It is worth mentioning that a uniform grid of 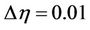 is satisfactory in obtaining sufficient accuracy with an error tolerance less than
is satisfactory in obtaining sufficient accuracy with an error tolerance less than  The more general formulations presented in this study can be readily simplified to various special cases considered in the previous works.
The more general formulations presented in this study can be readily simplified to various special cases considered in the previous works.
4. Results and Discussion
The effect of variable thermal conductivity on the MHD boundary layer flow and heat transfer in an electrically conducting power-law fluid over a non-linearly stretching sheet in the presence of heat source/sink parameter is investigated numerically. Numerical computation of the problem is obtained by Keller-Box method. To assess the accuracy of the computed values, the results for skin friction are compared with the values obtained by [8] for different values of power law index and the magnetic parameter for a linearly stretching sheet, i.e.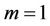 . It is observed that our results are in good agreement with the results obtained by the previous investigators as seen from the tabulated results in Table 1 for a viscous fluid. It is found from this table that the magnitude of
. It is observed that our results are in good agreement with the results obtained by the previous investigators as seen from the tabulated results in Table 1 for a viscous fluid. It is found from this table that the magnitude of  decreases when the power law index
decreases when the power law index 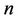 increases. Similarly, by varying
increases. Similarly, by varying 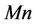 an excellent agreement is noted between present results and [8]. The effects of various non-dimensional parameters namely, the powerlaw index
an excellent agreement is noted between present results and [8]. The effects of various non-dimensional parameters namely, the powerlaw index , the magnetic parameter
, the magnetic parameter , the velocity exponent parameter
, the velocity exponent parameter  and the temperature exponent parameter
and the temperature exponent parameter , the modified Prandtl number
, the modified Prandtl number  and the heat source/sink parameter
and the heat source/sink parameter 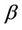 on the flow and heat transfer are shown graphically in the Figures 1-5.
on the flow and heat transfer are shown graphically in the Figures 1-5.
Figures 1(a)-(c) respectively, depict the effect of shear thinning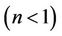 , Newtonian
, Newtonian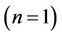 , and shear thickening
, and shear thickening  fluids on the horizontal velocity profiles
fluids on the horizontal velocity profiles  with
with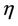 , for different values velocity exponent parameter
, for different values velocity exponent parameter 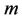 and the magnetic parameter
and the magnetic parameter . From the geometrical representation, we notice that increasing the values of magnetic parameter results in flattering of horizontal velocity profiles. The transverse contraction of the velocity boundary layer is due to the applied magnetic field which invokes the Lorentz force producing considerable opposition to the fluid motion. The effect of flattering of horizontal velocity as a consequence of increasing the strength of the magnetic field is observed for all values of velocity exponent parameter
. From the geometrical representation, we notice that increasing the values of magnetic parameter results in flattering of horizontal velocity profiles. The transverse contraction of the velocity boundary layer is due to the applied magnetic field which invokes the Lorentz force producing considerable opposition to the fluid motion. The effect of flattering of horizontal velocity as a consequence of increasing the strength of the magnetic field is observed for all values of velocity exponent parameter . The effect of increasing values of the velocity exponent parameter
. The effect of increasing values of the velocity exponent parameter 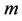 is to reduce the momentum boundary layer thickness, which tends to zero as the space variable
is to reduce the momentum boundary layer thickness, which tends to zero as the space variable  increases from the boundary surface. Physically,
increases from the boundary surface. Physically,  implies that the surface is decelerated from the slot,
implies that the surface is decelerated from the slot, 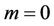 implies the continuous movement of a flat surface, and
implies the continuous movement of a flat surface, and  implies the surface is accelerated from the extruded slit. Horizontal velocity profiles
implies the surface is accelerated from the extruded slit. Horizontal velocity profiles 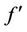 decreases and disclosing the fact that the effect of stretching of the exponent parameter
decreases and disclosing the fact that the effect of stretching of the exponent parameter 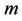 from negative values to positive
from negative values to positive
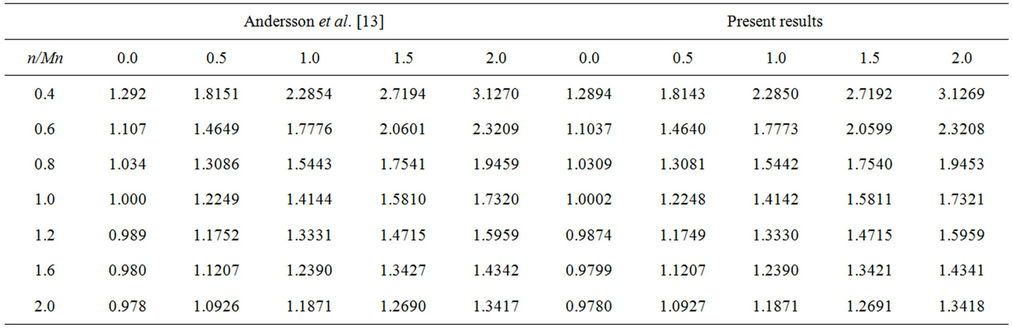
Table 1. Comparison of some of the values of skin-friction coefficient obtained by [13] with the present results for m = 1 for different values of n and Mn.

Figure 1. Velocity profiles for different values of stretching parameter (m) and magnetic parameter (Mn) with Npr = 1.0, r = 0.0 and β = 0.0 when (a) n = 0.8, (b) n = 1.0 and (c) n = 1.2.
values is to decelerate the velocity and hence reduces the momentum boundary layer thickness. This trend is notified for all types of fluids considered here namely, shear thinning (Figure 1(a)), Newtonian (Figure 1(b)) and shear thickening fluids (Figure 1(c)). Further it is observed from these Figures (1(a)-(c)) that the horizontal velocity profiles decrease with increasing values of power-law index
decrease with increasing values of power-law index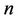 . The effect of increasing values of the power-law index parameter
. The effect of increasing values of the power-law index parameter  is to reduce the horizontal velocity and thereby reducing boundary layer thickness i.e. the thickness is much large for shear thinning fluids
is to reduce the horizontal velocity and thereby reducing boundary layer thickness i.e. the thickness is much large for shear thinning fluids  than that of Newtonian
than that of Newtonian 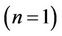 and shear thickening fluids
and shear thickening fluids 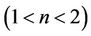 as clearly seen in Figures 1(a)-(c).
as clearly seen in Figures 1(a)-(c).
The graphs for the temperature profiles  with
with  for shear thinning, Newtonian and shear thickening fluids for different values of non-dimensional parameters governing the mathematical model, are shown graphically in Figures 2-5.
for shear thinning, Newtonian and shear thickening fluids for different values of non-dimensional parameters governing the mathematical model, are shown graphically in Figures 2-5.
Figures 2(a)-(c) show respectively, the shear thinning, Newtonian and shear thickening fluids on the temperature profiles 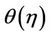 with
with 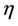 for different values of velocity exponent parameter
for different values of velocity exponent parameter  in the presence/absence of magnetic parameter
in the presence/absence of magnetic parameter . The effect of increasing values of velocity exponent parameter
. The effect of increasing values of velocity exponent parameter  is to decrease the temperature profile; however the effect is less in comparison to its effects over the flow. The graphs for the temperature profiles for different values of temperature exponent parameter
is to decrease the temperature profile; however the effect is less in comparison to its effects over the flow. The graphs for the temperature profiles for different values of temperature exponent parameter  and velocity exponent parameter
and velocity exponent parameter 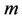 are plotted in Figures 3(a)-(c) for shear thinning, Newtonian and shear thickening fluids, respectively. From these figures we examine that the increase in the temperature exponent parameter
are plotted in Figures 3(a)-(c) for shear thinning, Newtonian and shear thickening fluids, respectively. From these figures we examine that the increase in the temperature exponent parameter 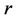 leads to decrease the temperature profiles. Physically, when
leads to decrease the temperature profiles. Physically, when 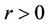 temperature flows from the stretching sheet into the ambient medium, when
temperature flows from the stretching sheet into the ambient medium, when 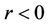 the wall temperature gradient positive and the temperature flows into the stretching sheet from the ambient medium and when
the wall temperature gradient positive and the temperature flows into the stretching sheet from the ambient medium and when  the thermal boundary conditions becomes isothermal. Figures 4(a)-(c) respectively, represents the temperature
the thermal boundary conditions becomes isothermal. Figures 4(a)-(c) respectively, represents the temperature  with the space variable
with the space variable  for several sets of values of the modified Prandtl number
for several sets of values of the modified Prandtl number  in the absence/presence of magnetic parameter
in the absence/presence of magnetic parameter 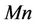 for the shear thinning (Figure 4(a)), Newtonian (Figure 4(b)) and shear thickening (Figure 4(c)). From these figures we scrutinize that the effect of an increase in the modified Prandtl number
for the shear thinning (Figure 4(a)), Newtonian (Figure 4(b)) and shear thickening (Figure 4(c)). From these figures we scrutinize that the effect of an increase in the modified Prandtl number  is to decrease the temperature
is to decrease the temperature 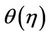 in the thermal boundary layer. This is because
in the thermal boundary layer. This is because

Figure 2. Temperature profiles for different values of stretching parameter (m) and magnetic parameter (Mn) with Npr = 1.0, r = 0.0 and β = 0.0 when (a) n = 0.8, (b) n = 1.0 and (c) n = 1.2.
Figure 3. Temperature profiles for different values of stretching parameter (m) and wall temperature parameter (r) with Npr = 1.0, Mn = 0.0 and β = 0.0 when (a) n = 0.8, (b) n = 1.0 and (c) n = 1.2.

Figure 4. Temperature profiles for different values of stretching parameter (m) and wall temperature parameter (r) with Npr = 1.0, Mn = 1.0 and β = 0.0 when (a) n = 0.8, (b) n = 1.0 and (c) n = 1.2.

Figure 5. Temperature profiles for different values of Prandtl number (Npr) and magnetic parameter (Mn) with r = –1.0, m = –0.3 and β = 0.0 when (a) n = 0.8, (b) n = 1.0 and (c) n = 1.2.
of the fact that the thermal boundary layer thickness decreases with an increase in the modified Prandtl number. This phenomenon is true even for zero/non-zero values of magnetic parameter . The effect of increasing values of the magnetic parameter
. The effect of increasing values of the magnetic parameter  is to increase the temperature profile in the presence of velocity exponent parameter. The effect of internal heat source/sink parameter
is to increase the temperature profile in the presence of velocity exponent parameter. The effect of internal heat source/sink parameter  on the temperature profile
on the temperature profile 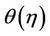 with the space variable
with the space variable  for increasing values of power-law index namely, shear thinning , Newtonian and shear thickening fluids respectively are shown graphically in Figures 5(a)-(c). From these graphs we analyzed that the temperature distribution is lower throughout the boundary layer for negative values of
for increasing values of power-law index namely, shear thinning , Newtonian and shear thickening fluids respectively are shown graphically in Figures 5(a)-(c). From these graphs we analyzed that the temperature distribution is lower throughout the boundary layer for negative values of  (heat sink) and higher for positive values of
(heat sink) and higher for positive values of  (heat source) as compared with the temperature profile in absence of heat source/sink parameter i.e.
(heat source) as compared with the temperature profile in absence of heat source/sink parameter i.e.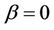 . Physically,
. Physically,  implies
implies  i.e. there will be a supply of heat to the flow region from the wall. Similarly
i.e. there will be a supply of heat to the flow region from the wall. Similarly 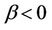 implies
implies 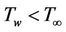 and there will be a transfer of heat from the flow to the wall. The effect of increasing the value of heat source/ sink parameter
and there will be a transfer of heat from the flow to the wall. The effect of increasing the value of heat source/ sink parameter 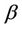 is to increase the temperature profile
is to increase the temperature profile 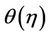 and this is even true for shear thinning, Newtonian and shear thickening fluids. .
and this is even true for shear thinning, Newtonian and shear thickening fluids. .
The values of , which signifies the local skin-friction
, which signifies the local skin-friction , are recorded in Table 1 for different values of the power-law index
, are recorded in Table 1 for different values of the power-law index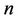 , the velocity exponent parameter
, the velocity exponent parameter 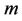 and the magnetic parameter
and the magnetic parameter . From Table 2, we observe that
. From Table 2, we observe that 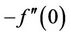 increases monotonically with increase in the magnetic field parameter
increases monotonically with increase in the magnetic field parameter  for various values of
for various values of . It is interesting to note that the magnitude of wall surface gradient decreases gradually with increasing power-law index for a fixed value of magnetic parameter
. It is interesting to note that the magnitude of wall surface gradient decreases gradually with increasing power-law index for a fixed value of magnetic parameter . The effect of power-law index on
. The effect of power-law index on 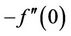 is significant in shear thinning fluid
is significant in shear thinning fluid 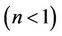 than shear thickening fluid
than shear thickening fluid . The effect of increasing the values of velocity exponent parameter
. The effect of increasing the values of velocity exponent parameter 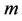 is to increase the magnitude of wall surface gradient and decreases with increasing the values of power-law index. This behavior is even true in the presence/absence of magnetic parameter. The heat transfer phenomenon is usually analyzed from the numerical value of the physical parameter, namely, wall temperature gradient
is to increase the magnitude of wall surface gradient and decreases with increasing the values of power-law index. This behavior is even true in the presence/absence of magnetic parameter. The heat transfer phenomenon is usually analyzed from the numerical value of the physical parameter, namely, wall temperature gradient  which in turn helps in the computation of the local Nusselt number
which in turn helps in the computation of the local Nusselt number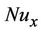 . Numerical results for wall temperature gradient for various values of temperature exponent
. Numerical results for wall temperature gradient for various values of temperature exponent  for different non-dimensional physical parameters
for different non-dimensional physical parameters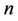 ,
, 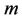 ,
,  , Npr,
, Npr,  are recorded in Table 3. It is observed that the effect of increasing the values of power-law index
are recorded in Table 3. It is observed that the effect of increasing the values of power-law index  is to increase the wall temperature gradient whereas reverse trend is seen with magnetic field parameter
is to increase the wall temperature gradient whereas reverse trend is seen with magnetic field parameter 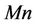 when
when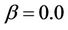 . The effect of increasing values of the temperature exponent parameter
. The effect of increasing values of the temperature exponent parameter 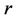 and the velocity exponent parameter
and the velocity exponent parameter 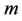 is to decrease the wall temperature gradient
is to decrease the wall temperature gradient . This result has significance in industrial applications to reduce expenditure on power supply in stretching the sheet just by increasing the magnetic field parameter
. This result has significance in industrial applications to reduce expenditure on power supply in stretching the sheet just by increasing the magnetic field parameter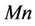 . Further, it is analyzed from Table 2 that the effect of modified Prandtl number
. Further, it is analyzed from Table 2 that the effect of modified Prandtl number 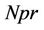 is to decrease the wall temperature gradient. In addition, the effect of increasing values of heat source/sink parameter
is to decrease the wall temperature gradient. In addition, the effect of increasing values of heat source/sink parameter  is to decrease the wall temperature gradient All results obtained here are consistent with the physical situations.
is to decrease the wall temperature gradient All results obtained here are consistent with the physical situations.
5. Conclusions
The problem of magneto-hydrodynamic flow and heat transfer of an electrically conducting non-Newtonian power-law fluid past a non-linearly stretching sheet is studied theoretically. The governing partial differential equations are transformed into ordinary differential equations by using an appropriate similarity transformation and the resulting boundary value problem is solved numerically by a second order finite difference scheme. The effects of various governing parameters such as the power-law index , the magnetic parameter
, the magnetic parameter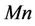 , the velocity exponent parameter
, the velocity exponent parameter 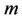 and the temperature exponent parameter
and the temperature exponent parameter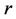 , the modified Prandtl number
, the modified Prandtl number 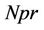 and the heat source/sink parameter
and the heat source/sink parameter 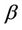 on the flow and heat transfer characteristics were examined. The numerical result for the skin friction is in good
on the flow and heat transfer characteristics were examined. The numerical result for the skin friction is in good
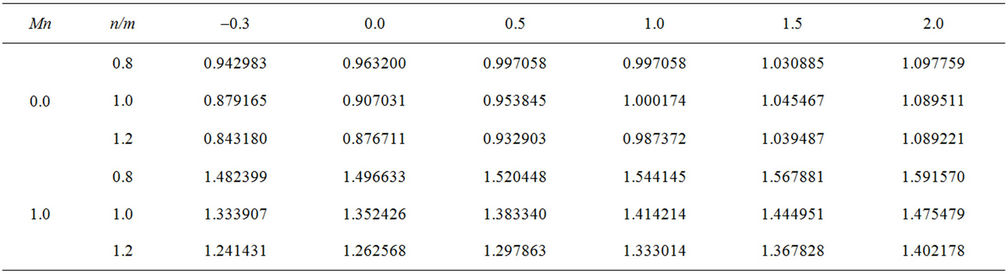
Table 2. Numerical values of skin-friction for different values of the physical parameters.


Table 3. Numerical values of wall temperature gradient for different values of the physical parameters.
agreement with earlier studies. Numerical results for the skin-friction coefficient, the local Nusselt number, the velocity and the temperature profiles are presented in graphs for several sets of values of the pertinent parameters. The following conclusions are drawn from the computed numerical values:
• The power-law index  is to increase the momentum boundary layer thickness and is to decrease the thermal boundary layer thickness for increasing values of power-law index namely, shear thinning, Newtonian and shear thickening fluids.
is to increase the momentum boundary layer thickness and is to decrease the thermal boundary layer thickness for increasing values of power-law index namely, shear thinning, Newtonian and shear thickening fluids.
• The effects of increasing values of velocity exponent parameter 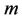 is to reduce the horizontal velocity and thereby reducing the momentum boundary layer thickness.
is to reduce the horizontal velocity and thereby reducing the momentum boundary layer thickness.
• The increasing value of magnetic parameter  results in flattering the horizontal velocity profiles and increase the temperature profile.
results in flattering the horizontal velocity profiles and increase the temperature profile.
• The increasing value of temperature exponent parameter 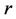 is to decrease the temperature profile.
is to decrease the temperature profile.
• The effect of modified Prandtl number  is to decrease the thermal boundary layer thickness and the wall temperature gradient.
is to decrease the thermal boundary layer thickness and the wall temperature gradient.
The internal heat source/sink parameter 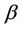 increases the temperature profile.
increases the temperature profile.
REFERENCES
- B. Vujannovic, A. M. Status and D. J. Djukiv, “A Variational Solution of the Rayleigh Problem for Power-Law Non-Newtonian Conducting Fluid,” Archive of Applied Mechanics, Vol. 41, No. 6, 1971, pp. 381-386.
- B. C. Sakiadis, “Boundary Layer Behavior on Continuous Solid Surfaces,” AIChE Journal, Vol. 7, No. 1, 1961, pp. 26-28. doi:10.1002/aic.690070108
- L. J. Crane, “Flow past a Stretching Plate,” Zeitschrift für Angewandte Mathematik und Physik, Vol. 21, No. 4, 1970, pp. 645-647. doi:10.1007/BF01587695
- P. S. Gupta and A. S. Gupta, “Heat and Mass Transfer on a Stretching Sheet with Suction or Blowing,” The Canadian Journal of Chemical Engineering, Vol. 55, No. 6, 1977, pp. 744-746. doi:10.1002/cjce.5450550619
- J. P. Jadhav and B. B. Waghmode, “Heat Transfer to Non-Newtonian Power-Law Fluid past a Continuously Moving Porous Flat Plate with Heat Flux,” Heat and Mass Transfer, Vol. 25, No. 6, 1990, pp. 377-380. doi:10.1007/BF01811562
- T. Sarpakaya, “Flow on Non-Newtonian Fluids in a Magnetic Field,” AIChE Journal, Vol. 7, 1961, pp. 26-28.
- K. B. Pavlov, “Magnetohydrodynamic Flow of an Incompressible Viscous Fluid Caused by Deformation of a Plane Surface,” Magninaya Gidrodinamika (USSR), Vol. 4, 1974, pp. 146-147.
- H. I. Andersson, K. H. Bech and B. S. Dandapat, “Magnetohydrodynamic Flow of a Power-Law Fluid over a Stretching Sheet,” International Journal of Non-Linear Mechanics, Vol. 27, No. 6, 1992, pp. 929-936. doi:10.1016/0020-7462(92)90045-9
- M. I. Char, “Heat and Mass Transfer in a Hydromagnetic Flow of a Visco-Elastic Fluid over a Stretching Sheet,” Journal of Mathematical Analysis and Applications, Vol. 186, No. 3, 1994, pp. 674-689. doi:10.1006/jmaa.1994.1326
- R. Cortell, “A Note on Magneto Hydrodynamic Flow of a Power-Law Fluid over a Stretching Sheet,” Applied Mathematics and Computation, Vol. 168, No. 1, 2005, pp. 557- 566. doi:10.1016/j.amc.2004.09.046
- T. C. Chaim, “Hydromagnetic Flow over a Surface with a Power-Law Velocity,” International Journal of Engineering Science, Vol. 33, No. 3, 1995, pp. 429-435. doi:10.1016/0020-7225(94)00066-S
- A. Ishak, R. Nazar and I. Pop, “Magnetohydrodynamic Stagnation-Point Flow towards a Stretching Vertical Sheet,” Magnetohydrodynamics, Vol. 42, 2006, pp. 17- 30.
- S. P. Anjali Devi and M. Thiyagarajan, “Steady Nonlinear Hydromagnetic Flow and Heat Transfer over a Stretching Surface of Variable Temperature,” Heat and Mass Transfer, Vol. 42, No. 8, 2006, pp. 671-677. doi:10.1007/s00231-005-0640-y
- R. Cortell, “Viscous Flow and Heat Transfer over a Nonlinearly Stretching Sheet,” Applied Mathematics and Computation, Vol. 184, No. 2, 2007, pp. 864-873. doi:10.1016/j.amc.2006.06.077
- J. P. Denier and P. P. Dabrowski, “On the Boundary Layer Equations for Power-Law Fluids,” Proceedings of the Royal Society of London, Vol. A, 2004, pp. 3143- 3158.
- A. Acrivos, M. J. Shah and E. E. Peterson, “Momentum and Heat Transfer in Laminar Boundary Layer Flows of Non-Newtonian Fluids past External Surfaces,” AIChE Journal, Vol. 6, No. 2, 1960, pp. 312-317. doi:10.1002/aic.690060227
- A. Acrivos, “A Theoretical Analysis of Laminar Natural Convection Heat Transfer to Non-Newtonian Fluids,” AIChE Journal, Vol. 6, No. 4, 1960, pp. 584-590. doi:10.1002/aic.690060416
- I. A. Hassanien, A. A. Abdullah and R. S. R. Gorla, “Flow and Heat Transfer in a Power-Law Fluid over a Non-Isothermal Stretching Sheet,” Mathematical and Computer Modelling, Vol. 28, No. 9, 1998, pp. 105-116. doi:10.1016/S0895-7177(98)00148-4
- H. I. Andersson and B. S. Dandapat, “Flow of a PowerLaw Fluid over a Stretching Sheet,” Stability and Applied Analysis of Continuous Media, Vol. 1, 1991, pp. 339-347.
- L. G. Grubka and K. M. Bobba, “Heat Transfer Characteristics of a Continuous Stretching Surface with Variable Temperature,” Journal of Heat Transfer, Vol. 107, No. 1, 1985, pp. 248-250. doi:10.1115/1.3247387
- T. Cebeci and P. Bradshaw, “Physical and Computational Aspects of Convective Heat Transfer,” Springer-Verlag, New York, 1984.
- H. B. Keller, “Numerical Methods for Two-Point Boundary Value Problems,” Dover Publications, New York, 1992.
Nomenclature
 constant
constant
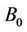 uniform magnetic field b;stretching rate, positive constant
uniform magnetic field b;stretching rate, positive constant
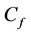 skin-friction
skin-friction
 strain tensor
strain tensor
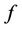 dimensionless stream function
dimensionless stream function
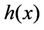 heat transfer coefficient
heat transfer coefficient
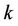 thermal conductivity
thermal conductivity
 consistency co efficient
consistency co efficient
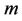 velocity exponent parameter
velocity exponent parameter
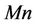 magnetic parameter
magnetic parameter
 power-law index
power-law index
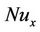 Nusselt number
Nusselt number
 modified Prandtl number
modified Prandtl number
 Peclet number
Peclet number
 local heat flux at the sheet p;pressure
local heat flux at the sheet p;pressure
 local Reynolds number r;temperature exponent parameter
local Reynolds number r;temperature exponent parameter
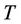 fluid temperature
fluid temperature
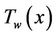 temperature of the stretching sheet
temperature of the stretching sheet
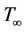 ambient temperature
ambient temperature
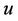 velocity in x direction
velocity in x direction
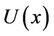 velocity of the stretching sheet
velocity of the stretching sheet
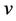 velocity in y-direction
velocity in y-direction
 horizontal distance
horizontal distance
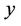 vertical distance
vertical distance
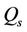 temperature-dependent volumetric rate of heat source
temperature-dependent volumetric rate of heat source
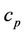 specific heat at constant pressure
specific heat at constant pressure
Greek Symbols
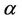 thermal diffusivity
thermal diffusivity
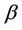 heat source/sink parameter
heat source/sink parameter
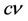 kinematic viscosity
kinematic viscosity
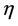 similarity variable
similarity variable
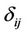 Kronecker delta
Kronecker delta
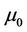 magnetic permeability
magnetic permeability
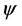 Stream function
Stream function
 density
density
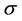 electrical conductivity
electrical conductivity
 shear stress
shear stress
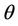 dimensionless temperature
dimensionless temperature
Subscripts
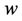 condition at the stretching sheet
condition at the stretching sheet
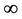 condition at infinity
condition at infinity
Superscript
' differentiation with respect to 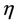
NOTES
*Corresponding author.

