ABSTRACT

In this paper first we prove common fixed point theorems for compatible and weakly compatible maps. Secondly, we prove common fixed point theorems for weakly compatible maps along with property (E.A.) and (CLRg) property respectively.

1. Introduction

In 1922, Banach proved a common fixed-point theorem which ensures under appropriate conditions, the existence and uniqueness of a fixed-point. This theorem has many applications, but suffers from one drawback—the definition requires that T be continuous throughout X. There then follows a flood of papers involving contractive definition that do not require the continuity of T. This result was further generalized and extended in various ways by many authors. This theorem provides a technique for solving a variety of applied problems in mathematical sciences and engineering.

In 1963, Gahler [1] introduced the concept of 2-metric spaces and claimed that a 2-metric is a generalization of the usual notion of a metric, but some authors proved that there is no relation between these two functions. Geometrically, a 2-metric d represents the area of a triangle whose vertices are x, y and z. Hsiao [2] have showed that contraction-like conditions on the operators in 2-metric spaces imply either the space is trivial or the operator is trivial.

In 1984, Dhage [3] introduced the concept of D-metric spaces. The situation for a D-metric space is quite different from 2-metric spaces. Geometrically, a D-metric D(x, y, z) represent the perimeter of the triangle with vertices x, y and z in R².

Recently, Mustafa and Sims [4] had shown that most of the results concerning Dhage’s D-metric spaces are invalid and they introduced an improved version of the generalized metric space structure and called it as Gmetric spaces. For more details on G-metric spaces one can refer to the papers [4-7].

Now we give preliminaries and basic definitions which are used throughout the paper.

In 2006, Mustafa and Sims [5] introduced the concept of G-metric spaces as follows:

Definition 1.1.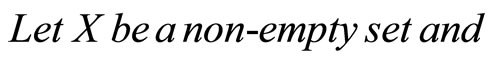

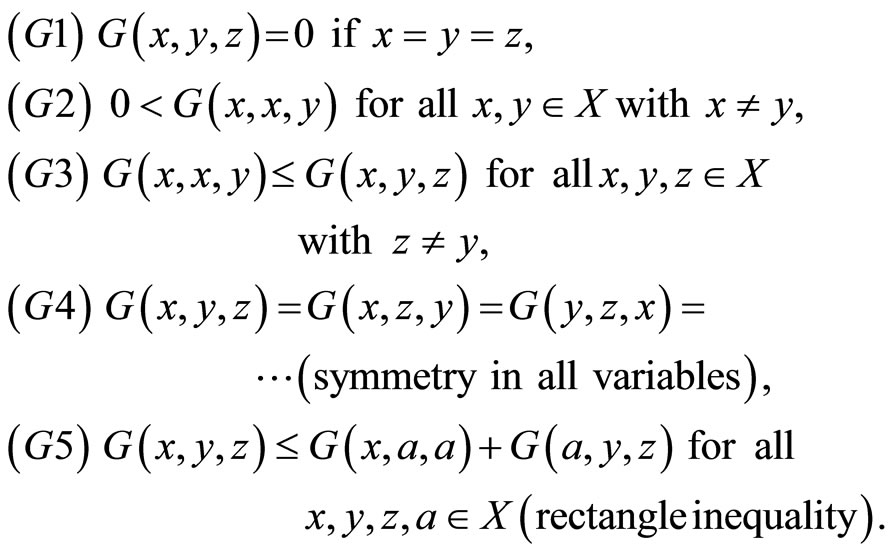
The function G is called a generalized metric or more specifically, a G-metric on X, and the pair (X, G) is called a G-metric space.

Let (X, G) be a G-metric space, {x_n} a sequence of points in X. we say that {x_n} is G-convergent to x if, i.e., for each 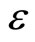> 0 there exists an N such that  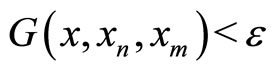for all m, n ≥ N. We call x the limit of the sequence and write

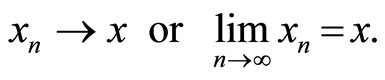
Proposition 1.1. Let (X, G) be a G-metric space. Then the following are equivalent:

Definition 1.2. Let (X, G) be a G-metric space. A sequence {x_n} is called G-Cauchy if, for each 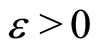there exist an (set of positive integers) such that .

Proposition 1.2. In a G-metric space (X, G) the following are equivalent:

1) The sequence {x_n} is G-Cauchy

2) for each there exists an (set of positive integers) such that

.

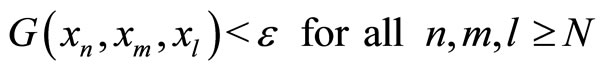Proposition 1.3. Let (X, G) be a G-metric space. Then the function G(x, y, z) is jointly continuous in all three of its variables.

Definition 1.3. A G-metric space (X, G) is called a symmetric G-metric space if G(x, y, y) = G(y, x, x) for all x, y in X.

Proposition 1.4. Every G-metric space defines a metric space by

Proposition 1.5. A G-metric space 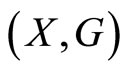is Gcomplete if and only if 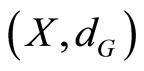is a complete metric space.

Proposition 1.6. Let 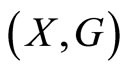be a G-metric space. Then, for any x, y, z, a in X it follows that:

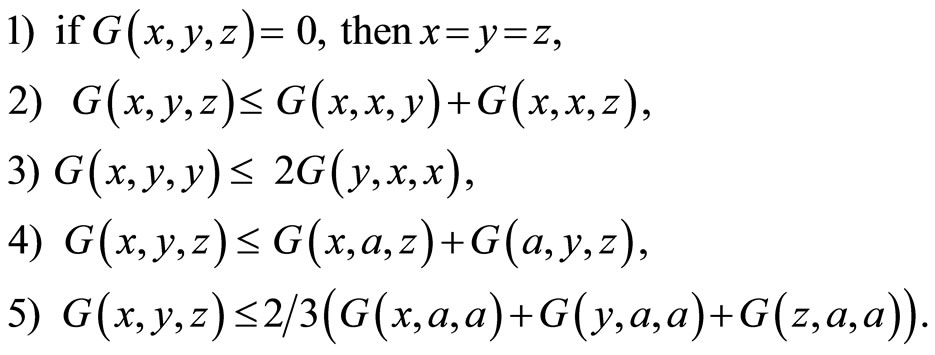
There has been a considerable interest to study common fixed point for a pair (or family) of mappings satisfying contractive conditions in metric spaces. Now, it is obvious that a fixed point of any map on metric spaces is a common fixed point of that map and identity map on the space. Several interesting and elegant results were obtained in this direction by various authors. It was the turning point in the “fixed point arena” when the notion of commutativity was used by Jungck [8] to obtain common fixed point theorems. While proving his result, Jungck [8] replaced identity map with a continuous map.

Theorem 1.1 [8]. Let T be a continuous mapping of a complete metric space into itself. Then T has a fixed point in X if there exist

From this result, it can be seen that a metrical common fixed point theorem generally involves conditions on commutativity, continuity, completeness and suitable containment of ranges of the involved maps besides an appropriate contraction condition and many authors in this domain are aimed at weakening one or more of these conditions.

In particular, now we look in the context of common fixed point theorems in G-metric spaces. Start with the following contraction conditions:

Let T be a mapping from a complete metric space into itself and consider the following conditions:

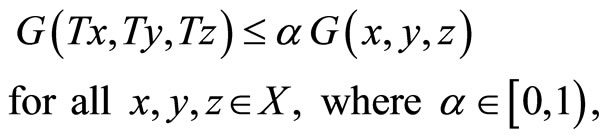(1.1)

It is clear that every self mapping T of X satisfying condition (1.1) is continuous. Now we focus to generalize the condition (1.1) for a pair of self maps S and T of X in the following way:

(1.2)

To prove the existence of common fixed points for (1.2), it is necessary to add additional assumptions such as construction of the sequence {x_n} and some mechanism to obtain common fixed point. Most of the theorems in literature have followed a similar pattern of maps: 1) contraction; 2) continuity of functions (either one or both); and 3) commuting pair of mappings were given. In some cases condition 2) can be relaxed but condition 1) and 3) are unavoidable.

In 1986, Jungck [9] introduced the concept of compatibility in metric spaces as follows:

Two self-mappings f and g of a metric space 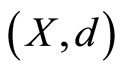are said to be compatible if

2. Compatible Maps

Recently, Choudhury et al. [10] introduced the notion of compatible maps in G-metric space as follows:

Let f and g be self maps of a G-metric space. The maps f and g are said to be compatible map if there exists a sequence

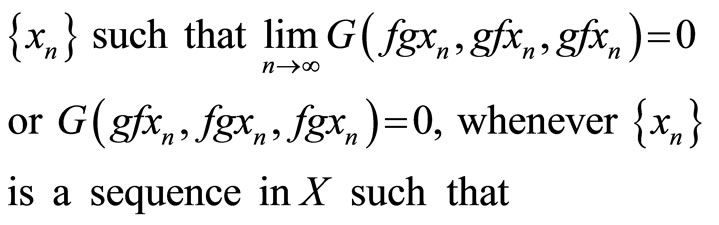
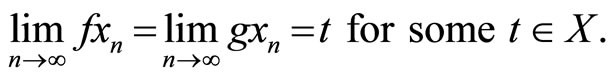
Example 2.1.

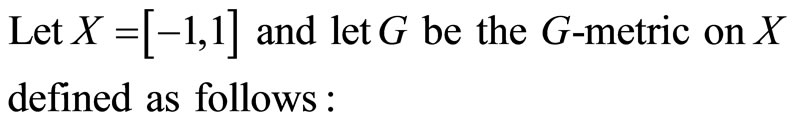
Now we come to our main result for a pair of compatible maps.

Theorem 2.1. Let be a complete G-metric space. Let f and g be self mappings of X satisfying the following conditions:

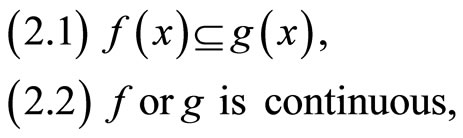
Then f and g have a unique common fixed point in X provided f and g are compatible maps.

Proof. Let be an arbitrary point in X. By (2.1), one can choose a point

From (2.3), we have

or

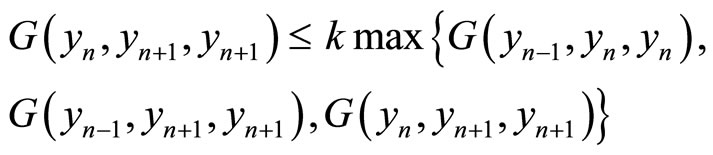
Case 1.

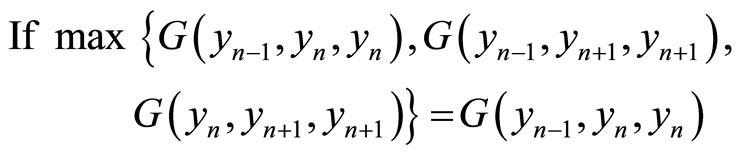
then, using (2.3), we getContinuing in the same way, we have

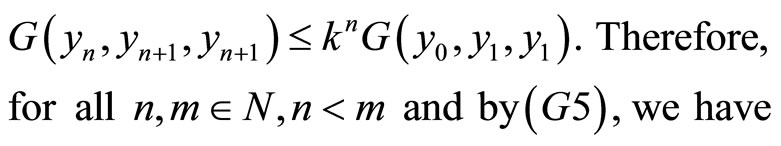
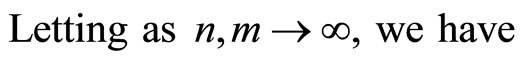
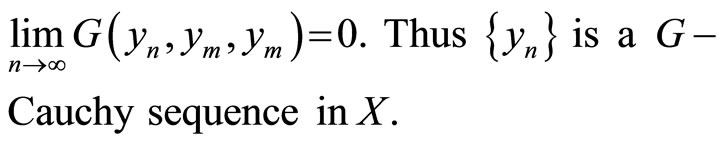
Case 2.

.

From (2.3) and using (G5) , one obtains

implies

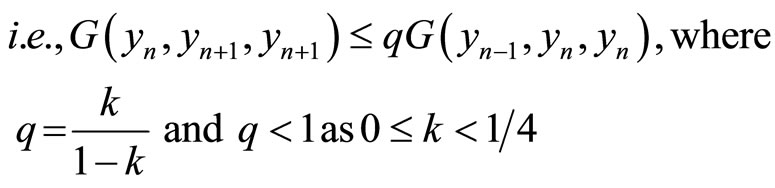
In view of Case 1, we have 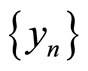is G-Cauchy sequence in X.

Case 3.

then, from (2.3), one obtains

Hence in all cases the sequence is a G-Cauchy sequence in X.

Since (X,G) is complete G-metric space, thereforethere exists a point 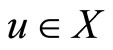such that, we have 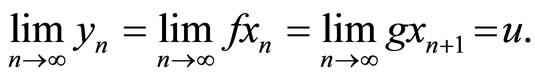Since one of the maps f or g is continuous, for definiteness one can assume that g is continuous, therefore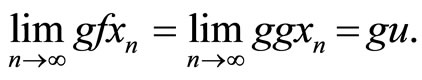Further, f and g are compatible, therefore,  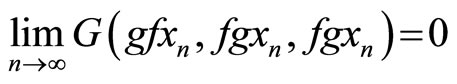implies 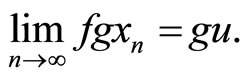Now we claim that gu = u, from (2.3), we have

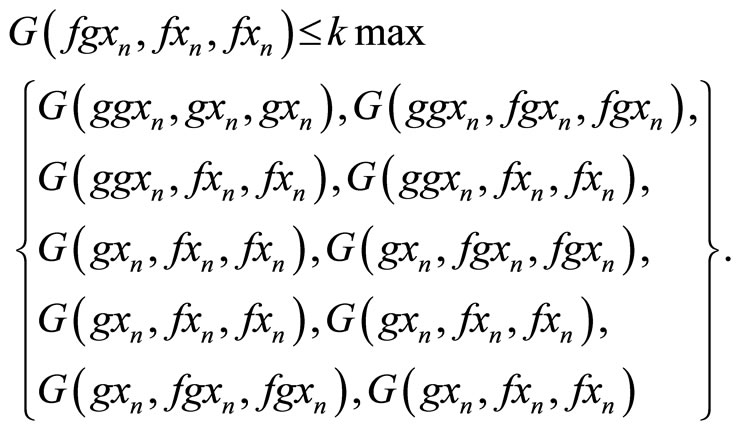
Proceeding limit as, and using Proposition 1.6, we have

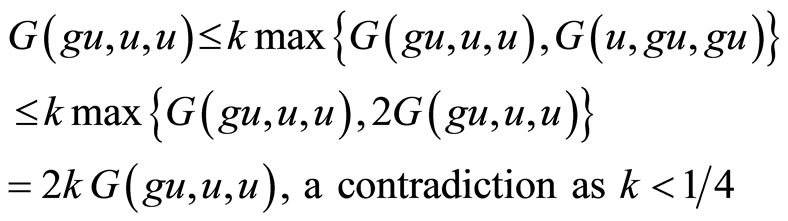
Hence gu = u, next we will show that gu = fu = u, for this purpose we put x = x_n, y = z = u in (2.3), we have

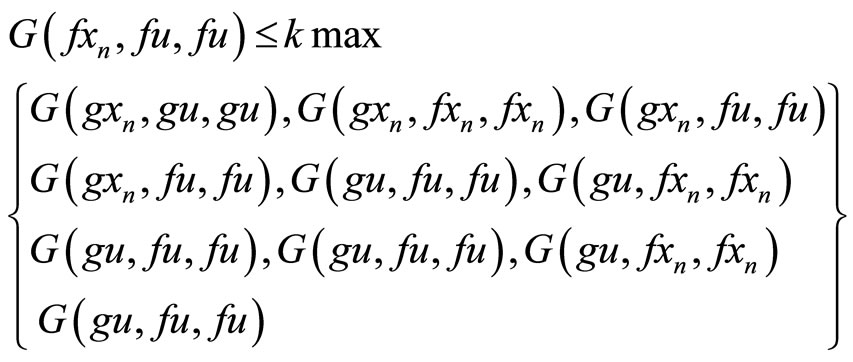
Proceeding limit as , we have

Hence fu = gu = u. Thus u is a common fixed point of f and g.

Uniqueness. We assume that be another common fixed point of f and g. Then

By using Proposition 1.6, we have 

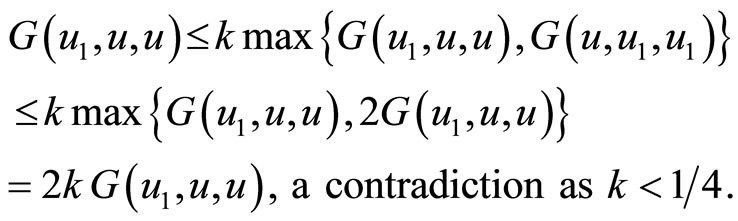
This demands that 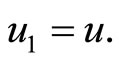Hence uniqueness follows.

Example 2.2. Let X = [−1, 1] and let G be the G-metric on X defined as follows:

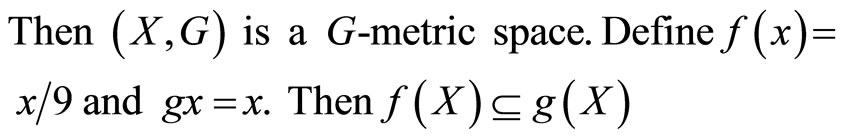
Also, inequality (2.3) holds for all x, y, z in X and 0 is the unique common fixed point of f and g.

Corollary 2.1. Let (X, G) be a complete G-metric space and let f and g be compatible mapping of X satisfying (2.1), (2.2) and  the following condition:

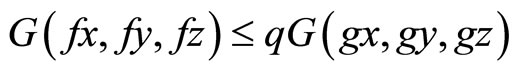
for every x, y, z in X and 0 < q < 1.

Then f and g have a unique common fixed point in X.

Proof: Proof follows easily from Theorem 2.1.

3. Weakly Compatible Maps

In 1996, Jungck [11] introduce the notion of weakly compatible mappings as follows:

Definition 3.1. Two maps f and g are said to be weakly compatible if they commute at coincidence points.

Example 3.1. Let X = [0, 3].

Then for any 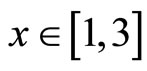, x is a coincidence point and fgx = gfx, showing that f, g are weakly compatible maps on [0, 3].

Theorem 3.1. Let f and g be weakly compatible self maps of a G-metric space (X, G) satisfying (2.1) and (2.3) and the following condition:

(3.1) any one of the subspace f(X) or g(X) is complete; Then f and g have a unique common fixed point in X.

Proof. From Theorem 2.1, we conclude that {y_n} is a G-Cauchy sequence in X. Since either f(X) or g(X) is complete, for definiteness assume that g(X) is complete subspace of X then the subsequence of {y_n} must get a limit in g(X). Call it be t. Let ug⁻¹t. Then gu = t as {y_n} is a G-Cauchy sequence containing a convergent subsequence, therefore the sequence {y_n} also convergent implying thereby the convergence of subsequence of the convergent sequence. Now we show that fu = t.

On setting x = x_n, y = u and z = u, in (2.3), we have

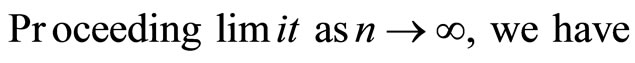
Hence fu = g u = t. Thus u is a coincident point of f and g. Since f and g are weakly compatible, it follows that fgu = gfu, i.e., ft = gt.

We now show that ft = t. Suppose that, therefore 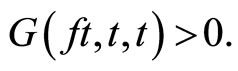Now put on setting x = t, y = u, z = u, in (2.3), we have

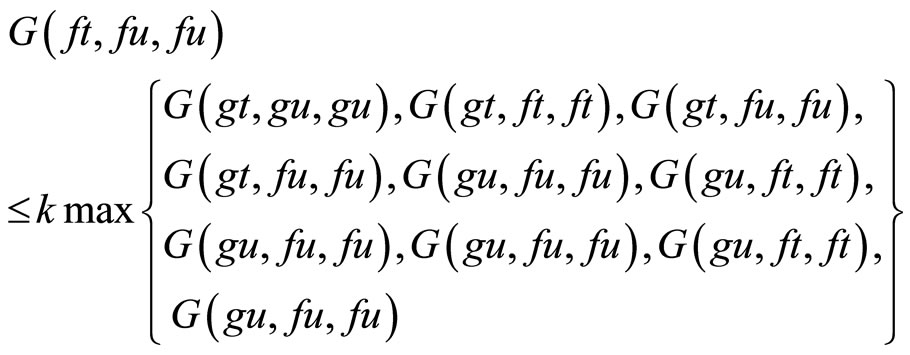
By using Proposition 1.6, we have

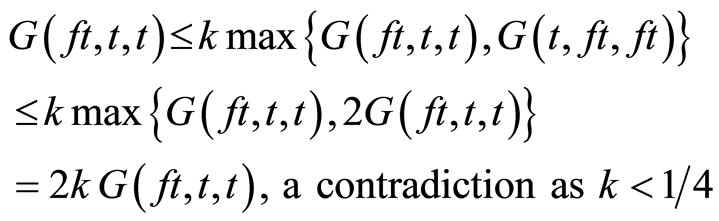
This demands that ft = t = gt, i.e., t is common fixed point of f and g. Uniqueness follows easily.

4. Property (E.A.) in G-Metric Spaces

Recently, Amari and Moutawakil [12] introduced a generalization of non compatible maps as property (E.A.) in metric spaces as follows:

Definition 4.1. Let A and S be two self-maps of a metric space (X, d) .The pair (A, S) is said to satisfy property (E.A.), if there exists a sequence{x_n} in X such that

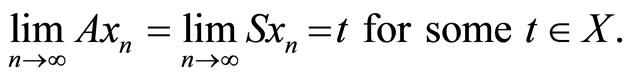
In similar mode, we use property (E.A.) in G-metric spaces.

Example 4.1 [12]. Let

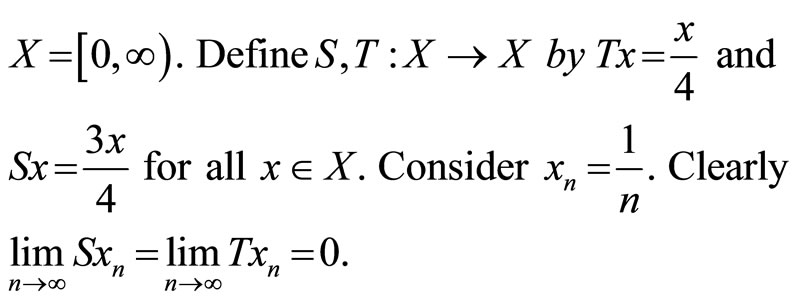
Then S and T satisfy property (E.A.).

Example 4.2 [12]. Let

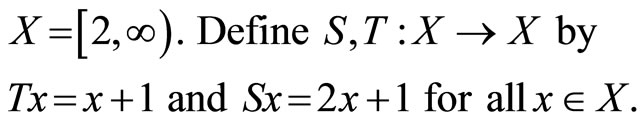
Suppose that the property (E.A.) holds. Then, there exists in X a sequence 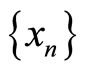satisfying

Therefore,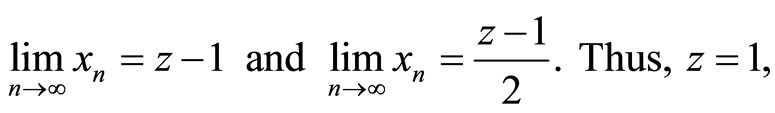a contradiction, since 1 is not contained in X. Hence S and T do not satisfy property (E.A.).

Notice that weakly compatible and property (E.A.) are independent to each other (for detail see, [13]).

Example 4.3. Let and be the usual metric space. Define

Thus the pair (f, g) satisfies property (E.A.). However, f and g are not weakly compatible as each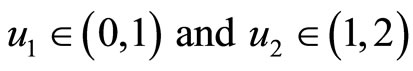are coincidence points of f and g, where they do not commute. Moreover, they commute at x = 0, 1, 2, ... but none of these points are coincidence points of f and g. Thus we can conclude that, property (E.A.) does not imply weak compatibility.

Now we prove a common fixed point theorem for a pair of weakly compatible maps along with property (E.A.).

Theorem 4.1. Let f and g be self maps of a G-metric space (X, G) satisfying (2.3) and the following conditions:

(4.1) f and g satisfy property (E.A.)

(4.2) g(X) is a closed subspace of X.

Then f and g have a unique common fixed point in X provided f and g are weakly compatible self maps.

Proof. Since f and g satisfy property (E.A.), therefore, there exists a sequence 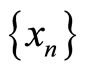in X such that

.

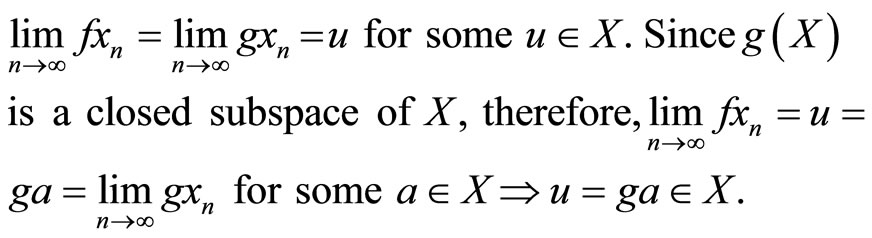
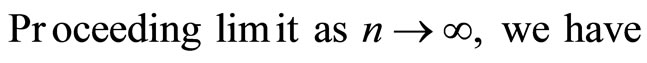
Hence fa = ga = u. Thus u is a coincident point of f and g. Since f and g are weakly compatible maps.

Rest of the proof follows easily from Theorem 3.1.

Corollary 4.1. Let f and g be self maps of a G-metric space (X, G) satisfying (4.1) and (4.2) and the following condition:

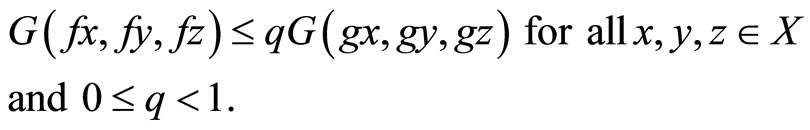
Then f and g have a unique common fixed point in X provided f and g be weakly compatible self maps.

Proof. Proof follows easily from Theorem 4.1.

Example4.1.

Then f and g satisfy property (E.A.). Also f(X) = {0, 1} and g(X) = {0, 2}.

Here we note that neither f(X) is contained in g(X) nor g(X) is contained in f(X) and Corollary 4.1 holds for 1/2 ≤ q < 1.

Remark 4.1. It can be observed that a pair of maps enjoying property (E.A.) relaxes the required containment of range of one mapping into the range of other which is utilized to construct the sequence of joint iterates. Moreover, it buys containment of ranges without any continuity requirements besides minimizes the commutativity conditions of the maps to the commutativity at their points of coincidence and it also allows replacing the completeness requirement of the space with a more natural condition of closeness of the range.

5. (CLRg) Property in G-Metric Spaces

Recently, Sintunavarat and Kumam [14] introduced a new property which is so called “Common Limit in the Range of g property” (i.e., (CLRg ) property) and defined as follow:

Definition 5.1 [14]. Suppose that 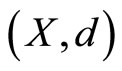is a metric space and. Two mappings f and g are said to satisfy the common limit in the range of g property if there exists a sequence in X such that

The common limit in the range of g property will be denoted by the (CLRg) property.

Example 5.1 [14].

Example 5.2 [14].

In similar mode, we use (CLRg) property in G-metric spaces.

Theorem 5.1. Let f and g be self maps of a G-metric space (X, G) satisfying (2.3) and the following condition: (5.1) f and g satisfy (CLRg ) property Then f and g have a unique common fixed point in X provided f and g are weakly compatible maps.

Proof. Since f and g satisfy (CLRg) property, therefore, there exists a sequence in X such that

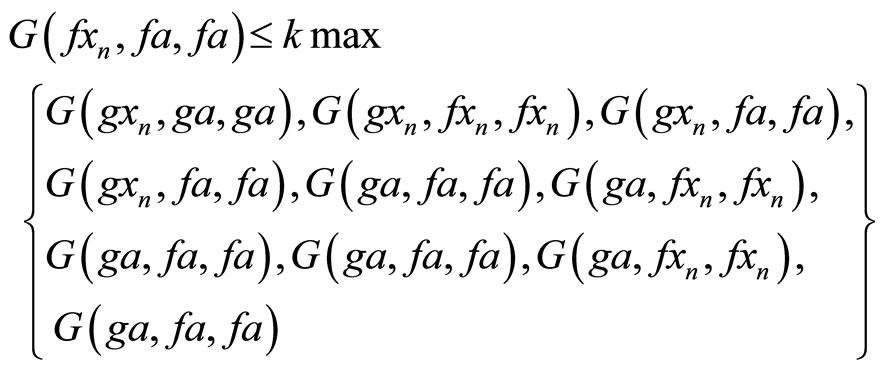
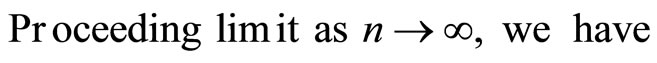
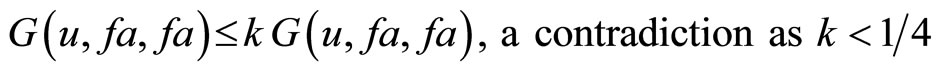
Hence fa = ga = u. Thus u is a coincident point of f and g. Since f and g are weakly compatible maps.

Rest of the Proof follows easily from Theorem 3.1.

Remark 5.1. We note that (CLRg) property relaxes the condition of closeness of range.

6. Acknowledgements

Authors (Sanjay Kumar, Naresh Kumar and S. K. Garg) would like to acknowledge University Grants Commission, Delhi, India for providing financial grant for the Major Research Project under Ref. No. 39-41/2010(SR).

REFERENCES

NOTES

^*Corresponding author.