Applied Mathematics
Vol.3 No.2(2012), Article ID:17390,5 pages DOI:10.4236/am.2012.32022
Generalized Thermoelasticity Problem of Material Subjected to Thermal Loading Due to Laser Pulse
1Mechanical Department, Faculty of Engineering and Islamic Architecture, Umm Al-Qura University, Makkah, Saudi Arabia
2Mathematics Department, Faculty of Education, Alexandria University, Alexandria, Egypt
3Mathematical Department, Faculty of Sciences, Umm Al-Qura University, Makkah, Saudi Arabia
Email: yousefanne@yahoo.com
Received November 18, 2011; revised December 29, 2011; accepted January 7, 2012
Keywords: Thermoelasticity; coupled thermoelasticity; generalized thermoelasticity; Non-Gaussian laser pulse
ABSTRACT
This work is devoted to a study of the induced temperature and stress fields in an elastic half space in context of classical coupled thermoelasticity and generalized thermoelasticity in a unified system of equations. The half space is considered to be made of an isotropic homogeneous thermoelastic material. The bounding plane surface is heated by a nonGaussian laser beam with pulse duration of 2 ps. An exact solution of the problem is first obtained in Laplace transform space. Since the response is of more interest in the transient state, the inversion of Laplace transforms have been carried numerically. The derived expressions are computed numerically for copper and the results are presented in graphical form.
1. Introduction
Although thermomechanical phenomena in the majority of practical engineering applications are adequately simulated with the classical Fourier heat conduction equation, there is an important body of problems that require due consideration of thermomechanical coupling: it is appropriate in these cases to apply the generalized theory of thermoelasticity. Serious attention has been paid to the generalized thermoelasticity theories in solving thermoelastic problems in place of the classical uncoupled/coupled theory of thermoelasticity.
The absence of any elasticity term in the heat conduction equation for uncoupled thermoelasticity appears to be unrealistic, since due to the mechanical loading of an elastic body, the strain so produced causes variation in the temperature field. Moreover, the parabolic type of the heat conduction equation results in an infinite velocity of thermal wave propagation, which also contradicts the actual physical phenomena. Introducing the strain-rate term in the uncoupled heat conduction equation, Biot extended the analysis to incorporate coupled thermoelasticity [1]. In this way, although the first shortcoming was over, there remained the parabolic type partial differential equation of heat conduction, which leads to the paradox of infinite velocity of the thermal wave. To eliminate this paradox generalized thermoelasticity theory was developed subsequently. Due to the advancement of pulsed lasers, fast burst nuclear reactors and particle accelerators, etc. which can supply heat pulses with a very fast time-rise [2,3]; generalized thermoelasticity theory is receiving serious attention. The development of the second sound effect has been nicely reviewed by Chandrasekharaiah [4]. At present mainly two different models of generalized thermoelasticity are being extensively used-one proposed by Lord and Shulman [5] and the other proposed by Green and Lindsay [6]. L-S (Lord and Shulman theory) suggests one relaxation time and according to this theory, only Fourier’s heat conduction equation is modified; while G-L (Green and Lindsay theory) suggests two relaxation times and both the energy equation and the equation of motion are modified.
The so-called ultra-short lasers are those with pulse duration ranging from nanoseconds to femtoseconds in general. In the case of ultra-short-pulsed laser heating, the high-intensity energy flux and ultra-short durationlaser beam, have introduced situations where very large thermal gradients or an ultra-high heating speed mayexist on the boundaries [7]. In such cases, as pointed out by many investigators, the classical Fourier model, whichleads to an infinite propagation speed of the thermal energy, is no longer valid [8]. The non-Fourier effect of heat conduction takes intoaccount the effect of mean free time (thermal relaxation time) in the energy carrier’s collision process, which caneliminate this contradiction. By employing the L-S model (Lord and Shulman) with one relaxation time,Sherief and Anwar [9] have obtained the distributions of thermal stresses and temperature for a generalizedthermoelastic problem in which an infinite elastic space was subjected to the influence of a continuous linesource of heat. The solution of the problem was obtained by applying the Hankel and Laplace integral transformssuccessively. Wang and Xu have studied the stress wave induced by nanoseconds, picoseconds, and femtoseconds laser pulses in a semi-infinite solid [10]. The solution takes into account the non-Fourier effect in heatconduction and the coupling effect between temperature and strain rate. It is known that characteristic elasticwaveforms are generated when a pulsed laser irradiates a metal surface. Point in case, McDonald hasstudied the importance of thermal diffusion to the thermoelastic wave generation [11]. Bagri and Eslami got the unified generalized thermoelasticity solution for cylinders and spheres [12].
The present investigation is devoted to a study of the induced temperature and stress fields in an elastic half space under the purview of classical coupled thermoelasticity and generalized thermoelasticity in a unified system of field equations. The half space continuum is considered to be made of an isotropic homogeneous thermoelastic material, the bounding plane surface being subjected to a Non-Gaussian laser pulse. An exact solution of the problem is first obtained in Laplace transform space. Since the response is of more interest in the transient state, the inversion of Laplace transforms have been carried numerically. The derived expressions are computed numerically for copper and the results are presented in graphical form.
2. Basic Equations and Formulation
All the field equations represented by (CTE), (L-S) and (G-L) can be formulated in the following unified system [13] and [14]:
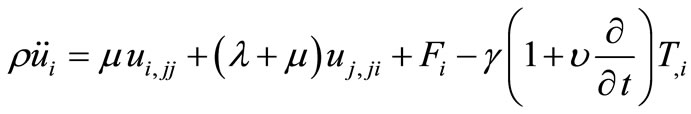 , (1)
, (1)
which constitute equation of motion where 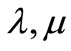 are Lame’s constants,
are Lame’s constants, 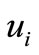 is the displacement component,
is the displacement component, 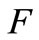 is the body force component,
is the body force component,  and
and 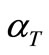 is the thermal expansion,
is the thermal expansion, ![]() is relaxation time, T is the temperature of the body and
is relaxation time, T is the temperature of the body and 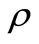 is the density.
is the density.
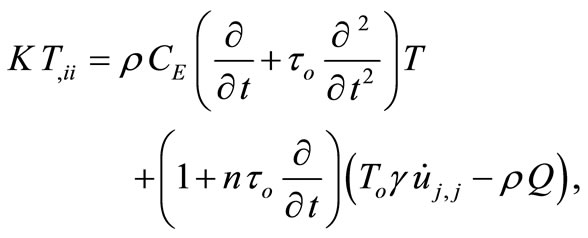 (2)
(2)
which constitute equation of heat conduction where K is the thermal conductivity, CE is the specific heat at constant strain, 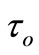 is relaxation time,
is relaxation time, 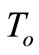 is the reference temperature, n is a parameter and Q is the heat source.
is the reference temperature, n is a parameter and Q is the heat source.
 . (3)
. (3)
which is called constitutive equation where 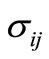 is the stress tensor and
is the stress tensor and 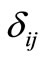 is the Kronecker function.
is the Kronecker function.
Equations (1)-(3) reduce to coupled thermoelasticity (CTE) when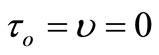 . Putting
. Putting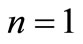 ,
, 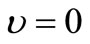 and
and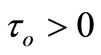 , the equations reduce to Lord-Shulman (L-S) model, while when
, the equations reduce to Lord-Shulman (L-S) model, while when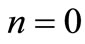 ,
, 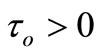 and
and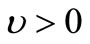 , the equations reduce to Green-Lindsay (G-L) model [13,14].
, the equations reduce to Green-Lindsay (G-L) model [13,14].
3. The Non-Gaussian Laser Pulse
We will consider the medium is heated uniformly by a laser pulse with non-Gaussian form temporal profile [7].
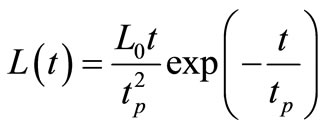 , (4)
, (4)
where  is a characteristic time of the laserpulse (the time duration of a laser pulse), L0 is the laser intensity which is defined as the total energy carried by a laser pulse per unit area of the laser beam, see Figure 1, [7].
is a characteristic time of the laserpulse (the time duration of a laser pulse), L0 is the laser intensity which is defined as the total energy carried by a laser pulse per unit area of the laser beam, see Figure 1, [7].
The conduction heat transfer in the medium can be modeled as a one-dimensional problem with an energy source 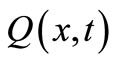 near the surface, i.e.
near the surface, i.e.
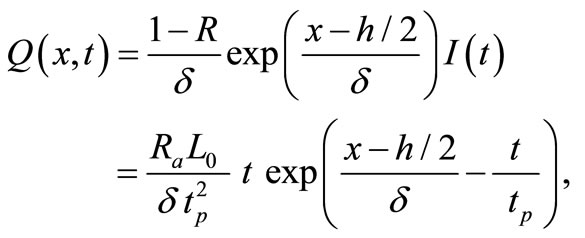 (5)
(5)
where ![]() is the absorption depth of heating energy and Ra is the surface reflectivity [7].
is the absorption depth of heating energy and Ra is the surface reflectivity [7].
When we consider the laser pulse lie on the surface of the mediumwhen 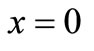 (see Figure 1), we get the energy source in the form
(see Figure 1), we get the energy source in the form
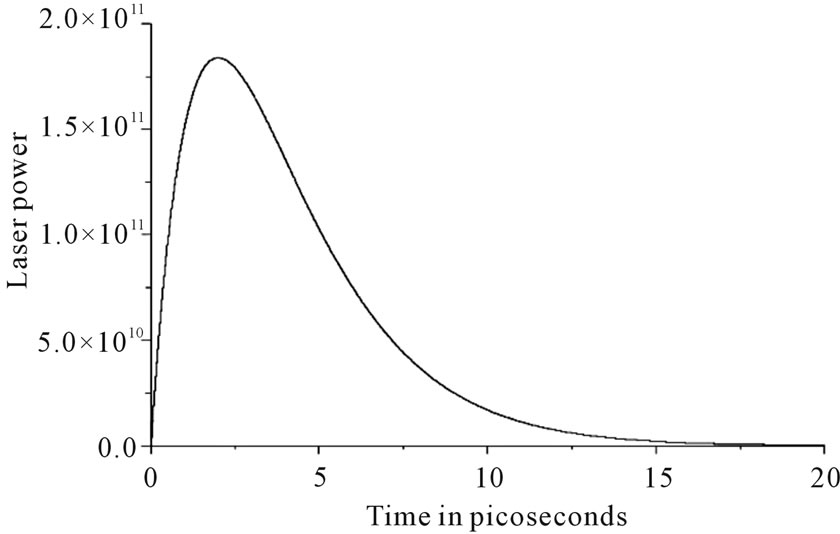
Figure 1. Temporal profile of laser power L/L0.
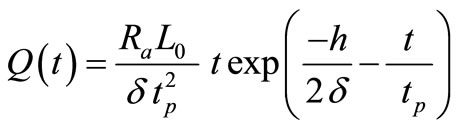 . (6)
. (6)
4. Formulation of the Problem
We consider half-space (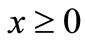 ) with the x-axis pointing into the medium with initial temperature distribution To. This half-space is irradiated uniformly the bounding plane (x = 0) by a laser pulse with non-Gaussian temporal profile as in (6). We assume that there is no body forces affecting the medium and all the state functions initially are equal to zero.
) with the x-axis pointing into the medium with initial temperature distribution To. This half-space is irradiated uniformly the bounding plane (x = 0) by a laser pulse with non-Gaussian temporal profile as in (6). We assume that there is no body forces affecting the medium and all the state functions initially are equal to zero.
The displacement vector has the components:
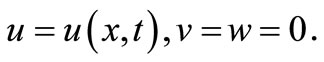 (7)
(7)
Hence, the governing equations (1)-(3) in one-dimensional will take the following forms:
The equation of motion
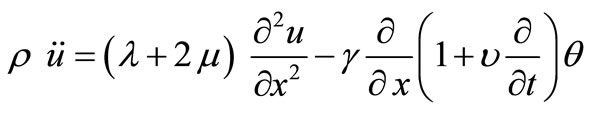 , (8)
, (8)
where 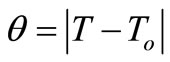 is the temperature increment.
is the temperature increment.
The heat equation:
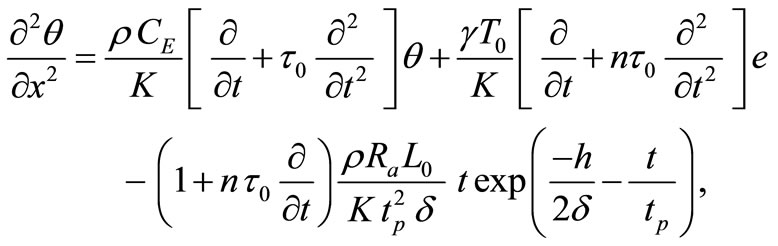 (9)
(9)
where
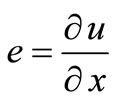 . (10)
. (10)
The constitute equation:
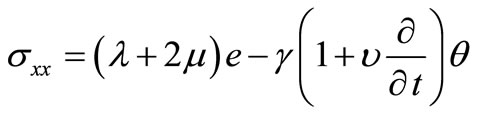 . (11)
. (11)
For simplicity, we will use the following non-dimensional variables Youssef (2006):
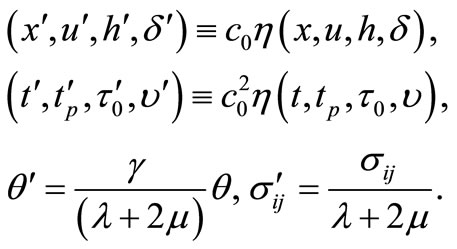 (12)
(12)
where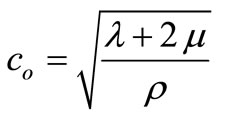 is the longitudinal wave speed and
is the longitudinal wave speed and 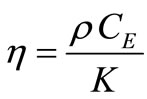 is the thermal viscosity.
is the thermal viscosity.
Hence, we have the following system of equations (we have dropped the prime for convenient)
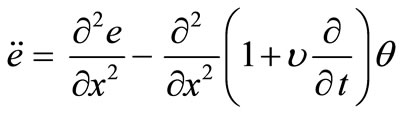 , (13)
, (13)
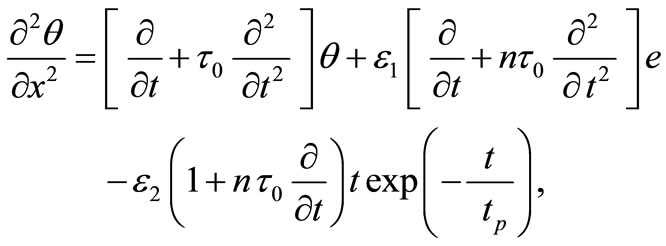 (15)
(15)
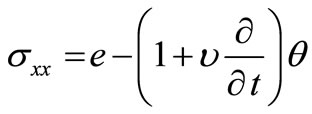 , (16)
, (16)
where 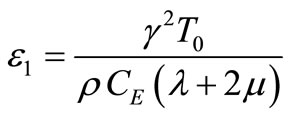 is the dimensionless thermoelastic coupling constant, and
is the dimensionless thermoelastic coupling constant, and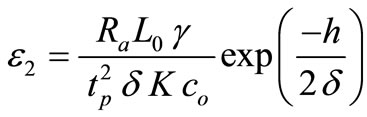 .
.
5. The Exact Solution of the Problem in the Laplace Transform Domain
Applying the Laplace transform for Equations (13)-(15) defined by the formula
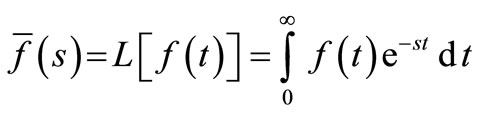 .
.
Hence, we obtain the following system of differential equations
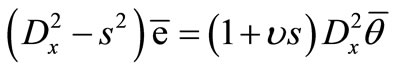 , (17)
, (17)
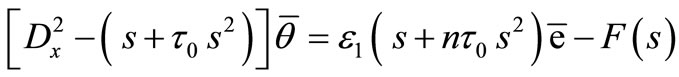 , (18)
, (18)
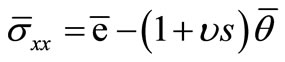 , (19)
, (19)
where all the state functions initially are equal to zero,
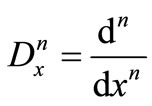 and
and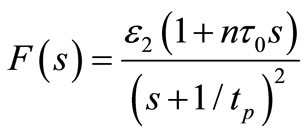 .
.
Eliminating  between the equations (17) and (18), we get
between the equations (17) and (18), we get
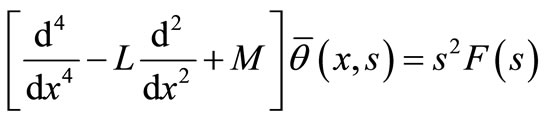 , (20)
, (20)
where 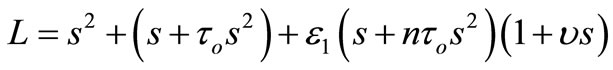 and
and 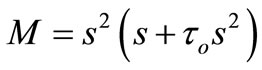 .
.
The solution of equation (20) takes the following form:
 . (21)
. (21)
where  are the roots of the characteristic equation
are the roots of the characteristic equation
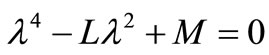 , (22)
, (22)
and
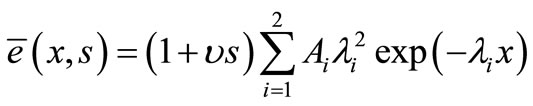 . (23)
. (23)
To get the value of the parameters 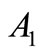 and
and 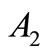 we have to apply the boundary conditions on the bounding plane
we have to apply the boundary conditions on the bounding plane 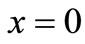 of the assumed half space as follows:
of the assumed half space as follows:
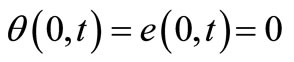 , (24)
, (24)
which gives after applying Laplace transform
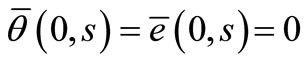 . (25)
. (25)
After applying the above boundary conditions, we get
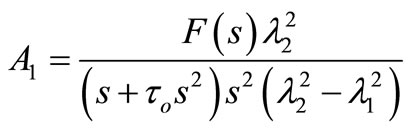
and
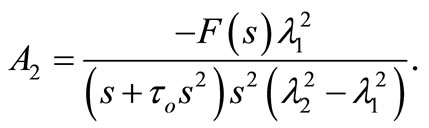
Finally, we can write the solution in the Laplace transform domain as follows:
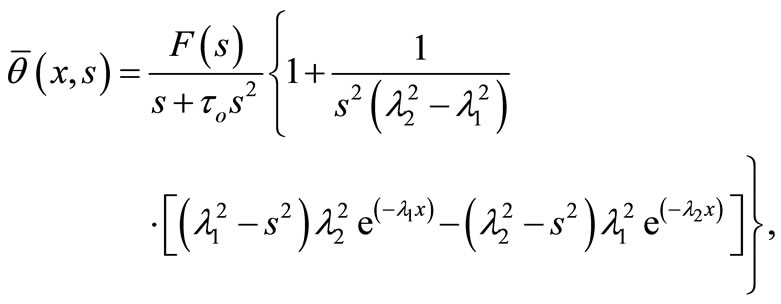 (26)
(26)
and
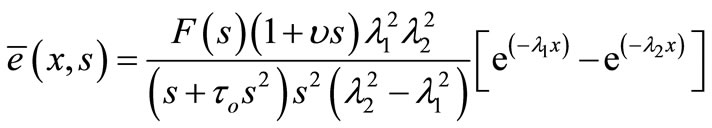 . (27)
. (27)
By using equations (19), (26) and (27), we get
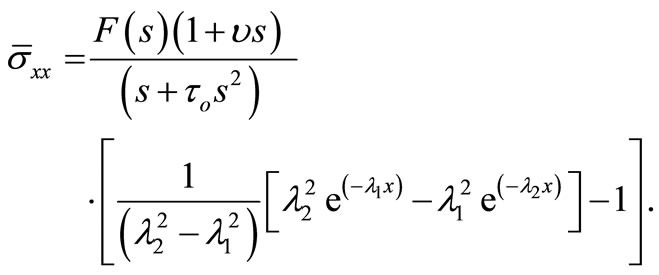 (28)
(28)
We get the displacement form equations (10) and (27) in the form
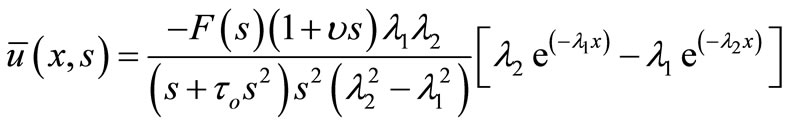 . (29)
. (29)
6. Numerical Results
In order to get the inversion of the Laplace transform, the Riemann-sum approximation method is used. In this method, any function in Laplace domain can be inverted to the time domain as
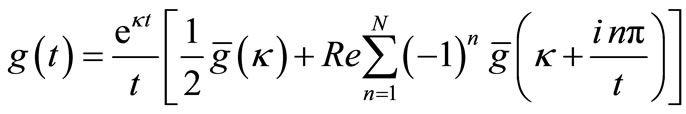 , (30)
, (30)
where Re is the real part and 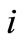 is imaginary number unit. For faster convergence, numerous numerical experiments have shown that the value of
is imaginary number unit. For faster convergence, numerous numerical experiments have shown that the value of ![]() satisfies the relation
satisfies the relation 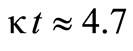 [8].
[8].
With a view to illustrating the analytical procedure presented earlier, we now consider a numerical example for which computational results are given. For this purpose, copper is taken as the thermoelastic material, [13]: ,
,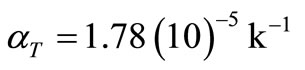 ,
,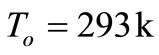
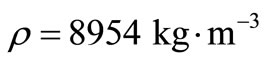 ,
,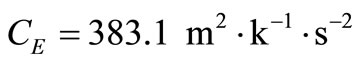 ,
, 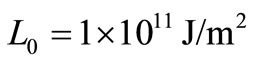 ,
,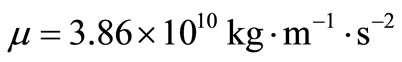 ,
, 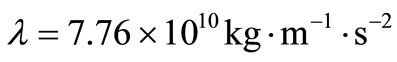 ,
,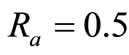 ,
, 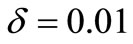
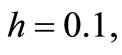 ,
, 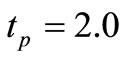 ,
, 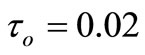 ,
, 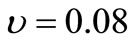 ,
, 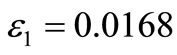 ,
, 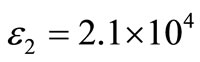 .
.
The computations were carried out for t = 0.2 and the temperature, the stress, the strain and the displacement distributions are represented graphically at different positions of x.
The figures 2-5 show that, the laser pulse makes the difference between the results in the context of the three studied models CTE, L-S and G-L is very clear and we can differentiate between them, while it was very difficult previously when we used thermal loading by using thermal shock or ramp-type heating as in [13,14].
7. Acknowledgements
The authors are grateful for the supports for this work
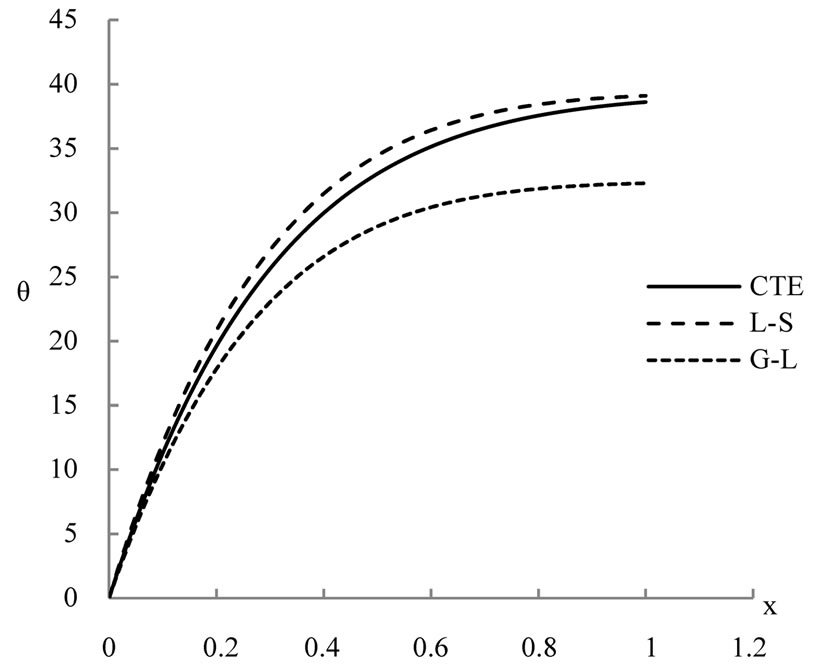
Figure 2. The temeperature distribution.
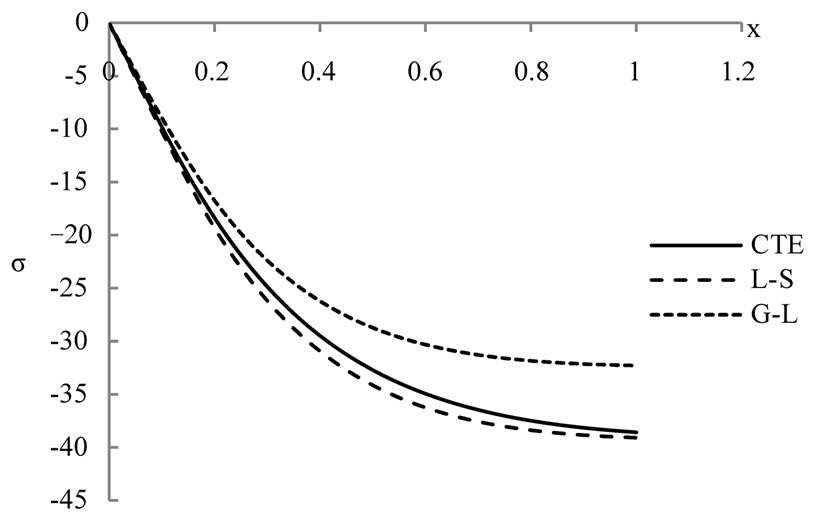
Figure 3. The stress distribution.
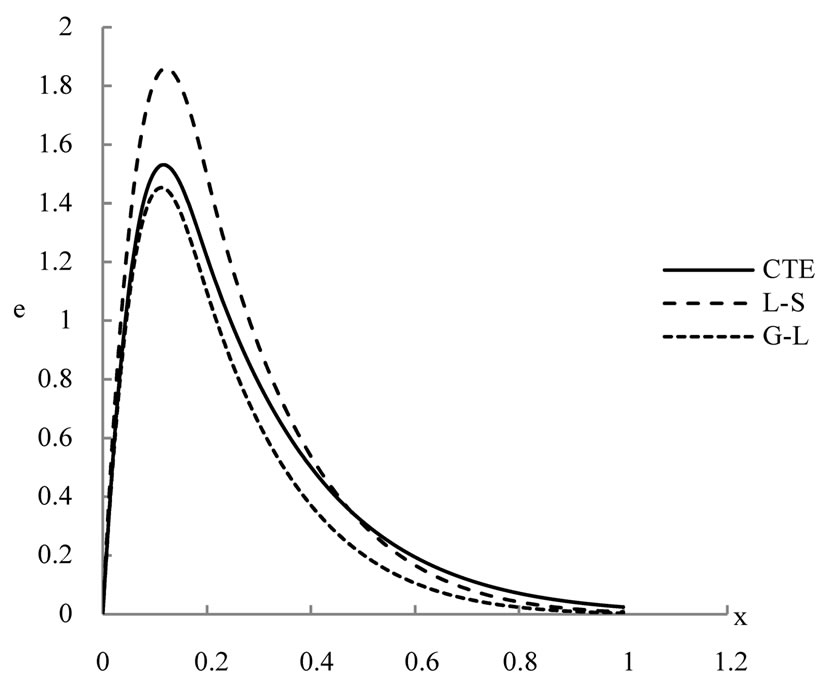
Figure 4. The strain distribution.
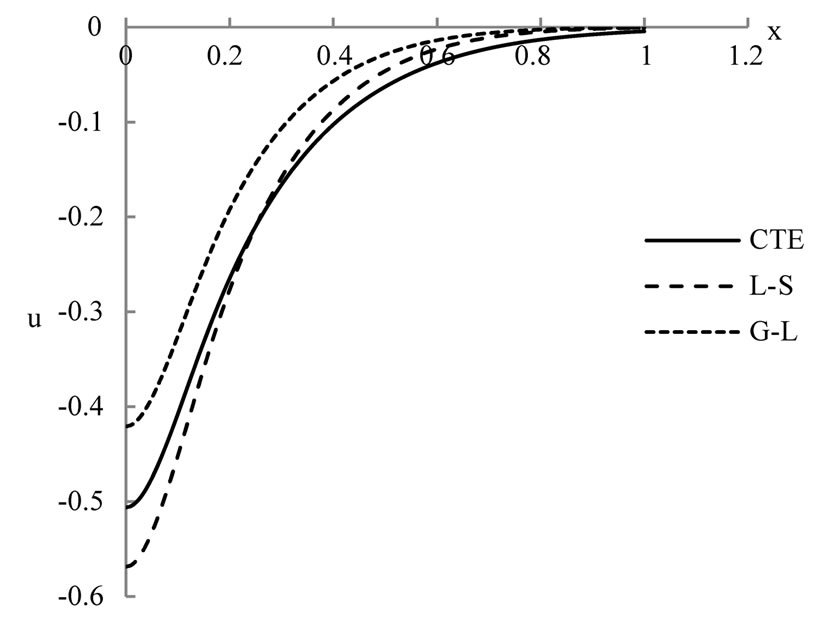
Figure 5. The displacement distribution.
provided by Institute of Scientific Research and Revival of Islamic Heritage, Umm Al-Qura University by grant number 42905012.
REFERENCES
- M. Boit, “Thermoelasticity and Irreversible Thermo-Dynamics,” Journal of Applied Physics, Vol. 27, 1956, pp. 240-251.
- H. Bargmann, “Recent Developments in the Field of Thermally Induced Waves and Vibrations,” Nuclear Engineering and Design, Vol. 27, No. 3, 1974, pp. 372-381.
- B. Boley, “In Thermal Stresses,” In: D. P. H. Hasselman and R. A. Heller, Eds., 1-ll. Plenum Press, New York, 1980. doi:10.1007/978-1-4613-3156-8_1
- D. S. Chandrasekharaiah, “Thermoelasticity with Second Sound: A Review,” Applied Mechanics Review, Vol. 39 No. 3, 1986, pp. 355-376. doi:10.1115/1.3143705
- H. Lord and Y. Shulman, “A Generalized Dynamical Theory of Thermoelasticity,” Journal of the Mechanics and Physics of Solids, Vol. 15, No. 5, 1967, pp. 299-307. doi:10.1016/0022-5096(67)90024-5
- A. E. Green and K. A. Lindsay, “Thermoelasticity,” Journal of Elasticity, Vol. 2, No. 1, 1972, pp. 1-7. doi:10.1007/BF00045689
- Y. Sun, D. Fang, M. Saka and A. K. Soh, “Laser-Induced Vibrations of Micro-Beams under Different Boundary Conditions,” International Journal of Solids and Structures, Vol. 45, No. 7-8, 2008, pp. 1993-2013. doi:10.1016/j.ijsolstr.2007.11.006
- D. Tzou, “Macro-to-Micro Heat Transfer,” Taylor & Francis, Washington DC, 1996.
- H. Sherief and M. Anwar, “Two-Dimensional Problem of a Moving Heated Punch in Generalized Thermoelasticity,” Journal of Thermal Stresses, Vol. 9, No. 4, 1986, 325-335. doi:10.1080/01495738608961910
- X. Wang and X. Xu, “Thermoelastic Wave Induced by Pulsed Laser Heating,” Applied Physics A: Materials Science & Processing, Vol. 73, No. 1, 2001, pp. 107-114. doi:10.1007/s003390000593
- F. A. McDonald, “On the Precursor in Laser-Generated Ultrasound Waveforms in Metals,” Applied Physics Letters, Vol. 56, No. 3, 1990, pp. 230-232. doi:10.1063/1.102839
- A. Bagri and M. R. Eslami, “A Unified Generalized Thermoelasticity; Solution for Cylinders and Spheres,” International Journal of Mechanical Sciences, Vol. 49, No. 12, 2007, pp. 1325-1338.
- H. M. Youssef, “Two-Dimensional Generalized Thermoelasticity Problem for a Half-Space Subjected to RampType Heating,” European Journal of Mechanics—A/Solids, Vol. 25, No. 5, 2006, pp. 745-763.
- H. M. Youssef and A. El-Bary, “Generalized Thermoelastic Infinite Layer Subjected to Ramp-Type Thermal and Mechanical Loading under Three Theories—State Space Approach,” Journal of Thermal Stresses, Vol. 32, No. 12, 2009, pp. 1293-1310. doi:10.1080/01495730903249276

