Applied Mathematics
Vol. 3 No. 7 (2012) , Article ID: 19869 , 7 pages DOI:10.4236/am.2012.37105
Soret and Dufour Effects on Unsteady MHD Mixed Convection Flow past a Radiative Vertical Porous Plate Embedded in a Porous Medium with Chemical Reaction
1Department of Mathematics, Birla Institute of Technology & Science, Pilani, India
2Department of Mathematics, University of Rajasthan, Jaipur, India
3Department of Mathematics, D. S. College, Aligarh, India
Email: bhupen_1402@yahoo.co.in
Received April 26, 2012; revised June 4, 2012; accepted June 11, 2012
Keywords: Dufour Effect; Soret Effect; MHD; Radiation; Chemical Reaction
ABSTRACT
The Soret and Dufour effects on unsteady MHD mixed convection flow past an infinite radiative vertical porous plate embedded in a porous medium in the presence of chemical reaction have been studied. A uniform magnetic field acts perpendicular to the porous surface. The Rosseland approximation has been used to describe the radiative heat flux in energy equation. The governing equations are solved numerically by applying explicit finite difference Method. The effects of various parameters on the velocity, temperature and concentration fields have been examined with the help of graphs.
1. Introduction
In recent years, the flows of fluid through porous media are of principal interest because these are quite prevalent in nature. Such flows have attracted the attention of a number of scholars due to their application in many branches of science and technology, viz., in the field of agriculture engineering to study the underground water resources, seepage of water in river-beds, in petroleum technology to study the movement of natural gas, oil and water through oil reservoirs, in chemical engineering for filtration and purification processes. The convection problem in porous medium has also important applications in geothermal reservoirs and geothermal energy extractions. A comprehensive review of the studies of convective heat transfer mechanism through porous media has been made by Nield and Bejan [1]. Hiremath and Patil [2] studied the effect on free convection currents on the oscillatory flow through a porous medium, which is bounded by vertical plane surface of constant temperature. Fluctuating heat and mass transfer on three-dimensional flow through a porous medium with variable permeability has been discussed by Sharma et al. [3].
Magnetohydrodynamics is currently undergoing a period of great enlargement and differentiation of subject matter. The interest in these new problems generates from their importance in liquid metals, electrolytes and ionized gases. Unsteady hydromagnetic free convection flow of Newtonian fluid has been investigated by Helmy [4]. Chaudhary and Sharma [5] considered combined heat and mass transfer by laminar mixed convection flow from a vertical surface with induced magnetic field. Hydromagnetic unsteady mixed convection and mass transfer flow past a vertical porous plate immersed in a porous medium was investigated by Sharma and Chaudhary [6]. El-Amin [7] considered the MHD free-convection and mass transfer flow in a micropolar fluid over a stationary vertical plate with constant suction.
Combined heat and mass transfer problems with chemical reaction are of importance in many processes and have, therefore, received a considerable amount of attention in recent years. In processes such as drying, evaporation at the surface of water body, energy transfer in wet cooling tower and the flow in a desert cooler, heat and mass transfer occur simultaneously. Chemical reaction can be codified as either homogeneous or heterogeneous processes. A homogeneous reaction is one that occurs uniformly through a given phase. In contrast, a heterogeneous reaction takes place in a restricted region or within the boundary of a phase. A reaction is said to be first order, if the rate of reaction is directly proportional to the concentration itself which has many applications in different chemical engineering processes and other industrial applications such as polymer production, manufacturing of ceramics or glassware and food processing [8]. Das et al. [9] considered the effects of first order chemical reaction on the flow past an impulsively started infinite vertical plate with constant heat flux and mass transfer. Muthucumarswamy and Ganesan [10] and Muthucumarswamy [11] studied first order homogeneous chemical reaction on flow past infinite vertical plate.
In the above mentioned studies the effects of heat sources/sinks and radiation have not been considered. Due to its great applicability to ceramic tiles production problems, the study of heat transfer in the presence of a source/sink has acquired newer dimensions. Actually, many processes in new engineering areas occur at high temperature and knowledge of radiation heat transfer becomes imperative for the design of the pertinent equipment. Nuclear power plants, gas turbines and the various propulsion devices for aircraft, missiles, satellites, and space vehicles are examples of such engineering areas. Kandasamy et al. [12] discussed heat and mass transfer effect along a wedge with heat source and concentration in the presence of suction/injection taking into account the chemical reaction of first order. Sharma et al. [13,14] have reported on the radiation effect with simultaneous thermal and mass diffusion in MHD mixed convection flow from a vertical surface. Sharma et al. [15,16] discussed radiation effect on free convective flow along a uniform moving porous vertical plate in the presence of heat source/sink and transverse magnetic field.
Due to the importance of Soret (thermal-diffusion) and Dufour (diffusionthermo) effects for the fluids with very light molecular weight as well as medium molecular weight many investigators have studied and reported results for these flows of whom the names are Eckert and Drake [17], Dursunkaya and Worek [18], Anghel et al. [19], Postelnicu [20] are worth mentioning. Recently, Alam and Rahman [21] studied the Dufour and Soret effects on steady MHD free convective heat and mass transfer flow past a semi-infinite vertical porous plate embedded in a porous medium.
In spite of all these studies, the Dufour and Soret effects on unsteady MHD mixed convection for a heat generating fluid with thermal radiation and chemical reaction has received little attention. Hence, the main object of the present investigation is to study the effect of a first-order homogeneous chemical reaction, thermal radiation, heat source, Dufour and Soret effects on the unsteady MHD mixed convection fluid flow past a vertical porous plate in the presence of suction. It is assumed that the plate is embedded in a uniform porous medium and moves with a constant velocity in the flow direction in the presence of a transverse magnetic field.
2. Mathematical Analysis
An unsteady two-dimensional flow of an incompressible and electrically conducting viscous fluid, along an infinite vertical porous flat plate embedded in a porous medium is considered. The x-axis is taken on the infinite plate, and parallel to the free-stream velocity which is vertical and the y-axis is taken normal to the plate. A magnetic field B0 of uniform strength is applied transversely to the direction of the flow. Initially the plate and the fluid are at same temperature  in a stationary condition with concentration level
in a stationary condition with concentration level 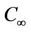 at all points. For t > 0, the plate starts moving impulsively in its own plane with a velocity U0, its temperature is raised to Tw and the concentration level at the plate is raised to Cw. The flow configuration and coordinate system are shown in the following Figure 1. The fluid is assumed to have constant properties except that the influence of the density variations with temperature and concentration, which are considered only in the body force term. Under the above assumptions, the physical variables are functions of y and t only.
at all points. For t > 0, the plate starts moving impulsively in its own plane with a velocity U0, its temperature is raised to Tw and the concentration level at the plate is raised to Cw. The flow configuration and coordinate system are shown in the following Figure 1. The fluid is assumed to have constant properties except that the influence of the density variations with temperature and concentration, which are considered only in the body force term. Under the above assumptions, the physical variables are functions of y and t only.
Assuming that the Boussinesq and boundary layer approximation hold and using the Darcy-Forchheimer model, the basic equations, which govern the problem, are given by:
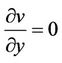 (1)
(1)
 (2)
(2)
 (3)
(3)
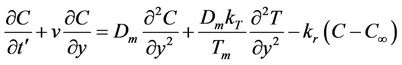 (4)
(4)
The radiative heat flux term by using Rosseland approximation [22,23] is given by
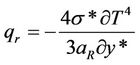 .
.
where, u and v are the Darcian velocity components in the xand y-directions respectively, t is the time,  is the kinematic viscosity, g is the acceleration due to gravity,
is the kinematic viscosity, g is the acceleration due to gravity, 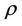 is the density,
is the density, 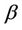 is the coefficient of volume expansion,
is the coefficient of volume expansion,  is the volumetric coefficient of expansion with concentration, K is the Darcy permeability, b is
is the volumetric coefficient of expansion with concentration, K is the Darcy permeability, b is
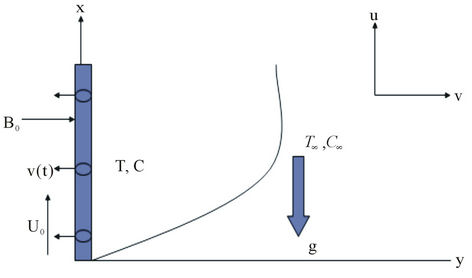
Figure 1. Flow configuration and coordinate system.
the empirical constant, B0 is the magnetic induction, T and  are the temperature of the fluid inside the thermal boundary layer and the fluid temperature in the free stream, respectively, while C and
are the temperature of the fluid inside the thermal boundary layer and the fluid temperature in the free stream, respectively, while C and 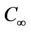 are the corresponding concentrations. Also,
are the corresponding concentrations. Also, 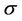 is the electric conductivity,
is the electric conductivity,  is the thermal diffusivity,
is the thermal diffusivity, 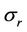 is StefanBoltzmann constant, Dm is the coefficient of mass diffusivity,
is StefanBoltzmann constant, Dm is the coefficient of mass diffusivity, 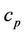 is the specific heat at constant pressure, Tm is the mean fluid temperature, kT is the thermal diffusion ratio and c is the concentration susceptibility, The term
is the specific heat at constant pressure, Tm is the mean fluid temperature, kT is the thermal diffusion ratio and c is the concentration susceptibility, The term  is assumed to be amount of heat generated or absorbed per unit volume Q0 is a constant, which may take on either positive or negative values, qr is the radiative heat flux in the y-direction,
is assumed to be amount of heat generated or absorbed per unit volume Q0 is a constant, which may take on either positive or negative values, qr is the radiative heat flux in the y-direction, 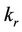 is chemical reaction parameter.
is chemical reaction parameter.
The equation of continuity (1) on integration gives
 .
.
Initially (t = 0) the fluid and the plate are at rest. Thus the no slip boundary conditions at the surface of the plate for the above problem for t > 0 are:
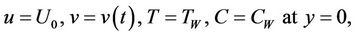 (5a)
(5a)
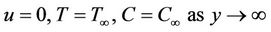 (5b)
(5b)
Now in order to obtain non-dimensional partial differential equations we are introducing following dimensionless variables and constants.
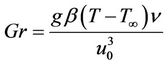
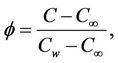
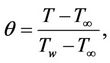
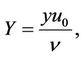
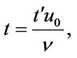
 ,
, 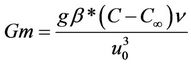 ,
, 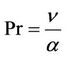 ,
,  ,
,  ,
, 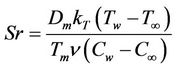 ,
, 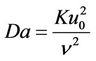 ,
,  ,
, 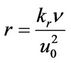
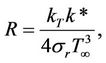
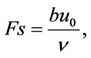 ,
, 
By introducing above dimensionless variables and constants the Equations (2)-(4) converted as follows
 (6)
(6)
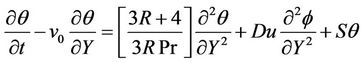 (7)
(7)
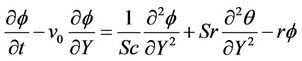 (8)
(8)
The corresponding boundary conditions for t > 0
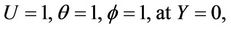 (9a)
(9a)
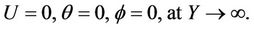 (9b)
(9b)
3. Numerical Solution
The unsteady, nonlinear coupled Equations (6)-(8) with conditions (9) are solved by using an explicit finite-difference scheme. Consider a rectangular region with y varying from 0 to Y max (= 6), where y max corresponds to Y = ∞ at which lies well outside the momentum and energy boundary layers. The region to be examined in (Y, t) space is covered by a rectilinear grid with sides parallel to axes with Y and Δt, the grid spacing in Y, and t directions, respectively. The grid points (Y, t) are given by (iΔY, kΔt). The finite-difference equations corresponding to (6)-(8) are given by

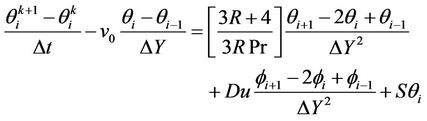
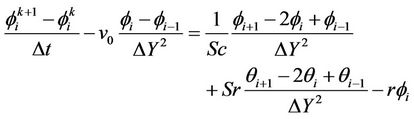
The coefficient appearing in difference equations are treated as constants. The finite-difference equations at every internal nodal point on a particular n-level constitute a tri-diagonal system of equations. These equations are solved by using the Thomas algorithm [24]. Computations are carried out until the steady-state solution is assumed to have been reached when the absolute difference between the values of velocity as well as temperature at two consecutive time steps are less than 10−8 at all grid points.
4. Results and Discussion
Numerical calculations have been carried out for different values of v0, Sr, Du, R, r, S, Da, M and for fixed values of Pr, Sc, Gr, Gm and Fs. The value of Pr is taken to be 0.71 which corresponds to air at 20˚C and 1 atmospheric pressure and the value of Sc is 0.22. Due to convection problem positive large values of Gr = 12 and Gm = 6 are chosen. The value of Fs is taken 0.09. The values of Dufour number and Soret number are chosen in such a way that their product is constant provided that the mean temperature Tm is kept constant as well. However, the values of v0, Da, R, S, r and M are chosen arbitrarily. The numerical results for the velocity, temperature and concentration profiles are displayed in figures.
The effects of suction parameter on the velocity field for Sr = 2.0, Du = 0.03, Da = 0.5 and M = 0.3 are shown in Figure 2. It is seen from this figure that the velocity profiles decrease monotonically with an increase of suction parameter which indicating the usual fact that suction stabilizes the boundary layer growth. The effects of suction parameter on the temperature and concentration field are displayed in Figure 3 and Figure 4 respectively. From Figure 3, it is noticed that the temperature decreases with an increase of suction parameter. From Figure 4, it is observe that the concentration increases with an increase of suction parameter close to the wall (approx. Y <= 0.5) whereas for Y >= 0.5, the concentration decreases with an increase in suction parameter. Sucking

Figure 2. Velocity profiles for different values of suction parameter (v0).

Figure 3. Temperature profiles for different values of suction parameter (v0).
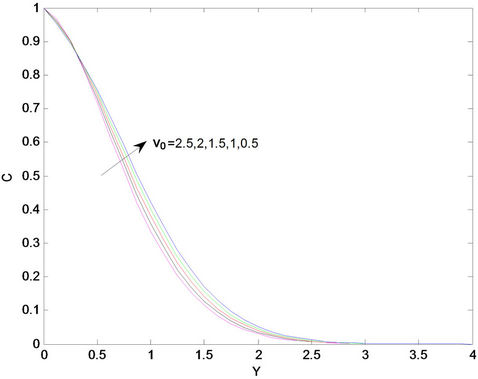
Figure 4. Concentration profiles for different values of suction parameter (v0).
decelerated fluid particles through the porous wall reduce the growth of the fluid boundary layer as well as thermal and concentration boundary layers.
The effects of Soret and Dufour numbers on the velocity field are shown in Figure 5. It is observed that an increase in Soret number and a decrease in Dufour number, the velocity profile is increasing. The effects of Soret and Dufour numbers on the temperature field are shown in Figure 6. It is noted that negligible effect of Dufour and Soret numbers on temperature profile. The effects of Soret and Dufour numbers on the concentration field are shown in Figure 7. It is also observed that with increase in Soret number and with decrease in Dufour number the concentration profile is increasing. For different values of radiation parameter R, the velocity profiles are plotted in Figure 8. Here, as the value of R increases the velocity increases, with an increasing in the flow boundary
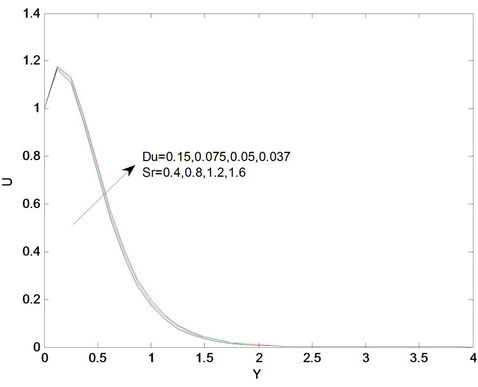
Figure 5. Velocity profiles for different values of Sr and Du.

Figure 6. Temperature profiles for different values of Sr and Du.

Figure 7. Concentration profiles for different values of Sr and Du.

Figure 8. Velocity profiles for different values of radiation parameter (R).
layer thickness. Thus, thermal radiation enhances convective flow. The effects of radiation parameter R on the temperature profiles are presented in Figure 9. From this figure we observe that, as the value of R increases the temperature profiles increases, with an increasing in the thermal boundary layer thickness. The effect of heat generation S on the velocity profiles is shown in Figure 10. From this figure, it is noted that the heat is generated the buoyancy force increases which induces the flow rate to the increase in the velocity profiles.
Figure 11 shows the variation of temperature profiles for different values of S. It is seen from this figure that temperature profiles increase with an increasing of heat generation parameter S. This result qualitatively agrees with expectation since the effect of internal heat generation is to increase the rate of heat transport to the fluid thereby increasing the temperature of the fluid. The influences of chemical reaction parameter r on the velocity profiles across the boundary layer are presented in Figure 12. We see that the velocity distribution across the boundary layer decreases with increasing of r. For different values of the chemical reaction parameter r, the concentration profiles plotted in Figure 13. It is obvious that the influence of increasing values of r, the concentration distribution across the boundary layer decreases. This shows that diffusion rate can be tremendously altered by chemical reaction.
5. Conclusions
In this paper we have studied Dufour and Soret effects on unsteady MHD free convection and mass transfer flow past a vertical porous plate in a porous medium with heat source and chemical reaction and radiation effect. From the present numerical study the following conclusions can be drawn:
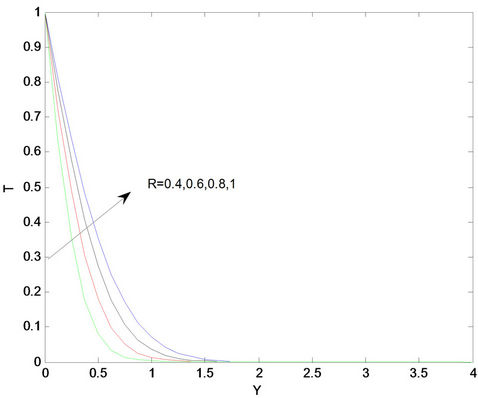
Figure 9. Temperature profiles for different values of R.
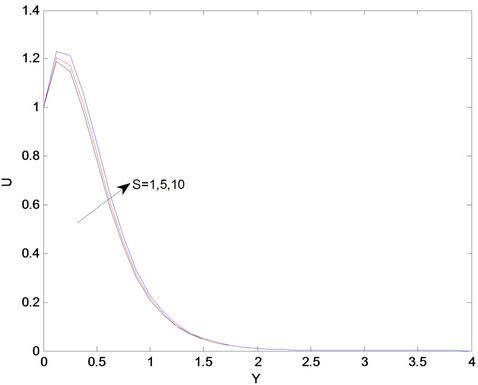
Figure 10. Velocity profiles for different values of heat source parameter (S).
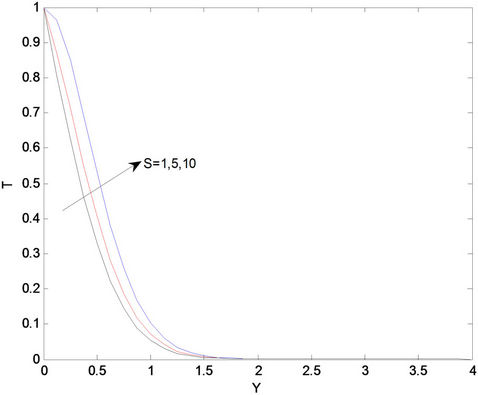
Figure 11. Temperature profiles for different values of S.
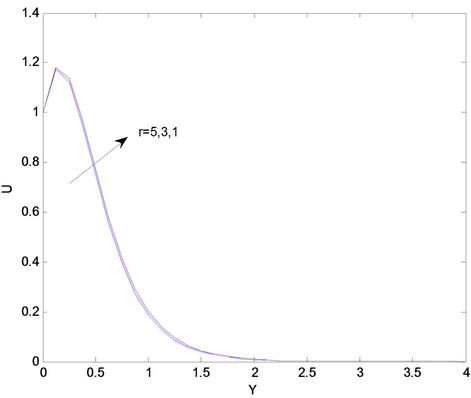
Figure 12. Velocity profiles for different values of chemical reaction parameter (r).
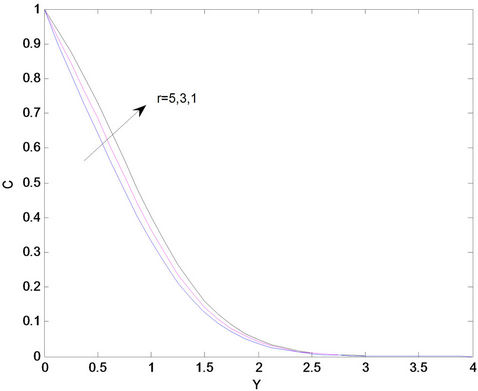
Figure 13. Concentration profile for different values of chemical reaction parameter (r).
• Suction stabilizes the hydrodynamic, thermal as well as concentration boundary layers growth.
• An increase in radiation parameter, the velocity and temperature profiles increase.
• With increasing heat source parameter, the velocity and temperature profiles are increasing.
• The velocity and concentration profiles decrease as an increase in chemical reaction parameter.
• For fluids with medium molecular weight (H2, air), Dufour and Soret effects should not be neglected.
REFERENCES
- D. A. Nield and A. Bejan, “Convection in Porous Media,” 2nd Edition, Springer-Verlag, Berlin, 1998.
- P. S. Hiremath and P. M. Patil, “Free Convection Effects on Oscillatory Flow of Couple Stress Field through a Porous Medium,” Acta Mechanica, Vol. 98, No. 1-4, 1993, pp. 143-158. doi:10.1007/BF01174299
- B. K. Sharma, R. C. Chaudhary and P. K. Sharma, “Fluctuating Mass Transfer on Three-Dimensional Flow through a Porous Medium with Variable Permeability,” Advances in Theoretical and Applied Mathematics, Vol. 2, No. 3, 2007, pp. 257-267.
- K. A. Helmy, “MHD Unsteady Free Convection Flow past a Vertical Porous Plate,” ZAMM, Vol. 98, No. 4, 1998, pp. 255-270. doi:10.1002/(SICI)1521-4001(199804)78:4<255::AID-ZAMM255>3.0.CO;2-V
- R. C. Chaudhary and B. K. Sharma, “Combined Heat and Mass Transfer by Laminar Mixed Convection Flow from a Vertical Surface with Induced Magnetic Field,” Journal of Applied Physics, Vol. 99, No. 3, 2006, pp. 34901-3410. doi:10.1063/1.2161817
- B. K. Sharma and R. C. Chaudhary, “Hydromagnetic Unsteady Mixed Convection and Mass Transfer Flow past a Vertical Porous Plate Immersed in a Porous Medium with Hall Effect,” Engineering Transactions, Vol. 56, No. 1, 2008, pp. 3-23.
- M. F. El-Amin, “Magnetohydrodynamic Free Convection and Mass Transfer Flow in Micropolar Fluid with Constant Suction,” Journal of Magnetism and Magnetic Materials, Vol. 234, No. 3, 2001, pp. 567-574. doi:10.1016/S0304-8853(01)00374-2
- E. L. Cussler, “Diffusion Mass Transfer in Fluid Systems,” 2nd Edition, Cambridge University Press, Cambridge, 1998.
- U. N. Das, R. K. Deka and V. M. Soundalgekar, “Effects of Mass Transfer on Flow past an Impulsively Started Infinite Vertical Plate with Constant Heat Flux and Chemical Reaction,” Forschung im Ingenieurwesen, Vol. 60, No. 10, 1994, pp. 284-287. doi:10.1007/BF02601318
- R. Muthucumarswamy and P. Ganesan, “First Order Chemical Reaction on Flow past an Impulsively Started Vertical Plate with Uniform Heat and Mass Flux,” Acta Mechanica, Vol. 147, No. 1-4, 2001, pp. 45-57. doi:10.1007/BF01182351
- R. Muthucumarswamy, “Effects of a Chemical Reaction on Moving Isothermal Vertical Surface with Suction,” Acta Mechanica, Vol. 155, No. 1-2, 2002, pp. 65-70. doi:10.1007/BF01170840
- R. Kandasamy, K. Periasamy and K. K. Prashu Sivagnana, “Effects of Chemical Reaction, Heat and Mass Transfer along Wedge with Heat Source and Concentration in the Presence of Suction or Injection,” International Journal of Heat and Mass Transfer, Vol. 48, No. 7, 2005, pp. 1388- 1394. doi:10.1016/j.ijheatmasstransfer.2004.10.008
- B. K. Sharma, A. K. Jha and R. C. Chaudhary, “Radiation Effect with Simultaneous Thermal and Mass Diffusion in MHD Mixed Convection Flow from a Vertical Surface with Ohmic Heating,” Romania Journal of Physics, Vol. 51, No. 7-8, 2006, pp. 715-727.
- B. K. Sharma, M. Agarwal and R. C. Chaudhary , “MHD Fluctuating Free Convective Flow with Radiation Embedded in Porous Medium Having Variable Permeability and Heat Source/Sink,” Journal of Technical Physics, Vol. 47, No. 1, 2006, pp. 47-58.
- B. K. Sharma, R. C. Chaudhary and M. Agarwal, “Radiation Effect on Temperature Distribution in Three-Dimensional Couette Flow with Injection or Suction,” Applied Mathematics and Mechanics, Vol. 28, No. 3, 2007, pp. 309-316. doi:10.1007/s10483-007-0304-z
- B. K. Sharma, R. C. Chaudhary and M. Agarwal, “Radiation Effect on Steady Free Convective Flow along a Uniform Moving Porous Vertical Plate in Presence of Heat Source/Sink and Transverse Magnetic Field,” Bulletin of Calcutta Mathematical Society, Vol. 100, 2008, pp. 529- 538.
- E. R. G. Eckert and R. M. Drake, “Analysis of Heat and Mass Transfer,” McGraw-Hill, New York, 1972.
- Z. Dursunkaya and W. M. Worek, “Diffusion-Thermo and Thermal-Diffusion Effects in Transient and Steady Natural Convection from Vertical Surface,” International Journal of Heat and Mass Transfer, Vol. 35, No. 8, 1992, pp. 2060-2065. doi:10.1016/0017-9310(92)90208-A
- M. Anghel, H. S. Takhar and I. Pop, “Dufour and Soret Effects on Free-Convection Boundary Layer over a Vertical Surface Embedded in a Porous Medium,” Studia Universitatis Babes-Bolyai: Mathematica, Vol. XLV, No. 4, 2000, pp. 11-21.
- A. Postelnicu, “Influence of a Magnetic Field on Heat and Mass Transfer by Natural Convection from Vertical Surfaces in Porous Media Considering Soret and Dufour Effects,” International Journal of Heat and Mass Transfer, Vol. 47, No. 6-7, 2004, pp. 1467-1472. doi:10.1016/j.ijheatmasstransfer.2003.09.017
- M. S. Alam and M. M. Rahman, “Dufour and Soret Effects on MHD Free Convective Heat and Mass Transfer Flow past a Vertical Flat Plate Embedded in a Porous Medium,” Journal of Naval Architecture and Marine Engineering, Vol. 2, No. 1, 2005, pp. 55-65.
- A. Raptis and C. V. Massalas, “Magnetohydrodynamic Flow past a Plate by the Presence of Radiation,” Heat and Mass Transfer, Vol. 34, No. 2-3, 1998, pp. 107-109. doi:10.1007/s002310050237
- C. Perdikis and E. Rapti, “Unsteady MHD Flow in the Presence of Radiation,” International Journal of Applied Mechanics and Engineering, Vol. 11, No. 2, 2006, pp. 383-390.
- J. D. Hoffman, “Numerical Methods for Engineers and Scientists,” McGraw-Hill, New York, 1992.

