ABSTRACT

In this paper we shall obtain some interesting extensions and generalizations of a well-known theorem due to Enestrom and Kakeya according to which all the zeros of a polynomial 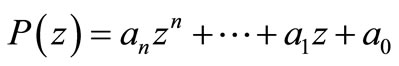satisfying the restriction 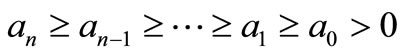lie in the closed unit disk.

1. Introduction and Statement of Results

The following results which is due to Enestrom and Kakeya [1] is well known in the theory of the location of the zeros of polynomials.

THEOREM A. Let

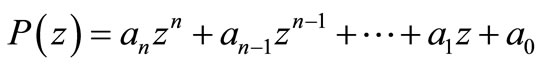be a polynomial of degree n, such that

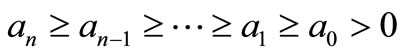, (1)

then 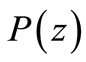does not vanish in.

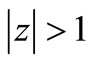In the literature [2-5] there exist some extensions and generalization of Enestrom-Kakeya Theorem. Joyal, Labelle and Rahman [6] extended this theorem to polynomials whose coefficients are monotonic but not necessarily non-negative by proving the following result:

THEOREM B. Let

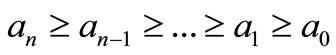
then the polynomial

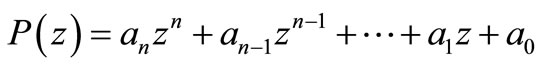
of degree n has all its zeros in

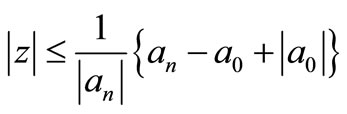(2)

Recently Aziz and Zarger [7] relaxed the hypothesis in several ways and among other things proved the following results:

THEOREM C. Let

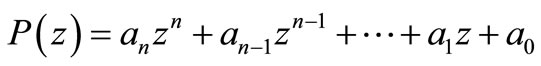
be the polynomial of degree n, such that for some k ≥ 1,

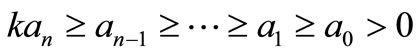(3)

then P(z) has all its zeros in

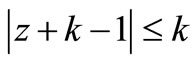(4)

The aim of this paper is to prove some extensions of Enestrom-Kakeya Theorem (Theorem-A) by relaxing the hypothesis in various ways. Here we shall first prove the following generalization of Theorem C which is an interesting extension of Theorem A.

2. Main Results

THEOREM 1.1. Let

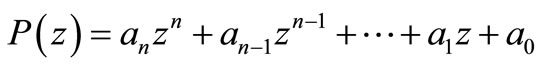be a polynomial of degree n. If for some positive numbers k and 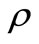with k ≥ 1, and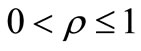

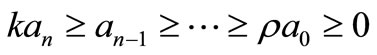(5)

then all the zeros of P(z) lie in the closed disk

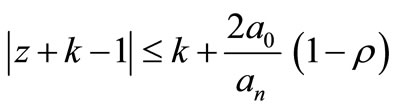(6)

If we take 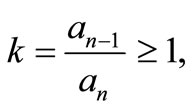in Theorem 1.1 we obtain the following result which is a generalization of Corollary 2 ([7]).

COROLLARY 1. Let

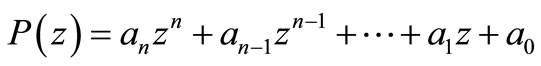be a polynomials of degree n. If for some positive real number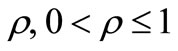

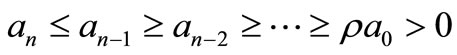(7)

then all zeros of P(z) lie in

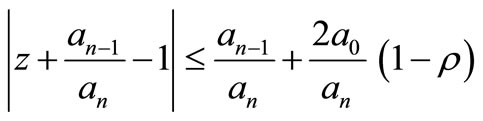
REMARK 1. Theorem 1.1 is applicable to situations when Enestrom-Kakeya Theorem gives no information. To see this consider the polynomial.

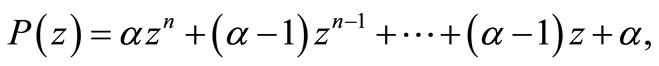
with is a positive real number. Here EnestromKakeya Theorem is not applicable to P(z) where as Theorem 1.1 is applicable with 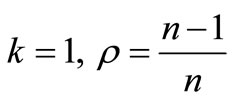and according to our result, all the zeros of P(z) lie in the disk.

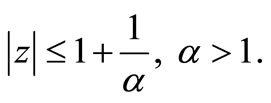
which is considerably better than the bound obtained by a classical result of Caushy ([4]) which states that all the zeros of P(z) lie in

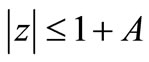
where

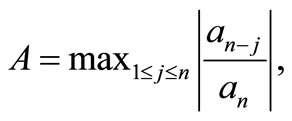
Next, we present the following generalization of corollary 1 which includes Theorem 4 of [6] as a special case and considerably improves the bound obtained by Dewan and Bidkham ([8], Theorem1) for t = 0 and .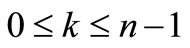

THEOREM 1.2. Let

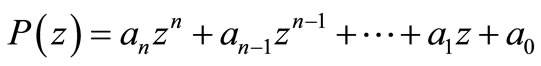be a polynomial of degree n. If for some positive number 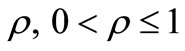and for some non-negative integer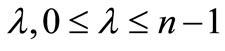

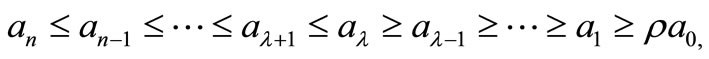(8)

then all the zeros of P(z) lie in

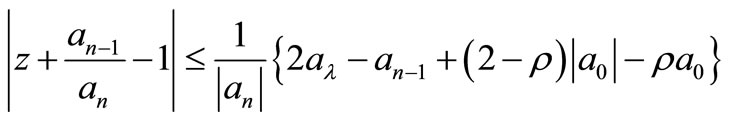(9)

Applying Theorem 1.2 to P(tz), we get the following result:

COROLLARY 2. Let

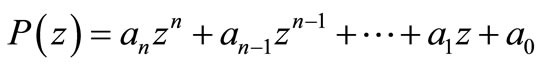be a polynomial of degree n. If for some positive numbers t and 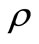with,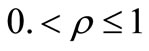

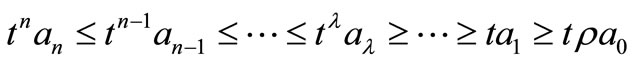
where 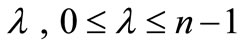is a non negative integer then all the zeros of P(z), lie in

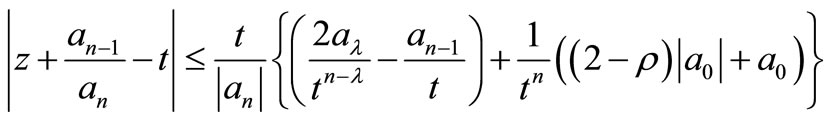
If we assume a₀ > 0, in Theorem 1.2, we obtain.

COROLLARY 3. Let

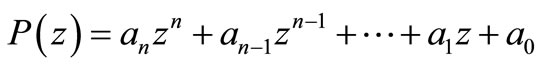be a polynomial of degree n. If for some positive numbers 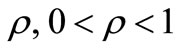and for same non-negative integer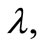

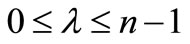
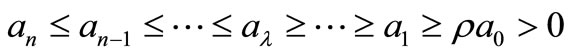
then all the zeros of P(z) lie in,

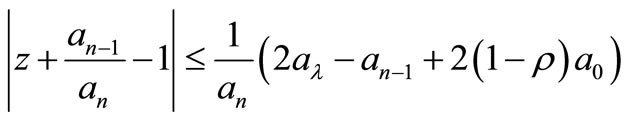(10)

Finally we present all following generalization of Theorem B due to Joyal, Labelle and Rahman which includes Theorem A as a special case.

THEOREM 1.3. Let

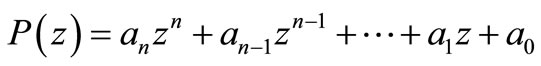be a polynomial of degree n, It for some positive number 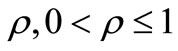and for some non-negative integer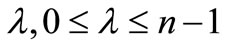

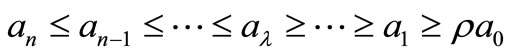
then all the zeros of P(z) lie in

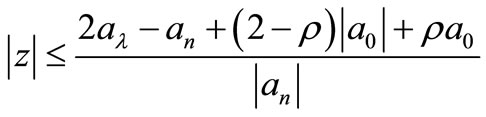(11)

REMARK 2. For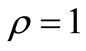, Theorem 1.3 reduces to Theorem B.

3. Proofs of the Theorems

PROOF OF THEOREM 1.1. Consider

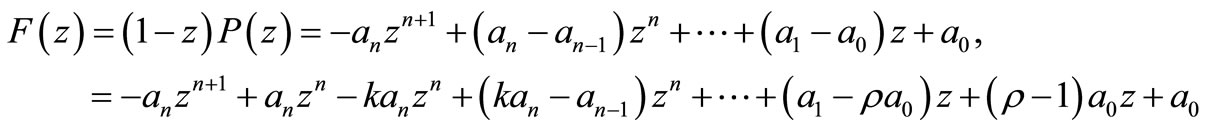
then for 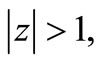we have

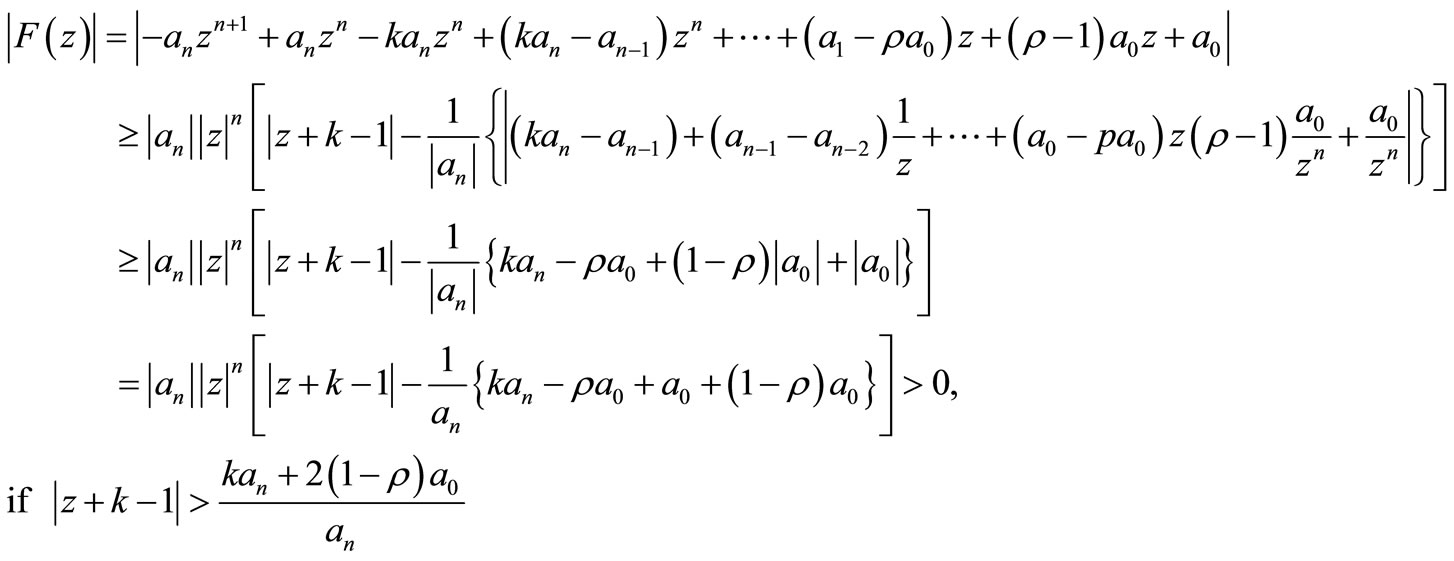
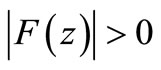this shows that if then, if

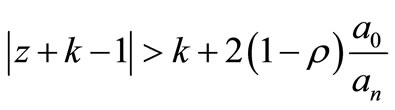
therefore all the zeros of F(z), whose modulus is greater than 1 lie in the closed disk

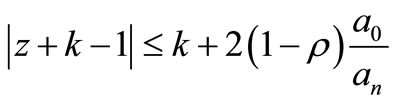
But those zeros of F(z) whose modules is less than or equal to 1 already satisfy the Inequality (6).

Since all the zeros of P(z) are also the zeros of F(z). therefore it follows that all the zeros of P(z) lie in the circle defined by (6). Which completes the proof of Theorem 1.1.

PROOF OF THEOREM 1.2. Consider

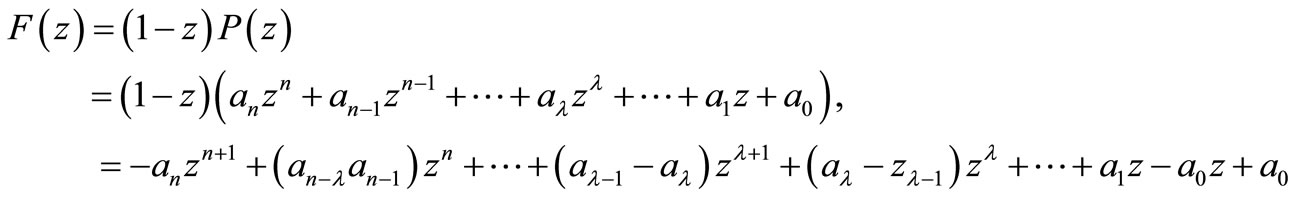
therefore, for 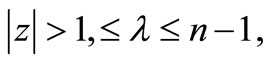and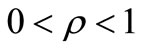,we have

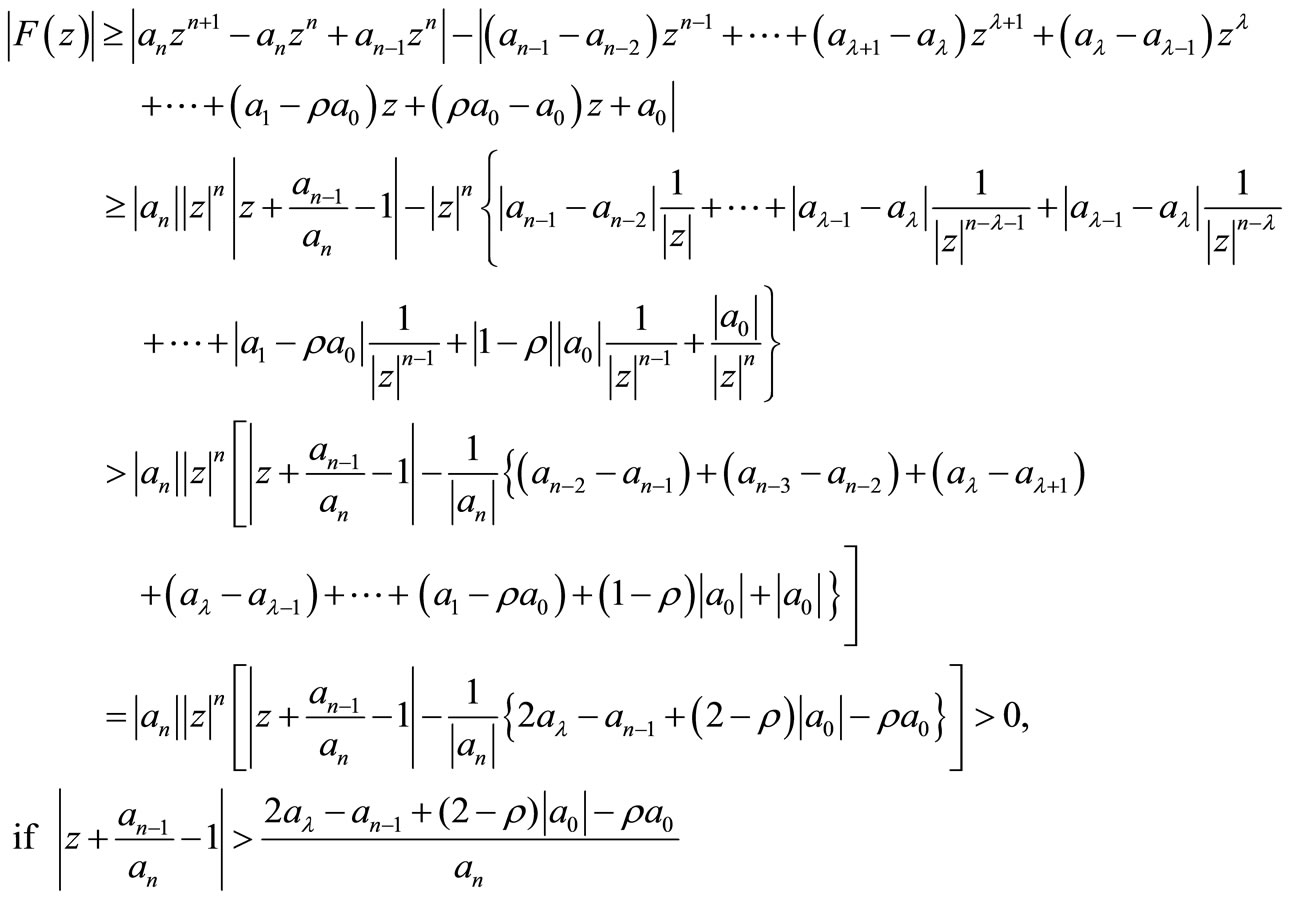
Therefore all the zeros of F(z) whose modulus is greater than 1 lie in the circle.

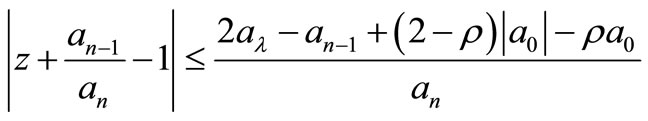
But those zeros of F(z) whose modulus is less than or equal to 1 already satisfy the Inequality (9).

Since all the zeros of P(z) are also the zeros of F(z), therefore it follows that all the zeros of P(z) lie in the circle defined by (9). This completes the proof of Theorem 1.2.

PROOF OF THEOREM 1.3. Consider

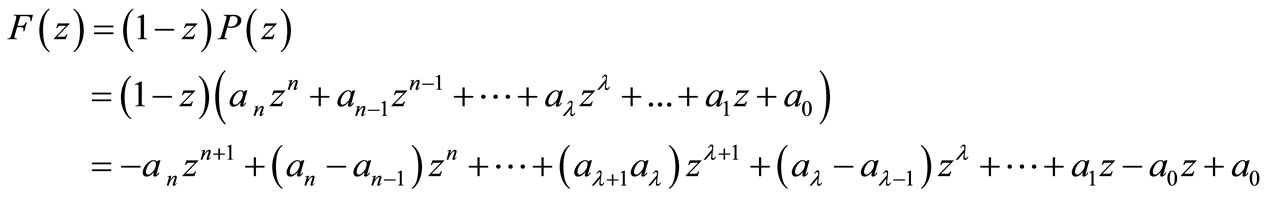
therefore, for 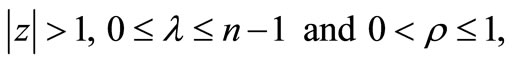we have

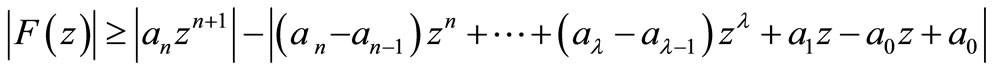
Proceeding similarly as in the proof of Theorem 1.2, we have

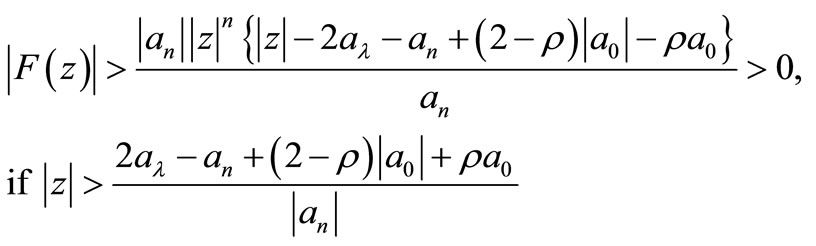
therefore all the zeros of F(z) whose modules is greater than 1 lie in the circle

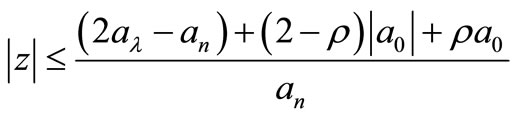
But those zeros of F(z) whose modulus is 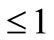already satisfy the (11). Since all the zeros of P(z) are also the zero of F(z), therefore it follows that all the zeros of P(z) lie in circle defined by (11) and hence Theorem 1.3 is proved completed.

4. Acknowledgements

The authors are grateful to the refree for useful suggestions.

REFERENCES