Received 10 January 2015; accepted 25 January 2015; published 29 January 2015

ABSTRACT

Anfinsen’s thermodynamic hypothesis is reviewed and misunderstandings are clarified. It really should be called the thermodynamic principle of protein folding. Energy landscape is really just the mathematical graph of the Gibbs free energy function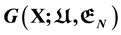, a very high dimensional hyper surface. Without knowing it any picture of the Gibbs free energy landscape has no theoretical base, including the funnel shape claims. New insight given by newly obtained analytic Gibbs free energy function 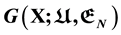of protein folding derived via quantum statistical mechanics are discussed. Disputes such as target-based or cause-based; what is the folding force, hydrophobic effect or hydrophilic force? Single molecule or ensemble of molecules to be used for the statistical physics study of protein folding, are discussed. Classical observations of 1970’s and 1980’s about global geometric characteristics of native structures of globular proteins turn out to have grabbed the essence of protein folding, but unfortunately have been largely forgotten.

Keywords:

Protein Folding, Gibbs Free Energy, Quantum Statistic, Single Molecule

1. Introduction

1.1. The Second Law of Thermodynamics

The Second Law of Thermodynamics states that in an isolated system the entropy will increase. For a spontaneous process in a system of constant temperature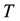, pressure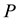, and composition, the equivalent statement of the second law of thermodynamics states that the Gibbs free energy will be lowered, and at the new equilibrium state it will be at a minimum. Indeed, this applies to any process or any chemical reaction with constant temperatures and pressure [1] . The Gibbs free energy has the form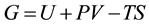, where 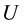is the internal energy, 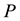the pressure, 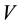the volume, 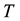the temperature, and 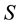the entropy, of the system. 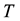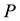Even and are not uniform in the system, moreover even they are not well defined in the system, the available free energy 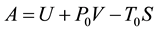will be lowered and goes to minimum as long as the heat bath of the system has well defined temperature and pressure and on the boundary of the system they are constants 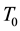and 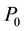respectively [2] . This fundamental principle was known long before.

1.2. Anfinsen’s Thermodynamics Hypothesis of Protein Folding

A good example of applying this fundamental principle to lift experimental results to guiding theory of further research is Anfinsen’s Thermodynamic Hypothesis of protein folding [3] . After many years of experimental work proved that the refolding process of ribonuclease is spontaneous, Anfinsen summarised: “The studies on the renaturation of the fully denatured ribonuclease required many supporting investigations to establish, finally, the generality which we have occasionally called the ‘thermodynamic hypothesis’. This hypothesis states that the three-dimensional structure of a native protein in its normal physiological milieu (solvent, pH, ionic strength, presence of other components such as metal ions or prosthetic groups, temperature, and other) is the one in which the Gibbs free energy of the whole system is lowest; that is that the native conformation is determined by the totality of the inter atomic interactions, and hence by the amino acid sequence, in a given environment.” [3] .

Once we know that protein folding is a spontaneous process, the thermodynamic hypothesis should be upgraded to thermodynamic principle. The thermodynamic principle makes the protein folding problem a pure physics problem, all biological knowledge needed is how to specify the physiological environment for a particular protein and how to reasonably simplify the environment for the further study.

But this has not been recognised so far, instead, it is thought that in biological problems such as protein folding theoretical consideration is unpractical. Coincidently, in the early 1970’s, the same time when the thermodynamic principle of protein folding was established by Anfinsen, computer entered research and played more and more important role in protein folding research. Theory was neglected, simulations became essential as if they were experiments, but many cannot satisfy the essential requirement to experiments in experimental sciences, the reproducibility, see [4] . Furthermore, theoretical background justification of these simulations were rarely questioned. One wonders that if the increasing computer power were really guided by the thermodynamics principle, perhaps today the mystery of protein folding phenomenon would not be really a mystery anymore.

1.3. Reasons of the Thermodynamic Principle of Protein Folding Is Neglected

Why the thermodynamics principle were not actively and persistently pursued?

1.3.1. Do Not Believe It

First, some do not think that the thermodynamic principle is correct. For example, in [5] it is claimed that Anfinsen’s theory was disapproved for long time because “other complexities of biological systems for example solvents of different compositions may affect the folding/unfolding of proteins, the role of high dielectric constant of water, chaperone assisted folding of proteins and existence of stable folding intermediates.”

All the reasons listed above to “disapprove” the thermodynamic principle belong to neglecting that in the thermodynamic principle of protein folding environment plays the same important role as the peptide chain of a protein. In fact, Anfinsen never claimed “that the primary amino acid sequence of polypeptides contains all of the necessary information to direct their folding into functional native proteins” [6] . Instead, Anfinsen stressed that “in a given environment”. Solvents of different compositions, particular properties of water, chaperones to assist folding, etc., are constitutes of environment. For example, globular proteins have the simplest environment which can be simplified as only water molecules surrounding a protein molecule. For proteins needing chaperones to assist folding, chaperone molecules must appear in the environment. For membrane proteins, the environment must be described as including three layers, the middle one is hydrophobic, and the other two are mainly water molecules. Some proteins would not fold in environments not including certain constitutes, does not disapprove the thermodynamic principle, rather the proteins are not in their “normal physiological milieu”. This is just one example that the generality of the thermodynamic principle is often misunderstood and then thought as wrong.

1.3.2. Misunderstandings Caused by Energy Landscape “Theory”

Second, the main reason of the thermodynamic principle was not pursued enough is because of confusions caused by the energy landscape “theory”, both the EL (potential energy landscape) and GEL (Gibbs energy landscape) “theories”. Indeed to minimise the Gibbs free energy one should have a Gibbs free energy function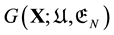, where the variable is a conformation of the protein, and the parameter is the physiological environment in which the protein is folding. Although many have tried to derive, for example, [7] , all failed.

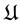
Without knowing, landscape “theories” take place, such as the GEL “theory”. In fact, the GEL “theory” really has no theory, and in principle cannot explain anything [8] . All its formulae for calculating Gibbs free energy are ad hoc, without any theoretical base. Terms such as random energy formula, minimally frustrated principle, are only borrowings from other field without discussion of justification, see [8] . Especially, although proteins fold in a fixed environment, GEL has several different temperatures to be used to calculate Gibbs free energies of different conformations, [9] , something wrong in principle. That is, if one invents a theory to explain a natural phenomenon, one cannot add something that is not in the natural phenomenon.

In fact, the GEL is just the graph of, a very high dimensional hyper-surface (the dimension is at least more than 200 for a 100 residue peptide chain) . Advocators of GEL fully understand this, for example, in [10] , it is stated that “In the filed of physical chemistry, the energy landscape of a protein-solvent system is defined as an energy function, where are variables specifying the protein microscopic states”. The GEL “theory” trying to produce pictures of the very high dimensions hypo-surface. Of course, nobody can penetrate the inhibiting high dimension of this hypo-surface, trying to show it as a two dimension surface give many misleading metaphors such as “funnel shaped”, cause more confusion than understanding.

Thus, if we know, depicting its graph only make trouble, we really do not need the GEL. If we do not know what is, GEL “theory” only makes ad hoc calculations of the Gibbs free energy of various conformations without theoretical base and without consistency. No wonder it caused more misunderstanding than understanding of the thermodynamic principle of protein folding.

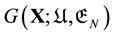
For example, in [1] it is claimed that pursuing of the thermodynamic principle (equivalented to GEL) leads to pitfalls, and the thermodynamic principle will not help to solve the protein folding problem [5] , [11] .

1.3.3. Lack of Mathematical Training

One of the main reasons of GEL, in fact, the thermodynamic principle, will not help solving the protein folding problem is that the second law of the thermodynamics cannot guarantee that the Gibbs free energy will have a global minimum [6] . Even though we do not have explicit formula, a little mathematical knowledge will help clarify this situation. For example, a lower semi-continuous function can always achieve its minimum on a compact set is a theorem in mathematics. Since any conformation’s diameter is uniformly bounded, the definition domain of certainly is contained in a compact set in higher dimensional Euclidean space. It is hard to imaging that a energy function is worse than lower semi-continuous, hence must have a global minimum. Besides, recently an analytic formula for monomeric globular proteins was derived via quantum statistics, [12] - [15] , and this function is certainly continuous, see (6). In [6] , to refute the funnel shape claim of GEL by suspecting the existence of global minimum is not a good argument.

1.3.4. Should the Native Structure Be Only a Local Minimum?

Another main reason of GEL will not help solving the protein folding problem is that the native structure of a protein maybe is only at a local minimum, instead of the global minimum of Gibbs free energy. This is possible, but in circumstances not against the second law of thermodynamics, hence will not negate the thermodynamic principle. In this case, the initial conformation will determine which minimal points will be achieved by the native structure. We should know more of the conformation of newly synthesised poly peptide chain in a cell. Is it alway the same conformation or does it vary with each individual molecule? If it is the former, then starting with other initial conformations may lead to local or global minima different to the native structure. If it is the later, then perhaps the native structure is really the unique global minimum, since starting from all initial conformations lead to the same native structure. Judged from the experiment results of ribonuclease denaturation/renatu- ration, denatured ribonuclease still hold about 1% biological function. Since there are 105 patterns of fulfilling the 4 disulphide bonds, we may infer that perhaps each of the 105 patterns has the similar percentage in the denatured state. Yet, all these initial conformations refold to the same native structure in which the protein has 100% biological function. Thus we can infer that for ribonuclease the really has a unique global minimum. Since this was the entire knowledge Anfinsen had been known, so he hypothesised that “lowest” Gibbs free energy. Considering certain initial conformation leads to certain minimiser, local or global, modifying the thermodynamic principle to admit local minimum will not harm the principle.

1.3.5. Mistaking Environment

A really legitimate concern about the thermodynamic principle is argued in [16] . It says that

“According to this hypothesis, if we define as the Gibbs free energy G of a folded protein in its native state N, is the global minimum of the protein’s free energy functional. However, can only be reached if N is the current equilibrium state for the native thermodynamic conditions. We describe the condition set as, where and are the equilibrium pressure and temperature for a protein in a state X with the conformation. We assume constant T and P and use the only microscopic solvent composition to define the present conditions for X. The Anfinsen’s thermodynamic hypothesis, therefore, seems to make sense. Indeed, from the Second Law (at constant T and P), a free energy change should be obtained for any thermodynamic pathway to relax the non-equilibrium state X to the folded native equilibrium state N with the respective free energies and. and are the native conformation and solvent composition, respectively. The possible pitfall is that is a non-equilibrium free energy because is not at equilibrium for. The real free energy change that has to be considered in a pathway where an intermediate state X has enough time to reach equilibrium is, where (We think this is an error for, otherwise) is the equilibrium free energy for. The Anfinsen’s thermodynamic hypothesis can, therefore, only hold with a good likeliness if. However, cases where is a deep minimum with cannot be excluded, which may lead to.”

The point is that the solvent composition is really varying with the conformation, i.e., there is not any common solvent composition, see the next section on the formula, where is the first water layer of the conformation and is part of the thermodynamic system for each conformation, and is really the Gibbs free energy of the thermodynamic system. As for equilibrium, the protein folding process should be considered as a quasi-static process, and as mentioned before, we only need the heat bath has a constant temperature and pressure, and in this case the second law of thermodynamics is that the available energy is getting its minims as stated in the beginning according to [2] .

After clarifying these suspicions on the thermodynamics principle, we will demonstrate what is the and look at some new insight it gives.

2. The Formula

We will not give the derivation of, which was done in [12] - [15] , with the same idea but progressively better understanding of the quantum physics. We concentrate on the rationals coming from the understanding of the thermodynamic principle of protein folding.

Our understanding of the thermodynamic principle is that it emphasises holistic view, it requires a single molecule method and quantum statistics instead of classical statistics to derive the Gibbs free energy formula.

2.1. The Function Cannot Be a Sum of Local Contributions

Unlike the potential energy function, the Gibbs free energy function, or, the GEL, is not pairwise additive as has been pointed in [6] . In fact, we cannot first consider local contributions and then sum them up to get the Gibbs free energy. This is emphasised by Anfinsen in the statement “that is that the native conformation is determined by the totality of the inter atomic interactions, and hence by the amino acid sequence, in a given environment.” [3] .

So that when trying to derive by the first principle, we cannot divide into several parts, consider each part, and sum up Gibbs free energies of all these parts. In fact, we even cannot take a coarse grained model of conformation to try to derive, because an atom’s contribution to the whole cannot be separated. Hence for us, a conformation is the atomic centres’ coordinates of all atoms of the given protein, witting as. For proteins with more than one poly peptide chains, all chains should be consider together, i.e., let, , , then.

2.2. Single Molecule Treatment Is Necessary

Like any computer simulation of protein folding, we describe only one protein molecule in various conformations, not an ensemble of (the same) protein molecules each taking a conformation. To derive, it is nature that one needs adopt the statistical physics. When applying statistics, naturally one thinks that there should be many copies of the same object, such as a protein molecule, to form an ensemble. This was pursued by many, see for example, [7] , where integrations on all molecular conformations of the ensemble except one was performed to get. With a not integrable integrand (in fact, it is in exponential form) and without clear delimitation of the integral domain, the obtained formula is a complicated unknown function buried in multi-dimensional integral. Worse still, is even not the Gibbs free energy. Nevertheless, the authors of [7] called it the effective energy and used it in many places as if is following the thermodynamic principle. This is a perfect example of starting from the thermodynamic principle and end up with metaphor expressions and endless computer simulations to cover up theoretical poverty. Following this trend, the protein folding problem will never be resolved.

Since one of the tasks of protein folding problem is to figure out the individual protein’s native structure, but in an ensemble of molecules, all available methods are actually neglecting the structures of individual molecule, we cannot use the ensemble method. Therefore, we have to take a single molecule, consider an arbitrary conformation of it, and to figure out a thermodynamic system which is tailor made for the conformation and contains the immediate surrounding environment of. Finally, the Gibbs free energy is the Gibbs free energy of the thermodynamic system.

2.3. Classical or Quantum Statistics?

We have to figure out how to do statistics on this thermodynamic system. Both classical and quantum statistics were tried, see [12] , with the classical result missing the volume contribution in formula (6). Consider that classical mechanics does not fit to describe physics of objects of molecule and even macro molecule size, we choose quantum statistics. Moreover, quantum statistics will allow we do further theoretical studies of protein folding, if we can handle the electronic density function defined in [17] , which we cannot do presently. This function holds the origins of our hydrophobicity level classification in subsection 2.6.

2.4. The Importance of Environment

Our tailor made thermodynamic system in fact contains the immediate surrounding environment of the conformation. Biological knowledge comes here to help us describe and make necessary and rationale simplifications of this immediate environment. For example, it is known for globular proteins, we can simply assume that in the physiological condition only water molecules immediately surrounding a conformation. For membrane proteins, the immediate environment should have at least three parallel layers, water molecules in the outer two layers and the middle is hydrophobic. For proteins needing chaperones’ help to fold, these chaperones must be contained in the immediate environment of the conformation. This is also the holistic view, without the chaperones, the protein is in a wrong environment and will either fold to another structure, or no structure at all, meaning many different conformations achieve the minimum of Gibbs free energy.

Since except for monomeric globular proteins, we have not figured out how to handle environment, our present function is only for monomeric globular proteins.

2.5. The Thermodynamic System for Monomeric Globular Proteins

Since only globular proteins allow us to simplify their physiological environment as consisting of only water molecules, we will only work on monomeric globular proteins here. A conformation of a polymeric globular protein is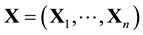,. Theoretically, our function can be generalised without any theoretical difficulty to polymeric globular proteins. But to apply it we will face the docking problem, i.e., consider and the relative positions between’s. This is too hard for now.

First, a conformation by definition lives in, but the textbook definition of a thermodynamic system is that it is a region in, see, for example, [18] . To create, we consider, where

is solid ball of radius and centred at. Essentially the together with its first layer of water molecules will be our. Here we assumed that each atom’s shape is a solid ball with van der Waals radius. Although the shape of each atom in is well defined by the theory of atoms in molecules [17] , what concerning us here is the overall shape of the structure. The cutoff of electron density in [17] , gives the overall shape of a molecular structure that is just like, a bunch of overlapping balls. Moreover, the boundary of the cutoff is almost the same as the molecular surface which was defined by Richards in 1977 [19] and in 1992 and 1993, [20] and [21] was shown to be a more suitable boundary surface of than other surfaces.

To explain the formula, we have to describe in details.

In general, any closed surface (connected, bounded, and has no boundary, for example, a sphere) will divide into three parts,

(1)

where is a bounded domain (connected open set) and a un-bounded domain, means the boundary of.

Rolling a sphere of radius on the boundary surface of will produce a molecular surface [19] . Let be the diameter of a water molecule and denote the molecular surface as. If is connected, then we can use in (1). If has multiple connected components, , such that is the largest component, i.e., all other components of are contained in (this is the case that has cavities, , each is large enough to hold a water molecule), then denote and. Thus, we always have

(2)

Let

(3)

be the first hydration shell surrounding. Then the tailor made thermodynamic system for the conformation is

(4)

2.6. Hydrophobicity Levels

Any Gibbs free energy formula should not only have fairly general form for all proteins, or at least a class of proteins such as monomeric globular proteins, but also must be able to distinguish different proteins. That means that if and are two different proteins with the same number of atoms, say. Then even simultaneously appears as conformations of both and, and are not identical in any neighbourhood of. In particular, even and have the same minimum values, and should have different natives structures, if they have native structures at all.

Hence, we should find a way to distinguish proteins by their peptide chains. The hardest task is that given a peptide chain, let be the number of amino acid appears in, shuffle the amino acid’s around we will have different amino acid sequences, the formula has to be able to distinguish all of these peptide chains. For example, there should be different minimi- sation problems in (9), though the minimisers may vary just slightly for some of them.

To this purpose, we divide atoms in a protein according to their hydrophobicity levels. Atoms in a protein molecule are naturally existing in atom groups or moieties which have different physicochemical properties. One of these properties is the electronic charge distributions caused the tendency of forming hydrogen bonds either with other moieties (intra-molecular) or with other molecules in the environment (inter-molecular). Accordingly, we can divide these atom groups or moieties into different levlels of hydrophobicity, from the most hydrophobic (cannot form hydrogen bond) to the most hydrophilic, say there are levels,. Then we can assign an atom into one hydrophobic level if belongs to an atom group. For example, we may assume that the classification is as in [22] , there are classes, C, O/N, O^?, N⁺, S. Unlike in [22] , we also classify every hydrogen atom into one of the hydrophobicity level groups. Note that this classification is independent of conformations, it only depends on the peptide chain.

For any compact (closed and bounded) set, let be the distance between the point and the subset. Define compact sets, , then. Define subsurfaces in,

(5)

where is the set of points that belong to but do not belong to.

To each hydrophobic level, there is a chemical potential, such that a water molecule touching will gain a Gibbs free energy. Similarly, there is a chemical potential for electrons inside. Let be the average number of water molecules that can simultaneously touching in a unit area, then will be chemical potential per unit area of. Moreover, since the curvature of is uniformly bounded for all conformations,’s do not depend on conformations.

2.7. The Formula

Let be the volume of and the area of a surface. Now we can write the analytic Gibbs free energy formula.

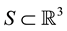
Theorem 1 Let be a monomeric globular protein with atoms and be a conformation. Let be the electronic charges in the nucleus of.

(6)

In [12] - [15] , the quantum statistical derivation first get a intermediate formula, which is much familiar but with new meaning for:

(7)

where and’s are mean numbers of electrons in and water molecules that touches. Moreover, there is a such that so define. Using and the volume decomposition

(8)

We get formula (6) from (7).

3. New Insight

3.1. Structure Prediction

With theoretically established, ab initio structure prediction not only becomes possible, but also simple. It is a pure mathematical problem of seeking the minimisers of. That is, let be the native structure, then

(9)

Or, in case that is only a local minimiser, it must satisfy:

(10)

As discussed before, in this situation, initial conformation is important. If the biological knowledge including the conformation of the nascent peptide chain, we should use it.

To solve (9) there is no need of searching landscapes as seen so important in GEL “theory” [9] . Just following the (the negative gradient of at) from any initial conformation to, and is a small positive number. If the GEL is really funnel shaped, the native structure will be reached eventually by this classical Newton’s fastest descending method.

When the native structure may take only a local minimum instead a global one, we have to try different initial conforms, to get as many as possible local minimisers (such that) by above Newton’s fastest descending method. The native structure must be one of the’s. Other information is needed to determine which one is.

Of course we can use another set of variables, i.e., the dihedral angles, including every routable dihedral angles, in main chain or side chains. Dihedral angles corresponding to a covalent bond inside a Bunsen ring is an example of not rotatable dihedral angle.

In fact, the dihedral angles are the most efficient variables in solving (9) and (10). For the explicit derivative formulae of, please see [23] and [13] .

3.2. Understanding the Folding Process

Theoretically derived can explain various phenomena in the folding process. For example, since the folding force is, i.e., the natural folding process will follow Newton’s fastest descending

path, the initial conformation determines the pathway of the folding. To test the shape of GEL, one can select as many as possible of initial conformations and apply the fastest descending method to find a solution of (10), i.e., a conformation such that. If all initial conformations lead to the same solution, then the landscape GEL is really funnel shaped. If we get many different’s, then which one is the native structure need to be further discussed with more information. But in this case if the conformation of the nascent peptide chain is alway the same, we still have a single folding pathway and even can also observes a classical two phase folding phenomenon.

Now consider an ensemble of conformations of the same protein,. This ensemble case is more familiar, and in fact is the only thermodynamic system appeared in protein folding literature so far. Single molecule phenomena, such as what is the shape of native structure, can never be deduced from such an ensemble system. Instead, the concern should be concentrated on knowing the collective phenomena such as folding rate

and folding time, etc. Then indeed we should consider the distribution. For example, the second law of thermodynamics indicates that there is a distribution such that when the proteins at full function state, for any distribution, it will be

(11)

where is the Gibbs free energy of the ensemble under distribution. The problem is, nobody knows, as Ben-Naim admitted in [24] . One suggestion is that we apply and try the Boltzmann distribution

(12)

The rational is that any conformation with will have much smaller,

thus less chance to appear in the full function state of the ensemble. Of course, this is only a conjecture and it is not so important to know, at least not as a claim made in [24] : “If one knew this distribution, then one could tell which conformations are more probable than the others under the given environment.” In fact, we now all know that in physiological situation the native structure is “more probable than the others under the given environment”, but, we still do not know the shape of the native structure. So to solve the protein folding problem, at least for the prediction of native structure from the knowledge of amino acid sequence, we have to know what is and solve (9) or (10) with whatever mathematical method.

3.3. Force of Folding

In [6] , the folding force is claimed as. In [6] it is also claimed that search the minimiser in GEL, such as in (9), is target-based, and identify the folding force is cause-based. In fact, target-based and cause-based are only artificial distinctions. We see that in solving (9), we do not have a target to subjectively approaching and if we use the fastest deciding method to find the minimiser, we are really cause-based, because we are explicitly using the force.

3.4. Understanding Denaturation and Refolding

If theoretically derived is known for any specific environment, for example, environments differ only in temperature values, can explain the denaturation and protein refolding by changing environments. Changing the environment to, say, the native structure of will no longer be a minimiser of in problem (9) or (10), therefore, is unstable in. Moreover,. By the same second law of thermodynamics, or thermodynamic principle, will force a minimisation of, resulting different minimisers other than. This is a theoretical explanation of denaturation. For certain types of proteins, when the environment changes back, or similar ones, refolding happens as the same procedures as in problem (9).

Furthermore, various thermodynamic functions, such as the entropy, can be obtained by the family. For example,

(13)

3.5. Hydrophobic, Hydrophilic, Which Is the Folding Force?

There is a hot debate in [6] on which one is the main folding force, hydrophobic effect or hydrophilic force? Once we know, moving along the force direction, will become smaller. The qualitative character of is that if the class is hydrophobic, then, and if is hydrophilic, then. Thus reducing hydrophobic areas (hydrophobic effect) or enlarging hydrophilic areas (hydrophilic force?) will reduce the Gibbs free energy.

In terms of the force, the situation is much more complicated. Consider the case of and, they contribute to a force pushing to a new conformation such that and. This well explains that both hydrophobic effect and hydrophilic force playing their roles in reducing the Gibbs free energy. But these are only two terms in, other terms’ values will eventually determine the sign of. And if, or, what will happen? So we have to adopt a holistic view of the folding force, both hydrophobic effect and hydrophilic force play their role, which is dominate depends on concrete circumstances.

To simplify the discussion of hydrophobic and hydrophilic effects (or force), we consider the simplest classification of hydrophobicity levels, i.e., , there are only hydrophobic and hydrophilic atom groups. Denote as the hydrophobic class, as the hydrophilic class. In this case, we have

(14)

Thus for fixed, enlarge is equivalent to reduce, no distinction between hydrophobic effect and hydrophilic force. In this case,

(15)

Since, the combination of hydrophobic effect and hydrophilic force is the effect of reducing the hydrophobic area. In [25] a simulation of reducing alone was performed, the result is very interesting. Secondary structures, such as helices, strands, turns, and hydrogen bonds appeared in obtained conformations with statistical significance [25] . Note that, when reducing, noth-

ing about secondary structure and hydrogen bond were considered. No calculation of the dihedral angles. No testing of positions of the donor and acceptor groups, let alone any intent to push them closer to form a hydrogen bond. Yet nevertheless, secondary structures and hydrogen bond appeared in statistical significance. Before this simulation, it was recognised that hydrogen bond must be explicitly modelled for helix formation and pairwise simulation without specifying hydrogen bonding cannot produce secondary structures [26] .

3.6. Continue a Classics Global View

If, then in the version (15) is an realisation of classical global view of the characteristics of global geometry of native structures of globular proteins. These characteristics are: 1) the native structure has smaller volume; 2) the native structure has smaller area; 3) the native structure has a better hydrophobic core or smaller hydrophobic area, [19] , [21] and [27] - [31] . These important observations were forgot after 1990’s, people were more interested in computer simulations based on force field, GEL, EL, etc. Based on these characteristics, a phenomenological model was formed with exactly the form of (15) with three positive coefficients, thus claim that simultaneously reducing volume, area, and hydrophobic area will eventual lead us to the native structure, see [32] and [25] . Moreover, the first two terms of formula (15) is the formula of the Gibbs free energy of a cavity in water, the two coefficients are pressure and surface tension [18] . First principle and phenomenology, both derived the same Gibbs free energy formula, can it be just a coincidence?

4. Conclusion

The reasons that over four decades Anfinsen’s thermodynamic hypothesis has been dismissed as leading to pitfalls, as disapproved, as no importance at all, are analysed and clarified. They are due to misunderstanding and inability in deriving a Gibbs free energy formula of protein folding. The misunderstandings mainly come from neglecting environment’s role that Anfinsen so emphasised. The inability of deriving a Gibbs free energy function of protein folding comes from using ensemble of conformations that neglected individual conformation’s 3-dimensional shape. The no importance dismiss came coincidently with various of computer simulation without theoretical discuss of their theoretical bases. Newly derived Gibbs free energy function is introduced, its roles in protein structure prediction and in explaining folding process are discussed. The derivation of is applying quantum statistics to thermodynamic systems tailor made for a single conformation and its immediate environment, following Anfinsen’s original single molecule orientation.

References