ABSTRACT

The metaphysical features of the mechanism for the integration of the information underlying protein folding were studied by applying principles of system logic theory. We conclude that it is not possible to predict all protein three-dimensional structures from protein sequences by one program only. This conclusion is validated in structural genomics in that we also cannot predict protein function from three-dimensional structure by one program only. Our theory also demonstrates that bioinformation flow from gene to biological function is an integration process, rather than an expression (translation) process. A system relationship between a gene and its biological function is also proposed.

1. INTRODUCTION

Protein folding describes the physical processes that determine the final three-dimensional structure of a linear chain of amino acids. Although an active area of research [1-6], many questions still remain obscure about how bioinformation within protein sequences is transformed into a specific three-dimensional structure.

Several unresolved issues in fundamental science hinder our research into protein folding. The first is our current understanding of the “system concept” which, at the present time, is essentially empirical. Although dynamic systems approaches [7-10] have revealed some of the nature of complex systems, our definitions have not matured sufficiently to provide a simple, reasonable and clear picture of the system concept. In my view, the nature of a system is still being sought by applying principles of elementary logic, which ignores the use of actual system theory itself.

Second is the theory for the origin of natural order. In the field of physics, the dominant view about this is the dissipative structure theory developed by Prigogine [11- 13]. However, this theory fails to give a reasonable explanation for protein folding, a typical process of the origin of natural order [5]. The key reason for this failure is that continuous supply of energy and exchange of materials between system and environment, which are prerequisite for the maintenance of dissipative structure, is unnecessary for protein dynamics system. Many schools of philosophy, such as Confucism, Taoism, Buddhism, and Hegel’s dialectics, have studied this [14]; however, these are not formulated according to scientific method and they are unable to handle scientific questions in the field. In biology, the logic cycle phenomenon (feedback regulation) has attracted much attention from scientists and a relationship among systems and the logic cycle has been proposed [15-18]. However, the axiomatic theory behind this has not yet been established.

Third is cybernetics [19]. All folded global proteins show hierarchical structure. Protein sequence and structure are the products of biological evolution, which makes a protein well structured and matched up with its biological function. The search for the causation-downward hierarchical structure is a challenging task for mathematicians, physicians, and biologists [20]. The relationship between different parts of a protein, in one aspect, reflects biological regulation mechanisms. However, there is no consensus about the relationship between physical laws and biological rules upon which a well-structured system is organized.

Overall, the study of these questions is in its embryonic stages. Contesting theories are still welcomed.

The dominant view of protein folding held by experimental scientists is that we can completely predict protein three-dimensional structure from protein sequence. The central task of molecular biology is therefore seen as elucidating secondary genetics codes (protein folding code) and many approaches have been taken [1-7]. The theoretical foundation underlying this belief is the linear relationship between a gene and a biological trait (here referring to protein sequence and protein structure), or the central dogma of molecular biology [21], and the observation that an unfolded protein can fold itself in vitro [1]. However, we are still far away from elucidating protein folding code either theoretically or practically [22]. As this hypothesis is not compatible with thermodynamics theory for protein folding [5,11,12,23], we might argue whether this property (structure) of protein folding is computable. If the answer is that it is not, then the question becomes how to demonstrate it logically.

Protein folding is a typical process for the origin of natural order [4,5]. The hierarchical structure of protein three-dimensional structure is formed and the information of protein folding is integrated at diversified levels within the protein hierarchical structure in protein folding. In this paper, we will discuss logic principles (metaphysical properties) of protein folding. Our conclusion is that we cannot predict all protein three-dimensional structure from protein sequences using only one program, nor can we predict protein function from protein threedimensional structure with only one program. This represents the logic limit of protein science [24]. Proteins, as well as biosignal networks, represent complex systems; therefore, the relationship between genes and biological functions can be only analyzed by system logic theory.

In order to demonstrate this rule mathematically, we need to formulate a logic system (referring here to system logic) and confirm it based upon well-known facts of protein folding (e.g., cooperation).

Briefly speaking, the conventional view of mathematics is formal logic (or symbolic logic), which is established based upon absolute and elementary concepts [25-27]. In substance, formal logic is unable to handle problems of a system, and in order to gain this ability, extra hypotheses (or conditions) may be introduced into the practice model of mathematics, allowing it to provide an approximate description of the properties of a system under a specific condition [6,28,29]. System logic can then be used to analyze properties of the system and their relationships.

2. PREREQUISITE FOR PROTEIN ALGORITHMICITY

If protein structure can be deduced logically from protein sequence, or in other words, if the bioinformational flow from protein sequence to protein structure is completely computable or algorithmic, then protein structure (S) could be expressed by the following equation.

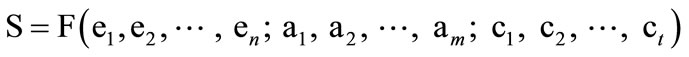(1)

where S represents protein structure, F is a mathematical function disregarding its formality, e represents a scientific element of axioms, a represents an axiom, and c represents a conditional parameter. In addition, F must be identical for all proteins. If these criteria cannot be met, the protein structure will show nonalgorithmicity.

3. THE COOPERATION PHENOMENON AND LOGIC CYCLE STRUCTURE

Multiple interactive connections occur within a protein, as well as in other biological systems. Mutual causality is a well-established fact of nature (16). Some scientists utilize terms such as feedback cycle regulation to describe these complex interactions in the field of biology [15,17,30]. This view, although correct, cannot be used to analyze the fundamental logic relationship between components of a system or the infrastructure of a system. The key theoretical flaw can be clearly seen in following expression, a well-known fact of biochemistry:

The regulating molecules of enzymes (inhibitors or activators) modulate modulating the protein conformation and dynamics state of an enzyme (acting as a conditional factor for enzyme activity). The relationship between the regulating site and enzyme activity is conditional logic, not absolute logic.

In protein folding, we have learned that the role of one amino acid residue is determined by another amino acid residue and vice versa [31,32]. In other words, the effect of residues is cooperative [33,34]. The strong coupling between secondary and tertiary structure formation in protein folding is a well known fact [35].

The logic relationship underlying this phenomenon can be expressed as follows:

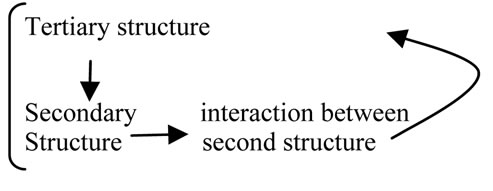
The tertiary structure of a protein is the result of protein folding; thus, it also acts as a conditional factor for protein folding.

We can thus formulate the logic cycle structure by the following expression mathematically:

In this expression, the result and condition are the same.

The mutual causality (feedback cycle regulation) can be expressed by specific logic cycle structures (a combined fashion of logic cycle structure).

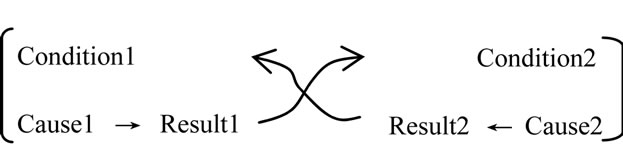
In a conventional view of mathematics, this logic cycle structure cannot be permitted.

4. THE ELEMENTARY CONCEPT OF PROTEIN FOLDING CANNOT BE ABSTRACTED (METHOD 1)

If we can abstract the elementary object (concept) of a property of protein folding, then it will be computable. If we can demonstrate that there is no elementary concept, then the property of protein folding is incomputable.

We suppose that cooperation (a type of logic cycle) occurs between residues A and residue B. We can formulate their relationship in following expression.

where a and b represent residues, A and B represent their roles. In other words, the effect of A is controlled by B and vice versa.

We can then express this relationship as follows:

A=F(B) and B=F'(A)

where A represents the role of residue A, F represents function, and B represents the role of residue B.

It is obvious that there is no solution for these equations. Thus, the elementary concept of protein folding cannot be abstracted theoretically. The property of protein folding therefore shows nonalgorithmicity.

5. THE SYSTEM THEORY

The above discussion reveals that properties of a system, which contains a logic cycle structure, cannot be described by elementary logic. Therefore, we have proposed the logic cycle structure as the infrastructure of a system or the scientific definition of a system concept.

We can then deduce properties of a system based upon this definition.

1) The structural change of a system and qualitative change: for two systems that are structurally differently, a transformation between them can be only processed catastrophically and this produces a qualitative change in the system. The cooperation phenomenon can be seen in system change.

2) Quantitative change of a system and stability of a system: a system can tolerate some degree of stimulus, and system properties will change to some degree, without inducing any structural change of the system. The limit of quantitative change of a system is called its system stability. The cooperation phenomenon cannot be seen in quantitative change.

3) A system has unlimited variables. This principle is the logic prerequisite for a system; otherwise the axiomatic theory cannot be established.

When we consider the relationship between two systems, we can deduce the following principles, and constructs a coherent system of system logic: Principle 1: the relationships of two systems construct a new system. Principle 2: within complex relationships of two systems, many models could be established under specific conditions and, within these models, the relationship between components of the systems can be written by elementary logic (or formal logic) that is computable. Principle 3: Among these models written in formal logic, which describe the relationship between systems mentioned in principle 2, some models are incompatible with each other in logic.

If we ignore the logic cycle structure of a system, the system logic will become the logic of elementary concepts or the conventional logic of mathematics.

6. THE NONALGORITHMICITY AND ALGORIMICITY OF PROTEIN FOLDING (METHOD 2)

Nonalgorithmicity and algorimicity of properties of a system can be clearly seen in system change.

Let us consider a simple case. The S (property of a system) is related to 3 factors: a, b and C, the C is conditional factor. We can then formulate the S of two systems as:

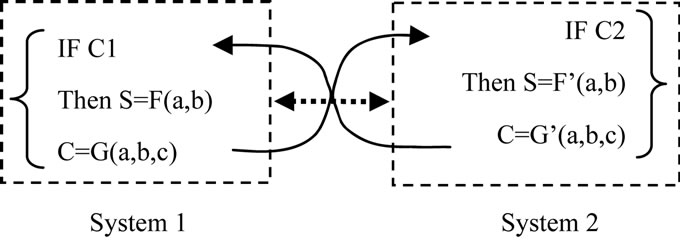
where F and G represent two different functions.

Even within both systems, S can be formulated (or computed). A unified S cannot be formulated (or computed, algorithmized).

Thus, we can conclude that S shows Nonalgorithmicity.

The study of protein structural change provides a good illustration of this [6]. It has shown that properties of the open and closed states of a channel can both be computed, but are described by different equations [5,6]. This view has been well confirmed theoretically and experimentally [36-38].

7. VALIDITY AND EXPLANATIONS

Our conclusion is certainly validated in many fields of science. In order to judge the nonalgorithmicity, two criteria must be met:

1) The infrastructure or logic cycle structure of a system needs to be identified. Cooperation or phasic change is a good indication for the existence of a system, but these may be induced by other mechanisms. It must be pointed out that the meanings of a system within our theory differ greatly from others. For example, because there is no infrastructure, gas cannot be recognized as one system according to our definition, although most people would consider it as one system.

2) The target property must be related to at least two different systems. In protein science, all protein is a complex dynamics system and shows hierarchical structure and cooperation of conformational change (system change) occur for all proteins, even small protein such as trypsin inhibitor [39]. Protein behavior cannot be analyzed by elementary logic—we must study it by system logic. According to system logic, we can explain it in plain language:

1) For a folded protein, there is at least one program that allows prediction of protein three-dimensional structure from the protein sequence.

2) No program exists for predicting all protein threedimensional structures from protein sequences.

3) We must predict different proteins (or protein structure families?) by different programs.

In protein science, these deductions are invalidated for peptides which show no cooperation phenomena or logic cycle structure in its conformational change.

The cooperation phenomenon is universal in protein conformational change (i.e., the logic cycle structure can be abstracted) and protein function is related to one type of protein conformation. Our conclusion is also validated in the structural genome [2,3]. We can revise this as follows:

1) For a protein function (or property), there is at least one program for finding the connection between it and the protein structure (conformation).

2) No program exists that predicts all protein functions from protein three-dimensional structures. In other words, the models that describe the relationship between protein function and conformation are incompatible with each other.

3) We must predict different protein functions by different programs.

Recently, the work of Dobbins et al. [28] has shown that a composite model is necessary to describe the diversity of conformational change observed during molecular recognition. This is exactly the prediction of our theory.

8. THE LOGIC INDEPENDENCY OF A SYSTEM

It is well known that protein, as well as most things in nature, shows hierarchical structure. The logic relationship between different properties of things at different levels has never been studied before in the field of mathematical logic, but this question had been discussed by several philosophical schools, such as Taoism, developed 2000 years ago. The logic discontinuity between different matters at different levels of nature is the theoretical foundation of the Li school, a dominant school of ancient Chinese philosophy. The main idea is that we cannot deduce the properties of advanced matter by applying principles of fundamental matters.

The logic independency of a system provides a reasonable answer for this phenomenon.

As the conditional change within the logic cycle structure of a system occurs at an advanced level in the hierarchical structure, and it cannot be traced back to any property of matter on fundamental level, the system has its own particular logic property that cannot be described by properties of matter at a fundamental level. This logic independency of a system reveals the utmost mechanism for the logic discontinuity between different levels of hierarchical structures of things.

A powerful proof is that protein stability does not control protein folding; some types of information of protein folding have nothing to do with protein structure [31,32,40].

9. SYSTEM RELATIONSHIPS BETWEEN GENES AND BIOLOGICAL FUNCTIONS

Protein folding is only one step among many in informational flow from a gene to biological function. A given biological function (which is usually defined at several different levels, from molecular function to biological role at the level of organisms) is not the property of a single protein, but the property of “functional modules”, or protein network, biosignal network, consisting of numerous macromolecules that interact with the given protein [41]. The functional module of a given function represents a specific system. Therefore, the conclusion obtained from system studies is also validated in our understanding of the relationship between a gene and its biological function.

Considerable debate is ongoing in genetics about the gene concept and the relationship between genes and biological functions [42-45]. No absolute definition has yet been proposed. We show that this question can be naturally resolved with system theory.

In Table 1, we list the coherence between system theory and knowledge of genetics obtained from experi

mental studies.

In this table, we can see that system theory agrees theoretically with the conclusions of experimental science.

The information stored in the genome is integrated at diverse levels in the hierarchical structures of biological organs (signal network). In a stricter meaning, the informational flow from gene to biological function is an integrated process, rather than an expression process. The conventional view of genetics—the linear relationship between gene and biological function—is merely the approximation of system logic. In other words, it is validated in many different models that cannot be unified theoretically and logically. Therefore, an absolute definition of the gene concept based upon system logic cannot be developed, meaning that we should seek its definition under a specific condition.

10. OTHER EVIDENCES

Studies on protein folding and protein structure have revealed many experimental phenomena which could be easily interpreted by system theory and were summarized as follows.

1) Folding of a protein is influenced by its entire environmental factors [46], which can modify or neutralize the effect of gene mutation on folding ability [47]. The logic cycle (conformation controls dynamics, and vice versa) could be clearly seen within process of folding. One environmental factor acts differently on different folding steps of a protein and different proteins. It is impossible to incorporate infinite factors of environment, which are not independent with each, into any axiomatic theory for protein folding written by elementary formal logic.

2) Some proteins can fold in vivo with help of chaperones [48]. It indicated that some protein sequences have no enough information for protein folding. Thus, there is no such program by which we can go from sequence to structure for all proteins.

3) The prion biology has provided powerful evidence for conclusion that a protein sequence can fold into many different structures [49]. The logic cycle structure (feedback regulation) can be clearly seen in the formation of prion. Therefore, information of a sequence can be differently integrated.

4) Some protein sequences are intrinsically unstructured [50], some are conditionally folded and some segments of a folded protein are unstructured. Many disordered segments fold on binding to their biological targets [51]. If we hope to predict structure of a protein, we must firstly know its coupled protein, and vice versa. Again there comes logic cycle phenomenon. According to system theory, the structure of a protein is logically determined by itself and coupled proteins; new type of conformation of a protein was generated on binding to their biological targets.

5) Protein is a developing system and new type of conformation (or new function) can emerge under different conditions [52]. If one program can predict many conformations of a protein from unique structure of a protein, it is with no use; if not, the rightness of it will be questionable.

6) Protein conformational change, or protein dynamics, is essential for enzyme (protein) activity [53,54]. Although there are significant correlations between protein dynamics and structure, the dynamics natures of a protein cannot be fully described and analyzed by protein three-dimensional structure theory.

REFERENCES