ABSTRACT

The 3-D structure of the β-adrenergic receptor with a molecular weight of 55,000 daltons is available from crystallographic data. Within one of the seven transmembrane ion channel helices in the β₂-receptor, one loop of a helix ACADL has previously been proposed as the site that explains β₂activity (fights acute bronchitis) whereas ASADL in the β₁-receptor at the correspondding site explains β₁-activity (cardiac stimulation). The α-agonist responsible for this selective reaction is only 0.5% of the receptor molecular weight, and only 1.5% of the weight of the transmembrane portion of the receptor. The understanding of the mechanism by which a small molecule on binding to a site on one single loop of a helix produces a specific agonist activity on an entire transmembrane ion channel is uncertain. A model of an α-helix is presented in which of pitch occurs at angles both smaller and larger than 180˚ n. Consequently, atomic coordinates in a peptide backbone α-helix match the data points of individual atom (and atom types) in the backbone. More precisely, eleven atoms in peptide backbone routinely equal one loop of a helix, instead of eleven amino acid residues equaling three loops of a helix; therefore, an α-helix can begin (or end) at any specific atom in a peptide backbone, not just at any specific amino acid. Wavefront Topology System and Finite Element Methods calculate this specific helical shape based only upon circumference, pitch, and phase. Only external forces which specifically affect circumference, pitch and/or phase (e.g. from agonist binding) can/will alter the shape of an α-helix.

1. INTRODUCTION

The crystallographic structure of the β₂-adrenergic receptor has 56,000 atoms, about a third of which are transmembrane a-helical backbone peptides [1-3]. Binding site specificity for β₂-adrenergic agonists results in stimulation of respiratory functions to treat acute bronchitis versus β₁-adrenergic agonists stimulation of cardiac output [4]. The size and molecular weight of these agonists is 0.5% of the size and weight of the receptor. Within one loop of one α-helix within the transmembrane region, the β₁-adrenergic agonists fit better to the sequence ACADL and β₁-agonists fit better to ASADL [5,6]. Changing only one receptor amino acid markedly alters agonist activity.

The ion channel portion of the receptor is composed of seven α-helical backbone peptides, each perpendicular to the lipid membrane: adjacent helices align anti-parallel, except the first and the last of the seven helices instead align parallel [7,8]. Although macromolecular processes such as shielding and hydrophobicity affect membrane potential [9,10], ion channels enable cross membrane signaling and intracellular communication [11,12]. The mechanism by which one small molecule agonists on associating with only one of the loops in only one of the α-helices would increase the amplitude of signaling for the entire macromolecular transmembrane domain of receptor is not at all self-evident.

Since the β₁-adrenergic binding across ACADL is selectively binding also across CAD, it is an assumption that the binding site requires one full loop of an α-helix. The sequence CAD is a little larger than half of a loop of the peptide backbone helix. The model of an α-helix in which the smallest structure is itself is actually a definition and therefore never experimentally accessible. A model of an α-helix is required in which the helix can be composed of smaller than 180˚ n steps. A model of a peptide backbone α-helix composed of parts smaller than one loop is required which can also be predictive structures and molecular level forces of larger, more complex biomolecules.

2. PRECISE MODEL OF (-HELIX

2.1. Geometry Describes (-Helical Shape

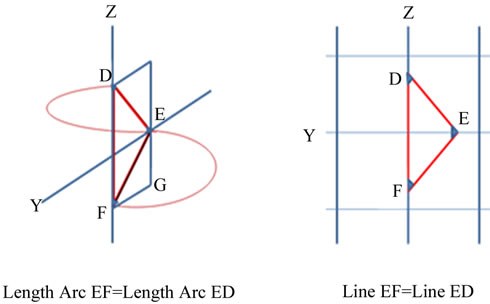
The geometric of an α-helix can be generated from only three data points. One loop of an a-helix is an arc FD both ends of which are in an YZ plane (Figure 1(a)). This arc can be divided in half at a point E such that arc EF = arc ED and FD and E forms an arc for 180˚, half of the length of the arc for 360˚.

Every helix intersects the YZ plane at three and only three points (Figure 1(b)). The distance FD is identical to FD in Figure 1(a) and point E is the same point E. The three points in the YZ plane form exactly three angles and three distances. EF = ED which forms an isosceles triangle. As both halves are identical, analysis of only half the arc and/or half the isosceles triangle are required to explain its properties. A point G is in the same YZ-plane as EFD and angle FGE is a right angle.

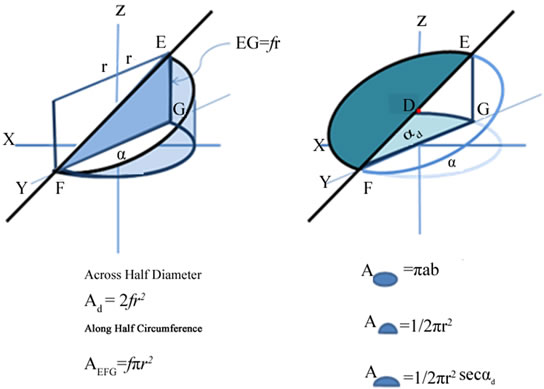
Four discretely different areas are present in any helix. Each arises from this same one triangle: the triangle in which angle FGE is a right angle (90˚); the hemi-circle with diameter FG; a triangle along the circumference of the circle with height EG, and half an ellipse across the length FE (Figure 2). The triangle along the circumference increases to height EG with an angle α; triangle across the diameter increases to height EG with an angle A triangle increasing in height a constant rate along the circumference of a circle produces the same curve as the ellipse. The triangles across diameter FG and along the arc FG produce exactly the same height EG.

The ratio of two distances has no units and pitch is a ratio, not a distance. The relative scale of dimension, not the absolute scale of dimensions, matters. Although pitch can be stated relative to the radius r or diameter d of a helix, pitch can as validly be stated as relative to the circumference (C) of the helix. One advantage of sta-

ting pitch relative to circumference is that pitch is a constant defined for any fraction of the (C) whereas pitch across the diameter (D) of a helix is invalid unless the p r is greater than or equal to 180^˚.

Since both the diameter FG and the arc FG are functions of r, and angles have no units, EF must be a function of r. The area of an ellipse is π, ab: a = r and b = FE_d/2 = FD. However FD = r sec α_d, thus the area of half an ellipse is 1/2 πr² sec α_d. The ratio of the areas of half a circle and half an ellipse is simply a constant: sec α_d = FE/FG. The ratio FE/EG is simply cosecant α_d. A pitch across a diameter simultaneously always forms a pitch along C.

The ratio of the areas of all the structures is directly proportional to r². Since the three data points F, G, and E are identical in each of the equations that define these shapes, equations forming shapes connecting these points cannot be independent of each other. An unexpected dilemma, however, arises when in comparing the two triangles (Figure 3).The area of the ellipse, the circle, and the triangle along C is proportional to π. Although 3a is a triangle, its area is always a factor times 1/2 πr². The unavoidable question is whether pitch across FD is also a function of π or independent of π.

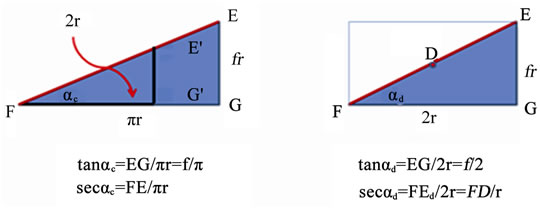
The pitch along half C is tan α_c = EG/πr; pitch across D is tan α_d = EG/2r. Let f be a dimensionless constant and EG = f r. Therefore, tan α_c = f/π and tan α_d = f/2. The ratio (tan α_d/tan α_c) = π/2. Alternatively, sec α_c = FE/pr where FE is the length along C and sec α_d = FE_d/2r = FD/r, where both FE_d and FD are lengths across D. Neither EG nor f are in these equations and (sec α_c/sec α_d) = (π/2) FE/FD.

The ratios include the factors π, f, FD, and the numbers 2. Let f = π/2 and a discrete and remarkably simple mathematical interrelationship among the four areas results (Table 1). The three ratios FD/r, FD/2r and FD/πr equal three secant functions which each corresponds to only one of three angles (α_r, α_d and α_c ).

2.2. Protein Peptide Helices

Pitch and diameter routinely are reported to two significant figures. The accepted value of pitch for peptides is 5.4 Å and the average diameter 2r is 3.5 Å [8]. Thus EG/2r = (2.7/3.5) = tan α_r; α_d = 37.65˚ and sec α_d = 1.263 = FE/3.5Å and FE= 4.420 Å; FD =2.210 Å; the length πr = 5.498 Å. The length arc FE = 6.125 Å. The angle of pitch is lower along C than across D (or across r) because the denominator of the ratio is larger along C.

The three secant functions are:

• tan α_r = 2.7/1.75; α_r = 57.05˚; sec α_r = 1.839;

• sec α_d = 4.420/3.5 = 1.263; α_d = 37.65˚

• sec α_c = 6.125/5.498 = 1.114; α_c = 26.16˚

For every 2pr length along C in peptide helices, a pitch of magnitude pr shows up in the +Z direction. The cross check is that tan (πr)/(2πr) = tan(0.5) = α_c =26.56˚. FD is a simultaneously a function of r and α_r, of r and α_{d ,} and of πr and α_c . Each ratio can be calculated within any selected precision. None of the ratios are in principle any more valid than any other ratio. The third ratio is the most useful because virtually all the empirical data on peptides is in the plane of the circumference, not in the plane of the diameter.

2.3. From π Radians to an α-Helix

A difficulty in this mathematical model arises on functions going from π to 2π  radians. An inclined plane in a Z direction across a Y diameter has no X component. Thus the same magnitude EG can be reached from both a clockwise and from a counter-clockwise direction. Continuing the same pitch for a second p radian distance requires asymmetry.

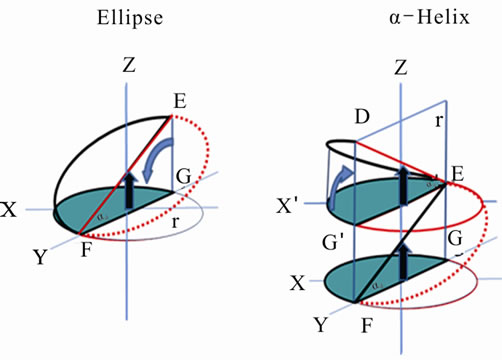
In the helix (Figure 4), the incline plane (sec α_c) is conserved along C for 2p radians. As a consequence, the path ends at D, not F. The value of maximum pitch on C is precisely twice maximum pitch of the ellipse. The line DG intersects the Z axis at height EG. Despite the back and forth of a tilt (in the Y plane), the net tilt on Z in any full cycle is zero.

In the ellipse, the path beginning at point F returns to the same point F path. The average magnitude in the Z direction is 1/2 EG, i.e. precisely half the magnitude in the helix. The ellipse is planar and its plane tilts α_d away from the Z axis in the YZ plane, creating a Z’-axis. There is no tilt in the XZ plane. When the direction of inclined planes in the second half is in the opposite direction, the cycle returns to the origin F, and an ellipse results. When first half and second half inclined plane is in the same direction, D is above F, and a helix results.

2.4. Molecular Distances within One Peptide Loop

One full loop of an α-helix contains 3.6 amino acids. The partial 0.6 amino acid could be above, below or partially above/partially below the complete three amino acids. Although a minimum of three data points are required to create an α-helix, 4.6 amino acid residues exist in every individual loop of a helix (the first is at point zero). In an alanine tetramer viewed from the Z-axis (Figure 5), the loop is about 0.6 amino acids short of 360˚. Every trimer contains sufficient information to generate half a helix. Eleven peptides equal three loops of an a-helix, thus (360˚) × (3/11) = 98.18˚. Three amino acids would equal 196.36˚, a bit larger than a semicircle.

Each step in this helix is ten atoms beginning from HN and ending with C=O. Starting at an NH₂ group and ending with an OH group is not actually part of the repeating pattern. A choice is required to deciding exactly which atoms define the helical shape. Atomic coordinates of the chiral centers (Figure 6(a)) unambiguously generates the helical shape and enables calculations of the parameters that fully define the specific geometric shape.

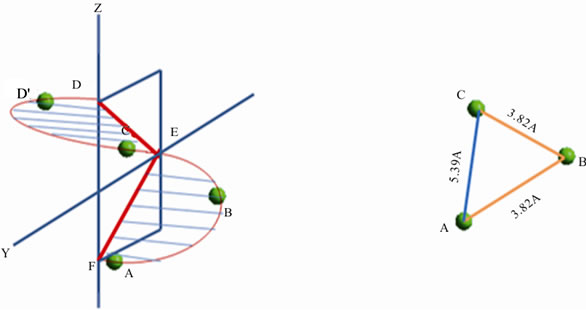
The position of three structurally equivalent atoms in the same peptide sequence corresponds to half a loop of an α-helix (Figure 6(b)) and three sites results in three molecular scale distances. The distance between two adjacent chiral centers in the peptide backbone is 3.82 Å; the longer distance between the first and third chiral center is 5.39 Å. The three data points/distances form an isosceles triangle. The data points in arc ABC are exactly those contained in arc ABCD. The same shape occurs in Figures 1 and 6. In Figure 1 all the data points happen

to be in the Y plane; in Figure 6, at most, only one of the data points can happen to be in the Y plane.

An additional precise and equally valid α-helix can be generated separately using each set of atomic coordinates from atoms containing the same [repeating] atom type (e.g. the amide H, the anomeric H, the amide N, the carbonyl C, and the carbonyl O). Every peptide trimer in an α-helical conformation contains a large abundant redundancy of information that should be readily accessible computationally. The three data points applied self-consistently will precisely generate one α-helix.

2.5. Molecular Distances for Multiple Loops

The length of twelve residue polyalanine forms three loops of a helix with 120 atoms. Viewed from the Z-axis, the average shape is a circle with a precise radius and height and shorter height. Three loops actually contain eleven residues, except one residue is one the origin. Viewed from the Z-axis, the residue at 0˚ and at 360˚ (the first and last amino acids) overlaps in position.

Every full loop of an a-helix contains eleven peptide backbone atoms, e.g. an amide group plus three residues or C-N-C^*-C-N-C^*-C-N-C^*-C-N = 2 + 3 + 3 + 3 = 11 atoms. This is the equals one atom in a peptide backbone short of four peptides (12 atom). However, everywhere along the helix, 11 atoms have the same pitch. This predicts the molecular forces that describe a peptide helix beginning from a C=O group would be equal to that beginning from an NH group, or from a chiral center C^* group. The average length of one loop of a backbone peptie will be constant independent of from which atom one starts to measure it.

The position of only three atoms [of the same atom type] (Figure 6(b)) is required to generate half a loop. Graphing only one data point per atom type for each of the residue (Figure 7) viewed from the Z-axis forms a circle. The diameter will be different depending upon the atom type, e.g. radius/diameter of the a-helix of the anomeric H is twice that of the amide H. No distances between any pairs of molecular coordinates intersect with and/or identify the geometric center of the helix. The data from a string of molecular coordinates generates multiple helices of varying diameters. Determining the circumferendce from the Y-axis can be computationally complicated, yet from the Z-axis it is readily accessible graphically.

3. GRAPHICAL METHODS

3.1. Peptides and Molecular Grids

Graphical methods developed for Engineering Visualization including Wavefront Topology and Finite Element Methods have been applied to geometric shape including helices [13-16]. A helical grid applied to a peptide helical backbone structure can be fitted to the same helical grid simply by changing the height and diameter of the grid, and more accurately by choosing atoms of a repeating atom type, e.g. the chiral centers of the same peptide sequence (Figure 8). Small changes in height in 2D equal a shift in phase in 3D.

Viewed from the Y-axis, the helical grid enables direct measurement of the pitch/radius ratio and/or radius/pitch ratio. The grid matches the quadrants of the helical peptide both where spatially chemical structure is and the

quadrants where chemical structure spatially is not. The inexactness of the fit is due to coordinates of multiple chemical structures being close to but not on the grid. In contrast, the coordinates of the same atom type (in this case the chiral center) fit much closer to the grid, i.e. amore exact radius/pitch ratio can be calculated. The data point sets in Figure 7 all uniquely conform to their own specific helical grid shape. For a helical shape to correlate with macromolecular structure, clearly the more the data points fit on the map, the better. Although a helical map can be a property of amino acid residues, a more accurate and more precise helical map is of the position of individual atoms within that amino acid. The helical maps of the different individual atom types composing the amino acid backbone need not be identical with each other and most often would probably not be identical.

3.2. The Problem of Phase

A helical structure and a grid with precisely the same pitch and radius [and the wrong phase] could have no data points in common. Unlike in a cylinder, at any Z-height, only one data point will be on its circumference. Beginning from any other data point on the initial circumference produces a parallel helix, not the same helix. Moving an intact YZ-map of parallel helices stepwise in the Z-direction is graphically equivalent to rotating the helix an angle in the XY-plane.

Since viewed from the Z-axis, a helix is a circle, guessing where the “circle” starts could seem strange. Yet observing empirical data (Figure 7) shows the distribution of the data points around the circle are NOT equal and one could visually [and correctly] guess where the helix actually starts, i.e. where two “adjacent” data points are clustered closest together. The reason this is possible is exactly because the height of the helix is maximum at this phase. The same would be true with only one loop of a helix.

The dilemma is that there are two equally viable choices for phase = 0 to occur. In Figure 1, for example, this data point can be either E or F. The height for Z cannot be mathematically determined without choosing a value (whether Z starts in the quadrant Y or -Y). Graphically, however, this is not a difficulty: the two heights are present and one can at any time measure either one.

The path along the circumference up an a-helix with secant (0˚) = 1 [zero pitch] is the circumference. Otherwise, the length of the path up (or down) the slope will always be longer than the circumference. At secant (26.5651˚) = 1.118, rise is a constant increase in distance over run and run is 2.000  and the hypotenuse length of the path is 1.118 time that of the circumference with no pitch. The affect of the longer path length is that the actual frequency per cycle is higher than measured at the circumference distance. Velocity along the longer distance and energy required to achieve the longer distance cannot be the same as going the shorter distance.

On every circular clock, the second hand will travel 1.25 times longer than 60 s to reach 75 s clockwise (cw). Ironically, if the second hand went in the opposite direction (ccw), the hand would reach the same location in only 45 s (0.75 times the rate of 60 s). The shorter distance corresponds to the slower rate, the longer distance to the more rapid rate, even though the average between the two unequal velocities is also a constant.

Measured in intervals of π/2, subtracting the difference between faster and slower periods is π/2 = [5/4π  – 3/4π]. Adding the magnitude of frequencies [5/4π + 3/4π] = 2π. Observations at 2π intervals (once per cycle of a α-helix) only identifies frequencies which co-add in one direction. Frequencies faster than 2π intervals will not be in the equation. Observations at p intervals would show up only as a phase shift of π/2, but in the opposite direction.

For a helix with (α_d) less than 26.5651˚, the phase will be smaller than π/2 For a helix with (α_c) larger than 26.5651˚, the phase will be larger than π/2. At (α_c) = 26.5651˚, the same forces that describe a circle in which (α_c) = 0˚ are present in the helix when (α_c) ≠ 0˚. In a circle, r is always positive and always in the XY-plane. At a distance of half a loop (πr) around the circumference, the sequence is (πr/2)_X + (πr/2)_Y. The third step in the sequence (if the path is a circle) is (πr/2)_X.

In the helix, the third step is ±(πr/2)_Z. One path is apparently faster, the other slower. Frequency ν has units of velocity and ν² has units of acceleration. Thus an increase in velocity of 1.118 corresponds to an increase in acceleration of 1.25. Since 1/4 (2π) = π/2, a pitch of 26.5651˚ increases by π/2 per cycle in one direction. In the opposite, direction ν² decreases by π/2 per cycle. The acceleration and deceleration depend upon direction up or down the inclined plane path. In a cylinder, height is independent of r. In an a-helix, the pitch is always dependent on r.

Drawn from a common origin, a sequence (πr/2)_X + (πr/2)_Y + (πr/2)_Z equals the sphape of a 3-D sphere. The sequence (πr/2)_X + (πr/2)_Y ± (αr/2)_Z, for an α-helix, contains exactly the same variables, except ±(πr/2)_Z is at/from the circumference of the circle, not at/from a common origin. The transition from a spherical to a helical mode requires energy to move from on the Z-axis to a distance r to a circumference. At (α_c) =26.5651˚, that amount of energy a known: half the energy from –X to +X (or from –Y to Y), i.e. 1/2 (πr)_X or 1/2 (πr)_Y. A constant (πr/2) unit of energy per half cycle is required for the α-helix to this component to remain on the circumference. Again, therefore the frequency selfconsistently in one direction must be slower in one direction, faster in the other.

With multiple loops/cycles, faster and slower frequencies will co-add: (πr)_X + (πr)_Y + (πr)_Z  requires (πr) n units of energy for every (πr)_X + (πr)_Y cycle. The maximum Z-component of force occurs at/from the site on the circumference in which the phase originated. Concomitantly, the minimum Z-component of force occurs from the graphical center of the α-helix, i.e. zero net charge occurs at the origin.

3.3. Graphical Solutions to Helical Measurements

An α-helix is mathematically definable from the same variables that define a circle: circumference, radius/diameter, pitch, and phase. Interestingly adding pitch and attmpting to holding radius/diameter and phase constant, a circle becomes a helix due to the circumference distance becoming longer. If pitch were a ± measurement from the plane of the circle, pitch would always be zero because half the distance would be above the plane, and an half below the plane. Graphically, in contrast, all physical distances between points are positive.

Pitch in a helix occurs parallel to the Z-axis. In molecular structures, however, atoms are only approximately aligned with the Z-axis. The NH group and the C = O group (3.6 amino acids later) do align in a helix, except the angle of alignment is not necessarily along the Z-axis.

Moreover, rarely is empirical data aligned with the preferred orientation from which to take desired measurements: the most accurate measurements of r or pr circumference is from the correct XY-plane. Orienting data graphically to any XY-plan in computer graphics software is routine and straightforward. In the Z-axis view of the helix (Figure 7), no line can be drawn between any two of the atoms that equals a diameter. There is physiccally no chemical structure at all in any peptide helix at either the center of the circle or the other end of the diameter.

The grid generated from graphical analysis contains three and only three variables: pitch, radius/diameter, and phase. Thus the input of molecular coordinates from the position of three atoms [e.g. of the same atom type] are fully sufficient to characterize an α-helix conformation. Since each atom type in a helical amino acid backbone (NHC^*HC = O) contains six atoms [except for each proline which has only five backbone atoms], there is a huge redundancy and interconnection of information about its shape even when only three amino residues are present. Three data point [of the same atom type] equal a little more than half a loop of the helix. Graphically, a fraction of a helix is identical in shape with whole helix, just displayed over a shorter interval.

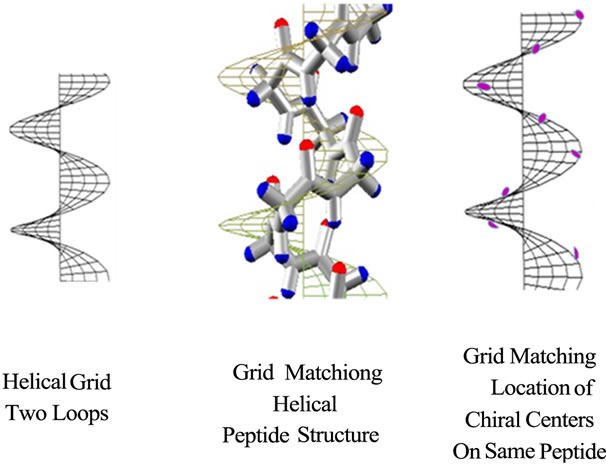
The YZ-dimension in the mesh in Figure 8(a) expanded in the Y-direction increases pitch, expanded in the X-direction increases radius. Only by proper and precise adjustment of these two dimensions can/will the mess align with the peptide backbone and its helical conformation (Figure 8(b)). A best fit occurs with half the data points are above the mesh, half below the mesh. Again, there is a huge redundancy and interconnection of the information. Choosing to display only the chiral centers of this helix, the graphical model shows very good

agreement between the mesh and the eight data points. The graphical model is the best fit for all eight data points and generated a precise value of pitch and diameter independent of any a priori prediction of where the other end of a diameter may be or where individual atoms must be to predict pitch. The same map can be used to correlate any set of coordinate data points which are in the same an α-helix conformation.

The radius to an amino acid residue has no precise physical meaning unless a site within its structure has been specifically defined (e.g. mathematically or graphically). In the model of an α-helix based on atoms within a peptide backbone, the radius ends at any individual atoms type will have a precise helical molecular structure, even if radius for different atom types can or will be different from each other.

4. BIOCHEMICAL CONSEQUENCES

4.1. Helical Shape and Agonist Effect

Pitch, diameter/radius, and phase fully define a helix. Thus these same variables could be the same components from which 1) to create a biophysical model that incurporates loops of a helical structure into explaining the electrical properties of ion channels and other nano structures, 2) to provide sites definitive 3D sites at which interactions of molecular structures and macromolecular forces can be evaluated and tested, and 3) to challenge the model that peptide helices are rigid cylinders that are discontinuous with and/or immune to/from other biophysical and biochemical processes.

In the presented model of a helix, only molecular and biophysical processes that affect pitch, diameter/radius or phase can/will disrupt the size and shape of an a-helix. Those which don’t, will not and parameters that do not affect the geometric shape of an a-helix are irrelevant to helical structure.

At the molecular level NH and C=O structures aligned with the Z-direction and contribute to both the diameter/radius and phase. The uniform shape of a helical geometry depends upon the self-consistent geometry, not on a particular mechanism distribution of molecular and/ or biophysical forces that cause the specific shape to be present.

Since each loop of a α-helix results in a net dipole in the Z-axis, the helix can function as a capacitor/battery. Again, the ground state capacitance at the center of a loop [or a number of loops] of a helix will have zero charge at its center. The capacitance of charge in helix is accessible measurement from Z– to Z+. The longer the distance between Z– and Z+, the larger it’s potential and capacitance.

Structurally at the same site, an agonist or an antagonist can bind perpendicular to an ion channel membrane helix. Four discretely different outcomes are possible: 1) binding could re-assign zero the electrical potential along the Z-axis from the center of the helix to this binding site; 2) binding could lower the electrical potential of the helix [an antagonistic effect]; 3) binding could raise/add to the electrical potential of the helix [an agonistic effect]; or 4) binding is effectively irrelevant to membrane structure.

At the molecular level, binding could also alter the shape of the helix. The radius, pitch, and/or phase could increase or decrease [or neither] on binding to agonists/antagonists. These effects would be in addition to, not in place of, the interactions along the Z-axis.

4.2. Transmembrance Capacitance

The contribution of a-helical structures to membrane ion channel capacitance in terms molecular structure could be complicated to calculate, i.e. many possible variables could be parameterized. Ion channel can contain multiple non-identical helices. The atomic/molecular site at which individual helical sequences begin and end in a membrane is unknown. Even the estimation of the number of loops that exist in each intra-membrane peptide helix sequence is uncertain.

Yet, even in this case, rise over run around half the circumference of the ion channel could provide a reasonable estimate of the charge on a membrane channel for each loop of a helix. Each a-helix within a membrane carries a considerable dipole moment, the effect of which can be approximated by placing 0.5 - 0.7 positive unit charge near the N-terminus and 0.5 - 0.7 negative unit charge near the C-terminus of the helix [11,12]. Each helix is comprised of five (or six) loops. This corresponds to ±1.0 - 1.4 eV difference for the membrane.

The dipolar forces in each anti-parallel pair of helices in a transmembrane ion channel are opposite in directions and can be assumed to be similar in magniture. The net charge on the membrane in the Z+ direction corresponds to the charge on the single (unpaired) helix in the membrane. This magnitude of this rise over run [i.e. the circumference of the transmembrane helix] could explain the the transmembrane ion potentential.

The diameter of the ion channel is about 70 Å, so πr = 110 Å. The pitch in each half loop of a helix is 1/2 (5.4 Å) = 2.7 Å. This ratio is (2.7/110) = 0.0245 which corresponds to tan (1.41˚). Since sec (1.41˚) = 1.00030, the rise along the circumference is 3.0 × 10⁻⁴ longer than with pitch = 0. The energy for l = (2πr) = 220 Å = 22 nm corresponds to about 400eV [17]. The increase in energy from the longer pathway along the α-helix is 400 eV × 3.0 × 10⁻⁴ = 0.12 eV per each half loop of an α-helix. As there are twelve half loops per six full loops, the membrane potential calculated purely from the pitch length increase is ±1.4 eV. Again at the middle of the membrane potential will be zero eV.

The observed membrane potential of β-adrenergic transmembrane ion channel can be estimate ed from only three variables of 1) circumference of the channel, 2) pitch above the circumference due to peptide structure per half loop, and 3) number of half loops/channel. Channels with five helical chains and containing the same peptide sequence would have a higher electrical potential both because the circumference is smaller and because [assuming the same rise] the denominator run in the ratio rise/run is shorter.

One intriguing implication of this model is that electrochemical potential is stored in chemical structure along one edge of ion channel [one of the helical peptide sequences], and not at the center of the channel. Just as interestingly, this model suggest in each loop of a peptide helix, the largest dipolar moment difference occur along one edge of the helix [where it starts and/to where it ends]; the opposite edge of the same helix would have zero dipolar moment difference in the same direction.

A model of a transmembrane ion is that the α-helical peptide chains are ordered regularly within the space of [and also oriented perpendicular to] a lipid cellular membrane. The a-helix is a known structural component in other peptides [18-20] in which at specific atomic sites protein folding beginning and ending an α-helix must be occurring. Graphics modeling techniques that generate peptide structures smaller than one loop of α-helix could predict where one loop [or n loops] begins/ends in more complicated protein macromolecular structures.

5. CONCLUSION

A model of a peptide helix as having a pitch in units of height (h) is fundamentally incorrect because pitch is not a constant, but a dimensionless ratio. The denominator in this ratio needs to be in the same units as h. Examples of a denominator are: r (radius), 2r = d (diameter) or pd (circumference). Pitch along circumference more closely fits the empirical data. A series of atomic coordinates corresponding to those of the same atom type are routinely present in the plane of the circumference, whereas very rarely will two atoms of the same atom type show up in the plane of a radius/diameter.

The size of a pixel sets a limit on the size things that can be detected in a graphic image. Similarly, the accuracy of the model with a “pixel size” of one peptide preclude precision in knowing the chemical structure of the 0.6 fraction in the 3.6 residues required to form one loop of an α-helix: the helix is the identical shape if the 0.6 residue is at the beginning or the end of peptide sequence (or even divided into partially at each end). Intrinsic to this “only single loops” model of a helix is that the discrete loops of a helix always end where there is no molecular structure [and correspondingly limited physical data correlating with actual molecular structure]. In contrast, 3.6 residues equal eleven atoms and eleven atoms equal one loop of an a-helix: and the length of eleven atoms in a peptide backbone helix is a physical measurement. With a “pixel size” as one atom, three sets of eleven atoms will have the same size/length and each has a structurally different sequence:

1) C-N-C*-C-N-C*-C-N-C*-C-N2) N-C*-C-N-C*-C-N-C*-C-N-C*3) C*-C-N-C*-C-N-C*-C-N-C*-CAtom sequence 1) has three chiral centers [C^*]; 2) has three amide nitrogens [N]; 3) has three carbonyl groups [C=O]. The length of the same eleven unit sequence along a cylindrical surface compared to the corresponding length along a circular circumference will on average be a constant as long as the helical shape is a constant. When all lengths happen to be equal, each of these sequences equally describes the same helical shape. When two or more of the lengths happen to be unequal, the same pattern repeats for every loop of a helix. One of the patterns could be more precisely/accurately reflect experimental data.

Identifying the site at which significant variance from the pattern that forms a particular a-helical shape enables assigning where the pattern begins/ends. A less precise model limits this assignment to a specific amino acid residue. In this proposed model, an α-helix can start and end at any peptide backbone atom as long as the pattern repeats every 360˚. Wavefront Topology System and Finite Element Method are algorithms that can be used to generate a helical shape at any angle or pitch or to calculate the parameters that of the radius, diameter, circumference and the rise/run ratio of pitch that best fit a data set. Data to calculate these constants does not require a full loop of an α-helix.

The b₂-adrenergic agonist requires only a fraction of the α-helix contained in the peptide backbone to have the specificity and selectivity required in its binding site. Interestingly [unless the structure is a double helix], on generating a helix in this model, the second half retains its empty mass. No information about the second [empty] half is required to generate the entire helix. The size and shape of each β-adrenergic agonist at the molecular level is comparable to the size and shape of this empty space.

In the cylinder model of an α-helix, a beginning half cycle and an ending half cycle can be added to a rigid cylinder of any possible height. In a cylinder, the height is always independent of the circumference.

Symmetry in a double helix would predict that dipolar forces composed a helix on the surface of a cylinder would average out to zero. The dipolar forces in a single helix do not need to equal zero.

In this more precise model, the height of a helix is never independent of its circumference. This model of structure and properties in any α-helix is built from steps smaller than one loop of a helix. In ordered structures smaller than one loop of a helix, resulting dipolar forces remain ordered within the loop. Repeating the half-loops of an α-helix, the molecular order and dipolar forces remain cumulative.

6. ACKNOWLEDGEMENTS

The authors acknowledge research funding from the European Union through the STEPS FP6 project (contract number FP6-500465) and also the partners in the STEPS project for their input. M. A. Tyndyk acknowledges funding from the Irish Research Council for Science, Engineering and Technology (IRCSET) through a Postdoctoral Fellowship. The authors acknowledge support from the Programme for Research in Third Level Institutions (PRTLI) administered by the Higher Education Authority.

REFERENCES