Wireless Engineering and Technology
Vol.3 No.4(2012), Article ID:24189,4 pages DOI:10.4236/wet.2012.34031
Performance of GA and PSO Aided SDMA/OFDM Over-Loaded System in a Near-Realistic Fading Environment
![]()
Department of Electronics and Communication Engineering, National Institute of Technology Calicut, Kozhikode, India.
Email: shahnaznitc@gmail.com, cka@nitc.ac.in
Received July 20th, 2012; revised August 18th, 2012; accepted August 29th, 2012
Keywords: Space Division Multiple Access (SDMA); Orthogonal Frequency Division Multiplexing (OFDM); GA; PSO; TGn Channel Model
ABSTRACT
In this work, two popular evolutionary algorithms such as genetic algorithm (GA) and particle swarm optimization (PSO) based SDMA-OFDM multi user detection (MUD) have been presented which overcome the limitations of classical detectors. They are simple to implement and their complexity in terms of decision-metric evaluations is very less compared to maximum likelihood detection (MLD). These techniques are shown to provide a high performance as compared to the other detectors especially in a rank-deficient scenario where numbers of users are high as compared to the base station (BS) antennas. In this scenario, Zero forcing (ZF) and minimum mean square error (MMSE) based MUDs exhibit severe performance degradation. To investigate almost realistic performance of a wireless communication system, it is important to use a proper channel model. Since the simulation parameters in this work are based on IEEE 802.11n wireless local area network (WLAN) standard, TGn is the channel model used.
1. Introduction
Orthogonal frequency division multiplexing (OFDM), which is the fundamental unit of all multi-carrier communication systems, has been receiving wide interest especially for high data-rate broadcast applications because of its robustness in frequency selective fading channel. The employment of multiple antennas at both the transmitter and the receiver, which is widely referred to as MIMO technique, constitutes a cost-effective approach to high-throughput wireless communications [1- 3].
SDMA based techniques as a subclass of MIMO systems, is one of the most promising techniques for solving the limitation of wireless communication systems. SDMA enables multiple users to simultaneously share the same bandwidth in different geographical locations. The exploitation of the spatial dimension makes it possible to identify the individual users, even when they are in the same time/frequency/code domains, thus increasing the system’s capacity [1,4]. Detection techniques especially in over-loaded situation pose many challenging issues. The higher the number of users to be supported, the more challenging the optimization task becomes, due to the exponentially increased number of dimensions to be estimated.
Most classic detection techniques suffer from specific limitations in rank-deficient scenarios. Suboptimal nonlinear MUDs based on successive interference cancellation (SIC) or parallel interference cancellation (PIC) techniques can also be used, but are prone to error propagation [1,5,6]. The family of GAs can be efficiently incorporated into SDMA-OFDM systems and thus solve many challenging issues. In literature, GA based technique with better convergence properties and lower computational complexities are discussed in detail. Possibility of applying optimization techniques other than GA led to the implementation of latest and robust stochastic PSO algorithm.
TGn is widely used channel for IEEE 802.11n wireless local area network (WLAN) standard, and is designed for indoor networks for bandwidths of up to 100 MHz, at frequencies of 2 and 5 GHz. Using TGn channel model, the actual performance in a high dispersive environment has been obtained. The proposed work has prime importance these days because the combination of SDMA and OFDM, with advantages of both, has emerged as a promising solution for future high data-rate wireless communication systems.
2. System Overview
2.1. SDMA System
In SDMA uplink MIMO channel model, U simultaneous mobile users employ one antenna each for the transmission, while the base station (BS) receiver has A antennas (Figure 1). At the kth subcarrier of the nth OFDM symbol received by the A element BS antenna array, we have the received complex signal vector y[n, k] which is constituted by the superposition of the independently faded signals associated with the U mobile users and contaminated by AWGN, expressed as
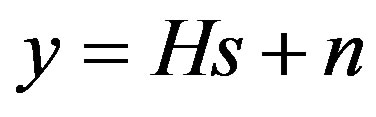 (1)
(1)
where the (Ax1) dimensional vector y, the (Ux1) dimensional vector s and the (Ax1) dimensional vector n are the received, transmitted and noise signals, respectively. The indices [n, k] have been omitted for notational convenience.
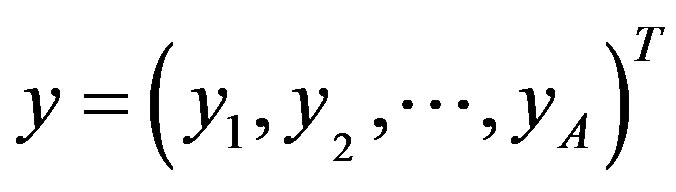

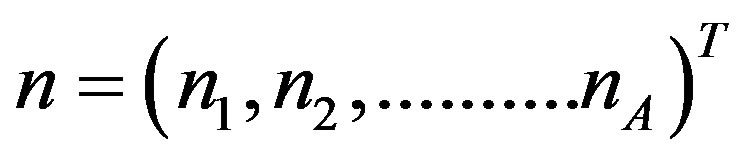
The (A × U) dimensional matrix H, which contains the frequency domain channel transfer functions (FD-CHTF) of the U users, is given by
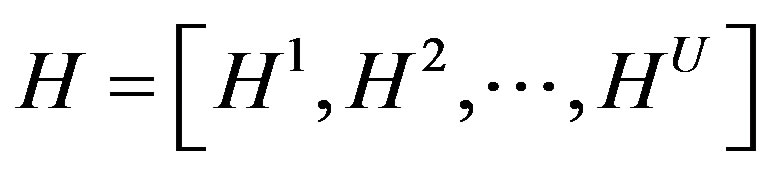
where  is the vector of the FD-CHTFs associated with transmission paths from uth user’s transmit antenna to each element of the A-element receiver antenna array which can be expressed as
is the vector of the FD-CHTFs associated with transmission paths from uth user’s transmit antenna to each element of the A-element receiver antenna array which can be expressed as
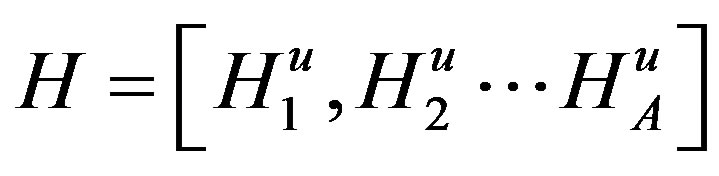
The FD-CHTFs, 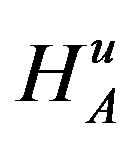 of the different users are assumed independent, stationary, complex Gaussian distributed processes with zero-mean and unit-variance.
of the different users are assumed independent, stationary, complex Gaussian distributed processes with zero-mean and unit-variance.

Figure 1. Schematic of the SDMA uplink model.
![]() In the MMSE-based MUD, the estimated signal vector
In the MMSE-based MUD, the estimated signal vector 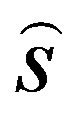 generated from the transmitted signal s of the U simultaneous users, obtained by linearly combining the signals received by the A different receiver antenna elements with the aid of the array weight matrix, is given by
generated from the transmitted signal s of the U simultaneous users, obtained by linearly combining the signals received by the A different receiver antenna elements with the aid of the array weight matrix, is given by
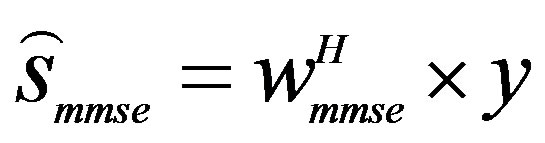 (2)
(2)
where y is the received signal vector and  is the weight matrix given by
is the weight matrix given by
 (3)
(3)
Here, I is the identity matrix and  is the AWGN noise variance. A block schematic of the MIMO-OFDM transceiver is shown in Figure 2. At the transmitter end, the trellis coded signals of U users
is the AWGN noise variance. A block schematic of the MIMO-OFDM transceiver is shown in Figure 2. At the transmitter end, the trellis coded signals of U users 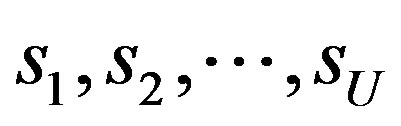 are applied to the IFFT-based OFDM modulators, followed by their transmission over the SDMA user specific Mobile Stations (MSs). At the Base Station BS, FFT-based OFDM demodulation is done at each element of the receiver antenna array. The demodulated outputs
are applied to the IFFT-based OFDM modulators, followed by their transmission over the SDMA user specific Mobile Stations (MSs). At the Base Station BS, FFT-based OFDM demodulation is done at each element of the receiver antenna array. The demodulated outputs 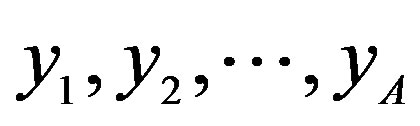 are then forwarded to the concatenated MMSE-GA MUD for separating the different users’ signals, followed by the independent FEC decoders.
are then forwarded to the concatenated MMSE-GA MUD for separating the different users’ signals, followed by the independent FEC decoders.
2.2. Optimization Metric for the GA and PSO Based MUD
The optimum ML-MUD uses an exhaustive search, which requires 2mU evaluations of the decision metric for finding the most likely transmitted U user symbol vector 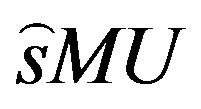
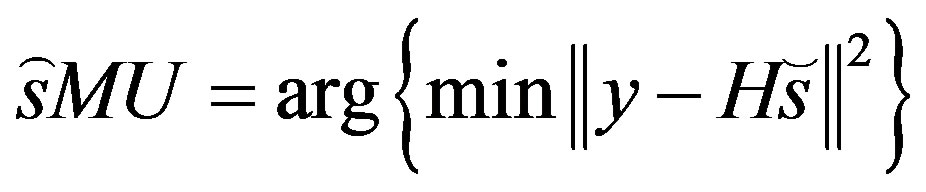 (4)
(4)
where, ∈ MU and the set of MU number of trial vectors are elements of MC that denotes the set containing the 2m number oflegitimate complex constellation points associated with the specific modulation scheme employed, while m denotes the number of bits per symbol. The optimum ML-based decision metric of Equation (4)
∈ MU and the set of MU number of trial vectors are elements of MC that denotes the set containing the 2m number oflegitimate complex constellation points associated with the specific modulation scheme employed, while m denotes the number of bits per symbol. The optimum ML-based decision metric of Equation (4)
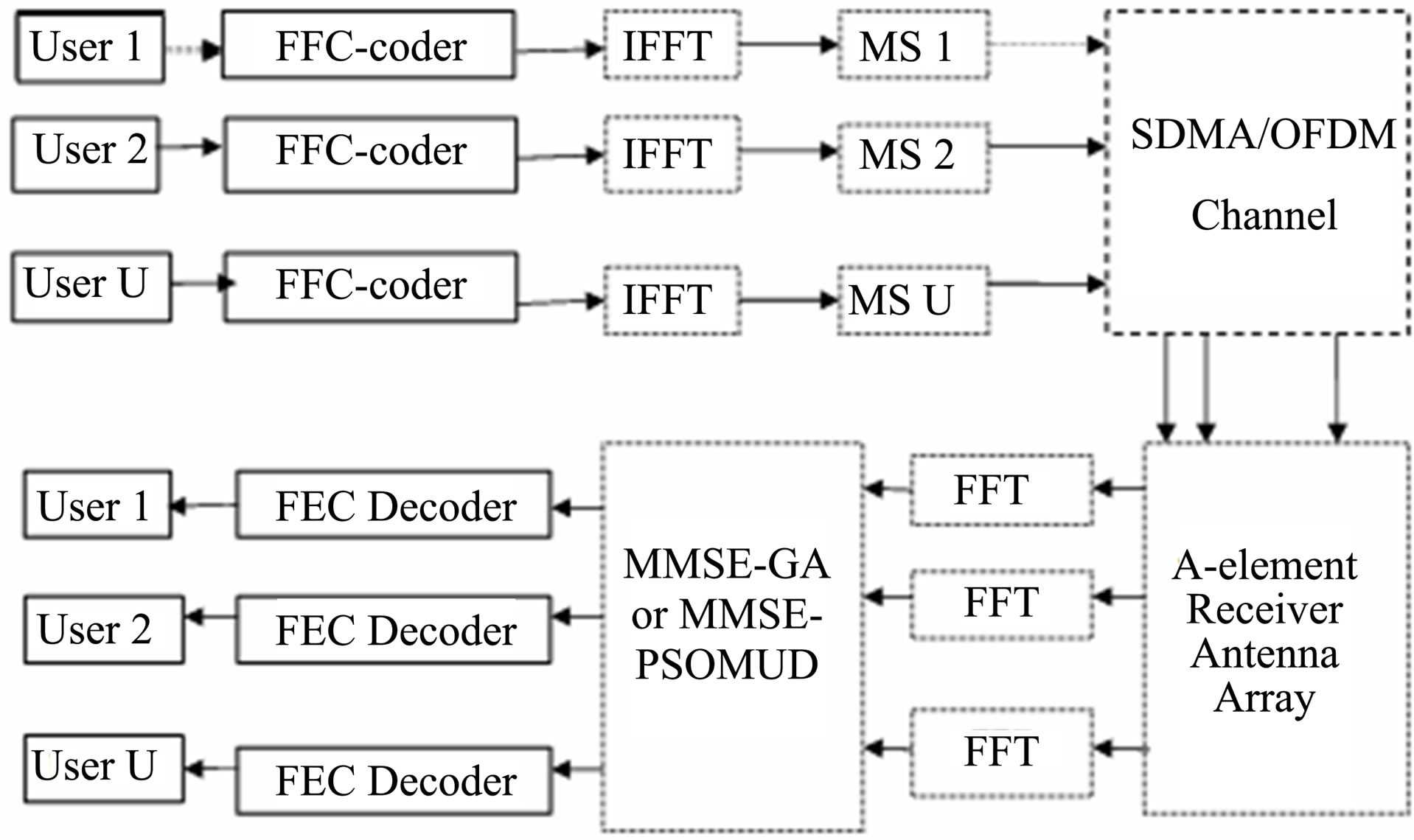
Figure 2. Schematic of the MMSE-GA or MMSE-PSO concatenated, multiuser detected SDMA-OFDM uplink system.
may also be used in the GA-MUD for the sake of detecting the estimated transmitted symbol vector  where the decision metric required for the ath receiver antenna, namely the antenna-specific objective function is defined by
where the decision metric required for the ath receiver antenna, namely the antenna-specific objective function is defined by
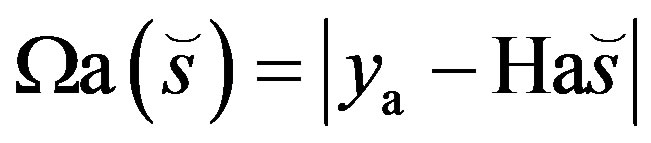 (5)
(5)
where ya is the received symbol at the input of the ath receiver at a specific OFDM subcarrier, while Ha is the ath row of the channel transfer function matrix H. The estimated transmitted symbol vector of the U users based on the knowledge of the received signal at the ath receiver antenna and a specific subcarrier is given by
 (6)
(6)
Since the Channel Impulse Responses (CIRs) of each of the A antennas are statistically independent, the U symbol vector that is considered optimum at antenna 1 may not be considered optimum at antenna 2. This implies that a decision conflict is encountered, which may be expressed as
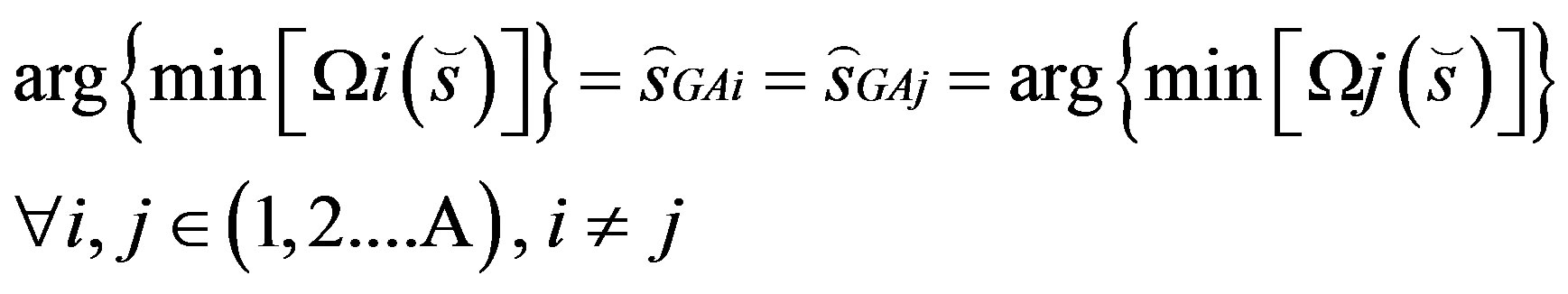 (7)
(7)
This decision conflict therefore leads to a so-called multi-objective optimization problem, since the optimization of the metrics may result in more than one possible U symbol solutions. In order to resolve this problem, we may combine the A number of antenna-specific U symbol metrics into a “joint” metric as follows
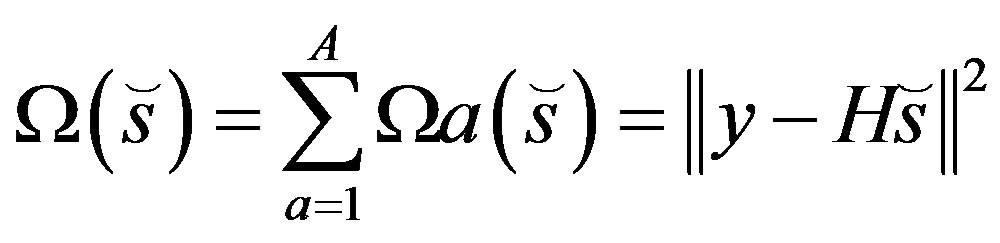 (8)
(8)
which is also called as the Objective Function of (OF) of GA.
2.3. TGn Channel Model
The IEEE 802.11n channel models are designed for indoor WLAN for bandwidths of up to 100 MHz, at frequencies of 2 and 5 GHz. The channel models comprise a set of 6 profiles, labeled A to F, which cover the scenarios of flat fading, residential, residential/small office, typical office, large office, and large space (indoors and outdoors) [7].
Each channel model has a path loss model including shadowing, and a MIMO multipath fading model, which describes the multipath delay profile, the spatial properties, the K-factor distribution, and the Doppler spectrum. Each channel model has a certain number of taps (one for model A, and 9 to 18 for models B-F). Each tap is characterized by a relative delay (with respect to the first path delay). Each model further comprises a number of clusters, which correspond to overlapping subsets of the tap delays. Each cluster is assigned a set of spatial properties like a mean angle of arrival (AoA), a mean angle of departure (AoD), an angular spread (AS) at the receiver, and an angular spread at the transmitter. These parameters assume the same values for all tap delays pertaining to a given cluster [7]. Refer to Figure 3. These parameters determine the transmit and receive correlation matrices associated with each tap delay.
3. Proposed MUD Methods
Optimization is the process of making something better. It consists of trying variations on an initial solution and using the information gained to improve the idea. Searching the cost surface (all possible function values) for the minimum cost lies at the heart of all optimization routines. The traditional methods have been tuned to quickly find the solution of a well behaved convex analytical function of only a few variables. For such cases calculus-based methods outperform the GA and PSO for quickly finding the minimum while the others are still analyzing the costs of the initial population. Also, movement from one variable set to another is based on some determinant sequence of steps. For these problems the optimizer should use the experience of the past and employ these quick methods. However, many realistic problems do not fall into this category. Evolutionary algorithms are more advantageous when there are large numbers of variables. In rank-deficient multi-user MIMOOFDM systems, the channel’s output phasor constellation often becomes linearly non separable. As a result, multiuser detection becomes a challenging multidimensional optimization problem. Higher the number of users to be supported, more challenging the optimization task becomes.
GA and PSO perform better than any other methods in this case. They have found numerous applications in wireless communication in recent years. They are based on evolutionary computing method as they generate new points in the search space by applying operators to current points and statistically moving toward more optimal
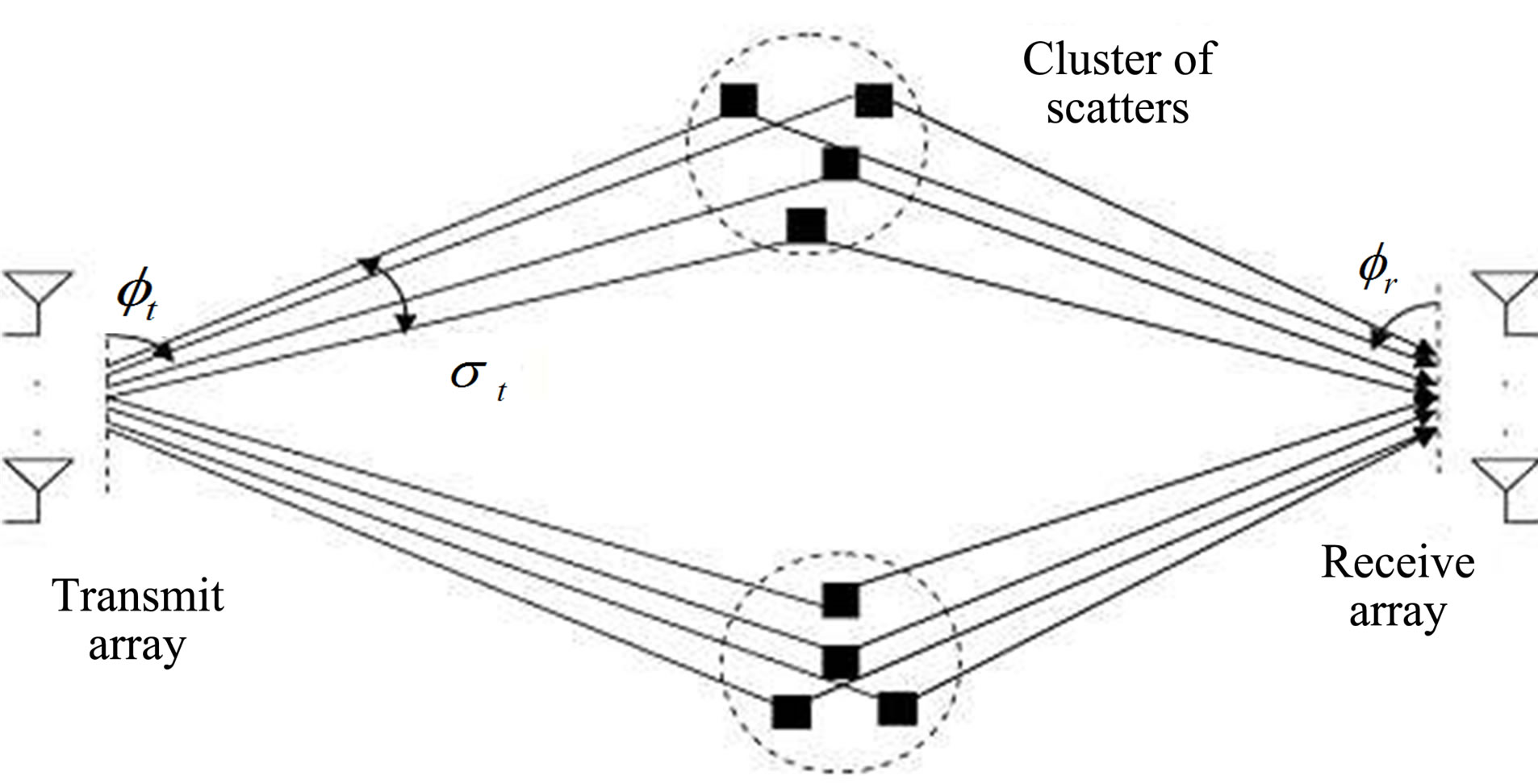
Figure 3. Cluster based channel model.
places in the search space. They rely on an intelligent search of a large but finite solution space using statistical methods. The algorithms do not require taking cost function derivatives and can thus deal with discrete variables and cost functions which are not continuous.
3.1. GA-Assisted SDMA-OFDM-MUD
The GA is an optimization and search technique based on the principles of genetics and natural selection [8]. They are part of evolutionary computing which is a rapidly growing area of artificial intelligence. Optimization is based on idea that evolution represents search for optimum solution set. A GA allows a population composed of many individuals to evolve under specified selection rules to a state that minimizes the cost function and thus maximizes the fitness.
In order to avoid an inefficient, entirely random search, GA-MUD uses a good initial guess of the estimated transmitted U symbol vectors to be detected. In SDMAOFDM system, GA commences its search for the optimum U symbol solution at the initial generation with the aid of the MMSE combiner [1]. Using GA, individuals of the g = 0th generation having a population size of X are created from the estimated length U transmitted symbol vector provided by the MMSE combiner, where the ith individual is expressed as

and 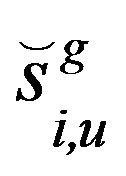 ϵ MC. G is the maximum generation index. The GA-based optimization selects some of the U symbol candidates from a total of X legitimate individuals in order to create a mating pool of T number of U symbol individuals. Two U symbol parent vectors are then combined using specific GA operations for the sake of creating another two U symbol offspring and this genetic evolution-like process of generating new U symbol offspring continues over G number of consecutive generations, so that the optimum symbol solution may be found. The selection of individuals for creating the mating pool containing T number of symbol parents is vital in determining the GA’s achievable performance. The mth U symbol individual is considered to be dominated by the nth individual, if the cost function calculated for mth individual is minimum compared to nth individual.
ϵ MC. G is the maximum generation index. The GA-based optimization selects some of the U symbol candidates from a total of X legitimate individuals in order to create a mating pool of T number of U symbol individuals. Two U symbol parent vectors are then combined using specific GA operations for the sake of creating another two U symbol offspring and this genetic evolution-like process of generating new U symbol offspring continues over G number of consecutive generations, so that the optimum symbol solution may be found. The selection of individuals for creating the mating pool containing T number of symbol parents is vital in determining the GA’s achievable performance. The mth U symbol individual is considered to be dominated by the nth individual, if the cost function calculated for mth individual is minimum compared to nth individual.
The selection process follows the strategy of Pareto Optimality. Two individuals in the mating pool are then selected as parents, based on their corresponding fitness values according to the fitness-proportionate selection scheme.
The selection of U symbol parents from the mating pool is repeated, which is followed by the uniform crossover, mutation and elitism operations, until a new population of offspring is created. Finally, the GA terminates after G-1 number of generations and thus the U symbol individual having the highest diversity-based fitness value will be considered as the detected U user transmitted symbol vector corresponding to the specific OFDM subcarrier considered.
3.2. PSO-Assisted SDMA-OFDM-MUD
Particle swarm optimization is a robust stochastic optimization technique based on the movement and intelligence of swarms [9]. It is similar to the continuous GA in that it begins with a random population matrix. But unlike the GA, PSO has no evolution operators such as crossover and mutation. The rows in the matrix are called particles (same as the GA chromosome). PSO applies the concept of social interaction to problem solving using a number of agents (particles) that constitute a swarm moving around in the search space looking for the best solution. It is inspired from underlying rules that enabled large numbers of birds to flock synchronously, often changing direction suddenly, scattering and regrouping. This model relied heavily on manipulation of inter-individual distances; that is, the synchrony of flocking behavior was thought to be a function of birds' efforts to maintain an optimum distance between themselves and their neighbors. Another motive for developing the simulation was to model human social behavior, which is of course not identical to fish schooling or bird flocking. One important difference is its abstractness. Birds and fish adjust their physical movement to avoid predators, seek food and mates, optimize environmental parameters such as temperature, etc. Humans adjust not only physical movement but cognitive or experiential variables as well.
As in the case of GA, output of MMSE is used to generate the initial population with random positions and velocities in the initialization block. The current searching point of each agent is set to pbest. The best evaluated value of pbest is set to gbest and agent number with best value is stored. Equation (8) is used as objective function and its value is calculated by each agent. If this value is less than the current pbest of the agent, the pbest is replaced by the current value. If the best value of pbest is less than the current gbest, the gbest is replaced by the best value and the agent number with its value is stored. The current searching point of each agent is changed using Equations (10) and (11). This process will continue until the termination criterion is finally met. The values of φ is taken as 0.7 and ∝1 and ∝2 are taken as 1.47.
The detection algorithm can be summarized as follows
1) Take the output of MMSE-MUD as initial particles (initial solution bit string) instead of selecting randomly from the solution space.
2) The algorithm parameters are initialized. Vi is initialized to zero and pbest and gbest are also initialized.
3) Evaluate the fitness of each particle
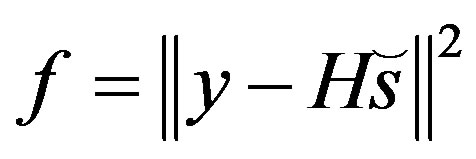
where 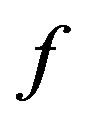 is same as Equation (8).
is same as Equation (8).
4) Find pbest and gbest.
5) Update velocity and position according to the following equations
 (9)
(9)
 (10)
(10)
4. Results and Discussion
4.1. Simulation Parameters
SDMA-OFDM system with 64 subcarriers and CP of 16 samples is considered for studying the BER Vs SNR performance in various scenarios. Band width considered is 20 MHz. Channel incorporates both AWGN and multipath Rayleigh fading. TGn channel model has been used as explained earlier. Both BPSK and QPSK modulation schemes were used alternatively. Ideal synchronization is assumed between the transmitter and the receiver. Trellis Coding (TC) has been used as FEC scheme for all simulations. Coding improves the performance very much.
4.2. Performance Evaluation of GA and PSO Based MUD
4.2.1. BER Performance under Fully-Loaded Scenario (U = 6, A = 6)
As a first step, BER performance of MUD using GA has been compared with MMSE and ML Detection under fully loaded scenario (Figure 4). Since the output of MMSE is taken as initial value for GA, performance is better for MMSE-GA detection than just MMSE detection and an improvement of 1.5 dB has been obtained. Here simple multipath Rayleigh fading channel has been considered.
It is clear from the plots that both outperform 6 × 6 MMSE and has an improvement of 2.2 dB at BER 10–3. When complexity and convergence of both optimization techniques are compared (Figure 5), it can be seen that PSO outperforms GA.(Table 1) That is metric evaluations required for GA; X × Y = 400 is more than that of PSO; swarm size = 40, no:of iterations = 5, so 40 × 5 = 200. The reason for reduction in complexity of PSO is that it does not require operations like mutation and crossover. PSO converges faster than GA since it attains a minimum cost with less no: of iterations as compared to GA. It is clear from Figure 6.
4.2.2. Performance Comparison under Over-Loaded Scenario (U = 8, A = 6)
Both techniques use output of 6 × 6 MMSE as initial
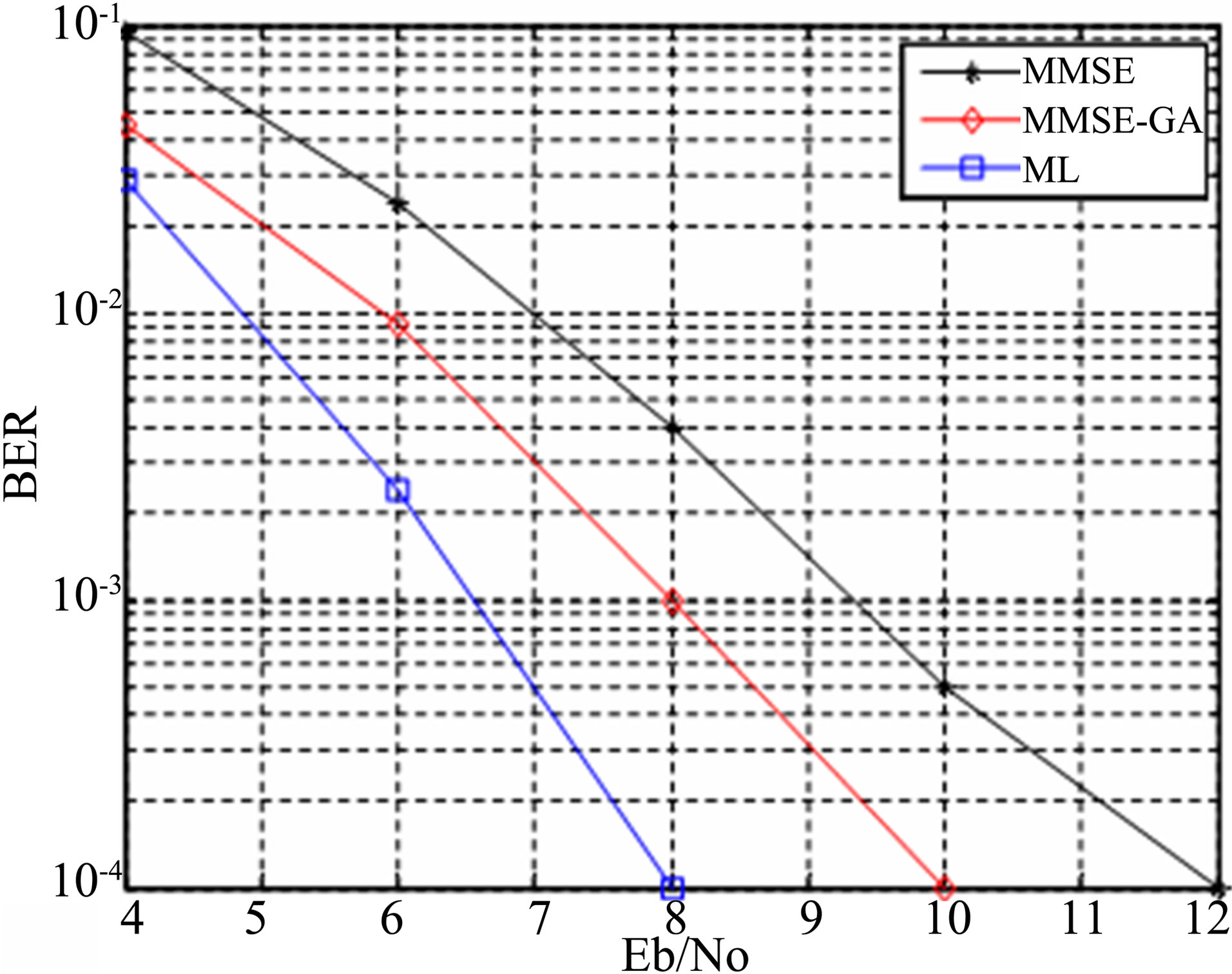
Figure 4. BER vs SNR graph of 2 × 2 QPSK multi-user MIMO-OFDM with genetic algorithm.
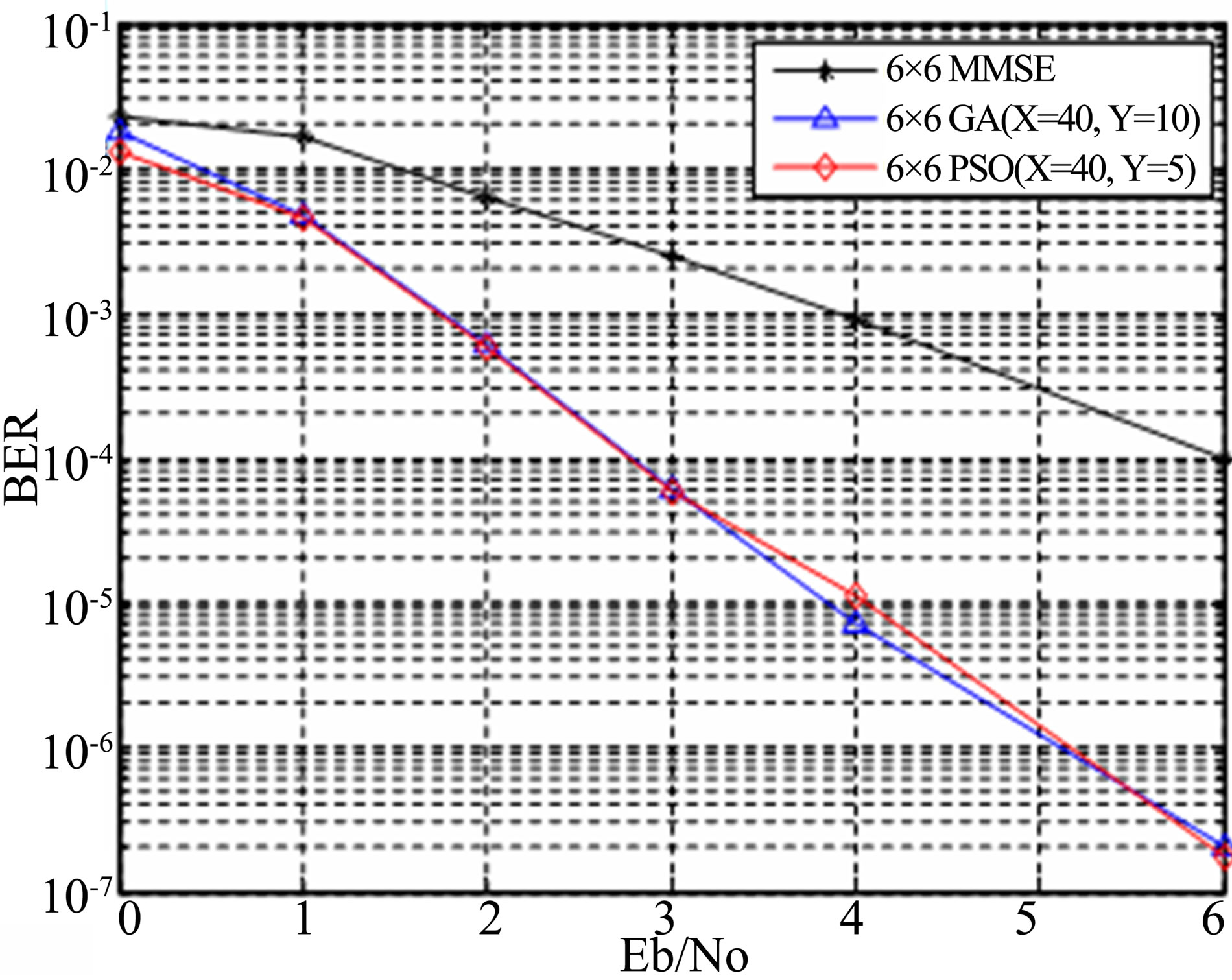
Figure 5. Performance comparison of GA and PSO in SDMA-OFDM-MUD when L = 8 and P = 6.

Table 1. GA parameters.
values. X = 50 and Y = 5 for both cases. For same parameters, PSO has about 0.4 dB performance improvement over GA due to less complexity and fast convergence compared to GA. The complexity is quantified here in terms of the maximal number of OF evaluations required by the ML, GA and PSO detection. In the overloaded scenario, for example, the corresponding complexity of the ML detection is M = 22 × 8 = 65,536 OF evaluations, while that of the GA or PSO aided detection is only X × Y = 500 × 5 = 2500 OF evaluations. A generalized plot based on numerical analysis for both GA and PSO MUD compared to ML MUD has been shown in Figure 7. For ML, complexity in terms of metric evaluations increases exponentially as number of users increases. Complexity of GA/PSO aided MUD required for maintaining a nearoptimum performance increases only slowly. From Figure 8 it is clear that the performance of MMSE-MUD is highly degraded as compared to GA and PSO aided MUDs. The channel parameters are as given in the Table 2.
In [1], authors use a different FEC scheme (TTCM) and so the performance is somewhat improved but with some increase in the over head. In our paper, much simpler FEC scheme has been used and more focus is given
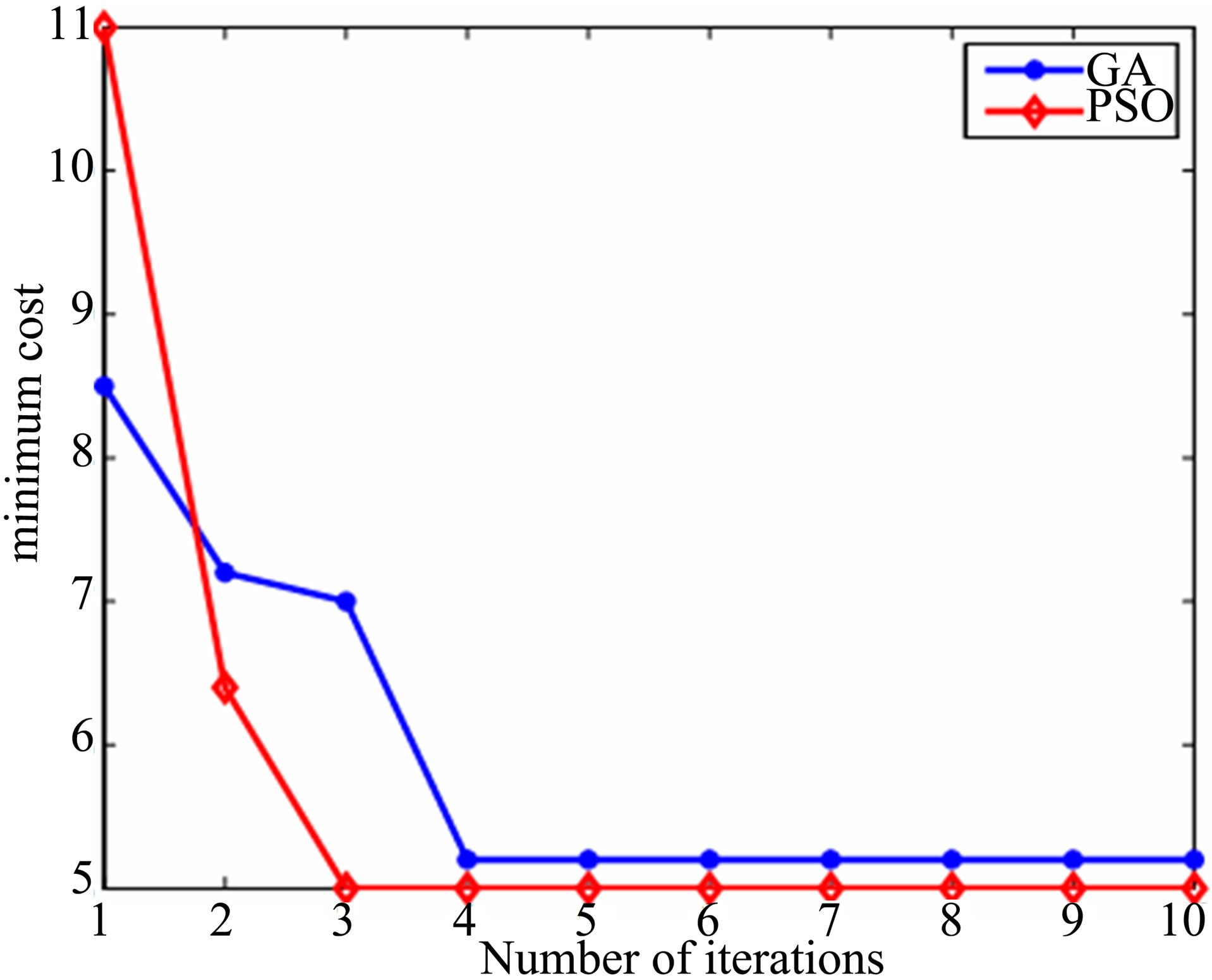
Figure 6. Convergence graphs of GA and PSO.
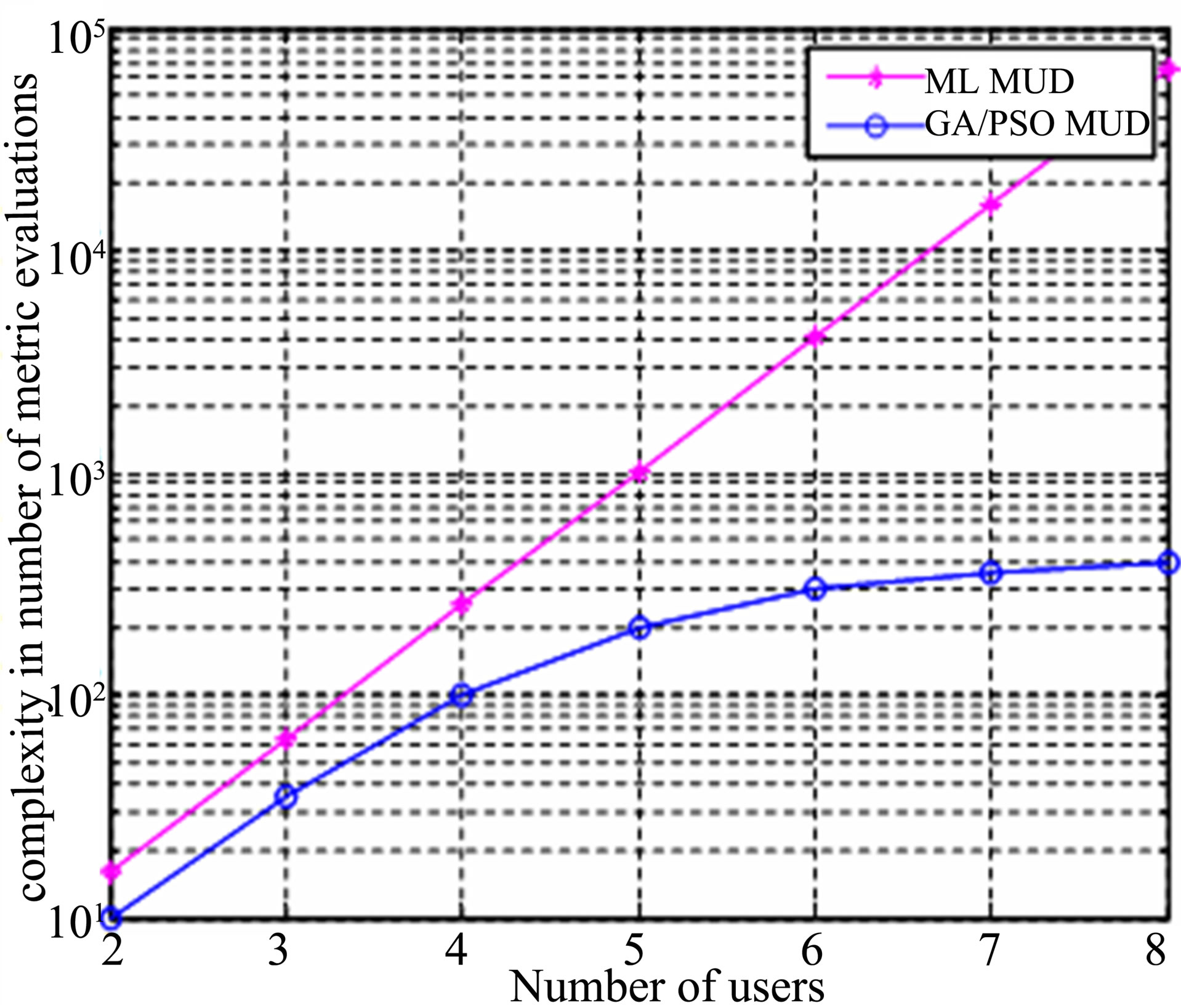
Figure 7. Complexity comparison in terms of number of OF evaluations.
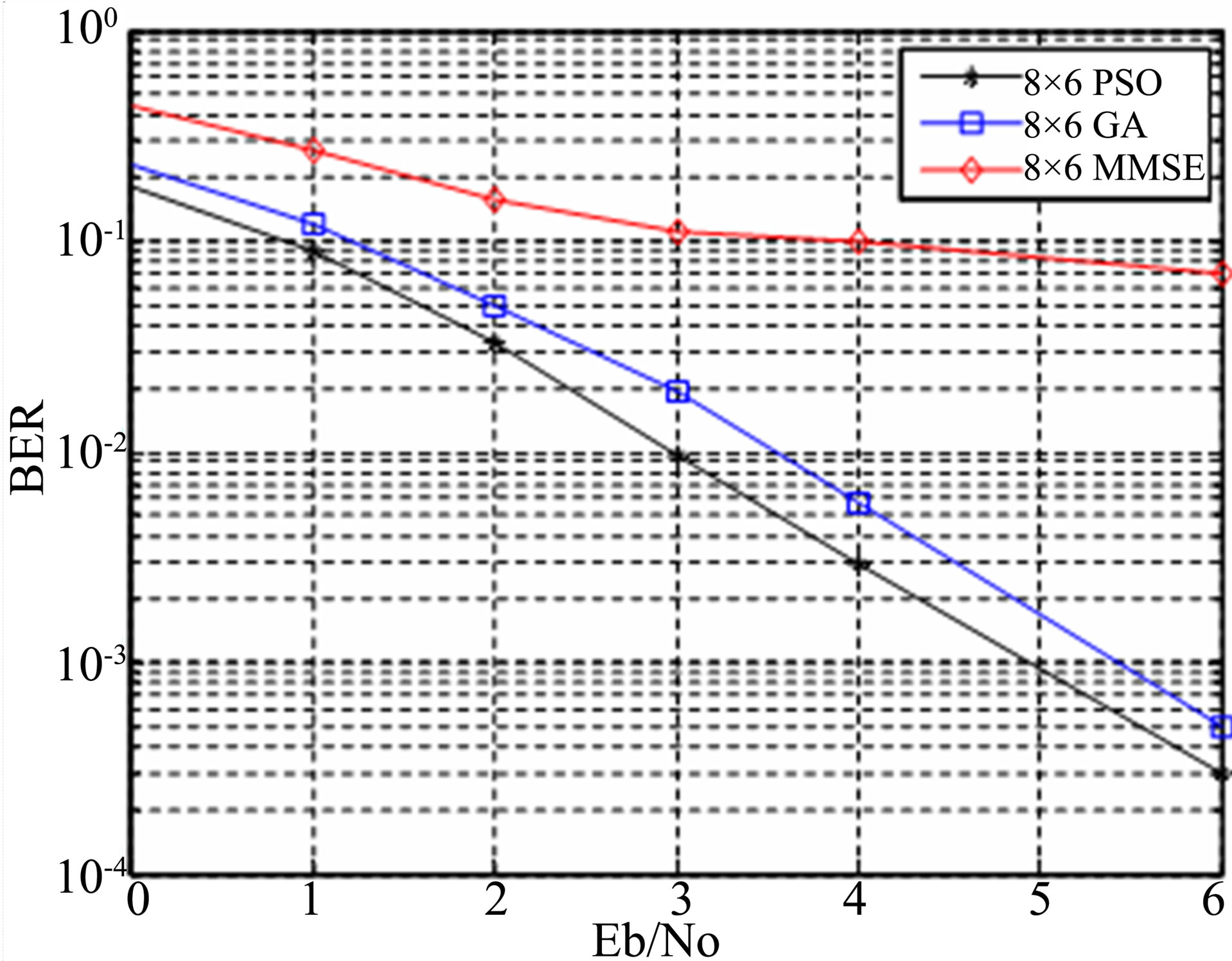
Figure 8. Performance comparison of both GA and PSO in SDMA-OFDM-MUD when L = 8 and P = 6.

Table 2. TGn simulation parameters.
to the newer optimization technique PSO which gives a marginal improvement over GA with reduced complexity. Similar works using latest optimization techniques and their comparative analysis are going on parallely in different scenarios based on MIMO-OFDM [2,10].
5. Conclusion
From the simulations conducted, it can be concluded that GA and PSO based SDMA-OFDM MUD, performs far better than conventional detection methods like ZF and MMSE and nears the performance of ML detection in a fully-loaded scenario. It became apparent that the high degradation in the performance of conventional methods during over-loaded scenario when number of users exceed number of receivers can be effectively solved using these evolutionary algorithm based MUDs. Using TGn channel model the actual performance in a high dispersive environment has been obtained. The associated complexity of the proposed GA and PSO aided detection is significantly lower than that of the ML detection. Both are very simple to implement and use MMSE-MUD output as their initial values. Among GA and PSO, latter displayed a marginal improvement over the other.
REFERENCES
- M. Jiang and L. Hanzo, “Multiuser MIMO-OFDM for Next-Generation Wireless Systems,” Proceedings of the IEEE, Vol. 95, No. 7, 2007, pp. 1430-1468.
- L. Hanzo, Y. Akhtman, L. Wang and M. Jiang, “MIMOOFDM for LTE, WiFi and WiMAX,” John Wiley & Sons, Hoboken, 2011.
- R. Prasad, “OFDM for Wireless Communications Systems,” Artech House Publishers, London, 2004.
- P. Vandenameele, “A Combined OFDM/SDMA Approach,” IEEE Journal on Selected Areas in Communications, Vol. 18, No. 11, 2000, pp. 795-825. doi:10.1109/49.895036
- P. A. Haris, E. Gopinathan and C. K. Ali., “Blind Successive Interference Cancellation for Multi-Carrier CDMA Systems in Indoor Wireless Networks,” WSEAS Transactions on Communications, Vol. 8, 2009, pp. 1192-1203.
- L. Hanzo, M. Munster, B. J. Choi and T. Keller, “OFDM and MC-CDMA for Broadband Multi-User Communications WLANs and Broadcasting,” IEEE Press/Wiley, Piscataway, 2003. doi:10.1002/9780470861813
- V. Erceg et al., “IEEE 802.11 Wireless LANs: TGn Channel Models,” 2004.
- R. L. Haupt and S. E. Haupt, “Practical Genetic Algorithms,” John Wiley and Sons, New York, 2004.
- J. Kennedy and R. C. Eberhart, “Particle Swarm Optimization,” Proceedings of International Conference on Neural Networks, Perth, 27 November-1 December 1995, pp. 1942- 1948.
- B. K. Praveen and S. Das, “Neural Network Based Multiuser Detection Techniques in SDMA-OFDM System,” Proceedings of Annual IEEE India Conference, Hyderabad, 16-18 December 2011, pp. 1-4. doi:10.1109/INDCON.2011.6139436

