Smart Grid and Renewable Energy
Vol.1 No.2(2010), Article ID:2600,10 pages DOI:10.4236/sgre.2010.12014
Composite Cost Function Based Solution to the Unit Commitment Problem
![]()
Department of Electrical Engineering, Annamalai University, Annamalainagar, India.
Email: anand_r1979@yahoo.com
Received May 29th 2010; revised June 29th 2010; accepted July 3rd 2010.
Keywords: Composite Cost Function, Generation Scheduling, Unit Commitment
ABSTRACT
This paper presents a new approach via composite cost function to solve the unit commitment problem. The unit commitment problem involves determining the start-up and shut-down schedules for generating units to meet the forecasted demand at the minimum cost. The commitment schedule must satisfy the other constraints such as the generating limits, spinning reserve, minimum up and down time, ramp level and individual units. The proposed algorithm gives the committed units and economic load dispatch for each specific hour of operation. Numerical simulations were carried out using three cases: four-generator, seven-generator, and ten-generator thermal unit power systems over a 24 h period. The produced schedule was compared with several other methods, such as Dynamic programming, Branch and bound, Ant colony system, and traditional Tabu search. The result demonstrated the accuracy of the proposed method.
1. Introduction
Unit commitment is to determine the commitment and generation levels of generating units over a period of time to minimize the total operation cost [1]. In solving the unit commitment problem, generally two basic decisions are involved, namely, the “unit commitment” decision and the “economic dispatch” decision. The “unit commitment” decision involves the determination of the generating units to be running during each hour of the planning horizon, considering the system capacity requirements, including the system constraints. The “economic dispatch” decision involves the allocation of the system demand and spinning reserve capacity among the operating units during each specific hour of operation. The unit commitment problem has commonly been formulated as a non-linear, large scale, mixed-integer combinatorial optimization problem with constraints. Research endeavours, therefore, have been focused on efficient, near-optimal solutions. A survey of literature on unit commitment methods reveals that various numerical optimization techniques have been employed to address the unit commitment problems.
An interior-point/cutting-plane method for non differentiable optimization is used to solve unit commitment problem [2]. This method has two advantages of subgradient and bundle methods that have better convergence characteristics and does not suffer from the parameter-tunning drawback. A parallel repair genetic algorithm has been proposed to solve unit commitment problem [3]. This algorithm provides a modeling framework less restrictive than previous approaches such as dynamic programming or lagrangian relaxation.
A new cooperative coevolutionary algorithm has been described for unit commitment problem which combines the basic ideas of LR and GA to form a novel two-level approach [4]. A successive sub problem solving method is developed and applied to solve the unit commitment problems with identical units [5]. The commitments of the identical units can be differentiated and the homogenous oscillations are avoided. The unit commitment problem has been solved with dual variable constraints [6].
An evolutionary programming based Tabu search has been applied to solve unit commitment problem [7]. The security constrained unit commitment problem is decomposed into two coordinated problems, based on benders decomposition, which include a master problem for optimizing UC and a sub problem for minimizing network violations [8]. The price-based unit commitment problem has been solved based on mixed integer programming [9].
The fuzzy logic based UC scheduling using absolutely stochastic simulated annealing have been proposed in which they introduce the sign bit vector to reduce economic load dispatch calculations [10]. An ant colony system approach for unit commitment problem has been proposed [11]. The algorithm implements the movement of ants in the search space and also discusses the accuracy of the solution with respect to the solution time.
The mixed-integer linear formulation for the unit commitment of thermal units have been applied to solve this problem, this method requires fewer binary variables and constraints than previously reported models, yielding a significant computational saving [12]. The unit commitment problem has been solved by Simulated Annealing and they maintained spinning reserve capacity, resulting in near-optimal UC solutions [13].
A Tabu search based hybrid optimization approach for a fuzzy modeled unit commitment problem has been proposed [14]. A unit commitment problem with probabilistic spinning reserve and interruptible load has been formulated [15]. Recently Bacterial foraging technique has been applied to solve unit commitment problem [16].
The artificial intelligence approaches Genetic Algorithm (GA), Evolutionary Programming (EP), Simulated Annealing (SA), Tabu Search (TS) and Expert Systems (ES) have been proposed to solve the UC problem and these methods require high computational time for large scale systems. This article presents a composite cost function based solution algorithm for solving unit commitment problem and it directly gives the units to be committed and the economic dispatch of the committed units while satisfying the equality and inequality constraints.
2. Problem Formulation
2.1 Nomenclature
ai , bi , ci Fuel cost coefficients unit i
Shi – cost Hot start cost in Rs
Sci – cost Cold start cost in Rs
c–s–hour Cold start hour in hours
MUi Minimum up time in hours
MDi Minimum down time in hours
N Number of generating units
Pi max Maximum output power of unit i in MW
Pi min Minimum output power of unit i in MW
Pit Power produced by unit i in time t
PGi Power generation of the plant i in MW
PDt Power demand at hour t in MW
PRt Spinning reserve requirement at hour t in MW
Rs Rupees
ini state Initial status of the unit in hours
SDi–cost Shut down cost in Rs
STi Start up cost in Rs
CCF Composite cost function
h hour
MW Mega Watt
i Index of generating units ( i = 1 ,2,….,N)
Xion (t) Duration of continuously ON of unit i in hour t
Xioff (t) Duration of continuously OFF of unit i in hour t
λ Incremental production cost
2.2 Unit Commitment Problem
Suppose there are N thermal units and the time horizon is T. The unit commitment problem is to determine the commitment and generation levels of all units over the period T so that the total generation cost is minimized. It is formulated as a mixed-integer optimization problem
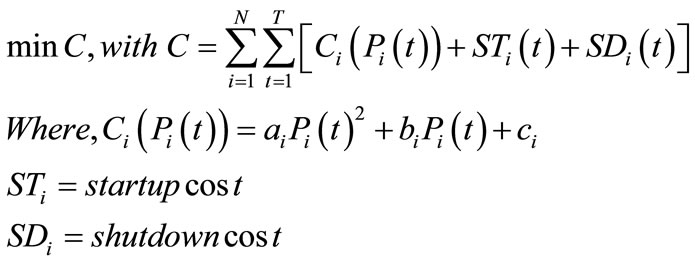 (1)
(1)
Subject to the following constraints.
2.3 Constraints
2.3.1 System Power Balance Constraint
The generated power from all the committed units must satisfy the load demand, which is defined as
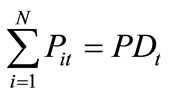 (2)
(2)
2.3.2 Generation Limit Constraints
Each unit has a valid generation range, which is represented as
 (3)
(3)
2.3.3 Spinning Reserve Constraints
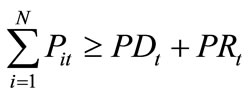 (4)
(4)
The total amount of power available at each hour must be greater than the load demanded. The reserve power available, denoted by PRt , is used when a unit fails or an unexpected increase in load occurs.
2.3.4 Initial Status Constraints
At the beginning of the schedule, the unit initial status must be taken into account.
2.3.5 Minimum Up and Down Time Constraints
Once a unit is committed/decommitted, there is a predefined minimum time after which it can be decommitted/ committed again.
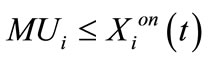 (5)
(5)
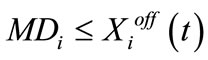 (6)
(6)
2.3.6 Startup Cost
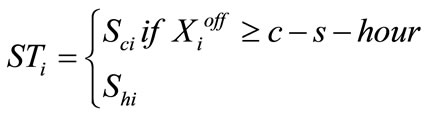 (7)
(7)
2.3.7 Ramp Level
From the beginning to end of the schedule the ramp level that is the output of the unit is maintained with in prescribed limits.
3. Composite Cost Function
The composite cost coefficients are derived as follows.
The total fuel cost of the ‘N’ unit system can be written as
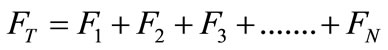 (8)
(8)
For most economical generation,
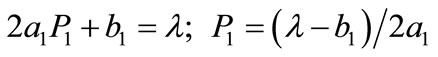

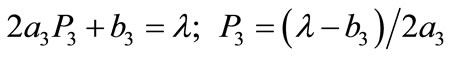
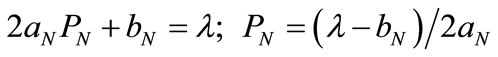
 (9)
(9)
where, 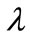 is the incremental production cost of the plant in MW.
is the incremental production cost of the plant in MW.
The total generation of the plant can be written as,
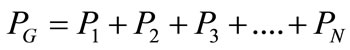
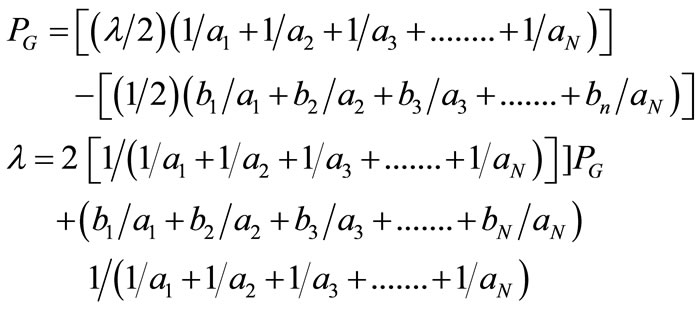 (10)
(10)
by comparing (9) & (10)
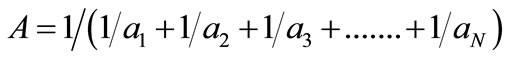
 (11)
(11)
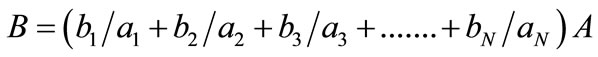 (12)
(12)
The fuel cost can be rewritten as
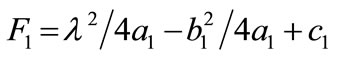 ;
;
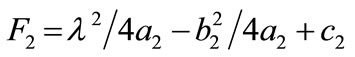 ;
;
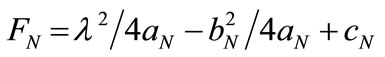 ;
;
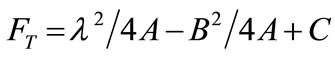 (13)
(13)
From (13)
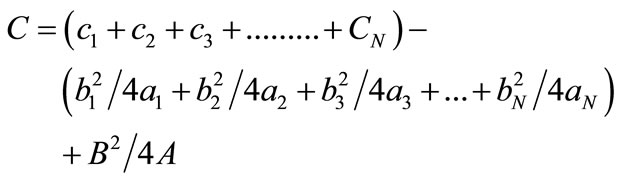 (14)
(14)
4. Description of CCF Based Unit Commitment and Economic Dispatch
The detailed computational flow of the proposed methodology is presented as a flow chart in Figure 1 and the algorithmic steps of CCF based solution for unit commitment problem are presented as follows.
Step 1: Read the unit characteristics, cost coefficients and load.
Step 2: Generate the possible binary combinations using 2n, where n is the number of generating units.
Step 3: Choose the possible combinations to satisfy the power demand and spinning reserve constraints for first hour.
Step 4: Compute CCF coefficients and λ for each combination.
Step 5: Evaluate the generation of units for each combination.
Step 6: Compute the total operating cost for each combination.
Step 7: Choose a combination with minimum total operating cost.
Step 8: If it is last hour go to step 9 else increase the hour and go to step 3.
Step 9: Print the unit commitment schedule and dispatches.
5. Results and Discussion
The proposed technique has been implemented in MATLAB on a 2.10 GHz core 2 Duo processor PC. The performance of the algorithm has been evaluated through simulation. Simulation studies have been carried out on four-generator [11], seven-generator [14] and ten-generator [11] sample systems. Before proceeding to the dispatch of demand to generators, careful selection of units is important. In the proposed method first generate the possible binary combinations using 2n, where n is the number of generating units. For the four unit system, the possible binary combinations are 0000 to 1111. The first combination is not necessary because all the units are off. The maximum generation value is substituted in the combinations where the unit was on and the total generation of the each combination is obtained.
The first hour load demand is 410 MW. The possible binary combinations are five, such as 0110, 0111, 1011, 1110, 1111 having generations of 630, 610, 690, 440, 550 MW. For each combination CCF coefficients for committed units, lambda, power generation and total operating cost are obtained. Then the combination 1111 is chosen for first hour because its operating cost is low (Rs.862/-). Hence for the first hour the unit combination is 1111 and the economic schedule for the committed unit is P1 = 72 MW, P2 = 138 MW, P3 = 140 MW and P4 = 60 MW. In case if there is any violation of power limit, the power is fixed at its maximum limit or minimum limit. Then the CCF coefficients, lambda, power generation and total operating cost are obtained. The same procedure is continued for next hour.
5.1 IEEE 4-Unit Test System
The proposed approach has been tested on a sample system consisting of four generating units. Table 1 summarizes the committed units, operating cost and start up cost. The committed unit shows that there was no need to add startup and shut down cost because all the units were ON
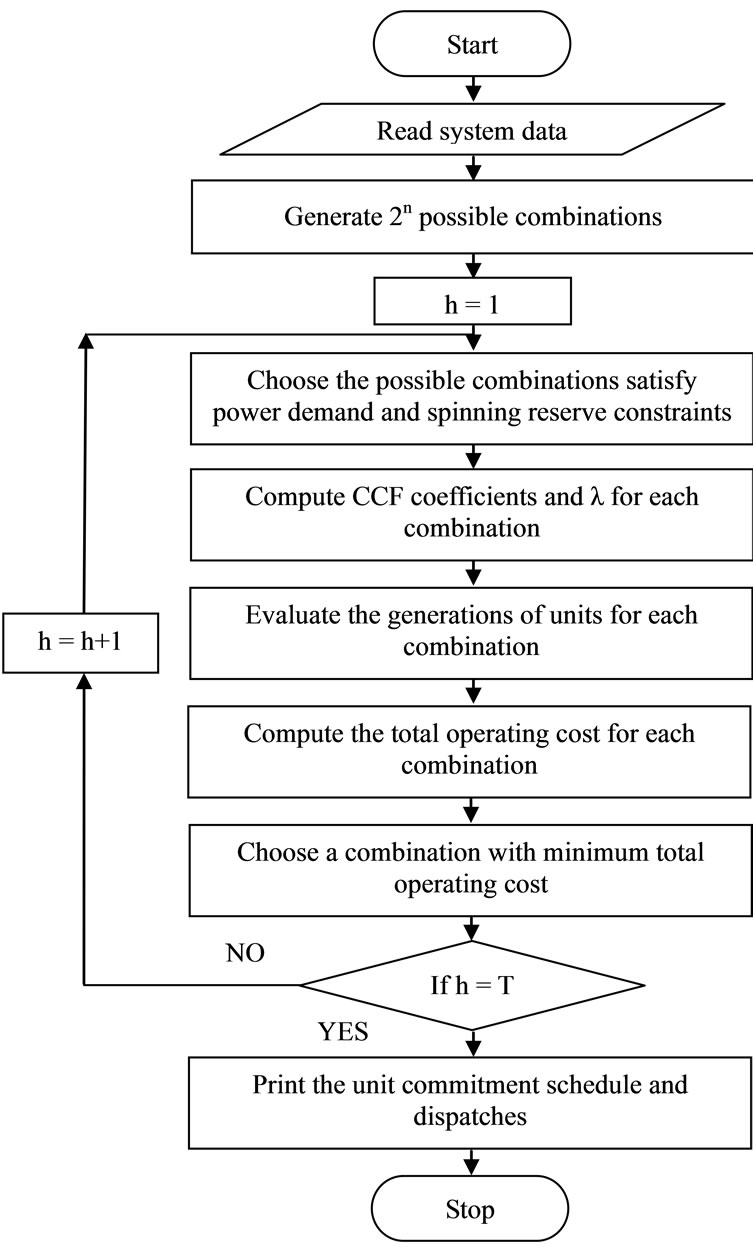
Figure 1. Flow chart of the proposed method
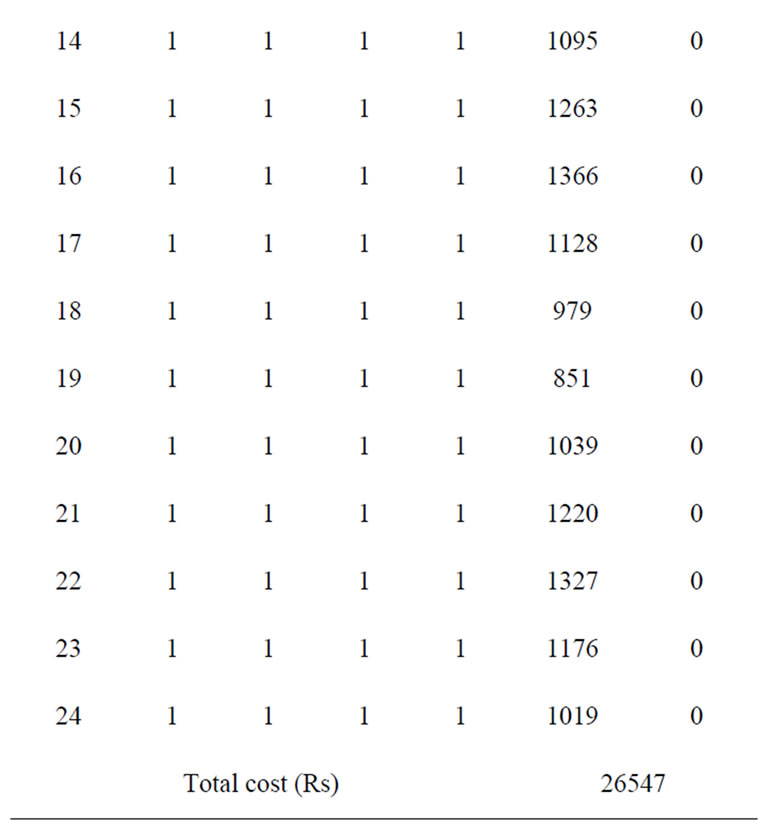
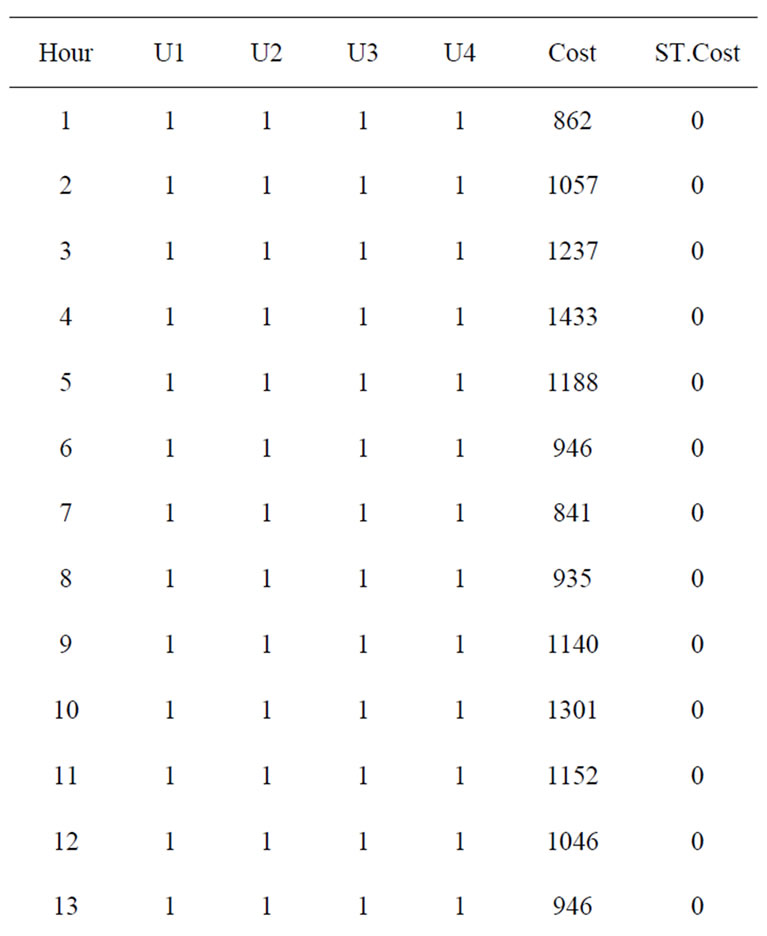
Table 1. Committed units and cost for 4-unit system
during entire 24 hour. Table 2 gives the optimum generation schedule for various system demands. The ramp level should be maintained for entire 24 hour. The results do not show any violation of reserve and power demand constraints. The proposed method in comparison with Dynamic Programming (DP), Branch and bound and Ant colony system as shown in the Table 3. It is clear from
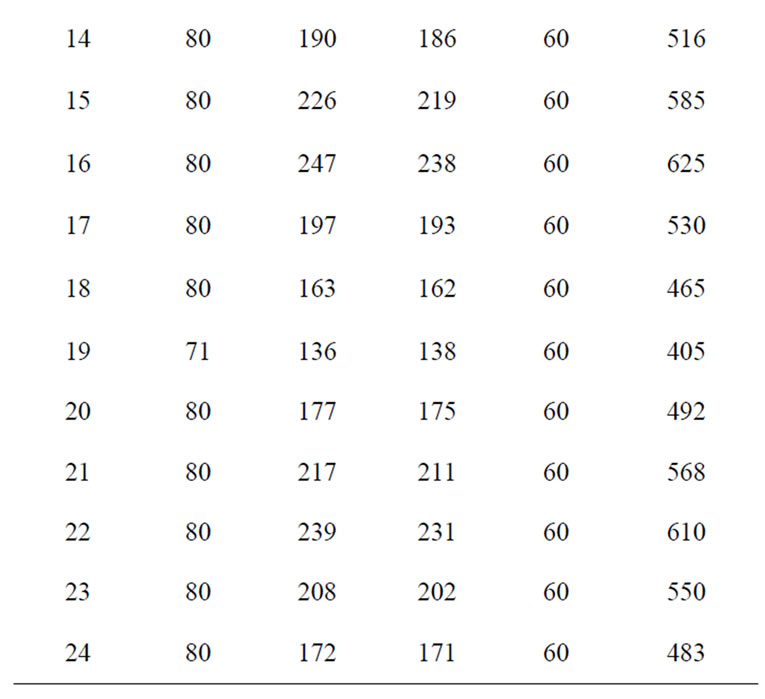
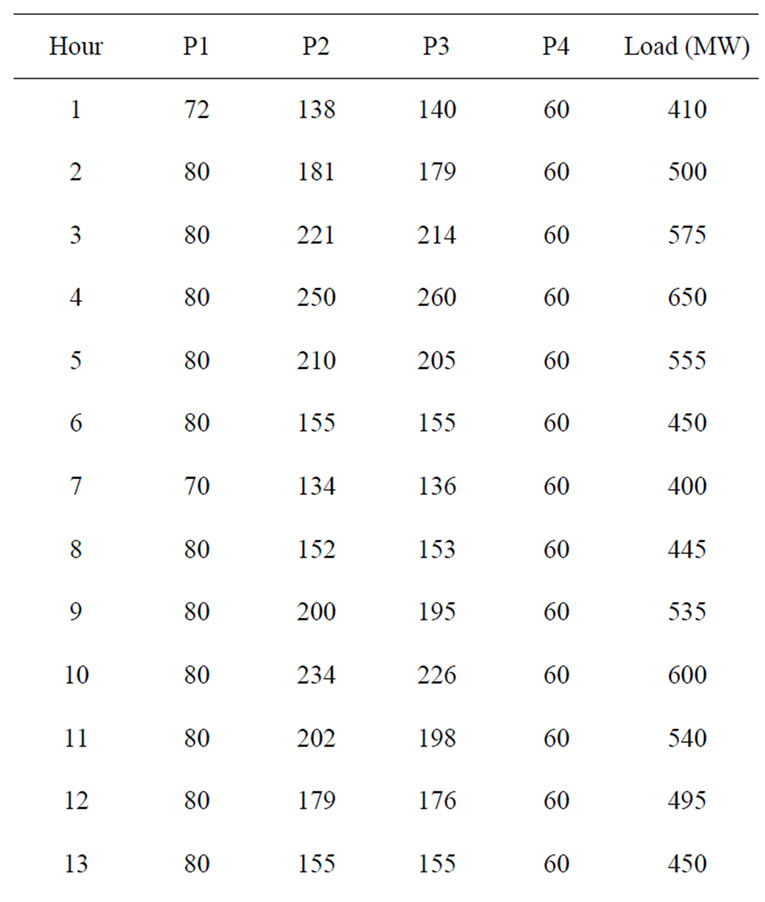
Table 2. Economic Schedule of committed units for 4-unit system
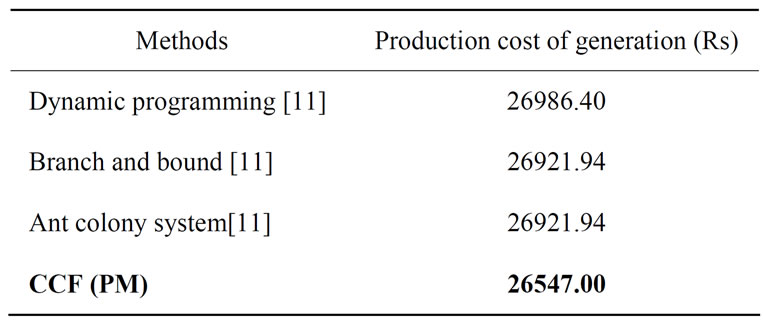
Table 3. Comparison results of cost of generation for 4-unit system
the comparison, that the proposed approach gives the better optimum solution for all load demands when compared to the other methods reported in Reference [11].
5.2 IEEE 7-Unit Test System
The proposed approach has been tested on a sample system the optimum generation schedule for various system de consisting of seven generating units. Table 4 summarizes the committed units, operating cost and start up cost. The committed units show that it is necessary to add the start up cost at Hour 10 and Hour 24. Table 5 gives mands. The results do not show any violation of reserve and power demand constraints. In this article [14] there is no shutdown cost and ramp level for any generating units. The proposed method is compared with Tabu Search (TS) and the comparison is shown in Table 6. It is clear from the comparison, that the proposed approach gives the better optimum solution for all load demands when compared to the other method reported in Reference [14].
5.3 IEEE 10-Unit Test System
The proposed approach has been tested on a sample system consisting of ten generating units. Table 7 summarizes the committed units, operating cost and start up cost. The committed units shows that it is necessary to add startup cost Hour 4 and shutdown cost at Hour 1, Hour 20 and Hour 24. Table 8 gives the optimum generation schedule for various system demands. The ramp level should be maintained for entire 24 hour. The results do not show any violation of reserve and power demand constraints. The proposed method in comparison with Dynamic Programming (DP), Branch and bound and Ant colony system as shown in the Table 9. It is clear from the comparison, that the proposed approach gives the better optimum solution for all load demands when compared to the other methods reported in Reference [11].
The data are obtained for four generator [11], sevengenerator [14] and ten-generator [11] as reported in references. From the results, it was clear that the proposed approach provides solution with close agreement with conventional method. The composite cost function-based solution method has the following distinctive features.
1) The conventional methods gives the committed units and total production cost only but the proposed method gives the committed units, cost and economic schedule for committed units.
2) The proposed approach directly express the optimum generation of each unit using CCF coefficients. Hence the computation time for unit commitment and economic schedule becomes an easy task.
3) The iterative steps are completely eliminated.
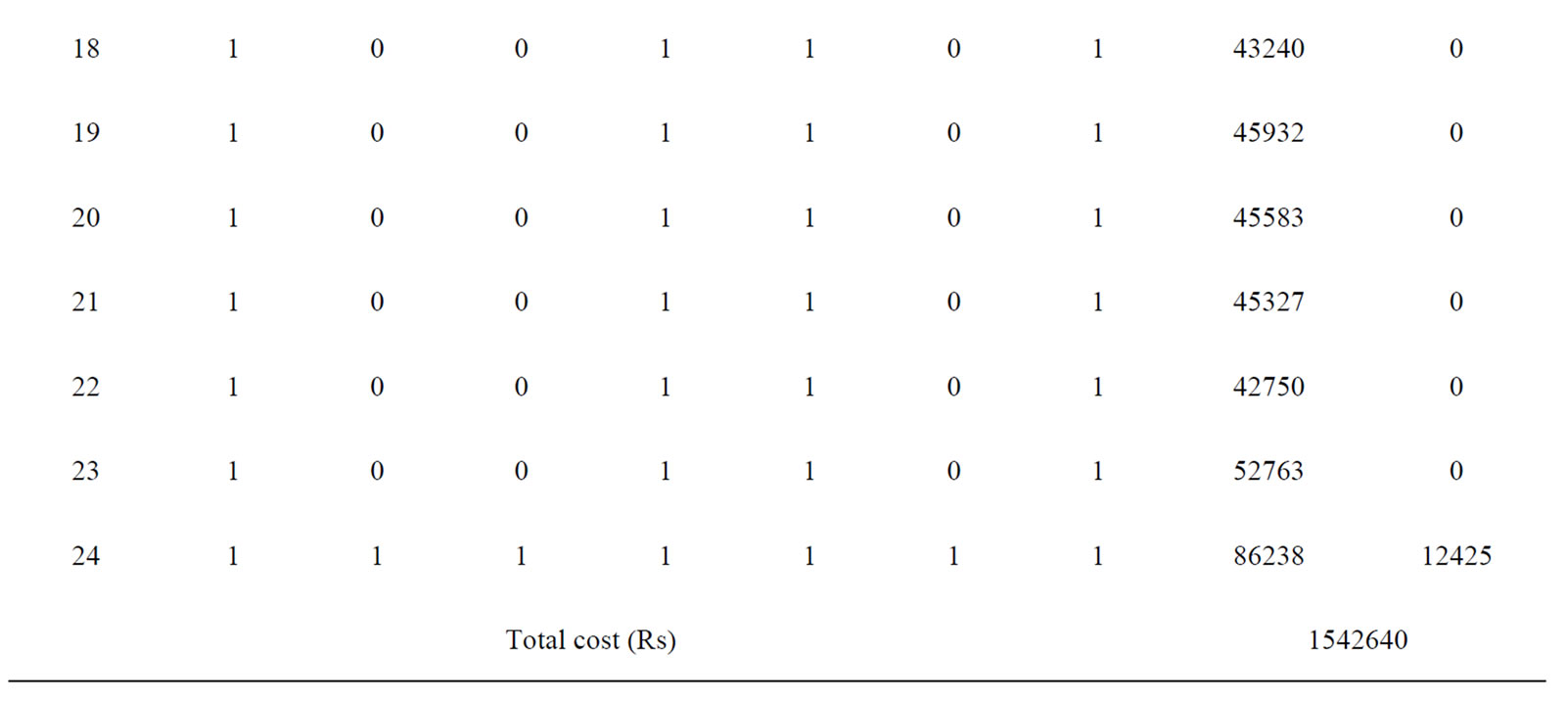
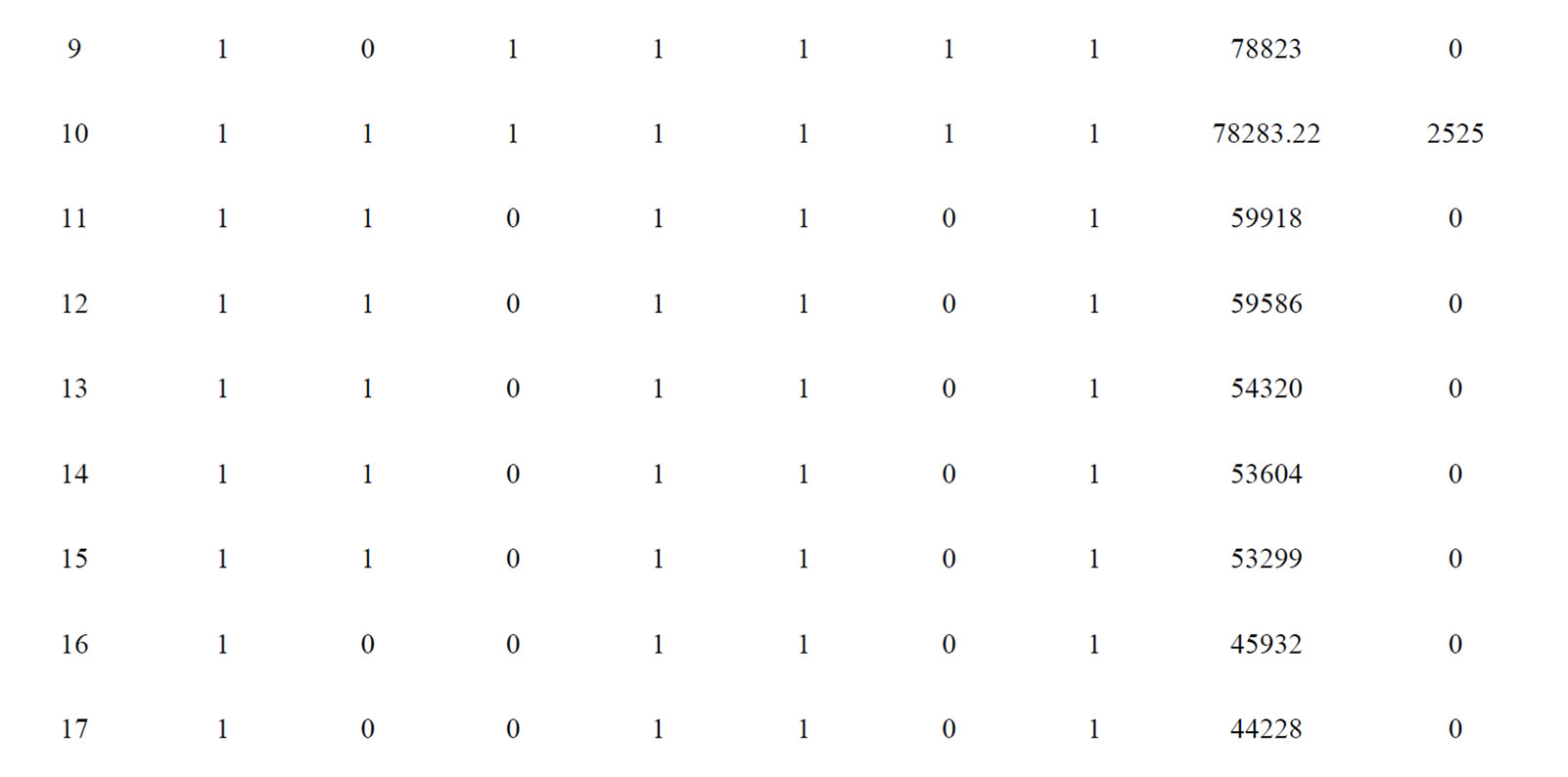
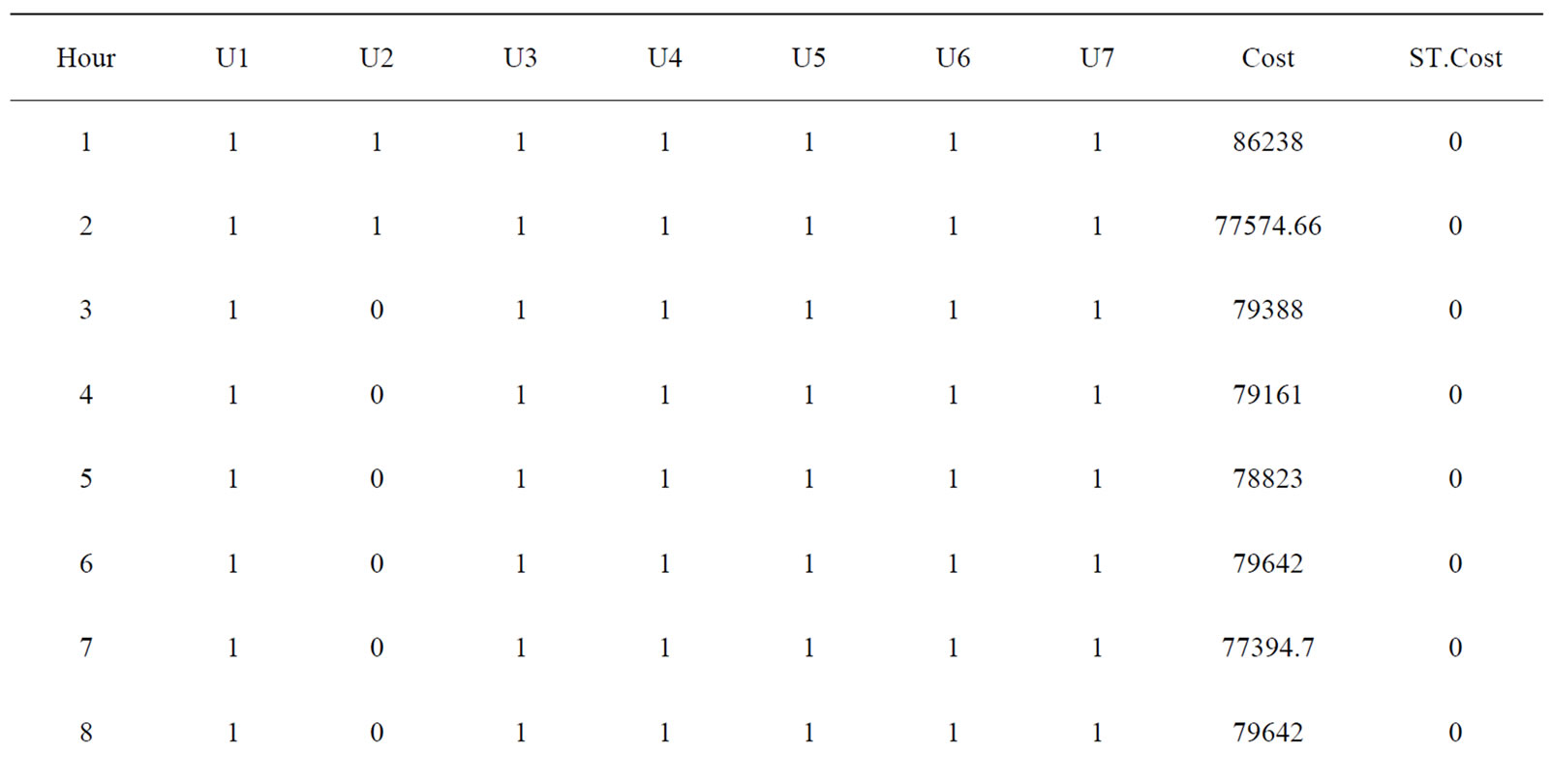
Table 4. Committed units and cost for 7-unit system
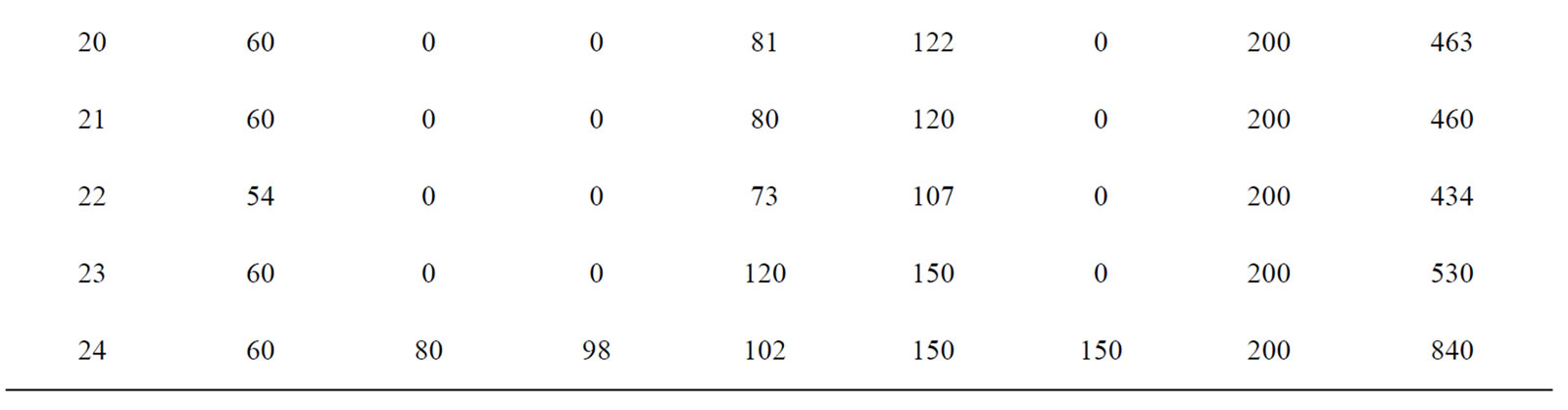
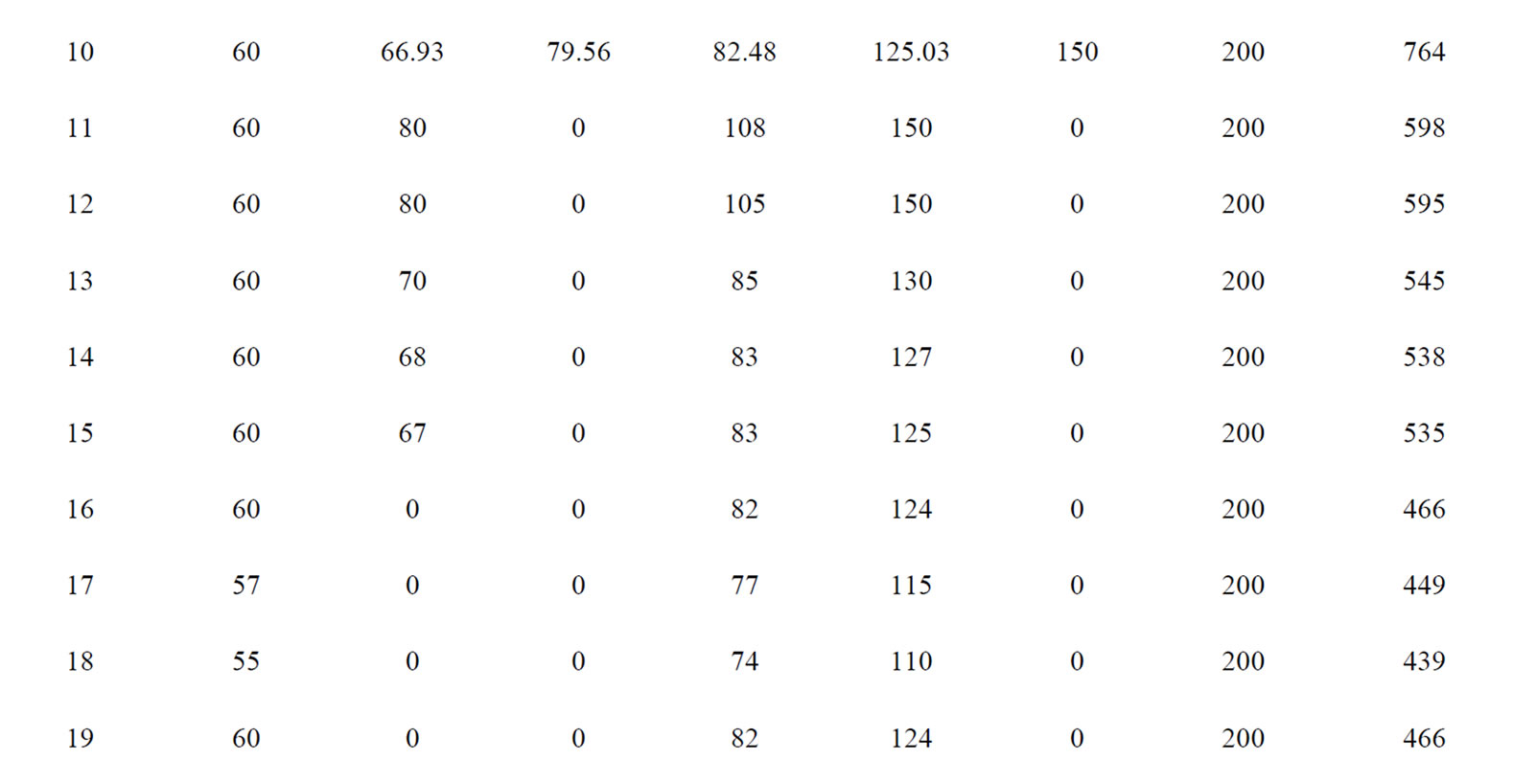
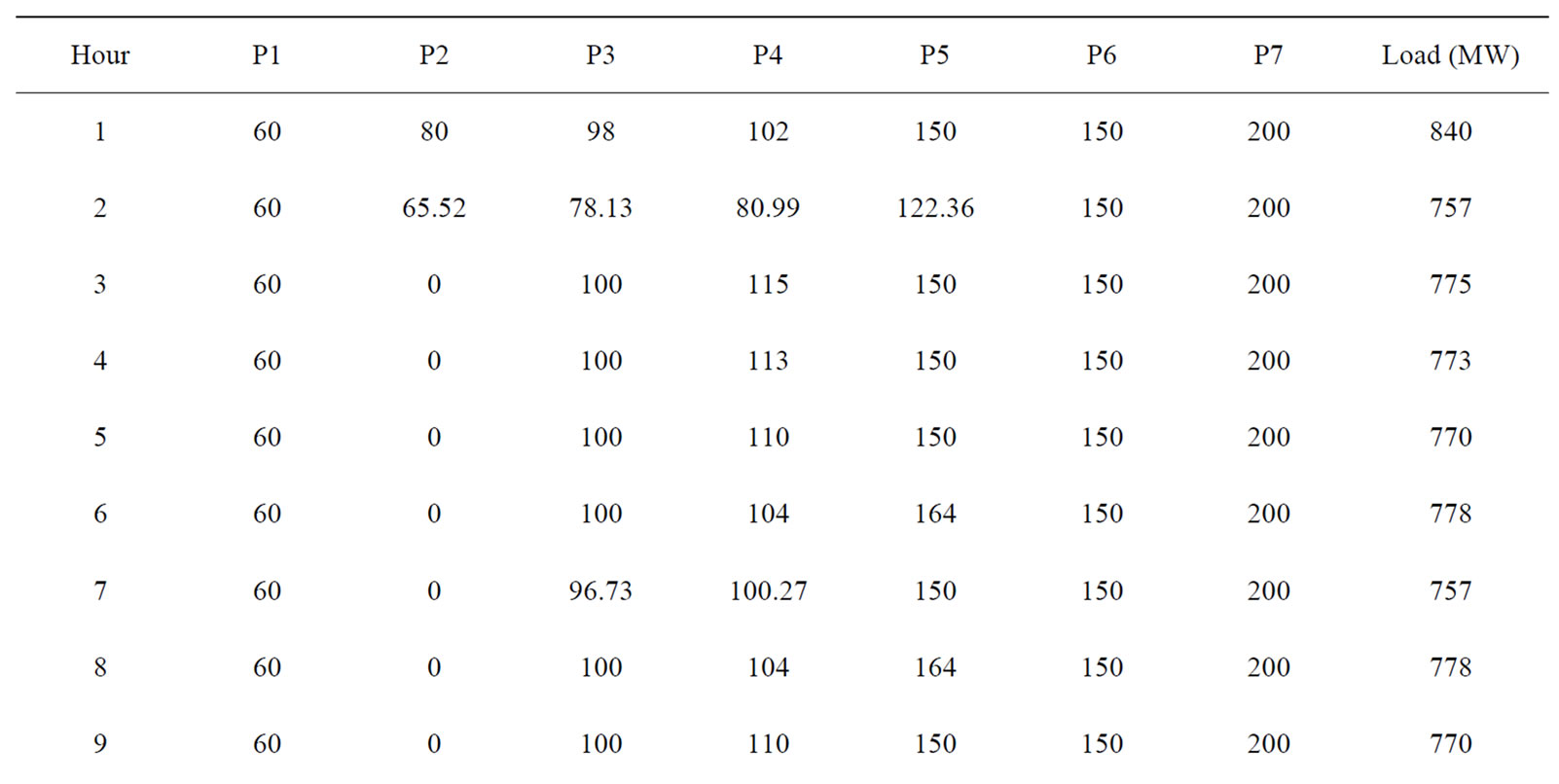
Table 5. Economic Schedule of committed units for 7-unit system

Table 6. Comparison results of cost of generation for 7–unit system
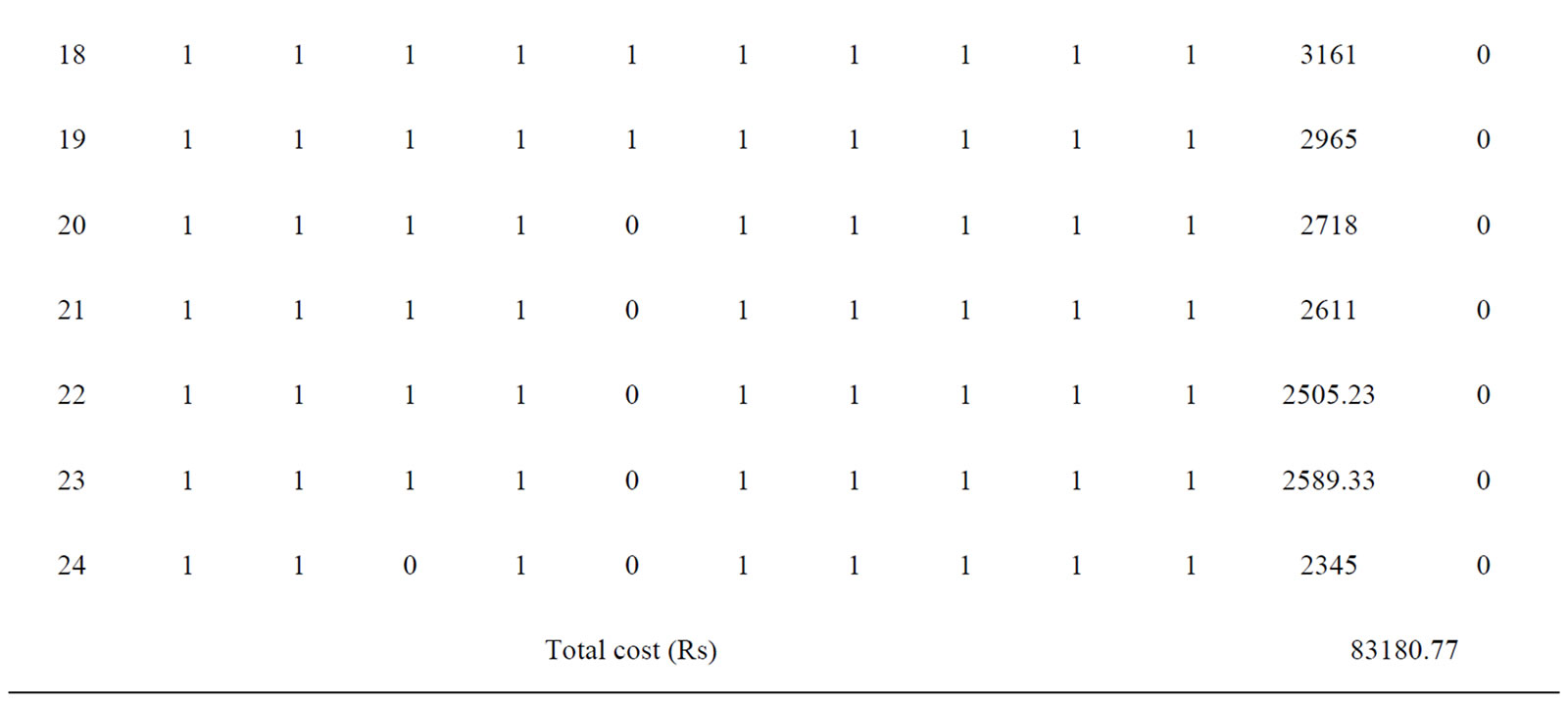
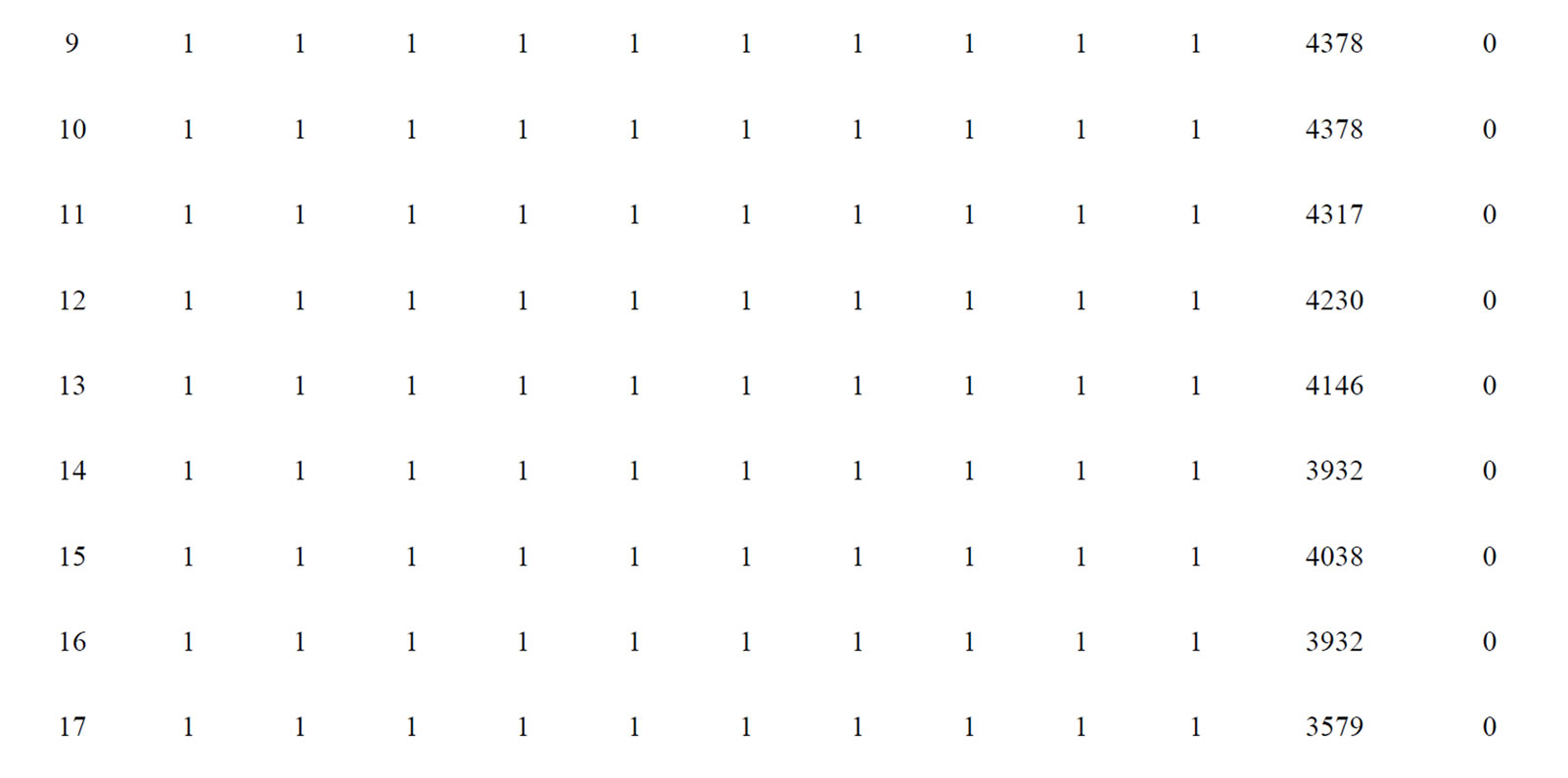
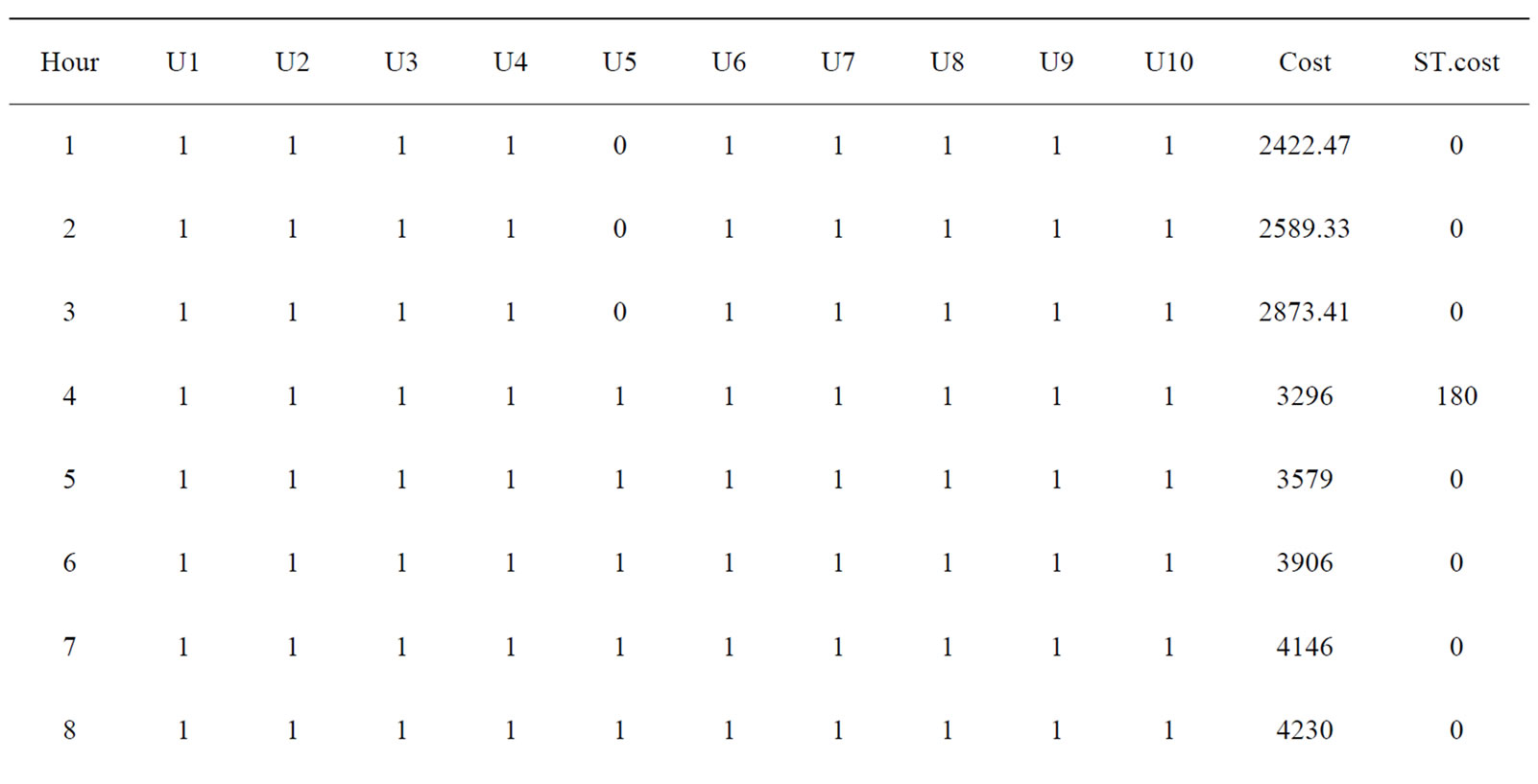
Table 7. Committed units and cost for 10-unit system
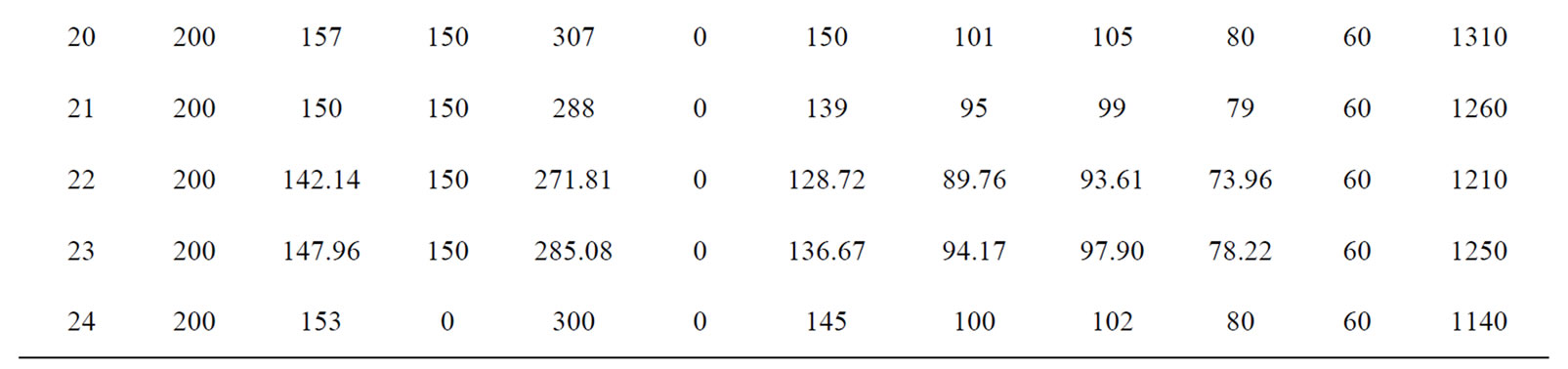
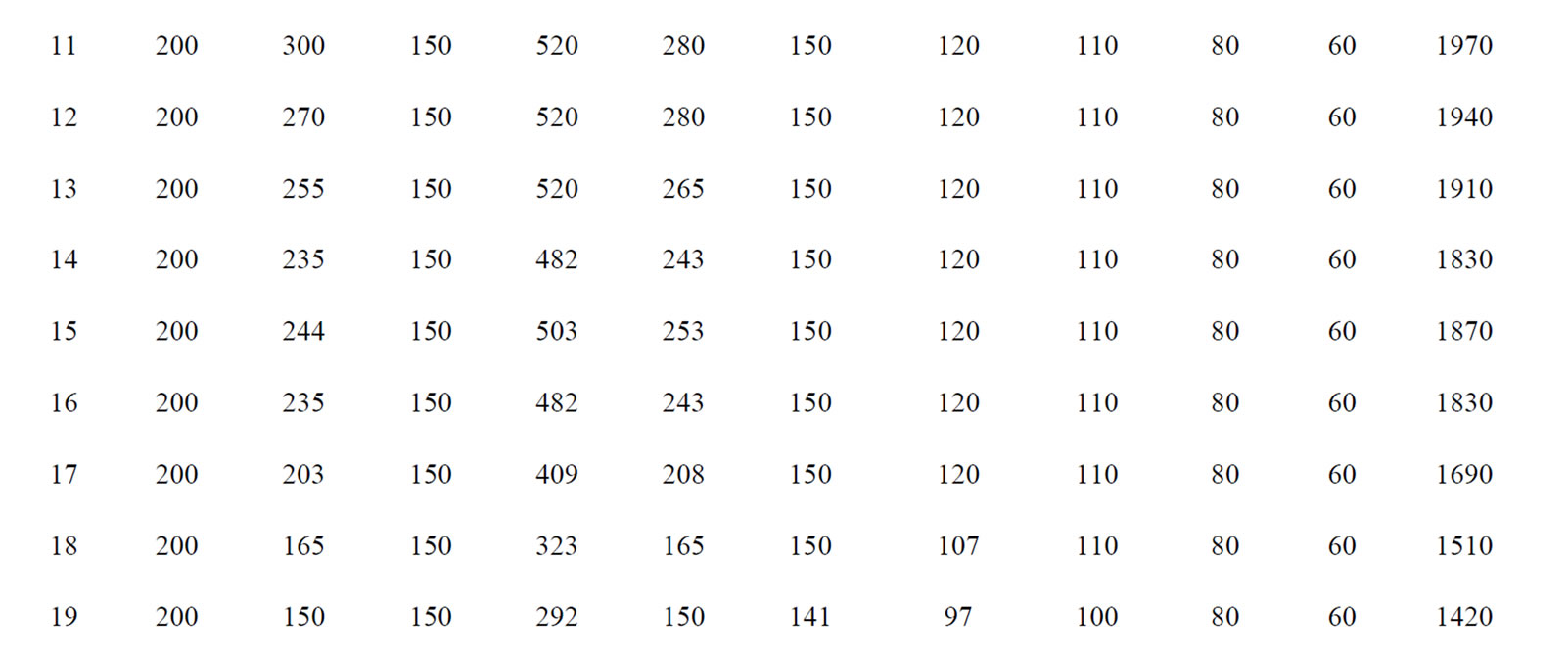

Table 8. Economic Schedule of committed units for 10-unit system

Table 9. Comparison results of cost of generation for 10-unit system
6. Conclusions
An effective, robust unit commitment solution is a necessary contribution to the operating on/off plans of the generating units. In this paper, a new composite cost function based solution algorithm for solving the unit commitment problem is presented. The proposed algorithm uses the composite cost coefficients to select the committed units and give the economic schedule for each specific hour. This new algorithm produces better results than the Branch and bound, Dynamic programming, Ant colony, and Tabu search methods in addition to satisfaction of the system constraints. The proposed algorithm is most suitable for system having smaller number of units. From the results, it is clear that the proposed method provides the quality solution with low cost and has a potential for on-line implementation.
7. Acknowledgements
The authors gratefully acknowledge the authorities of Annamalai University, Annamalainagar, Tamilnadu, India, for their continued support, encouragement, and the extensive facilities provided to carry out this research work.
REFERENCES
- A. J. Wood and B. F. Wollenberg, “Power Generation, Operation and Control,” Wiley, New York, 1984.
- M. Madrigal and V. H. Quintana, “An Interior–Point/Cutting-Plane Method to Solve Unit Commitment Problems,” IEEE Transactions on Power Systems, Vol. 15, No. 3, August 2000, pp. 1022-1027.
- J. M. Arroyo and A. J. Conejo, “A Parallel Repair Genetic Algorithm to Solve the Unit Commitment Problem,” IEEE Transactions on Power Systems, Vol. 17, No. 4, November 2002, pp. 1216-1224.
- H. Y. Chen and X. F. Wang, “Cooperative Coevolutionary Algorithm for Unit Commitment,” IEEE Transactions on Power Systems, Vol. 17, No. 1, February 2002, pp. 128-133.
- Q. Z. Zhai, X. H. Guan and J. Cui, “Unit Commitment with Identical Units: Successive Subproblem Solving Method Based on Lagrangian Relaxation,” IEEE Transactions on Power Systems, Vol. 17, No. 4, November 2002, pp. 1250-1257.
- A. L. Motto and F. D. Galiana, “Unit Commitment with Dual Variable Constraints,” IEEE Transactions on Power Systems, Vol. 19, No. 1, February 2004, pp. 330-338.
- C. C. A. Rajan and M. R. Mohan, “An Evolutionary Programming-Based Tabu Search Method for Solving the Unit Commitment Problem,” IEEE Transactions on Power Systems, Vol. 19, No. 1, February 2004, pp. 577- 585.
- B. Lu and M. Shahidehpour, “Unit commitment with Flexible Generating Units,” IEEE Transactions on Power Systems, Vol. 20, No. 2, May 2005, pp. 1022-1034.
- T. Li and M. Shahidehpour, “Price-Based Unit Commitment: A Case of Lagrangian Relaxation Versus Mixed Integer Programming,” IEEE Transactions on Power Systems, Vol. 20, No. 4, November 2005, pp. 2015-2025.
- A. Y. Saber, T. Senjyu, T. Miyagi, N. Urasaki and T. Funabashi, “Fuzzy Unit Commitment Scheduling Using Absolutely Stochastic Simulated Annealing,” IEEE Transactions on Power Systems, Vol. 21, No. 2, May 2006, pp. 955-964.
- S. P. Simon, N. P. Padhy and R. S. Anand, “An Ant Colony System Approach for Unit Commitment Problem,” Electrical Power and Energy Systems, Vol. 28, No. 5, 2006, pp. 315-323.
- M. Carrion and J. M. Arroyo, “A Computationally Efficient Mixed-Integer Linear Formulation for the Thermal Unit Commitment Problem,” IEEE Transactions on Power Systems, Vol. 21, No. 3, August 2006, pp. 1371- 1378.
- D. N. Simopoulos, S. D. Stavroula and C. D. Vournas, “Reliability Constraints Unit Commitment Using Simulated Annealing,” IEEE Transactions on Power Systems, Vol. 21, No. 4, November 2006, pp. 1699-1706.
- A. A. Victoire and A. E. Jeyakumar, “A Tabu Search Based Hybrid Optimization Approach for a Fuzzy Modelled Unit Commitment Problem,” Electric Power Systems Research, Vol. 76, No. 6-7, 2006, pp. 413-425.
- F. Aminifar, M. Fotuhi-Firuzabad and M. Shahidehpour, “Unit Commitment with Probabilistic Spinning Reserve and Interruptible Load Considerations,” IEEE Transactions on Power Systems, Vol. 24, No. 1, February 2009, pp. 388-397.
- M. Eslamian, S. H. Hosseinian and B. Vahidi, “Bacterial Foraging Solution to the Unit-Commitment Problem,” IEEE Transactions on Power Systems, Vol. 24, No. 3, August 2009, pp. 1478-1488.

