Creative Education
Vol.5 No.9(2014), Article ID:46255,11 pages DOI:10.4236/ce.2014.59081
Possibilities of Augmented Reality Use in Mathematics Aiming at a Meaningful Learning
Carlos Vitor de Alencar Carvalho1,2,3, Bruno Morais Lemos2,3
1State University Center of Western Rio de Janeiro, Rio de Janeiro, Brazil
2Severino Sombra University, Vassouras, Brazil
3Geraldo di Biase University Center, Barra do Piraí, Brazil
Email: carloscarvalho@uezo.rj.gov.br, cvitorc@gmail.com, bruno.mathematic@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 9 March 2014; revised 9 April 2014; accepted 16 April 2014
ABSTRACT
This article aims to present various softwares in mathematics teaching, where visualization of mathematical objects is done by using Augmented Reality. This is a computational technique in which virtual objects are added in a real environment, allowing an enrichment of the information for students to visualize concepts and test hypotheses with the teacher, providing a more playful and meaningful investigative environment. Meaningful learning is the theoretical framework that guides the development and software use. Such softwares are characterized as potentially meaningful materials that allied to the student’s prior knowledge and their will to learn establishes the basic pillars of the theory.
Keywords:Augmented Reality, Educational Software, Mathematics Teaching, Meaningful Learning

1. Introduction
This article aims to present various softwares in mathematics teaching, where visualization of the mathematical objects is done by using Augmented Reality. The softwares were developed at EUCLIDES Laboratories, linked to the Professional Master’s Degree Program in Mathematics Education of Severino Sombra University (USS), in Vassouras, Rio de Janeiro, Brazil.
According to Lemos and Carvalho (2010), nowadays, computers are becoming common in everyday life. Education is one of the areas in which computers has been used as a complementary tool for teaching. The use of educational software with an easy usage interface view and scientific vision resources became an interesting manner to be this complementary support in mathematic teaching and as it is described in the Meaningful Learning Theory (MLT), it is also a potentially meaningful material. The idea of a potential meaningful material was proposed by David Ausubel in (MLT) and according to Moreira and Massini (2001), it is one of the basis for meaningful learning. The others equally important pillars are subsumers (previous knowledge) and the willingness to learn, i.e., the intentionality. Moreira and Massini also indicate that meaningful learning occurs when the new knowledge presented in a logic manner interacts with the learner previous knowledge, (subsumers), i.e., with the individual cognitive structure, thus being assimilated and contributing to give a meaning to new the knowledge. Therefore, the potential meaningful material acts as a tooling for subsumers organization and presentation of the new knowledge. In Figure 1, there is a brief conceptual map of MLT.
Thus, the next section of this article describes some details about the Augmented Reality technique. Then, details about development and the use of SISEULER, MATERIALDOURADORA, TABUADARA and SISFRAC software will be presented. The last section presents conclusions.
2. The Augmented Reality (AR)
The Augmented Reality Term (AR) is defined by Milgram and Kishino (1994) as a subset of Mixed Reality (MR), and it can be located within a virtuality continuum, in which in one of the ends is the Real Environment (RE) and the other the Virtual Reality Environment. In this continuum an application is classified as Augmented Reality or Augmented Virtuality (AV) according to the level of interaction between the real and virtual worlds, as shown in Figure 2.
In the AR case there is the dominance of the real above the virtual, in which the match scene enrichment is done with virtual targets. All the software shown in the following items were developed by using the C language, and for the construction of virtual designs, it was used the OpenGL graphic system (Woo, 1999). The identification development for markers was made by using the ARToolkit library (ARToolkit, 2006).
The ARToolkit is a software library developed in C language by the Human Interface Technology Laboratory at the University of Washington. The software helps the programmer to build fast applications in AR area. ARToolkit uses computer vision techniques to calculate the camera’s point of view in relation to the square markers that contains a pattern on the inside (Figure 3), allowing its correct register.
Markers are squares that can be printed in any type of printer. In the center of the square there must be a non-
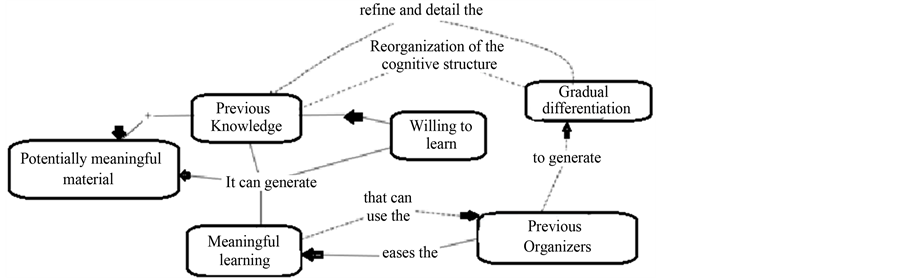
Figure 1. Meaningful Learning Theory Concept Map. Extracted from Guedes and Carvalho (2012).

Figure 2. Virtuality continuum. Adapted from Milgram and Kishino (1994).

Figure 3. Example of a marker used in software developed with Augmented Reality. Source: Research data.
symmetrical picture with high contrast. For each software developed, it was created various markers. There are three basic and fundamental characteristics in these applications: real and virtual matching (with predominance of real), real-time interaction, three-dimensional images and functioning. In summary, it is described as follows: the real environment is captured by the video camera (webcam), the marker is identified and if its correctly registered and implemented in the application code, it may serve to analyze the problem (for example, the composition with other markers) or to display in one or various markers a virtual image.
According to Kirner and Tori (2004), the webcam use is the simplest way to accomplish images captures to integrate them to the virtual image. Thus, the next sections will present the details about the development and the use of software addressed in this article.
3. SISEULER
SISEULER software (Lemos, 2011) was implemented with the aim to develop a recreational activity, to promote the teaching of Euler’s Formula. Firstly, various markers are provided to develop the activity with the system, note that one marker is destined to the image exhibition (marker results). The other markers correspond to the number of vertices, faces and edges of any polyhedron. To exemplify, markers will be described as: 8V, 6F, 12A, 4V, 4F, 6A, 6V, 8F, 20V, 12F, 20F, 12V e 30ª. These markers represent respectively, 8 vertices, 6 faces, 12 edges, 4 vertices, 4 faces, 6 edges, 6 vertices, 8 faces, 20 edges, 12 faces, 20 faces, 12 vertices and 30 edges. In Lemos (2013) markers and SISEULER software are available to be downloaded.
By placing these markers in the designated space, the student will be able to understand that a three-dimensional image will be shown only if there is a relation with the number of vertices, edges and faces. Currently the software is able to recognize the relations related to the platonic polyhedral, in other words, cube, tetrahedron, octahedron, dodecahedron and icosahedrons. Even knowing that Euler’s Formula is a necessary condition for the existence of a convex polyhedral, the approach with AR can be quite profitable for the theme.
To illustrate its use, while developing this activity, initially a suggestion for the teacher is to perform a didactic intervention, guiding the student firstly to put the “R” marker in the space for the result, the 8V marker in the space for the number of vertices, the 6F marker in the space for the number of faces and then, using the remaining markers, find out which one of them should be placed in the space for the number of edges.
By placing these markers in the designated areas, the student will notice that when the marker 12 A is introduced; the software will draw, as reward, a virtual cube on the marker results (Figure 4). At this moment the teacher can draw the attention to the name of the virtual geometric solid projected on the top of the marker results.
At this moment, the suggestion for the teacher who is in charge of the activity is to distribute a booklet. This guide (key manual) is available at Lemos (2013) and it contains the function keys that can be used. These keys display only the vertices (Figure 5), the edges (Figure 6) and the faces of the virtual geometric solids. Furthermore, the student will be able to rotate the virtual prism by pressing the keys: r, a, d, w or s.

Figure 4. Recognition of the Cube relationship.

Figure 5. Cube vertice projection.

Figure 6. Cube edges projection.
The teacher also may highlight that the cube can be manipulated. At this point, it is important to note that markers may present occlusion problems, so the student must not put the hand or any other object on the marker of the camera vision field, thus blocking its recognition (Figure 7).
Then, by using an analogous methodology, the teacher will be able to explore other platonic solids. Arbitrarily this activity suggests that the next solid to be constructed is the tetrahedrons, so the teacher should ask the students to place the 4 V marker in the vertices areas, the 4F in the faces areas and after let the students find out which marker related to the number of edges will project the next polyhedron.
Figure 8 shows how the software identifies the markers related to the tetrahedron and how the user can manipulate the image for a better perception. Figure 9 shows the virtual tetrahedron with edge exhibition only.
After the tetrahedron recognition, the mediator of the activity should remind the students that they can use the keys listed in the booklet to better exploit the tetrahedron properties that they might register in a table, the number of vertices, faces, edges and the name of the virtual polyhedron projection.
It is believed to be important for the students to make trials with the given markers and be able to find the appropriate relationship by themselves, because it will be through this experiment and meaningful process that they will build the knowledge.

Figure 7. Virtual cube manipulation.
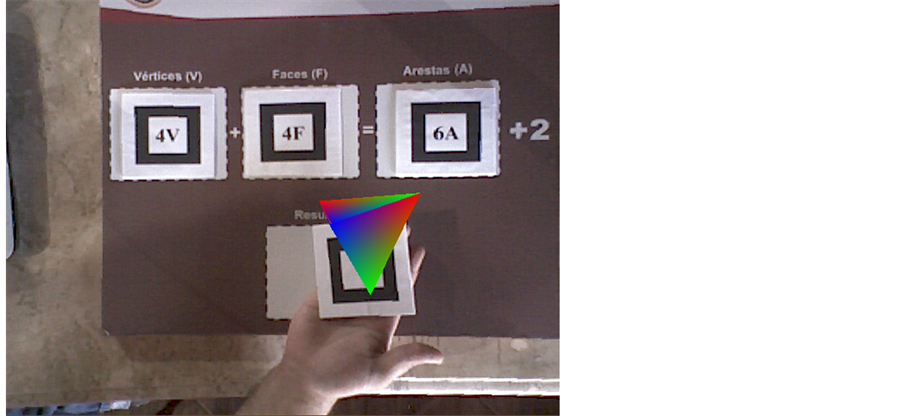
Figure 8. Virtual tetrahedron recognition and manipulation.

Figure 9. Virtual tetrahedron with edge exhibition only.
4. DouradoRA Material
DouradoRA Material aims to promote the teaching-learning of the decimal-positional numbering system. The main idea is that students in a recreational way understand the decomposition of a number in units, tens, hundreds and thousands.
The system allows, further than the three-dimensional vision of the golden pieces of the material, the enlargement or reduction of the objects by the activation of the “x” key (enlargement) and “z” (reduction), and the rotation in clockwise rotation in the three Cartesian axes using the (“q”, “w” e “e”) keys. When the “n” key is active, a menu exhibits options for the activities with the software, described as follows:
1. Decomposition of a number;
2. Formation of a set of ten animation;
3. Formation of a set of hundred animation;
4. Formation of a set of thousand animation.
In this first system version, the understanding of the number relationship with the pieces of the golden material in AR was privileged from the decomposition of the number into units, tens, hundreds and thousands. As described in the previous section, when the “n” key is pressed, the system exhibits a menu for activities with the software. In Options 2, 3 and 4, the user will be able to see, by means of an animation, the decomposition of the set of ten, the set of hundred and the set of thousand.
In the case of ten, ten units are displayed. From the moment the user press the “p”, the formation of the set of ten bar animation is displayed. To enhance and easy the understanding, it would be interesting that such source be used with the concrete golden material. Similarly there has been made animations for the set of hundred and for the set of thousand compositions. Option 1 allows the user to indicate a number between 1 and 9999. This number is decomposed in unit, ten, hundred and million. Then, such amounts are drawn in a mixed environment. Figures 10-12 display decompositions for numbers: 79 (7 × 10 + 9 × 1), 567 (5 × 100 + 6 × 10 + 7 × 1) 3189 (3 × 1000 + 1 × 100 + 8 × 10 + 9 × 1).
5. TabuaraRA
TabuadaRA software uses the golden material concept for the development and study of the multiplication of a couple of numbers. It makes use of the main core of the software development Material DouradoRA (Carvalho & Lemos, 2011). The software allows the vision of the numbers that takes part in the multiplication and as well as the result of the multiplication with the Golden material pieces. In this aspect, the visualization is a great advantage, because it eases the understanding of the relationships that most of times are abstract. Basically, the TabuadaRA requires three markers, two numbers that will be multiplicated and the marker where the result will displayed. Figures 13-16 exhibit some operations made with TabuadaRA software. More software details are available at Souza et al. (2013).

Figure 10. AR view of the Number 79.
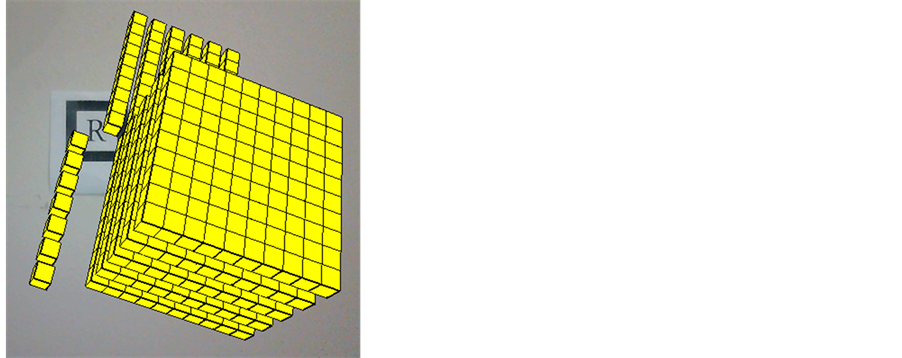
Figure 11. AR view of the number 657.
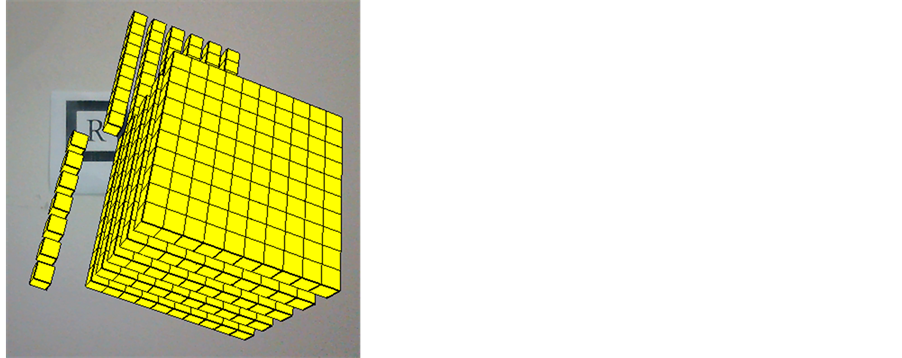
Figure 12. AR view of the number 3190.

Figure 13. AR view of the 8 × 5 product.

Figure 14. AR view of the 2 × 3 product.

Figure 15. AR view of the 2 × 7 product.
6. TabuaraRA
SISFRAC software (Silva, 2013) was developed to exhibit in a simplest and objective way the representation of fractions, covering mainly new students in the studies of fractions. The first SISFRAC version was implemented to display the proper fractions. Many markers available at the moment represent fractions 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 1/9, 2/6, 2/12, 2/8, 4/8, 4/15, 3/7, 5/9. Figures 17-19 exhibit fractions 1/2 and 1/9 by means of SISFRAC software.
7. Conclusion
Originally, this article presented software SISEULER, MATERIALDOURADORA, TABURADARA and SISFRAC. These softwares were developed entirely or with the authors’ participation. SISEULER started to be developed in 2009 and the acquired knowledge during its creation was used as a base technology for the development of the other ones. In the case of SISEULER, workshops were made to verify if the software could contribute for the teaching of Euler’s Formula, bringing positive results regarding its educational relevance. More information about these workshops is available at Lemos (2011). The other software:
MATERIALDOURADORA, TABUADARA and SISFRAC were developed as an undergraduation course com-

Figure 16. AR view of the 9 × 4 product.

Figure 17. Fraction ½ view-SISFRAC software.

Figure 18. Fraction1/7 view—SISFRAC software.

Figure 19. Fraction 1/9 view—SISFRAC software.
pletion assignment, under the supervision of the authors. These softwares have not been tested in educational environment, but it is believed that it can contribute for the teaching of mathematic topics in which they are co-related to. In the future, there is an expectation to add new features to all of the quoted software and test its usage in educational settings. It is also important to highlight that the development of the mentioned software was based on the Meaningful Learning Theory, in which new knowledge is based on the knowledge acquired by the learner and thus it can be realized through the software mentioned, the display and manipulation of mathematical objects in 3D through Augmented Reality, promotes the conjecture and construction of the knowledge by the student and may contribute significantly to the education.
Acknowledgements
The first author thanks CNPq for financial support (process 310282/2012-8).
References
- ARToolKit version 2.71 (2006). http://www.hitl.washington.edu/artoolkit/download/
- Carvalho, C. V. A., & Lemos, B. M. (2011). MaterialDouradoRA—Um software para o ensino-aprendizagem do sistema de numeração decimal-posicional através da Realidade Aumentada. Realidade Virtual, 4, 57-70.
- Guedes, M., de F. dos S., & Carvalho, C. V. A. (2012). CONSTRUFIG3D e VISUALFIG3D: softwares potencialmente significativos para o ensino da geometria espacial. Revista de Educação, Ciências e Matemática, 2, 38-55.
- Kirner, C. & Tori, R. (2004). Realidade Virtual: Conceitos e Tendências. São Paulo: J. Garcia Comunicação Visual.
- Lemos, B. M. (2011). SISEULER: Um software para apoio ao ensino da Relação de Euler. Dissertação (Mestrado Profissional em Educação Matemática) Vassouras: Universidade Severino Sombra.
- Lemos, B. M. (2013). https://sites.google.com/site/siseuler/
- Lemos, B. M., & Carvalho, C. V. A. (2010). Uso da Realidade Aumentada para apoio ao entendimento da relação de Euler. RENOTE: Revista Novas Tecnologias na Educação, 8, 1-10.
- Milgram, P., & Kishino, E. A. (1994). Taxonomy of Mixed Reality Visual Displays. IEICE Transactions on Information and Systems. http://etclab.mie.utoronto.ca/people/paul_dir/IEICE94/ieice.html
- Moreira, M. A., & Masini, S. F. E. (2001). Aprendizagem significativa: a teoria de David Ausabel. São Paulo: Centauro.
- Silva, T. R. (2013) SISFRAC—Um software para apoio ao ensino de frações utilizando realidade aumentada. Trabalho de Conclusão de Curso. (Graduação em Sistema de Informação). Vassouras: Universidade Severino Sombra.
- Souza, B. S., Lemos, B. M., & Carvalho, C. V. A. (2013) Um Software em Realidade Aumentada para o ensino da tabuada. Realidade Virtual, 6, 34-48.
- Woo, M., Neider, J., Davis, T., & Shreiner, D. (1999) OpenGL Programming Guide, Third Edition (OpenGL, Version 1.2), 800 p. Boston, MA: Addison-Welsey.

