Energy and Power Engineering
Vol.6 No.9(2014), Article
ID:49574,12
pages
DOI:10.4236/epe.2014.69023
Robust
 Observer-Based Tracking Control for the Photovoltaic Pumping System
Observer-Based Tracking Control for the Photovoltaic Pumping System
Iliass Ouachani1,2, Abdelhamid Rabhi3, Ahmed El Hajjaji3 ,Belkassem Tidhaf1, Smail Zouggar2
1Laboratory of Embedded Electronic Systems and Renewable Energy, University Mohammed First, Oujda, Morocco
2Laboratory of Electrical Engineering and maintenance High School of Technology, University Mohammed First, Oujda, Morocco
3Laboratory of Modelisation of Information and Systems, University of Picardie Jules Verne, Amiens, France
Email: iliassdoct@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 June 2014; revised 29 July 2014; accepted 12 August 2014
Abstract
In this paper, we propose a
 robust observer-based control DC motor based on a photovoltaic pumping system. Maximum power point tracking is achieved via an
algorithm using Perturb and Observe method, with array voltage and current being used to generate the reference voltage which
should be the PV panel’s operating voltage to get maximum available power. A Takagi-Sugeno (T-S) observer has been proposed
and designed with non-measurable premise variables and the conditions of stability are given in terms of Linear Matrix Inequality
(LMI). The simulation results show the effectiveness and robustness of the proposed method.
robust observer-based control DC motor based on a photovoltaic pumping system. Maximum power point tracking is achieved via an
algorithm using Perturb and Observe method, with array voltage and current being used to generate the reference voltage which
should be the PV panel’s operating voltage to get maximum available power. A Takagi-Sugeno (T-S) observer has been proposed
and designed with non-measurable premise variables and the conditions of stability are given in terms of Linear Matrix Inequality
(LMI). The simulation results show the effectiveness and robustness of the proposed method.
Keywords:Photovoltaic, Pumping System, Fuzzy Controller,  , Takagi-Sugino (TS) Fuzzy Model, Observer, Stability, Linear Matrix Inequalities (LMIs), Maximum Power Point Tracking (MPPT), Unmeasurable Premise Variables
, Takagi-Sugino (TS) Fuzzy Model, Observer, Stability, Linear Matrix Inequalities (LMIs), Maximum Power Point Tracking (MPPT), Unmeasurable Premise Variables

1. Introduction
The standalone photovoltaic pumping systems have become a favorable solution for water supply. It earns a more market share, particularly in rural areas that have a substantial amount of insolation and have no access to an electric grid. The maximization of these systems via maximum power point tracking (MPPT) has been sufficiently exploited in the literature [1] . As a result, most commercial photovoltaic pumping systems either use conventional MPPT control (P & dO, Incremental) or not use the MPPT control [2] . For a better optimization of the energy, a pump controller is necessary. For photovoltaic pumping systems, the pump controller is essentially a DC-DC, the duty ratio is controlled by a tracking system of the maximum power point tracking (MPPT) [3] [4] . This is used to adjust the motor armature voltage and in turn the motor speed and the hydraulic power of the pump according to the irradiation level. Different types of dc-dc converters have been employed including the buck converter [5] [6] and the boost converter [7] depending on the voltage rating of the motor and the PV array.
Based on these works, we propose in this paper a  observer-based on tracking controller based on TS representation of the PV pumping system, where the weighting functions depend on non-measurable premise variables [8] -[10] . Sufficient conditions, based on Lyapunov approach and the convex optimization techniques, are formulated as an efficient one step LMI [11] to avoid the complexity of separate design steps and can be solved using MATLAB software. The block diagram of a DC pumping system is shown in Figure 1 [12] .
observer-based on tracking controller based on TS representation of the PV pumping system, where the weighting functions depend on non-measurable premise variables [8] -[10] . Sufficient conditions, based on Lyapunov approach and the convex optimization techniques, are formulated as an efficient one step LMI [11] to avoid the complexity of separate design steps and can be solved using MATLAB software. The block diagram of a DC pumping system is shown in Figure 1 [12] .
The structure of this paper is organized as follows. In Section II we describe the process of getting a T-S fuzzy model of PV system, with the DC motor pumping [13] . Section III presents the proposed control design. The stability conditions of the closed loop system are proposed in this section in terms of LMIs. In Section IV, we present the proposed strategy of the observer and the controller. In Section V, the simulation results are presented and discussed. Finally, conclusions are made in Section VI.
2. Model of Pumping System
The water pumping system is considered in this work as a standalone system, without batteries. This is a complex and nonlinear system. The complete model is difficult to use in control applications. We need an easy model to use for the synthesis of observers and controllers. It also allows estimating or adjusting the values of dynamic parameters in real time. The system consists of a single PV module, an MPPT System, and a DC water pump. In the literature, different models of PV and of the pump were used. Figure 2 shows the equivalent circuit of the boost of the PV system with water pump.
The system [3] average model is given in (1):
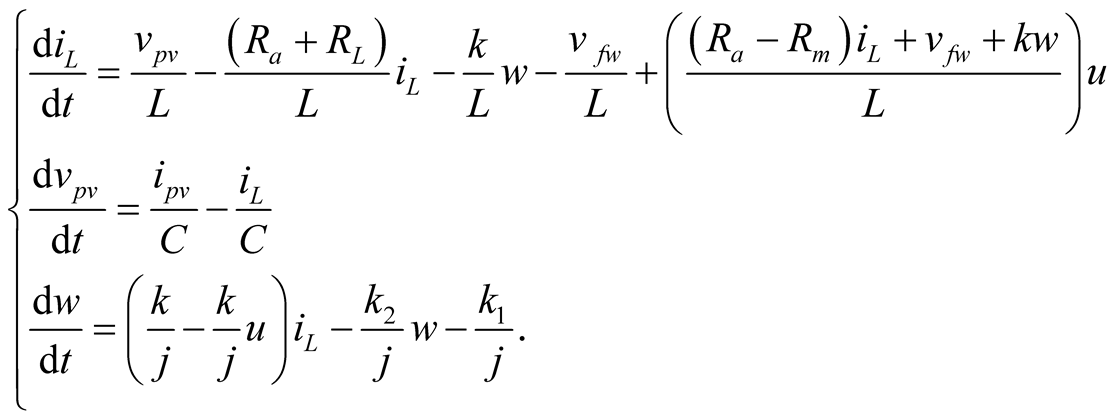 (1)
(1)
where 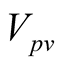 and
and 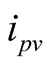 refer to the PV panel voltage and current respectively.
refer to the PV panel voltage and current respectively.![]() ,
, 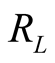 and
and ![]() are the self-inductance, resistance and current.
are the self-inductance, resistance and current.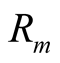 is a resistance characterizing IGBT lost.
is a resistance characterizing IGBT lost.
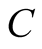 ,
, 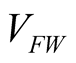 and
and ![]() are the input capacitance, the diode forward voltage and speed.
are the input capacitance, the diode forward voltage and speed. ![]() is the control input. Considering the PV current as an exogenous input, we get the state representation (2).
is the control input. Considering the PV current as an exogenous input, we get the state representation (2).
 (2)
(2)
In order to guarantee zero steady state regulation error, we develop an integral T-S fuzzy control. Let 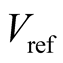 be a constant reference, the objective is to achieve that
be a constant reference, the objective is to achieve that  when
when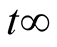 . To this end, we introduce an added state variable to account for the integral of output regulation error. Let us define the new state variable as (3):
. To this end, we introduce an added state variable to account for the integral of output regulation error. Let us define the new state variable as (3):
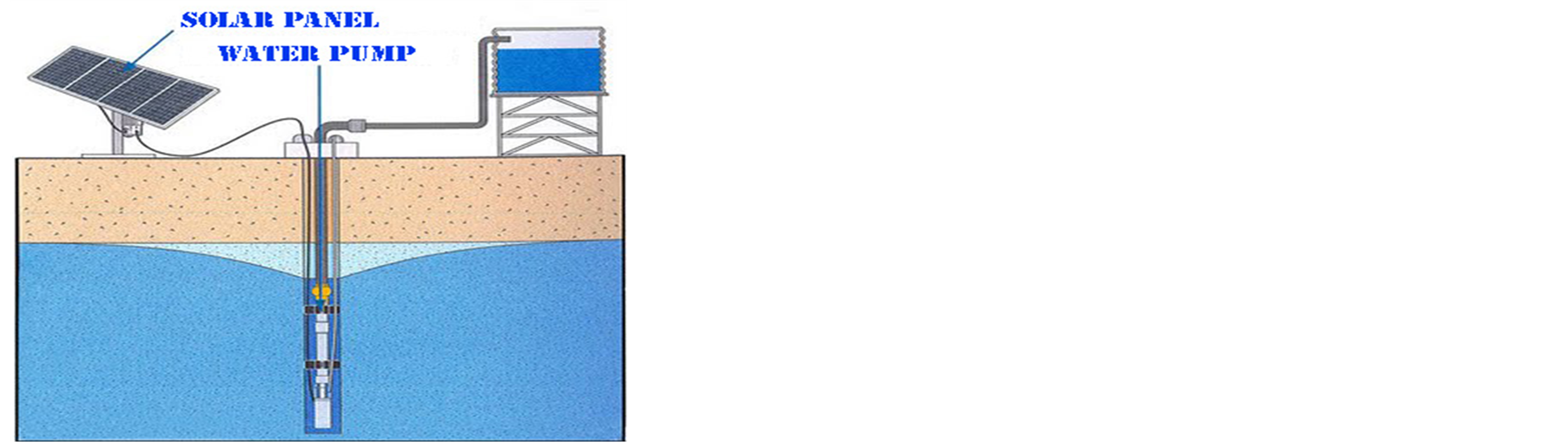
Figure 1. PV pumping system.

Figure 2. Model of PV system with a motor-pump load.
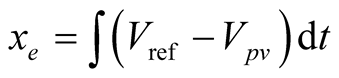 (3)
(3)
The new augmented state vector then becomes:
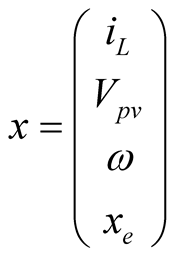 (4)
(4)
So this second integrator included previous to the input would make it smoother, benefiting the implementation, and therobustness [14] .
The augmented system can be written as (5):
 (5)
(5)
where
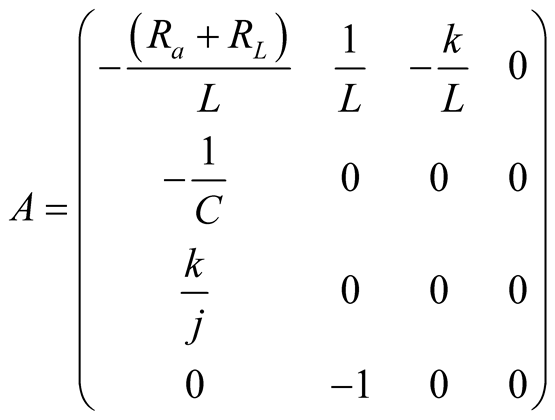 ;
; 
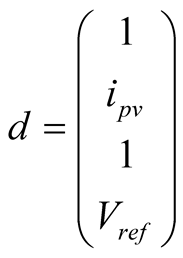 ;
; 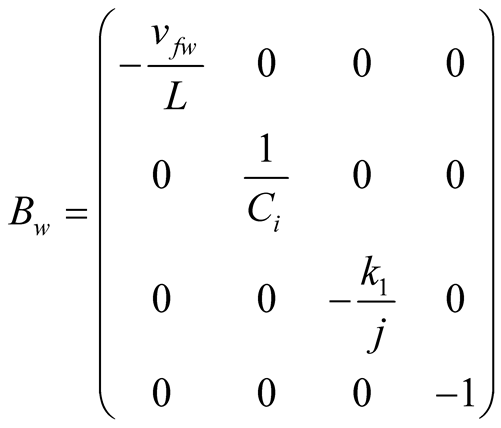
3. Control Strategy
In this work two control strategies are studied.
3.1. Perturb and Observe Algorithm
The P&P algorithm acts periodically by giving a perturbation to operating voltage  and observing the power variation
and observing the power variation 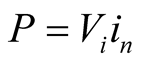 order to deduct the direction of evolution to give to the voltage reference
order to deduct the direction of evolution to give to the voltage reference . Taking into account power-voltage characteristic curve
. Taking into account power-voltage characteristic curve 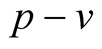 obtained under given conditions, the goal is to track the operating point at the MPP as shown in Figure 3. This algorithm measures at each
obtained under given conditions, the goal is to track the operating point at the MPP as shown in Figure 3. This algorithm measures at each ![]() instant variable
instant variable  and
and 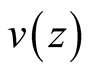 and calculates
and calculates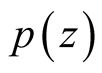 , then compares with the power calculated at
, then compares with the power calculated at 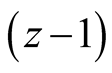 instant
instant .
.
For all the operating points where the power and current variations are positive, the algorithm that continued to perturb the system in the same direction of perturbation is reversed. The increasing of reference voltage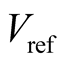 , otherwise, if these variations are negative, the direction of perturbation is reversed. The increasing or decreasing of reference
, otherwise, if these variations are negative, the direction of perturbation is reversed. The increasing or decreasing of reference  is done by tracking step
is done by tracking step . The flow chart of the P&O algorithm is presented in Figure 4. Theoretically, the algorithm is simple to implement in its basic form. However, it was noticed some oscillations around the MPP in steady state operating and this causes power loss [15] . Its functioning depends on the tracking step size applied to voltage reference
. The flow chart of the P&O algorithm is presented in Figure 4. Theoretically, the algorithm is simple to implement in its basic form. However, it was noticed some oscillations around the MPP in steady state operating and this causes power loss [15] . Its functioning depends on the tracking step size applied to voltage reference . For the same sample time of the system, the oscillations and consequently the power loss could be minimized if the tracking step would continuously get smaller [16] . Nevertheless, the response of the algorithm becomes slower.
. For the same sample time of the system, the oscillations and consequently the power loss could be minimized if the tracking step would continuously get smaller [16] . Nevertheless, the response of the algorithm becomes slower.

Figure 3. Power-Voltage characteristic of PV panel.

Figure 4. Flow chart of the P&O algorithm.
3.2. Takagi-Sugino Fuzzy Model
In this section, we present T-S fuzzy control approach that ensures robust regulation under disturbance. Consider a general nonlinear system as follows:
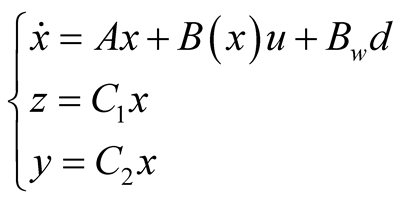 (6)
(6)
![]() is the controlled output variable and
is the controlled output variable and ![]() is the output vector.
is the output vector.
By observing the functions of ,
, 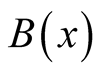 , the fuzzy premise variables are chosen as
, the fuzzy premise variables are chosen as  and
and . Then, the system (2)-(5) can be represented by the following T-S fuzzy rules: IF
. Then, the system (2)-(5) can be represented by the following T-S fuzzy rules: IF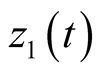 is
is 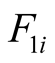 and
and 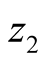 is
is , then [17] .
, then [17] .
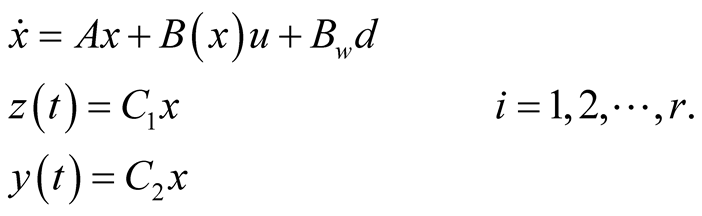 (7)
(7)
where  are the fuzzy sets,
are the fuzzy sets, ![]() is the number of fuzzy rules, and
is the number of fuzzy rules, and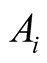 ,
, 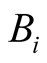 ,
,  , and
, and 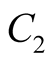 are appropriate subsystem matrices.
are appropriate subsystem matrices.
The global T-S model is then inferred as follows:
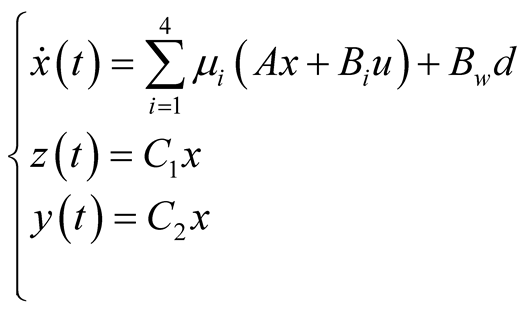 (8)
(8)
where ,
, 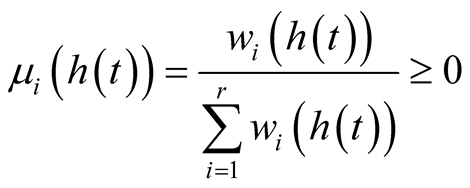 , with
, with 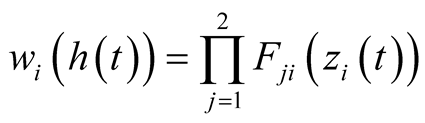 so that
so that  for all
for all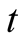 . To obtain an exact fuzzy representation of dynamic (2), the membership functions of
. To obtain an exact fuzzy representation of dynamic (2), the membership functions of ![]() and
and 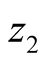 should be chosen so that
should be chosen so that 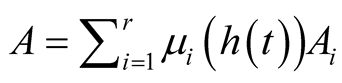 and
and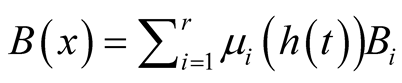 . For simplification, let us write the membership function in the general form [18] .
. For simplification, let us write the membership function in the general form [18] .
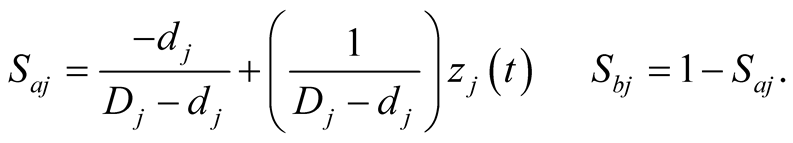
where  and
and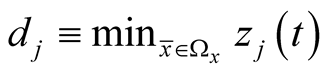 , for
, for 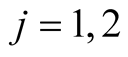 and the discussion set:
and the discussion set:  . (Note that
. (Note that 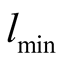 and
and 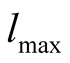 are the lower and upper bounds of variable
are the lower and upper bounds of variable 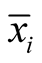 respectively).
respectively).
Hence, functions 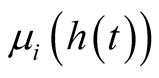 are the weighting functions depending on variable
are the weighting functions depending on variable 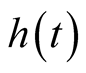 which can be measurable (as the input or the output of the system) or unmeasurable variables [19] [20] (as the state of the system) and verify the following properties:
which can be measurable (as the input or the output of the system) or unmeasurable variables [19] [20] (as the state of the system) and verify the following properties:

In the following, we assume that the weighting functions depend on the system state. Then, TS fuzzy system (7) becomes:
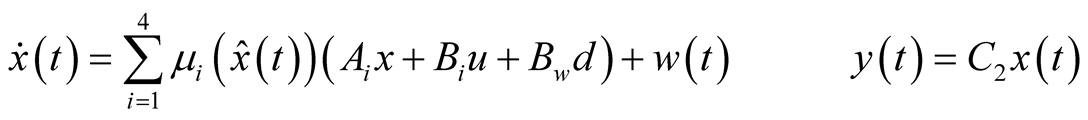 (9)
(9)
where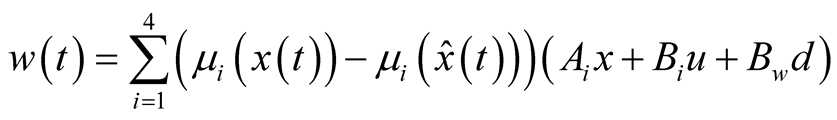 .
.
4. Fuzzy Observer Based Tracking Controller
The aim of this section is the design of the observer-based tracking control of the photovoltaic Pumping System. As the motor speed model states are not fully measurable, the designed state feedback control is based on the estimated states. We define the fuzzy controller as follows:
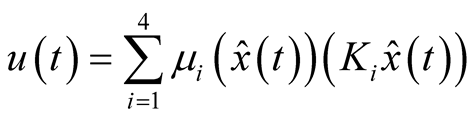 (10)
(10)
where  is the estimated state and
is the estimated state and 
 are the controller gains to be determined. Based on T-S fuzzy model of solar pump (1), the structure of the observer is defined as:
are the controller gains to be determined. Based on T-S fuzzy model of solar pump (1), the structure of the observer is defined as:
 (11)
(11)
where 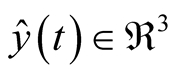 is the estimated output,
is the estimated output, 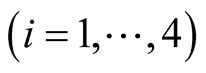
 are the observer gains to be determined.
are the observer gains to be determined.
Let’s define error of state estimation as ; then, we can find the estimation error dynamics as follows:
; then, we can find the estimation error dynamics as follows:
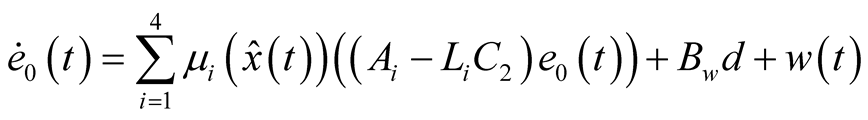 (12)
(12)
Augmented system ; can be written as
; can be written as
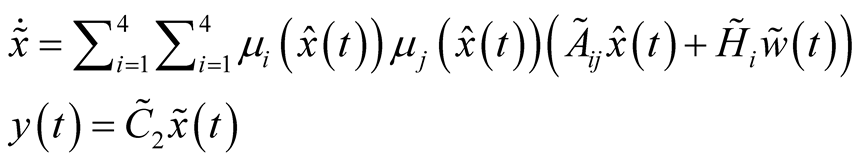 (13)
(13)
with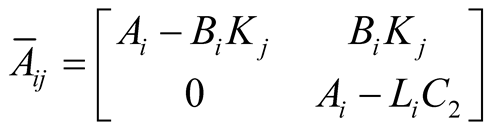 ;
;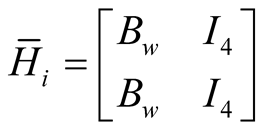 ;
; ;
; .
.
The estimation error asymptotically converges around zero and satisfies the following  performance under zero initial conditions:
performance under zero initial conditions:
 (14)
(14)
where 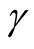 is the desired disturbance attenuation parameter.
is the desired disturbance attenuation parameter.
Theorem 1: if there exists symmetric matrices ,
,  , matrices
, matrices 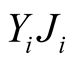 and a prescribed
and a prescribed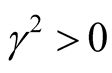 , such that the following LMI holds [21] :
, such that the following LMI holds [21] :
 (15)
(15)
where
 (16)
(16)
Controller gains 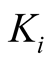 and observer gains
and observer gains  are given by:
are given by:
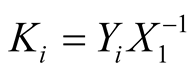 (17)
(17)
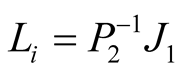 (18)
(18)
Proof
Consider the following Lyapunov function candidate:
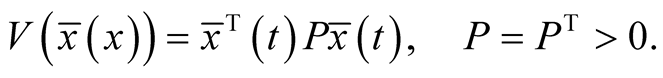 (19)
(19)
The time derivate of  (12) is given by
(12) is given by

The closed loop system with controller-based observer is stable and has  norm limited by
norm limited by ![]() if and only if:
if and only if:
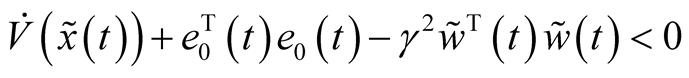 (20)
(20)
Therefore, we have
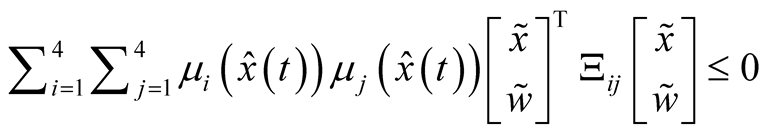 (21)
(21)
where ,
,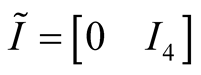 .
.
Inequality (19) is satisfied if condition 20 holds:
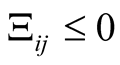 (22)
(22)
Let us consider thefollowing particular form of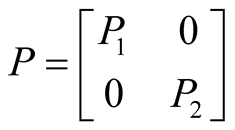 ,
, 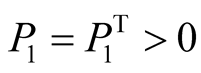 ,
, 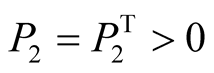 Then after simple manipulation, inequality (17) can be reformulated as:
Then after simple manipulation, inequality (17) can be reformulated as:
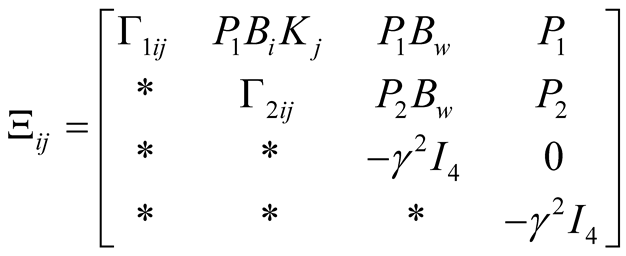 (23)
(23)
with
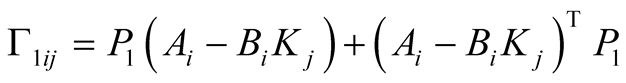 and
and .
.
It should be noted that condition (18) is nonlinear with respect variables  and
and  Then, the objective is to formulate (18) in LMI constraints.
Then, the objective is to formulate (18) in LMI constraints.
Hence, after partitioning the matrix inequality shown in (18),  becomes:
becomes:
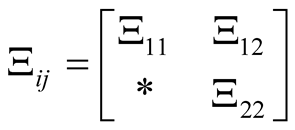 (24)
(24)
 is the upper right block of (22) and
is the upper right block of (22) and 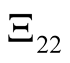 is the lower right block of (22).
is the lower right block of (22).
Lemma 1: (Congruence) Let two matrices 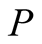 and
and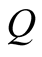 , if
, if  is positive definite and if
is positive definite and if 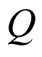 is afull column rank matrix, then matrix
is afull column rank matrix, then matrix  is positive definite.
is positive definite.
 and
and 
Post and pre-multiplying inequality (21) by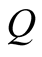 , it follows that (23) can be rewritten as:
, it follows that (23) can be rewritten as:
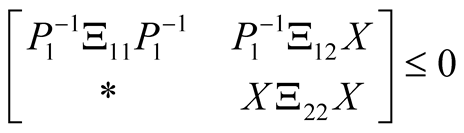 (25)
(25)
Lemma 2: Considering  a matrix
a matrix 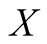 and a scalar
and a scalar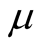 , the following holds [21] [22] :
, the following holds [21] [22] :
 (26)
(26)
By substituting (22) into (21) and using the Schur complement, then inequality (21) holds if (23), displayed below, is satisfied:
 (27)
(27)
By changing matrices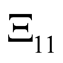 ,
,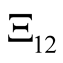 and
and  by their expressions from (19) and considering
by their expressions from (19) and considering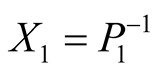 ,
,  we obtain an LMI in (14).
we obtain an LMI in (14).
5. Simulation Results
To illustrate the proposed method, the Observer based robust controller law is tested by considering the T-S Model of the photovoltaic pumping. The controller is tested by simulation. This section shows the efficiency of the designed control of system through computer simulations.
Figure 5 and Figure 6 present the climatic conditions on one day (temperature and solar irradiance).
To validate our approach, we compare these results with those given by the classical P&O method.
In Figure 7, the simulation result shows that the power obtained in our case is better than using the P&O method.
Figure 8 shows the comparison of motor speed using the two methods. We can see the difference and the importance of our approach.
Finally, the water flow obtained by the two methods is presented in Figure 9.
The errors of state estimation are given in Figure 10, where all errors asymptotically converge to zero.
The Simulation results showing the confusion of the P&O algorithm with reference voltage perturbation by a step increase in solar irradiance (Figure 11).
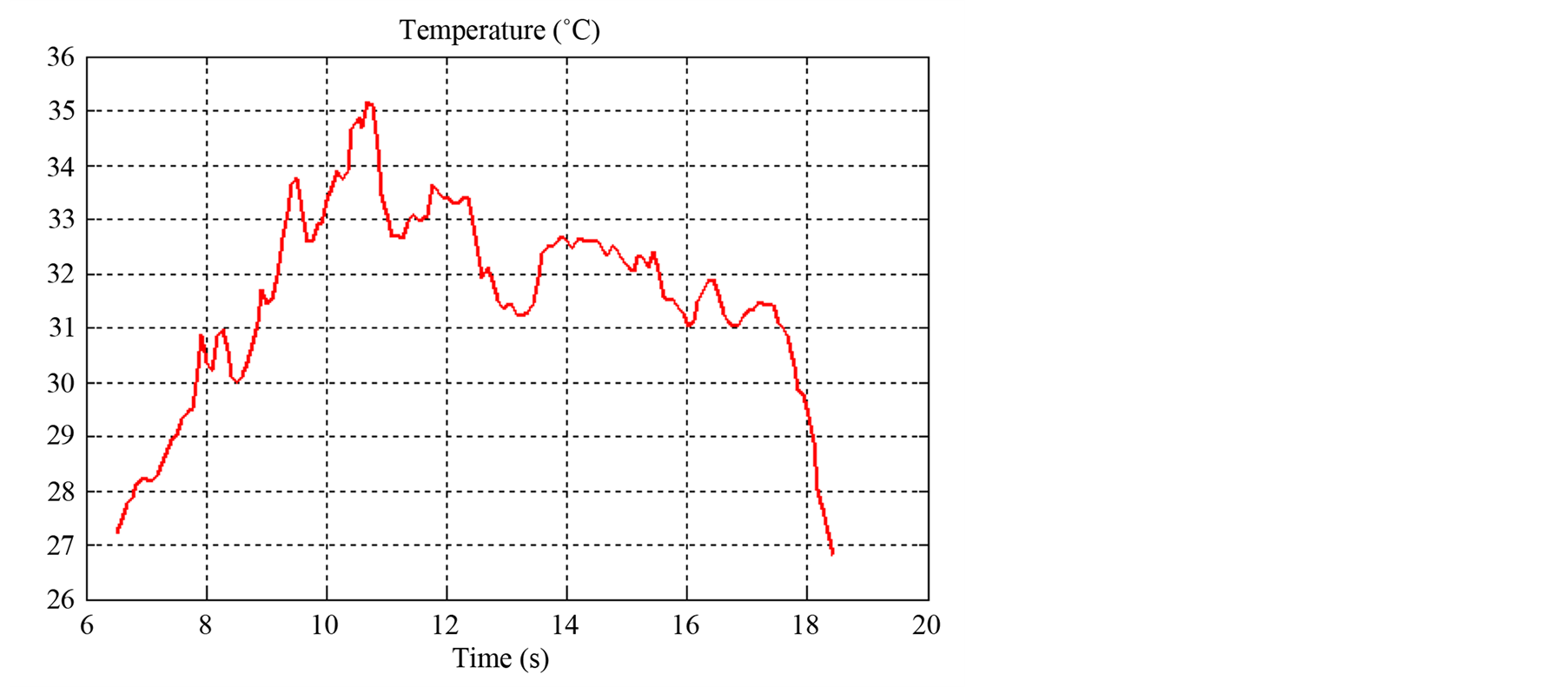
Figure 5. Temperature for a day.
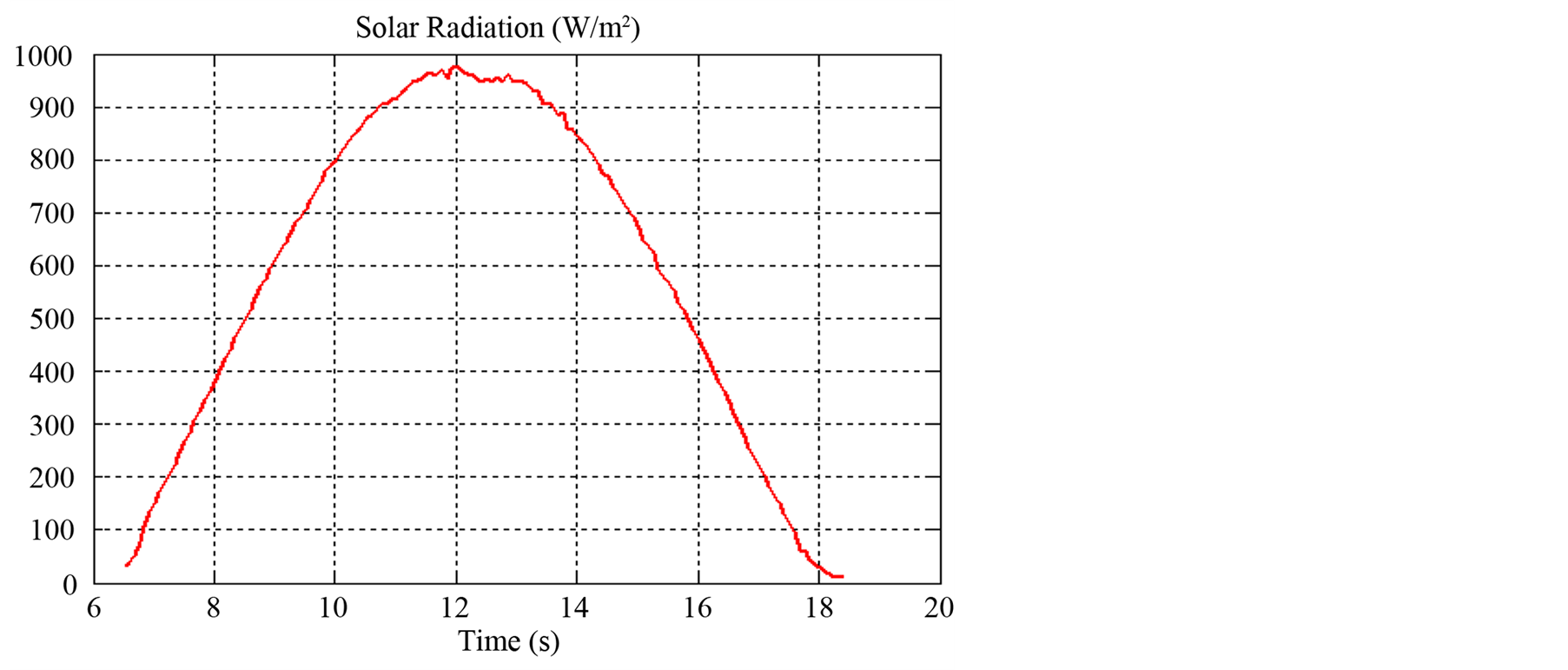
Figure 6. The solar irradiance for a day.

Figure 7. Maximum power obtained by two methods.

Figure 8. Simulated motor speed.
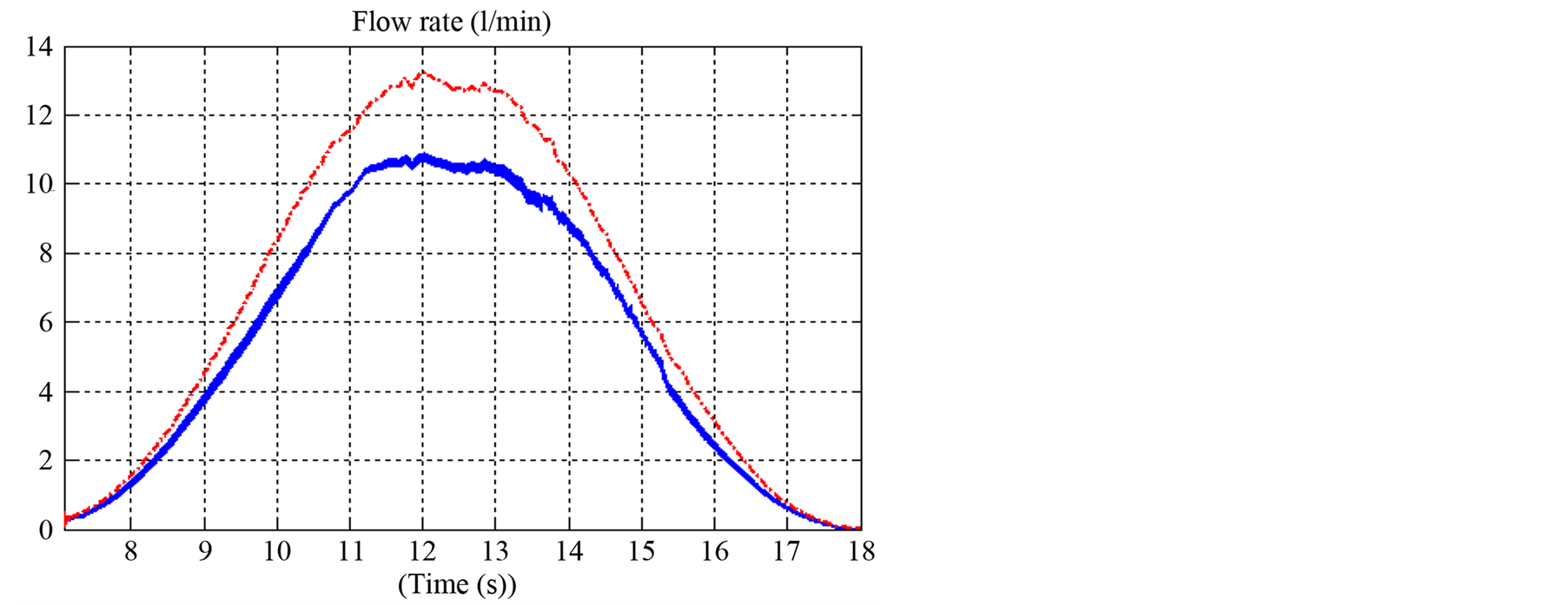
Figure 9. Simulated flow rate.
 (a)
(a) (b)
(b) (c)
(c)
Figure 10. Estimation error of (a) inductance current; (b) PV array Voltage; and (c) Motor speed.
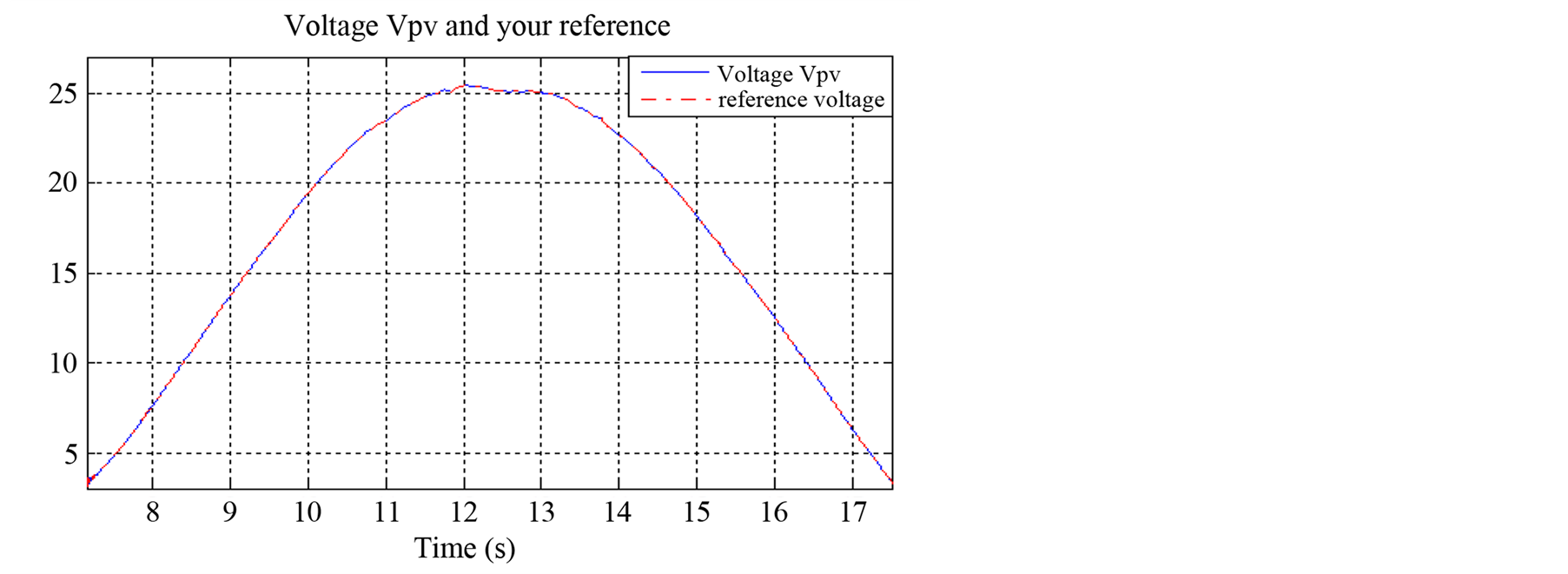
Figure 11. Voltage Vpv and your reference.
6. Conclusion
In this paper, a robust  observer-based tracking control of the photovoltaic Pumping System has been proposed. The designed controller ensures the optimum of power and guarantees a better flow of water. The stability conditions are given in terms of LMIs, which can be solved in one single step-procedure to determine the observer and the controller gains. From simulation results, the performances of the designed robust observer-based controller are satisfactory and the capability of this controller is shown under critical situations. To put that in perspective, we will test this control law on a test branch that we are developing in our laboratory.
observer-based tracking control of the photovoltaic Pumping System has been proposed. The designed controller ensures the optimum of power and guarantees a better flow of water. The stability conditions are given in terms of LMIs, which can be solved in one single step-procedure to determine the observer and the controller gains. From simulation results, the performances of the designed robust observer-based controller are satisfactory and the capability of this controller is shown under critical situations. To put that in perspective, we will test this control law on a test branch that we are developing in our laboratory.
References
- Arrouf, M. (2007) Optimisation de l’Ensemble Onduleur, Moteur et Pompe, Branches sur un Genérateur Photo-volta?que. Thèse de Doctorat, Université Mentouri de Contrainte, Constantine.�
- Khalil, H.K. (2000) Universal Integral Controllers for Minimum-Phase Nonlinear System. IEEE Transactions on Automatic Control, 45, 490-494.
- Elgendy, M.A., Zahawi, B. and Atkinson, D.J. (2012) Assessment of Perturb and Observe MPPT Algorithm Implementation Techniques for PV Pumping Applications. IEEE Transactions on Sustainable Energy, 3, 21-23.
- Elgendy, M.A., Zahawi, B. and Atkinson, D.J. (2010) Comparison of Directly Connected and Constant Voltage Controlled Photovoltaic Pumping Systems. IEEE Transactions on Sustainable Energy, 1, 184-192.
- Hadji Arab, A., Benghanem, M. and Chenlo, F. (2006) Motor-Pump System Modelization. Renewable Energy, 31, 905-913.
- Elgendy, M.A., Zahawi, B. and Atkinson, D.J. (2008) Analysis of the Performance of DC Photovoltaic Jumpings Systems with Maximum Power Point Tracking. IET International Conference on Power Electronics, Machines and Drives, York, 2008, 426-430.
- Akbaba, M. (2006) Optimum Matching Parameters of an MPPT Unit Based for a PVG-Powered Water Pumping System for Maximum Power Transfer. International Journal of Energy Research, 30, 395-409. http://dx.doi.org/10.1002/er.1157
- Ghorbel, H., Souissi, M., El Hajjaji, A. and Chaabane, M. (2011) Design of Multi-Observers for Takagi-Sugeno Systems with Unmeasurable Premise Variables: Descriptor Approach. International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Sousse, 18-20 December 2011, 250-256.
- Ichalal, D., Marx, B., Ragot, J. and Maquin, D. (2009) State Estimation of Nonlinear Systems Using Multiple Model Approach. American Control Conference (ACC), St. Louis, 10-12 June 2009, 4636-4641.
- Nagy, A., Marx, B., Mourot, G., Schutz, G. and Ragot, J. (2010) State Estimation of Two-Time Scale Multiple Models with Unmeasurable Premise Variables. Application to Biological Reactors. 49th IEEE Conférences on Décisions and Control, 15-17 December 2010, 5689-5694.
- Oudghiri, M., Chadli, M. and El Hajjaji, A. (2007) One-Step Procedure for Robust Output H1 Fuzzy Control. 15th Mediterranean Conference on Control and Automation, Athens, 27-29 June 2007, 1-6.
- Ouachani, I., Rabhi, A., El Hajjaji, A., Tidhaf, B. and Zouggar, S. (2013) A Robust Control Method for a DC Motor-Based Photovoltaic Pumping. Proceedings of the 3rd International Conference on System and Control, Algiers, 29-31 October 2013, 720-726.
- Ouachani, I., Rabhi, A., Tidhaf, B., Zouggar, S. and Elhajjaji, A. (2013) Optimization and Control for a Photovoltaic Pumping System. 2nd International Conference on Renewable Energy Research and Applications, Madrid, 20-23 October 2013, 734-739.
- Lian, K.-Y., Ouyang, Y.-L. and Wu, W.-L. (2008) Realization of Maximum Power Tracking Approach for Photovoltaic Array Systems Based on T-S Fuzzy Method. IEEE International Conference on Fuzzy Systems, Hong Kong, 1-6 June 2008, 1874-1879.
- Takagi, T. and Sugeno, M. (1985) Fuzzy Identification of Systems and Its Applications to Modeling and Control. IEEE Transactions on Systems, Man and Cybernetics, SMC-15, 116-132. http://dx.doi.org/10.1109/TSMC.1985.6313399
- Chiu, C.-S. (2010) T-S Fuzzy Maximum Power Point Tracking Control of Solar Power Generation Systems. IEEE Transactions on Energy Conversion, 25, 1123-1132.
- Ichalal, D., Marx, B., Ragot, J. and Maquin, D. (2007) Conception de multi-observateurs variables de décision non mesurables. 2 Journes Doctorales/Journes Nationales MACS, Reims.
- Boyd, S., El Ghaoui, L., Feron, E. and Balakrishnan, V. (1994) Linear Matrix Inequalities in System and Control Theory. SIAM, Philadelphia. http://dx.doi.org/10.1137/1.9781611970777
- Ichalal, D. (2009) Estimation et diagnostic de system non lineaires decrits par un modèle de Takagi-Sugeno. Institut National Polytechnique de Lorraine, Frensh.
- Guerra, T., Kruszewski, A., Vermeiren, L. and Tirmant, H. (2006) Conditions of Output Stabilization for Nonlinear Models in the Takagi-Sugeno’s Form. Fuzzy Sets and Systems, 157, 1248-1259. http://dx.doi.org/10.1016/j.fss.2005.12.006
- Tafticht, T., Agbossou, K., Doumbia, M.L. and Cheriti, A. (2008) An Improved Maximum Power Point Tracking Method for Photovoltaic Systems. Renew Energy, 33, 1508-1516. http://dx.doi.org/10.1016/j.renene.2007.08.015
- Locment, F., Sechilariu, M. and Houssamo, I. (2010) Energy Efficiency Experimental Tests Comparison of P&O Algorithm for PV Power System. Proceedings of 14th International Power Electronics and Motion Control Conference, Ohrid, 6-8 September 2010, T12-89-T12-95.

