Communications and Network
Vol.5 No.1(2013), Article ID:28238,7 pages DOI:10.4236/cn.2013.51005
Fuzzy Voice Coding with Significant Impulses Modeling and Redundant Waveform Recycling
Microelectronics Department, Escuela Superior de Ingeniería Mecánica y Eléctrica Culhuacán, Ciudad de México, México
Email: *jcnet21@yahoo.com, persia311@hotmail.com, jcsanchezgarcia@gmail.com
Received September 4, 2012; revised October 6, 2012; accepted November 8, 2012
Keywords: Coding; Signal Processing; Fuzzy Logic; Algorithms; Pattern Recognition
ABSTRACT
This paper proposes a voice codification based on two algorithms that make the wave form codification in time domain. The first uses the significant impulse model (SIM), which has as a goal to operate as an endpoint detector and as a dawn sampling, through the detection and selection of the significant valleys and crests; the second algorithm, is a redundant wave-form recycler (RWR) that uses an architecture based on fuzzy logic with an accumulative memory. The fuzzy algorithm obtains the similitude grade between the redundant wave forms, this with the objective of save into an knowledge base the patterns, based on the no supervised learning and when there are into memory, automatically there will be used to identified their arrive respect to the input signal, substituting the input block by the correspondent pattern into memory. This decoding process is using the SIM interpolation with a memory in accordance to the RWR.
1. Introduction
The voice signals digitalization to each sample, has given rise to the conventional coding techniques as PCM, which is based on the scalar quantization [1]. However, when a set of values of a waveform is quantized jointly as a single vector or entity, the process is known as vector quantization (VQ) [2]. This entity is encoded by a binary word, which is an approximation of the original vector. Each vector is encoded in comparison with a set of reference vectors stored, known as patterns [3]. Each pattern is used to represent the input vectors that are somehow identified as “similar” to this pattern [1]. The best set of patterns in the codebook, i.e. the set of reference patterns stored in memory is selected by the encoding process in accordance with an adequate fidelity measure, and a binary word is used to identify this pattern in the codebook of patterns [2].
The size and definition of the population of the codebook or training (updated during the measurement) has two critical parameters that determine the efficiency of a VQ [1-5]. There are several models that reduce both storage and computational load, but the problem is that those do not always match with the vector patterns of the incoming signal due to a phase shift [1-8].
This paper proposes two algorithms that change the perspective of VQ to adjust the patterns to the input vectors [3,4] for the input vectors recycling, used for redundancy. These algorithms are the SIM (significant impulse model) which prevents the phase shift and reduces the number of samples for voice modeling and RWR that achieves non-trained patterns recognition through the same signal recycling.
2. General Architecture
The speech coder first receives the signal into the RWR process in order to fit the voice signal by the MIS algorithm. The RWR makes a quantization of the signal which is presented as a vector and compared with patterns storage in the memory. The differences between them are evaluated by a fuzzy system; if the distances are great enough to be accepted as “similar” the system chooses this pattern to be used or in other hand the pattern is discarded as “similar” then the RWR calls another pattern in memory. This process is repeated until any of the following two cases occurs: find a pattern in memory “similar” to the input vector or can’t find any pattern which satisfies the conditions of similarity. For the first case the input vector is encoded using an index that identifies this pattern in the memory, making an adjustment in proportion using the coding that is performed by the SIM.
The Figure 1 shows the general architecture of the adaptation vector quantizer, which replaces the training patterns for recycling, adding components allowing an adequate fidelity measure into the comparison and effi-

Figure 1. Block diagram of speech coder.
cient recycling.
A binary word is needed to identify the coding algorithm performed. The decoding chooses a linear interpolation for the SIM or an i-adjusted vector magnitude σ in the case of the RWR (this process is illustrated in Figure 2).
3. Significant Impulse Modeling
To use linear interpolation for decoding, the signal is modeled based on its direction and strength properties, to allow omitting pulses having the same direction and close strength. This will reduce the number of samples needed to reproduce a signal. Although the linear correlation has good enough results when using these features to find the relationship between two signals, the modeling is not always equally benefited, particularly at high frequencies, since it adds some components to the signal, having noise. The Figure 3 shows the SIM flow diagram.
See the comparison into the Figure 4, complaining the requirements of a voice signal.
To achieve this modeling process we use the fuzzy logic if-then rules in terms of the direction and strength or magnitude. The Equations (1) and (2) show this rules respectively.
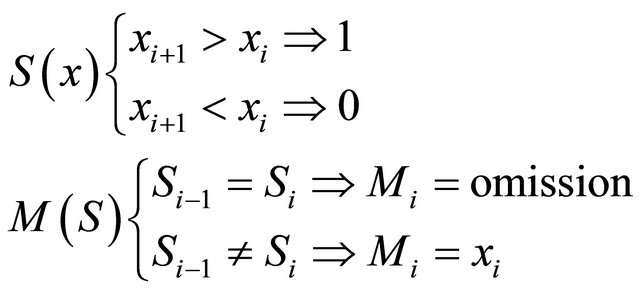 (1)
(1)
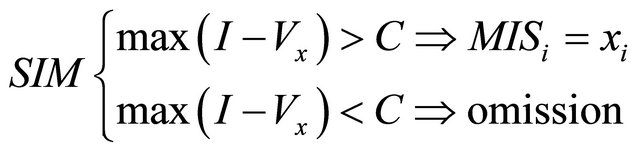 (2)
(2)
where xi is the ith sample of the signal, S(x) is the signal direction and M is the direction model. Likewise, I is the vector formed by interpolation of samples skipped by M, and Vx is the vector formed by the omitted samples M.

Figure 2. Block diagram of speech decoder.
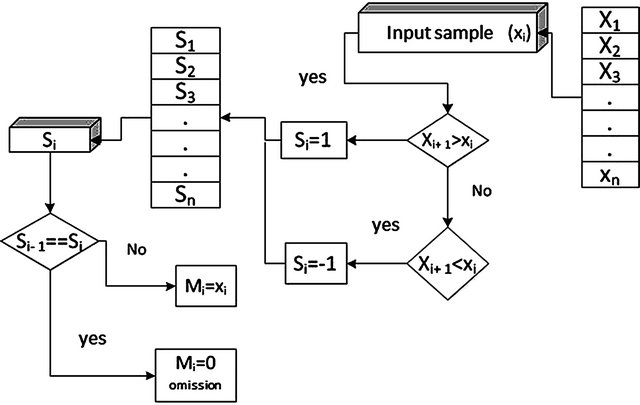
Figure 3. SIM flowchart.
4. SIM Simulations
The C constant determines the samples reduction degree needed into the SIM. The C adjustment is in accordance of the signal/noise ratio. So, in low noise conditions (approximately 16 dB) needs a samples reduction near of 50% and a correlation coefficient value greater than 0.99. As this way the benefits of a “down-sampling” (in terms of reducing samples) is obtained without lose the voice quality (see Figure 4). This reduced modeling of excitation sequences can be found in the RPE algorithm [9]. The Figure 5 shows this process.
Once the signal is modeled by the SIM the number of
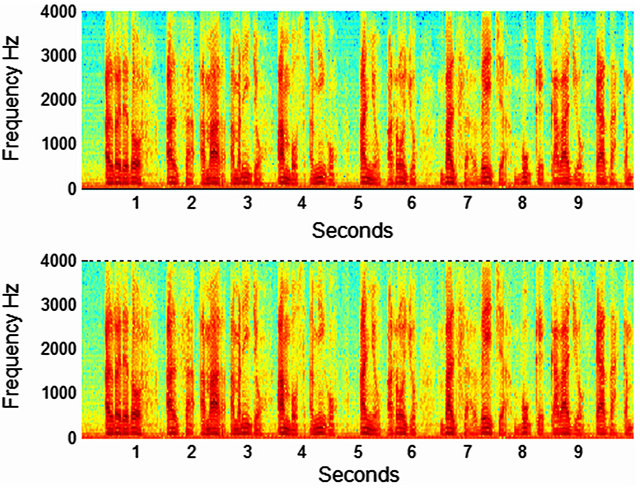
Figure 4. Spectrum comparison between the original signal (above) and the linear modeling (below).
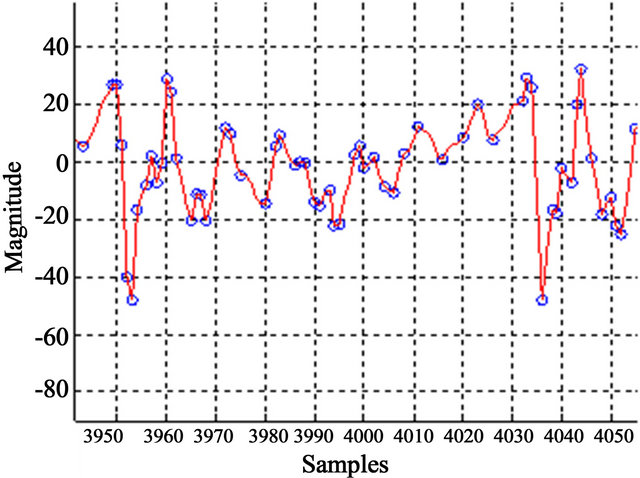
Figure 5. Comparison between the original signal and its modeled.
significant changes in the signal are count for determine if a signal frame is voiced or unvoiced with similar results than a zero crossing detector.
5. Redundant Waveform Recycling
To make a description of the RWR, we assume that the size of the frame is 11.25 ms, since this is approximately the greatest average elongation that a pattern can have [3, 10]. The pattern searching using the RWR is based on the premise of comparing the patterns having a frame of the incoming signal that is shifted one sample per iteration. However, this assumption implies a large computational loading, because the number of iterations. One solution is to increase the number of shifted samples per iteration, but this could involve problems into the pattern recognition stage. The solution proposed in this paper is to shift the frame of the signal into each significant permutation, causing the number of samples displaced in order to switch in accordance to the changes in the signal, where such changes are described by the SIM. The Figure 6 shows the RWR architecture [11,12].
The knowledge base optimized by the histogram, whichis limited in size without significant reduction of the performance pattern detection. As show in Figure 7, the knowledge base has a reduction in approximately one quarter, maintaining the higher occurrence patterns.
In accordance with the conditions described above, the patterns are compared in terms of its direction and strength. The effect has previously been defined by the SIM and the difference in magnitude is defined by Equation (3). How-
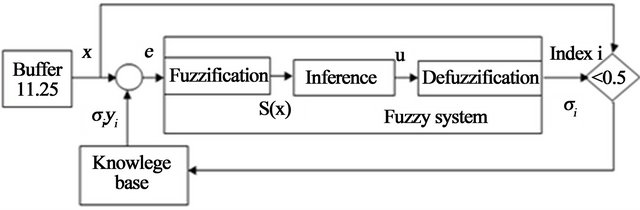
Figure 6. RWR block diagram.
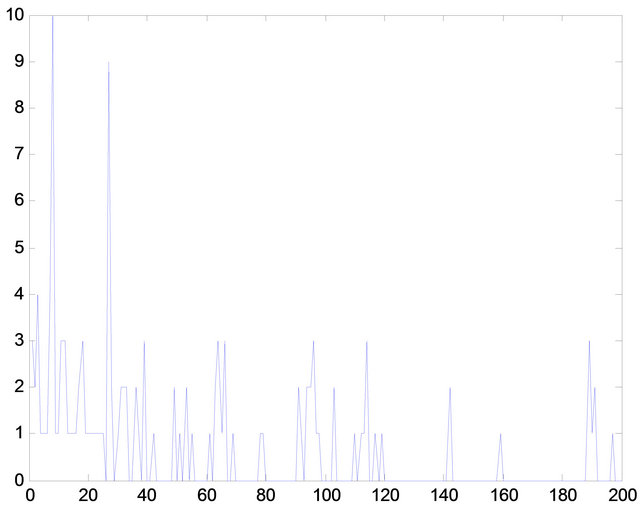
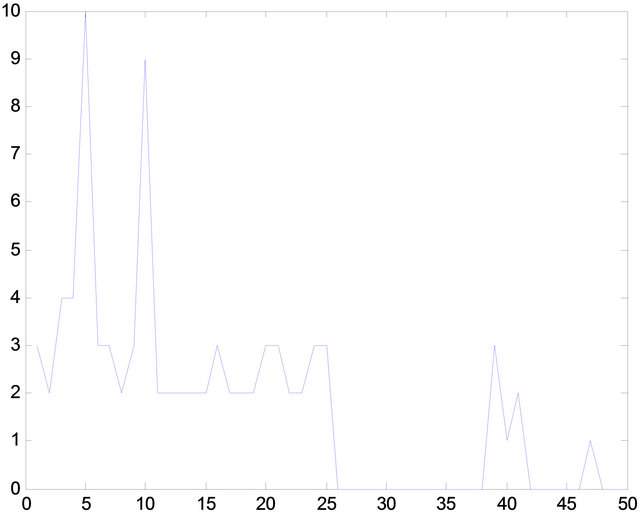
Figure 7. Histogram comparison between knowledge base no-optimized (above) and optimized one (below).
ever, before any comparison it is necessary to standardize their scales obeying the Equation (4).
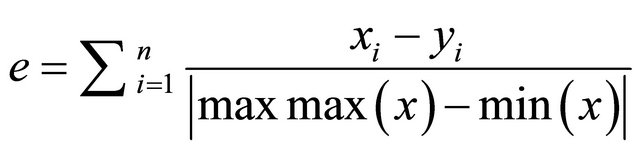 (3)
(3)
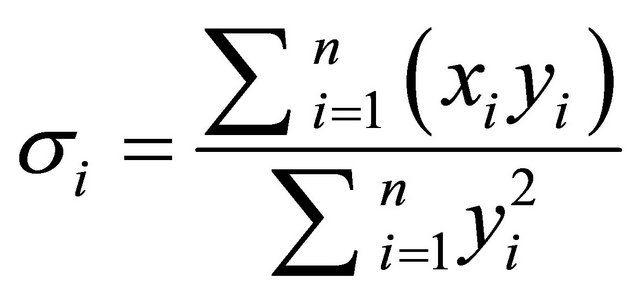 (4)
(4)
The comparisons were evaluated by a fuzzy Mamdani algorithm. The membership functions (MF) are sigmoidal (as shown in Figures 8 and 9), these determine the degree of the antecedent and its correspondence of every rule, since there are two rules (direction and difference) using the “and” fuzzy operator to unify. Once the antecedent is defined by a single number, the consequent is defined by aggregation of two rules: with the pattern “similar” or “different”, each of them with their respective membership function. Finally the centroid method is used in order to do the defuzzification process
[12-14].
The output of the fuzzy system requires a condition of “likeness” (see Equation (5)) to allow a more subjective comparison of the waveform.
 (5)
(5)
where SC is the coded signal, SD is the output of the fuzzy system, P is the size of the displacement and L is the length of the pattern.
Finally Figure 10 show the behavior of the Membership functions.
6. RWR Simulations
Using a voice signal of 30 seconds containing words in Spanish phonetics [11], the RWR achieve the recycling of many patterns in speech frames, between 20% and
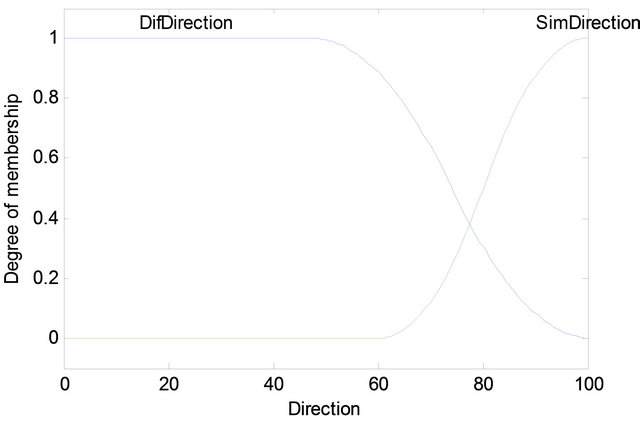
Figure 8. MF for direction.
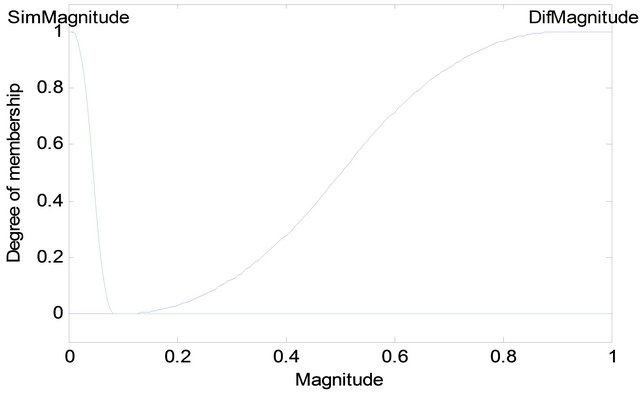
Figure 9. MF for difference in magnitude.
70% of them, depending on whether the frame is mostly voiced or mostly unvoiced. The size of the knowledge base depends of this frame. The Figure 8 shows the last syllable of the Spanish word segment “alrededor” with an elongation of about 166.6 ms, which 90 ms were recycled in 8 patterns, each of them with 11.25 ms (see Figure 8 using the minimum segments of the black line) [14]. This saves about 50% of the voice frame. In addition, the SIM reduction only needs 22.6 ms of the originnal frame for modeling 166.6 ms of the speech; this implies a total compression rate of 0.13. The Figure 11 shows the unvoiced and voiced frames.
As in Figure 10, the correlation between recycled patterns and the original signal is not perfect, but something more important than a perfect correlation is that significant changes are in phase. This means that it is possible reproduce the majority of the frequency components. The fuzzy comparator achieves this purpose in most of the cases [15]. For to obtain the best approximation into the correlation, the process use a minimum error distance in order to classify the signal pattern as seen into the Figure 12.
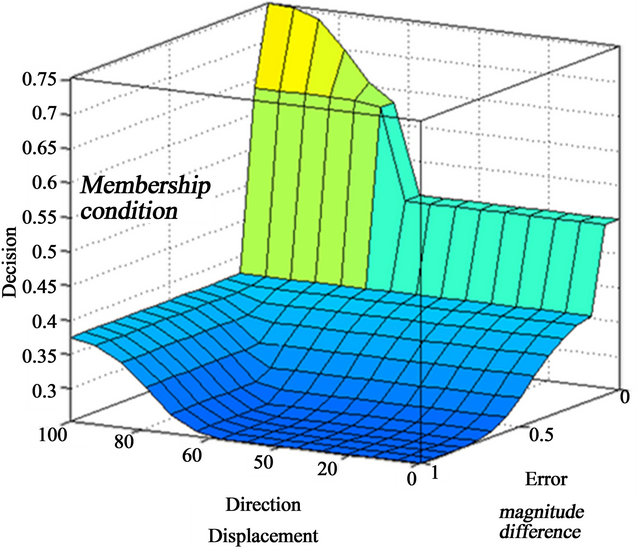
Figure 10. Membership function behavior.
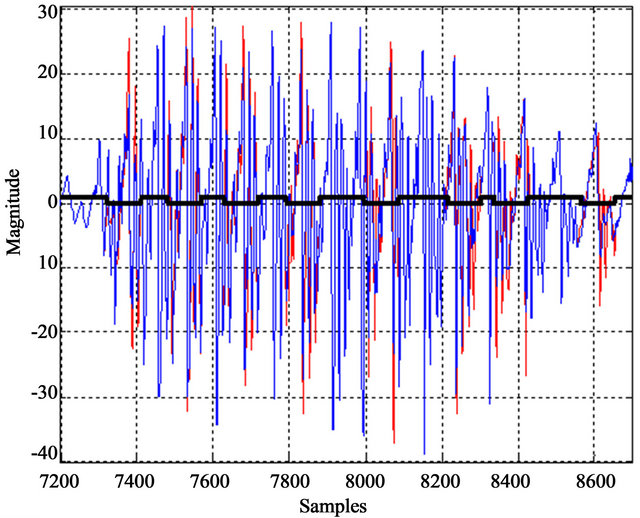
Figure 11. Comparison between the original speech and the reconstructed signal by RWR and SIM.
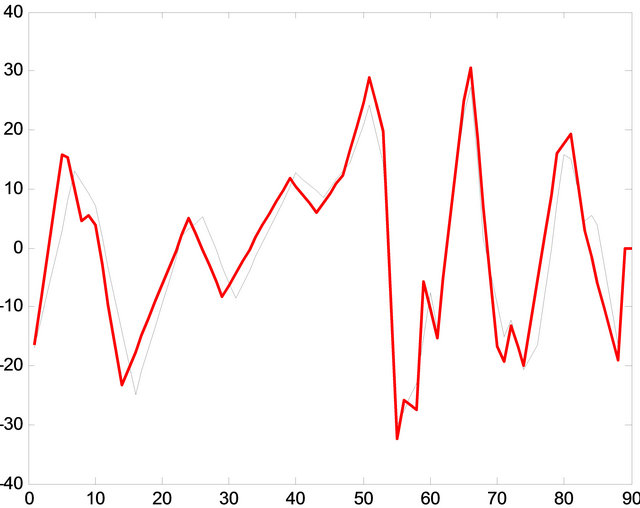
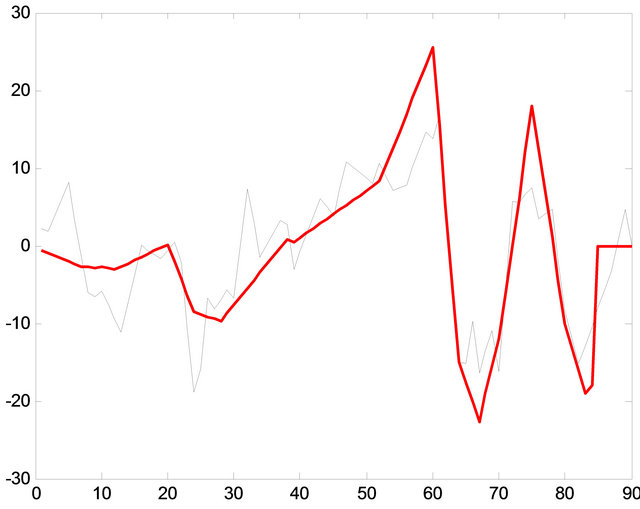
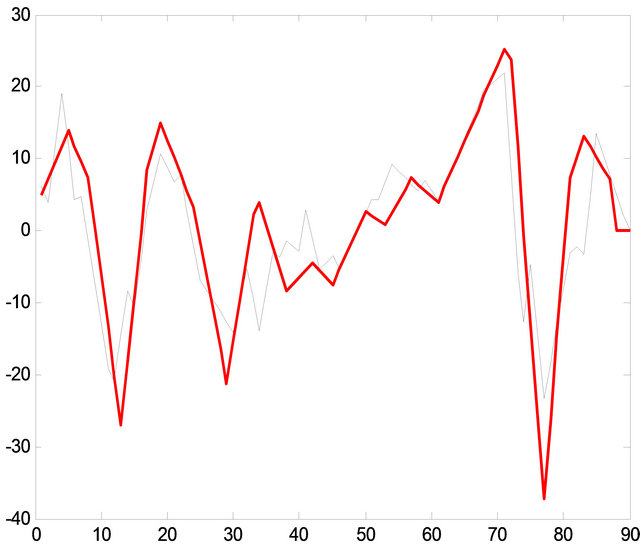
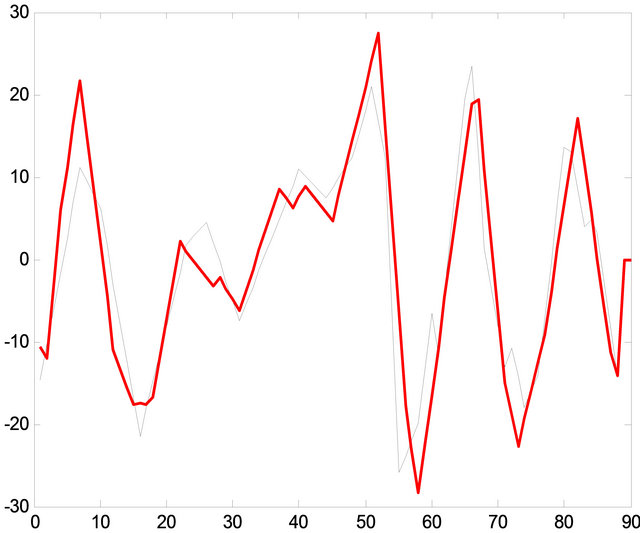
Figure 12. Comparison between the original signal and the 8 patterns recycled.
7. Conclusions
The algorithms mentioned above are simulated with a input speech signal into the architecture with sampling frequency of 8 KHz and 8 bits of resolution. Under these conditions the compression rates range is from 0.2 to 0.125 for the SIM and between 0.7 and 0.2 for the RWR are achieved. Having a joint with a compression ratio up to 0.04 achieved. The decoded voice quality can be improved with a 3 KHz low pass filter applied to the reconstructed signal. With an acceptable quality at compression rate of 0.15 according to the MOS (Mean Opinion Score) test applied on a population of 20 people.
By this way the architecture suggests that the process for defining an input vector through a window, which is displaced in relation to the changes in the voice signal, greatly discards the similar waveforms described as patterns, due loss of their synchronization in its window, involving a more complex detection using an algorithm that forces their detection.
REFERENCES
- A. Gersho and V. Cuperman, “Vector Quantization: A pattern-Matching Technique for Speech Coding,” IEEE Communications Magazine, Vol. 21, No. 9, 1983, pp. 15- 21.
- J. Makhoul, S. Roucos and H. Gish, “Vector Quantization in Speech Coding,” Proceedings of the IEEE, Vol. 73, No. 11, 1985, pp. 1551-1588.
- A. M. Kondoz, “Digital Speech Coding for Low Bit Rate Communication Systems,” 2nd Edition, John Wiley & Sons, Chichester, 2004. doi:10.1002/0470870109
- A. Vasuki and P. Vanathi, “A Review of Vector Quantization Techniques,” IEEE Potentials, Vol. 25, No. 4, 2006, pp. 39-47.
- N. B. Karayiannis, “A Methodology for Constructing Fuzzy Algorithms for Learning Vector Quantization,” IEEE Transactions on Neural Networks, Vol. 8, No. 3, 1977, pp. 505-518.
- C. E. Pedreira, “Learning Vector Quantization with Training Data Selections,” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 28, No. 1, 2006, pp. 157-162.
- C. W. Tsai, C.Y. Lee, M. C. Chiang and C. S. Yang, “A Fast VQ Codebook Generation Algorithm via Pattern Reduction,” Pattern Recognition Letters, Vol. 30, No. 7, 2009, pp. 653-660.
- G. E. Tsekouras, D. Darzentas, I. Drakoulaki and A. D. Niros, “Fast Fuzzy Vector Quantization,” IEEE International Conference on Fuzzy Systems, Barcelona, 18-23 July 2010, pp. 1-8. doi:10.1109/FUZZY.2010.5584446
- P. Kroon, E. Deprettere, R. Sluyter, AT&T Bell Laboratories, “Regular-Pulse Excitation—A Novel Approach to Effective and Efficient Multipulse Coding of Speech,” IEEE Transactions on Acoustics, Speech and Signal Processing, Vol. 34, No. 5, 1986, pp. 1054-1063.
- I. McLoughlin, “Applied Speech and Audio Processing with Matlab® Examples,” Cambringe University Press, Cambringe, 2009. doi:10.1017/CBO9780511609640
- I. J. Hualde, “The Sounds of Spanish,” Cambrindge University Press, Cambringe, 2005.
- E. Mamdani, “Applications of Fuzzy Algorithms for Control of Simple Dynamic Plant,” Proceedings of the Institution of Electrical Engineers, Vol. 121, No. 12, 1974, pp.1585-1588.
- L. Zadeh, “Fuzzy Sets, Information and Control,” Information and Control, Vol. 8, No. 3, 1965, pp. 338-353. doi:10.1016/S0019-9958(65)90241-X
- T. Takagi and M. Sugeno, “Fuzzy Identification of Systems and Its Applications to Modelling and Control,” IEEE Transactions and Systems, Man, and Cybernetics, Vol. 15, No. 1, 1986, pp. 116-132. doi:10.1109/TSMC.1985.6313399
- K. M. Passino, “Fuzzy Control,” Addison Wesley, Boston, 1998.
NOTES
*Corresponding author.

