Int'l J. of Communications, Network and System Sciences
Vol.3 No.2(2010), Article ID:1267,7 pages DOI:10.4236/ijcns.2010.32020
Community Analysis of Social Network in MMOG
School of Electric & Information Engineering, Beijing Jiaotong University, Beijing, China
Email: pangsheng_bjtu@yahoo.com.cn, changjiachen@sina.com
Received November 6, 2009; revised November 29, 2009; accepted December 27, 2009
Keywords: MMOG, Behavior, Community, Social Network
Abstract
Massive Multiplayer Online Games (MMOG) have attracted millions of players in recent years. In MMOG, players organize themselves voluntarily and fulfill collective tasks together. Because each player can join different activities, one player may show different social relationship with others in different activities. In the paper we proposed the incremental label propagation algorithm to search the cliques accurately and quickly. Then we analyzed community structure characteristics on multi-activities. It's shown that the existing guild organization cannot satisfy the requirements of multi-activities in MMOG, which motivates us to devise new community communication channels and platforms in future.
1. Introduction
About ten years ago, Internet grows explosively in China. Making friends through online chatting is fabulous and very popular at that time. Though a “net friend”, who is sitting in front of a certain PC at the other side of the wire, is mysterious and dangerous maybe, this platform indeed creates a new way to make friends. Nowadays, Internet has become a widely used tool for us to communicate with others. Similarly, the massive multiplayer online games (MMOG) also provide us a platform for making friends as well as entertaining. In MMOG, the virtual relationship network of the players resulted from their behaviors, which we call “relationship network” in briefly in this paper, has also become part of the real social relationship network of people, and the virtual world is becoming a field for the study of social behavior [1,2]. On the other hand, the players' behaviors in terms of their interaction can affect the performance of the game’s network system [3,4].
We name players of the game as nodes, and the players who participate in the same activities at the same time as neighbors. Thus the relationship network structure is formed. According to the pattern of multiple activities in the WoW, we divide these activities into two categories: Player vs. Environment (PVE) and Player vs. Player (PVP). PVE is composed of raid activities and party ones, while PVP contains battle ground activities. To show the characteristics of the players’ behaviors and reveal the unreasonable point of the existing policies and organizational style of the game, we go deep into the relationship network in the pattern of multiple activities in the World of Warcraft (WoW).
In the paper we proposed the time-based incremental label propagation algorithm to reveal the community structure of relationship network formed in one activity. And then we analysed the characteristic of overlap between these structures of different activities. Our major contributions are as follows:
1) Most networks will evolve with time instead of keeping unchanged in reality. Therefore, we proposed the time-based incremental label propagation algorithm, which is based on label propagation algorithm [5]. Our time-based algorithm will only take the local changed vertexes into consideration. The computation time is greatly decreased, while vertex (edge) is added, deleted or modified. The algorithm will definitely converge since the original version of label propagation algorithm converges.
2) Just as in real life, the clique of friends is different from the clique of workmates. In MMOG, there is little correlation among network structures of different activities. However, it is the overlap of these structures of different activities that extend the whole relationship network which turns the path reachable from unreachable. This indicates that the present guild organization cannot meet the requirements of multi-activities, which motivates us to devise new community communication channels and platforms in future.
The paper is organized as follows. In Section 2 we will present some related works on MMOG. We will go on to introduce the WoW and trace collection in Section 3. In Section 4, the time-based incremental abel propagation algorithm will be proposed, and we will present the characteristics of multi-layer network structures which orrespond to multiple activities in Section 5. We will give some oncluding remarks and future work in Section 6.
2. Related Work
This work analyzes the player relationship network resulted from the players’ behavior in terms of their interaction. We adopt the measurement traces of Shaolong Li’s work [6], and put our emphasis on the characteristics of multi-activities in the paper.
2.1. Players’ Behaviors Analysis
As the virtual relationship network has also become part of the real social relationship network, many studies focus on psychological factors. N. Ducheneaut [1] observed player-to-player interaction in two locations in the game Star Wars Galaxies. They analyzed user interaction patterns, mainly gestures and utterances, and discussed how they were affected by the structure of the game. In [7], the authors believed it was important to study social interactions within the virtual communities. They examined the WoW as an online community, and investigated the degree to which it exhibits characteristics of a new tribalism.
However, it is equally important to understand users’ behavior for network researchers, because how users act determines how well network systems perform, such as online games. In [3], authors analyzed player behavior in term of their social interaction, and revealed several featured patterns of player interaction. And then they proposed some suggestions to improve game system based on their studies. Tobias Fritsch [2] defined “hardcore” player and classified four game types (FPS, RTS, RPG and SG). They analyzed “hardcore” players’ distribution of age and education level respectively for the four game types. The results of their statistical analysis can be used to improve the current game design and retail strategies. Lia C. Rodrigues [8] employed self-organizing maps to find clusters from MMOG, and designed a fuzzy system to improve the performance of the algorithm. But the algorithm must be trained for every MMOG before using it.
2.2. Clique Finding
The GN algorithm [9], proposed by Newman and Girvan in 2004 is used to find cliques in the graph, which is substantially classic and widely-used. GN algorithm has two definitive features: firstly, it involves iterative removal of edges from the network to split it into communities, the edges removed being identified using any one of possible “edge betweenness” measures; secondly, these measures are, crucially, recalculated after each removal. They also propose a measure to estimate the strength of the community structure found by our algorithms, which gives us an objective metric for choosing the number of communities into which a network should be divided. They also demonstrate that GN algorithm is highly effective at discovering community structure in both computer-generated and real-world network data [9,10]. But the disadvantage is the high time complexity of calculation, thus it is only applicable in small-scale network.
Raghavan proposed a localized community detection algorithm [5] based on label propagation. Each node is initialized with a unique label and at every iteration step of the algorithm each node adopts a label that a maximum number of its neighbors have, with ties broken uniformly randomly. As the labels propagate through the network in this manner, densely connected groups of nodes form a consensus on their labels. At the end of the algorithm, nodes having the same labels are grouped together as communities, as shown in Figure 1. The advantage of this algorithm over the others is its simplicity and time efficiency. Its time complexity can reach nearly linear time. In the paper we modified the algorithm to meet the demands of real time analysis and demonstrations.
Nearly all the community detecting methods cant tell us when the communities found are good ones or which of the divisions are the best ones for a given network. To answer these questions, Newman and Girvan define a measure of the quality of a particular division of a network modularity [11], denoted by Q, which is a numerical index to assess how good a particular division is. For a division with g groups, a g £ g matrix e is defined whose element eij is the fraction of edges in the original network that connect vertices in group i to those in group j. ai which is the sum of any row (or column) of e corresponds to the fraction of links connected to group i. Then the modularity is defined as follows:
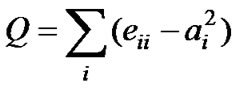 (1)
(1)
Physically, Q is the fraction of all edges that lie within communities minus the expected value of the same quantity in a graph in which the vertices have the same degrees but edges are placed at random without regard for the communities. A value of Q = 0 indicates that the community structure is no stronger than would be expected by random chance and values other than zero represent deviations from randomness. Local peaks in the modularity during the progress of the community struc-
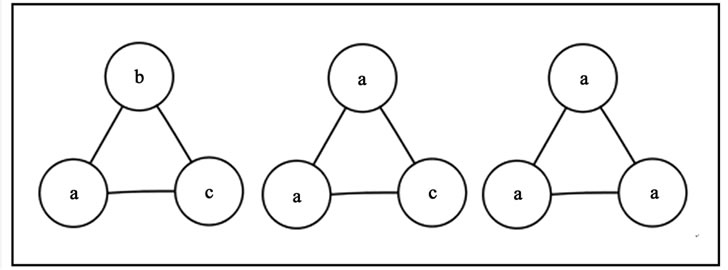
Figure 1. An example of label propagation algorithm.
ture algorithm indicate particularly good divisions of the network. The definition and application of the modularity is independent of the particular community structure algorithm used, and it can therefore also be applied to any other algorithm [3]. In practice, the modularity Q typically falls in the range from about 0.3 to 0.7 [9].
3. Game Virtual World and Datasets
World of Warcraft (WoW) is one of the most popular MMOGs, which has attracted 11.5 millions players online till Dec. 24, 2008. The virtual game world consists of many kinds of regions, and those game world regions can be classified into two categories: some regions which can be reached by all players are called world regions, while the others which only accept group players who must join in a team are called dungeons. Thus, we can identify which dungeons and activities the players are participating by the locations of them. At the same time, one dungeon can accept multiple groups simultaneously, but each group is in its independent environment. Therefore, players of the same group can not be in another group dungeon environment, while players in the same dungeon may belong to different groups. By the way, almost all players in one dungeon leave with their teammates concurrently.
To get application-level traces, we set up a monitor as a client. The monitor is a PC which is equipped with a 2.4 GHz Pentium 4 CPU and 1GB RAM. The monitor is attached to game program as a plugin. The modified client disguises itself as a normal player, who sends requests to game server periodically. A little like database query, the client can initiate many kinds of requests according to different query conditions, such as level, race and profess sion. Every response includes the information about all players who satisfy the query standard. The information contains the profile of each player: level, race, profession, location, guild, name, and online time. A round of complete scan for players lasts for 10 minutes which contain about 1200 requests.
The datasets record the information from the servernamed ‘AoLaJiEr’ in the 2nd (Beijing) game district be

Table 1. Datasets statistics (WoW).

Table 2. Region statistics (WoW).
tween Apr. 9, 2006 and Apr. 16, 2006. There are 221053 items in total and each of them records state information of one online player at that moment. There are 91 record hours and 7137 players involved in our datasets. Table 1 and Table 2 display data statistics of our collected traces.
4. Time-Based Incremental Label Propagation Algorithm
In reality most networks will evolve with time instead of keeping unchanged. For example, in P2P networks, every client will go online and off-line from time to time, thus the topology of the overlay networks will definitely change with the dynamics of these peers. Upon every change of the networks, traditionally the algorithm has to run again to get the results. The disadvantage of this kind of algorithms is its high computational cost and long time consumption. To deal with the above problems, we propose the incremental label propagation algorithm.
4.1. Method
The label propagation algorithm was proposed in [5]. It’s a fast algorithm which tries to find out the cliques with nearly linear time complexity. The idea is rather simple. Each vertex will be allocated the label (group) number randomly at first, and then the label will be changed based on the neighbors’ labels. The vertex will be given the label which the majority of its neighbors have. The algorithm iterates until no change can be made. The label propagation algorithm is proposed in the following steps:
1) bInitialize the labels at all nodes in the network. For a given node, its label is n.
2) Arrange the nodes in the network in a random sequence X.
3) Each node changes its label to maximum number of the same label among its neighbors in the order of sequence X.
4) Iterate the above two steps 2 and 3 until no labels can be changed.
It has been proved that it works well for static networks. However, in reality most networks will evolve with time instead of keeping unchanged. For example, in P2P networks, every client will go online and off-line from time to time, thus the topology of the overlay networks will definitely change with the dynamics of these peers. Upon every change of the networks, traditionally the algorithm has to run again to get the results. The disadvantage of this kind of algorithms is its high computational cost and long time consumption.
To deal with the above problems, we propose the timebased incremental label propagation algorithm in the paper. The algorithm tries to deal with the network changes incrementally. That is, when the new vertex (edge) joins or the old vertex (edge) leaves the network, the algorithm will be executed locally instead of globally. Our idea is simple, but it works effectively. Time domain is discretized into time intervals of the same length. For each round, the algorithm only considers the vertexes or edges changed in previous interval. The algorithm will be run locally and iteratively until no labels can be changed.
In our algorithm, we add the time interval sequence as well as the label number in the label. Thus, a vertex can be labeled as (t, g) in which t denotes the time sequence while g represents the group this vertex belongs to. When the new edge is added, the labels of the two vertexes which are adjacent to the edge will both be updated. It should be noted that, when there are two different labels which same number of neighbors have, the vertex will follow the label which has bigger t. Then these updated vertexes will calculate the new labels until no changes can be made. One example which adopts our time-based incremental label propagation algorithm is drawn in Figure 2.
The formal time-based incremental label propagation algorithm can be defined as follows:
1) For each new edge which is added during time interval t, the two vertexes which are incident to the edge will be labeled as (t, m) and (t, n). These two vertexes are recorded as the new labeled nodes.
2) All new labeled nodes and their neighbors are added to the vertex calculation sequence X in terms of random order.
3) Each element in sequence X is fetched one by one and the new label is determined according to the original label propagation algorithm. Similarly, vertexes whose labels are changed will be recorded as new labeled nodes. If there are two or more different labels with same number of neighbors, we will follow the label of the neighbors with bigger t.
Iterate the above two steps 2 and 3 until no labels can be changed.
4.2. Validity of the Algorithm
Newman [11] proposed that the divisions of the network can be evaluated using a measure they call modularity Q. We use a real network and the modularity to prove our algorithm’s validity.
The network of the well-known “karate club study of Zachary includes 34 vertices, as shown in Figure 3(a). This network is divided into two communities correctly by our algorithm, as shown in Figure 4. The value of the modularity Q for this partition is 0.488, which is better than the value 0.381 reported by A. Clauset [12]. The number 3 vertex is grouped correctly with our method, whereas it is grouped wrongly by GN algorithm [11].
However, the algorithm does not converge at the unique result, when the random calculate sequence X is different. In Figure 3(a), the partition of the network is exactly same with the real community structure. But the result of Figure 3(b) is different from the real structure.
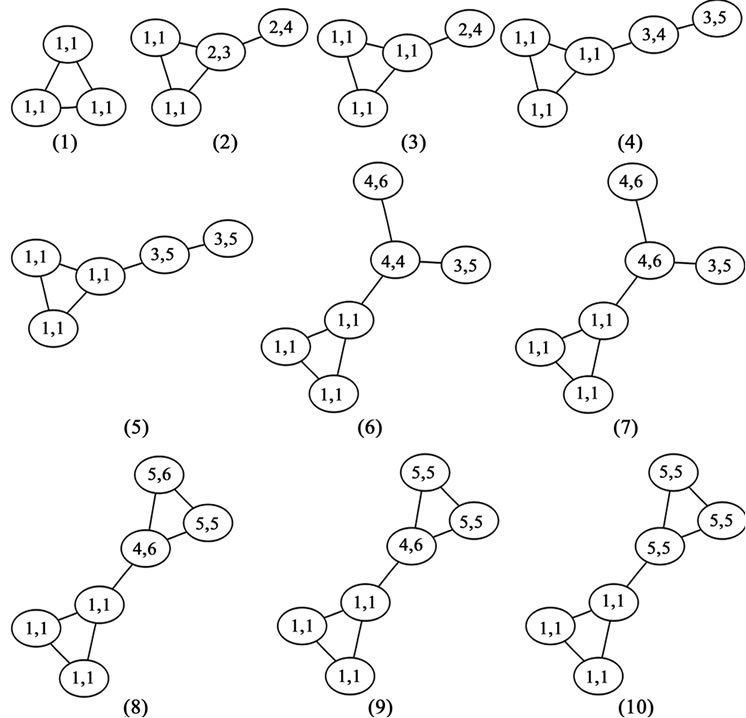
Figure 2. An example of time-based incremental label propagation algorithm.
 (a)
(a)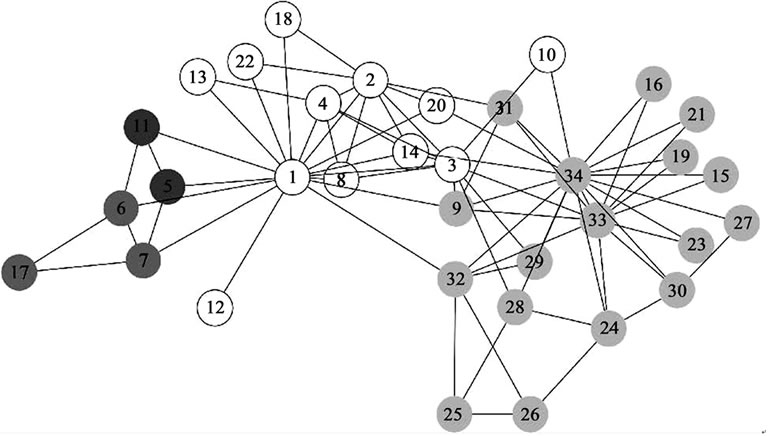 (b)
(b)
Figure 3. The network of friendships between individuals in the karate club study of Zachary [9]. The administrator and the instructor are represented by nodes 1 and 33, respectively.The communities can be identified by their shades of grey colors. (a) The result is same with real community structure; (b) The result is different from the real community structure.
4.3. Time Complexity
Label propagation algorithm takes near-linear time run its completion [5]. Each iteration of the label propagation algorithm takes linear tim in the number of edges O(m)).They also found 95% of the nodes or more are classified correctly by the end of iteration 5. When the algorithm terminates, it is possible that two or more disconnected groups of nodes have the same label (the groups are connected in the network via other nodes of different labels). In such case, after the algorithm terminates one can run a simple breadth-first search on the sub-networks of each individual groups to separate the disconnected communities. This requires an overall time of O(m + n).
When the new edge is added, the labels of the two vertexes which are adjacent to the edge will both be updated. The vertexes of the new-added edges and their neighbor vertexes are added into local random calculation sequence 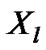 It just takes time in the number of local edges connected to the local vertexes (
It just takes time in the number of local edges connected to the local vertexes (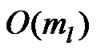 ). Similarly to the propagation algorithm, the overall time is
). Similarly to the propagation algorithm, the overall time is 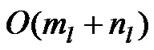 in the worst case.
in the worst case.
5. Structure Analysis on Multi-Activities
Players can participate in different activities at any time, therefore, for each activity we can get the network of players. For example, in 2006, WoW can provide players with raid activity, party activity and battle ground activity. Among them, only well-organized guilds can play the raid activity, while the party and battle ground activities are free for every player. However, it will be revealed that the players in battle ground are strongly organized too. Thus, different activities which WoW provides combined with the behaviors of the players will result in the network structure of multiple layers, and each layer corresponds to one activity.
Based on our traces, we preprocess our traces for the convenience of better analysis. Because players with short online time and low level will not possible to participate in all activities, the core network is composed of players with long online time. We only take the 60-level players who kept online for 240 minutes a week in five big guilds as the objects for network structure analysis.
In general, the average shortest length of WoW player network is 3.097 and the clustering coefficient is 0.553,

Table 3. Table type styles.
which show that the network is rather dense for players above 30 online minutes a week. Table 3 shows the player number and online time statistics for multiple activities. It’s revealed that the numbers of players who take only one or two (and above) activities are 879 and 848 respectively. The number is similar while the total online time is greatly different (the latter is 1.85 times of the former)! It indicates that attracting players to take multiple activities will increase their online time effectively, and the profits of the game operators will be greatly improved for the time-based charging strategies in most MMOG games.
In the section we choose datasets of 60-level players who come from 5 large guilds and play 240 minutes per week as our research targets. The goal of the section is to analyze the community structures of different activities and the relationship among these structures.
 (a)
(a) (b)
(b)
Figure 4. Guild vs. activities. (a) Original graph for all activities. (b) Structure graph for all activities.
5.1. Multi-Layer Player Networks
In WoW a player can only take one kind of activity at one time slot, however, a player can take different activities at different time slots. Therefore, supposing we draw a relationship network for each activity, some players who take several kinds of activities can exist in multiple relationship networks. If we project all these layers of
 (a)
(a)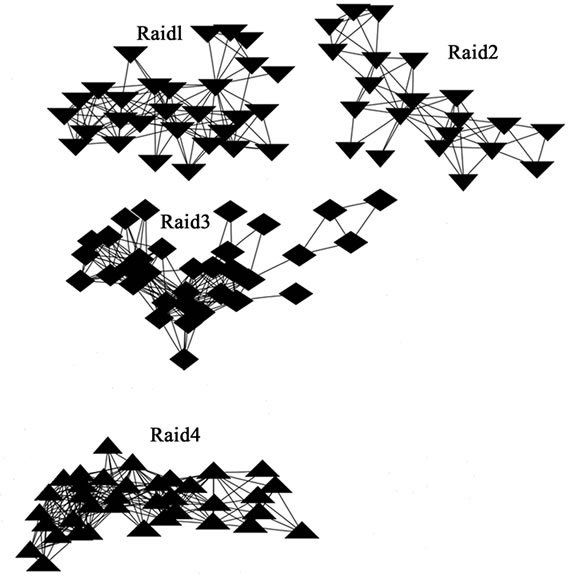 (b)
(b) (c)
(c)
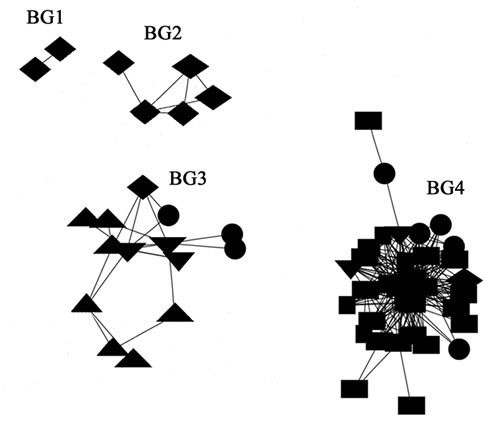
Figure 5. Guild vs. activities. (a) Battle ground activity subgraph; (b) Raid activity subgraph; (c) Party activity subgraph.
networks into one plane, we will get the whole player network. In Figures 4(a) and (b), it’s plotted the whole player network. The independent relationship networks of battle ground, raid and party activities are drawn in
Figure 5(a), (b) and (c) respectively. Some clusters of players only attend one activity, such as BG4 in (a), Raid1 and Raid2 in (b). However, it’s the players who take multiple activities that make the whole player network connectable. For example, the cluster BG3 in (a) connects cluster Raid3 and cluster.
Furthermore, considering the extent of overlap between two clusters, we define the overlap coefficient correspondingly. Suppose that there are 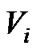 players in i cluster and
players in i cluster and 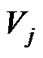 ones in j cluster, the number of players who are in both clusters is
ones in j cluster, the number of players who are in both clusters is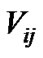 , thus the overlap coefficient
, thus the overlap coefficient  is defined as
is defined as . We choose two relationship networks of raid and battle ground activities, and calculate the overlap coefficient between any two clusters from different activities. The maximum and average coefficient for these clusters are 0.182 and 0.022, respectively, which indicates that there are overlaps among the clusters from different activities.
. We choose two relationship networks of raid and battle ground activities, and calculate the overlap coefficient between any two clusters from different activities. The maximum and average coefficient for these clusters are 0.182 and 0.022, respectively, which indicates that there are overlaps among the clusters from different activities.
5.2. Guild Organization vs. Activities
There are strong cluster characteristics in battle ground and raid activities, which can be observed in Figure 5(a) and (b) respectively. From the design philosophy of WoWraid activity will definitely show strong cluster effect because the task must be well organized in advance. To our surprise, from the random organized battle ground activity, we can also observe the effect, and the clustering coefficient of BG4 is rather high (0.581). The cluster is gradually formed instead of planned beforehand.
In addition, in Figure 4 and Figure 5 different node shapes are adopted and they represent different guilds in WoW. Guild in an in-game organization is for real-time communication and chatting. In WoW a player can only join in one guild. This mechanism does works well in some activities, such as raid activities in Figure 5(b). However, in some activities, one cluster is often composed of players who come from several guilds, such as BG3 and BG4 Figure 5(a) in battle ground activity, though there is strong connectivity in the cluster.
To measure the relationship between guild structures and activities, we propose the concept of guild organization coefficient . Firstly, the clusters are found by the time-based incremental label propagation algorithm. In a cluster, if there are fewer guilds in the cluster, or there is higher ratio of nodes in the biggest guild, the cluster shows stronger organization. The definitions of the parameters are shown in Table 4. We define the guild organization coefficient as the average of
. Firstly, the clusters are found by the time-based incremental label propagation algorithm. In a cluster, if there are fewer guilds in the cluster, or there is higher ratio of nodes in the biggest guild, the cluster shows stronger organization. The definitions of the parameters are shown in Table 4. We define the guild organization coefficient as the average of 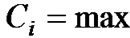
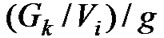 throughout all clusters in certain activity.
throughout all clusters in certain activity.
In Table 5 we list the guild organization coefficient on each activity. The guild organization coefficient for wellorganized activity, such as raid activity, is 1. Though there is no need for the organization of party activity, the coefficient reaches to 0.536, too. For battle ground activity, we have shown in previous subsection that stable organization is required since there are strong clusters in the activity. However, the relative low coefficient (0.376) shows that the present guild organization cannot meet this requirement. In all, the guild regulations should be developed according to the activities for player may play different activities with different swarm of players. The limit that one player can only join in one guild should be eliminated.
6. Conclusions
In the paper, we measured one of the most popular MMOG called WoW and traced the behaviors of many players. It’s revealed the structure characteristics how the players are organized. The overlap among different activities can make the whole player network connectable. Some key players who are active in multiple activities take responsibility to connect players of these activities. Furthermore, there are some activities which show great organization while some don’t. In addition, the guild organization works well for some activities and doesn’t for some others. New policies and organization style should be promoted.
In the future, we will collect datasets for longer time and try to analyze these characteristics theoretically. We’ll also try to propose a network structure model to satisfy the development of multi-activities.
7. Acknowledgment
This work is supported by China 973 2007CB307101 and the National Natural Science Foundation of China (60772043, 60672069).
8. References
[1] N. Ducheneaut and R. J. Moore, “The social side of gaming: A study of interaction patterns in a massively multiplayer online game,” In CSCW’04: Proceedings of the 2004 ACM Conference on Computer Supported Cooperative Work, pp. 360–369, 2004.
[2] T. Fritsch, B. Voigt, and J. Schiller, “Distribution of online hardcore player behavior (How hardcore are you?) ,” Netgames’06, 2006.
[3] K. T. Chen and C. L. Lei, “Network game design: Hints and implications of player interaction,” Netgames’06, 2006.
[4] K. Luyten, K. Thys, S. Huypens, and K. Coninx, “Telebuddies on the move: Social stitching to enhance the networked gaming experience,” Netgames’06, 2006.
[5] U. N. Raghavan, R. Albert, and S. Kumara, “Near linear time algorithm to detect community structures in largescale networks,” Physical Review E, Vol. 76, 036106, 2007.
[6] S. L. Li, C. J. Chen, and L. Li, “Using group interaction of players to prevent in-game cheat in network games,” First International Symposium on Data, Privacy and E-Commerce, pp. 47–49, 2007.
[7] T. W. Brignall, III, and T. L. Van Valey, “An online community as a new tribalism: The world of warcraft,” Proceedings of the 40th Annual Hawaii International Conference on System Sciences, 2007.
[8] L. C. Rodrigues, C. A. M. Lima, P. P. B. de Oliveira, and P. N. Mustaro, “Clusterization of an online game community through self-organizing maps and an evolved fuzzy system,” Fourth International Conference on Natural Computation, 2008.
[9] M. E. J. Newman and M. Girvan, “Finding and evaluating community structure in networks,” Physics Review E, Vol. 69, 026113, 2004.
[10] M. E. J. Newman, “Detecting community structure in network,” The European Physical Journal B - Condensed Matter, Vol. 38, No. 2, 2004.
[11] M. E. J. Newman, “Modularity and community structure in networks,” Physics 0602124, Vo1, 17, February 2006.
[12] Clauset, M. E. J. Newman, and C. Moore, “Finding community structure in very large networks,” Physics Review E, Vol. 70, 06111, 2004.

