ABSTRACT

4-bit linear relations play an important role in cryptanalysis of 4-bit crypto S-boxes. 4-bit finite differences have also been a major part of cryptanalysis of 4-bit S-boxes. Existence of all 4-bit linear relations have been counted for all of 16 input and 16 output 4-bit bit patterns of 4-bit Crypto S-boxes said as S-boxes has been reported in Linear Cryptanalysis of 4-bit S-boxes. Count of existing finite differences from each element of output S-boxes to distant output S-boxes have been noted in Differential Cryptanalysis of S-boxes. In this paper a brief review of these two cryptanalytic methods for 4-bit S-boxes has been introduced in a very lucid and conceptual manner. Two new analysis techniques, one to search for the existing linear approximations among the input vectors (IPVs) and output Boolean functions (BFs) of a particular S-box has also been introduced in this paper. The search is limited to find the existing linear relations or approximations in the contrary to count the number of existent linear relations among all 16, 4-bit input and output bit patterns within all possible linear approximations. Another is to find number of balanced BFs in difference output S-boxes. Better the number of Balanced BFs, Better the security.

Keywords:

Linear Cryptanalysis, Differential Cryptanalysis, Substitution Boxes, S-Boxes, Cryptography, Cryptanalysis

1. Introduction

Substitution boxes or S-boxes have been a part of block ciphers from the birth of Commercial Computer Cryptography by Horst Feistel in IBM Research [1] . A 4-bit S-box contains 16 elements [2] . If they are unique and distinct then the S-box has been termed as 4-bit crypto S-box. A 4-bit Crypto S-box contains 16 unique and distinct elements vary from 0 to F in hex and index of each element which are unique and distinct also. They also vary from 0 to F in hex and follow a monotonically increasing sequential order. The elements of a Crypto 4-bit S-box may be sequential or partly sequential or non-sequential in order [2] . The elements of index of S-box also construct an identity Crypto S-box and termed as input S-box. A brief Literature survey of related literatures has been given in Section 2.

In Differential Cryptanalysis of 4-bit Crypto S-boxes the 16 distant input S-Boxes have been obtained by xor operation with each of 16 input differences varies from 0 to F in hex to 16 elements of input S-box. The 16 distant S-boxes have been obtained by shuffling the elements of the original S-box in a certain order in which the elements of the input S-boxes have been shuffled in concerned distant input S-boxes. The 16 elements of each S-box and the elements in corresponding position of corresponding distant S-box has been xored to obtain the Difference S-box. The Difference S-Box may or may not be a Crypto S-Box since it may not have all unique and distinct elements in it. The count of each element from 0 to F in Difference S-box has been noted and put in Difference Distribution Table (DDT) for analysis of the S-box [3] [4] . The concept has been reviewed in Subsection 3.3 of Section 3.

In this paper a new algorithm using 4-bit BFs for Differential Cryptanalysis of 4-bit S-boxes have been introduced. An input S-box can be decomposed into four 4-bit Input Vectors (IPVs) with Decimal Equivalents 255 for 4^th IPV, 3855 for 3^rd IPV, 13,107 for 2nd IPV, and 21,845 for 1st IPV respectively. Now we complement all IPVs one, two, three and four at a time to obtain 16, 4-bit Distant input S-boxes. Each of four Output BFs is shifted according to the Shift of four IPVs of input S-boxes to form four IPVs of Distant input S-boxes to obtain Distant S-boxes. The four 4-bit output BFs of S-boxes are xored bitwise with four 4-bit BFs of Distant S-boxes to obtain four 4-bit Difference BFs. For 16 Distant Output S-boxes there are 64 Difference BFs. Difference BFs are checked for balanced-ness i.e. for at most uncertainty. The Table in which the balanced-nesses of 64 Difference BFs have been noted is called as Differential Analysis Table (DAT). The Theory has been elaborated in Subsection 3.4 of Section 3.

In Linear Cryptanalysis of 4-bit S-boxes, every 4-bit linear relations have been tested for a particular 4-bit Crypto S-box. The presence of each 4-bit unique linear relation is checked by satisfaction of each of them for all 16, 4-bit unique input bit patterns and corresponding 4-bit output bit patterns, generated from the index of each element and each element respectively of that particular Crypto S-box. If they are satisfied 8 times out of 16 operations for all 4-bit unique input bit patterns and corresponding 4-bit output bit patterns, then the existence of the 4-bit linear equation is at a stake. The probability of presence and absence of a 4-bit linear relation both are (=8/16) 1/2. If a 4-bit linear equation is satisfied 0 times then it can be concluded that the given 4-bit linear relation is absent for that particular 4-bit Crypto S-box. If a 4-bit linear equation is satisfied 16 times then it can also be concluded that the given 4-bit linear relation is present for that particular 4-bit Crypto S-box. In both the cases full information is adverted to the cryptanalysts. The concept of Probability Bias was introduced to predict the randomization ability of that 4-bit S-box from the probability of presence or absence of unique 4-bit linear relations. The result is better for cryptanalysts if the probability of presence or absences of unique 4-bit linear equations are far away from 1/2 or near to 0 or 1. If the probabilities of presence or absence of all unique 4-bit linear relations are 1/2 or close to 1/2, then the 4-bit Crypto S-box is said to be linear cryptanalysis immune, since the existence of maximum 4-bit linear relations for that 4-bit Crypto S-box is hard to predict [3] [4] . Heys also introduced the concept of Linear Approximation Table (LAT) in which the numbers of times, each 4-bit unique linear relation have been satisfied for all 16, unique 4-bit input bit patterns and corresponding 4-bit output bit patterns of a crypto S-box have been noted. The result is better for a cryptanalysts if the numbers of 8s in the table are less. If numbers of 8s are much more than the other numbers in the table then the 4-bit Crypto S-box is said to be more linear cryptanalysis immune [3] [4] .

In another look an input S-box can be decomposed into four 4-bit Input Vectors (IPVs) with Decimal Equivalents 255 for 4th IPV, 3855 for 3^rd IPV, 13,107 for 2nd IPV, and 21,845 for 1st IPV respectively. The S-box can also be decomposed into 4, 4-bit Output BFs (OPBFs). Each IPV can be denoted as an input variable of a linear relation and OPBF as a output variable and “+” as xor operation. Linear relations have been checked for satisfaction and 16-bit output variables (OPVs) due to linear relations have been checked for balancedness. Balanced OPVs indicates, out of 16 bits of IPVs and OPBFs, 8 bits satisfies the linear relation and 8 bits is out of satisfaction, i.e. best uncertainty. 256 4-bit Linear relations have been operated on 4, 16-bit IPVs and 4, 16-bit OPBFs and 256 OPVs have been generated. The count of number of 1s in OPVs have been put in Linear Approximation Table or LAT. Better the number of 8s in LAT, better the S-box security [3] [4] . The concept has been reviewed in brief in Subsection 4.2. of Section 4.

In this paper a new technique to find the existing Linear Relations or Linear Approximations for a particular 4-bit S-box has been introduced. If the nonlinear part of the ANF equation of a 4-bit output BF is absent or calculated to be 0 then the equation is termed as a Linear Relation or Approximation. Searching for number of existing linear relations through this method is ended up with Number of Existing Linear Relations. I.e. the goal to conclude the security of a 4-bit bijective S-box has been attended in a very lucid manner by this method. The method has been described in Subsection 4.3 of Section 4.

Result and Analysis of all four algorithms have been given in Section 5. The conclusion and Acknowledgements have been made in Section 6 and Section 7 respectively.

2. Literature Survey

In this section an exhaustive relevant Literature survey with their specific references has been introduced to crypto literature. In Section 2.1 the relevant topic has been cryptography and cryptology, in Section 2.2 the topic has been Linear Cryptanalysis, in Section 2.3 the topic has been Differential Cryptanalysis, in Section 2.4 the topic has been cryptanalysis of stream ciphers and at last in Section 2.5 the relevant topic has been Strict Avalanche Criterion (SAC) of substitution boxes.

2.1. Cryptography and Cryptology

In end of Twentieth Century a bible of Cryptography had been introduced [5] . The various concepts involved in cryptography and also some information on cryptanalysis had been provided to Crypto-community in late nineties [6] . A simplified version of DES that has the architecture of DES but has much lesser rounds and much lesser bits had also been proposed at the same time. The cipher has also been better for educational purposes [7] . Later in early twenty first century an organized pathway towards learning how to cryptanalyze had been charted [8] . Almost at the same time a new cipher as a candidate for the new AES, main concepts and issues involve in block cipher design and cryptanalysis had also been proposed [9] that is also a measure of cipher strength. A vital preliminary introduction to cryptanalysis has also been introduced to cryptanalysts [10] . At the same time somewhat similar notion as [10] but uses a more descriptive approach and focused on linear cryptanalysis and differential cryptanalysis of a given SPN cipher had been elaborated [11] . Particularly, it discusses DES-like ciphers that had been extended with it [12] . Comparison of modes of operations such as CBC, CFB, OFB and ECB had also been elaborated [13] . A new cipher called Camelia had been introduced with its cryptanalysis technique to demonstrate the strength of the cipher [14] . History of Commercial Computer Cryptography and classical ciphers and the effect of cryptography on society had also been introduced in this queue [15] . The requirements of a good cryptosystem and cryptanalysis had also been demonstrated later [16] . Description of Rijndael, the new AES provides good insight into many creative cryptographic techniques that increases cipher strength had been included in literature. A bit Later a highly mathematical path to explain cryptologic concepts had also been introduced [17] . Investigation of the security of Ron Rivest’s DESX construction, a cheaper alternative to Triple DES had been elaborated [18] . A nice provision to an encyclopedic look at the design, analysis and applications of cryptographic techniques had been depicted later [19] and last but not the least a good explanation on why cryptography has been hard and the issues which cryptographers have to consider in designing ciphers had been elaborated [20] . Simplified Data Encryption Standard or S-DES is an educational algorithm similar to Data Encryption Standard (DES) but with much smaller Parameters [21] [22] . The technique to analyze S-DES using linear cryptanalysis and differential cryptanalysis has been of interest of crypto-community later [21] [22] . The encryption and decryption algorithm or cipher of twofish algorithm had been introduced to crypto community and a cryptanalysis of the said cipher had also been elaborated in subject to be a part of Advance Encryption Algorithm proposals [23] .

2.2. Some Old and Recent References on Linear Cryptanalysis

The cryptanalysis technique to 4-bit crypto S-boxes using linear relations among four, 4-bit input Vectors (IPVs) and four, output 4-bit Boolean Functions (OPBFs) of a 4-bit S-box have been termed as linear cryptanalysis of 4-bit crypto S-boxes [3] [4] . Another technique to analyze the security of a 4-bit crypto S-box using all possible differences had also been termed as Differential cryptanalysis of 4-bit crypto S-boxes [3] [4] . The search for best characteristic in linear cryptanalysis and the maximal weight path in a directed graph and correspondence between them had also been elaborated with proper example [24] . It had also been proposed that the use of correlation matrix as a natural representation to understand and describe the mechanism of linear cryptanalysis [25] . It was also formalized the method described in [26] and showed that at the structural level, linear cryptanalysis has been very similar to differential cryptanalysis. It was also used for further exploration into linear cryptanalysis [27] . It had also been provided with a generalization of linear cryptanalysis and suggests that IDEA and SAFER K-64 have been secure against such generalization [28] . It had been surveyed to the use of multiple linear approximations in cryptanalysis to improve efficiency and to reduce the amount of data required for cryptanalysis in certain circumstances [29] . Cryptanalysis of DES cipher with linear relations [26] and the improved version of the said cryptanalysis [26] with 12 Computers had also been reported later [30] . The description of an implementation of Matsui’s linear cryptanalysis of DES with strong emphasis on efficiency had also been reported [31] . In early days of this century The cryptanalytic attack based on multiple Linear Approximations to AES candidate Serpent had also been reported [32] . Later A Technique to prove security bounds against Linear and Differential cryptanalytic attack using Mixed-Integer Linear Programming (MILP) had also been elaborated [33] . Later to this on the strength of two variants of reduced round lightweight block cipher SIMON-32 and SIMON-48 had been tested against Linear Cryptanalysis and had been presented the optimum possible results [34] . Almost at the same time the strength of another light weight block ciphers SIMECK had been tested against Linear Cryptanalysis [35] . The fault analysis of light weight block cipher SPECK and Linear Cryptanalysis with zero statistical correlation among plaintext and respective cipher text of reduced round lightweight block cipher SIMON to test its strength had also been introduced in recent past [36] .

2.3. Old and Recent References on Differential Cryptanalysis

The design of a Feistel cipher with at least 5 rounds that has been resistant to differential cryptanalysis had been reported to crypto community [37] . The exploration of the possibility of defeating differential cryptanalysis by designing S-boxes with equiprobable output XORs using bent functions had been reported once [38] . The description of some design criteria for creating good S-boxes that are immune to differential cryptanalysis and these criteria are based on information theoretic concepts had been reported later [39] . It had been Introduced that the differential cryptanalysis on a reduced round variant of DES [40] and broke a variety of ciphers, the fastest break being of two-pass Snefru [41] and also described the cryptanalysis of the full 16-round DES using an improved version [40] [42] . It had been shown that there have been DES-like iterated ciphers that does not yield to differential cryptanalysis [43] and also introduced the concept of Markov ciphers and explained its significance in differential cryptanalysis. It had also been Investigated that the security of iterated block ciphers shows how to and when an r-round cipher is not vulnerable to attacks [44] . It had also been proposed that eight round Twofish can be attacked and investigated the role of key dependent S-boxes in differential cryptanalysis [45] . It had been on the same line with [38] but proposed that the input variables be increased and that the S-box be balanced to increase resistance towards both differential and linear cryptanalysis [46] . Early in this century in previous decade estimation of probability of block ciphers against Linear and Differential cryptanalytic attack had been reported. Later a new Algebraic and statistical technique of Cryptanalysis against block cipher PRESENT-128 had been reported [47] . Almost 3 year later a new technique entitled Impossible Differential Cryptanalysis had also been reported [48] . A detailed Comparative study of DES based on the strength of Data Encryption (DES) Standard against Linear and Differential Cryptanalysis had been reported later [49] . At last Constraints of Programming Models of Chosen Key Differential Cryptanalysis had been reported to crypto community [50] .

2.4. Linear and Differential Cryptanalysis of Stream Ciphers

In late 20th century A Stepping Stone of the Differential-Linear cryptanalysis method that is a very efficient method against DES had also been grounded [51] . The relationship between linear and differential cryptanalysis and present classes of ciphers which are resistant towards these attacks had also been elaborated [52] . Description of statistical cryptanalysis of DES, a combination and improvement of both linear and differential cryptanalysis with suggestion of the linearity of S-boxes have not been very important had been depicted [53] . Later in 21^st century description of analysis with multiple expressions and differential-linear cryptanalysis with experimental results of an implementation of differential-linear cryptanalysis with multiple expressions applied to DES variants had also been proposed [54] . At the same time the attack on 7 and 8 round Rijndael using the Square method with a related-key attack that can break 9 rounds Rijndael with 256 bit keys had been described [55] . In Late or almost end of 20th century the strength of stream ciphers have been tested against Differential Cryptanalytic attack [56] . Later the strength of them had also been tested against Linear Cryptanalytic attack [57] . A separate method of linear cryptanalytic attack had been reported once [58] . At least 6 years later the strength of stream cipher Helix had been tested against Differential Cryptanalytic attack [59] . Later the strength of stream ciphers Py, Py6, and Pypy had also been tested again Differential Cryptanalytic attack [60] . Recently the test of strength of stream cipher ZUC against Differential Cryptanalytic attack had also been reported to crypto community [61] .

2.5. Strict Avalanche Criterion (SAC) of S-Boxes

In beginning Strict Avalanche Criterion of 4-bit Boolean Functions and Bit Independence Criterion of 4-bit S-boxes had been introduced [62] and Design of Good S-boxes based on these criteria had also been reported later [63] . In end of 20th century the construction of secured S-boxes to satisfy Strict Avalanche Criterion of S-boxes had been reported with ease [64] . The Test of 4-bit Boolean Functions to satisfy higher order strict Avalanche Criterion (HOSAC) have had also been illustrated [65] . In early twenty first century the analysis methods to Strict Avalanche Criterion (SAC) had been reported. A new approach to test degree of suitability of S-boxes in modern block ciphers had been introduced to crypto-community [66] . 16, 4-bit S-boxes had also been tested for optimum linear equivalent classes later [67] . The strength of several block ciphers against several Cryptanalytic attacks had been tested and reported later [68] . Recently the Key dependent S-boxes and simple algorithms to generate key dependent S-boxes had been reported [69] . An efficient cryptographic S-box design using soft computing algorithms have had also been reported [70] . In recent past the cellular automata had been used to construct good S-boxes [71] .

3. A Brief Review of Differential Cryptanalysis of 4-Bit S-Boxes and a New Technique with Boolean Functions for Differential Cryptanalysis of 4-Bit S-Boxes

The given 4-bit Crypto S-box has been described in Sub-section 3.1. The relation Between 4-bit Crypto S-boxes and 4-bit BFs has been illustrated in Subsection 3.2., The Differential Cryptanalysis of 4-bit Crypto S-boxes and DDT or Differential Distribution Table has been illustrated in Subsection 3.3. The Differential Cryptanalysis of 4-bit S-boxes with 4-bit BFs has been described in Subsection 3.4.

3.1. 4-Bit Crypto S-Boxes

A 4-bit Crypto S-box can be written as Follows in Table 1, where the each element of the first row of Table 1, entitled as index, are the position of each element of the S-box within the given S-box and the elements of the 2^nd row, entitled as S-box are the elements of the given Substitution box. It can be concluded that the 1^st row is fixed for all possible Crypto S-boxes. The values of each element of the 1^st row are distinct, unique and vary between 0 to F in hex. The values of the each element of the 2^nd row of a Crypto S-box are also distinct and unique and also vary between 0 to F in hex. The values of the elements of the fixed 1^st row are sequential and monotonically increasing where for the 2^nd row they can be sequential or partly sequential or non-sequential. Here the given Substitution box is the 1^st 4-bit S-box of the 1^st S-Box out of 8 of Data Encryption Standard [2] [72] [73] .

3.2. Relation between 4-Bit S-Boxes and 4-Bit Boolean Functions

Index of Each element of a 4-bit Crypto S-box and the element itself is a hexadecimal number and that can be converted into a 4-bit bit sequence that are given in column 1 through G of row 1 and row 6 under row heading Index and S-box respectively. From row 2 through 5 and row 7 through A of each column from 1 through G of Table 2 shows the 4-bit bit sequences of the corresponding hexadecimal numbers of the index of each element of the given Crypto S-box and each element of the Crypto S-box itself. Each row from 2 through 5 and 7 through A from column 1 through G constitutes a 16 bit, bit sequence that is a 16 bit long input vectors (IPVs) and 4-bit output BFs (OPBFs) respectively. column 1 through G of Row 2 is termed as 4^th IPV, Row 3 is termed as 3^rd IPV,

Row 4 is termed as 2^nd IPV and Row 5 is termed as 1^st IPV whereas column 1 through G of Row 7 is termed as 4^th OPBF, Row 8 is termed as 3^rd OPBF, Row 9 is termed as 2^nd OPBF and Row A is termed as 1^st OPBF [2] . The decimal equivalent of each IPV and OPBF are noted at column H of respective rows.

3.3. Review of Differential Cryptanalysis of 4-Bit Crypto S-Boxes [3] [4]

In Differential Cryptanalysis of 4-bit Crypto S-boxes, Elements of 4-bit input S-box (ISB) have been xored with a particular 4-bit Input Difference (ID) to obtain a Distant input S-box (DISB). The Distant S-boxes (DSB) have been obtained from original S-box (SB) by shuffling the elements of SB in such order in the way in which the elements of ISB have been shuffled to obtain DISB for a Particular ID. Each element of Difference S-box (DFSB) have been obtained by the xor operation of corresponding elements of SB and DSB. The Count of each Hexadecimal number from 0 to F have been put into the concerned cell of Differential Distribution Table or DDT. As the number of 0s in DDT increases, information regarding concerned Output Difference (OD) increases so the S-box has been determined as weak S-box. The 4-bit Sequence of each element of ISB, ID, DISB, DSB, DFSB have been given in BIN ISB, BIN ID, BIN DISB, BIN DSB, BIN DFSB respectively.

The Column 1 in Table 3 from row 1 through G shows the 16 elements of ISB in a monotonically increasing sequence or order. The ISB can also be concluded as an Identity 4-bit S-box. The elements of 1^st 4-bit S-box, out of 4 of 1^st S-Box of Data Encryption Standard (DES) out of 8, has been considered as S-box (SB), in column 7 from row 1 through G. The elements of ID, DISB, DSB, DFSB has been shown in row 1 through G of Column 3, 5, 9 and C of Table 3 respectively. The 4-bit Binary equivalents of each elements of ISB, ID, DISB, SB, DSB, DFSB, has been shown in row 1 through G of column 2, 4, 6, 8, A and B of Table 3 respectively.

The review has been done in two different views; The S-box view has been described in subsec.3.3.1. in which the concerned column of interest are row 1 through G of column 1, 3, 5, 7, 9 and C respectively. The 4-bit binary pattern view has also been described in subsec.3.3.2 in which concerned column of interest are row 1 through G of column 2, 4, 6, 8, A and b respectively. The Pseudo Code of two algorithms with their time complexity comparison has been illustrated in Subsection 3.3.3.

3.3.1. S-Box View of Differential Cryptanalysis of 4-Bit Crypto S-Boxes

The S-box with a particular input difference or ID from 0 to F in which all elements have the same value “B” in hex, is not a Crypto Box but an S-box and is shown in row 1 through G of Column 3 of Table 3. The Distant input S-box (DISB) is shown in row 1 through G of column 5 of the said table. In DISB each row element from row 1 through G is obtained by the xor operation of the elements in corresponding positions of each element of DISB from row 1 through

G of Column 1 (ISB) and Column 3 (ID) respectively. In ISB for each row element from row 1 through G of Column 1 just in corresponding position from row 1 through G of Column 7, there is an element of SB. Now in DISB the elements of ISB have been shuffled in a particular order and In DSB the corresponding elements of SB has also been shuffled in that particular order. Each element of the Difference S-Box or DFSB from row 1 through G of column C. has been obtained by xor operation of each element in corresponding positions from row 1 through G of Column 7 and row 1 through G of Column 9 respectively. The repetition of each existing elements in DSB have been counted and put into Difference Distribution Table or DDT. It is shown in Table 4 as follows,

The count of each existing elements in DFSB have been put into Difference Distribution Table as follows, in row 2 of Table 5. For Input Difference (ID) = “B” and Output Difference from 0 through F of row 1.

3.3.2. 4-Bit binary Pattern View of Differential Cryptanalysis of 4-Bit Crypto S-Boxes

The corresponding 4-bit bit patterns of input S-box elements (ISB) has been shown from row 1 through G of Column 2 in Table 3 and termed as Bin ISB. The Particular Input Difference “1101” is shown in each row from 1 through G of Column 4 in Table 3. The Distant 4-bit input bit patterns are shown from row 1 through G of Column 6 (Bin DISB) are obtained by the xor operation of the

elements in corresponding positions of each element of BIN DISB from row 1 through G of Column 2 (Bin ISB) and Column 4 (Bin ID) respectively. In Bin ISB for each element from row 1 through G of Column 2 in corresponding position from row 1 through G of Column 8, there is an element of Bin SB. Now in Bin DISB the elements of ISB have been shuffled in a particular order and in Bin DSB the corresponding elements of SB has also been shuffled in that particular order. Each element from row 1 through G of Column 11 has been obtained by xor operation of each element in corresponding positions from row 1 through G of Column 8 and row 1 through G of Column 10 respectively. The repetition of each existing elements in Bin DFSB have been counted and put into Difference Distribution Table or DDT. It is shown in Table 6.

The count of each existing elements in Bin DFSB have been put into the Differential Distribution Table as follows, in row 2 of Table 7(a) for Binary Input Difference (Bin ID) “1101” and Output Difference from 0 through F of row 1. The Total DDT or Difference Distribution table for 16 IDs for the given S-box has been shown below in Table 7(b).

3.3.3. Pseudo Code for Differential Cryptanalysis of 4-bit Crypto S-Boxes and its Time Complexity Analysis

The Pseudo Code of Algorithm for 4-bit binary pattern view with Time Complexity has been depicted in Subsection 3.3.3.1, the Pseudo Code of algorithm for S-box view with Time Complexity has been depicted in Subsection 3.3.3.2 and The comparison of time complexity of two algos has been given in Subsection 3.3.3.

1) Pseudo Code of Algorithm of Differential Cryptanalysis 4-bit binary pattern view

The Pseudo Code has been given as follows,

Start. // Start of Pseudo Code

// Variable Declarations, Two Dimensional Array ISB is for 4-bit bit patterns for Input S-box, IDIFF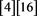 is for 4-bit bit patterns of Input Difference, Three Dimensional Array ODIFF 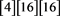is for all 4-bit bit patterns of Output Difference for 16 IDIFFs.

Step 0A: int ISB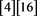; int IDIFF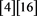; int ODIFF;

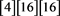// Variable Declarations, ISB’ is for 4-bit bit patterns of All elements of 16 distant ISBs. OSB is for 4-bit bit patterns of the given S-box or Output S-box, OSB’ is for 4-bit bit patterns of All elements of 16 distant OSBs, DDT is for Difference Distribution Table, and Count is for count of each element in ODIFF for 16 OSBs.

Step 0B: int ISB’; int OSB; int OSB’; int DDT; int Count;

// Differential Cryptanalysis Block.

Step 01: For I =1:16; For J =1:16; For K =1:4; // Start of For Loop I, J, K respectively

ISB’[K][I][J] = ISB[K][J]^IDIFF[K][I];

OSB’[K][I][J] = OSB[ISB’[K][I][J]];

ODIFF[K][I][J] = OSB[K][J]^ OSB’[K][I][J];

End For K. End For J. End For I.// End of For loop K, J, I respectively

// Generation of Difference Distribution Table.

Step 02: For I =1:16 For J =1:16 For K =1:4 // Start of For Loop I, J, K respectively

DDT[I][J]= Count[ISB[K][J]];

End For K. End For J. End For I. // End of For loop K, J, I respectively

Stop. // End of Pseudo Code

Time Complexity of the Given Algorithm. Since Differential Cryptanalysis block contains 3 nested loops so the time Complexity of the Algorithm has been O(n³).

2) Pseudo Code of Algorithm of Differential Cryptanalysis S-Box View

The Pseudo Code has been given as follows,

Start. // Start of Pseudo Code

// Variable Declarations, One Dimensional Array ISB is for for Input S-box in Hex, IDIFF is for Input Difference in Hex, Three Dimensional Array ODIFF is for all Output Difference in Hex for 16 IDIFFs.

Step 0A: int ISB[16]; int IDIFF; int ODIFF;

// Variable Declarations, ISB’ is for All elements in Hex of 16 distant ISBs. OSB is for elements in Hex of the given S-box or Output S-box, OSB’ is for All elements in Hex of 16 distant OSBs, DDT is for Difference Distribution Table, and Count is for count of each element in ODIFF for 16 OSBs.

Step 0B: int ISB’; int OSB; int OSB’; int DDT; int Count.

// Differential Cryptanalysis block

Step 01: For I =1:16; For J =1:16; // For Loop I and J respectively.

ISB’[I][J] = ISB[J]^IDIFF[I];

OSB’[I][J] = OSB[ISB’[I][J]];

ODIFF[I][J] = OSB[J]^ OSB’[I][J];

End For J. End For I.// End of For Loop J and I respectively.

Step 02: For I =1:16; For J =1:16 // For Loop I and J respectively.

DDT[I][J]= Count[ISB[J]];

End For J. End For I. // End of For Loop J and I respectively.

Stop. // End of Pseudo Code

Time Complexity of the Given Algorithm. Since Differential Cryptanalysis block contains 2 nested loops so the time Complexity of the Algorithm has been O(n²).

3) Comparison of Time Complexity of Two views of Differential Cryptanalysis of 4-bit S-boxes

The Comparison of time complexity of two algos has been given in Table 7(c) as follows,

It can be concluded from the comparison that the Execution Time reduces in S-box view than the 4-bit Binary Pattern view. So in can be concluded from above review work that the execution time of Differential Cryptanalysis depends upon the view of the algorithm and the S-box view has been proved to be a better algorithm than 4-bit binary pattern view algorithm.

3.4. Differential Cryptanalysis of 4-Bit Bijective Crypto S-Boxes Using 4-Bit BFs

The Procedure to obtain four Input Vectors (IPVs) and Four Output BFs (OPBFs) from the elements of a particular 4-bit Crypto S-box has been described in section 2.1. The procedure to obtain distant Input Vectors (DIPVs) and Distant Output BFs (DOPBFs) for a particular Input Difference (ID) of the said S-box has been described with example in section 3.4.1. Generation of Difference 4-bit BFs, Analysis of Algorithm and Generation of Difference Analysis Algorithm in Subsection 3.4.2, Subsection 3.4.3 and Subsection 3.4.4 respectively. The Differential Analysis Table of the given S-box, Pseudo Code of Algorithm with Time Complexity and Comparison of Time complexity of three Algos have been given in Subsection 3.4.5, Subsection 3.4.6 and Subsection 3.4.7 respectively.

3.4.1. Distant Input BFs (DIBFs) and Distant Output BFs (DOBFs) Generation from IBFs and OBFs for a Specific ID

Within 4 bits of binary input difference (Bin ID), 1 in position p means do complement of p^th IPV and 0 means no operation on p^th IPV. Similarly in the given example 1 in position 4 of Bin ID, as in position 4 from row 1 through G of column 4 of Table 9 indicates do complement of 4-bit IPV, IPV4 i.e. CIPV4 and 0 in position 3 as in position 3 from row 1 through G of column 4 of table.3. means no operation on 4-bit IPV, IPV3 (CIPV3) or CIPV3 = IPV3. Similarly 1 in respective positions 2 and 1 as in positions 2 and 1 from row 1 through G of column 4 of Table 9 means do complement 4-bit IPV, IPV2 (CIPV2) and do complement of 4-bit IPV, IPV1 (CIPV1) respectively. CIPV4, CIPV3, CIPV2 and CIPV1 for Input S-box (ISB) and Input Difference (ID) have been shown from row 1 through G of Column 1 and Column 3 of Table 9 respectively.

Here the 4^th OPBF has been taken as an example of OPBF and termed as OPBF. Since complement of 4^th IPV means interchanging each 8 bit halves of 16 bit long 4^th IPV so The 2, 8 bit halves of OPBF have been interchanged due to complement of 4^th IPV. The resultant OPBF has been shown from column 1 through G of row 6 in Table 9. Again No Operation on 3^rd IPV means CIPV3 = IPV3 so resultant OPBF is as same as STEP1 and has been shown from column 1 through G of row 7 in Table 9. Next to it, the complement of 2^nd IPV means interchanging each 2 bit halves of each 4 bit halves of each 8 bit halves of resultant OPBF. The resultant OPBF has been shown from column 1 through G of row 8 in Table 9. Again the complement of 1^st IPV means interchanging each bit of each 2 bit halves of each 4 bit halves of each 8 bit halves of resultant OPBF, The resultant OPBF After operation has been shown in column 1 through G of row 9 in Table 9. The Complemented OPBF has been the resultant OPBF of STEP4 and has been shown from column 1 through G of row A in Table 9.

3.4.2. Generation of Difference Boolean Functions or DBFs for a Certain ID

The DBFs of each OPBF have been generated by bitwise Xor of OPBFs and the corresponding COPBFs. The corresponding DBFs of OBPF4, OBPF3, OBPF2, OPBF1 are denoted as DIFF4, DIFF3, DIFF2, DIFF1 respectively. Generation of 4^th DBF of ID “1011” has been shown in column 1 through G of row 3 of Table 10.

3.4.3. Analysis

If the DBFs are balanced then the number of bits changed and remains unchanged among corresponding bits of OPBFs and COPBFs is maximum. So uncertainty of determining a particular change in bits is maximum. As the number of balanced DBFs are increased among 64 (=2⁴ × 4) possible DBFs then the security will increase. The number of 1s or balanced-ness of the above DBF shown from row 1 through G of row 3 of Table 10 has been shown in Column 2 of row 2 of Table 11.

3.4.4. DBFs Generation and Derivation of a Particular Row of Differential Analysis Table (DAT) for a Certain ID

Four IPVs in the order IPV4, IPV3, IPV2 and IPV1 for the S-box given in Table 1 and four CIPVs, CIPV4, CIPV3, CIPV2 and CIPV1 for a certain ID “1011” have been shown from column 1 through G of row 1, 2, 3, 4, 5, 6, 7 and 8 respectively in Table 12. Four OPBFs in the order OPBF4, OPBF3, OPBF2 and OPBF1 for the S-box given in Table 1 and four COPBFs COPBF4, COPBF3, COPBF2 and COPBF1 for a certain ID “1011” have been shown from column 1 through G of row 9, A, B, C, D, E, F and G respectively in Table 12. The resultant DBFs, DIFF4, DIFF3, DIFF2, DIFF1, have been shown in column 1 through G of row H, I, J, K of Table 12. The number of 1s or Balanced-ness of four DBFs have been shown in row from Column 2 through 5 of row 1 in Table 13.

3.4.5. Differential Analysis Table or DAT

The Balanced-ness of four DBFs for each ID have been shown from column 2 through 5 of row 2 through H of DAT or Table 14.

3.4.6. Pseudo Code for Differential Cryptanalysis of 4-Bit Crypto S-Boxes and Its Time Complexity Analysis

The Pseudo Code has been given as follows,

Start. // Start of Pseudo Code

// Variable Declarations, One Dimensional Array ISB is for Input S-box in Hex, IDIFF is for Input Difference in Hex, Three Dimensional Array ODIFF is for all Output Difference in Hex for 16 IDIFFs. Bin_ODIFF is for all 4-bit bit patterns of Output Difference for 16 IDIFFs.

Step 0A: int ISB; int IDIFF; int ODIFF;

// Variable Declarations, ISB’ is for All elements in Hex of 16 distant ISBs. OSB is for elements in Hex of the given S-box or Output S-box, OSB’ is for All elements in Hex of 16 distant OSBs, DAT is for Difference Analysis Table, and Count is for count of each element in ODIFF for 16 OSBs.

Step 0B: int ISB’; int OSB; int OSB’; int DAT; int Count.

// Differential Cryptanalysis block

Step 01: For I =1:16; For J =1:16; // For Loop I and J respectively.

ISB’[I][J] = ISB[J]^IDIFF[I];

OSB’[I][J] = OSB[ISB’[I][J]];

ODIFF[I][J] = OSB[J]^ OSB’[I][J];

For K=1:4 Bin_ODIFF[K][I][J] = Hex to Binary(ODIFF[I][J])

End For J. End For I.// End of For Loop J and I respectively.

Step 03: For I =1:4; For J =1:16; For K = 1:16 // For Loop I and J respectively.

DAT[I][J]= Count[Bin_ODIFF[I][J][K]];

End For J. End For I. // End of For Loop J and I respectively.

Stop. // End of Pseudo Code

Time Complexity of the Given Algorithm. Since Differential Cryptanalysis block contains 2 nested loops so the time Complexity of the Algorithm has been O(n²).

3.4.7. Comparison of Time Complexity of Two Views of Differential Cryptanalysis of 4-Bit S-Boxes and Differential Cryptanalysis with 4-Bit BFs

The Comparison of time complexity of three algos has been given in Table 15 as follows.

It can be concluded from the comparison that the Execution Time reduces in S-box view and With 4-bit BFs than the 4-bit Binary Pattern view. So it can be concluded from above review work and new algorithm that the execution time of Differential Cryptanalysis depends upon the view of the algorithm and the S-box view has been proved to be a better algorithm than 4-bit binary pattern view algorithm. The with 4-bit BFs algo has also been proved to be the better one since The DAT table construction is less time consuming than DDT construction since DDT constitutes of 256 entries while DAT constitutes of 64 entries so it can also be concluded from comparison that Differential Cryptanalysis with 4-bit BFs has been proven to be the best algorithm among 3 Algorithms since it takes less execution time among three algorithms.

4. A Brief Review of Linear Cryptanalysis of 4-Bit crypto S-Boxes and a New Technique with Boolean Functions for Linear Cryptanalysis of 4-Bit Crypto S-Boxes or Linear Approximation Analysis

The review of related relevant property of 4-bit BFs, Algebraic Normal form of 4-bit BFs has been illustrated in Subsection 4.1. The review of Linear Cryptanalysis of 4-bit Crypto S-boxes has been described in brief in Subsection 4.2. At last the new technique to analyze 4-bit S-boxes by 4-bit Linear Approximations or Linear Approximation Analysis has been described in brief in Subsection 4.3.

4.1. A Review of Boolean Functions (BF) and Its Algebraic Normal Form (Anf)

A 4-bit Boolean Function (BF) accepts 4 bits as input {x₁x₂x₃x₄} having 16 combinations of decimal values varying between 0 and 15 and provides 1-bit output for each combination of input. The input-output relation is given in a Truth Table which provides 16-bit output vector corresponding to four 16-bit input vectors, each one attached to x₁, x₂, x₃ and x₄. The 4-bit BF is a mapping from (0,1)⁴ to (0,1)¹ and its functional relation, F(x) can be expressed in Algebraic Normal Form (anf) with 16 coefficients as given in Equation (1) below,

$\begin{array}{c}F\left(x\right)=a_0+\left(a_1\cdot x_1+a_2\cdot x_2+a_3\cdot x_3+a_4\cdot x_4\right)\\ +(a_5\cdot x_1\cdot x_2+a_6\cdot x_1\cdot x_3+a_7\cdot x_1\cdot x_4+a_8\cdot x_2\cdot x_3+a_9\cdot x_2\cdot x_4+a_{10}\cdot x_3\cdot x_4)\\ +(a_{11}\cdot x_1\cdot x_2\cdot x_3+a_{12}\cdot x_1\cdot x_2\cdot x_4+a_{13}\cdot x_1\cdot x_3\cdot x_4+a_{14}\cdot x_2\cdot x_3\cdot x_4)\\ +a_{15}\cdot x_1\cdot x_2\cdot x_3\cdot x_4\end{array}$ (1)

where x represents the decimal value or the hex value of 4 input bits represented by {x₁x₂x₃x₄}, BF assumes 1-bit output, “.” and “+” represent AND and XOR operations respectively. Here a₀ is a constant coefficient, (a₁ to a₄) are 4 linear coefficients, and (a₅ to a₁₅) are 11 nonlinear coefficients of which (a₅ to a₁₀) are 6 non-linear coefficients of 6 terms with 2-AND-operated-input-bits, (a₁₁ to a₁₄) are 4 nonlinear coefficients of 4 terms with 3-AND-operated-input-bits and a₁₅ is a non-linear coefficient of one term with 4-AND-operated-input-bits. The 16 binary ANF coefficients, from a₀ to a₁₅ are marked respectively as anf.bit0 to anf.bit15 in ANF representation and are evaluated from the 16-bit output vector of a BF designated as bf.bit0 to bf.bit15 using the following relations as given in Equation (2),

$anf.bit0=bf.bit0;$

$anf.bit1=anf.bit0+bf.bit8;$

$anf.bit2=anf.bit0+bf.bit4;$

$anf.bit3=anf.bit0+bf.bit2;$

$anf.bit4=anf.bit0+bf.bit1;$

$anf.bit5=anf.bit0+anf.bit1+anf.bit2+bf.bit12;$

$anf.bit6=anf.bit0+anf.bit1+anf.bit3+bf.bit10;$

$anf.bit7=anf.bit0+anf.bit1+anf.bit4+bf.bit9;$

$anf.bit8=anf.bit0+anf.bit2+anf.bit3+bf.bit6;$

$anf.bit9=anf.bit0+anf.bit2+anf.bit4+bf.bit5;$

$anf.bit10=anf.bit0+anf.bit3+anf.bit4+bf.bit3;$

$\begin{array}{c}anf.bit11=anf.bit0+anf.bit1+anf.bit2+anf.bit3+anf.bit5\\ +anf.bit6+anf.bit8+bf.bit14;\end{array}$

$\begin{array}{c}anf.bit12=anf.bit0+anf.bit1+anf.bit2+anf.bit4+anf.bit5\\ +anf.bit7+anf.bit9+bf.bit13;\end{array}$

$\begin{array}{c}anf.bit13=anf.bit0+anf.bit1+anf.bit3+anf.bit4+anf.bit6\\ +anf.bit7+anf.bit10+bf.bit11;\end{array}$

$\begin{array}{c}anf.bit14=anf.bit0+anf.bit2+anf.bit3+anf.bit4\\ +anf.bit8+anf.bit9+anf.bit10+bf.bit7;\end{array}$ (2)

The DEBF (Decimal Equivalent of BF) varies from 0 through 65,535 and each decimal value is converted to a 16-bit binary output of the Boolean function from bf.bit0 through bf.bit15. Based on the binary output of a BF, the ANF coefficients from anf.bit0 through anf.bit15 are calculated sequentially using Equation (2).

4.2. A Review on Linear Cryptanalysis of 4-Bit Crypto S-Boxes [3] [4]

The given 4-bit Crypto S-box has been described in sub-section 4.2.1. The relation of 4-bit S-boxes with 4 bit BFs and with Linear Approximations are described in Sub-section 4.2.2 and 4.2.3 respectively. LAT or Linear Approximation Table has also been illustrated in Section 4.2.4. Agorithm of Linear Cryptanalysis with Time Complexity Analysis has been described in Section 4.2.5.

4.2.1. 4-Bit Crypto S-Boxes

A 4-bit Crypto S-box can be written as Follows in Table 16, where the each element of the first row of Table 16, entitled as index, are the position of each element of the S-box within the given S-box and the elements of the 2^nd row, entitled as S-box, are the elements of the given Substitution box. It can be concluded that the 1^st row is fixed for all possible Crypto S-boxes. The values of each element of the 1^st row are distinct, unique and vary between 0 to F in hex. The values of the each element of the 2^nd row of a Crypto S-box are also distinct and unique and also vary between 0 to F in hex. The values of the elements of the fixed 1^st row are sequential and monotonically increasing where for the 2^nd row they can be sequential or partly sequential or non-sequential. Here the given Substitution box is the 1^st 4-bit S-box of the 1^st S-Box out of 8 of Data Encryption Standard [2] [72] [73] .

4.2.2. Relation between 4-bit S-Boxes and 4-Bit Boolean Functions (4-Bit BFs)

Index of Each element of a 4-bit Crypto S-box and the element itself is a hexadecimal number and that can be converted into a 4-bit bit sequence that are given in column 1 through G of row 1 and row 6 under row heading Index and S-box respectively. From row 2 through 5 and row 7 through A of each column from 1 through G of Table 17 shows the 4-bit bit sequences of the corresponding hexadecimal numbers of the index of each element of the given Crypto S-box and each element of the Crypto S-box itself. Each row from 2 through 5 and 7 through A from column 1 through G constitutes a 16 bit, bit sequence that is a 16 bit long input vectors (IPVs) and 4-bit output BFs (OPBFs) respectively. column 1 through G of Row 2 is termed as 4^th IPV, Row 3 is termed as 3^rd IPV, Row 4 is termed as 2^nd IPV and Row 5 is termed as 1^st IPV whereas column 1 through G of Row 7 is termed as 4^th OPBF, Row 8 is termed as 3^rd OPBF, Row 9 is termed as 2^nd OPBF and Row A is termed as 1^st OPBF [2] . The decimal equivalent of each IPV and OPBF are noted at column H of respective rows.

4.2.3. 4-bit Linear Relations

The elements of input S-box have been shown under column heading ‘I’ and the Input Vectors have been shown under field IPVs (Input Vectors) and subsequently under column headings 1, 2, 3 and 4. The 4^th input vector has been depicted under column heading “4”, 3^rd input vector has been depicted under column heading “3”, 2^nd input vector has been depicted under column heading “2” and 1^st input vector has been depicted under column heading “1”. The elements of S-box have been shown under column heading “SB” and the Output 4-bit BFs are shown under field OPBFs (Output Boolean Functions) and subsequently under column headings 1, 2, 3 and 4. The 4^th Output BF has been

depicted under column heading “4”, 3^rd Output BF has been depicted under column heading “3”, 2^nd Output BF has been depicted under column heading ‘2’ and 1^st Output BF has been depicted under column heading “1”.

The IPEs or Input Equations are all possible xored terms that can be formed using four IPVs 4, 3, 2 and 1. On the other hand OPEs are possible xored terms that can be formed using four OPVs 4, 3, 2 and 1. All possible IPEs and OPEs are listed under the column and also row heading (IPE = OPE) from row 2 through H and column 1 through G respectively. Each cell is a linear equation equating IPE to OPE. Such as L_1+2+4,2+3 is the linear equation formed by IPE “1 + 2 + 3” i.e. the xored combination of three IPVs 1, 2 and 4 and OPE “2 + 3” i.e. the xored combination of two OPBFs 2 and 3. The 256 possible 4-bit Linear Equations are shown in Table 19.

4.2.4. Linear Approximation Table (LAT)

According to Heys each linear equation is tested for each of 16, 4-bit patterns shown in each row under the field IPVs and subsequently under the column headings 1, 2, 3 and 4 and the corresponding 16, 4-bit patterns under field OPBFs and subsequently under the column headings 1, 2, 3 and 4. If a linear equation satisfies 8 times out of 16 then the existence of the linear equation is highly unpredictable. That is the probability is 1/2. If the numbers of satisfaction of each linear equation is noted in respective cells of Table 20 then it is called as Linear Approximation Table or LAT. The Linear Approximation Table for the given S-box has been shown in table 20.

4.2.5. Pseudo Code of Algorithm with Time Complexity Analysis of Linear Cryptanalysis of 4-Bit Crypto S-Boxes

The algorithm to execute the linear cryptanalysis for 4-bit Crypto S-boxes following Heys [3] [4] considers 4-bit Boolean variables Ai and Bj whose i and j are the decimal indices varying from 0 to 15 and Ai and Bj are taking corresponding bit values from [0000] to [1111]. The algorithm to fill the (16 × 16) elements of the LAT is,

for(i=0;i<16;i++){

A=0;

for(k=0;k<16;k++) A=A+(Ai0.Xk0+Ai1.Xk1+Ai2.Xk2+Ai3.Xk3)%2;

for(j=0;j<16;j++){

B=0;

for(k=0;k<16;k++)B=B+(Bj0.Yk0+Bj1.Yk1+Bj2.Yk2+Bj3.Yk3)2;

Sij = (A+B)%2;

if (Sij==0) Cij++; Nij = Cij - 8;

}

}

Time Complexity of the given Algorithm. Since the Pseudo Code contains two nested loops so the time complexity of the given algorithm has been O(n²).

4.3. Linear Approximation Analysis

A Crypto 4-bit S-box (1^st 4-bit S-box out of 32 4-bit S-boxes of DES) has been described in Sub-section 4.3.1. The Table for four input vectors, Output 4-bit BFs and corresponding ANFs has been depicted in Sub-section 4.3.2. The analysis has been described in Sub-section 4.3.3. The result of Analysis has been given in Sub-section 4.3.4.

4.3.1. 4-bit Crypto S-Boxes

A 4-bit Crypto S-box can be written as Follows in Table 21, where the each element of the first row of Table 21, entitled as index, are the position of each element of the S-box within the given S-box and the elements of the 2^nd row, entitled as S-box, are the elements of the given Substitution box. It can be concluded that the 1^st row is fixed for all possible Crypto S-boxes. The values of each element of the 1^st row are distinct, unique and vary between 0 to F in hex. The values of the each element of the 2^nd row of a Crypto S-box are also distinct and unique and also vary between 0 to F in hex. The values of the elements of the fixed 1^st row are sequential and monotonically increasing where for the 2^nd row they can be sequential or partly sequential or non-sequential. Here the given Substitution box is the 1^st 4-bit S-box of the 1^st S-Box out of 8 of Data Encryption Standard [2] [72] [73] .

4.3.2. Input Vectors (IPVs)-Output BFs (OPBFs)-Algebraic Normal Forms (ANFs)

The elements of input S-box have been shown under column heading ‘ISB’ and the Input Vectors have been shown under the field IPVs (Input Vectors) and subsequently under column headings 1, 2, 3 and 4. The 4^th input vector has been depicted under column heading “4”, 3^rd input vector has been depicted under column heading “3”, 2^nd input vector has been depicted under column heading “2” and 1^st input vector has been depicted under column heading “1”. The elements of S-box have been shown under column heading “OSB” and the Output 4-bit BFs have been shown under field OPBFs (Output Boolean Functions) and subsequently under column headings 1, 2, 3 and 4. The 4^th Output BF has been depicted under column heading “4”, 3^rd Output BF has been depicted under column heading “3”, 2^nd Output BF has been depicted under column heading “2” and 1^st Output BF has been depicted under column heading “1”. The corresponding ANFs for 4 OPBFs, OPBF-4^th, OPBF-3^rd, OPBF-2^nd, OPBF-1^st, are depicted under field “ANFs” subsequently under column heading 4, 3, 2 and 1 respectively of Table 22.

4.3.3. Linear Approximation Analysis (LAA)

An Algebraic Normal Form or ANF equation is termed as Linear Equation or Linear Approximation if the Nonlinear Part or NP (i.e. The xored value of all product terms of Equation (2) for corresponding 4 bit values of IPVs, with column heading 4, 3, 2, 1) is 0 and The Linear part or LP for corresponding 4 bit values of IPVs, with column heading 4, 3, 2, 1 is equal to corresponding BF bit values. The corresponding ANF coefficients of output BFs F(4), F(3), F(2), and F(1) are given under row heading ANF(F4), ANF(F3), ANF(F2) and ANF(F1)

respectively from row 2 through 5 and column 4 through J. In which Column 4 of row 2 through 5 gives the value of Constant Coefficient (a₀ according to Equation (2)) of ANF(F4), ANF(F3), ANF(F2) and ANF(F1) respectively. Column 5 through 8 of row 2 through 5 gives the value of respective Linear Coefficients more specifically a₁, a₂, a₃, a₄ (according to Equation (2)) of ANF(F4), ANF(F3), ANF(F2) and ANF(F1). They together termed as LP or Linear Part of the respective ANF Equation. Column 9 through J of row 2 through 5 gives the value of respective Non-Linear Coefficients more specifically a₅ to a₁₅ (according to Equation (2)) of ANF(F4), ANF(F3), ANF(F2) and ANF(F1). They together termed as NP or Non-Linear Part of the respective ANF Equation.

The 4^th, 3^rd, 2^nd, 1^st IPV for the given S-box have been noted in the Field ‘IPVs’ under column heading 4, 3, 2, 1 respectively from row 8 through M of Table.23. The 4 output BFs F4, F3, F2, F1 are noted at column 4, 8, C, G from row 8 through M respectively. The corresponding LP, NP, Satisfaction (SF) values (LP = BF)are noted at column 5 through 7, 9 through B, C through F and H to J from row 8 through M respectively of Table 23.

4.3.4. Results

Total Number of Existing Linear Approximations: 21.

4.3.5. Pseudo Code with Time Complexity Analysis of the Linear Approximation Analysis Algorithm

The Nonlinear Part for the given analysis has been termed as NP. The ANF coefficients are illustrated through array anf[16]. IPVs are termed as x₁, x₂, x₃, x₄ for IPV1, IPV2, IPV3, IPV4 respectively. The Pseudo Code of algorithm of the above analysis is given below,

Start.

Step 1. NP = (anf[5].&x₁&x₂)^(anf[6]&x₁ &x₃₎+(anf[7]&x₁ &x₄)+(anf[8] &x₂ &x₃)+(anf[9]&x₂ &x₄)+(anf[10]&x₃ &x₄)(anf[11]&x₁ &x₂ &x₃)+(anf[12]&x₁ &x₂ &x₄)+(anf[13]&x₁&x₃ &x₄) +(anf[14] &x₂ &x₃ &x₄)+(anf[15]&x₁ &x₂ &x₃ &x₄))

Step 2. LP= anf[0] ^(anf[1].&x₁)^ (anf[2].&x₂)^ (anf[3].&x₃)^ (anf[4].&x₄).

Step 3. if(NP==0&& BF(x₁x₂x₃x₄₎ == LP) then Linear equation.

else Nonlinear equation.

Stop.

Time Complexity. Since the analysis contains no loops so the Time complexity of the algorithm has been O(n).

4.3.6. Comparison of Execution time Complexity of Linear Cryptanalysis of 4-Bit Crypto S-Boxes and Linear Approximation Analysis of 4-Bit S-Boxes

The Comparison of time complexity of two algorithms has been given in Table 24 as follows,

It can be concluded from the comparison that the Execution time reduces in Linear Approximation Analysis than the Linear Cryptanalysis of 4-bit Crypto S-boxes. So in can be concluded from above review work that the execution time of 4-bit LA Algorithm is much less that 4-bit LC Algorithm so 4-bit LA algorithm has been proved to be much better algorithm.

5. Result and Analysis and Security Criterion for all Four Algorithms of 4-Bit Crypto S-Boxes

In this section The Analysis Criterion of Differential Cryptanalysis of 4-bit S-boxes has been described in Subsection 5.1 and The Analysis Criterion of Differential Cryptanalysis with 4-bit BFs of 4-bit S-boxes has been described in Subsection 5.2. The same of Linear Cryptanalysis of 4-bit S-boxes has been illustrated in Subsection 5.3 and at last The Analysis Criterion of Linear Approximation Analysis of 4-bit S-boxes has been depicted in Subsection 5.4. The Result and Analysis of Results of Four Algorithms on 32 DES 4-bit S-boxes has been described in brief in Section 5.5.

5.1. The Analysis Criterion of Differential Cryptanalysis of 4-Bit S-Boxes

In Difference Distribution Table there have been 256 cells, i.e. 16 rows and 16 columns. Each row has been for each input difference varies from 0 to F. Each column in each row represents each output difference varies from 0 to F for each input difference. 0 in any cell indicates absence of that output difference for subsequent input difference. Such as 0 in 2^nd cell of Table 7(b) of relevant DDT means for input difference 0 the corresponding output difference o is absent. If number of 0 is too low or too high it supplies more information regarding concerned output difference. So an S-box is said to be immune to this cryptanalytic

attack if number of 0s in DDT is close to 128 or half of total cells or 256. In the said example of 1^st DES 4-bit S-box total number of 0s in DDT are 168. That is close to 128. So the S-box has been said to be almost secure from this attack.

5.2. The Analysis Criterion of Differential Cryptanalysis with 4-Bit BFs

As total number of balanced 4-bit BFs increases in Difference Analysis Table or DAT the security of S-box increases since balanced 4-bit BFs supplies at most uncertainty. Since Number of 0s and 1s in balanced 4-bit BFs are equal i.e. they are same in number means determination of each bit has been at most uncertainty. In the said example of 1^st DES 4-bit S-box total number of 8s in DAT are 36. That is close to 32 half of total 64 cells. So the S-box has been said to be almost less secure from this attack.

5.3. The Analysis Criterion of Linear Cryptanalysis of 4-Bit S-Boxes

In Linear Analysis Table or LAT there are 256 cells for 256 possible 4-bit linear relations. The count of 16, 4-bit binary conditions to satisfy for any given linear relation has been put into the concerned cell. 8 in a cell indicate that the particular linear relation has been satisfied for 8 4-bit binary conditions and remain unsatisfied for 8, 4-bit binary conditions. That is at most uncertainty. In the said example of 1^st DES 4-bit S-box total number of 8s in LAT have been 143. That is close to 128. So the S-box has been said to be less secure from this attack.

5.4. The Analysis Criterion of Linear Approximation Analysis of 4-Bit S-Boxes

The value of ⁿC_r has been maximum when the value of r is ½ of the value of n (when n is even). Here the maximum number of linear approximations is 64. So if the total satisfaction of linear equation is 32 out of 64 then the number of possible sets of 32 linear equations has been the largest. Means if the total satisfaction is 32 out of 64 then the number of possible sets of 32 possible linear equations is ⁶⁴C₃₂. That is maximum number of possible sets of linear equations. If the value of total No of Linear Approximations is closed to 32 then it is more cryptanalysis immune. Since the number of possible sets of linear equations are too large to calculate. As the value goes close to 0 or 64 it reduces the sets of possible linear equations to search, that reduces the effort to search for the linear equations present in a particular 4-bit S-box. In this example total satisfaction is 21 out of 64. Which means the given 4-bit S-Box is not a good 4 bit S-Box or not a good Crypt analytically immune S-Box.

If the values of total number of Existing Linear equations for a 4-bit S-Box are 24 to 32, then the lowest numbers of sets of linear equations are 250,649,105,469,666,120. This is a very large number to investigate. So the 4-bit S-Box is declared as a good 4-bit S-Box or 4-bit S-Box with good security. If it is between 16 through 23 then the lowest numbers of sets of linear equations are 488526937079580. This not a small number to investigate in today’s computing scenario so the S-boxes are declared as medium S-Box or S-Box with medium security. The 4-bit S-Boxes having existing linear equations less than 16 are declared as Poor 4-bit S-Box or vulnerable to cryptanalytic attack.

5.5. The Result and Analysis of Results of Four Algorithms on 32 DES 4-Bit S-Boxes

The four algorithms have been operated on 32 DES 4-bit S-boxes as shown Table 25. No-ELR stands for Number of existing linear Relations, N8-LAT stands for number of 8s in Linear Analysis Table, No-DDT stands for number of 0s in Difference Distribution Table and N8-DAT stands for number of balanced (8-8) 4-bit BFs in Difference Analysis Table. The Discussion has been given below,

6. Discussion

Out of 32 DES S-boxes 1 have 17, 3 have 21, 4 have 22, 1 have 23, 3 have 24, 3 have 25, 1 have 26, 2 have 27, 3 have 28, 2 have 29, 2 have 30 and 1 have 31 Existing Linear Relations i.e. 24 S-boxes out of 32 have been less secure from this attack and 8 out of 32 have been immune to this attack. Again out of 32 DES S-boxes 1 have 126, 2 have 127, 2 have 130, 1 have 132, 2 have 133, 2 have 134, 1 have 135, 4 have 136, 2 have 137, 2 have 138, 1 have 141, 5 have 143, 1 have 144, 1 have 145, 1 have 147, 1 have 151, 1 have 154 and 1 have 158 8s in LAT. That is All S-boxes are less immune to this attack. Again out of 32 DES S-boxes 1 have 159, 1 have 160, 1 have 161, 4 have 162, 1 have 164, 8 have 166, 13 have 168, 1 have 173 and 2 have 174 0s in DDT. That is all S-boxes have been secured from this attack. At last out of 32 DES S-boxes 1 have 0, 3 have 18, 2 have 21, 2 have 27, 10 have 30, 12 have 36, 1 have 39 and 1 have 42 8s in DAT i.e. they have been less secure to this attack. The comparative analysis has proved that Linear Approximation analysis has been the most time efficient cryptanalytic algorithm for 4-bit S-boxes.

7. Conclusion

In this paper, a detailed discussion on four cryptanalytic attacks on 4-bit Crypto S-boxes has been done. From their point of view of execution time of algorithms, the new attack Linear Approximation Analysis has been the best. A detail Analysis of 32 DES 4-bit S-boxes has also been included in this paper and it has been proved that DES S-boxes have constructed with the knowledge of Differential Cryptanalysis of 4-bit Crypto S-boxes. All S-boxes are unsecure to rest of three attacks. So we cannot Consider DES S-boxes as cryptographically secure S-boxes.

Acknowledgements

For This exhaustive work we want to acknowledge the continuous encouragement of Prof.(Dr.) Amlan Chakrabarti, Dean Faculty Council of Engineering and Technology, University of Calcutta and the infrastructure provided by Prof.(Dr.) Debatosh Guha, Head Dept. Department of Radio Physics and Electronics, University of Calcutta. We also acknowledge TEQIP-Phase-II, University of Calcutta for providing financial support upto 30^th November 2016.

Cite this paper

Dey, S. and Ghosh, R. (2018) A Review of Existing 4-Bit Crypto S-Box Cryptanalysis Techniques and Two New Techniques with 4-Bit Boolean Functions for Cryptanalysis of 4-Bit Crypto S-Boxes. Advances in Pure Mathematics, 8, 272-306. https://doi.org/10.4236/apm.2018.83015

References

NOTES

*A review of existing 4-bit crypto S-box cryptanalysis techniques.