Advances in Pure Mathematics
Vol.06 No.13(2016), Article ID:72955,15 pages
10.4236/apm.2016.613075
Banach Limits Revisited*
Diethard Pallaschke1, Dieter Pumplün2
1Institute of Operations Research, Karlsruhe Institute of Technology (KIT), Karlsruhe, Germany
2Faculty of Mathematics and Computer Science, Fern Universität Hagen, Hagen, Germany

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: November 13, 2016; Accepted: December 20, 2016; Published: December 23, 2016
ABSTRACT
Order unit normed linear spaces are a special type of regularly ordered normed linear spaces and therefore the first section is a short collection of the fundamental results on this type of normed linear spaces. The connection between order unit normed linear spaces and base normed linear spaces within the category of regularly ordered normed linear spaces is described in Section 2, and Section 3 at last, contains the results on Banach limits in an arbitrary order unit normed linear space. It is shown that the original results on Banach limits are valid for a greater range.
Keywords:
Order Unit Normed Spaces, Base Normed Spaces, Banach Limits

1. Introduction
Most, if not all, publications where Banach limits are investigated take place in an order unit normed real linear space. Order unit normed linear spaces are a special type of regularly ordered normed linear spaces and therefore the first section is a short collection of the fundamental results on this type of normed linear spaces, for the reader's convenience. The connection between order unit normed linear spaces and base normed linear spaces within the category of regularly ordered normed linear spaces is described in Section 2, and Section 3 at last, contains the results on Banach limits in an arbitrary order unit normed linear space. It is shown that the original results on Banach limits are valid in a for greater range. For a further generalisation of vector valued Banach limits in a different direction we refer to a recent paper of R.Armario, F. Kh. Garsiya-Pacheko and F. Kh Peres-Fernandes [1] .
2. Regularly Ordered Normed Linear Spaces
An ordered normed linear space 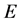 with order
with order 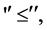 norm
norm 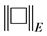 and order cone
and order cone  is called regularly ordered iff the cone
is called regularly ordered iff the cone 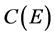 is
is 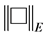 -closed and proper and
-closed and proper and 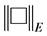 is a Riesz norm, i.e. if
is a Riesz norm, i.e. if
(Ri 1) For 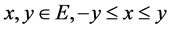 implies
implies 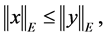 i.e.
i.e. 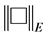 is absolutely mo- notone, and
is absolutely mo- notone, and
(Ri 2) For x Î E with 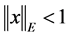 there exists a
there exists a 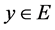 with
with  and
and 
hold. (see [2] [3] ).
Lemma 1. Let, for an ordered linear space  with proper and
with proper and 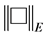 -closed cone
-closed cone  (Ri 1) hold. Then each of the following two conditions is equivalent to (Ri 2)
(Ri 1) hold. Then each of the following two conditions is equivalent to (Ri 2)
(Ri 3) For 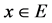 and
and 



(Ri 4) For any
holds.
Proof. The proof is straightforward. Condition (Ri 2) implies that 




hence (Ri 3) is proved for
(Ri 3) implies that 

Because of (Ri 3), for 






In [3] K. Ch. Min introduced regularly ordered normed spaces as a natural and canonical generalization of Riesz spaces. A crucial point in this generalization was the definition of the corresponding homomorphisms compatible and most closely related to the structure of these spaces, such that, in addition, the set of these special homomorphisms is again a regularly ordered normed linear space in a canonical way. This is done by
Definition 1. If 


The set
is a linear space by the obvious operations. One introduces the cone
which is obviously proper and generates 










Lemma 2. Let 




holds.
Proof. For 



and
hence
□
Now, we proceed to define the norm 


Proposition 1. For regularly ordered normed spaces 




Proof. The proof that 








Using 

and, multiplying by −1

Adding (i) and (ii) yields
hence
and
Now 



hence 





□
In the following 

3. Order Unit and Base Ordered Normed Linear Spaces
The order unit normed linear spaces are a special type of regularly ordered normed linear spaces , as are the base normed linear spaces [3] [4] . For investigating a special type of mathematical objects, however, it is always best to use the type of mappings most closely related to the special structure of the objects (the Bourbaki Principle). Hence, for investigating order unit normed spaces we do not look at the full subcategory of Reg-Ord generated by the order unit normed spaces but introduce a more special type of regular linear mappings. The same method, by the way, has been successful for another type of regularly ordered spaces, namely the base normed (Banach) spaces (cp. [3] [5] [6] ).
Definition 2. For two order unit normed linear spaces 

and
Proposition 2. Let 

i) 





ii) 

Proof. (1) Let 















Let 
Then
follows, i.e.
which proves that 
Now 







(ii) This follows from (i) (see [7] , 3.9 p. 128). □
Corollary 1. For order unit normed linear spaces
is a base-normed ordered linear space with base 



Proof. That 



□
Remark 1. If 




Definition 3. The order unit normed linear spaces together with the linear mappings 

There is an equally important subcategory of Reg-Ord, the category of based normed linear spaces.
Definition 4. A base normed ordered linear space “base normed linear space” for short, is a regular ordered linear space 





The elements of 





is a base normed space of special mappings from 

What remains in this connection is to investigate special morphisms particularly adapted to these subcategories between spaces belonging to two different of these subcategories Ord-Unit and BN-Ord. We start this with investigating the intersection of these subcategories.
Proposition 3. Let 



Proof. If 
















Hence, the isomorphism is 

It should be noted that this isomorphism is an isomorphism in the category Ord- Unit of order unit normed spaces and also in BN-Ord. So, loosely speaking,
Now the “general connection” between Ord-Unit and BN-Ord is investigated via the morphisms:
Proposition 4. If 


Proof. Define 











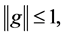


















This is a slightly different version of the proof of Theorem 1 in Ellis [7] .
Surprisingly a corresponding result also holds if 

Proposition 5. If 


Proof. Define
where 






that is 


For 





Obviously 



from which 

□
It is interesting that by defining the subspaces 






There are different ways to generalize the structure of 





4. Banach Limits
For the introduction of Banach Limits we first prove, following a proof method of W. Roth in [12] , Theorem 2.1, a special variant of the Hahn-Banach Theorem for order unit normed linear spaces.
Theorem 6. (Hahn-Banach Theorem for Order Unit Spaces) Let 



i) 
ii) 
iii) For any 




iv) 

v) For any 



Then there exists a positive linear functional 
a) 
b)
c)
d)
for 
Proof. Define
Obviously 



Let 

As 


holds.
If 




Let 


As obviously 










Define for
As, for 

Taking 



implying

Now, the remaining equations in the assertion will be proved for 


contributing
to 

contributing
to the definition of 

To show the invariance of 



contributing
to
An inequality 

and
as contribution to

Verbatim, this proof carries over to the equation

A new function is now introduced by

If 


For




and

follows which implies in, particular, 


Taking 


in particular 



follows i.e. monotonicity.
Consider now, for
then
i.e.
Now for
and
The mapping
is, for fixed 

holds because for 


We now show that 


contributing
to 



Hence
This implies

The proof of the remaining two equations of the assertions follows almost verbatim this pattern of proof and one gets:
and (6) implies 


because of (6) and the minimality of
Now, looking again at the definition (4) of 



which together with (1) yields 

Now, for
and
and since 

which implies 


Banach limits are almost always defined as continuous extensions of a continuous linear functional in an order unit normed space. Hence, for the introduction of Banach limits we need Theorem 6 in a continuous form. Surprisingly Theorem 6 already contains all the necessary continuity conditions as the following Corollary shows:
Corollary 2. Let the assertions (i)-(v) of Theorem 6 be satisfied and put 


i) 


ii) 

iii) Any 
Proof. i): Obviously, 




ii): 















implying the continuity of 




It is remarkable that with respect to the continuity properties, the continuity of 

Definition 5. With the notations of Corollary 2 any such 
One defines


Proposition 7. For 
i) 


ii) 



iii) 

Proof. i): Let 
all abstract convex combinations, then, for 

ously 


satisfied, too.
ii): One first proves that 














iii): Obviously, 



□
Because 

is a proper cone and
is a base normed ordered linear space. To simplify notation, we will write 

Theorem 8. If the norm induced by 





is a compact, base normed Saks space (see [13] , Theorem 3.1) and an isometrical subspace of
Proof. As 



The result of Theorem 8 is essentially the definition of a functor from any category with objects satisfying the assertions of Theorem 6 to the category of compact, base normed Saks spaces ( [13] , Theorem 3.1). This functor will be investigated by the authors in a forthcoming paper.
5. Summary
The main result of the paper offers a Hahn-Banach theorem for order unit normed spaces (Theorem 6) from which novel conclusions on Banach limits are drawn. The result of Theorem 8 gives rise to the definition of a functor which goes from any category with objects satisfying the assertions of Theorem 6 into the category of compact, base normed Saks spaces.
Cite this paper
Pallaschke, D. and Pumplün, D. (2016) Banach Limits Revisited. Advances in Pure Mathematics, 6, 1022-1036. http://dx.doi.org/10.4236/apm.2016.613075
References
- 1. Armario, R., Garcia-Pacheco, F.J. and Pérez-Fernández, F.J. (2013) On Vector-Valued Banach Limits. Functional Analysis and Its Applications, 47, 82-86. (In Russian) (Transl. (2013) Functional Analysis and Its Applications, 47, 315-318.)
- 2. Davis, R.B. (1968) The Structure and Ideal Theory of the Predual of a Banach Lattices. Transactions of the AMS, 131, 544-555.
https://doi.org/10.1090/S0002-9947-1968-0222604-8 - 3. Min, K.Ch. (1983) An Exponential Law for Regular Ordered Banach Spaces. Cahiers de Topologie et Géometrie Differentielle Catégoriques, 24, 279-298.
- 4. Wong, Y.C. and Ng, K.F. (1973) Partially Ordered Topological Vector Spaces. Oxford Mathematical Monographs, Clarendon Press, Oxford.
- 5. Pumplün, D. (1999) Elemente der Kategorientheorie. Spektrum Akademischer Verlag, Heidelberg, Berlin.
- 6. Pumplün, D. (2002) The Metric Completion of Convex Sets and Modules. Results in Mathematics, 41, 346-360.
https://doi.org/10.1007/BF03322777 - 7. Jameson, C. (1971) Ordered Linear Spaces. Lecture Notes in Mathematics (Volume 141), Springer, Berlin.
- 8. Pumplün, D. (1995) Banach Spaces and Superconvex Modules. In: Behara, M., et al. (Eds.), Symposia Gaussiana, de Gruyter, Berlin, 323-338.
https://doi.org/10.1515/9783110886726.323 - 9. Pumplün, D. and Röhrl, H. (1989) The Eilenberg-Moore Algebras of Base Normed Spaces. In: Banaschewski, Gilmour, Herrlich, Eds., Proceedings of the Symposium on Category Theory and its Applications to Topology, University of Cape Town, Cape Town, 187-200.
- 10. Ellis, E.J. (1966) Linear Operators in Partially Ordered Normed Vector Spaces. Journal of the London Mathematical Society, 41, 323-332.
https://doi.org/10.1112/jlms/s1-41.1.323 - 11. Klee Jr., V.L. (1954) Invariant Extensions of Linear Functionals. Pacific Journal of Mathematics, 4, 37-46.
- 12. Roth, W. (2000) Hahn-Banach Type Theorems for Locally Convex Cones. Journal of the Australian Mathematical Society Series A, 68, 104-125.
https://doi.org/10.1017/S1446788700001609 - 13. Pumplün, D. (2011) A Universal Compactification of Topological Positively Convex Sets and Modules. Journal of Convex Analysis, 8, 255-267.
- 14. Pumplün, D. (2003) Positively Convex Modules and Ordered Normed Linear Spaces. Journal of Convex Analysis, 41, 109-127.
NOTES
*Dedicated to Reinhard Börger, a brilliant and enthusiastic mathematician full of new ideas.














































































































