Advances in Pure Mathematics
Vol.06 No.03(2016), Article ID:63990,12 pages
10.4236/apm.2016.63014
New Generalized  -Expansion Method Applications to Coupled Konno-Oono Equation
-Expansion Method Applications to Coupled Konno-Oono Equation
Md. Nur Alam1*, Fethi Bin Muhammad Belgacem2
1Department of Mathematics, Pabna University of Science & Technology, Pabna, Bangladesh
2Department of Mathematics, Faculty of Basic Education, PAAET, Al-Ardhiya, Kuwait
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).



Received 10 November 2015; accepted 24 February 2016; published 29 February 2016
ABSTRACT
The new generalized 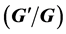 -expansion method is one of the powerful and competent methods that appear in recent time for establishing exact solutions to nonlinear evolution equations (NLEEs). We apply the new generalized
-expansion method is one of the powerful and competent methods that appear in recent time for establishing exact solutions to nonlinear evolution equations (NLEEs). We apply the new generalized 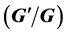 -expansion method to solve exact solutions of the new coupled Konno-Oono equation and construct exact solutions expressed in terms of hyperbolic functions, trigonometric functions, and rational functions with arbitrary parameters. The significance of obtained solutions gives credence to the explanation and understanding of related physical phenomena. As a newly developed mathematical tool, this method efficiency for finding exact solutions has been demonstrated through showing its straightforward nature and establishing its ability to handle nonlinearities prototyped by the NLEEs whether in applied mathematics, physics, or engineering contexts.
-expansion method to solve exact solutions of the new coupled Konno-Oono equation and construct exact solutions expressed in terms of hyperbolic functions, trigonometric functions, and rational functions with arbitrary parameters. The significance of obtained solutions gives credence to the explanation and understanding of related physical phenomena. As a newly developed mathematical tool, this method efficiency for finding exact solutions has been demonstrated through showing its straightforward nature and establishing its ability to handle nonlinearities prototyped by the NLEEs whether in applied mathematics, physics, or engineering contexts.
Keywords:
New Generalized 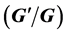 -Expansion Method, Coupled Konno-Oono Equations, Nonlinear Partial Differential Equation
-Expansion Method, Coupled Konno-Oono Equations, Nonlinear Partial Differential Equation

1. Introduction
Various physical, mechanical, chemical, biological, engineering and some economic laws and relations appear mathematically in the form of differential equations which are linear or nonlinear, homogeneous or inhomogeneous. Almost all differential equations relating physical phenomena are nonlinear. Methods of solutions of linear differential equations are reasonably easy and well avowed. In contrast, the techniques of solutions of nonlinear differential equations are less obtainable and in general, approximations are generally used. Nonlinearity is a fascinating element of nature, today; many scientists observe nonlinear science as the most important frontier for the fundamental understanding of nature. The analytical solutions of such equations are of fundamental importance to reveal the inner structure of the phenomena. The world around us is inherently nonlinear. For instance, nonlinear evolution equations (NEEs) are widely used as models to describe complex physical phenomena in various fields of sciences, especially in fluid mechanics, solid-state physics, plasma physics, plasma waves and biology, etc. One of the basic physical problems for those models is to obtain their travelling wave solutions. In particular, various methods have been utilized to explore different kinds of solutions of physical models described by nonlinear partial differential equations (NPDEs). In the numerical methods, stability and convergence should be considered so as to avoid divergent or inappropriate results. However, in recent years, a variety of effective analytical and semi-analytical methods have been developed to be used for solving NLEEs, such as the inverse scattering transform method [1] , the  -expansion method [2] [3] , the modified simple equation method [4] [5] , the Sumudu transform method [6] -[8] , the homogeneous balance method [9] [10] , the Darboux transformation method [11] , the Backlund transformation method [12] , the complex hyperbolic function method [13] [14] , the
-expansion method [2] [3] , the modified simple equation method [4] [5] , the Sumudu transform method [6] -[8] , the homogeneous balance method [9] [10] , the Darboux transformation method [11] , the Backlund transformation method [12] , the complex hyperbolic function method [13] [14] , the  -expansion method [15] -[25] , the improved
-expansion method [15] -[25] , the improved 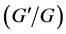 -expansion method [26] , the collocation method [27] [28] , the similarity reductions method [29] [30] , the homotopy analysis method [31] [32] , the spectral-homotopy analysis method [33] -[35] , the Hermite-Pade approximation method [36] and so on.
-expansion method [26] , the collocation method [27] [28] , the similarity reductions method [29] [30] , the homotopy analysis method [31] [32] , the spectral-homotopy analysis method [33] -[35] , the Hermite-Pade approximation method [36] and so on.
Naher and Abdullah [37] introduced a new approach of 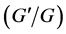 -expansion method and a new approach of generalized
-expansion method and a new approach of generalized 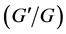 -expansion method for a reliable treatment of the nonlinear evolution equations. Afterwards, many researchers investigated many nonlinear PDEs to construct traveling wave solutions via this powerful
-expansion method for a reliable treatment of the nonlinear evolution equations. Afterwards, many researchers investigated many nonlinear PDEs to construct traveling wave solutions via this powerful 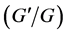 -expansion method. For example, Alam and Akbar [38] [39] applied this method for finding traveling wave solutions of the KP-BBM equation, the (3 + 1)-dimensional potential-YTSF equation, the (2 + 1)-dimen- sional Zakharov-Kuznetsov equation. Alam et al. [40] [41] concerned about this method to construct traveling wave solutions of the strain wave equation in microstructured solids, the (3 + 1)-dimensional mKdV-ZK equation and the (1 + 1)-dimensional compound KdVB equations. The objective of this article is to look for new study relating to the new generalized
-expansion method. For example, Alam and Akbar [38] [39] applied this method for finding traveling wave solutions of the KP-BBM equation, the (3 + 1)-dimensional potential-YTSF equation, the (2 + 1)-dimen- sional Zakharov-Kuznetsov equation. Alam et al. [40] [41] concerned about this method to construct traveling wave solutions of the strain wave equation in microstructured solids, the (3 + 1)-dimensional mKdV-ZK equation and the (1 + 1)-dimensional compound KdVB equations. The objective of this article is to look for new study relating to the new generalized  expansion method for solving the new coupled Konno-Oono equation to make the goodwill and helpfulness of the method obvious.
expansion method for solving the new coupled Konno-Oono equation to make the goodwill and helpfulness of the method obvious.
Our aim in this paper is to present an application of the new generalized 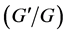 -expansion method to the new coupled Konno-Oono equation to be solved by this method for the first time.
-expansion method to the new coupled Konno-Oono equation to be solved by this method for the first time.
The rest of the paper is organized as follows: In Section 2, we give the description of the new generalized 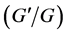 -expansion method. In Section 3, we apply this method to the new coupled Konno-Oono equation with discussion and Graphical representations of the solutions. Conclusions are given at last.
-expansion method. In Section 3, we apply this method to the new coupled Konno-Oono equation with discussion and Graphical representations of the solutions. Conclusions are given at last.
2. Description of the Method
Let us consider a general nonlinear PDE in the form
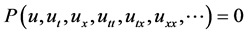 , (1)
, (1)
where  is an unknown function, P is a polynomial in
is an unknown function, P is a polynomial in 
Step 1: We combine the real variables x and t by a complex variable


where V is the speed of the traveling wave. The traveling wave transformation (2) converts Equation (1) into an ordinary differential equation (ODE) for

where Q is a polynomial of u and its derivatives and the superscripts indicate the ordinary derivatives with respect to
Step 2: According to possibility Equation (3) can be integrated term by term one or more times, yields constant(s) of integration. The integral constant may be zero, for simplicity.
Step 3: Suppose the traveling wave solution of Equation (3) can be expressed as follows:

where either 








where 

where the prime stands for derivative with respect to
Step 4: To determine the positive integer N, taking the homogeneous balance between the highest order nonlinear terms and the derivatives of the highest order appearing in Equation (3).
Step 5: Substitute Equation (4) and Equation (6) including Equation (5) into Equation (3) with the value of N obtained in Step 4, we obtain polynomials in 







Step 6: Suppose that the value of the constants 





Using the general solution of Equation (6), we have the following solutions of Equation (5):
Family 1: When 


Family 2: When 


Family 3: When 


Family 4: When 


Family 5: When 


3. The New Coupled Konno-Oono Equation
The new coupled Konno-Oono equation: In this section, we will put forth the new generalized 

Now let us suppose that the traveling wave transformation equation be

The Equation (13) reduces Equation (12) into the following ODEs


By integrating (15) with respect to

where P is a constant of integration.
Substituting Equation (16) into Equation (14), we get

Taking the homogeneous balance between highest order nonlinear term 



where 
Substituting Equation (18) together with Equations (5) and (6) into Equation (17), the left-hand side is converted into polynomials in 









where 
Substituting Equation (19) into Equation (18), along with Equation (7) and simplifying, our traveling wave solutions become, if 



and
and
Substituting Equation (19) into Equation (18), along with Equation (8) and simplifying yields exact solutions, if 



and
and
Substituting Equation (19) into Equation (18), along with Equation (9) and simplifying, our obtained solution becomes:
and
Substituting Equation (19) into Equation (18), together with Equation (10) and simplifying, yields following traveling wave solutions, if 




and

and
Substituting Equation (19) into Equation (18), along with Equation (11) and simplifying, our exact solutions become, if 



and

and

where
Khan and Akbar [43] investigated solutions of the the new coupled Konno-Oono equation by the modified simple equation method and obtained only eight solutions (A1)-(A8) (see appendix). Moreover, in this article eighteen solutions of the new coupled Konno-Oono equation are constructed by applying the new approach of generalized 



4. Graphical Representations of the Solutions
The graphical illustrations of the solutions are depicted in the Figures 1-6 with the aid of commercial software Maple.
Figure 1. Single soliton of 


Figure 2. Multiple soliton of 







Figure 3. Compacton of 







Figure 4. Singular soliton of 









Figure 5. Singular periodic solution of 







Figure 6. Periodic solutions of 







5. Conclusion
The new generalized 



Acknowledgements
F.B.M. Belgacem is pleased to acknowledge the continued support of the Public Authority Applied Education and Training Research Department (PAAET RD).
Cite this paper
Md. NurAlam,Fethi Bin MuhammadBelgacem, (2016) New Generalized (G'/G)-Expansion Method Applications to Coupled Konno-Oono Equation. Advances in Pure Mathematics,06,168-179. doi: 10.4236/apm.2016.63014
References
- 1. Ablowitz, M.J. and Clarkson, P.A. (1991) Soliton, Nonlinear Evolution Equations and Inverse Scattering Method. Cambridge University Press, New York.
http://dx.doi.org/10.1017/CBO9780511623998 - 2. Yang, Y.J. (2013) New Application of the (G’/G,1/G)-Expansion Method to KP Equation. Applied Mathematical Sciences, 7, 959-967.
- 3. Li, L.X., Li, E.Q. and Wang, M.L. (2010) The (G’/G,1/G)-Expansion Method and Its Application to Traveling Wave Solutions of the Zakharov Equations. Applied Mathematics, 25, 454-462.
http://dx.doi.org/10.1007/s11766-010-2128-x - 4. Jawad, A.J.M., Petkovic, M.D. and Biswas, A. (2010) Modified Simple Equation Method for Nonlinear Evolution Equations. Applied Mathematics and Computation, 217, 869-877.
http://dx.doi.org/10.1016/j.amc.2010.06.030 - 5. Khan, K., Akbar, M.A. and Alam, M.N. (2013) Traveling Wave Solutions of the Nonlinear Drinfel’d-Sokolov-Wilson Equation and Modified Benjamin-Bona-Mahony Equations. Journal of the Egyptian Mathematical Society, 21, 233-240.
http://dx.doi.org/10.1016/j.joems.2013.04.010 - 6. Belgacem, F.B.M., Karaballi, A.A. and Kalla, S.L. (2003) Analytical Investigations of the Sumudu Transform and Applications to Integral Production Equations. Mathematical Problems in Engineering, 2003, 103-118.
- 7. Belgacem, F.B.M. (2006) Introducing and Analyzing Deeper Sumudu Properties. Nonlinear Studies, 13, 23-41.
- 8. Belgacem, F.B.M. and Karaballi, A.A. (2006) Sumudu Transform Fundamental Properties Investigations and Applications. Journal of Applied Mathematics and Stochastic Analysis, 2006, Article ID: 91083.
- 9. Zayed, E.M.E., Zedan, H.A. and Gepreel, K.A. (2004) On the Solitary Wave Solutions for Nonlinear Hirota-Sasuma Coupled KDV Equations. Chaos, Solitons and Fractals, 22, 285-303.
http://dx.doi.org/10.1016/j.chaos.2003.12.045 - 10. Wang, M.L. (1996) Exact Solutions for a Compound KdV-Burgers Equation. Physics Letters A, 213, 279-287.
http://dx.doi.org/10.1016/0375-9601(96)00103-X - 11. Matveev, V.B. and Salle, M.A. (1991) Darboux Transformation and Solitons. Springer, Berlin.
http://dx.doi.org/10.1007/978-3-662-00922-2 - 12. Miura, M.R. (1978) Backlund Transformation. Springer, Berlin.
- 13. Zayed, E.M.E., Abourabia, A.M., Gepreel, K.A. and Horbaty, M.M. (2006) On the Rational Solitary Wave Solutions for the Nonlinear HirotaCSatsuma Coupled KdV System. Journal of Applied Analysis, 85, 751-768.
http://dx.doi.org/10.1080/00036810600604789 - 14. Chow, K.W. (1995) A Class of Exact Periodic Solutions of Nonlinear Envelope Equation. Journal of Mathematical Physics, 36, 4125-4137.
http://dx.doi.org/10.1063/1.530951 - 15. Wang, M., Li, X. and Zhang, J. (2008) The (G’/G)-Expansion Method and Traveling Wave Solutions of Nonlinear Evolution Equations in Mathematical Physics. Physics Letters A, 372, 417-423.
http://dx.doi.org/10.1016/j.physleta.2007.07.051 - 16. Alam, M.N. and Akbar M.A. (2015) A Novel (G’/G)-Expansion Method for Solving the (3+1)-Dimensional Modified KdV-Zakharov-Kuznetsov Equation in Mathematical Physics. International Journal of Computing Science and Mathematics, 6, 404-415.
http://dx.doi.org/10.1504/IJCSM.2015.071812 - 17. Feng, J., Li, W. and Wan, Q. (2011) Using (G’/G)-Expansion Method to Seek the Traveling Wave Solution of Kolmogorov-Petrovskii-Piskunov Equation. Applied Mathematics and Computation, 217, 5860-5865.
http://dx.doi.org/10.1016/j.amc.2010.12.071 - 18. Alam, M.N. (2015) Exact Solutions to the Foam Drainage Equation by Using the New Generalized -Expansion Method. Results in Physics, 5, 168-177.
http://dx.doi.org/10.1016/j.rinp.2015.07.001 - 19. Guo, S. and Zhou, Y. (2010) The Extended (G’/G)-Expansion Method and Its Applications to the Whitham-Broer-Like Equations and Coupled Hirota-Satsuma KdV Equations. Applied Mathematics and Computation, 215, 3214-3221.
http://dx.doi.org/10.1016/j.amc.2009.10.008 - 20. Zhu, S.D. (2008) The Generalizing Riccati Equation Mapping Method in Nonlinear Evolution Equation: Application to (2+1)-Dimensional Boiti-Leon-Pempinelle Equation. Chaos, Solitons & Fractals, 37, 1335-1342.
http://dx.doi.org/10.1016/j.chaos.2006.10.015 - 21. Alam, M.N., Akbar, M.A. and Mohyud-Din, S.T. (2014) A Novel (G’/G)-Expansion Method and Its Application to the Boussinesq Equation. Chinese Physics B, 23, Article ID: 020203.
http://dx.doi.org/10.1088/1674-1056/23/2/020203 - 22. Shakeel, M., Ul-Hassan, Q.M. and Ahmad, J. (2014) Applications of the Novel (G’/G)-Expansion Method for a Time Fractional Simplified Modified MCH Equation. Abstract and Applied Analysis, 2014, Article ID: 601961.
- 23. Hafez, M.G., Alam, M.N. and Akbar, M.A. (2014) Exact Traveling Wave Solutions to the Klein-Gordon Equation Using the Novel (G’/G)-Expansion Method. Results in Physics, 4, 177-184.
http://dx.doi.org/10.1016/j.rinp.2014.09.001 - 24. Alam, M.N. and Akbar, M.A. (2014) A New (G’/G)-Expansion Method and Its Application to the Burgers Equation. Walailak Journal of Science and Technology, 11, 643-658.
- 25. Zayed, E.M.E. (2009) New Traveling Wave Solutions for Higher Dimensional Nonlinear Evolution Equations Using a Generalized (G’/G)-Expansion Method. Journal of Physics A: Mathematical and Theoretical, 42, Article ID: 195202.
http://dx.doi.org/10.1088/1751-8113/42/19/195202 - 26. Zhang, J., Jiang, F. and Zhao, X. (2010) An Improved (G’/G)-Expansion Method for Solving Nonlinear Evolution Equations. International Journal of Mathematics, 87, 1716-1725.
http://dx.doi.org/10.1080/00207160802450166 - 27. Saliman, A.A. (2004) Collocation Solution of the Kortewegde Vries Equation Using Septic Splines. International Journal of Computer Mathematics, 81, 325-331.
http://dx.doi.org/10.1080/00207160410001660817 - 28. Soliman, A.A. and Hussein, M.H. (2005) Collocation Solution for RLW Equation with Septic Spline. Applied Mathematics and Computation, 161, 623-636.
http://dx.doi.org/10.1016/j.amc.2003.12.053 - 29. Bluman, G.W. and Kumei, S. (1989) Symmetries and Differential Equations. Springer-Verlag, New York.
http://dx.doi.org/10.1007/978-1-4757-4307-4 - 30. Olver, P.J. (1986) Applications of Lie Groups to Differential Equations. Springer-Verlag, New York.
http://dx.doi.org/10.1007/978-1-4684-0274-2 - 31. Domairry, G., Mohsenzadeh, A. and Famouri, M. (2009) The Application of Homotopy Analysis Method to Solve Nonlinear Differential Equation Governing Jeffery-Hamel Flow. Communications in Nonlinear Science and Numerical Simulation, 14, 85-95.
http://dx.doi.org/10.1016/j.cnsns.2007.07.009 - 32. Joneidi, A.A., Domairry, G. and Babaelahi, M. (2010) Three Analytical Methods Applied to Jeffery-Hamel Flow. Communications in Nonlinear Science and Numerical Simulation, 15, 3423-3434.
http://dx.doi.org/10.1016/j.cnsns.2009.12.023 - 33. Motsa, S.S., Sibanda, P., Awad, F.G. and Shateyi, S. (2010) A New Spectral-Homotopy Analysis Method for the MHD Jeffery-Hamel Problem. Computers & Fluids, 39, 1219-1225.
http://dx.doi.org/10.1016/j.compfluid.2010.03.004 - 34. Makukula, Z.G., Sibanda, P. and Motsa, S.S. (2010) A Note on the Solution of the von Kármán Equations Using Series and Chebyshev Spectral Methods. Boundary Value Problems, 2010, Article ID: 471793.
- 35. Sibanda, P., Makukula, Z.G. and Motsa, S.S. (2010) A Novel Numerical Technique for Two-Dimensional Laminar Flow between Two Moving Porous Walls. Mathematical Problems in Engineering, 2010, Article ID: 528956.
- 36. Makinde, O.D. and Mhone, P.Y. (2006) Hermite-Padé Approximation Approach to MHD Jeffery-Hamel Flows. Applied Mathematics and Computation, 181, 966-972.
http://dx.doi.org/10.1016/j.amc.2006.02.018 - 37. Naher, H. and Abdullah, F.A. (2013) New Approach of (G’/G)-Expansion Method and New Approach of Generalized (G’/G)-Expansion Method for Nonlinear Evolution Equation. AIP Advances, 3, Article ID: 032116.
http://dx.doi.org/10.1063/1.4794947 - 38. Alam, M.N. and Akbar, M.A. (2014) The New Approach of Generalized (G’/G)-Expansion Method for Nonlinear Evolution Equations. Ain Shams Engineering Journal, 5, 595-603.
http://dx.doi.org/10.1016/j.asej.2013.12.008 - 39. Alam, M.N. and Akbar, M.A. (2013) Exact Traveling Wave Solutions of the KP-BBM Equation by Using the New Approach of Generalized (G’/G)-Expansion Method. Springer Plus, 2, 617.
http://dx.doi.org/10.1186/2193-1801-2-617 - 40. Alam, M.N., Akbar, M.A. and Mohyud-Din, S.T. (2014) General Traveling Wave Solutions of the Strain Wave Equation in Microstructured Solids via the New Approach of Generalized (G’/G)-Expansion Method. Alexandria Engineering Journal, 53, 233-241.
http://dx.doi.org/10.1016/j.aej.2014.01.002 - 41. Alam, M.N., Akbar, M.A. and Hoque, M.F. (2014) Exact Traveling Wave Solutions of the (3+1)-Dimensional mKdV-ZK Equation and the (1+1)-Dimensional Compound KdVB Equation Using New Approach of the Generalized (G’/G)-Expansion Method. Pramana—Journal of Physics, 83, 317-329.
http://dx.doi.org/10.1007/s12043-014-0776-8 - 42. Konno, K. and Oono, H. (1994) New Coupled Integrable Dispersion-Less Equations. Journal of the Phusical Society of Japan, 63, 377-378.
http://dx.doi.org/10.1143/JPSJ.63.377 - 43. Khan, K. and Akbar, M.A. (2013) Traveling Wave Solutions of Some Coupled Nonlinear Evolution Equations. Mathematical Physics, 2013, Article ID: 685736.
Appendix: Khan and Akbar’s Solutions [43]
We bring to the reader’s attention that Equation (16) regarding v(x,t) above is the same as Equation (10) in Khan and Akbar [43] , where the authors manged established exact solutions of the new coupled Konno-Oono equation by using the modified simple equation method which are as follows (see Equation (23) for u(x,t), in [43] ):

We can freely choose the constants A and B. Therefore, setting


Again, Setting


If




NOTES
*Corresponding author.



































