Advances in Pure Mathematics
Vol.05 No.13(2015), Article ID:61179,8 pages
10.4236/apm.2015.513073
Some Inequalities on Polar Derivative of Polynomial Having No Zero in a Disc
Barchand Chanam
Department of Basic Sciences and Humanities, National Institute of Technology, Manipur, India

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 30 September 2015; accepted 14 November 2015; published 17 November 2015

ABSTRACT
Let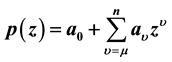 ,
, 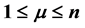 , be a polynomial of degree n having no zero in
, be a polynomial of degree n having no zero in ,
, 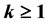 , then Qazi [Proc. Amer. Math. Soc., 115 (1992), 337-343] proved
, then Qazi [Proc. Amer. Math. Soc., 115 (1992), 337-343] proved
 .
.
In this paper, we first extend the above inequality to polar derivative of a polynomial. Further, as an application of our result, we extend a result due to Dewan et al. [Southeast Asian Bull. Math., 27 (2003), 591-597] to polar derivative.
Keywords:
Polynomials, Inequalities, Polar Derivative of a Polynomial, Zeros

1. Introduction and Statement of Results
Let 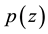 be a polynomial of degree n. Then according to the well-known Bernstein’s inequality [1] .
be a polynomial of degree n. Then according to the well-known Bernstein’s inequality [1] .
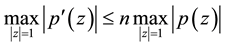 . (1.1)
. (1.1)
Equality holds in (1.1) if and only if 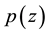 has all its zeros at the origin.
has all its zeros at the origin.
If we restrict ourselves to the class of polynomials having no zero in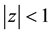 , then inequality (1.1) can be sharpened. It was conjectured by Erdös and later verified by Lax [2] that if
, then inequality (1.1) can be sharpened. It was conjectured by Erdös and later verified by Lax [2] that if 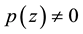 in
in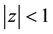 , then (1.1) can be replaced by
, then (1.1) can be replaced by
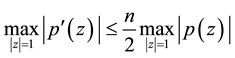 . (1.2)
. (1.2)
Inequality (1.2) is best possible and equality attains for ,
, .
.
Malik [3] extended (1.2) by considering the class of polynomials  of degree n not vanishing in
of degree n not vanishing in


Qazi [4] considered a more general class of polynomials



Theorem A. If



Inequality (1.4) is sharp and equality holds for the polynomial 

By involving

Theorem B. If



Inequality (1.5) is best possible for 


Remark 1. Theorem B proved by Dewan et al. [5] seems to have a deficiency in the sense that for 

Let 




The polynomial 




The polynomial 




Aziz [9] extended (1.3) to the polar derivative of 






Inequality (1.8) is best possible and equality holds for 


Further, by considering a more general class of polynomials

having no zero in




In this paper, we first extend Theorem A to polar derivative of a polynomial, which gives an improvement of (1.9). More precisely, we prove.
Theorem 1. If





Equality in (1.10) holds for 



Remark 2. To prove that the bound of Theorem 1is better than that of (1.9), it is sufficient to prove that
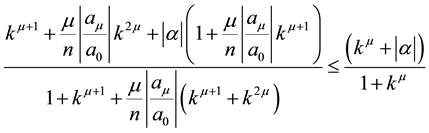
i.e. equivalently,
i.e.
which is true since


Further, if we put 
Corollary 1. If 





Remark 3. Inequality (1.13) is the corresponding polar derivative version of a result proved by Govil et al. ( [11] , Inequality (10)).
Remark 4. As mentioned earlier, inequality (1.13) improves inequality (1.8) and is evident from Remark 2, for the paticularcase
It is of interest that as an application of Theorem 1, we have been able to obtain an independent proof of a re-
sult proved by Mir and Dar ( [12] , Theorem 1), which involves 
rivative which also improves upon Theorem 1 for
Theorem 2. If






Equality occurs in (1.11) for 



If we divide both sides of the above inequalities (1.11) and (1.12) by 

Remark 5. For
Corollary 2. If 





Inequality (1.14) is best possible for


Remark 6. It is obvious that Corollary 2 is an improvement of Corollary 1.
2. Lemmas
The following lemmas are required in the proofs of the theorems.
Lemma 2.1. If 


where

The above lemma is a special case of a result due to Govil and Rahman [13] .
Lemma 2.2. If 



Proof of Lemma 2.2. The proof of this lemma is simple and follows as a part ( [10] , proof of Theorem 1), but for the sake of completeness, we outline it. Let


Now, for every real or complex number



This implies on
which completes the proof of Lemma 2.2.
Lemma 2.3. If



and

Lemma 2.3 is due to Qazi ( [4] , Proof and Remark of Lemma 1).
3. Proofs of the Theorems
Proof of Theorem 1. On

and by inequality (2.4) of Lemma 2.3, we have

Combining (3.1) and (3.2), we obtain for

which gives for

Now, if


Inequality (3.3) when combined with Lemma 2.2, gives for 

which is equivalent to

from which Theorem1 follows.
Proof of Theorem 2. First, we prove inequality (1.11).
Let





















which implies

Let 


Now, we choose the argument of 

Then (3.5) becomes
Finally, making 
For




zero in




Cite this paper
BarchandChanam, (2015) Some Inequalities on Polar Derivative of Polynomial Having No Zero in a Disc. Advances in Pure Mathematics,05,796-803. doi: 10.4236/apm.2015.513073
References
- 1. Bernstein, S. (1926) Lecons sur les propriétésextrémaleset la meilleure approximation des fonctions analytiques d’une variablereele. Gauthier Villars, Paris.
- 2. Lax, P.D. (1944) Proof of a Conjecture of P. Erdös on the Derivative of a Polynomial. Bulletin of the American Mathematical Society, 50, 509-513.
http://dx.doi.org/10.1090/S0002-9904-1944-08177-9 - 3. Malik, M.A. (1969) On the Derivative of a Polynomial. Journal of the London Mathematical Society, 1, 57-60.
http://dx.doi.org/10.1112/jlms/s2-1.1.57 - 4. Qazi, M.A. (1992) On the Maximum Modulus of Polynomials. Proceedings of the American Mathematical Society, 115, 337-343.
http://dx.doi.org/10.1090/S0002-9939-1992-1113648-1 - 5. Dewan, K.K., Singh, H. and Yadav, R.S. (2003) Inequalities Concerning Polynomials Having Zeros in Closed Exterior or Closed Interior of a Circle. Southeast Asian Bulletin of Mathematics, 27, 591-597.
- 6. Laguerre, E. (1898) Oeuvres. 1 Gauthier-Villars, Paris.
- 7. Pólya, G. and Szegö, G. (1925) Aufgaben and Lehratzeaus der Analysis. Springer-Verlag, Berlin.
- 8. Marden, M. (1949) Geometry of the Zeros of Polynomials in a Complex Variable. Math. Surveys, No.3. Amer. Math. Soc., Providence, R.I.
- 9. Aziz (1988) Inequalities for the Polar Derivative of a Polynomial. Journal of Approximation Theory, 55, 183-193.
http://dx.doi.org/10.1016/0021-9045(88)90085-8 - 10. Dewan, K.K. and Singh, B. (2006) Inequalities for the Polar Derivative of a Polynomial. Journal of Combinatorics, Information and System Sciences, 31, 317-324.
- 11. Govil, N.K., Rahman, Q.I. and Schmeisser, G. (1979) On the Derivative of a Polynomial. Illinois Journal of Mathematics, 23, 319-329.
- 12. Mir, A. and Dar, B. (2014) On the Polar Derivative of a Polynomial. Journal of the Ramanujan Mathematical Society, 29, 403-412.
- 13. Govil, N.K. and Rahman, Q.I. (1969) Functions of Exponential Type Not Vanishing in a Half-Plane and Related Polynomials. Transactions of the American Mathematical Society, 137, 501-517.
http://dx.doi.org/10.1090/S0002-9947-1969-0236385-6







