Advances in Pure Mathematics
Vol.05 No.09(2015), Article ID:57895,10 pages
10.4236/apm.2015.59052
An Exact Mathematical Picture of Quantum Spacetime
Mohamed S. El Naschie
Department of Physics, University of Alexandria, Alexandria, Egypt
Email: Chaossf@aol.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 July 2015; accepted 10 July 2015; published 13 July 2015
ABSTRACT
Using von Neumann’s continuous geometry in conjunction with A. Connes’ noncommutative geometry an exact mathematical-topological picture of quantum spacetime is developed ab initio. The final result coincides with the general conclusion of E-infinity theory and previous results obtained in the realm of high energy physics. In particular it is concluded that the quantum particle and the quantum wave spans quantum spacetime and conversely quantum particles and waves mutates from quantum spacetime.
Keywords:
E-Infinity, Quantum Spacetime, Noncommutative Geometry, Fractals, Transfinite Set Theory, Von Neumann Continuous Geometry, Cantor Sets, Fusion Algebra, Zero Point Energy, Vacuum Fluctuation, Quantum Field Theory, Casimir Effect, Dark Energy

1. Introduction
Modern philosophy has always had a privileged place for the picture theory as exemplified for instance by the work of Ludwig Wittgenstein [1] . In the present work we seek to give an exact mathematical-topological picture for quantum spacetime [2] - [38] . Ours tools to achieve such a picture are primarily the dimensional function of von Neumann’s continuous geometry as developed further by A. Connes in his noncommutative geometry to describe Penrose fractal tiling universe [8] [9] . In addition we will be using various results from the mathematical and the physical E-infinity theory as well as a variety of other powerful mathematical techniques and theories including the Menger-Urysohn dimensional theory, fuzzy sets, deterministic chaos, fusion algebra and chaotic fractals [4] [10] [22] . In addition we stress that we adopt in the present work a view point which is relatively nearer to the source theory of Schwinger [35] than the popular Feynman diagrams method [10] [13] . One important objective and implicit message of the present paper is that pure mathematics is essentially pure “physics” and is indispensible for the advancement of applied science and engineering. Thus as on previous occasions [34] , we felt it important to address the readers of advanced pure mathematical research using advanced mathematical language in the hope of reaching this enormously important community.
2. E-Infinity Quantum Spacetime: A Minimalistic Exact Mathematical-Topological Picture
The following presupposes a modest degree of familiarity with the Cantorian and fractal spacetime theories of Ord, Nottale and El Naschie as well as the fundamental work of May and Connes [1] - [4] . Starting from von Neumann-Connes’ dimensional function [8]
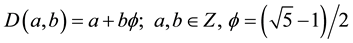
it is surprisingly straight forward and simple to picture the topology of quantum spacetime (see Figure 1 and Figure 2). Following the above function, which is the pillar of John von Neumann and Alain Connes’ continuous noncommutative geometry, it was rather surprising how accurately and simply we can draw a definite picture based on a pre-quantum particle given by the bi-dimension [4] [8] [10] [11]
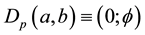
and a pre-quantum wave
Figure 1. The quantum spacetime E-infinity hierarchy. It consists of three main layers. We have first an infinite number of zero and empty sets with an average bi-dimension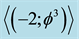 . This is the outer circle representing quantum spacetime. Inside this we have the quantum wave given by the bi-dimension
. This is the outer circle representing quantum spacetime. Inside this we have the quantum wave given by the bi-dimension
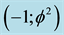 which is the empty set. Finally inside the quantum wave as its inner eye, we have the zero set quantum particle with the bi-dimension
which is the empty set. Finally inside the quantum wave as its inner eye, we have the zero set quantum particle with the bi-dimension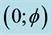 . The above picture also gives us an almost trivial resolution for quantum wave collapse. This is so because to “locate” QP we must somehow penetrate QW. Since QW is the empty set, the slightest touch would convert it to a non-empty set. Consequently QW disappears and metamorphose into QP. This is the observed mysterious state vector reduction which as the reader sees, is not mysterious at all within this topological set theoretical picture.
. The above picture also gives us an almost trivial resolution for quantum wave collapse. This is so because to “locate” QP we must somehow penetrate QW. Since QW is the empty set, the slightest touch would convert it to a non-empty set. Consequently QW disappears and metamorphose into QP. This is the observed mysterious state vector reduction which as the reader sees, is not mysterious at all within this topological set theoretical picture.
Figure 2. Banach-Tarski sphere decomposition Cantorian spacetime of E-infinity theory that is considered here to model our actual spacetime may be envisaged advantageously as in this artist impression. This is basically a two dimensional projection in which each of the larger balls (circles) are a zero set
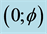 representing the quantum particle while the surface (circumference) represents the empty set
representing the quantum particle while the surface (circumference) represents the empty set
 which in turn represents the quantum wave [1] [17] . This wave is then surrounded by an infinite hierarchy of smaller (fractal) spheres (surfaces), which may be seen as the emptier set
which in turn represents the quantum wave [1] [17] . This wave is then surrounded by an infinite hierarchy of smaller (fractal) spheres (surfaces), which may be seen as the emptier set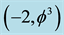 , i.e. the surface of the empty set quantum wave. Remarkably the average set of all zero and empty sets is an expectation value equal
, i.e. the surface of the empty set quantum wave. Remarkably the average set of all zero and empty sets is an expectation value equal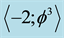 . In other words
. In other words
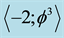 is our quantum spacetime, which is the cobordism of the quantum wave, which in turn is the cobordism of the quantum particle, floating and propagating with the help of its wave in our Cantorian E-infinity spacetime [1] [2] [10] [11] . It is likewise remarkable that
is our quantum spacetime, which is the cobordism of the quantum wave, which in turn is the cobordism of the quantum particle, floating and propagating with the help of its wave in our Cantorian E-infinity spacetime [1] [2] [10] [11] . It is likewise remarkable that
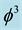 is simultaneously equal to the topological Casimir force as well as the topological mass of the ordinary energy of spacetime. Thus all matter and energy manifestations in our cosmos are essentially a manifestation of the zero point energy of the vacuum of spacetime. To obtain Einstein maximal energy density we just need to find first the topological energy density by adding Kaluza-Klein D = 5 to
is simultaneously equal to the topological Casimir force as well as the topological mass of the ordinary energy of spacetime. Thus all matter and energy manifestations in our cosmos are essentially a manifestation of the zero point energy of the vacuum of spacetime. To obtain Einstein maximal energy density we just need to find first the topological energy density by adding Kaluza-Klein D = 5 to
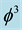 of the spacetime vacuum and find the fractal Kaluza-Klein dimension
of the spacetime vacuum and find the fractal Kaluza-Klein dimension
 then multiply this with the average Cantorian interval speed of light
then multiply this with the average Cantorian interval speed of light
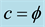 squared. The result is
squared. The result is

enveloping the pre-quantum particle and floating in a quantum spacetime resembling the well known golden mean proportioned Penrose fractal tiling universe termed by Connes X quotient space given by the expectation (average) bi-dimension [11] [12] [18]

In the above the bi-dimension consists of two numbers [9] [18] . The first is the topological inductive Menger- Urysohn dimension, i.e. a consistent refinement of the ordinary topological dimension while the second number is the Hausdorff dimension corresponding to the said Menger-Urysohn topological dimension [1] - [5] [8] . It is remarkable that

also on passing that while the classical deterministic triadic Cantor set has


this slight difference, by pure chance or providence, happens to impact calculations and theory positively be- yond the wildest expectations. On reflection however this is in agreement with the number theoretical expectation and befitting the highly structured E-infinity golden mean ring involved in the von Neumann-Connes dimensional function [8] - [11] . However it is fair to say that the notation of the dimensional function is slightly
cumbersome and does not make the value of a and b which gives us for instance the zero set


Fibonacci growth law. This is mainly the reason for why we opt here for the far more convenient bijection notation of E-infinity theory. Thus the dimensional function could far more conveniently be rewritten as [4] [5] [11]
where


exactly as should be. For the quantum pre-wave on the other hand, we have to realize that the empty set must be

exactly as expected. Now without the need to work through a tedious recursive calculation, we can work out


and
which is the famous expectation value of the Hausdorff dimension f our E-infinity Cantorian spacetime core. Next we can move towards drawing an exact topological picture of our spacetime.
Let us start with the simplest thing which we could in principle hold in our hand, namely the quantum pre- particle



This corresponds to the world sheet of superstring theory, albeit a fractal one. We must not confuse ourselves by not remembering that this circle represents a point of topological dimension zero and Hausdorff dimension




our



That way we have developed in projection a remarkable picture made of three concentric circles as can be seen in Figure 1 and Figure 2. The first part of this picture is that of a circle representing the quantum pre-par-
ticle


so that the inversion is obviously

exactly as expected. Now we can go on drawing circles around circles and each circle is essentially the surface, i.e. cobordism of the circle inside it and could continue this process indefinitely so that in the limit we would have at minus infinity
as mentioned much earlier on. The inverse is clearly an infinite dimensional space but in the two dimensional project this is a zero cobordism, i.e. a surface beyond which there is absolutely “not only nothing” but not even nothing.
Now comes a most probably unexpected observation that has far reaching implications. We saw from our analysis that the surface of the zero set









wave but simply and somewhat unexpectedly it is our quantum, micro, fractal or what ever other names one likes to give it, spacetime. This picture is extremely simple, in fact far simpler than we expected and herein may lay the difficulties of arriving at a simple but profound picture as the one at hand. Our universe consists of a
quantum pre-particle

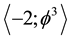


same time, nothing but the pre-spacetime itself on average as manifestly clear from Figure 1 and the accompanied artist impression of Figure 2. Thus the definite logical conclusion must be that the quantum particle and the quantum wave spans spacetime and in turn spacetime gives birth to the quantum particle and the quantum wave. On the count of the conclusion above it becomes natural that the gravity is the curvature of spacetime in Einstein’s relativity and that vacuum fluctuation of spacetime is the source of near infinite zero point energy [11] [12] .
3. Indistinguishability Condition of Quantum Cantorian Spacetime
The preceding analysis and conclusion are truly profound so that we have to study their further consequences and implications in more detail. We start by noting that while the inversion of the quantum particle Hausdorff dimension




In both cases one finds the same result, namely the expectation value of the Hausdorff dimension of spacetime
This fact is fundamental to understanding the paradoxical outcome of the two-slit experiment with quantum particles as discussed on numerous previous occasions. By contrast in the present work we focus the light on another related aspect that reflects another interesting relation to superstrings and related theories. It is obvious that




4. The E-Infinity Exactness Is for Being Fuzzy
Pondering E-infinity fuzziness and contrasting this to its exactness we arrive at the following dialectic conclusion:
On the one hand irrationality gives E-infinity dynamics stability which Hamiltonian systems lack but without having friction dissipative “energy” losses. On the other hand having the golden mean as the organizing center gives us two advantages. First a number which is the worse possible to approximate using rational numbers and in this sense it is maximally irrational, yet the arithmetic of the golden mean is maximally simple because the golden mean ring is maximally highly structured, as is well known from the mathematical E-infinity theory. Furthermore, it is well known that the complexity measure of maximal disorder is equal to that of maximal order so that having golden mean irrationality as the basis of our theory represents a coincidentia-oppositorium uniting the usually un-unitable similar to Fittegel dialectic philosophy, getting the best of all opposed worlds so that at the end the golden mean irrationality fuzziness becomes the hallmark of exactness as in fuzzy logic of Lotfi Zada which introduces fuzzy techniques to the quality control of Japan’s car industry, making it more reliable than any comparable car production in the USA at that time [36] . We note on passing the deep relation between fuzzy logic and our own theory of fractal logic [37] .
5. Nano Universes as Casimir-Dark Energy Reactors
Fusion was observed almost exclusively on the sun or in a hydrogen bomb test explosion. That is definitely the most important single reason for people to suppose that only hot fusion reactors are a viable possibility towards this highly sought after possibility for a major almost infinite source of relatively clean energy. However an almost trivial point seems to have been overlooked in this otherwise convincing argument, namely how did the sun and not only the sun but all these stars and galaxies come into being? Well the traditional answer is a small or big bang scenario or the creational scenarios described in the Bible and Koran in impressive metaphoric language. However this is then not as convincing an argument for a scientific philosopher nor a religious thinker as we thought and a big bang could actually be conceived without the need for the heat of billions of suns as large as our sun. In fact we have advanced sometime ago a cold big bang scenario based on Banach-Tarski theorem of paradoxical decomposition [22] which is even more in harmony with logic and religion. It is thus our thesis here that our present set theoretical analysis of spacetime and its relation to the quantum particle and the quantum wave gives us the possibility of constructing a nano universe ab initio from which the latent Casimir energy could be extracted from its outer surface where by Dvoretzky’s theorem 96% of the energy is concentrated [16] . Let us elaborate this vital point a little bit more. It is almost self evident that the Casimir energy and ordinary energy is one and the same thing. It is all simply a matter of boundary conditions. On the nano scales the boundary condition is given by the two Casimir plates. However ordinary energy, and I must hasten to say and dark energy, are produced by the cosmic boundary condition of the universe. This cosmic boundary condition is by its definition a one-sided boundary like a Möbiusstrip [38] . It is the boundary which has an inside but no outside. Consequently the Casimir energy and Casimir force of the nano scale accumulates and ramifies at the end of the universe. Ninety six percent of this energy is then concentrated at the surface of the universe, that is to say at the boundary of the universe. The rest of the energy is what is inside the universe and we call it ordinary energy because we can measure it while the dark energy part of the total energy, being concentrated at the edge of the universe which for all practical purposes is at infinity, cannot be measured directly and we perceive its effects only as a negative pressure forcing the universe to accelerate its expansion. In other words Casimir energy, dark energy and ordinary energy are basically one and the same thing, manifested however in different ways depending on scale and topology of spacetime. We could do a back of an envelope calculation to come to this momentous result. Let us start with Einstein’s space of general relativity. It is 4 dimensional, D = 4. However deeper investigation shows that this D = 4 smooth spacetime is a deceptively simple picture because the core of this spacetime is basically a fractal with a dimensionality



sion in this case is equal to the sum of all the dimension functions [23] which means


6. Conclusion
In this paper we made little attempt to cover the vast literature but some additional important references are given for the sake of completeness [39] - [102] . Starting from the zero set a hierarchy of empty sets with increasing degrees of emptiness were found using von Neumann-Connes dimensional function which accurately describes Penrose fractal tiling universe as well as Klein’s compactified modular cures alike. Going this road to its ultimate logic, an exact mathematical-topological picture of quantum-fractal spacetime is developed from which it becomes evident that spacetime is not only the stage upon which physical phenomena involving matter and radiation takes place but it is the very stuff of which matter is made. This is the very reason why we can build a basically nano universe to function as a reactor from which free energy could be extracted [11] [12] [38] [97] [101] [102] . One final word, designing and developing a Casimir-dark energy reactor which would be the greatest achievement of human civilization to give humanity a practically infinite source of energy [89] cannot be more expensive than the needless wars which Nobel Laureate J. Stiglatz described in his book [87] and which cost the USA tax payer alone three trillion dollars.
Cite this paper
Mohamed S. ElNaschie, (2015) An Exact Mathematical Picture of Quantum Spacetime. Advances in Pure Mathematics,05,560-570. doi: 10.4236/apm.2015.59052
References
- 1. Wittgenstein, L. (1922) Tractatus Logico-Philosophicus. With Introduction by B. Russel. London-Kegan Paul, Trench, Trubner & Co. Ltd., New York Harcourt, Brace & Co. Inc.
- 2. He, J.-H. (2014) A Tutorial Review on Fractal Spacetime and Fractional Calculus. International Journal of Theoretical Physics, 53, 3698-3718. http://dx.doi.org/10.1007/s10773-014-2123-8
- 3. Auffray, J.-P. (2014) Quantum Meteorites: An Extemporaneous Description of the System of the World. Journal of Modern Physics, 6, 878-889. http://dx.doi.org/10.4236/jmp.2015.67092
- 4. Nottale, L. (1996) Scale Relativity and Fractal Spacetime: Application to Quantum Physics, Cosmology and Chaotic Systems. Chaos, Solitons & Fractals, 7, 877-938.
http://dx.doi.org/10.1016/0960-0779(96)00002-1 - 5. El Naschie, M.S. (2004) A Review of E-Infinity and the Mass Spectrum of High Energy Particle Physics. Chaos, Solitons & Fractals, 19, 209-236. http://dx.doi.org/10.1016/S0960-0779(03)00278-9
- 6. El Naschie, M.S. (2013) The Quantum Gravity Immirzi Parameter—A General Physical and Topological Interpretation. Gravitation and Cosmology, 19, 151-155.
http://dx.doi.org/10.1134/S0202289313030031 - 7. Peter May, J. (1977) E-Infinity Ring Spaces and E-Infinity Spectra. Lecture Notes in Mathematics, Springer, Berlin.
- 8. Witten, E. (1998) D-Branes and K-Theory. Journal of High Energy Physics, 12, 1-35.
- 9. Connes, A. (2000) Noncommutative Geometry Year 2000. Geometric and Functional Analysis. Special Volume, Birkhauser-Verlag, 481-599. http://dx.doi.org/10.1007/978-3-0346-0425-3_3
- 10. Penrose, R. (2004) The Road to Reality. Jonathan Cape, London.
- 11. El Naschie, M.S. (2015) Kerr Black Hole Geometry Leading to Dark Matter and Dark Energy via E-Infinity Theory and the Possibility of Nano Spacetime Singularities Reactor. Natural Science, 7, 210-225.
http://dx.doi.org/10.4236/ns.2015.74024 - 12. El Naschie, M.S. (2015) The Casimir Topological Effect and a Proposal for a Casimir-Dark Energy Nano Reactor. World Journal of Nano Science & Engineering, 5, 26-33.
http://dx.doi.org/10.4236/wjnse.2015.51004 - 13. Schwinger, J. (1994) Cold Fusion Theory: A Brief History of Mine. A Talk Read in an Evening Session B Eugene Mallove at the Fourth International Conference on Cold Fusion ICCF4, Maui, 6-9 December 1994. Printed Online by Infinity Energy—The Magazine of New Energy Science & Technology (2014-2015).
www.infinite-energy.com/iemagazine1/colfusthe-html - 14. Jiang, X.L., Zhou, X.P. and Peng, W.M. (2014) Extraction of Clean and Cheap Energy from Vacuum. Materials for Renewable Energy & Environment, 2, 467-471.
- 15. El Naschie, M.S. (1999) From Implosion to Fractal Spheres. A Brief Account of the Historical Development of Scientific Ideas Leading to the Trinity Test and Beyond. Chaos, Solitons & Fractals, 10, 1955-1965. http://dx.doi.org/10.1016/s0960-0779(99)00030-2
- 16. El Naschie, M.S. (2015) Banach Spacetime-Like Dvoretzky Volume Concentration as Cosmic Holographic Dark Energy. International Journal of High Energy Physics, 2, 13-21.
http://dx.doi.org/10.11648/j.ijhep.20150201.12 - 17. El Naschie, M.S. (2005) On 336 Kissing Spheres in 10 Dimensions, 528 P-Brane States in 11 Dimensions and the 60 Elementary Particles of the Standard Model. Chaos, Solitons & Fractals, 24, 337-457.
http://dx.doi.org/10.1016/j.chaos.2004.09.071 - 18. El Naschie, M.S. (2014) From E = mc2 to E = mc2/22—A Short Account of the Most Famous Equation in Physics and Its Hidden Quantum Entanglement Origin. Journal of Quantum Information Science, 4, 284-291. http://dx.doi.org/10.4236/jqis.2014.44023
- 19. Schwinger, J. (1975) Casimir Effect in Source Theory. Letters in Mathematical Physics, 1, 43-47.
http://dx.doi.org/10.1007/BF00405585 - 20. Finkelstein, D. (1996) Quantum Relativity. Springer, Berlin.
http://dx.doi.org/10.1007/978-3-642-60936-7 - 21. ‘tHooft, G. (2014) The Cellular Automata Interpretation of Quantum Mechanics: A View on the Quantum Nature of Our Universe, Compulsory or Impossible? http://arxiv.org/abs/1405.1548
- 22. El Naschie, M.S. (1995) Banach-Tarski Theorem and Cantorian Micro Spacetime. Chaos, Solitons & Fractals, 5, 1503-1508. http://dx.doi.org/10.1016/0960-0779(95)00052-6
- 23. El Naschie, M.S. (2009) Wild Topology, Hyperbolic Geometry and Fusion Algebra of High Energy Particle Physics. Chaos, Solitons & Fractals, 13, 1935-1945.
- 24. Gillet, H. (1981) Riemann-Roch Theorem for Higher Algebraic K-Theory. Advances in Mathematics, 40, 203-289. http://dx.doi.org/10.1016/s0001-8708(81)80006-0
- 25. Kodiyalam, V. and Saunder, V. (2001) Topological Quantum Field Theories from Subfactors. Chapman & Hall/CRC, Bacaraton and London.
- 26. Witten, E. (1988) Topological Quantum Field Theory. Communications in Mathematical Physics, 117, 353-386. http://dx.doi.org/10.1007/bf01223371
- 27. Baez, J.C. and Dolan, J. (1988) Higher-Dimensional Algebra III: n-Categories and the Algebra of Opetopes. Advances in Mathematics, 135, 145-206.
- 28. May, J.P. (2009) What Precisely Are E-Infinity Rings and E-Infinity Spectra.
http://arxiv.org/abs/0903.2813 - 29. Ketov, S.V. (1995) Conformal Field Theory. World Scientific, Singapore.
- 30. Duplantier, B. and Rivasseau, V., Eds. (2003) Poincaré Seminar 2002: Vacuum Energy—Renormalization. Birkhauser, Basel. http://dx.doi.org/10.1007/978-3-0348-8075-6
- 31. Saller, H. (2006) Operational Quantum Theory I and II. Springer, Heidelberg.
- 32. Milonni, P.W. (1994) The Quantum Vacuum: An Introduction to Quantum Electrodynamics. Academic Press, Boston. http://dx.doi.org/10.1119/1.17618
- 33. Connes, A. and Marcolli, M. (2008) Noncommutative Geometry, Quantum Fields and Motives. American Mathematical Society, Providence and Hindustan Book Agency, New Delhi.
- 34. El Naschie, M.S. (2014) From Highly Structured E-Infinity Rings and Transfinite Maximally Symmetric Manifolds to the Dark Energy Density of the Cosmos. Advances in Pure Mathematics, 4, 641-648.
http://dx.doi.org/10.4236/apm.2014.412073 - 35. Fried, H.M. (2014) Modern Functional Quantum Field Theory. World Scientific, Singapore.
http://dx.doi.org/10.1142/8544 - 36. Zadeh, L. (1996) Fuzzy Sets, Fuzzy Logic and Fuzzy Systems. World Scientific, Singapore.
http://dx.doi.org/10.1142/2895 - 37. El Naschie, M.S., Olsen, S., He, J.H., Nada, S., Marek-Crnjac, L. and Helal, A. (2012) On the Need for Fractal Logic in High Energy Quantum Physics. International Journal of Modern Nonlinear Theory and Application, 1, 84-92. http://dx.doi.org/10.4236/ijmnta.2012.13012
- 38. El Naschie, M.S. (2015) The Casimir Effect as a Pure Topological Phenomenon and the Possibility of a Casimir Nano Reactor—A Preliminary Design. American Journal of Nano Research and Application, 3, 33-40.
- 39. El Naschie, M.S. (2000) On Nishina’s Estimate of the Critical Mass for Fussion and Early Nuclear Research in Japan. Chaos, Solitons & Fractals, 11, 1809-1818.
http://dx.doi.org/10.1016/S0960-0779(99)00172-1 - 40. El Naschie, M.S. (2000) Remarks on Heisenberg’s Farm-Hall Lecture on the Critical Mass of Fast Neutron Fission. Chaos, Solitons & Fractals, 11, 1327-1333. http://dx.doi.org/10.1016/S0960-0779(99)00136-8
- 41. El Naschie, M.S. and Hussein, A. (2000) On the Eigenvalue of Nuclear Reaction and Self-Weight Buckling. Chaos, Solitons & Fractals, 11, 815-818. http://dx.doi.org/10.1016/S0960-0779(99)00106-X
- 42. El Naschie, M.S. (2000) Elastic Buckling Loads and Fission Critical Mass as an Eigenvalue of a Symmetry Breaking Bifurcation. Chaos, Solitons & Fractals, 11, 631-629.
http://dx.doi.org/10.1016/S0960-0779(99)00063-6 - 43. El Naschie, M.S. (2000) On the Zel’dovich-Khuriton Critical Mass for Fast Fission. Chaos, Solitons & Fractals, 11, 819-824. http://dx.doi.org/10.1016/S0960-0779(99)00113-7
- 44. El Naschie, M.S. (2000) On the Eigenvalue of Transport Reaction Involving Fast Neutrons. Chaos, Solitons & Fractals, 11, 929-934. http://dx.doi.org/10.1016/S0960-0779(99)00066-1
- 45. El Naschie, M.S. (2000) Heisenberg’s Critical Mass Calculations for an Explosive Nuclear Reaction. Chaos, Solitons & Fractals, 11, 987-997. http://dx.doi.org/10.1016/S0960-0779(99)00110-1
- 46. El Naschie, M.S. (1998) Chaos and Fractals in Nano and Quantum Technology. Chaos, Solitons & Fractals, 9, 1793-1802.
- 47. El Naschie, M.S. (2006) Nanotechnology for the Developing World. Chaos, Solitons & Fractals, 30, 769-773. http://dx.doi.org/10.1016/j.chaos.2006.04.037
- 48. El Naschie, M.S. (2007) The Political Economy of Nanotechnology and the Developing World. International Journal of Electrospun Nanofibrers and Applications, 1, 41-50.
- 49. El Naschie, M.S. (1998) Some Tentative Proposals for the Experimental Verification of Cantorian Micro Spacetime. Chaos, Solitons & Fractals, 9, 143-144. http://dx.doi.org/10.1016/S0960-0779(97)00175-6
- 50. Johnston, H. (2012) Physicists Solve Casimir Conundrum. Physicsworld.com., July 18, 2012.
- 51. Rencroft, S. and Swain, J. (1998) What Is the Casimir Effect? Scientific American, June 22, 1998.
- 52. Wongjun, P. (2015) Casimir Dark Energy, Stabilization and the Extra Dimensions and Gauss-Bonnet Term. The European Physical Journal C, 75, 6.
- 53. El Naschie, M.S. (2007) A Review of Application and Results of E-Infinity. International Journal of Nonlinear Science & Numerical Simulation, 8, 11-20. http://dx.doi.org/10.1515/IJNSNS.2007.8.1.11
- 54. Smolin, L. (2001) The Strong and the Weak Holographic Principles. Nuclear Physics B, 601, 209-247.
http://dx.doi.org/10.1016/s0550-3213(01)00049-9 - 55. El Naschie, M.S. (2006) Holographic Dimensional Reduction Centre Manifold Theorem and E-Infinity. Chaos, Solitons & Fractals, 29, 816-822. http://dx.doi.org/10.1016/j.chaos.2006.01.013
- 56. Misner, C., Thorne, K. and Wheeler, J.A. (1973) Gravitation. Freeman, New York.
- 57. El Naschie, M.S. (2003) Kleinian Groups in E-Infinity and Their Connection to Particle Physics and Cosmology. Chaos, Solitons & Fractals, 16, 637-649.
http://dx.doi.org/10.1016/S0960-0779(02)00489-7 - 58. El Naschie, M.S. (2005) A Guide to the Mathematics of E-Infinity Cantorian Spacetime Theory. Chaos, Solitons & Fractals, 25, 935-964. http://dx.doi.org/10.1016/j.chaos.2005.02.029
- 59. El Naschie, M.S. (2004) The Concepts of E-Infinity: An Elementary Introduction to the Cantorian-Fractal Theory of Quantum Physics. Chaos, Solitons & Fractals, 22, 495-511.
http://dx.doi.org/10.1016/j.chaos.2004.02.028 - 60. El Naschie, M.S. (2003) Complex Vacuum Fluctuation as a Chaotic “Limit” Set of any Kleinian Group Transformation and the Mass Spectrum of High Energy Particle Physics via Spontaneous Self Organization. Chaos, Solitons & Fractals, 17, 631-638.
http://dx.doi.org/10.1016/s0960-0779(02)00630-6 - 61. El Naschie, M.S. (2003) Modular Groups in Cantorian E-Infinity High-Energy Physics. Chaos, Solitons & Fractals, 16, 353-366. http://dx.doi.org/10.1016/S0960-0779(02)00440-X
- 62. El Naschie, M.S. (1994) On Certain “Empty” Cantor Sets and Their Dimensions. Chaos, Solitons & Fractals, 4, 293-296. http://dx.doi.org/10.1016/0960-0779(94)90152-X
- 63. He, J.-H., Xu, L., Zhang, L.-N. and Wu, X.-H. (2007) Twenty Six Dimensional Polytope and High Energy Spacetime Physics. Chaos, Solitons & Fractals, 33, 5-13. http://dx.doi.org/10.1016/j.chaos.2006.10.048
- 64. El Naschie, M.S. (1994) Is Quantum Space a Random Cantor Set with a Golden Mean Dimension at the Core? Chaos, Solitons & Fractals, 4, 177-179. http://dx.doi.org/10.1016/0960-0779(94)90141-4
- 65. El Naschie, M.S. (2008) Mathematical Foundation of E-Infinity via Coxeter and Reflection Groups. Chaos, Solitons & Fractals, 37, 1267-1268. http://dx.doi.org/10.1016/j.chaos.2008.02.001
- 66. El Naschie, M.S. (1995) Banach-Tarski Theorem and Cantorian Micro Spacetime. Chaos, Solitons & Fractals, 5, 1503-1508. http://dx.doi.org/10.1016/0960-0779(95)00052-6
- 67. El Naschie, M.S. (1995) On the Initial Singularity and the Banach-Tarski Theorem. Chaos, Solitons & Fractals, 5, 1391-1392. http://dx.doi.org/10.1016/0960-0779(95)99645-2
- 68. El Naschie, M.S. (1998) COBE Satellite Measurement, Hyper Spheres, Superstrings and the Dimension of Spacetime. Chaos, Solitons & Fractals, 9, 1445-1471.
http://dx.doi.org/10.1016/S0960-0779(98)00120-9 - 69. El Naschie, M.S. (2001) Infinite Dimensional Branes and the E-Infinity Toplogy of Heterotic Superstrings. Chaos, Solitons & Fractals, 12, 1047-1055. http://dx.doi.org/10.1016/S0960-0779(00)00130-2
- 70. El Naschie, M.S. (2007) Ji-Huan He’s Ten Dimensional Polytope and High Energy Particle Physics. International Journal of Nonlinear Science & Numerical Simulation, 8, 475-476.
http://dx.doi.org/10.1515/ijnsns.2007.8.4.475 - 71. El Naschie, M.S. (1999) Hyper-Dimensional Geometry and the Nature of Physical Spacetime. Chaos, Solitons & Fractals, 10, 155-158. http://dx.doi.org/10.1016/S0960-0779(98)00235-5
- 72. Finkelstein, D. (1982) Quantum Sets and Clifford Algebras. International Journal of Theoretical Physics, 21, 489-503.
- 73. El Naschie, M.S. (2002) Derivation of the Threshold and Absolute Temperature Tc = 273.16 K from the Topology of Quantum Spacetime. Chaos, Solitons & Fractals, 14, 1117-1120.
http://dx.doi.org/10.1016/S0960-0779(02)00053-X - 74. El Naschie, M.S. (2008) Quarks Confinement via Kaluza-Klein Theory as a Topological Property of Quantum-Classical Spacetime Phase Transition. Chaos, Solitons & Fractals, 35, 825-829.
http://dx.doi.org/10.1016/j.chaos.2007.08.057 - 75. El Naschie, M.S. (2002) On a Class of General Theories for Higher Energy Particle Physics. Chaos, Solitons & Fractals, 14, 649-668. http://dx.doi.org/10.1016/S0960-0779(02)00033-4
- 76. He, J.-H. (2009) Hilbert Cube Model for Fractal Spacetime. Chaos, Solitons & Fractals, 42, 2754-2759. http://dx.doi.org/10.1016/j.chaos.2009.03.182
- 77. Lomas, R. (1999) The Man Who Invented The Twentieth Century, Nicola Tesla, Forgotten Genius of Electricity. Headline Books, London.
- 78. Helal, M., Marek-Crnjac, L. and He, J.-H. (2013) The Three Page Guide to the Most Important Results of M.S. El Naschie’s Research in E-Infinity Quantum Physics. Open Journal of Microphysics, 3, 141-145.
http://dx.doi.org/10.4236/ojm.2013.34020 - 79. Ho, M.-W., El Naschie, M.S. and Vitiello, G. (2015) Is Spacetime Fractal and Quantum Coherent in the Golden Mean. Global Journal of Science Frontier Research—A: Physics and Space Science, 15, 61-80.
- 80. El Naschie, M.S. (2009) The Theory of Cantorian Spacetime and High Energy Particle Physics (An Informal Review). Chaos, Solitons & Fractals, 41, 2635-2646.
http://dx.doi.org/10.1016/j.chaos.2008.09.059 - 81. Marek-Crnjac, L. and He, J.-H. (2013) An Invitation to El Naschie’s Theory of Cantorian Spacetime and Dark Energy. International Journal of Astronomy and Astrophysics, 3, 464-471.
http://dx.doi.org/10.4236/ijaa.2013.34053 - 82. El Naschie, M.S. (2013) A Resolution of Cosmic Dark Energy via Quantum Entanglement Relativity Theory. Journal of Quantum Information Science, 3, 23-26. http://dx.doi.org/10.4236/jqis.2013.31006
- 83. El Naschie, M.S. (2013) What Is the Missing Dark Energy in a Nutshell and the Hawking-Hartle Quantum Wave Collapse. International Journal of Astronomy & Astrophysics, 3, 205-211.
http://dx.doi.org/10.4236/ijaa.2013.33024 - 84. El Naschie, M.S. (2013) Topological-Geometrical and Physical Interpretation of the Dark Energy of the Cosmos as a “Halo” Energy of the Schrodinger Quantum Wave. Journal of Modern Physics, 4, 591-596.
http://dx.doi.org/10.4236/jmp.2013.45084 - 85. Peat, F.D. (1983) In Search of Nikola Tesla. Ashgrove Publications, London & Bath.
- 86. Susskind, L. and Lindesay, J. (2005) The Holographic Universe. World Scientific, Singapore.
- 87. Stiglitz, J. and Bilmes, L. (2008) The Three Trillion Dollar War: The True Cost of The Iraq Conflict. Allen-Lane, Penguin Books, London.
- 88. El Naschie, M.S. (2013) A Unified Newtonian-Relativistic Quantum Resolution of Supposedly Missing Dark Energy of the Cosmos and the Constancy of the Speed of Light. International Journal of Modern Nonlinear Theory & Application, 2, 43-54. http://dx.doi.org/10.4236/ijmnta.2013.21005
- 89. Malek, C. (2015) Abu Dhabi Crown Prince Details UAE Leaders’ Vision of Future without Oil. The National Newspaper, UAE, February 10, 2015.
http://www.thenational.ae/uae/government/abu-dhabi-crown-prince-details-uae-leaders-vision-of-future-without-oil?utm_content='%20vision%20of%20future%20without%20oil - 90. Zee, A. (2003) Quantum Field Theory in a Nutshell. Princeton University Press, Princeton.
- 91. Duplantier, B. and Rivasseau, V., Eds. (2003) Vacuum Energy-Renormalization. Birkhauser, Basel.
- 92. Milonni, P.W. (1994) The Quantum Vacuum. Academic Press, Boston.
- 93. Parsegian, V.A. (2006) van der Waals Forces. Cambridge University Press, Cambridge.
- 94. Huang, K. (2007) Fundamental Forces of Nature. World Scientific, Singapore.
http://dx.doi.org/10.1142/6447 - 95. Wapner, L.M. (2005) The Pea and the Sun. A.K. Peters Ltd., Wellesley.
- 96. Auffray, J.-P. (2014) E-Infinity Dualities, Discontinuous Spacetime, Xonic Quantum Physics and the Decisive Experiment. Journal of Modern Physics, 1427-1436.
http://dx.doi.org/10.4236/jmp.2014.515144 - 97. El Naschie, M.S. (2015) The Cantorian Monadic Plasma behind the Zero Point Vacuum Spacetime Energy. American Journal of Nano Research and Application, 3, 66-70.
- 98. Auffray, J.-P. (2015) E-Infinity, the Zero Set, Absolute Space and the Photon Spin. Journal of Modern Physics, 6, 536-545.
- 99. Tang, W., Li, Y., Kong, H.Y. and El Naschie, M.S. (2014) From Nonlocal Elasticity to Nonlocal Spacetime and Nanoscience. Bubbfil Nano Technology, 1, 3-12.
- 100. El Naschie, M.S. (2014) Dark Energy via Quantum Field Theory in Curved Spacetime. Journal of Modern Physics and Applications, 2, 1-7.
- 101. El Naschie, M.S. (2015) A Cold Fusion-Casimir Energy Nano Reactor Proposal. World Journal of Nano Science and Engineering, 5, 49-56. http://dx.doi.org/10.4236/wjnse.2015.52007
- 102. El Naschie, M.S. (2015) A Casimir-Dark Energy Nano Reactor Design—Phase I. Natural Science, 7, 287-298. http://dx.doi.org/10.4236/ns.2015.76032















