Received 30 April 2015; accepted 27 June 2015; published 30 June 2015

ABSTRACT

This paper, divided into three parts (Part II-A, Part II-B and Part II-C), contains the detailed factorizational theory of asymptotic expansions of type (*)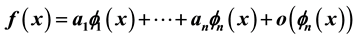, , 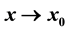, 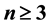where the asymptotic scale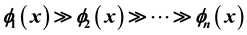, , 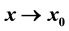is assumed to be an extended complete Chebyshev system on a one-sided neighborhood of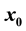. It follows two previously published papers: the first, labelled as Part I, contains the complete (elementary but nontrivial) theory for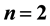; the second is a survey highlighting only the main results without proofs. All the material appearing in §2 of the survey is here reproduced in an expanded form, as it contains all the preliminary formulas necessary to understand and prove the results. The remaining part of the survey―especially the heuristical considerations and consequent conjectures in §3― may serve as a good introduction to the complete theory.

Keywords:

Asymptotic Expansions, Formal Differentiation of Asymptotic Expansions, Factorizations of Ordinary Differential Operators, Chebyshev Asymptotic Scales

1. Introduction

Following the line of thought in [1] , case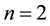, we develop in this paper a general analytic theory of asymptotic expansions of type

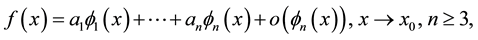(1.1)

where

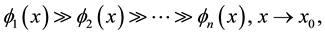(1.2)

and the Hardy notation 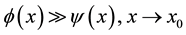is alternative to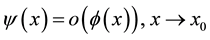. For the reader’s convenience, the paper has been divided into three parts: the present Part II-A contains all the general results obtainable through two approaches based on different special factorizations (called “canonical factorizations”) of the nth-order differential operator whose kernel is spanned by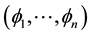. Our results are characterizations of (1.1) via integro-differential conditions useful for applications unlike the trivial characterization by means of the existence (as finite numbers) of the following n limits defining the coefficients:

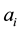(1.3)

the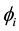’s being supposed non-vanishing on a deleted neighborhood of.

Our theory parallels: 1) the classical Taylor’s formula at a point; 2) the theory of polynomial expansions at systematized in [2] ; 3) the theory of asymptotic expansions in real powers developed in [3] [4] from the standpoint of formal differentiability. A survey [5] , previously published in this journal, contains the main results with no proofs and may be conveniently used to gain a quick view of the (rather long) detailed theory. The introductions in [1] [2] and [5] contain other comments; moreover, the heuristic considerations with related conjectures in §3 of [5] are quite helpful to properly grasp the presented results. Here, we only mention that our theory consists in studying (1.1) not by itself but matched to other expansions obtained by formal application of certain differential operators and we give a brief outline of the content.

・ In §2, we collect all the preliminary material concerning factorizations of a disconjugate operator and the nonvanishingness of various Wronskians involving certain bases of its kernel. The scale of comparison functions is practically assumed to form an extended Chebyshev system on some left deleted neighborhood of and various properties are systematized around the concept of Chebyshev asymptotic scale.

・ In §3, we exhibit the operators used in formal differentiation together with some of their elementary properties.

・ In §4, we state characterizations of a set of asymptotic expansions obtained from (1.1) by formal applications of the differential operators implicitly defined by the “unique” canonical factorization, termed by us of type (I), which chronologically is the first to be introduced, studied and applied.

・ In $5, we do the same job for the differential operators implicitly defined by a special canonical factorization termed by us of type (II) and constructed using the given asymptotic scale.

・ In $6, all proofs are collected.

・ In Part II-B, we specialize the results to the important class of functions satisfying a differential inequality linked to the scale, so obtaining many nice characterizations.

・ In Part II-C, we exhibit two algorithms for constructing the canonical factorizations upon which our theory is built. These algorithms are simple to describe, admit of “natural” asymptotic interpretations (also showing the appropriateness of the used differential operators) and are of considerable help in building examples and counterexamples concerning formal differentiation of asymptotic expansions.

Occasionally, an asymptotic expansion

(1.4)

will be called “incomplete”―with respect to the given scale, of course―whereas (1.1) will be called “complete”, and these locutions refer to the specified growth-order of the remainder and not to the terms effectively present in the expansion i.e. those with non-zero coefficients. In both approaches, characterizations of incomplete expansions via a differential operator whose kernel is spanned by the “complete” basis are less simple than those of complete expansions presented in the survey [5] and will be illustrated in the present paper.

We stress that the guiding thread of our work is “formal differentiation of asymptotic expansions”, a theme going back to the early 20th century (Landau, Hardy, Boas and others), but usually referring to the use of standard derivatives. The factorizational approach clearly shows that formal differentiation is admissible only if one uses suitable differential operators strictly linked to the involved scale together with related factorizations. The case of standard derivatives is very special and is highlighted in Part II-B and Part II-C.

Notations

・ is absolutely continuous on each compact subinterval of I;

・ ;

・ For, we write, meaning that x runs through the points wherein exists as a finite number. Applying L’Hospital’s rule in such a context means using Ostrowski’s version [6] valid for absolutely continuous functions;

・ denotes the extended real line;

・ If no ambiguity arises, we use the following shorthand notations or similar ones:

wherein each integral or, alternatively, may be a proper or improper integral. A notation such as “convergent” means that exists as a Lebesgue integral for some and each

and that the exists in, so defining the improper integral;

・ The symbol denotes the Wronskian determinant of the ordered i-tuple , times differentiable at the specified point x; denotes the Wronskian viewed as the operator on a specified interval;

・ Two acronyms systematically used are T.A.S. = “Chebyshev asymptotic scale” as in Def. 2.1, and C.F. = “canonical factorization” defined in Proposition 2.1-(iv) and (v);

・ Propositions are numbered consecutively in each section irrespective of their labelling as lemma, theorem and so on.

2. Canonical Factorizations of Disconjugate Operators and Chebyshev Asymptotic Scales

Our theory is built upon appropriate integral representations stemming from a special structure of the asymptotic scale: practically this n-tuple forms a fundamental system of solutions of a disconjugate equation on a one-sided neighborhood of such that certain Wronskians do not vanish thereon, a property granted by a result by Levin [7] which justifies our definition of Chebyshev asymptotic scale. We preliminarly recall some facts about factorizations of differential operators.

In this section, denotes a linear ordinary differential operator of type

(2.1)1

(2.1)2

where denotes the class of functions Lebesgue-summable on every compact subinterval of J. The matters to be discussed depend on the property of disconjugacy and several characterizations involving factorizations are collected in the next proposition where special locutions are defined in the statement itself. For general properties about disconjugacy we refer to the book by Coppel [8] and the paper by Levin [7] , and for facts concerning canonical factorizations we refer to the papers by Trench [9] and the author [10] [11] .

Proposition 2.1 (Disconjugacy on an open interval via factorizations). For an operator of type (2.1)_1,2, , on an open interval, bounded or not, the following properties are equivalent:

1) is disconjugate on in the sense that: every nontrivial solution of has at most zeros on counting multiplicities or, equivalently, has at most distinct zeros on.

2) has a fundamental system of solutions on, , satisfying Pólya’s W-property

(2.2)

or equivalently has solutions satisfying (2.2) for.

3) has a Pólya-Mammana factorization on i.e.

(2.3)

where the’s are suitable functions such that

(2.4)

4) has a “canonical factorization (C.F. for short) of type (I) at the endpoint a” i.e. a factorization of type (2.3)-(2.4) with the additional conditions

(2.5)a

and a similar “C.F. of type (I) at the endpoint b”, i.e. with the’s satisfying

(2.5)b

5) For each c, , has a “C.F. on the interval which is of type (II) at the endpoint a” i.e. a factorization (2.3)-(2.4) valid on the interval and with the’s satisfying

(2.6)a

and has a “C.F. on the interval which is of type (II) at the endpoint b” i.e. a factorization (2.3)-(2.4) valid on the interval and with the’s satisfying

(2.6)b

Remarks. 1) In the definition of a C.F. conditions (2.5) or (2.6) are required to hold for the index i running from 1 to: there are no conditions on and. Factorizations in properties 3)-4) are global i.e. valid on the whole given interval, whereas property 5) claims the existence of local C.F.’s of type (II). The existence of a global C.F. of type (II) at a or at b is a special circumstance ([10] , Th. 3.11, p. 163).

2) A global C.F. of type (I) at a specified endpoint does always exist for a disconjugate operator on an open interval and is “essentially” unique in the sense that the functions are determined up to multiplicative constants with product 1, Trench [9] . The situation is quite different for C.F.’s of type (II). For example the operator has no global C.F. on of type (II) at any of the endpoints for it admits of only “one” (up to constant factors) Pólya-Mammana factorization on namely

(2.7)

which is a special contingency characterized in ([10] , Th. 3.3) and in ([11] , Th. 7.1). But the operator thought of as acting on the space, or even on the space, has infinitely many “essentially” different C.F.’s of type (II), for instance the following ones

(2.8)

which are C.F.’s of type (II) at both the endpoints “0” and “” whatever the choice of the constant. For, we get a factorization on which is a C.F. of type (I) at “0” and of type (II) at “”; for we have nonglobal factorizations which are of type (II) at.

C.F.’s are naturally linked to bases of ker forming asymptotic scales at one or both endpoints and the following results, due to Levin ([7] , §2), highlight important properties of the Wronskians constructed with an asymptotic scale.

Proposition 2.2 (Wronskians of asymptotic scales and their hierarchies).

(I) (Results involving a differential operator). Let be an operator of type (2.1)_1,2 disconjugate on an open interval. Then:

1) Its kernel has some basis satisfying

(2.9)

2) For each such basis

(2.10)

noticing the reversed order of the’s in the Wronskians.

3) For any strictly decreasing set of indexes i.e. such that

(2.11)

we have

(2.12)

and in particular we have the inequalities

(2.13)

4) For each k, , and for any two distinct and strictly increasing sets of indexes and such that, we have

(2.14)

Notice the ordering of the’s and the’s in (2.14): if each has a growth-order at greater than that of the corresponding then the same is true for the Wronskians. In the claim 3), we have a different ordering of the’s as this grants the positivity of the Wronskians in (2.12).

(II) (Results involving scales with less regularity). Let be functions of class satisfying conditions (2.9) and condition

(2.15)

and let there exist an integer such that

(2.16)

where the symbol denotes the Wronskian determinant wherein the column involving has been suppressed. Then the following inequalities hold true

(2.17)

(2.18)

together with the above-stated properties in 3) and 4). Notice that in (2.17)-(2.18) the signs of the Wronskians are well defined even if they remain undefined in the assumptions (2.15)-(2.16).

To visualize (2.14), we list a few asymptotic scales at constructed with the Wronskians:

(2.19)

(2.20)

It is quite important to note the order of the’s forming the asymptotic scale in (2.9); if we mantain the same ordering in the analogous statement for, i.e., then the Wronskians in (2.10) and in (2.12) to (2.18) are the same, the essential point being the relative growth-orders of the’s. From the point of view of asymptotic expansions the correct numbering is that adopted by us irrespective of the limiting process.

The above results substantiate the following definition of special asymptotic scales wherein we merely fix the neighborhood of b left undefined in Proposition 2.2 whose part (I) grants the existence of such scales whereas part (II) implies a lot of useful properties even for scales with less regularity. From now on the interval will be denoted as in the two-term theory [1] .

Definition 2.1 (Chebyshev asymptotic scales). The ordered n-tuple of real-valued functions is termed a “Chebyshev asymptotic scale” (T.A.S. for short) on the half-open interval, , , provided the following properties are satisfied:

(2.21)

(2.22)

(2.23)

(2.24)

Whenever the’s satisfy the stronger regularity condition

(2.25)

they remain associated to the operator

(2.26)

which is the unique linear ordinary differential operator of type (2.1)_1,2, acting on the space and such that

Remarks. 1) Condition (2.21) is the usual regularity assumption in approximation theory (Chebyshev systems and the like), whereas in matters involving differential equations/inequalities it is natural to assume (2.25).

2) Choosing an half-open interval in this definition is a matter of convenience: the point involved in the asymptotic relations is characterized as the endpoint not belonging to the interval, possibly, whereas the other endpoint marks off an interval whereon the inequalities involving the Wronskians are satisfied and these in turn allow certain integral representations valid on the whole given interval and essential to our theory. These remarks make evident the analogous definition for an interval where:, and.

3) In the above definition we have merely supposed the nonvanishingness of various functions instead of specifying their signs as in Proposition 2.2; this avoids restrictions that are immaterial in asymptotic investigations. If the’s are strictly positive near then Levin’s theorem provides the exact signs of certain Wronskians.

4) As concrete examples of such asymptotic scales on the reader may think of scales whose non- identically zero and infinitely-differentiable functions are represented by linear combinations, products, ratios and compositions of a finite number of powers, exponentials and logarithms. As a rule such functions and their Wronskians have a principal part at which can be expressed by products of similar functions, hence they do not vanish on a neighborhood of.

When comparing our notations with other authors’ results the reader must carefully notice the numbering of the’s in the asymptotic scale (2.23) and in the Wronskians (2.24); the next proposition contains various additional properties of a T.A.S. and, in particular, it claims that conditions (2.21)-(2.24) imply the nonvanishingness of the reversed Wronskians:

(2.27)

though the converse generally fails as it may be easily checked for the scale

(2.28)

which satisfies (2.27) on whereas

Proposition 2.3 (Several characterizations and additional properties of T.A.S.’s). Let the ordered n-tuple of real-valued functions satisfy conditions (2.21)-(2.22)-(2.23).

(I) The following are equivalent properties:

1) is a T.A.S. on, i.e. (2.24) hold true.

2) Both sets of inequalities (2.24) and (2.27) hold true.

3) The ordered n-tuple, with proper choices of the constants, is an extended complete Chebyshev system on.

4) The n-tuple admits of an integral representation of the form

(2.29)

with suitable functions subjected to the following regularity conditions

(2.30)

If this is the case the’s are unique and may be expressed in terms of the’s on by the formulas

(2.31)

Conversely we have the following formulas for the Wronskians of the’s

(2.32)

(II) For a T.A.S. on we have the inequalities

(2.33)

(2.34)

for any set of indexes satisfying (2.11) and we also have the hierarchies between the Wronskians stated in Proposition 2.2-4) and referred to in the present context. Whenever the’s are strictly positive then all the Wronskians in (2.27) are strictly positive on by (2.10), but not necessarily all the Wronskians in (2.24); in this case the inverted n-tuple is an extended complete Chebyshev system on. On the contrary, if the given n-tuple is an extended complete Chebyshev system on i.e. all the Wronskians in (2.24) are strictly positive on, then (2.29) and (2.31) imply that the’s have alternating signs, namely:.

Part (I) of Proposition 2.3 generalizes a classical result, ([12] , Ch. XI, Th. 1.2, p. 379), which characterizes those special asymptotic scales formed by functions with zeros of increasing multiplicities (namely) at an endopint of a compact interval; also refer to ([12] , Ch. I]) and to [13] for locutions and facts about Chebyshev systems. Notice that formulas (2.31) in themselves are well defined if the n-tuple satisfies (2.21) and (2.24); under the addditional assumption (2.23) they establish a one-to-one correspondence between the’s and the’s. For a T.A.S. on the integrals in (2.29) are obviously replaced by, the’s in (2.31) for are defined without the minus sign and the coefficient is absent in (2.32). If all the Wronskians in (2.24) are strictly positive on then the same is true for all the’s.

Under condition (2.25) formulas in Proposition 2.3-2) are related to C.F.’s of type (II) at. We collect in the next proposition all the facts essential to develop our theory of asymptotic expansions focusing on C.F’s rather than on integral representations of the given scale because we need both types of C.F.’s and the layout of Proposition 2.3 does not suit a C.F. of type (I).

Proposition 2.4 (Formulas concerning T.A.S.’s linked to differential operators). Let the ordered n-tuple satisfy conditions (2.21) to (2.25), hence the operator in (2.26) is disconjugate on the open interval and enjoys the properties in Propositions 2.1 and 2.2-(I). Moreover, as an operator acting on, it has the following further properties:

1) Define the following functions on:

(2.35)

Then, the’s satisfy the following regularity conditions:

(2.36)

Their reciprocals, left apart and, may be expressed as derivatives of certain ratios

(2.37)

on the interval, and

(2.38)

Our operator admits of the following factorization on:

(2.39)

which is a global C.F. of type (II) at both endpoints T and.

2) Our T.A.S. (apart from the signs) admits of the following integral representation in terms of the’s:

(2.40)

hence the’s, besides being everywhere non-zero on, have the same order of growth at T, namely

(2.41)

In the special case where all the Wronskians in (2.24) are strictly positive, i.e. when is an extended complete Chebyshev system on, then the’s have alternating signs, namely

(2.42)

3) Analogously we define the following functions on:

(2.43)

They satisfy the same regularity conditions on the half-open interval as the’s do in (2.36) and their reciprocals may be expressed as derivatives of the following ratios analogous to those in (2.37):

(2.44)

on the interval. Moreover:

(2.45)

(2.46)

hence the associated factorization

(2.47)

is (up to constant factors) “the” global C.F. of type (I) at and it turns out to be of type (II) at T.

4) The special fundamental system of solutions to defined by

(2.48)

satisfies the asymptotic relations:

(2.49)

Relations (2.49) uniquely determine the fundamental system up to multiplicative constants. (In the terminology used by the author [10] , [11] the n-tuple is a “mixed hierarchical system” on whereas Levin ([7] , p. 80) would call it a “doubly hierarchical system” because he uses different arrangements for asymptotic scales at the left or right endpoints ([7] , p. 59).) Whenever the’s are strictly positive then the same is true for all the Wronskians appearing in (2.43) hence the absolute values are redundant; in this case it is the inverted n-tuple which forms an extended complete Chebyshev system on.

The construction of the two above factorizations starting from the given expressions of the coefficients or is the classical procedure by Pólya [14] . Notice that the functions’s in (2.47), which are unique (constant factors apart) by a mentioned result by Trench, may be recovered from many different asymptotic scales and not just from one! The main feature of the above proposition is that we can express all the properties of our basic operator (at least those needed in our theory) in terms of the a-priori given Chebyshev asymptotic scale. The use of absolute values in the definitions of the’s and’s has the advantage of avoiding their use in the everywhere-present integral representations; and we must use them in at least one of the definitions as the two sets of Wronskians cannot have one and the same sign.

A quick proof of the existence of C.F.’s. The global existence of C.F.’s of type (I) was for the first time proved by Trench [9] by an original procedure which was subsequently adapted by the author [10] to show the local existence of C.F.’s of type (II). Trench’s result played a historical role as it had a great impact on the asymptotic theory of ordinary differential equations. Levin’s theorem easily implies both Trench’s result about global existence (but not uniqueness) and the existence of a particular local C.F.’s of type (II) in the case of disconjugate operators: see the proof of Proposition 2.4. However we must point out that Trench’s procedure, independent of properties of Wroskians, applies to a larger class of operators ([9] , §1). As far as C.F.’s of type (II) are concerned the present quick approach does not yield a C.F. of type (II) at b for each interval, as asserted in Proposition 2.1-5.

3. The Special Operators Associated to Canonical Factorizations

In this section, we collect some facts concerning those special operators associated to canonical factorizations: properties and formulas which our theory is constructed upon. We do not report the heuristic considerations which justify our approach and show how “natural” the obtained results are; we refer the reader to ([5] , §3) for the heuristic approach and the related conjectures which will be proved in this paper.

Referring to the factorization of type (I) in (2.47), with the’s in (2.43), we define the differential operators acting on:

(3.1)

which satisfy the recursive formula

(3.2)

And referring to the factorization of type (II) in (2.39), with the’s in (2.35), we define the differential operators acting on:

(3.3)

which satisfy the recursive formula

(3.4)

We call L_k [respectively M_k] “the weighted derivative of order k with respect to the weights, [respectively]”, in preference to the (some-times used) generic locutions of “quasi-derivatives or generalized derivatives” with no reference to the n-tuples of weights. The operator of order zero is included for convenience. Now representations (2.40) and (2.47) imply that:

(3.5)

hence there exist never-vanishing functions such that:

(3.6)

It follows that L_k and M_k preserve the hierarchy (2.23), namely we have the following asymptotic scales:

(3.7)

(3.8)

for each fixed k,. For they respectively reduce to

(3.9)

(3.10)

both equivalent to (2.23). Hence if we apply any n-tuple of operators L_k and M_k, , to an asymptotic expansion with an identically-zero remainder i.e. to a linear combination

(3.11)

we get again an asymptotic expansion with a zero remainder and in this sense we may say that “the asymptotic expansion (3.11) is formally differentiable times with respect to the n-tuples of weights and” neglecting the nth-order weighted derivatives which yield identically-zero expressions. Beside this the operators M_k have a remarkable asymptotic link with the coefficients in (3.11) as claimed in the following

Proposition 3.1 (The coefficients of an asymptotic expansion with zero remainder). Referring to the T.A.S. in Proposition 2.4 and to the special factorization (2.39) the following facts hold true for the differential operators M_k in (3.3):

(I) The’s satisfy the following relations:

(3.12)

(3.13)

(3.14)

(3.15)

(II) For a fixed k, , we have the logical equivalence:

(3.16)

if and only if

(3.17)

being the same as in (3.16) and as in (3.13). If (3.16)-(3.17) hold true on a left neighborhood of then the following limits exist as finite numbers and

(3.18)

where, for h = k, (3.18) is the identity (3.16).

(III) In the special case wherein all the Wronskians in (2.24) are strictly positive then the constants in (3.13)- (3.14) have the values:

(3.19)

We stress that the equivalence “(3.16) Û (3.17)” is an algebraic fact based on (3.12)-(3.13) whereas the inference “(3.16)-(3.17) Þ (3.18)” is an asymptotic property whose validity requires that be an asymptotic scale at and that the operators be defined as specified.

4. The First Factorizational Approach

We start from the “unique” C.F. of our operator on the interval of type (I) at, i.e. identity (2.47) with conditions (2.45)-(2.46) and the’s satisfying the same conditions as do the’s in (2.36). We consider the fundamental system (2.48). By (2.49) the ordered n-tuple is an asymptotic scale at but it cannot coincide (constant factors apart) with the given scale as (2.41) and (2.49) are incompatible. However (2.23) and (2.49) imply that the two scales are linked by the following relations

(4.1)

with suitable nonzero constants, hence

(4.2)

and viceversa

(4.3)

with suitable constants. In this approach the appropriate differential operators to be used are the’s defined in (3.1) and here are some elementary properties of these operators.

Lemma 4.1. The following relations are checked at once:

(4.4)

(4.5)

(4.6)

(4.7)

Hence, we have the following chains of asymptotic relations:

(4.8)

The first chain in (4.8) coincides with the second chain in (2.49) apart from the ordering and the factor. As the first term in each chain is the constant “1” all the other terms diverge to.

Lemma 4.2. If a solution of satisfies the asymptotic relation

(4.9)

for some and some nonzero constant c then the following relations hold true:

(4.10)

(4.11)

Moreover,

(4.12)

with the’s defined in (4.1). It follows from (4.1) and (4.10) that all relations in (4.8) hold true after replacing by hence, consistently with (3.7), we have the asymptotic scales:

(4.13)

Last, with the’s defined in (4.1), we have the identity

(4.14)

Lemma 4.3. Any function admits of a representation of type

(4.15)

with suitable constants. From (4.6), (4.12) and (4.15) we infer at once the following representations of the weighted derivatives of f with respect to the weight functions:

(4.16)

(4.17)

By (4.13) the linear combination in the right-hand side of (4.16) is in itself an asymptotic expansion at for each fixed k.

We shall now characterize various situations wherein relations (4.16)-(4.17) become asymptotic expansions. In the following two theorems we state separately three cases of a single claim lest a unified statement be obscure. The reader is referred to the first remark after Theorem 4.4 to grasp the meaning of the differentiated asymptotic expansions which exhibit a special non-common phenomenon.

Theorem 4.4 (Asymptotic expansions formally differentiable according to the C.F. of type (I)). Let .

(I) The following are equivalent properties for a suitable constant:

1) The set of asymptotic relations

(4.18)

2) The single asymptotic relation

(4.19)

which is the explicit form of the relation in (4.18) for.

3) The improper integral

(4.20)

Under condition (4.20) we have the representation formula

(4.21)

(II) For a fixed the following are equivalent properties for suitable constants (the same in each set of conditions):

4) The set of asymptotic expansions as:

(4.22)

5) The second group of asymptotic expansions in (4.22), i.e.

(4.23)

where we point out that the last meaningful term in the right-hand side is a constant.

6) The following improper integral, involving “i” iterated integrations,

(4.24)

Under condition (4.24), we have the representation formula

(4.25)

for, as well as the corresponding formulas for the functions with, obtained by suitable differentiations of (4.25): see remark 3 below.

Remarks. 1) Relations in (4.22) may be read as follows. The first relation, involving, is equivalent to the asymptotic expansion

(4.26)

and the relations involving, with, state that (4.26) can be formally differentiated times in the sense of formally applying the operators to the remainder in (4.26). In so doing one arrives at the expansion

(4.27)

where. The process of formal differentiation, from the order up to, goes on according to the following rule: in (4.27) and in each expansion in (4.23) the last term is constant and is lost after one further weighted differentiation while the remainder preserves its simple growth-order estimate of “”. So the first expansions, i.e. those involving have the same number of meaningful terms whereas each of the other expansions is deprived of the last meaningful term at each successive differentiation. We rewrite more explicitly the expansions in (4.22) to better highlight the dynamics of this process:

(4.28)

The loss of the last meaningful term, where it occurs, is caused by formula (4.12) for which, after renaming the indexes, reads

(4.29)

Notice that in the second group of expansions in (4.28) i.e. those with remainder “”, the meaningful terms disappear one after one in reversed order if compared with Taylor’s formula.

2) It is shown in §6, after the proof of Theorem 4.4, that the set (4.23) is not equivalent in general to the single relation

(4.30)

as in part (I) of the theorem (case).

3) Suitable weighted differentiations of (4.25) yield integral representations of the remainders in the differentiated expansions of orders greater than and these representations are numerically meaningful. On the contrary, if, then successive integrations of (4.25) contain some constants not uniquely defined hence the corresponding representations are of no numerical use without additional information on f.

For the subset of (4.22) involving the operators is empty and here is an explicit and expanded statement.

Theorem 4.5 (The case in Theorem 4.4). For the following are equivalent properties:

1) The set of asymptotic expansions as for suitable constants:

(4.31)

where the last term in each expansion is lost in the successive expansion.

2) The improper integral

(4.32)

3) There exist n real numbers and a function Lebesgue-summable on such that

(4.33)

If this is the case is determined up to a set of measure zero and

(4.34)

The phenomenon described in (4.28) and (4.31) is intrinsic in the theory; it occurs even in the seemingly elementary case of real-power expansions, ([4] , Th. 4.2-(ii), p. 181, and formula (7.2), p. 195), where the asymptotic scale enjoys the most favourable algebraic properties. This type of formal differentiation of an asymptotic expansion does not frequently occur in the literature though the results in this section show that it is one of the possible natural situations. An instance (not inserted in a general theory) is to be found in a paper by Schoenberg ([15] , Th. 3, p. 258) and refers to the asymptotic expansion

(4.35)

5. The Second Factorizational Approach and Estimates of the Remainders

Now we face our problem starting from a C.F. of type (II) at. Referring to Proposition 2.4 the most natural choice is the special C.F. of in (2.39), with the’s in (2.35) and satisfying conditions (2.36). According to the Conjectures formulated in ([5] , §3) we shall characterize a set of asymptotic expansions, involving the operators defined in (3.3), wherein each coefficient of the first expansion may be found by an independent limiting process instead of the recursive formulas (1.3), and the existence of the sole last coefficient implies the existence of all the preceding coefficients. In this new context a representation of the following type is appropriate for any function:

(5.1)

with suitable constants. Applying the operators to (5.1) we get the following representations of the weighted derivatives of f with respect to the weight functions:

(5.2)

Warning! To simplify formulas and to leave no ambiguity about the signs of the involved quantities we assume throughout this section that the Wronskians in (2.24) are strictly positive. Hence, by (3.19), and the last relation in (5.2) explicitly is

(5.3)

By (3.8), the ordered linear combination in (5.2),

(5.4)

is an asymptotic expansion at for each fixed Unlike §4 we first state here the result concerning a complete asymptotic expansion, i.e. of type (1.1), because it is the most expressive result in this paper and characterizes the simple circumstance that via a set of n asymptotic expansions. Always refer to Proposition 3.2 for properties of the’s.

Theorem 5.1 (Complete expansions formally differentiable according to a C.F. of type (II) ). Let our T.A.S. be such that all the Wronskians in (2.24) are strictly positive and let.

(I) The following are equivalent properties:

1) There exist n real numbers such that:

(5.5)

(5.6)

where the first term in each expansion is lost in the successive expansion, just the same phenomenon as in Taylor’s formula. Notice that the relation that would be obtained in (5.6) for differs from relation in (5.5) by the common factor.

2) All the following limits exist as finite numbers:

(5.7)

where the’s coincide with those in (5.5).

3) The single last limit in (5.7) exists as a finite number, i.e.

(5.8)

and (5.8) is nothing but the relation in (5.6) for which reads

4) The improper integral

(5.9)

and automatically also the iterated improper integral

(5.10)

5) There exist n real numbers and a function Lebesgue-summable on such that

(5.11)

where, by (2.35),. In this case is determined up to a set of measure zero and

(5.12)

(II) Whenever properties in part (I) hold true we have integral representation formulas for the remainders

(5.13)

namely,

(5.14)

(5.15)

for From (5.14) we get the following estimate of wherein the order of smallness with respect to is made more explicit than in Theorem 4.5 (formula in (2.40) for is used):

(5.16)

Under the stronger hypothesis of absolute convergence for the improper integral we get

(5.17)

Similar estimates can be obtained for the’s.

Remarks. 1) As noticed in ([4] , Remark 1 after Th. 4.1, pp. 179-180) the remarkable inference “3) Þ 2)” is true for the special operator stemming out from a C.F. of type (II) at but not for any th-order differential operator originating from an arbitrary factorization of.

2) Condition (5.9) involves the sole coefficient which admits of the explicit expression in (2.35) in terms of

(5.18)

hence (5.9) can be rewritten as

(5.19)

For the ratio inside the integral equals and we reobtain the result in ([1] ; condition (5.15), p. 265).

3) In Theorem 4.5, generally speaking, no such estimates as in (5.16)-(5.17) can be obtained due to the divergence of all the improper integrals in (4.33) if the innermost integral is factored out.

4) Theorem 5.1 changes the perspective of the elementary characterizations in (1.3) of the coefficients: in (1.3) the’s are defined recursively whereas in (5.7) each has its own independent expression and, moreover, the existence of, as the limit in (5.8), implies the existence of

In the following result about incomplete expansions formal differentiation is in general legitimate a number of times less than the “length” of the expansion (see Remark 2 after the statement).

Theorem 5.2 (A result on incomplete asymptotic expansions). Let our T.A.S. be such that all the Wronskians in (2.24) are strictly positive and let.

(I) For a fixed the following are equivalent properties:

1) There exist i real numbers such that:

(5.20)

(5.21)

2) All the following limits exist as finite numbers:

(5.22)

where the’s coincide with those in (5.20)-(5.21).

3) The single last limit in (5.22) exists as a finite number, i.e.

(5.23)

and (5.23) coincides with the relation in (5.21) for

4) The improper integral (involving n−i+1 iterated integrations)

(5.24)

and automatically also the iterated improper integral

(5.25)

(II) For the theorem simply asserts that the asymptotic relation

(5.26)

holds true for some real number iff the improper integral

(5.27)

Remarks. 1) We shall see in the proof of Theorem 5.2, formula (7.44), that the representations of the quantities, , contain some unspecified constants not determinable through the sole condition (5.24) which, for this reason, grants neither explicit representations nor numerical estimates of the remainders of the expansions in (5.20)-(5.21).

2) As concerns estimates of the quantities for, the situation is as follows. By (3.13)-(3.14), the representation in (5.2) for has the form:

(5.28)

for some constant c. If, as converges to a real number then we may apply Theorem 5.2 with i replaced by; but if is unbounded and oscillatory no asymptotic relation more expressive than (5.28) can be obtained generally speaking. On the contrary a favourable situation occurs when it is known a priori that either converges or diverges to and the corrresponding estimates are reported in Part II-B of this paper, Theorems 8.3-8.4.

Theorem 5.3 (The analogue of Theorems 5.1-5.2 with “O”-estimates). Let our T.A.S. be such that all the Wronskians in (2.24) are strictly positive, let and let be fixed. The following are equivalent properties:

1) There exist real numbers such that:

(5.29)

(5.30)

2) All the following relations hold true:

(5.31)

where the’s coincide with those in (5.29)-(5.30).

3) It holds true the single last relation in (5.31) i.e.

(5.32)

4) We have the following estimate instead of condition (5.24):

(5.33)

For condition (5.32) reads

(5.34)

and representation (5.11)-(5.12) must be replaced by

(5.35)

For the theorem simply asserts that the asymptotic relation

(5.36)

holds true iff

(5.37)

6. Proofs

Proof of Proposition 2.1. For the equivalence of the two properties in 1), see Coppel ([8] , Prop. 3, p. 82). “1) Û 2)” is proved in Levin ([7] , Th. 2.1, p. 66) where the interval I is explicitly stated to be open not in the statement of the cited theorem but at the outset of §2 on p. 58; “2) Û 3)” is the classical result by Pólya [14] ; “1) Û 4)” is the fundamental result by Trench [9] ; “1) Þ 5)” is to be found in ([10] , Th. 2.2, p. 162) whereas the converse rests on the trivial fact that disconjugacy on is equivalent to disconjugacy on every compact subinterval of.

Proof of Proposition 2.2. Part (I) is contained in ([12] , Th. 2.1, p. 66) with reverse numbering of the’s whereas part (II) follows from ([12] , Lemma 2.6, pp. 63-64, and Remarks on p. 67 concerning the hierarchies of the Wronskians), here again with reverse numbering of the’s. Levin’s results are valid for an open interval and this is stated explicitly at the outset of §2 in ([7] , p. 58); moreover, the tacit assumption of strict positivity of the functions forming the scale is agreed in a long list of notations and terminology in ([7] , §1, p. 57, item 20).

Proof of Proposition 2.3. 1) Þ 2). Let be an extension of of class, , such that

(6.1)

In particular, we have

(6.2)

and we may apply part (II) of Proposition 2.2 (regardless of the signs) because the second condition in (6.2) coincides with the condition in (2.16) for. So, we infer the inequalities:

(6.3)

which imply (2.27). Proposition 2.2 also implies all the claims in part (II).

1) Û 3). We refer to the standard definition of the concept of “extended complete Chebyshev system on a generic interval J”, based on the maximum number of zeros for their linear combinations, see, e.g., ([12] , Ch. I). A classical result states the equivalence between an ordered n-tuple forming such a system on J and the strict positivity of the Wronskians on J. This is proved, e.g., in ([12] , Ch. XI, Th. 1.1, p. 376) for a compact interval J, but the argument is valid for any interval as observed, e.g., by Mazure ([13] , Prop. 2.6). This equivalence is a general fact involving only inequalities (2.24).

2) Þ 4). Here, we are retracing the steps of the proof in ([12] , Ch. XI, Th 1.2, pp. 379-380) in a way that includes in one proof the expressions given in (2.31). First, inequalities (2.24) grant that the functions, , are well defined on and satisfy (2.29). The second expression for, in (2.30), is a classical identity, see ([8] , Lemma 4, p. 87) for a synthetic proof under our regularity assumptions. Moreover, inequalities (2.24) and (2.27) together grant, by Proposition 2.2-(II), the asymptotic relations (2.14), hence

(6.4)

This implies three facts: 1) the convergence of the improper integrals

(6.5)

2) the representations for; 3) the identity

(6.6)

Before using induction, we prove the representation of to highlight the role of (6.6). We have

(6.7)

whence

(6.8)

which implies the representation of in (2.28). To prove the representations of for, we proceed by induction supposing to have proved our inference 2) Þ 4) for any i-tuple forming a T.A.S. on; hence, our representations hold true for and we must prove it for. Putting

(6.9)

we immediately infer from (1.5) and from (2.14) referred to that

(6.10)

(6.11)

(The n-tuple is sometimes called the “reduced system”). Moreover, (6.6) and (6.10) imply

(6.12)

We may now apply our inductive hypothesis inferring that

(6.13)

where the’s are defined by the expressions on the right of (2.30) with the’s replaced by the’s and (6.10) implies

(6.14)

and (6.13) becomes

(6.15)

which, by (2.23), gives the sought-for formula for. Formulas (2.32) may be proved quite simply, in alternative to the inductive argument suggested in ([12] , p. 380), using the second expressions for the’s given in (2.31); putting for brevity,

(6.16)

we have as in ([8] , p. 92):

(6.17)

hence,

(6.18)

and this shows the converse inference “4) Þ 2)”.

Proof of Proposition 2.4. 1)-2). Properties in (2.36) follow directly from the assumptions, and relations in (2.37) are a standard fact as remarked in the preceding proof. As concerns (2.38), the continuity of the’s at the endpoint T implies, whereas from (2.37) we get

(6.19)

Factorization (2.39) is then the classical factorization arising from (2.35) and discovered for the first time by Pólya [14] . Representations (2.40) are contained in Proposition 2.3 with different notations. In general, by (2.12), the calculations in (6.19) prove the existence of a C.F. of type (II) at valid on a suitable left neighborhood of.

3) The very same reasonings prove the properties of the’s; the proof of (2.45) is similar to that in (6.19)

(6.20)

and in general, by (2.10), these calculations prove the existence of a C.F. of type (I) at valid on the whole open interval where the given operator is assumed disconjugate. The claims in 4) are trivial.

Proof of Proposition 3.2. Relations (3.12) to (3.14) are directly checked using representations (2.40). Relation (3.15) follows from the second relation in (3.6) replacing u by and using (3.13). If (3.16) holds true for some sufficiently regular f, then (3.4) implies and (3.17) follows from (3.12)-(3.13). The converse trivially follows again from (3.12)-(3.13). Now suppose (3.16)-(3.17) to be true on the left of; relation

(3.18) for is nothing but the obvious relation

For, we use all relations (3.12), (3.13), (3.14) and get from (3.17)

(6.21)

where the remainder “” is for.

Proof of Lemma 4.2. From the chain, we get

(6.22)

for suitable constants, hence

(6.23)

now (4.10) follows from (4.7), and (4.11) follows from (4.4). If in (6.22) we replace by we have and the identities in (4.12) follow from (4.4) and (4.5). The identity in (4.12) for, i.e., together with the first relation in (3.5) imply (4.14).

Proof of Theorem 4.4. Part (I). From (4.12) and (4.17), with, we infer at once the equivalence “(ii) Û (iii)” as well as representation in (4.21). The inference “1) Þ 2)” being obvious let us prove the converse simply

denoting by L our operator. We shall repeatedly use the recursive formula (3.2) in the form

(6.24)

If (4.19) holds true we have (4.21), and representations in (4.16) can be rewritten as

(6.25)

Now we have

(6.26)

by (4.1) and (4.10) And after substituting into (6.25), we get

(6.27)

where, and the coefficient

(6.28)

is independent of k. To show that c coincides with the appearing in (4.19) we may suitably integrate (4.19) to obtain, by (3.1),

(6.29)

Part (II). Case. We must prove the equivalence of the following three contingencies:

(6.30)

(6.31)

(6.32)

First, we prove “(6.31) Û (6.32)”. If (6.32) holds true then, by part (I) of our theorem, we have all relations in (4.18) and in particular the second relation in (6.31). Moreover we can rewrite representation in (4.16) for in the form

(6.33)

where is just the same as in the second relation in (6.31) and is a suitable constant. This yields the first relation in (6.31) because is a nonzero constant by (4.12). Viceversa if relations in (6.31) hold true then, by part (I), we have representation in (4.21) by which we replace the quantity in the first equality in (6.33). Denoting by suitable constants we get

(6.34)

By comparison with the first relation in (6.31) we get (6.32) because is a constant. As the inference “(6.30) Þ (6.31)” is obvious it remains to prove the converse. Using (6.24) and integrating the first relation in (6.31), we get (with suitable constants)

(6.35)

as is a nonzero constant and diverges

Here, the constant is meaningless as the comparison functions are divergent as. Iterating the procedure we get all relations in (6.30). By induction on i and the same kind of reasonings our theorem is proved for each.

Proof of Theorem 5.1. 1) Þ 2). Relation (5.5) implies the existence of

, and each relation in (5.6) implies the relation in (5.7) with the

same value of k because of (3.13)-(3.14). 2) Þ 3) is obvious. 3) Û 4). It follows from (5.3) that the limit in (5.8) exists in iff (5.9) holds true and, in this case, (5.3) can be written as

(6.36)

where, as above,.

4) Þ 1). We have already proved (6.36) which is (5.6) for together with an integral representation of the remainder. For the recursive formula (3.4) gives

(6.37)

whence, by (6.36) and (2.38), we get

(6.38)

for a suitable constant. By (3.13)-(3.14) this is nothing but

(6.39)

which is the relation in (5.6) for with a representation of the remainder. In a similar way for we start from

(6.40)

and integrate (6.38) after dividing by, so getting

(6.41)

for a suitable constant. By (3.13)-(3.14), this can be rewritten as

(6.42)

with a suitable constant. An iteration of the procedure gives all relations in (5.6) together with the representation formulas (5.11)-(5.12) for and (5.15) for “1) Þ 5)” has been proved. The last inference “5) Þ 1)” and (5.12) are trivially proved by applying the operators to (5.11).

Proof of Theorem 5.2. 1) Þ 2) follows from (3.13)-(3.14). 2) Þ 3) is obvious. 3) Û 4): by (3.13)-(3.14) the representation in (5.2) for has the form

(6.43)

whence our equivalence follows at once. If this is the case (5.2) can be rewritten as

(6.44)

where is uniquely determined by (5.23) but are non-better specified constants not determinable by the sole condition (5.23).

4) Þ 1). As in the corresponding inference in Theorem 5.1 we integrate (6.44) starting from

(6.45)

whence, by (2.38), (3.4) and (3.14), we get

(6.46)

where the constant, which includes all the constants from integration of the various terms, is uniquely determined by (5.22). By iteration of the procedure we get all relations in (5.20)-( 5.21). Relation (5.28) easily follows from (6.44) by (3.13)-(3.14).

Proof of Theorem 5.3. This is almost a word-for word repetition of the proofs of Theorems 5.1-5.2. 1) Þ 2). For this is included in the same inference in Theorems 5.1-5.2; whereas the relation in (5.30) for just reads. “2) Þ 3)” is obvious. “3) Û 4)” follows from (6.43). To show “4) Þ 1)” we use (6.45) and the representation in (5.2) for instead of (6.44) as in the proof of Theorem 5.2. Due to the convergence of we may still apply the operator so getting, instead of (6.46),

(6.47)

By iteration, we get all relations in (5.28)-(5.29).

Acknowledgements

The author thanks the referees for their valuable suggestions.

References

Corrections of Misprints in Previous Papers

In the above reference [1] :

・ On p. 255, first line under title of §4: “gaphs” reads “graphs”.

・ On p. 260: the reader may notice that (4.29)₂ is just a reformulation of (4.27).

・ On p. 261, first line from above: delete “t” in locution “t limit position”.

・ On p. 266: there is a redundant sign of absolute value “|” inside the integrals in (5.27) and (5.28).

・ On p. 284: in the right-hand side of formula (8.26) the quantity must be replaced by.

・ On p. 286: in reference [7] the article pages are missing, namely, 173-218; and in reference [13] the correct article pages are 319-327.

In the above reference [5] :

・ On p. 3: in the right-hand side of formula (2.3) the symbol u is missing in the innermost position so that the formula correctly reads:

・ On p. 19: in reference [7] the correct article pages are 319-327.