Advances in Pure Mathematics
Vol.05 No.06(2015), Article ID:56727,9 pages
10.4236/apm.2015.56035
Equivalence of K-Functionals and Modulus of Smoothness Generated by a Generalized Dunkl Operator on the Real Line
Reem Fahad Al Subaie1, Mohamed Ali Mourou2
1Department of Mathematics, College of Sciences for Girls, University of Dammam, Dammam, Kingdom of Saudi Arabia
2Department of Mathematics, Faculty of Sciences of Monastir, University of Monastir, Monastir, Tunisia
Email: rmalsubaei@uod.edu.sa, mohamed_ali.mourou@yahoo.fr
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 April 2015; accepted 25 May 2015; published 28 May 2015
ABSTRACT
This paper is intended to establish the equivalence between K-functionals and modulus of smooth- ness tied to a Dunkl type operator on the real line.
Keywords:
Differential-Difference Operator, Generalized Fourier Transform, Generalized Translation Operators, K-Functionals, Modulus of Smoothness

1. Introduction
Consider the first-order singular differential-difference operator on the real line
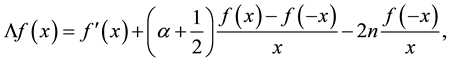
where 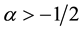 and
and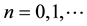 . For
. For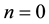 , we regain the differential-difference operator
, we regain the differential-difference operator
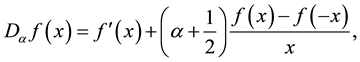
which is referred to as the Dunkl operator with parameter 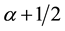 associated with the reflection group
associated with the reflection group 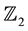 on
on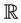 . Such operators have been introduced by Dunkl [1] -[3] in connection with a generalization of the classical theory of spherical harmonics. The one-dimensional Dunkl operator
. Such operators have been introduced by Dunkl [1] -[3] in connection with a generalization of the classical theory of spherical harmonics. The one-dimensional Dunkl operator  plays a major role in the study of quantum harmonic oscillators governed by Wigner’s commutation rules [4] -[6] .
plays a major role in the study of quantum harmonic oscillators governed by Wigner’s commutation rules [4] -[6] .
The authors have developed in [7] [8] a new harmonic analysis on the real line related to the differential-dif- ference operator 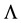 in which several classical analytic structures such as the Fourier transform, the translation operators, the convolution product, ..., were generalized. With the help of the translation operators tied to
in which several classical analytic structures such as the Fourier transform, the translation operators, the convolution product, ..., were generalized. With the help of the translation operators tied to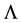 , we construct in this paper generalized modulus of smoothness in the Hilbert space
, we construct in this paper generalized modulus of smoothness in the Hilbert space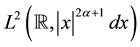 . Next, we define Sobolev type spaces and K-functionals generated by
. Next, we define Sobolev type spaces and K-functionals generated by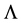 . Using essentially the properties of the Fourier transform associated to
. Using essentially the properties of the Fourier transform associated to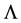 , we establish the equivalence between K-functionals and modulus of smoothness.
, we establish the equivalence between K-functionals and modulus of smoothness.
In the classical theory of approximation of functions on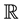 , the modulus of smoothness are basically built by means of the translation operators
, the modulus of smoothness are basically built by means of the translation operators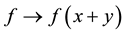 . As the notion of translation operators was extended to various contexts (see [9] [10] and the references therein), many generalized modulus of smoothness have been discovered. Such generalized modulus of smoothness are often more convenient than the usual ones for the study of the connection between the smoothness properties of a function and the best approximations of this function in weight functional spaces (see [11] -[13] and references therein).
. As the notion of translation operators was extended to various contexts (see [9] [10] and the references therein), many generalized modulus of smoothness have been discovered. Such generalized modulus of smoothness are often more convenient than the usual ones for the study of the connection between the smoothness properties of a function and the best approximations of this function in weight functional spaces (see [11] -[13] and references therein).
In addition to modulus of smoothness, the K-functionals introduced by J. Peetre [14] have turned out to be a simple and efficient tool for the description of smoothness properties of functions. The study of the connection between these two quantities is one of the main problems in the theory of approximation of functions. In the classical setting, the equivalence of modulus of smoothness and K-functionals has been established in [15] . For various generalized modulus of smoothness these problems are studied, for example, in [16] -[19] . It is pointed out that the results obtained in [16] emerge as easy consequences of those stated in the present paper by simply taking
2. Preliminaries
In this section, we develop some results from harmonic analysis related to the differential-difference operator

The one-dimensional Dunkl kernel is defined by

where
is the normalized spherical Bessel function of index



Furthermore, we have the Laplace type integral representations:


where

The following properties will be useful for the sequel.
Lemma 1 1) For all

2) There is 



3) For all

4) For all
Proof. Assertions (1) and (2) are proved in [16] . By (1), (4) and the fact that
we have
Clearly the integral above is null only for

we get
By (6),
Moreover,
which concludes the proof.
Notation 1 Put
We denote by






The topology of 








Clearly 



For 


Definition 1 The generalized Fourier transform of a function 
Remark 1 If 




Theorem 1 The generalized Fourier transform 


where
Theorem 2 1) For every 
2) The generalized Fourier transform 


Definition 2 The generalized Fourier transform of a distribution 
Theorem 3 The generalized Fourier transform 


Lemma 2 If 
is a tempered distribution

with
Proof. The fact that 

where
which completes the proof.
Lemma 3 Let 




Proof. Identity (8) may be found in [7] . If 
But by (8),
So
which ends the proof.
Notation 2 From now on assume


More explicitly, 




Proposition 1 For 

Proof. From the definition of 
By (7) and (9),
with
with
Definition 3 The generalized translation operators


where
with 
Proposition 2 Let 



Furthermore,

3. Equivalence of K-Functionals and Modulus of Smoothness
Definition 4 Let 

The generalized modulus of smoothness is defined by
where
I being the unit operator.
The generalized K-functional is defined by
The next theorem, which is the main result of this paper, establishes the equivalence between the generalized modulus of smoothness and the generalized K-functional:
Theorem 4 There are two positive constants 

for all 

In order to prove Theorem 4, we shall need some preliminary results.
Lemma 4 Let 



Proof. The result follows easily by using (11), (12) and an induction on m.
Lemma 5 For all 


Proof. By (10), (14), Lemma 1 (4) and Theorem 2 we have
which is the desired result.
Notation 3 For 

Proposition 3 Let 

1) The function 


for all
2) For all


where
Proof. The fact that 
which is proved in [7] . Assertion (2) is a consequence of (16) and Theorem 2.
Lemma 6 There is a positive constant 
for any 

Proof. By (17) and Theorem 2, we have
By Lemma 1 (2) there is a constant 

for all 

which achieves the proof.
Corollary 1 For all 

where c is as in Lemma 6.
Lemma 7 There is a positive constant 
for every 

Proof. By (17) and Theorem 2 we have
Put
By L’Hôpital’s rule,
This when combined with Lemma 1 (3) entails
Therefore
by virtue of (14) and Theorem 2.
Corollary 2 For any 

where C is as in Lemma 7.
Proof of Theorem 4. 1) Let 

Calculating the supremum with respect to 

with
2) Let 

Since 

with
References
- Dunkl, C.F. (1989) Differential-Difference Operators Associated to Reflection Groups. Transactions of the American Mathematical Society, 311, 167-183. http://dx.doi.org/10.1090/S0002-9947-1989-0951883-8
- Dunkl, C.F. (1991) Integral Kernels with Reflection Group Invariance. Canadian Journal of Mathematics, 43, 1213- 1227. http://dx.doi.org/10.4153/CJM-1991-069-8
- Dunkl, C.F. (1992) Hankel Transforms Associated to Finite Reflection Groups. Contemporary Mathematics, 138, 128- 138. http://dx.doi.org/10.1090/conm/138/1199124
- Kamefuchi, S. and Ohnuki, Y. (1982) Quantum Field Theory and Parastatistics. University of Tokyo Press, Springer- Verlag, Tokyo, Berlin.
- Rosenblum, M. (1994) Generalized Hermite Polynomials and the Bose-Like Oscillator Calculus. Operator Theory: Advances and Applications, 73, 369-396. http://dx.doi.org/10.1007/978-3-0348-8522-5_15
- Yang, L.M. (1951) A Note on the Quantum Rule of the Harmonic Oscillator. Physical Review Letters, 84, 788-790. http://dx.doi.org/10.1103/PhysRev.84.788
- Al Sadhan, S.A., Al Subaie, R.F. and Mourou, M.A. (2014) Harmonic Analysis Associated with A First-Order Singular Differential-Difference Operator on the Real Line. Current Advances in Mathematics Research, 1, 23-34.
- Al Subaie, R.F. and Mourou, M.A. (2014) Inversion of Two Dunkl Type Intertwining Operators on R Using Generalized Wavelets. Far East Journal of Applied Mathematics, 88, 91-120.
- Mourou, M.A. and Trimèche, K. (2003) Transmutation Operators and Paley-Wiener Theorem Associated with a Singular Differential-Difference Operator on the Real Line. Analysis and Applications, 1, 43-69. http://dx.doi.org/10.1142/S0219530503000090
- Trimèche, K. (1981) Transformation intégrale de Weyl et théorème de Paley-Wiener associés à un opérateur différentiel singulier sur
. Journal de Mathématiques Pures et Appliquées, 60, 51-98.>http://html.scirp.org/file/5-5300892x222.png" class="200" />. Journal de Mathématiques Pures et Appliquées, 60, 51-98.
- Platonov, S.S. (2000) Generalized Bessel Translations and Certain Problems of the Theory of Approximation of Functions in the Metrics of L2,α. I. Trudy Petrozavodskogo Gosudarstvennogo Universiteta, Seriya Matematika, 7, 70-82.
- Platonov, S.S. (2001) Generalized Bessel Translations and Certain Problems of the Theory of Approximation of Functions in the Metrics of L2,α. II. Trudy Petrozavodskogo Gosudarstvennogo Universiteta, Seriya Matematika, 8, 1-17.
- Potapov, M.K. (1998) Application of the Operator of Generalized Translation in Approximation Theory. Vestnik Mos- kovskogo Universiteta, Seriya Matematika, Mekhanika, 3, 38-48.
- Peetre, J. (1963) A Theory of Interpolation of Normed Spaces. Notes de Universidade de Brasilia, Brasilia.
- Berens, H. and Buter, P.L. (1967) Semi-Groups of Operators and Approximation. Grundlehren der mathematischen Wissenschaften, 145, Springer, Berlin.
- Belkina, E.S. and Platonov, S.S. (2008) Equivalence of K-Functionnals and Modulus of Smoothness Constructed by Generalized Dunkl Translations. Izvestiya Vysshikh Uchebnykh Zavedenii Matematika, 8, 3-15.
- Dai, F. (2003) Some Equivalence Theorems with K-Functionals. Journal of Approximation Theory, 121, 143-157. http://dx.doi.org/10.1016/S0021-9045(02)00059-X
- Ditzian, Z. and Totik, V. (1987) Moduli of Smoothness. Springer-Verlag, New York. http://dx.doi.org/10.1007/978-1-4612-4778-4
- Löfstróm, J. and Peetre, J. (1969) Approximation Theorems Connected with Generalized Translations. Mathematische Annalen, 181, 255-268. http://dx.doi.org/10.1007/BF01350664


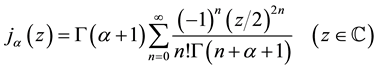






















































 . Journal de Mathématiques Pures et Appliquées, 60, 51-98.>http://html.scirp.org/file/5-5300892x222.png" class="200" />. Journal de Mathématiques Pures et Appliquées, 60, 51-98.
. Journal de Mathématiques Pures et Appliquées, 60, 51-98.>http://html.scirp.org/file/5-5300892x222.png" class="200" />. Journal de Mathématiques Pures et Appliquées, 60, 51-98.