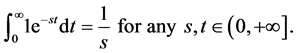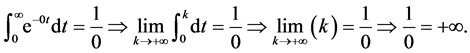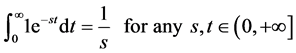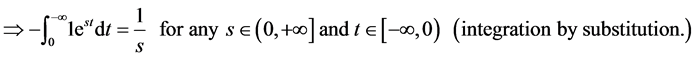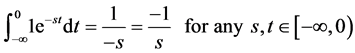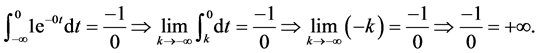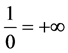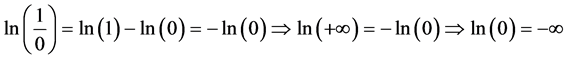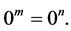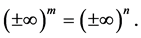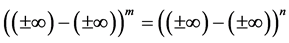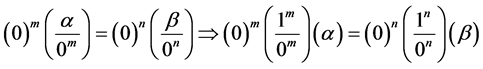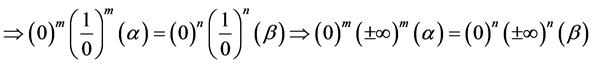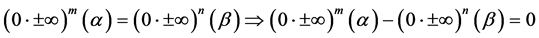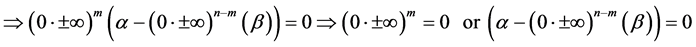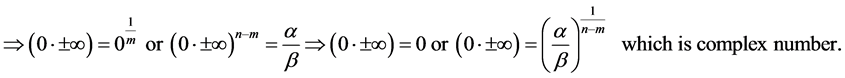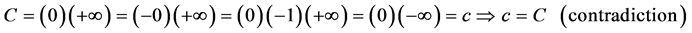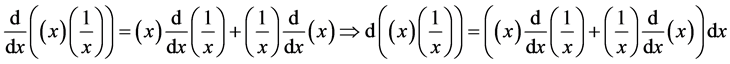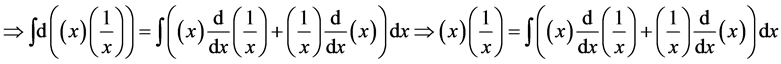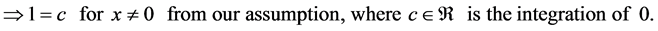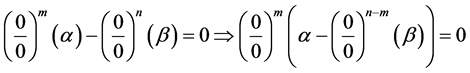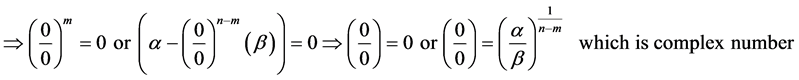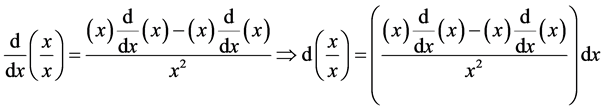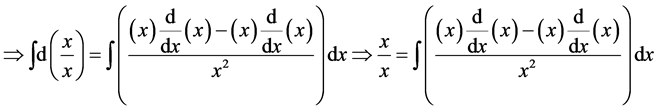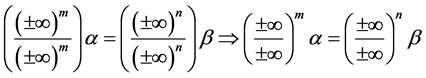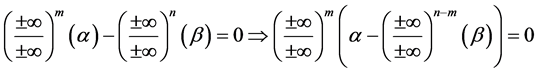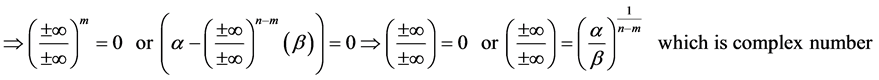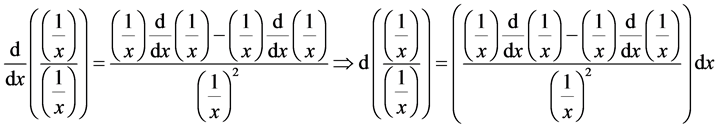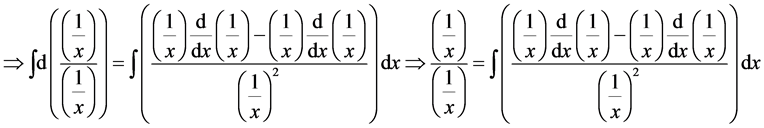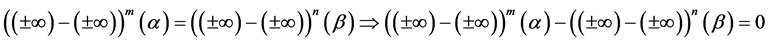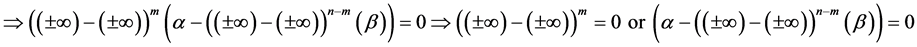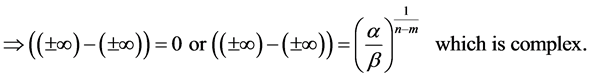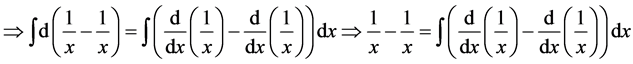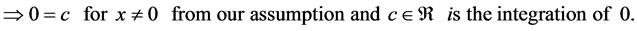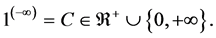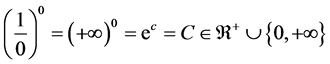Advances in Pure Mathematics
Vol.06 No.08(2016), Article ID:68947,9 pages
10.4236/apm.2016.68043
Indeterminate Forms
Dagnachew Jenber
University of Addis Ababa Science and Technology, Addis Ababa, Ethiopia

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 April 2016; accepted 22 July 2016; published 25 July 2016
ABSTRACT
In this paper, I’m going to discuss on why are ,
, 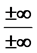 ,
, 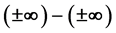 ,
, 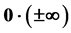 ,
, 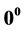 ,
, 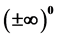 , and
, and 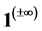 indeterminate form using simple calculus and algebra.
indeterminate form using simple calculus and algebra.
Keywords:
Integration, Differentiation, Simple Algebra

1. Introduction
There are so many things that they are undetermined/indeterminate. Our universe is too complex to model mathe- matically because most of them are undetermined/indeterminate, but we have mathematical model for indeter- minate things itself called indeterminate forms. For example, the weight and height of human beings is indeter- minate because we can’t say the weight or height of human being is this much.
Everything we don’t know is infinitely many times more than everything we know. From something we know we can creat something we don’t know and that gonna be something we know and using this something we know we can creat another something we don’t know and it will continue and never ending. For example, let the only thing we know is hydrogen and oxgen but if we combine two hydrogen and one oxgen we can creat another thing, say water and by combining alot of water together we can creat another thing, say river, lake, ocean etc and also if we add something in to the river or lake or ocean we may creat another living things that we haven’t seen them before and we can continue in such away that creating something we don’t know from something we know.
Someone may ask the main question, “What is the thing before something ?”. In other words, where is our universe comes from? Is our universe comes from something or from nothing? If we assume that our universe is created by God and then some one may ask, “Where God comes from and where he was before he creat the universe?” and Some one may answer for this question like “Before God there is nothing and God comes from nothing”. This may indicates that there is something from nothing [1] - [13] . If there is something from nothing and we know that after something we will have an endless thing, so what is the common thing from nothing and an endless thing? according to our hypothesis it should be something. Therefore if we denote nothing by 0 and
something by c, then 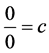 since there is something from nothing and if there is something and using algebra,
since there is something from nothing and if there is something and using algebra, 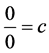 implies
implies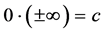 , where
, where 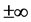 is the notation for an endless thing/idea and in mathematics language
is the notation for an endless thing/idea and in mathematics language
which means doesn’t exist. Here we can’t say anything about nothing while nothing exists but invisible. Till
now the first and the only thing we imagine about c is, c might be God or Big-bang. To be something exist there should be nothing exist first. Empty-space doesn’t imply that nothing and vice versa since nothing is not mea- surable and not observable but existance [1] - [13] . In this paper, I am going to discuss on the proof of indeter- minate things in our universe mathematically called indeterminate forms.
In calculus and other branches of mathematical analysis, limits involving algebraic combination of functions in an independent variable may often be evaluated by replacing these functions by their limits; if the expression obtained after this substitution does not give enough information to determine the original limit, it is said to take on an indeterminate form. The term was originally introduced by cauchy’s student Moigno in the middle of the 19th century.
The indeterminate forms typically considered in the literature are denoted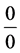 ,
,  ,
, 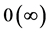 ,
, 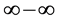 ,
, 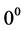
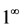

2. Why Is 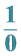
Definition: The function 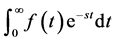
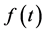
Theorem 1. The number 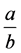
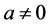
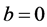

Proof. We know that the laplace transform of 1 is equal to 
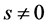
But if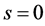
Therefore 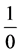

Corollary 1. 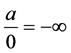
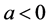
Proof. 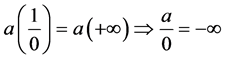
Theorem 2. The number 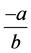

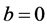

Proof. We know that the laplace transform of 1 is equal to 
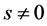
Let’s replace s by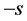
But if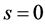
Therefore 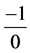
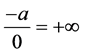
Corollary 2. 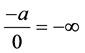
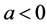
Proof. 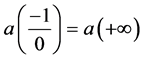
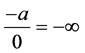
Theorem 3. 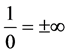
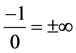
Proof. Easily sketched from Theorem 1-2 and Corollary 1-2.
Theorem 4. The function 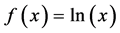
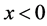

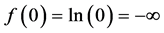
Proof. From above Theorem-1 we have,
If we take natural logarithm both sides of this equation we get,
3. Why Is 
Remark: For every natural numbers m and n such that 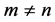
1.
2.
3.
4.
Theorem 5. The number 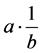
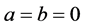
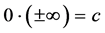
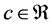
Proof. Let’s take any arbitrary constants 
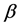
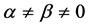
We know that 
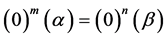
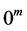
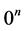
this implies that for every natural numbers m and n
From this we must therfore conclude that 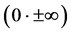
Theorem 6. If 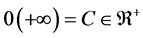


Proof. Suppose
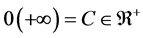
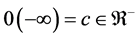
Therefore
This theorem shows that 
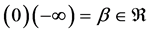
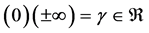
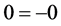
Theorem 7. The number 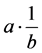
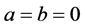
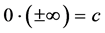
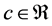
Proof. Suppose 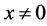
Therefore 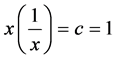
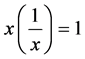
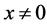
Let’s suppose that 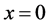
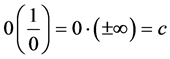

Thus 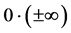
4. Why Is 
Theorem 8. The number 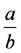
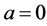
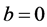
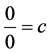
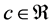
Proof. Let’s take any arbitrary constants 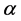

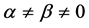
We know that 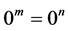
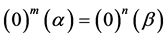
this implies that for every natural numbers m and n,
From this we must therefore conclude that 
Theorem 9. The number 
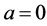
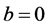


Proof. Since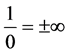
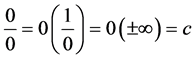
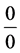
Theorem 10. The number 
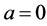
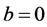

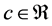
Proof. Suppose 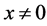
but from our assumption
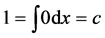
Therefore 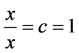
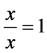
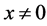
Let’s suppose that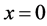
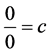
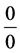
Thus 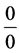
5. Why Is 
Theorem 11. The number 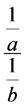
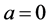
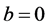
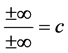
Proof. Let’s take any arbitrary constants 
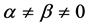
We know that 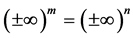
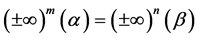
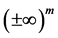
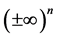
this implies that for every natural numbers m and n such that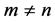
From this we must therefore conclude that 
Theorem 12. The number 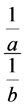
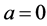
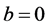
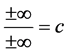

Proof. Suppose 
but from our assumption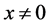
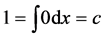
Therefore 

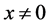
Let’s suppose that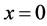
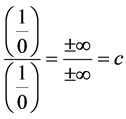
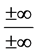
Thus 
6. Why Is 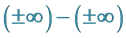
Theorem 13. The number 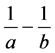
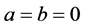
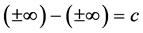
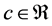
Proof. Let’s take any arbitrary constants 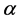
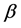

We know that 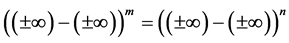
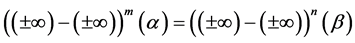
Thus for every natural numbers m and n such that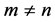
From this we must therefore conclude that 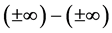
Theorem 14. The number 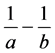

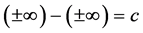
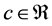
Proof. Suppose 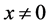
Therefore 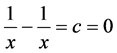

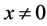
Let’s suppose that 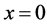
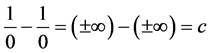
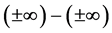
Thus 
7. Why Is 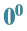
Theorem 15. The number 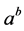
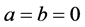
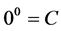
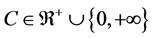
Proof. We know that 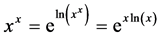
But if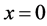
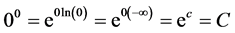
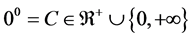
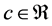

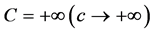
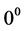
8. Why Is 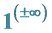
Theorem 16. The number 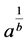
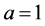


Proof. We know that 
But if 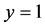
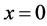
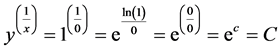
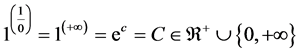
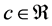


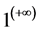
Corollary 3.
Proof. We know that 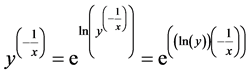
But if 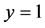
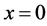
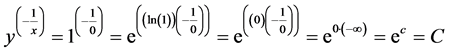
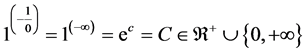
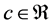
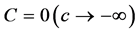
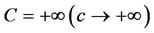
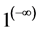
9. Why Is 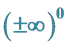
Theorem 17. The number 
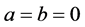
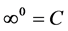
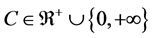
Proof. We know that 
But if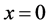

for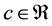
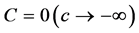

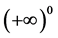
Corollary 4.
Proof. We know that 
But if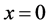


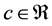

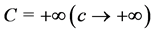
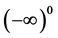
Cite this paper
Dagnachew Jenber, (2016) Indeterminate Forms. Advances in Pure Mathematics,06,546-554. doi: 10.4236/apm.2016.68043
References
- 1. Reynosa, P. (2016) Some of the Changes Lawrence M. Krauss Should Make to the Second Edition of “A Universe from Nothing”. Huffington Post.
- 2. Krauss, L.M. (2012) A Universe from Nothing: Why There Is Something Rather than Nothing. Free Press, New York, 183.
- 3. Andersen, R. (2014) Has Physics Made Philosophy and Religion Obsolete?
http://www.theatlantic.com/ - 4. Krauss, L. After Word from Lawrence Krauss’ New Book—A Universe from Nothing.
- 5. Lawrence Krauss’s 2009 Lecture. A Universe from Nothing.
- 6. “Non Fiction Best Sellers”. The New York Times.
- 7. Albert, D. (2012) On the Origin of Everything. The New York Times Sunday Book Review.
- 8. A Universe from Nothing?—Cosmic Variance: Cosmic Variance.
http://blogs.discovermagazine.com/ - 9. Physicist George Ellis Knocks Physicists for Knocking Philosophy, Falsification, Free Will/ Cross Check, Scientific American Blog Network.
http://blogs.scientificamerican.com/ - 10. Kohli, L.S. (2014) Comments on: A Universe from Nothing. arXiv.1405.6091 [physics.gen-ph].
- 11. Scharf, C. (2012) Cosmology: Plucked from the Vacuum. Nature, 481, 440.
- 12. Nelson, S. (2012) A Universe from Nothing. Review. The A.V. Club.
- 13. Brooks, M. (2012) The Paradox of Nothing. New Scientist, 213.
- 14. Indeterminate Form-Wikipedia.
https://en.m.wikipedia.org - 15. Rotando, L.M. and Korn, H. (1977) The Indeterminate Form 00. Mathematics Magazine, 50, 41-42.
http://dx.doi.org/10.2307/2689754