Received 18 January 2015; accepted 9 February 2015; published 13 February 2015

ABSTRACT

The object of the present paper is to investigate various argument results of analytic and multivalent functions which are defined by using a certain fractional derivative operator. Some interesting applications are also considered.

Keywords:

Multivalent Analytic Functions, Argument, Integral Operator, Fractional Derivative Operator

1. Introduction

Let 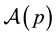denote the class of functions 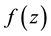of the form

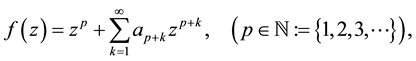(1.1)

which are analytic in the open unit disk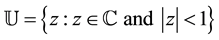. Also let 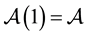denote the class of all analytic functions 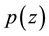with 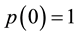which are defined on.

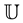Let a, b and c be complex numbers with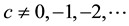. Then the Gaussian hypergeometric function 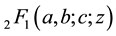is defined by

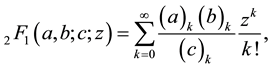(1.2)

where 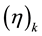is the Pochhammer symbol defined, in terms of the Gamma function, by

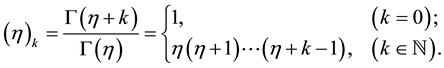
The hypergeometric function 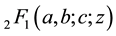is analytic in 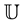and if a or b is a negative integer, then it reduces to a polynomial.

There are a number of definitions for fractional calculus operators in the literature (cf., e.g., [1] and [2] ). We use here the Saigo type fractional derivative operator defined as follows ([3] ; see also [4] ):

Definition 1. Let 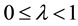and. Then the generalized fractional derivative operator of a function is defined by

(1.3)

The function is an analytic function in a simply-connected region of the z-plane containing the origin, with the order

for, and the multiplicity of is removed by requiring that to be real when.

Definition 2. Under the hypotheses of Definition 1, the fractional derivative operator of a function is defined by

(1.4)

With the aid of the above definitions, we define a modification of the fractional derivative operator by

(1.5)

for and. Then it is observed that also maps onto itself as follows:

(1.6)

It is easily verified from (1.6) that

(1.7)

Note that, and, where is the fractional derivative operator defined by Srivastava and Aouf [5] .

In this manuscript, we drive interesting argument results of multivalent functions defined by fractional derivative operator.

2. Main Results

In order to establish our results, we require the following lemma due to Lashin [6] .

Lemma 1 [6] . Let be analytic in, with and . Further suppose that and

(2.1)

then

(2.2)

We begin by proving the following result.

Theorem 1. Let, and, and let. Suppose that satisfies the condition

(2.3)

then

(2.4)

Proof. If we define the function by

(2.5)

then is analytic in, with and. Making use of the logarithmic differentiation on both sides of (2.5), we have

(2.6)

By applying the identity (1.7) in (2.6), we observe that

Hence, by using Lemma 1, we conclude that

which completes the proof of Theorem 1.

Remark 1. Putting, and in Theorem 1, we obtain the result due to Lashin ([6] , Theorem 2.2).

Taking and in Theorem 1, we have the following corollary.

Corollary 1. Let, and. Suppose that satisfies the condition

then

Theorem 2. Let, , and. Suppose that satisfies the condition

(2.7)

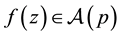
then

(2.8)

Proof. If we set

(2.9)

then is analytic in, with and. By using the logarithmic differentiation on both sides of (2.9), we obtain

Thus, in view of Lemma 1, we have

which evidently proves Theorem 2.

Remark 2. Setting and in Theorem 2, we get the result obtained by Goyal and Goswami ([7] , Corollary 3.6).

Putting in Theorem 2, we obtain the following result.

Corollary 2. Let. Suppose that satisfies the condition

then

Finally, we consider the generalized Bernardi-Libera-Livingston integral operator defined by (cf. [8] [9] and [10] )

(2.10)

Theorem 3. Let, , and, and let. Suppose that satisfies the condition

(2.11)

then

(2.12)

Proof. From (2.10) we observe that

(2.13)

If we let

(2.14)

then is analytic in, with and. Differentiating both sides of (2.14) logarithmically, it follows that

(2.15)

Hence, by applying the same arguments as in the proof of Theorem 1 with (2.13) and (2.15), we obtain

which proves Theorem 3.

Acknowledgements

This work was supported by Daegu National University of Education Research Grant in 2014.

References