Received 5 January 2015; revised 20 January 2015; accepted 23 January 2015

ABSTRACT

This paper presents building one-parameter motion by complex numbers on a time scale. Firstly, we assumed that 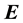and 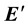were moving in a fixed time scale complex plane and and 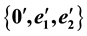were their orthonormal frames, respectively. By using complex numbers, we investigated the delta calculus equations of the motion on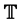. Secondly, we gave the velocities and their union rule on the time scale. Finally, by using the delta-derivative, we got interesting results and theorems for the instantaneous rotation pole and the pole curves (trajectory). In kinematics, investigating one-parameter motion by complex numbers is important for simplifying motion calculation. In this study, our aim is to obtain an equation of motion by using complex numbers on the time scale.

Keywords:

Complex Numbers, Kinematic, Time Scales, Pole Curve

1. Introduction

The calculus on time scales was initiated by B. Aulbach and S. Hilger in order to create a theory that can unify discrete and continuous analysis, [1] . Some preliminary definitions and theorems about delta derivative can be found in the references [2] - [4] .

In this study, some properties of motion in references [5] - [7] are investigated by using time scale complex planes. We find delta calculus equations of the motion and finally we get some results about the pole curves.

2. Preliminaries

A time scale is an arbitrary nonempty closed subset of the real numbers.

Definition 2.1. Let be any time scale. The forward jump operator is defined by

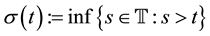
and the backward jump operator is defined by

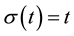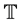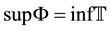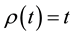In this definition, we put (i.e., if has a maximum t) and (i.e., if has a minimum t), where denotes the empty set. If, we say that t is right-scat- tered, while if we say that t is left-scattered. Points that are right-scattered and left-scattered at the same time are called isolated. Also if and, then t is called right-dense, and if and, then t is called left-dense. Points that are right-dense and left-dense at the same time are called dense.

Finally, the graininess function is defined by

If is a function, then we define the function by

Let us define the interior of relative to which is a function that maps into to be the set

Definition 2.2. Assume is a function and let. Then we define to be the number (pro- vided it exists) with the property that given any ε > 0, there is a neighborhood U of t (i.e. for some) such that

We call the delta (or Hilger) derivative of f at t. Moreover, we say that f is delta (or Hilger) differentiable on provided exists for all.

Theorem 2.1. Assume is a function and let. Then we have the following:

1) If f is differentiable at t, then f is continuous at t.

2) If f is continuous at t and t is right-scattered, then f is differentiable at t with

3) If t is right-dense, then f is differential at t if the limit

exists as a finite number. In this case a given

4) If f is differentiable at t then

Theorem 2.2. Assume are differentiable at. Then:

1) The sum is differentiable at t with

2) For any constant, is differentiable at t with

3) The product is differentiable at t with

4) If then is differentiable at t with

5) If, then is differentiable at t with

In the reference [3] , the chain rule on time scales is given for various cases.

Theorem 2.3. Assume is continuous, is delta differentiable on, and is continuously differentiable. Then, there exists in the real interval with

Theorem 2.4. Let be continuously differentiable and suppose is delta differentiable. Then is delta differentiable and the formula

holds.

Theorem 2.5. Assume that is strictly increasing function and is a time scale. Let. If and exist for, then

(2.1)

Definition 2.3. For the given time scales and, let us set

(2.2)

where is the imaginary unit. The set is called the time scale complex plane.

Definition 2.4. For, we define the cylinder transformation by

and for, let.

Definition 2.5. If, then we define the exponential function by

where the cylinder transformation is introduced in Definition 2.4.

Theorem 2.6. If then

1) and;

2);

3);

4);

5);

6);

7);

8);

Theorem 2.7. Assume for

Theorem 2.8. If then

Theorem 2.9. If and then

3. One Parameter Motion and Hilger Complex Numbers on a Time Scale

Assume that is a time scale. Let us set the time scale complex plane for as

(3.1)

Here, let and be moving in a fixed time scale complex plane. The motion is called as one-parameter planar motion by the complex numbers on the time scale and denoted as for a planar motion of E relative to E′. and be their orthonormal frames, respectively. We suppose that is fixed, then we say that moves with respect to, , are the functions of a time scale parameter t. Let and be the position vectors of a point X in the plane, as following we can write the coordinates of the point X by using complex numbers on the time scale with respect to a fixed or moving plane and, respectively. So:

The translation vector can be written as the following equation on a fixed plane:

by using the definition of the time scale complex plane. The translation vector is more suitable as

for doing the formulas symmetric on the moving plane.

Thus, is equivalent to the vector. Let be a rotation angle between the vectors and (or the time scale complex planes and), in Figure 1. So we can find the equation

(3.2)

For any point, the vector is

(3.3)

By substituting in the Equation (3.3)

(3.4)

Then, we can obtain the vector as follows:

Here, assume the functions

are -differentiable functions and the parameter t is defined as on the time scale. We will cal- culate the formulas for a fixed or moving plane.

Definition 3.1. A velocity vector of the point X with respect to E is called -relative velocity vector of the point X on the time scale. The equation of relative -velocity vector is

(3.5)

for the moving time scale complex plane.

Definition 3.2. A velocity vector of the point X with respect to E is called -relative velocity vector of the point X on the time scale. The equation of the relative -velocity vector is

(3.6)

(3.7)

for the fixed time scale complex plane.

Definition 3.3. A velocity vector of the point X with respect to the time scale complex plane on the planar motion which belongs to a curve of the point on is called the -absolute velocity vector of the point X on the time scale and is denoted by.

Definition 3.4. On the planar motion, while the point X is fixed on the moving time scale complex plane (i.e.), a velocity vector of the point X is called the -dragging velocity vector of this point on the time scale and is denoted by.

So, we obtain the -absolute velocity, i.e. the velocity of X with respect to the plane, from the Equation (3.4) using Equation (3.2).

by Theorem 2.5. Also

and using Theorem 2.7, we have

Here, is called a delta-angular velocity of the motion on a time scale, and remembering Equations (3.3) and (3.7), we can find the dragging velocity vector of the point X

(3.8)

(3.9)

with the restriction, from Equation (3.2) by taking the -derivative with respect to the parameter t, we get the following equation.

and using Equation (3.2), we get

(3.10)

Theorem 3.1. A -absolute velocity vector is equal to adding a -relative velocity vector and -dragging velocity vector on the motion, i.e.

(3.11)

Proof. By using Equation (3.10) and Equation (3.5), we can get the following equations:

and thus, we get the relation of the velocities:

We have

We will calculate here using Equation (3.9) and Equation (3.10);

and

(3.12)

Theorem 3.2. There is only one point at which the -dragging velocity is zero for any instant, i.e. which is fixed on the both of the planes and, with the restriction on the motion.

Proof. The points at which the -dragging velocity vector is zero for any instant have to stay fixed for not only the plane, but also for the plane on the motion. By taking for fixed and moving planes, from (3.15) and (3.8):

(3.13)

(3.14)

we can obtain the following complex vectors;

(3.15)

(3.16)

which are given -instantaneous rotation pole P on both coordinate systems. Because, the affine axioms, are the end-points of, , respectively.

Definition 3.5. The point which corresponds to the position vector is called the for- ward pole or the instantaneous rotation pole or the instantaneous rotation center for the moving plane on the time scale motion, in Figure 2.

Definition 3.6. The point which corresponds to the position vector is called the for- ward pole or the instantaneous rotation pole or the instantaneous rotation center for the fixed plane on the time scale motion, in Figure 2.

We can get the following equations from Equation (3.15) and Equation (3.16):

(3.17)

(3.18)

By eliminating and from Equation (3.13) and Equation (3.14), the dragging velocity becomes as following:

(3.19)

(3.20)

and;

4. Conclusions

Result 4.1. Two results for the -dragging velocity of the point on the moving plane can be obtained as follows:

1) Since scalar product of the vector is

and the vector is zero, these vectors are perpendicular.

2) The length of the vector can be calculated as follows:

here denotes for the length of. From this result, we get the following theorem:

Theorem 4.1. On the motion, the points X of the moving plane E draw trajectories on the fixed time scale complex plane which their normals (trajectory normals) pass from the instantaneous rotation pole.

Theorem 4.2. Every point of X of the moving plane E is doing rotational movement (instantaneous rotation movement) with a -centered, -angular velocity and p factor on instant t.

Since X is an arbitrary point of the time scale complex plane E, we can give the following theorem:

Theorem 4.3. A one-parameter motion consists of rotation with angular velocity and p factor around the instantaneous rotation pole of the moving plane E on t instant, i.e. the plane E rotates with the angle and the factor p around the point on the time element.

Theorem 4.4. The velocity vectors of the instantaneous rotation pole which draws the forward pole curves on the moving and fixed planes is the same vector at each instant t.

Theorem 4.5. On one-parameter planar motion the moving pole curve of the plane E rolls onto the fixed pole curve of the plane without sliding.

Result 4.2. Without being depended on time, a motion occurs by rolling, without sliding, the curve of E onto the curve of.

References