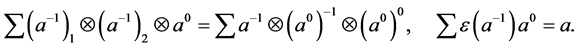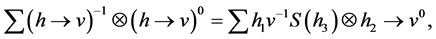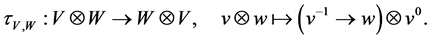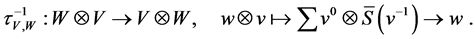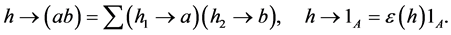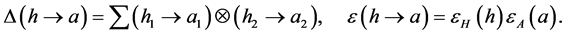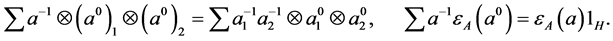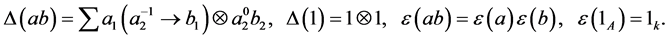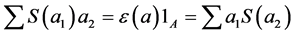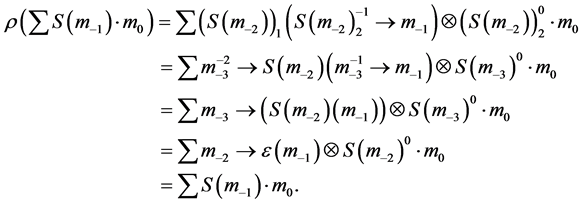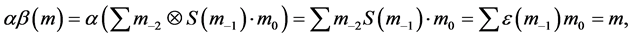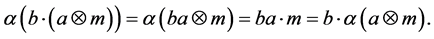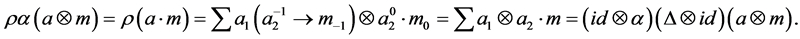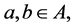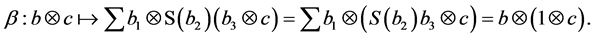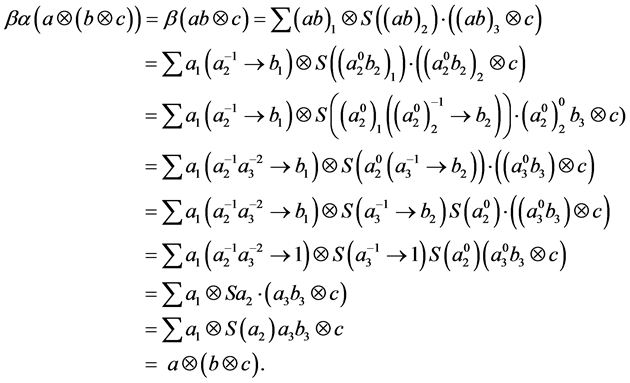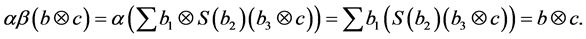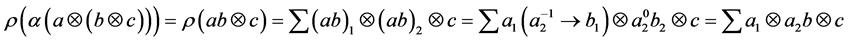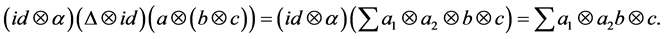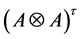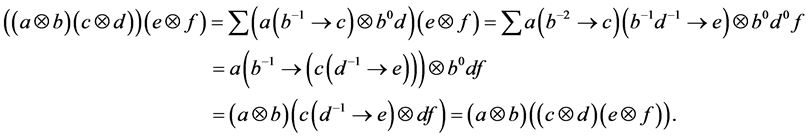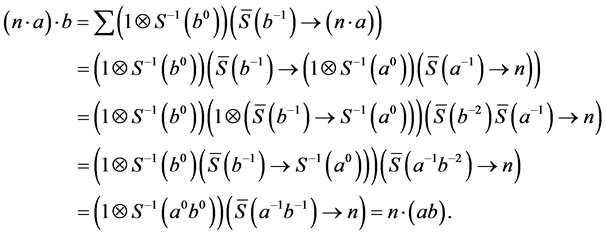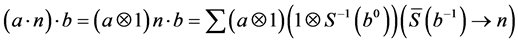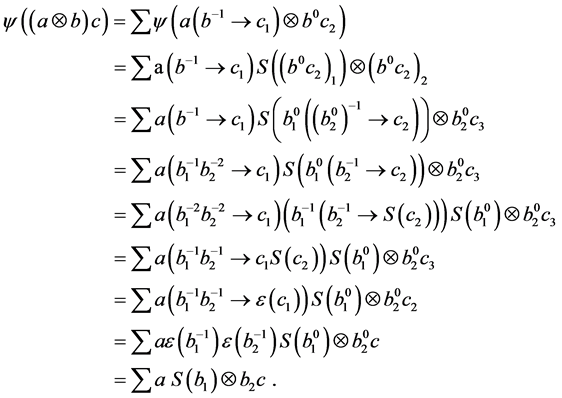Advances in Pure Mathematics
Vol.04 No.09(2014), Article ID:50203,6 pages
10.4236/apm.2014.49060
The Freedom of Yetter-Drinfeld Hopf Algebras
Yanhua Wang
School of Mathematics, Shanghai University of Finance and Economics, Shanghai, China
Email: yhw@mail.shufe.edu.cn
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 August 2014; revised 2 September 2014; accepted 13 September 2014
ABSTRACT
In this paper, the fundamental theorem of Yetter-Drinfeld Hopf module is proved. As applications, the freedom of tensor and twisted tensor of two Yetter-Drinfeld Hopf algebras is given. Let A be a Yetter-Drinfeld Hopf algebra. It is proved that the category of A-bimodule is equivalent to the category of  -twisted module.
-twisted module.
Keywords:
Hopf Algebra, Hopf Module, Yetter-Drinfeld Module, Yetter-Drinfeld Hopf Algebra

1. Introduction
Let 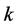 be a field and
be a field and 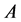 an algebra. A left
an algebra. A left 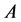 -module is a
-module is a 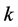 -vector space
-vector space 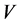 together with a
together with a 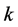 -linear map
-linear map 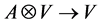 such that
such that  and
and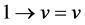 . The category of left
. The category of left  -module is denoted by
-module is denoted by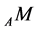 . Dually, let
. Dually, let 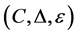 be a coalgebra. A left
be a coalgebra. A left 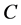 -comodule is a
-comodule is a 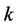 -vector space
-vector space 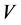 together with a
together with a 
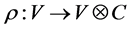
The category of left 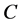

Assume that 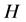
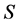

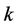
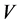
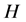
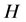
for all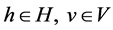
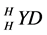
The map is a braiding in 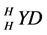
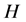
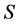
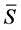
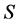
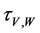
Let 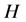
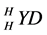
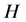

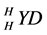
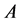
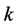
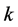
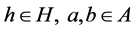
(a1) 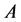
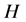
(a2) 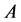
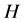
(a3) 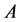
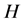
(a4) 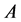
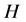
(a5) 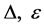
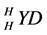
(a6) There exists a 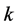
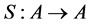
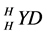
One easily get that 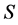
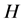
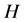
Yetter-Drinfeld Hopf algebras are generalizations of Hopf algebras. Some important properties of Hopf algebras can be applied to Yetter-Drinfeld Hopf algebra. For example: Doi gave the trace formular of Yetter-Drin- feld Hopf algebras in [6] and studied Hopf module in [7] ; Chen and Zhang constructed Four-dimensional Yetter-Drinfeld module algebras in [8] ; Zhu and Chen studied Yetter-Drinfeld modules over the Hopf-Ore Extension of Group algebra of Dihedral group in [9] ; Alonso Álvarez, Fernández Vilaboa, González Rodríguez and Soneira Calvoar considered Yetter-Drinfeld modules over a weak braided Hopf algebra in [10] , and so on.
Hopf module fundamental theorem plays an important role in Hopf algebras. This theory can be generalized to Yetter-Drinfel Hopf algebras.
Theorem 1.1. Let 
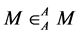

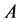
Note that Theorem 1.1 was appeared in [7] , but we give a different proof with Doi’s here.
Let 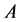


then 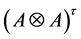
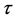
Theorem 1.2. Let 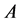
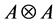
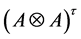

We also proved the category of Yetter-Drinfeld. 
Theorem 1.3. Let 

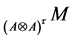
2. The Freedom of Yetter-Drinfeld Hopf Algebras
In this section, we require 
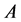
Definition 2.1. Let 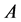
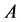
1) 

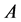
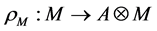
2) 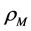

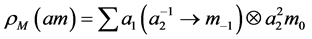
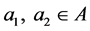
Note that 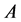
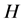
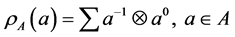
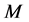
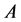
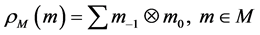
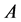
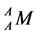
Define 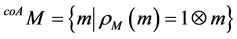
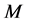
Theorem 2.2. Let 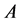

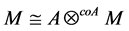
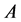
Proof: We define 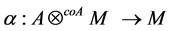
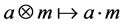

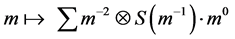
First, we show that 
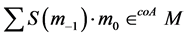
So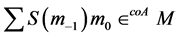
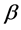
We will show that 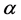
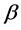
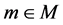
Hence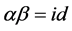
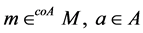
which show that 
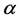
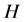
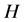
Next, we show that 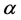

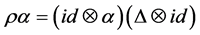
This complete the proof.
Proposition 2.3. We have 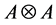
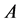
Proof: 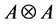

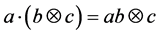
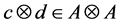
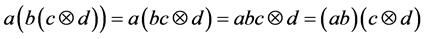

module structure of 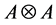
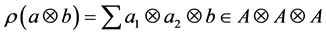

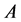
Theorem 2.4. Let 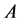
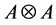
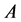
Proof: Apply 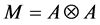
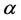
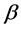
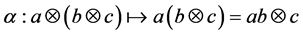
Next, we show that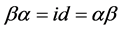
and
Hence, we have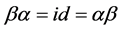
Moreover, 

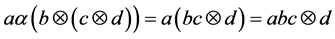
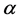
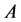
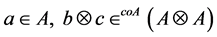
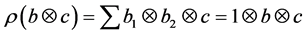
and
In a word, 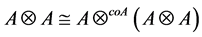

3. Twist Yetter-Drinfeld Hopf Module
Let 
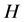
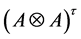
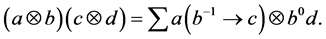
Lemma 3.1. Let 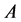
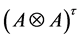
Proof: We only need to check the associativity of
And 
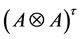
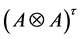
Remark 3.2. 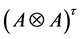
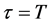
Denote the 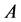
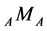


Theorem 3.3. Let 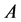
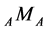

equivalent.
Proof: we are going to construct the functor 
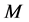
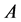
We denote the two-side action on 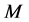


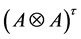
We claim that the action is well-defined, i.e.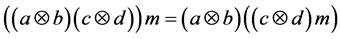
and
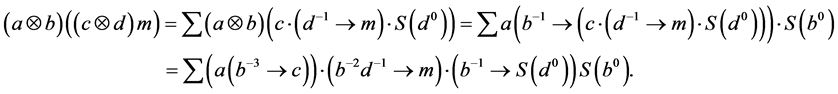
By comparing the above two identities, we have 
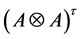
Moreover, we have the functor 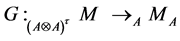
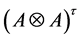
define 
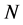
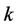
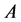
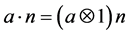

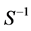
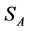
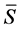
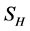
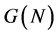
Hence, 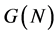

and
therefore, 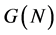
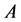


Let 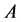


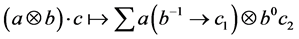
Recall that if 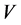
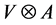
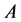
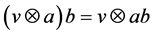
Theorem 3.4. The right 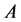
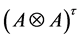
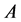
Proof: Let 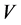
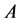
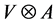
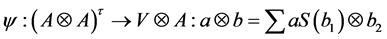
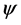
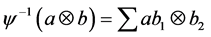
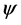
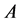
In fact, we have
Note that the right 
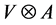
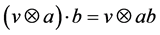
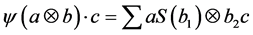
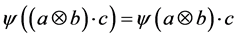
Acknowledgements
Supported by the National Nature Science Foundation of China (Grant No. 11271239).
References
- Dascalescu, S., Nastasescu, C. and Raianu, S. (2001) Hopf Algebras; An Introduction. Marcel Dekker, Inc., New York.
- Montgomery, S. (1993) Hopf Algebras and Their Actions on Rings. CBMS Regional Conf. Series in Math. 82, American Mathematical Society, Providence, RI.
- Sweedler, M.E. (1969) Hopf Algebras. Benjamin, New York.
- Yetter, D.N. (1990) Quantum Groups and Representation of Monoidal Categories. Mathematical Proceedings of the Cambridge Philosophical Society, 108, 261-290. http://dx.doi.org/10.1017/S0305004100069139
- Sommerhauser, Y. (2002) Yetter-Drinfeld Hopf Algebras over Groups of Prime Order. Vol. 1789, Springer, Berlin.
- Doi, Y. (2000) The Trace Formula for Braided Hopf Algebras. Communications in Algebra, 28, 1881-1895. http://dx.doi.org/10.1080/00927870008826933
- Doi, Y. (1998) Hopf Module in Yetter-Drinfeld Module Categories. Communications in Algebra, 26, 3057-3070. http://dx.doi.org/10.1080/00927879808826327
- Chen, H.X. and Zhang, Y. (2006) Four-Dimensional Yetter-Drinfeld Module Algebras. Journal of Algebra, 296, 582- 634. http://dx.doi.org/10.1016/j.jalgebra.2005.08.011
- Zhu, H. and Chen H.X. (2012) Yetter-Drinfeld Modules over the Hopf-Ore Extension of Group Algebra of Dihedral Group. Acta Mathematica Sinca, 28, 487-502. http://www.cnki.com.cn/Article/CJFDTotal-ACMS201203007 http://dx.doi.org/10.1007/s10114-011-9777-4
- Alonso Álvarez, J.N., Fernández Vilaboa, J.M., González Rodríguez, R. and Soneira Calvoar, C. The Monoidal Category of Yetter-Drinfeld Modules over a Weak Braided Hopf Algebra. arXiv: 1203.2474. http://arxiv.org/abs/1203.2474