Advances in Pure Mathematics
Vol.05 No.05(2015), Article ID:55720,7 pages
10.4236/apm.2015.55028
The Initial Boundary Value Problem for Modified Zakharov System
Lang Li, Shaomei Fang*
Department of Mathematics, South China Agricultural University, Guangzhou, China
Email: *dz90@scau.edu.cn
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 July 2014; accepted 10 April 2015; published 16 April 2015
ABSTRACT
In this paper, we consider the initial boudary value problem for modified Zakharov system in 3 dimensions with small initial condition. By using the continuity lemma and the linear interpolation theory, together with the properties of Sobolev spaces and the Galerkin method, we obtain the existence and uniqueness of the global solution.
Keywords:
Modified Zakharov System, Galerkin Method, A Prior Estimate

1. Introduction
In this paper, we study the global existence and uniqueness of solutions for a modified Zakharov system with initial boundary value conditions as follows.
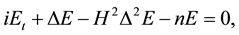 (1.1)
(1.1)
 (1.2)
(1.2)
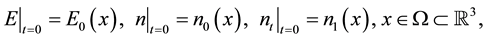 (1.3)
(1.3)
 (1.4)
(1.4)
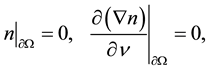 (1.5)
(1.5)
where  represents the slowly varying envelope of the electric field,
represents the slowly varying envelope of the electric field, 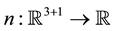 denotes deviation of the ion density from its mean, and H is the dimensionless quantum parameter given by the ratio of the ion plasmon and electron thermal energies.
denotes deviation of the ion density from its mean, and H is the dimensionless quantum parameter given by the ratio of the ion plasmon and electron thermal energies.
The classical Zakharov system was derived by Zakharov to describe the propagation of Langmuir waves in a plasma [1] . In the past decade, a large amount of work has been devoted to the existence problem for the classical Zakharov system. For instance, the Fourier restriction norm method, applies to this problem, and under appropriate assumption on the data, several existence results have been established. The local well-posedness of this problem on  in the energy space
in the energy space 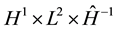 was first obtained by Bourgain and Colliander [2] , which was improved to
was first obtained by Bourgain and Colliander [2] , which was improved to 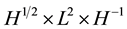 by Ginibre, Tsutsumi and Velo [3] . Recently, Bejenaru, Herr, Holmer and Tataru have obtained local well-posedness in
by Ginibre, Tsutsumi and Velo [3] . Recently, Bejenaru, Herr, Holmer and Tataru have obtained local well-posedness in  [4] . Another approach was initiated by Colliander, Keel, Stafflani, Takaoka, and Tao in [5] , called the I-method. This method was successfully applied by these authors to the Kdv and modified Kdv equation. In [6] , this method was also used to construct global solutions for the one dimensional Zakharov system.
[4] . Another approach was initiated by Colliander, Keel, Stafflani, Takaoka, and Tao in [5] , called the I-method. This method was successfully applied by these authors to the Kdv and modified Kdv equation. In [6] , this method was also used to construct global solutions for the one dimensional Zakharov system.
However, some important effects, such as quantum effects, have been ignored in the classical Zakharov system. The importance of quantum effects in ultrasmall electronic devices, dense astrophysical plasma systems and laser plasmas has produced an increasing interest on the investigation of the quantum counterpart of some of plasma physics phenomena [7] . By using a quantum fluid approach, Garcia has obtained the following modified Zakharov system [8] :
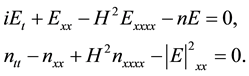
Recently, S. You and B. Guo have considered the existence and uniqueness of the global solution to the initial boundary value problem for the above system in 1 dimension and 2 dimensions, respectively [9] [10] . Motivated by their result, we consider the global existence of solutions in 3 dimensions with small initial condition. As is standard, the problem is to obtain a prior estimate of higher derivatives of solutions in some suitable function spaces. To overcome higher dimensional difficulty, we use continuity lemma and the linear interpolation theory, together with the properties of Sobolev spaces to handle it.
Now we give some notations:
-For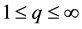 , we denote by
, we denote by  or simply
or simply , the space of all q times integrable functions in
, the space of all q times integrable functions in 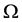 equipped with norm
equipped with norm 

-Let 
-We denote by C a positive constant which may change from one line to the next line.
2. A Prior Estimates
To study the smooth solution of the modified Zakharov system, we introduce function



with initial condition

and boundary condition


Lemma 2.1. Assume that

Proof. Multiplying Equation (2.1) by


Since
Taking the imaginary part of Equation (2.7), then we have
Lemma 2.2. [11] (Continuity lemma) Assume that 

If 



Lemma 2.3. [11] (Gargliardo-Nirenberg inequality) Assume that 




where
Lemma 2.4. Assume that 

Proof. Multiplying Equation (2.1) by


Since
then taking the real part of Equation (2.8), we have

where we have used the fact
Similarly, multiplying Equation (2.2) by


i.e.

Adding Equation (2.9) to Equation (2.11), we deduce
Set 
therefore, using Young’s inequality, we have

Choosing 

Set 


if the initial condition is small enough. Substituting it into Equation (2.12), we have
Lemma 2.5. Assume that 

Proof. Differentiating Equation (2.1) with respect to t, and then multiplying it by


Since
Taking the imaginary part of Equation (2.13) yields
therefore, using Hölder’s inequality and Sobolev imbedding, we have

Differentiating Equation (2.2) with respect to t, and then multiplying it by

i.e.
therefore

Adding Equation (2.14) to Equation (2.15), we have
Using Gronwall’s inequality, we have
From Equation (2.1), Equation (2.2), and Equation (2.3), it easily get
3. Existence and Uniqueness of Global Solution
Theorem 3.1. Assume that 
Proof. We first give the proof of the uniqueness of the solution. Suppose 

therefore



with initial condition

Multiplying Equation (3.1) by

taking the imaginary part yields
therefore

Multiplying Equation (3.3) by

Since
therefore

Adding Equation (3.5) to Equation (3.6), we have
Using Gronwall’s inequality and the initial condition Equation (3.4), we can obtain
Next we show the existence of the solution.
By using the Garlerkin method, choose basic functions 


where the undetermined coefficients 
with initial conditions
According to the basic theory of ordinary differential equations, the above equations have a unique local solution.
Similarly to the proof of Lemma 2.1 and Lemma 2.4, we have
By compactness argument, we can choose subsequences, still denoted by 
















Indeed
By using the density of 

Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 11271141, No. 11426069 and No.61375006).
References
- Zakharov, V.E. (1972) The Collapse of Langmuir Waves. Soviet Physics―JETP, 35, 908-914.
- Bourgain, J. and Colliander, J. (1996) On Well-Posedness of Zakharov System. International Mathematics Research Notices, 11, 515-546. http://dx.doi.org/10.1155/S1073792896000359
- Ginibre, J., Tsutsumi, Y. and Velo, G. (1997) On the Cauchy Problem for Zakharov System. Journal of Functional Analysis, 151, 384-436. http://dx.doi.org/10.1006/jfan.1997.3148
- Bejenaru, I., Herr, S., Holmer, J. and Tataru, D. (2009) On the 2d Zakharov System with L2 Schrodinger Data. Nonlinearity, 22, 1063-1089. http://dx.doi.org/10.1088/0951-7715/22/5/007
- Colliander, J., Holmer, J. and Tzirakis, N. (2008) Low Regularity Global Well-Posedness for the Zakharov and Klein- Gordon-Schrodinger Systems. Transactions of the American Mathematical Society, 9, 4619-4638. http://dx.doi.org/10.1090/S0002-9947-08-04295-5
- Pecher, H. (2005) Global Solutions with Infinite Energy for the One-Dimensional Zakharov System. Electronic Journal of Differential Equations, 41, 1-18.
- Guo, C.H., Fang, S.M. and Guo, B.L. (2013) Long Time Behavior of the Solutions for the Dissipative Modified Zakharov Equations for Plasmas with a Quantum Correction. Journal of Mathematical Analysis and Applications, 403, 183-192. http://dx.doi.org/10.1016/j.jmaa.2013.01.058
- Garcia, L.G., Haas, F., de Oliveira, L.P.L. and Goedert, J. (2005) Modified Zakaharov Equations for Plasmas with a Quantum Correction. Physics of Plasmas, 12. http://dx.doi.org/10.1063/1.1819935
- You, S.J., Guo, B.L. and Ning, X.Q. (2012) Initial Boundary Value Problem for Modified Zakharov Equations. Acta Mathematica Scientia, 32B, 1455-1466.
- You, S.J., Guo, B.L. and Ning, X.Q. (2012) Initial Boundary Value Problem for Generalized Zakharov Equations. Applied Mathematics, 57, 581-599. http://dx.doi.org/10.1007/s10492-012-0035-6
- Guo, B.L., Gan, Z.H. and Zhang, J.J. (2011) Zakharov Equations and Its Solitary Wave Solutions. Science Press.
NOTES
*Corresponding author.



















































