Received 5 April 2014; revised 5 May 2014; accepted 12 May 2014

ABSTRACT

Some derived categories and their deformed versions are used to develop a theory of the ramifi- cations of field studied in the geometrical Langlands program to obtain the correspondences between moduli stacks and solution classes represented cohomologically under the study of the kernels of the differential operators studied in their classification of the corresponding field equations. The corresponding D-modules in this case may be viewed as sheaves of conformal blocks (or co-invariants) (images under a version of the Penrose transform) naturally arising in the framework of conformal field theory. Inside the geometrical Langlands correspondence and in their cohomological context of strings can be established a framework of the space-time through the different versions of the Penrose transforms and their relation between them by intertwining operators (integral transforms that are isomorphisms between cohomological spaces of orbital spaces of the space-time), obtaining the functors that give equivalences of their corresponding categories. The different cycles and co-cycles obtained through of Penrose transform apparatus and their relation with different classes of Hecke category 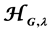carry us to conjecture that unique geometrical pictures in field theory to different cohomological classes of the sheaves in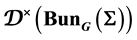, are geometrical objects belonging to the global Langlands category (let mono- dromic or not) corresponding to a system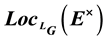, is the objects included in a category that involves a category of quasi-coherent sheaves on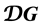, of certain fibers on the generalized flag manifolds that are 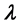-twisted D-modules of the flag variety.

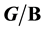Keywords:

Geometrical Langlands Correspondence, Hecke Categories, Moduli Stacks, Penrose Transforms, Quasi-Coherent Sheaves

1. Introduction

The extensions given by a global Langlands correspondence between the Hecke sheaves category on an adequate moduli stack and the holomorphic 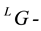bundles category with a special connection (Deligne connection), establish a viewing of the 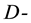modules as sheaves of conformal blocks (or co-invariants) (images under a version of the Penrose transform [1] -[3] ) naturally arising in the framework of conformal field theory. But in the 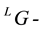bundles category context is done necessary the development of structures more fine whose basis let be the derived category on 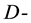modules of operators (that is to say, consider the sheaf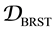) applied to the geometrical Langlands correspondence to obtain the “quantum” geometrical Langlands correspondence that we want (we want to obtain a differential operators theory (being these germs of our sheaves) from a point of view of BRST-coho- mology that includes the theory QFT (Quantum Field theory), the SUSY (Super-symmetry theory) and HST (heterotic string theory) to be applied in field theory)¹.

In more general sense, the conjectured to the group 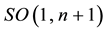[1] , and their application in the obtaining of Cěch complexes obtained in the tacking of strings through super-conformally spaces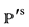, given in the corollary by [2] [3] , could establish that the Penrose-Ward transform is done evident when the inverse images of the 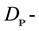modules that are quasi-coherent 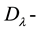modules established by the diagram [1] (Verma modules diagram in this conjecture to the group [1] [4] [5] ), results naturally inside of vector bundle language as image of the degeneration of cycles given inside of a manifold signed in the equivalences of moduli spaces of the theorem 4.1 given in [3] . Likewise the duality between string theories (string and branes) stay established through of the intertwining operators of the Penrose transform in all different dualities field/particle and the conformally and holonomy levels required in invariance of the space-time field theory. finally we can explain the relation between certain branes (for example branes [6] ) and twisted modules on the space moduli resulting to be these relations those obtained by the functores [7] that from the deformation theory we want describe deformations with compact support in. Then topologically the derived category of the moduli space and the category of certain branes classes consigned in the moduli space stay related, giving place to a class of objects in a moduli space Then the geometrical Langlands ramifications are consigned in Hecke correspondences whose Hecke categories are the given by the theorem 4.2. [2] and enunciated in the section 3 of this work. Finally we can to say, that the techniques of localization functors used to produce global categories of Hecke eigensheaves from local categories using the technique of integral transform is accord with the Langlands data structure given by the affine Hecke categories [8] [9] , which are required to conform a representation theory of affine Kac-Moody algebras that will complete the research on geometrical Langlands correspondence.

2. Derived Categories in Geometrical Langlands Ramifications Problem

¹Remember that this is a correspondence between flat holomorphic bundles of the worldsheet (hypersurface) and Hecke eigensheaves on the moduli space of holomorphic bundles on where

We interpret the Hecke eigensheaves and Hecke operators (elements of the Hecke algebras [3] ) of the geometric Langlands program in terms of the correlation functions of purely bosonic local operators in the holomorphic twisted sheaves on the complex flag manifold

Then by the Recillas conjecture [1] and using the extensions discussed in the Section 3, we can to obtain this geometrical correspondence on

First, the election of the derived sheaves to one theory of sheaf cohomology on modules to the geometrical Langlands correspondence must be established in first instance, satisfying the Kashiwara’s theorem on correspondence between quasiequivarintsmodules and some kind of representation spaces which must be modules. This has been established through certain generalized versions of the Penrose transform presented in [10] -[12] that determine algebraic Zuckerman functors² of generalized Verma modules [7] .

Let a quasi-equivariant--module belonging to the subcategory of modules given by (category of the equivariant-modules). Then to obtain equivalences between the different classes of modules establishing the isomorphism between the categories and where must be the restricted Zuckerman functor to the subcategory of left equivariant-modules to obtain the derived category that is product of a trianguled subcategory (as the given in [3] ) for a factor category that determine us the Harish-Chandra functor between the categories. These equivalences in analogy to the established in (9) take the shape to the specific modules

(1)

considering the moduli space as base,

(2)

If we consider then, from the group. equivariant module on the flag manifold provide integral kernels and thus integral transforms, to know

(3)

where such that where and, are Higgs fields on either side of the open string [7] , which are implicitly these kernels?

From the perspective of the Zuckerman functors produced from the Penrose transform, the kernels associated with the modules are those characterized for the Recillas conjecture [1] and to some points of the Lie algebra are completed by the Szegö operator.

Proposition 2. 1. (F. Recillas). The equations with non-flat differential operators can be solved by the corresponding Szegö kernels associated with Harish-Chandra modules [13] , of corresponding spherical functions on homogeneous space. The Szegö operator complete in some points of the Lie algebra [14] , to the Penrose transform to the case with compact.

Proof. Some results of representation theory obtained by the seminar of representation theory of real reductive Lie groups IM/UNAM (2000-2007) [13] [15] .

One geometrical argument is the condition established in the kernel of equivalences inside the moduli space, which is analogous to the given by the isomorphism of the Penrose transform discussed in foot of page 2, in the Section 2, in [3] . The idea is extend the harmonic condition to the functions to differential operators of derived sheaves that are in cohomology, such that the equivalences in (2) are defined by certain functors due to the duality between the resolution and meromorphic version of the Cousin complex³ associated to (bundle of lines associated to the flag manifold then, is a Borel subgroup) These is the way of the classification of the differential operators with their moduli stacks. Then we obtain to good approach by Penrose transforms to different classes of field solutions always and when the moduli stacks let be orbifolds produced as branes or string orbifolds.

Theorem (F. Bulnes). 2. 1 [3] . The derived category of quasiequivariantmodules can be identify for twisted Hecke category if, is a derived version of the category of Harish-Chandra to certain Proof. [3] .

²A simple consequence of the construction of equivariant Zuckerman functors as given by is the following lemma which generates said functors for cohomological process:

Lemma. Assuming that H, is a reductive subgroup of K, and being V, a Harish-Chandra module in the category then

³Cousin Dolbeault theory refers to the complex Dolbeault infinite dimension.

3. Penrose Transforms Framework to Ramifications

After we generalize the functors to the functors which are the Hecke functors defined as the integral transforms [7]

(4)

with the correspondence rule given as:

(5)

We can enounce the following theorem explained and proved in [7] :

Theorem 3.2 (F. Bulnes). The derived category of quasi-equivariant-modules shaped with the generalized and extended Verma modules given by can be identify for critically twisted sheaf category of modules on moduli stack (singularity) identified by the Hecke category (geometric Langlands correspondence) if this is an image of integral transforms acting on ramifications of the Hecke category (for example) on the flag variety with weight corresponding to twisted differential operators on

Proof. [7] .

Then as example of some consequences that derive of the classification of differential operators proposed by the theorem 3.2, to the solution of the corresponding field equations (using the philosophy of Langlands program to field ramifications) is the following short Table 1 of the Penrose transforms framework⁴ to ramifications:

4. Some Results

⁴Radon-Schmid transform, classic Penrose transform, twistor transform, Penrose-Radon transform, Radon transform, module transform, module transform and Penrose-Ward transform.

⁵Here, is the Hecke category that assigns the categories of quasi-coherent sheaves on the stack of. Also this Hecke category is that is the twisted Hecke category consisting of the natural integral transforms acting on categories of twisted modules of the flag variety (see the theorem 2.2). This theorem also comes to strengthen the conclusion obtained in the theorem 3.1, and establish a correspondence between the open curves of the moduli stacks of bundles as and Hecke algebras.

is the loop group that acts naturally on every one the categories in the Frenkel notation [17] .

If we use the topological gauge theory through of a scheme on Stein manifolds of a complex Riemannian manifold of the space-time, using the generalization given by Gindikin conjectures formulated in the Section 7 in [1] . Then we have the following result from [7] [16] to the geometrical Langlands correspondences:

Theorem 4.1 (F. Bulnes). Consider the classes of Hecke category satisfying the geometrical

a. The Penrose-Ward transform for this case maps very naturally 1-gerbes over the hyper-plane twistor space to solutions to the self-dual string equation.

Langlands correspondences given by

(6)

(as was established in the Theorem 4.1 [7] ). The unique geometrical pictures in field theory to different cohomological classes of the sheaves in, are the co-cycles (images under different Penrose transform versions):

a) Orbi-folds or,

b) Strings as twisted hyperlines and twisted hyper-planes or,

c) Super-twistor surfaces (from complex 2- and 3-dimension spaces).

Proof. The functor given in the theorem 3.2, applied to a quasi-coherent module, belongs to the category, determining a geometrical Langlands correspondence given by, which is the image of the integral transform (Radon-Penrose transform) acting for ramifications of, , (for example) on the flag manifold [3] . But such twisted Hecke category, is itself a Calabi-Yau algebra [9] . Then by the duality of the cycles on (equivariant modules on the flag variety), this category is the given by certain orbifolds of. Then is satisfied a). In particular, if we realize an extension by local cohomology [18] , that is to say, to ramifications of, we have by the theorem 4. 2 in [3] , that

(7)

where is a holomorphic sheaf. By duality of the Calabi-Yau manifolds, the derived category under the Penrose transform results equivalent to the space of twisted strings. Indeed, the Verdier duality (that extends equivalences to deformed derived categories as certain class of coherent categories) [19] [20] , establishes equivalences between categories of objects that are modules in different scales inside the field theory from a point of view of bundle of lines, worldsheets from and all space time (for example branes and strings)). Then we have that strings are in this context twisted hyperlines (curves of the moduli space belonging to the category) and twisted hyperplanes from the Penrose-Ward transform (twistor matrix model [21] ). Then is satisfied b). In particular, using inverse and direct images of the Penrose transform on the corresponding Hochschild cohomology we have that their derived center is the endomorphism to, (theorem A. 2, of appendix) that is to say, a bundle of lines of the twisted bundle of lines. Their functor is realized by the corresponding Penrose transform [8] ⁶. To the twisted Hecke category and electing a correct character, these centers are Drinfeld centers in derived algebraic geometry [9] .

Finally, using the proper to generalized flag manifolds that appear in the modules, that are in the ramifications given in as the sheaf ⁷ (which to certain conditions can be Grothendieck alteration [22] ) we have that the Penrose transform to these sheaves is:⁸

(8)

⁶Theorem. Let be a finite orbit stack. Then is canonically self-dual as a module category and so for any module category, there is a canonical equivalence

when, consists of modules on a stack the above equivalence is realized by the usual formalism of integral transforms.

Here is the nilpotent cone and is the Springer resolution. Both space are used to construct the Steinberg manifold

⁷Here is the Springer fiber defined by the space

⁸Here is the nilpotent cone and is the Springer resolution. Both space are used to construct the Steinberg manifold

where these images are co-cycles of the ramifications of the category which is the Hecke category that assigns the categories of quasi-coherent sheaves on the stack of. But the hypersurface , is the admissible space-time from a point of view of the B-model string theory where the correspondences between categories of quasi-coherent sheaves on the stack of, and sheaves of branes as branes are duals under scheme of Penrose transform functor by mirror homology [6] , since the duality between string theories and branes (for example strings and branes) stay established through of the intertwining operators of the Penrose transform in all different dualities field/particle and the conformally and holonomy levels required in invariance of the space-time field theory, resulting to be these relations they obtained by the functores. Certain maps from the 2-surface to a super-manifold give, result from the 2-dimen- sional branes models, for example in electromagnetism by the moduli space Physically the super-manifold is interpreted as space-time and each map is interpreted as the embedding of the string in space-time. Finally we can say that there is no restriction on the number of dimensions of space-time, other than that it must be even because space-time is a generalized Kähler manifold. However all correlation functions with world-sheets that are not spheres vanish unless the complex dimension of the space-time is three, and so space-times with complex dimension three are the most interesting. This is fortunate for phenomenology, as phenomenological models often use a physical string theory compactified on a complex 3-dimensional space.

5. Conclusions

The obtaining of a first approaching through the integral geometry methods of the different geometrical pictures that defines the different actions of loop group, in the geometrical Langlands program (that is to say,

through the equivalences of categories [7] under duality of the cycles on (

equivariant modules on the flag variety)) can help to a best viewing of the space-time through of a ramified field that can determined by the ramifications defined in the context of the coherent modules that can be mapped in the order of the invariance and holomorphicity through a modules transform between categories of induced G-invariants modules. One generalized version of the Penrose transform on induced invariant modules was obtained considering the Szëgo kernels associated with Harish-Chandra modules [1] , in the images of the Penrose transform on an extension of the cohomology (the Dolbeault algebra). Then the ramified field can be defined of the point of view of the connections as, where the ramification is covered by the Lie algebra which has a natural interpretation in deformation theory, that describes deformations with compact support in an open set of the bundle on (hypersurface) determined as a co-cycle in the Theorem 4.1, of this work. Then topologically the derived category of the moduli space and the category of certain branes classes consigned in the moduli space stay related, giving place to a class of objects in moduli space

“The true source of the transformations and determination of all field interactions in the space-time born from a field that can be ramified under the same scheme of connections that involves the Deligne connection adding other connection on singularities (that is to say, of other secondary sources) to certain, calculated by the local geometrical Langlands correspondence under certain hypothesis on the character in the moduli stacks correlating with the Dolbeault algebra on, which must be the image of integral transforms acting on ramifications of a category of Hecke on ,with weight corresponding to twisted differential operators on”

Acknowledgements

I grateful the invitation offered for the “Sophus Lie” Conference Center, in Norway and the Engineering Information Institute of China to give a cycle of talks related with the contents of this mathematical research paper. Also I grateful the financing and moral supports to realize the present research work to the director of TESCHA, Demetrio Moreno Arcega, M. in L.

References

Some Technical Notation

―Twisted sheaf of differential operators to our, given by

―Set of equivalence classes of bundles with a connection on This space shape a bijection with the set of gauge equivalence classes of the ramified operators, as defined in [7] [17].

―the derived category on modules of operators applied to the geometrical Langlands correspondence to obtain the “quantum” geometrical Langlands correspondence.

of bi-equivariant modules on a complex reductive group.

―It’s the category of the twisted Hecke categories.

―Character sheaves used as Drinfeld centers in derived algebraic geometry. Their use connects different cohomologies in the Hecke categories context.

Appendix

One topological gauge theory can be useful if we establish a scheme on Stein manifolds of a complex Riemannian manifold of the space-time, using furthermore the generalization by Gindikin conjectures formulated in the Section 7 in [1]. Then we have the following result in [5]:

Theorem (F. Bulnes). A. 1. [23]. In the integral operator cohomology on complex Riemannian manifolds the following statements are equivalent:

The open sets and are orbits in and their integrals are generalized integrals to M.

Exist an integral operator such that

and then

being and fiber of the double fibration in integral geometry.

Proof. [5] [23].

In one more general sense, is a complex variety with regular singularities which can be topologically surveyed through the Stein manifolds as the defined in this before result.

Theorem [8]. A. 2. For any the category of character sheaves is equivalent to both the abelianization and center of the twisted Hecke category The equivalences fit into natural adjoin commutative diagrams

The same results hold for the monodromic Hecke category. Here, and, are corresponding functors whose image are in a category of holomorphic sheaves.

NOTES

^*Postdoctoral fellowship by State of Mexico Government and some results presented in Norway JNMP-conference 2013.