ABSTRACT

Recent developments in mathematics have in a sense organized objects of study into categories, where properties of mathematical systems can be unified and simplified through presentation of diagrams with arrows. A category is an algebraic structure made up of a collection of objects linked together by morphisms. Category theory has been advanced as a more concrete foundation of mathematics as opposed to set-theoretic language. In this paper, we define a pseudo-category on the class of isotonic spaces on which the idempotent axiom of the Kuratowski closure operator is assumed.

1. Introduction

Virtually every branch of modern mathematics can be unified in terms of categories and in doing so revealing deep insights and similarities between seemingly different areas of mathematics. Categories were introduced by Eilenberg and Mac Lane in 1945. A category has two basic properties, the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets whose objects are sets and whose arrows are functions. Generally, objects and arrows may be abstract entities of any kind and the notion of category provides a fundamental and abstract way to describe mathematical entities and their relationships. This is the central idea of category theory, a branch of mathematic which seeks to generalize all of mathematics in terms of objects and arrows independent of what the object and arrows represent.

2. Literature Review

2.1. Kuratowski Closure Operator

A closure operator is an arbitrary set-valued, set-function where 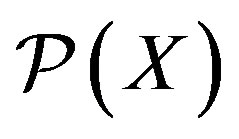is the power set of a non-void set that satisfies some closure axioms [1]. Consequently, various combinations of the following axioms have been used in the past in an attempt to define closure operators [2]. Let.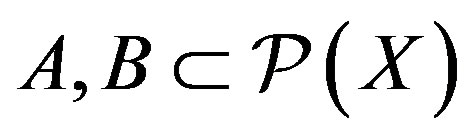

1) Grounded: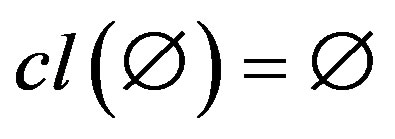

2) Expansive: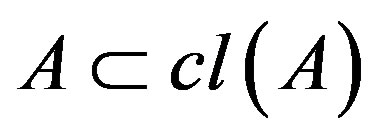

3) Sub-additive:. This axiom implies the Isotony axiom: implies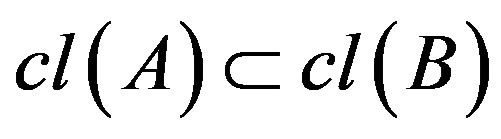

4) Idempotent:

The structure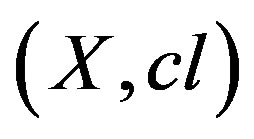, where satisfies the first three axioms is called a closure space [2].

2.2. Isotonic Space

A closure space satisfying only the grounded and the Isotony closure axioms is called an isotonic space [3]. This is the space of interest in this study and clearly, it is more general than a closure space.

In a dual formulation, a space 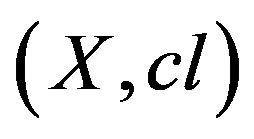is isotonic if and only if the interior function satisfies;

1).

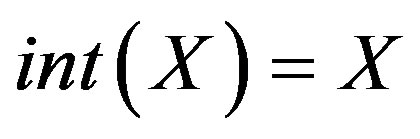2) implies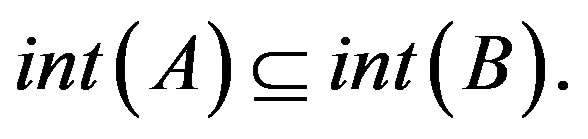

2.3. Category

A category has objects 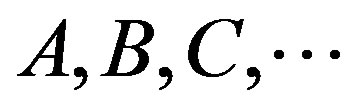and arrows 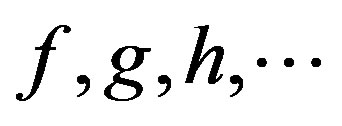such that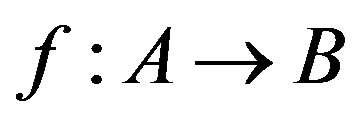, i.e. and. Two arrows and such that 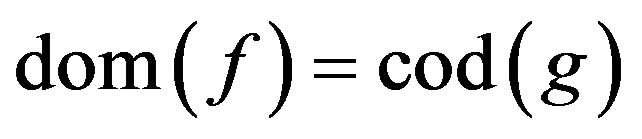are said to be composable [4].

Axioms of a Category

According to [5], the following are the axioms of a category;

1) If 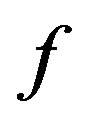and are composable, then they must have a composite which is the arrow shown 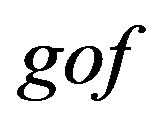shown in the diagram below

The arrow 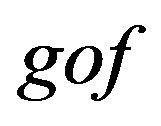goes from the 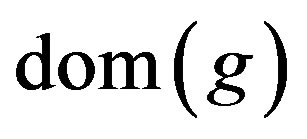to the such that 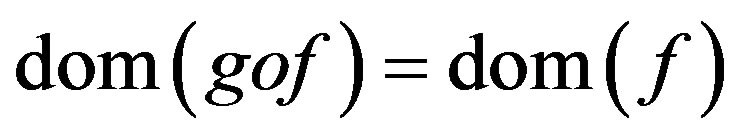and the

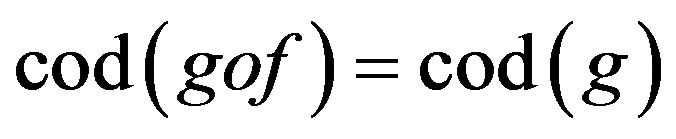
1) For every object there exists the identity arrow.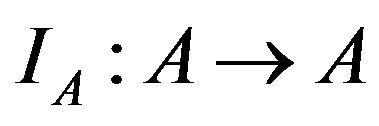

2) Composition is associative. This can be represented in as shown below;

3. Main Results

3.1. Quasi-Isotone Space

A closure space 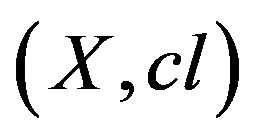with a closure operator is called a quasi-isotone space if the closure operator satisfies the following three Kuratowski closure axioms 1)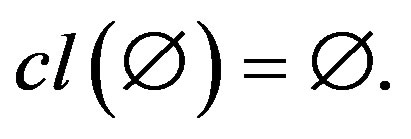

2) For 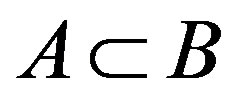implies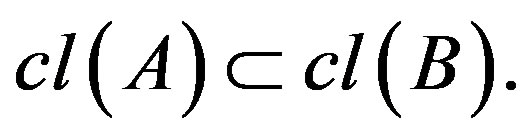

3).

The third axiom is called the idempotent axiom. It will become very useful while defining the pseudo-category on the quasi-isotone space.

3.2. Pseudo-Category

To define a pseudo-category on the class of quasi-isotone space, we firstly need to identify the objects and morphisms on this class of spaces. The objects are the closure operators such that they obey the three Kuratowski axioms above.

Next is to define the morphisms on the category. The arrows linking the objects together are 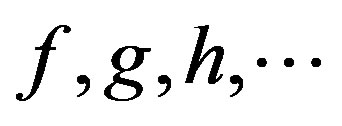such that. More explicitly, the arrow 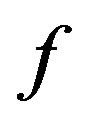may be represented diagrammatically by;

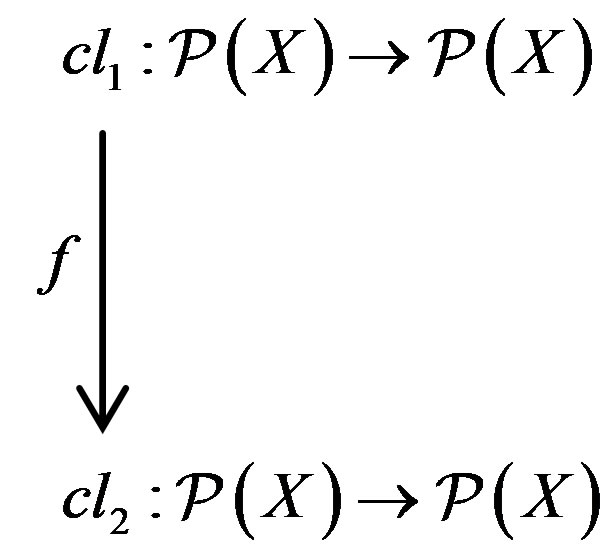
Therefore, the pseudo-category on quasi-isotone space has as objects the closure operators 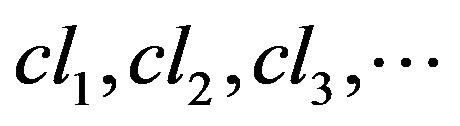and such that 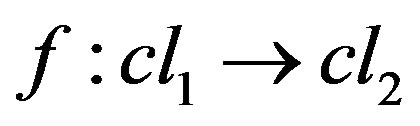as the morphisms. Of course two arrows 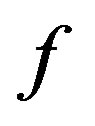and such that are said to be composable

Axioms of the Pseudo-Category

1) If 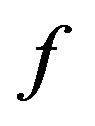and are composable, then they must have a composite which is the arrow shown in the diagram below

The arrow 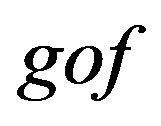goes from the 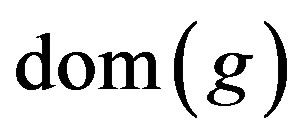to the 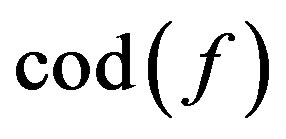such that 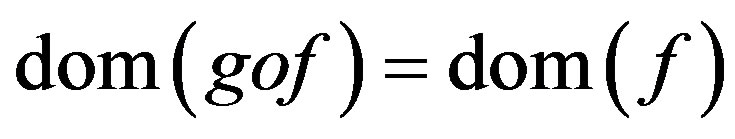and the

.

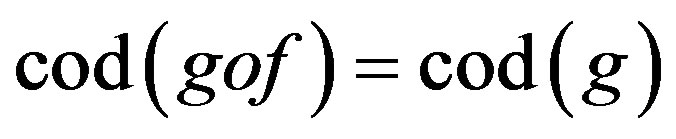2) For every object there exists the identity arrow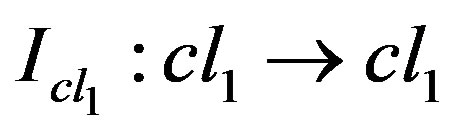. The existence of this identity arrow is guaranteed by the idempotent axiom defined on the quasi-isotone axiom. Indeed, the name pseudo-category for this structure is adopted since the idempotent axiom is not exactly an identity function.

3) Composition is associative. This can be representedas in the diagram below:

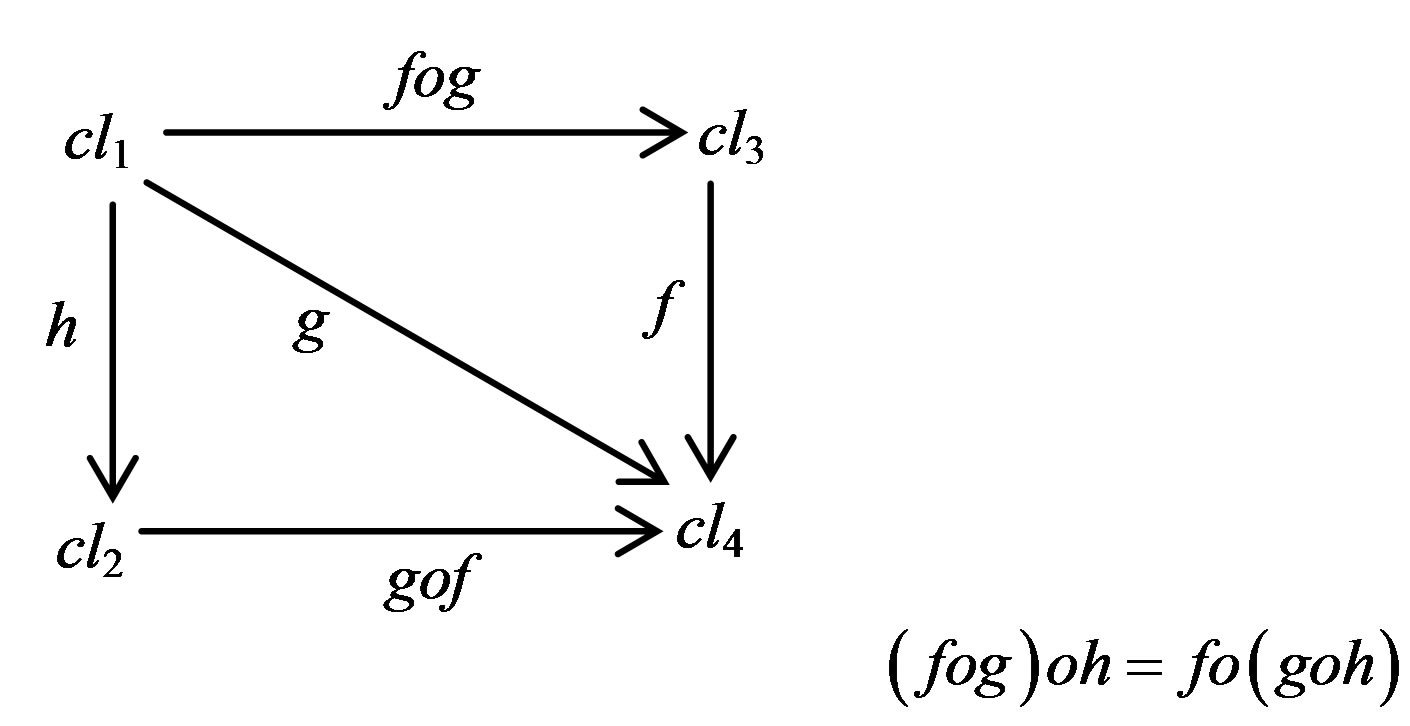
4. Remark

Other notions of a category may also be defined on the pseudo-category of quasi-isotone spaces. They include functors, natural transformations, adjunctions among others.

5. Conclusion

On a space defined by the Kuratowski closure axioms, it is possible to define a category-like structure in a very natural and straightforward way. This will enable some mathematical analysis to be extended onto closure spaces.

REFERENCES

[1]       W. J. Thron, “What Results Are Valid on Cech-Closure Spaces,” Topology Proceedings, Vol. 6, No. 3, 1981, pp. 135-158.

[2]       T. A Sunitha, “A Study of Cech Closure Spaces,” Doctor of Philosophy Thesis, School of Mathematical Sciences, Cochin University of Science and Technology, Cochin, 1994.

[3]       A. K. Elzenati and E. D. Habil, “Connectedness in Isotonic Spaces,” Turkish Journal of Mathematics, Vol. 30, No. 3, 2006, pp. 247-262.

[4]       C. McLarty, “Elementary Categories, Elementary Toposes,” Oxford University Press, Oxford, 1992.

[5]       S. MacLane, “Category for the Working Mathematician,” 2nd Edition, Springer-Verlag Inc., New York, 1998.